Stiffness Characteristics and Analytical Model of a Flange Joint with a Spigot
Abstract
:1. Introduction
- We designed and built an experimental instrument to research the angular bending stiffness characteristics of a flange joint with a spigot.
- Based on the experimental method, our previous FE model and study is validated.
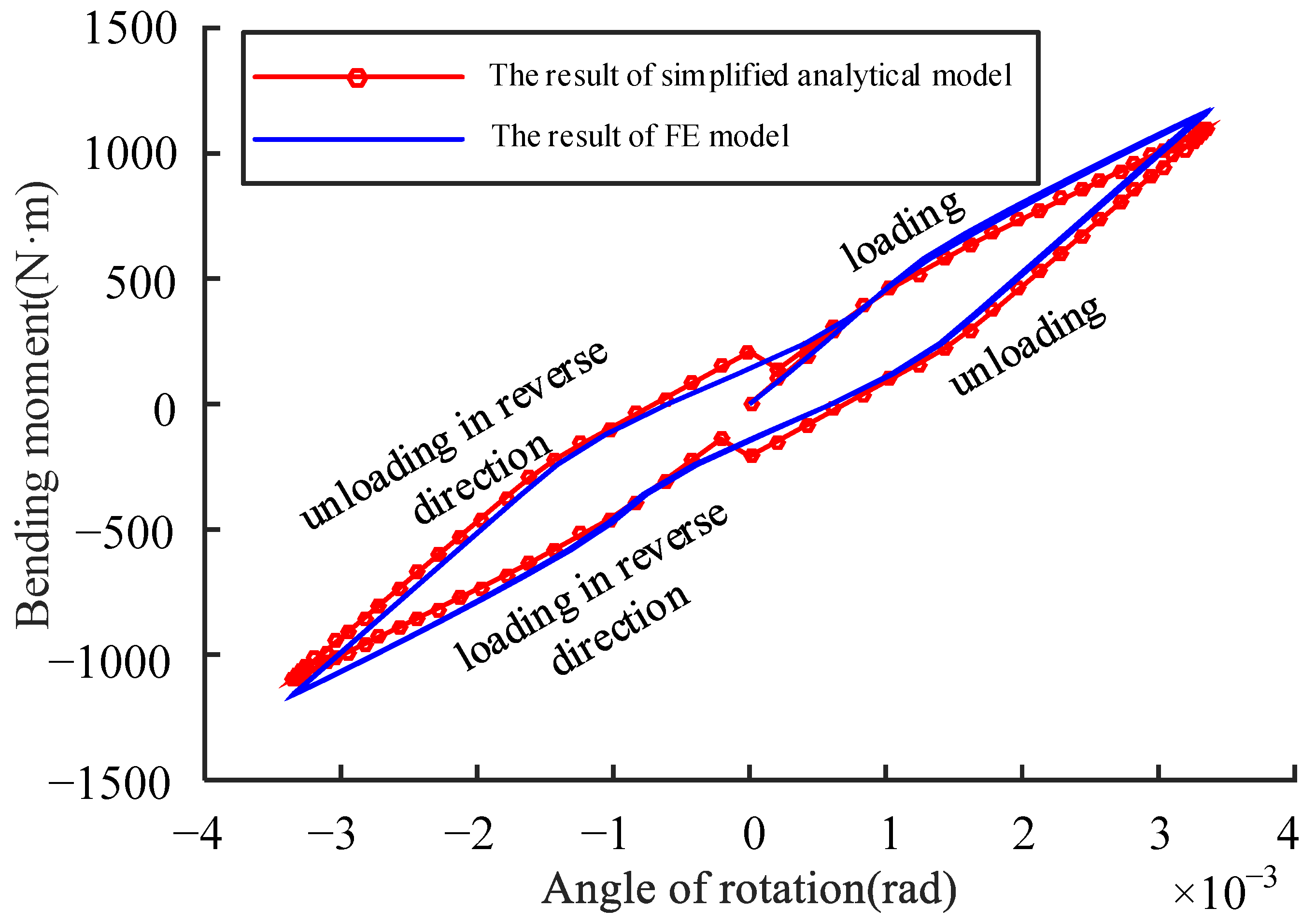
- From the viewpoint of convenient engineering applications, we proposed a simplified analytical model for the deformation and sliding of the flange contact interface. The accuracy and applicability are verified by comparison with the FE model and experimental test results. It can simulate the stiffness characteristics of a flange joint with a spigot well.
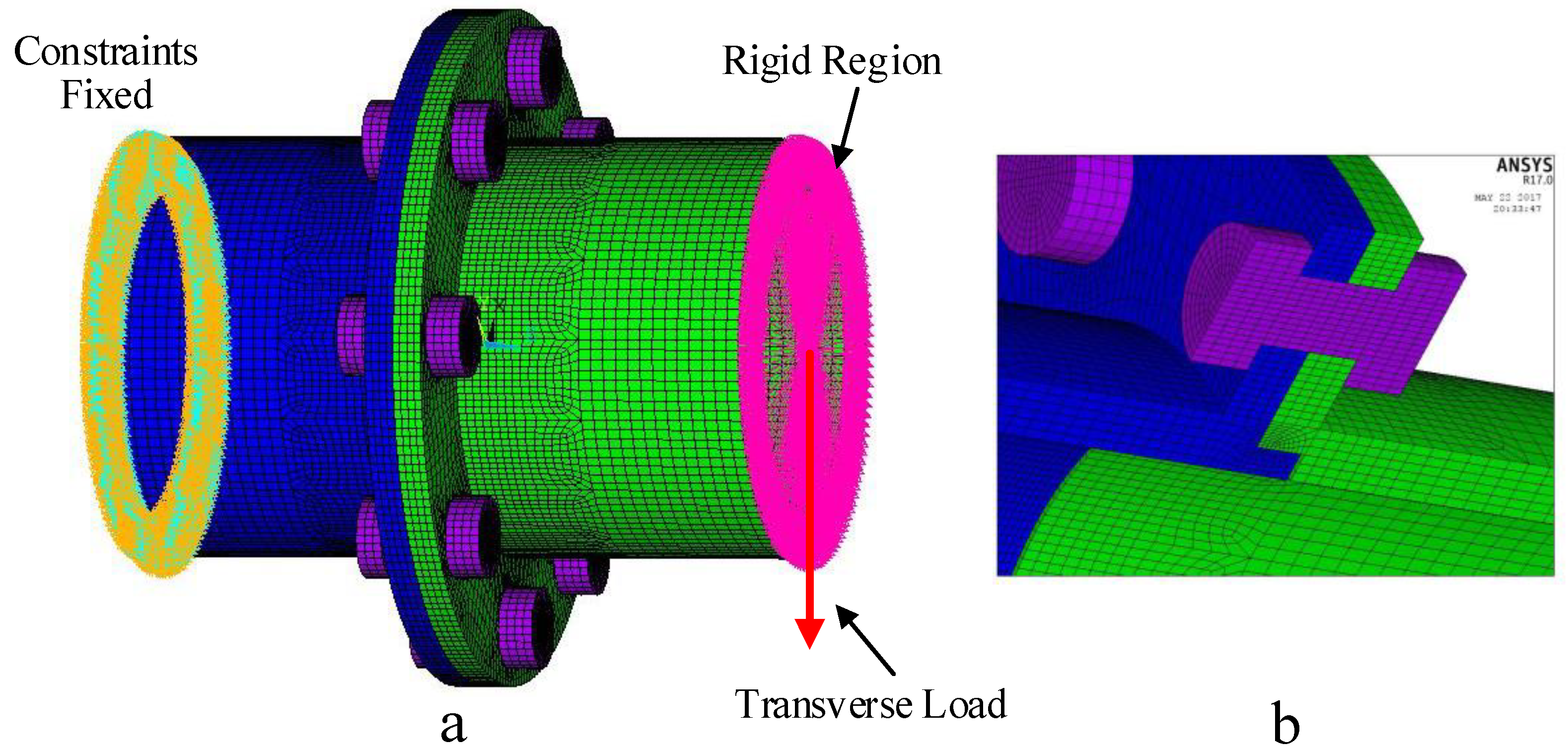
2. FE Modeling and Analysis of Flange Joint with a Spigot
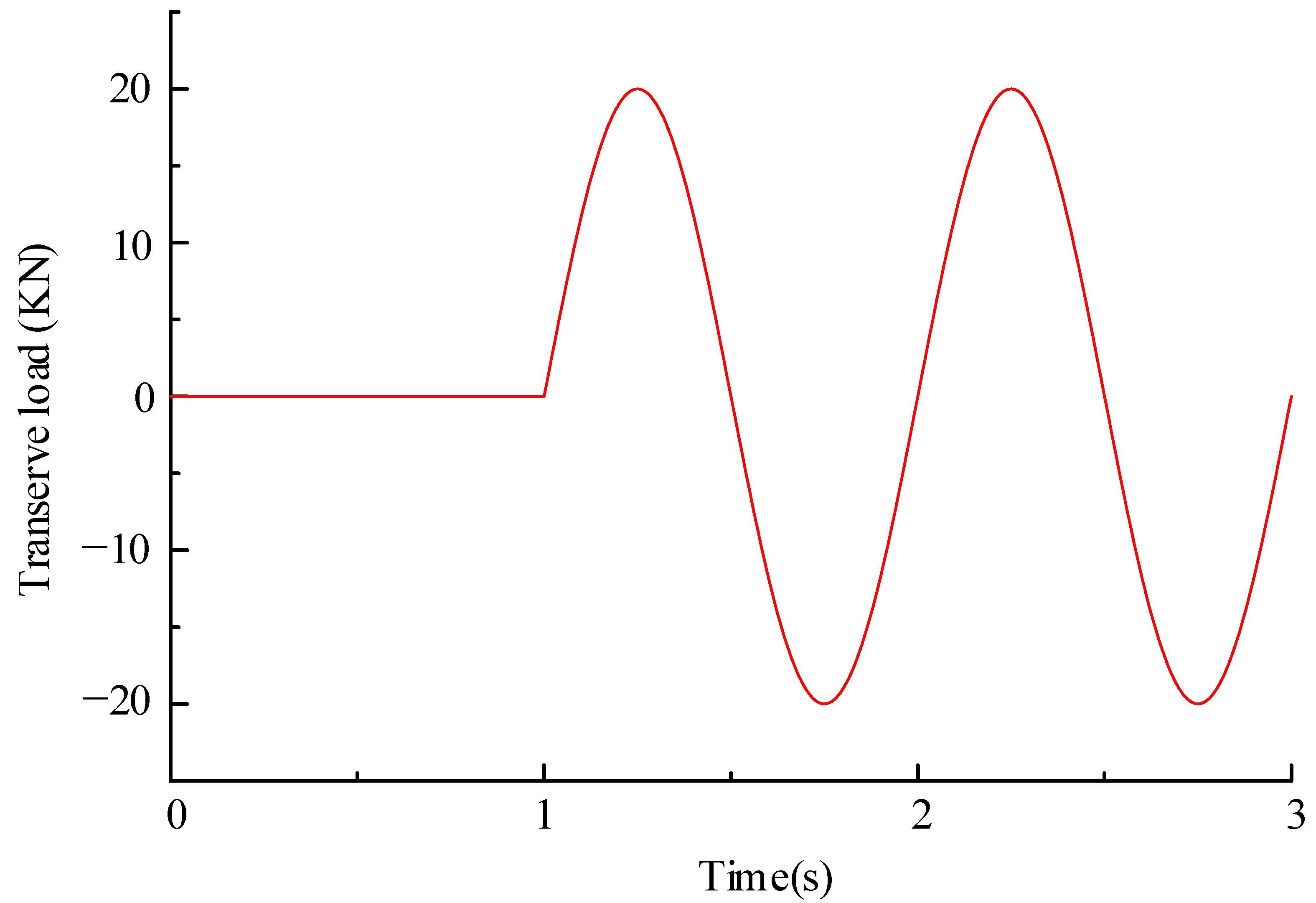
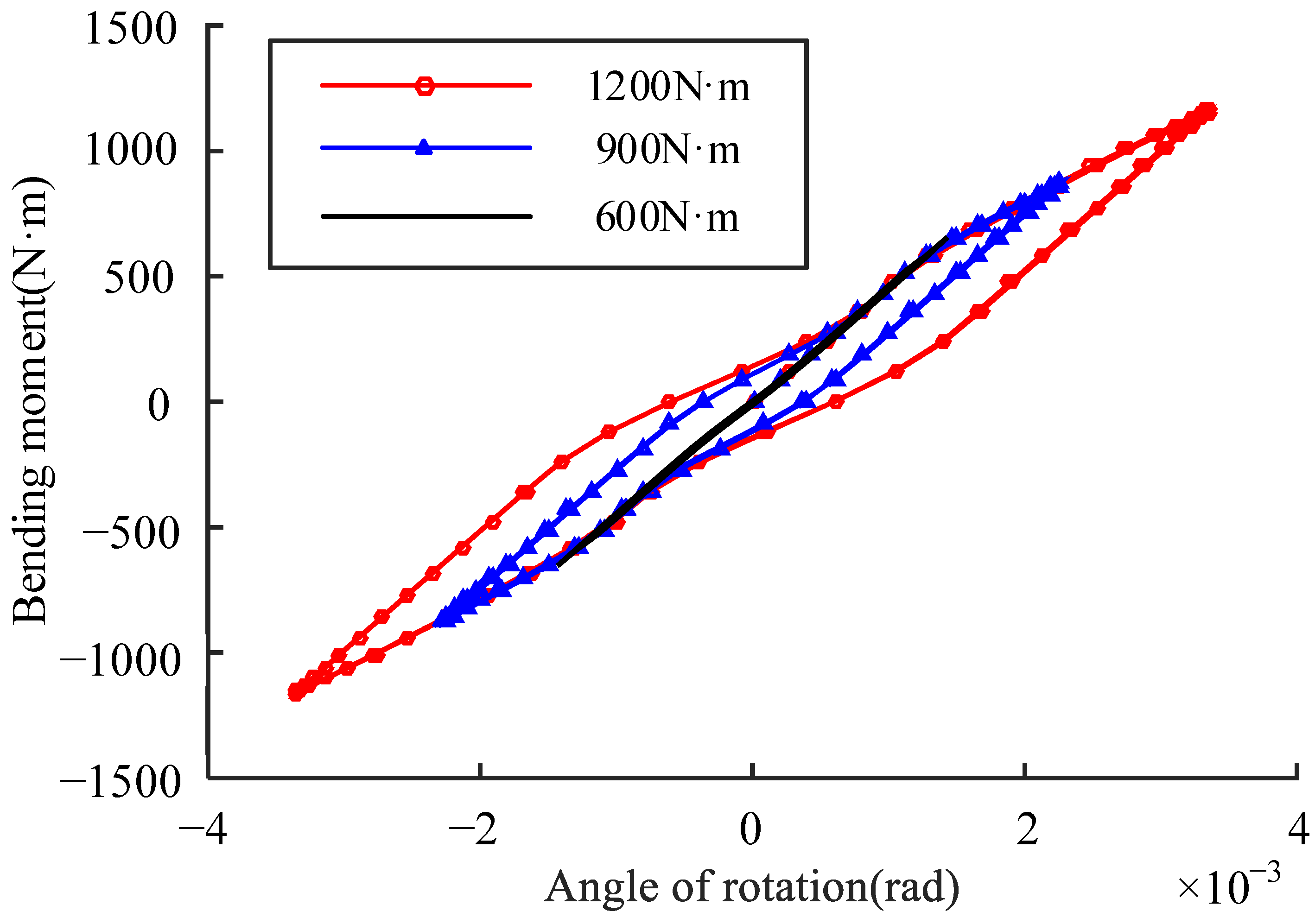
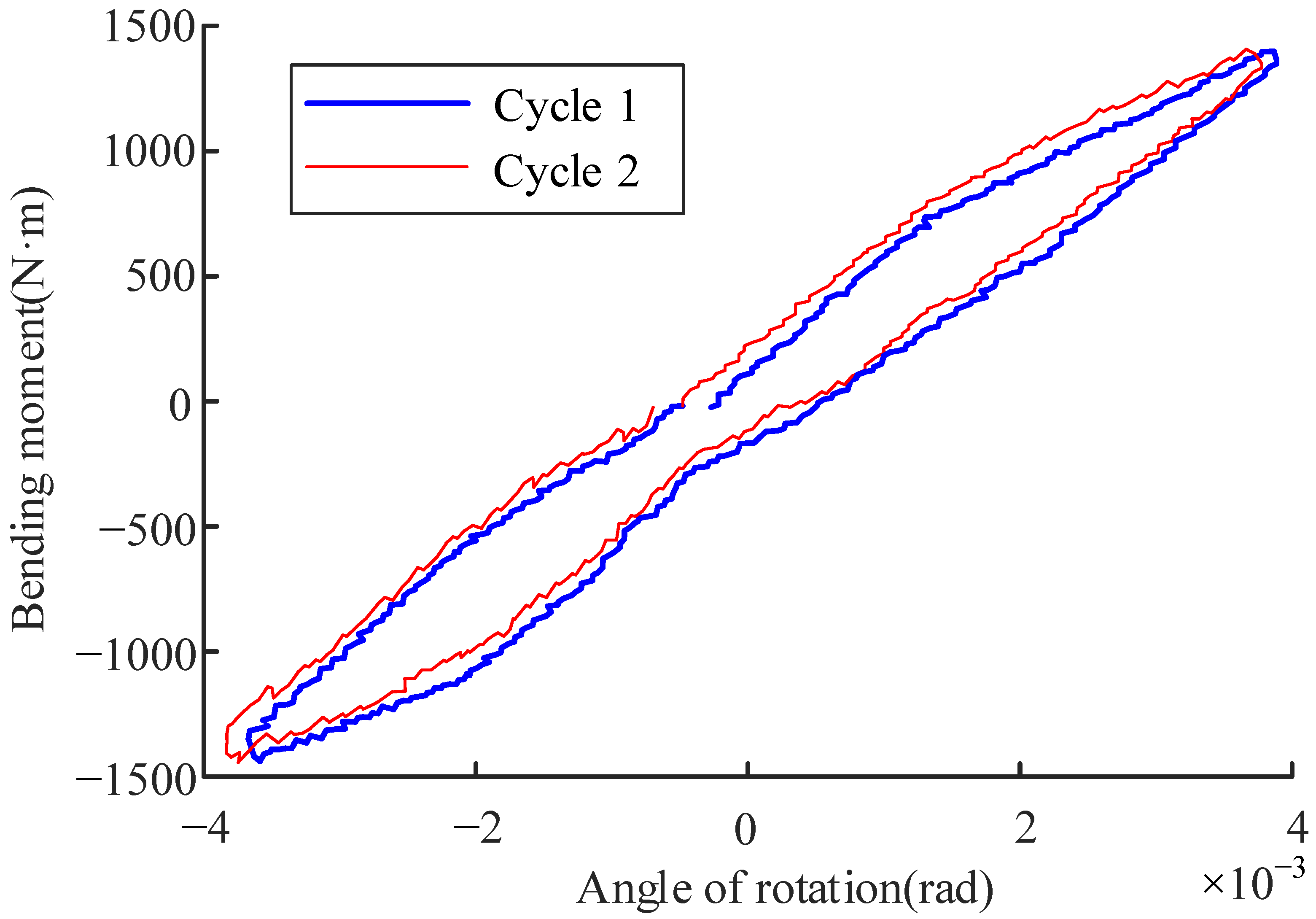
3. Experimental Verification
4. Simplified Analytical Modeling and Analysis
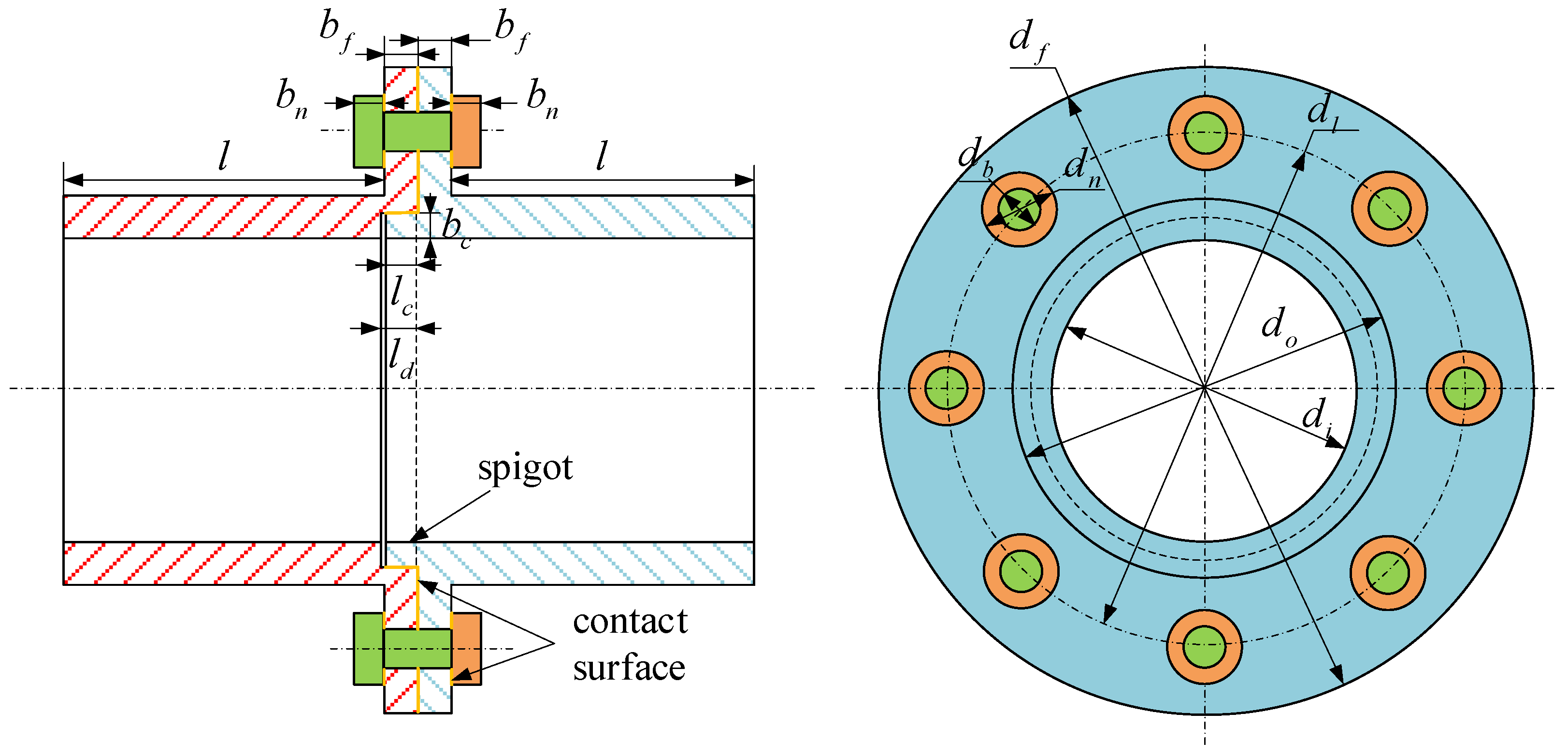
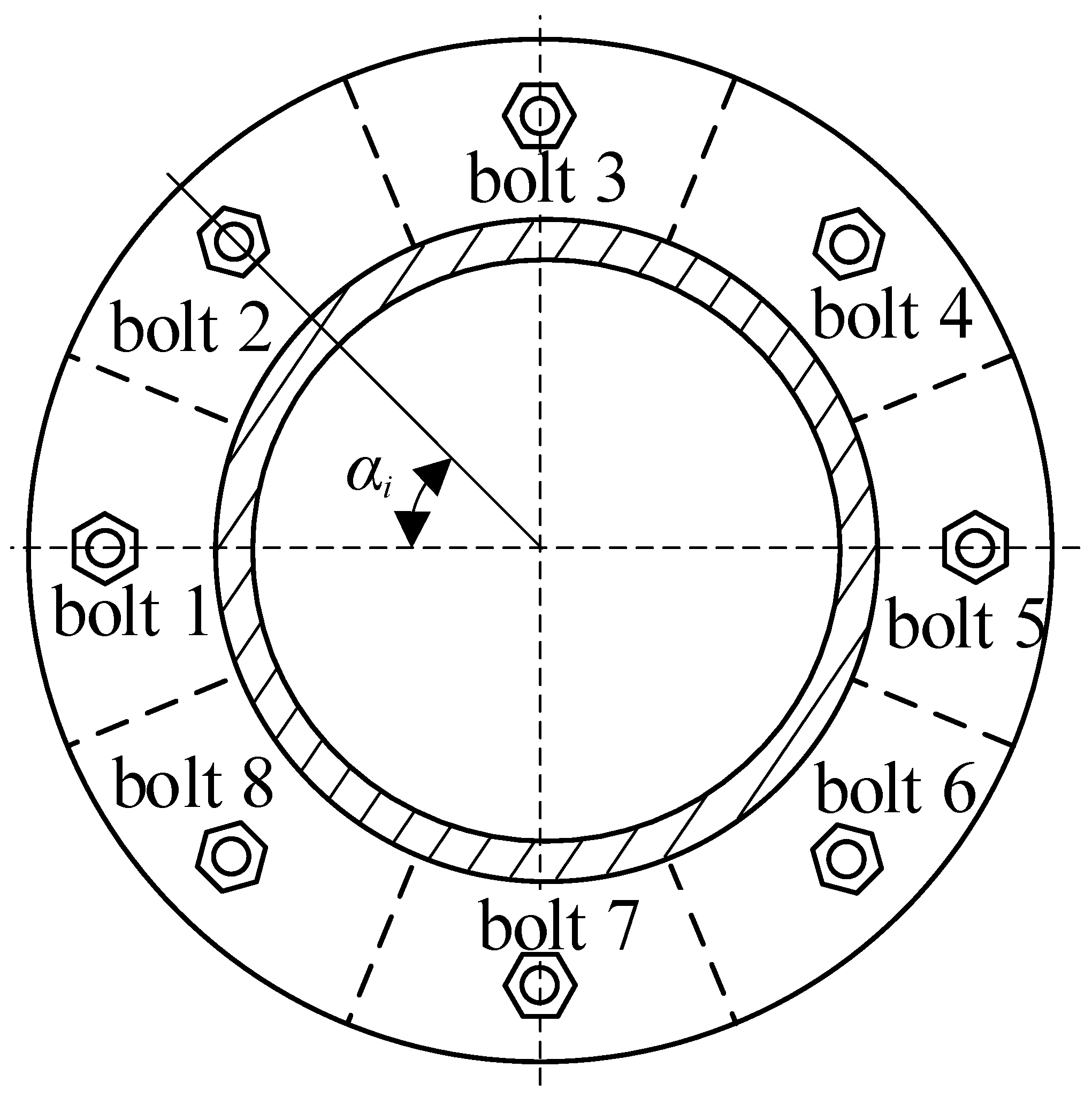
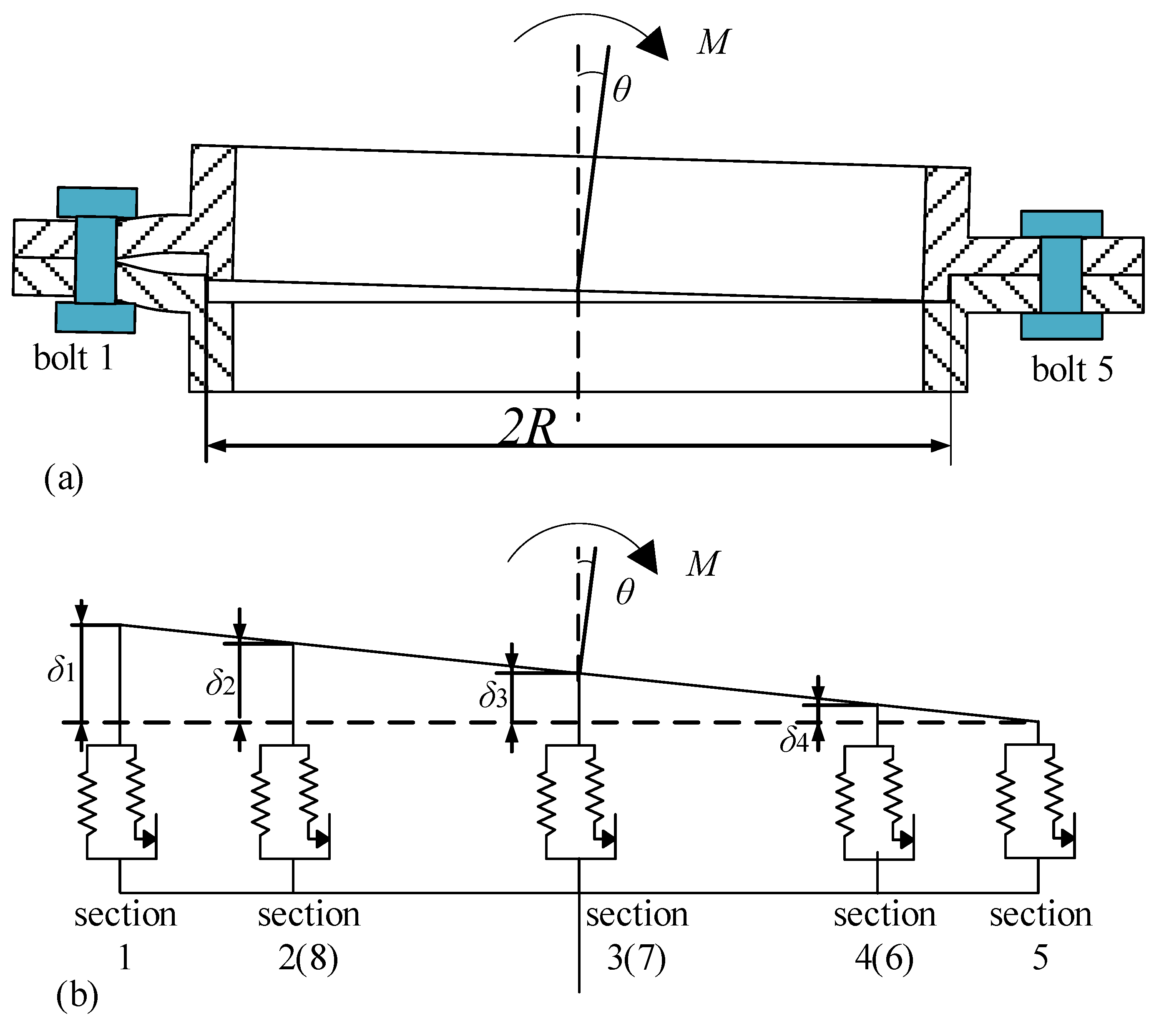
4.1. Division of the Sections of a Flange Joint
- The flange, bolts, and spigot conform to the small deformation assumption;
- The cylinder is assumed to be rigid;
- The flange is assumed to be a plane when the joint is subject to a bending load;
- Every section is independent, and there is no interaction between the two adjacent sections;
- As the compression stiffness is much larger than the tension stiffness, the section’s deformation under compression force is ignored [6].
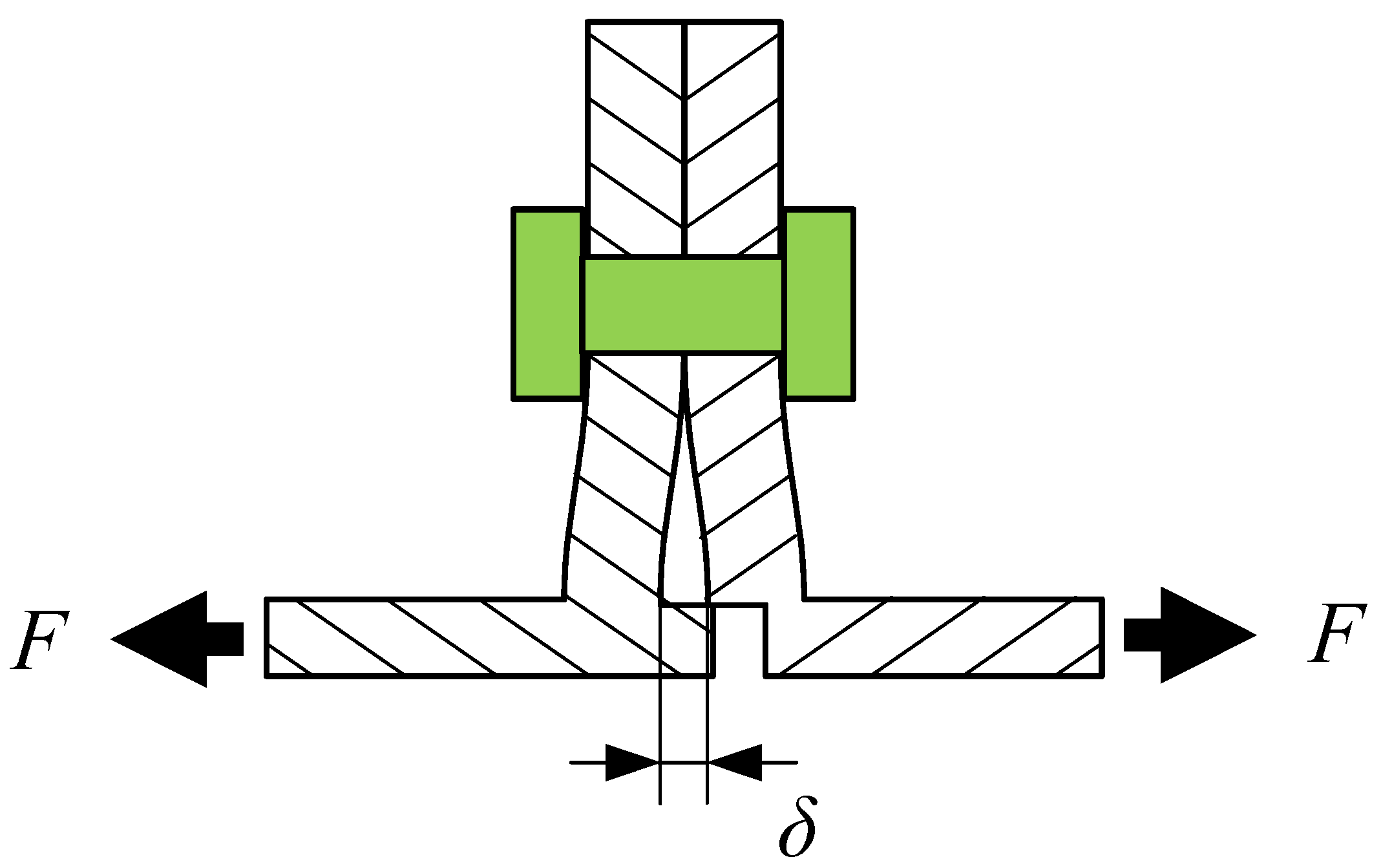
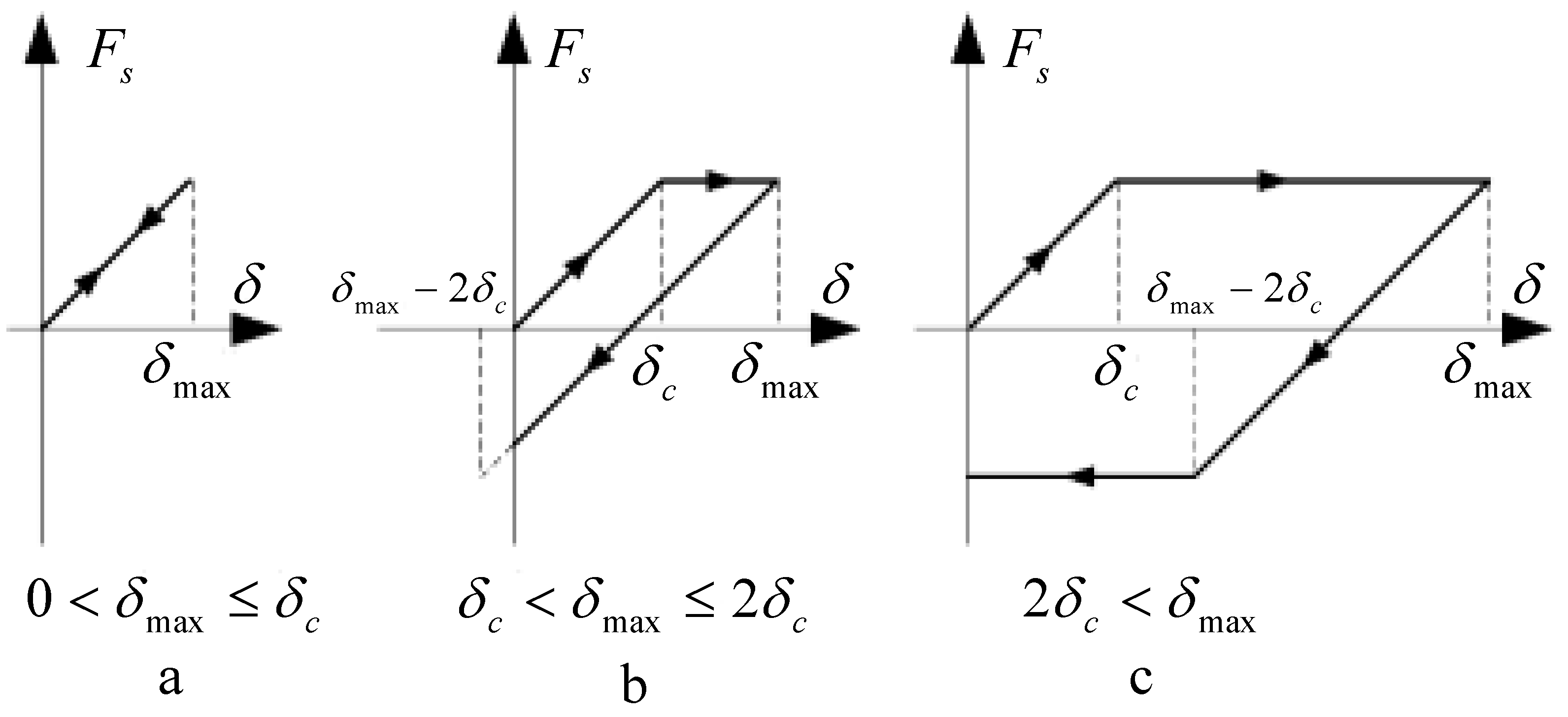
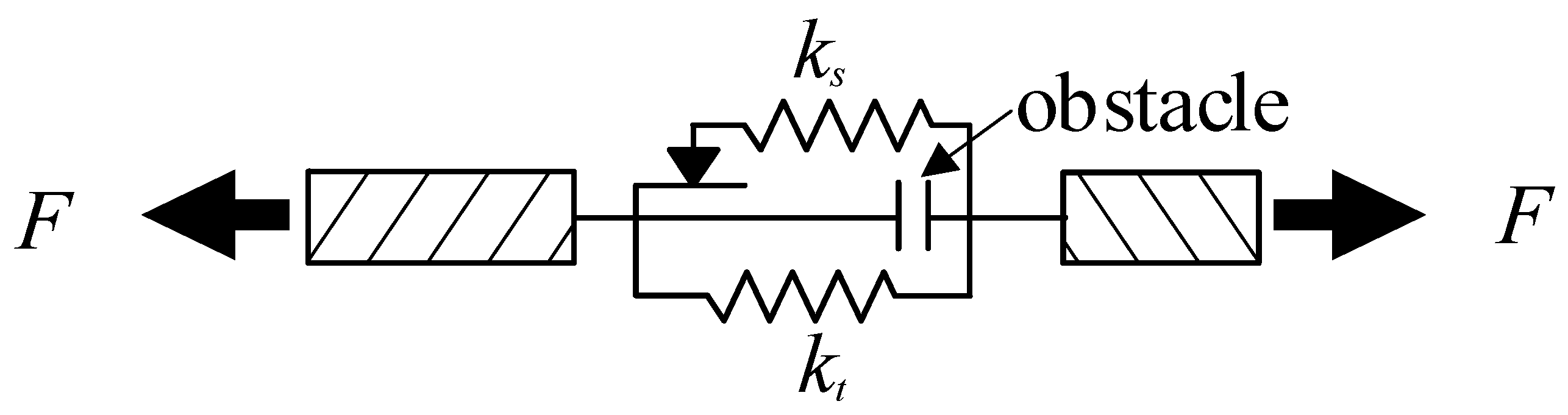
4.2. Force and Displacement of the Spigot
4.3. Building of the Analytical Model
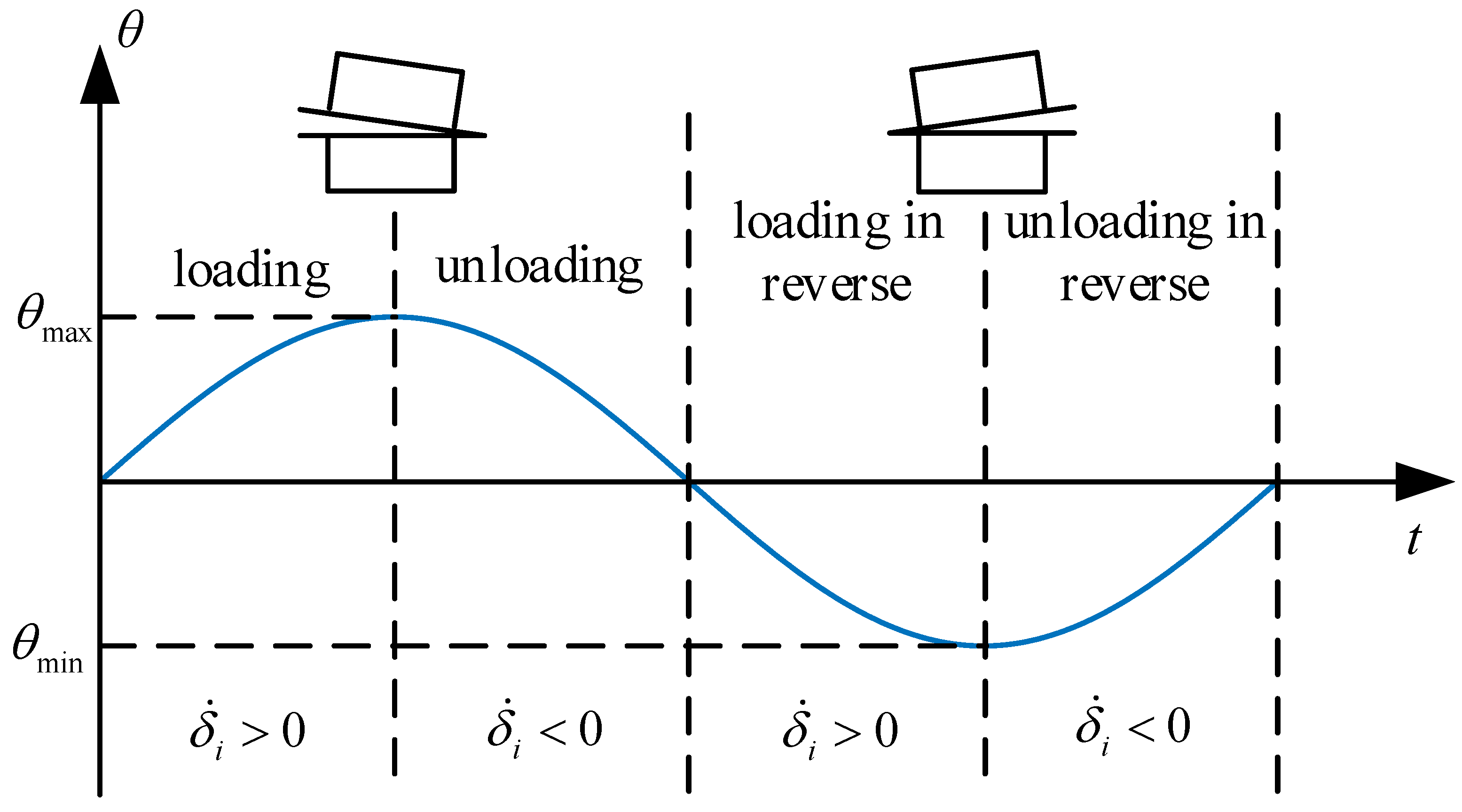
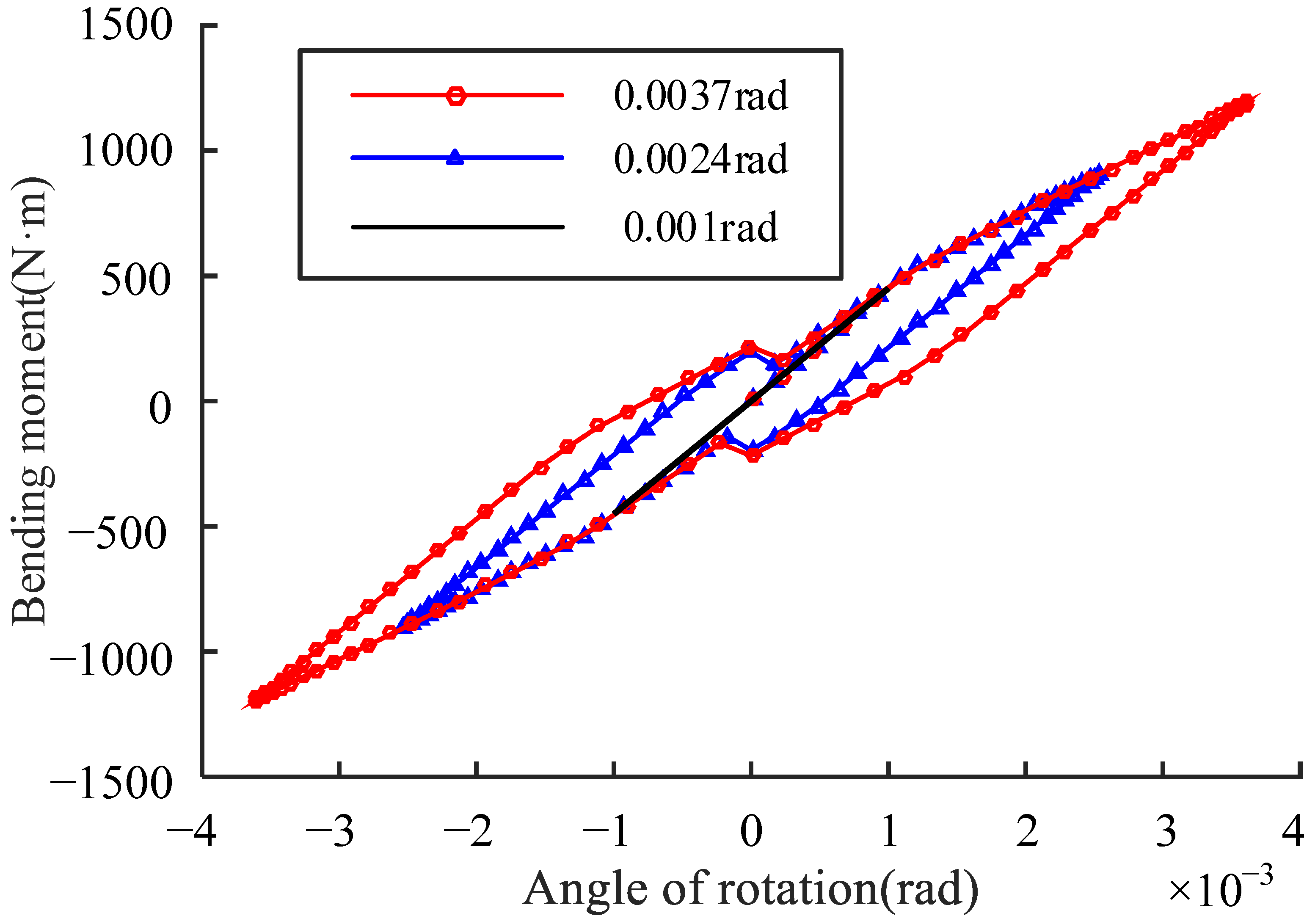
4.4. Simulation
5. Conclusions
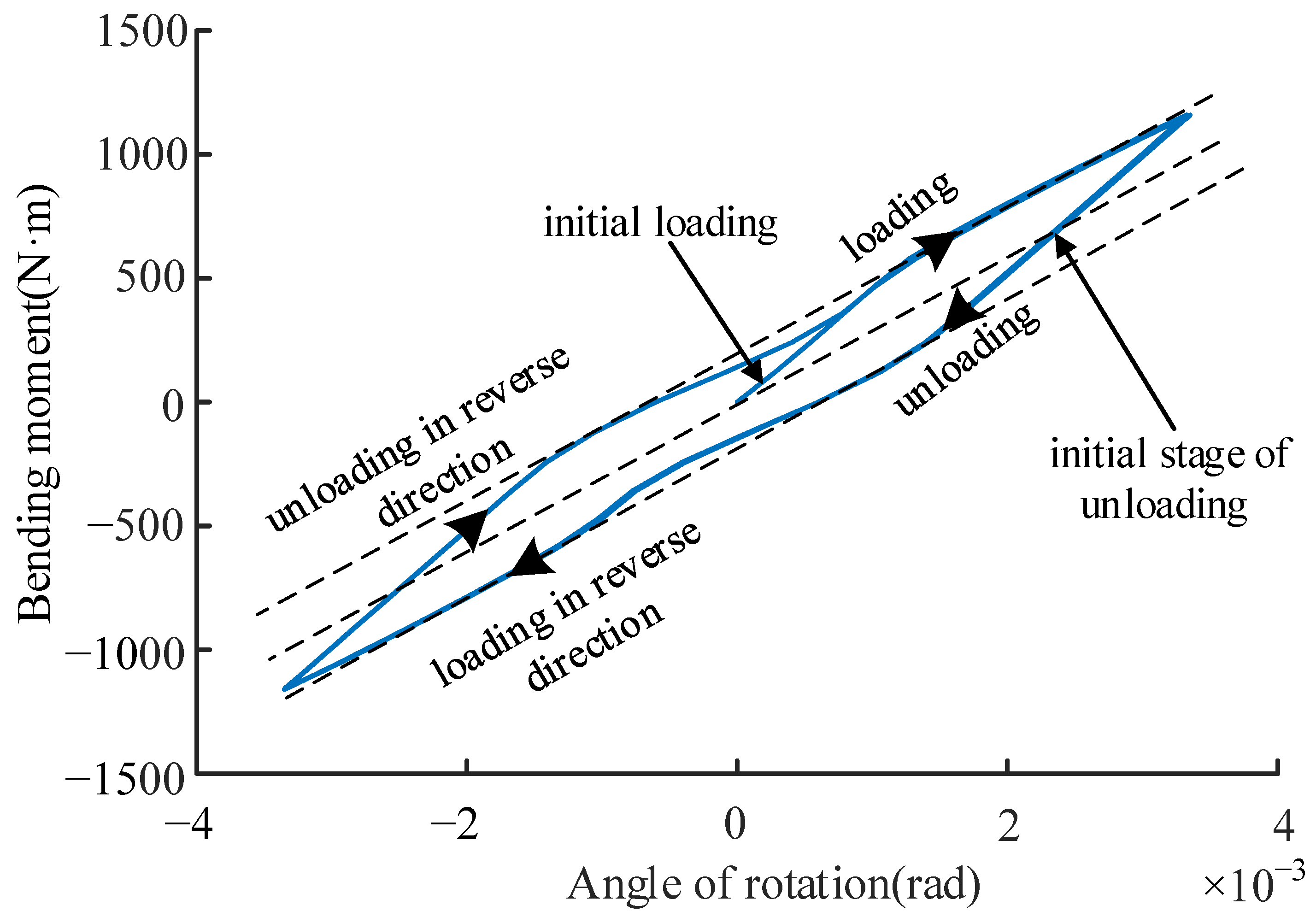
- When the load applied on the flange joint is large enough to cause the sliding of the contact surface of the spigot, hysteresis characteristics of the flange joint appear.
- The experiment established in this paper verifies the validity of the stiffness characteristics obtained by FE analysis.
- The proposed simplified analytical model can be utilized to simulate the deformation and sliding status of the contact surface of the spigot.
- The hysteresis stiffness characteristics of the flange joint with a spigot can be obtained through the analytical model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Bending stiffness before a change in the initial loading stage | |
| Bending stiffness after a change in the initial loading stage | |
| Tangential contact stiffness of the spigot | |
| Contact stiffness of the flange plate | |
| Displacement of the flange plate | |
| Total tension force, tangential force of the spigot, tangential force of the flange plate | |
| Contact pressure | |
| Sliding friction coefficient | |
| Peak value of displacement load | |
| Critical value of displacement load | |
| Angle of rotation for the flange plate | |
| Displacement of the section | |
| Velocity of the section | |
| Tension force of the section | |
| Bending moment | |
References
- Sun, W.; Guan, Z.; Chen, Y.; Pan, J.; Zeng, Y. Modeling of Preload Bolted Flange Connection Structure for Loosening Analysis and Detection. Shock Vib. 2022, 2022, 7844875. [Google Scholar] [CrossRef]
- Marek, P.; Pawlicki, J.; Mościcki, A. Tightness Problems at the Flange Connection in Transient Temperature and High Pressure Condition. Eng. Fail. Anal. 2022, 133, 105986. [Google Scholar] [CrossRef]
- Zhu, L.; Bouzid, A.-H.; Hong, J. A Method to Reduce the Number of Assembly Tightening Passes in Bolted Flange Joints. J. Manuf. Sci. Eng. 2021, 143, 121006. [Google Scholar] [CrossRef]
- El Masnaoui, W.; DaidiÉ, A.; Lachaud, F.; Paleczny, C. Semi-Analytical Model Development for Preliminary Study of 3D Woven Composite/Metallic Flange Bolted Assemblies. Compos. Struct. 2021, 255, 112906. [Google Scholar] [CrossRef]
- Nassiraei, H. Local Joint Flexibility of CHS X-Joints Reinforced with Collar Plates in Jacket Structures Subjected to Axial Load. Appl. Ocean Res. 2019, 93, 101961. [Google Scholar] [CrossRef]
- Nassiraei, H. Geometrical Effects on the LJF of Tubular T/Y-Joints with Doubler Plate in Offshore Wind Turbines. Ships Offshore Struct. 2022, 17, 481–491. [Google Scholar] [CrossRef]
- Zacal, J.; Folta, Z.; Struz, J.; Trochta, M. Influence of Symmetry of Tightened Parts on the Force in a Bolted Joint. Symmetry 2023, 15, 276. [Google Scholar] [CrossRef]
- Jamia, N.; Jalali, H.; Taghipour, J.; Friswell, M.I.; Haddad Khodaparast, H. An Equivalent Model of a Nonlinear Bolted Flange Joint. Mech. Syst. Signal Process. 2021, 153, 107507. [Google Scholar] [CrossRef]
- Qin, Z.; Han, Q.; Chu, F. Bolt Loosening at Rotating Joint Interface and Its Influence on Rotor Dynamics. Eng. Fail. Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Song, Y. Modeling, Identification and Simulation of Dynamics of Structures with Joints and Interfaces. Ph.D. Thesis, University of Illinois, Urbana-Champaign, IL, USA, 2004. [Google Scholar]
- He, K.; Zhu, W.D. Detecting Loosening of Bolted Connections in a Pipeline Using Changes in Natural Frequencies. J. Vib. Acoust. 2014, 136, 034503. [Google Scholar] [CrossRef]
- Yao, X.; Wang, J.; Zhai, X. Research and Application of Improved Thin-Layer Element Method of Aero-Engine Bolted Joints. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 823–839. [Google Scholar] [CrossRef]
- Luan, Y.; Guan, Z.-Q.; Cheng, G.-D.; Liu, S. A Simplified Nonlinear Dynamic Model for the Analysis of Pipe Structures with Bolted Flange Joints. J. Sound Vib. 2012, 331, 325–344. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, D.; Zhu, X.; Hong, J. Study on the Stiffness Loss and the Dynamic Influence on Rotor System of the Bolted Flange Joint. In Proceedings of the Volume 7A: Structures and Dynamics, Düsseldorf, Germany, 16 June 2014; American Society of Mechanical Engineers: Düsseldorf, Germany, 2014; p. V07AT31A020. [Google Scholar]
- Bouzid, A.-H.; Vafadar, A.K.; Ngô, A.D. On the Modeling of Anisotropic Fiber-Reinforced Polymer Flange Joints. J. Press. Vessel Technol. 2021, 143, 061506. [Google Scholar] [CrossRef]
- Ahmadian, H.; Jalali, H. Identification of Bolted Lap Joints Parameters in Assembled Structures. Mech. Syst. Signal Process. 2007, 21, 1041–1050. [Google Scholar] [CrossRef]
- Iranzad, M.; Ahmadian, H. Identification of Nonlinear Bolted Lap Joint Models. Comput. Struct. 2012, 96–97, 1–8. [Google Scholar] [CrossRef]
- Bograd, S.; Reuss, P.; Schmidt, A.; Gaul, L.; Mayer, M. Modeling the Dynamics of Mechanical Joints. Mech. Syst. Signal Process. 2011, 25, 2801–2826. [Google Scholar] [CrossRef]
- Oldfield, M.; Ouyang, H.; Mottershead, J.E. Simplified Models of Bolted Joints under Harmonic Loading. Comput. Struct. 2005, 84, 25–33. [Google Scholar] [CrossRef]
- Ouyang, H.; Oldfield, M.J.; Mottershead, J.E. Experimental and Theoretical Studies of a Bolted Joint Excited by a Torsional Dynamic Load. Int. J. Mech. Sci. 2006, 48, 1447–1455. [Google Scholar] [CrossRef]
- Van-Long, H.; Jean-Pierre, J.; Jean-François, D. Behaviour of Bolted Flange Joints in Tubular Structures under Monotonic, Repeated and Fatigue Loadings I: Experimental Tests. J. Constr. Steel Res. 2013, 85, 1–11. [Google Scholar] [CrossRef]
- Firrone, C.M.; Battiato, G.; Epureanu, B.I. Modelling the Microslip in the Flange Joint and Its Effect on the Dynamics of a Multi-Stage Bladed Disk Assembly. In Proceedings of the Volume 7A: Structures and Dynamics, Seoul, Republic of Korea, 13 June 2016; American Society of Mechanical Engineers: Seoul, Republic of Korea, 2016; p. V07AT32A032. [Google Scholar]
- Shi, W.; Zhang, Z. An Improved Contact Parameter Model with Elastoplastic Behavior for Bolted Joint Interfaces. Compos. Struct. 2022, 300, 116178. [Google Scholar] [CrossRef]
- He, L.; Li, T. Undamped Non-Linear Vibration Mechanism of Bolted Flange Joint under Transverse Load. J. Asian Archit. Build. Eng. 2023, 22, 1507–1532. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Chen, L. Dynamic Characteristics of the Flange Joint with a Snap in Aero-Engine. Int. J. Acoust. Vib. 2018, 23, 168–174. [Google Scholar] [CrossRef]
- Shuguo, L.; Yanhong, M.; Dayi, Z.; Jie, H. Studies on Dynamic Characteristics of the Joint in the Aero-Engine Rotor System. Mech. Syst. Signal Process. 2012, 29, 120–136. [Google Scholar] [CrossRef]
- Yu, P.; Li, L.; Chen, G.; Yang, M. Dynamic Modelling and Vibration Characteristics Analysis for the Bolted Joint with Spigot in the Rotor System. Appl. Math. Model. 2021, 94, 306–331. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, D.; Guo, X.; Ai, Y. Stiffness and Geometry Characteristics of Flange Connection with Bolt Failure and Its Influence on Rotor Dynamics. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 095440622211474. [Google Scholar] [CrossRef]





| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 2.5 mm | 58 mm | ||
| 3 mm | 40 mm | ||
| 27.5 mm | 30 mm | ||
| 2.5 mm | 49 mm | ||
| 1.7 mm | 7 mm | ||
| 2 mm | 5 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, J.; Liu, Y.; Wang, Z.; Long, Y. Stiffness Characteristics and Analytical Model of a Flange Joint with a Spigot. Symmetry 2023, 15, 1221. https://doi.org/10.3390/sym15061221
Liu H, Wang J, Liu Y, Wang Z, Long Y. Stiffness Characteristics and Analytical Model of a Flange Joint with a Spigot. Symmetry. 2023; 15(6):1221. https://doi.org/10.3390/sym15061221
Chicago/Turabian StyleLiu, Hao, Jianjun Wang, Yu Liu, Zhi Wang, and Yifu Long. 2023. "Stiffness Characteristics and Analytical Model of a Flange Joint with a Spigot" Symmetry 15, no. 6: 1221. https://doi.org/10.3390/sym15061221
APA StyleLiu, H., Wang, J., Liu, Y., Wang, Z., & Long, Y. (2023). Stiffness Characteristics and Analytical Model of a Flange Joint with a Spigot. Symmetry, 15(6), 1221. https://doi.org/10.3390/sym15061221





