Abstract
We investigated the influence of precession angle, energy filtering and sample thickness on the structural parameters of amorphous SiO2 thin films from the electron reduced density functions obtained by applying precession electron diffraction. The results demonstrate that the peak positions in the electron reduced density functions are generally insensitive to the studied experimental conditions, while both precession angle and energy filtering influence peak heights considerably. It is also shown that introducing precession with small angles of up to 2 degrees and energy filtering results in higher coordination numbers that are closer to the expected theoretical values of 4 and 2 for Si and O, respectively, for data obtained from a thicker sample.
1. Introduction
Amorphous structures are an important class of materials for a number of applications, e.g., optical fibres [1] and biological scaffolds [2]. Understanding these materials’ properties and building meaningful structure–property correlations depends on the accurate determination of atomistic structures. Due to the structural complexity of amorphous materials, describing an averaged building block or structure is one of the more generally used approaches to assess these structures [3]. Diffraction techniques are among the experimental techniques that are suitable for obtaining an averaged structure [4,5,6]. In this approach, the diffraction pattern can be converted into a pair distribution function (PDF) that describes an averaged structure, and this can be subsequently used to build an atomistic model.
Diffraction techniques have been applied extensively to determine atomic structures using various types of radiation including X-rays, neutrons and electrons. The major advantage of electron diffraction is that electrons have larger scattering cross sections (than X-rays), with the ability to form fine probes of controlled geometry. This enables the observation of the local atomic structure of materials from very small volumes when compared to those required for X-ray and neutron diffraction [7]. In addition, the imaging mode in a transmission electron microscope (TEM) allows for the straightforward selection of the sample area of interest from where the diffraction data are collected.
Electron reduced density function (eRDF) analysis, which is equivalent to pair distribution function (PDF) analysis, is a direct way to characterise the atomistic structure of amorphous thin films by recording and analysing diffraction patterns in a TEM.
The kinematic scattering approximation is often used when comparing atomistic models to experimental electron diffraction data, a practice which assumes that only one elastic scattering event occurs for each electron passing through the specimen [8]. However, in practice, the electrons can be scattered multiple times and scattering events can be inelastic, with characteristic energy losses.
The contribution of inelastic scattering can be removed by energy filtering [9]. Additionally, precession electron diffraction (PED) has been shown to reduce the effect of multiple scattering when interpreting diffraction data from crystalline samples [10,11,12].
The contributions of both multiple and inelastic scattering are expected to increase with sample thickness and therefore this is an important factor that will influence the results of an RDF analysis based on the kinematic scattering approximation.
Whilst eRDF analysis has been extensively applied in various studies [13,14,15,16,17], the effect of various experimental parameters on the eRDF analysis and especially on the refined atomistic models has not been systematically investigated for amorphous materials. The purpose of this study is to quantify the influence of precession angle in PED, together with the effects of energy filtering and sample thickness on the eRDF of amorphous SiO2 thin films and, subsequently, on the determined structural parameters.
Electron Reduced Density Function (eRDF)
The total electron scattering intensity, for a particular arrangement of different atomic species for all orientations of the sample can be calculated using Equation (1) [18], where is the atomic scattering factor, is the scattering vector and is the distance between two atoms.
Following Cockayne [7], this function can be rewritten in terms of a pair distribution function, , by integrating over the sample volume which is directly related to the local average density, (Equation (2)).
In Equation (2), the atomic scattering intensity term, , represents the atoms scattering independently and the second term describes the deviation from the mean intensity when the local density at deviates from the mean density . Used to extract the RDF, the reduced scattering intensity function is defined as in Equation (3).
Finally, the function is Fourier-transformed to give the eRDF, (Equation (4)).
In practice, the eRDF (Equation (5)) is calculated by the integration of the reduced scattering function over an experimentally limited range of q between and . In this case, to reduce the influence of data truncation on the Fourier transform, the data are multiplied by an exponential function with a small artificial temperature factor b, which is usually set at b = 0.02:
2. Materials and Methods
2.1. Experimental
Electron diffraction data were collected from amorphous SiO2 films samples with two different thickness of 234 Å and 471 Å (purchased from Agar Scientific Ltd., Essex, UK). The thicknesses were determined using an ARM-200CF TEM (JEOL, Akishima, Japan) from the field of electron energy loss spectroscopy (EELS) at 200 kV using the log–ratio technique [19] by averaging over three windows in each film sample. A Libra 120 TEM (Zeiss, Oberkochen, Germany), operating at 120 kV with an in-column energy filter, was used to collect diffraction data and electron diffraction patterns were recorded on a TRS full-frame 16-bit 2 k × 2 K-pixel CCD camera, with a camera length of 144 mm and a 5 μ condenser aperture giving a parallel nanobeam of 150 nm in diameter. The diffraction patterns were energy-filtered at the zero-loss peak, with a slit width of 20 eV. A NanoMEGAS Digistar P1000 was used for precession electron diffraction. When collecting diffraction patterns, a beam stop was used to block the central beam in order to collect scattering intensity data at larger scattering angles while avoiding the risk of damaging the CCD during long exposures.
2.2. eRDF Analysis
The calculation of eRDF curves from the experimental data was performed using the free open source eRDF Analyser software [20], which is one of several similar software suites available, including ProcessDiffraction [21], SUePDF [22], ePDF tools [23], and RDF Tools [24].
The eRDF Analyser provides an interactive graphical user interface and allows users to mask beam stops or any distorted areas, which are then excluded from the calculation of the final results. It also allows for the optimisation of the position of the centre of the diffraction pattern in the experimental diffraction data. Identifying the position of the centre is important for computing an accurate azimuthally averaged intensity distribution function, .
A polycrystalline aluminum specimen (SPI Supplies, West Chester, PA, USA) was used as a standard to calibrate the diffraction patterns. A customised automated fitting routine provided in the eRDF Analyser software was used to extract the atomic scattering background for calculations of the reduced scattering intensities according to Equation (3). This was performed based on least-squares fitting of the atomic scattering curve, with either the full range or the last third of the experimental data selected as the region of fitting. The reduced scattering intensity function was obtained from Equation (3), and the eRDF curve was obtained by a Fourier transform of following Equation (5). These functions were subsequently used in a reverse Monte Carlo refinement [25] to obtain an atomistic model, from which average coordination numbers and average bond lengths were calculated. The reduced scattering functions were obtained in the same range from 1.541 to 18.355 Å−1, with a 0.014 Å−1 step to facilitate comparison between experiments.
2.3. Structure Refinement
Model structures were obtained from matched reduced scattering functions calculated from the model using Equation (6). Then, they were filtered to remove the contribution of frequencies, resulting in unphysically short distances in the RDF below 1 Å to the corresponding experimental scattering intensities, as described by McGreevy [25] and performed previously [26].
Initially, a small model of SiO2 with 102 atoms was prepared by random dense packing of atoms approximated as soft spheres, in a cubic cell with a lattice parameter corresponding to a density of 2.3 g cm−3.
DFT calculations using the CASTEP code [27] were used to perform liquid quench molecular dynamics (MD) simulations using on-the-fly-generated pseudopotentials within the generalized gradient approximation using the Perdew–Burke–Ernzerhof exchange–correlation functional [28]. The generated pseudopotentials are a function of atomic species and, once generated in the beginning of the calculations, do not change during simulations. MD simulations were performed using a canonical (constant NVT) ensemble. The starting model was first melted at 3000 K for 2 ps. It was then simulated at 2000 K for 10 ps, and then further quenched to 400 K, reducing the temperature by 200 K in 5 ps equilibration steps. Finally, the structure was equilibrated at 300 K for 10 ps. The total simulation time was therefore 62 ps, with time steps of 2 fs throughout. The temperature was controlled using an implementation of the Nosé–Hoover thermostat [29]. The electron density was only sampled at the gamma point, with the pseudopotential energy cut-off set at 300 eV.
A larger model of 816 atoms for SiO2 was constructed from the smaller model, obtained in the DFT MD simulations at 300 K, by assembling 2 × 2 × 2 small models with random orientations. These larger models were then used in RMC refinements. Small displacements of atoms in each of the RMC refinement steps were used to retain the structural features from the MD simulation, such as the preferred bond types and bond angle distributions. An example of a refined model is shown in Figure 1

Figure 1.
An example of SiO2 model of 816 atoms after RMC refinement.
Unfiltered and filtered reduced scattering intensity functions are shown in Figure 2a. The filter is a low-order polynomial contribution to the background that cannot be fit to the refinements as it would mean the presence of unphysically close interatomic distances [25]. A comparison of the RDF obtained from the refined model to the experimental one computed from filtered scattering intensities is shown in Figure 2b.
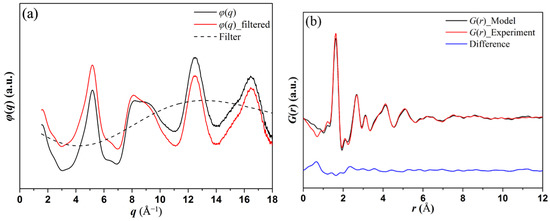
Figure 2.
(a) φ(q) filtering and (b) comparison between experimental and model G(r) curves.
3. Results
Figure 3 shows a typical selected area diffraction pattern acquired from polycrystalline aluminium and amorphous SiO2 films without energy filtering. The patterns were obtained with the central beam shifted to the corner of the detector to maximize the recorded scattering angles. The thinnest part of the beam stopper was used to block the unscattered beam in order to collect the scattered intensity at low angles. A pixel calibration factor of 0.00223 Å−1 was determined using the eRDF Analyser by first identifying and refining the centre of the diffraction pattern obtained without energy filtering and then calculating and relating the peak positions to the known reflections of polycrystalline Al, as summarised in Table 1.
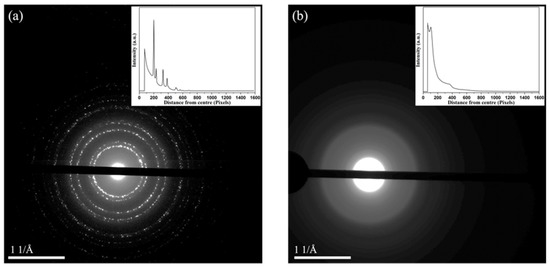
Figure 3.
Typical electron diffraction patterns of (a) polycrystalline Al and (b) amorphous SiO2 specimen with azimuthally averaged total scattering intensities shown inset.

Table 1.
Computed pixel calibration factors for polycrystalline Al.
3.1. Influence of Specimen Thickness
Figure 4 compares the results of atomic scattering background fitting to the total experimental scattered intensity curves , and , recorded from amorphous SiO2 specimens with thicknesses of 234 Å and 471 Å, in experiments with 0° precession (no precession) and without energy filtering. Noticeable differences are observed in scattering intensities (Figure 4) at low scattering angles (q from 2 to 6 Å−1) when comparing the data from the 471 Å film to the 234 Å data. This is due to the atomic scattering background for thinner specimens fitting better through the oscillations of the total scattered intensity curve in this region due to there being a smaller contribution from multiple and inelastic scattering, as seen in Figure 4. In the curves, the first peak corresponds to the Si-O distances, while the second and third peaks are due to a mixture of Si…O, Si…Si and O…O distances. The determined Si-O bond length of 1.61–1.63 Å also agrees with the value of 1.612(7) Å drawn from an X-ray diffraction study [30]. Measurements of peak position and height are given in Table 2. The maximum difference in peak positions for the two sample thicknesses is observed for the second peak and is about 0.03 Å, or less than 2%. The peak heights, however, show larger deviations for the two films, being of 12.6%, 6.4% and 21.9% for the first, second and third peaks, respectively. The peak heights were defined as the peak amplitude in the calculated eRDF curves. The significance of large change in the peak heights is that it affects the coordination numbers that can be calculated from the results.
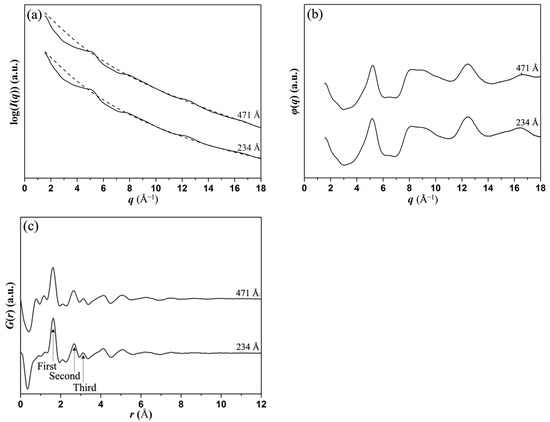
Figure 4.
Influence of specimen thickness on atomic scattering background fitting to (a) I(q), (b) φ(q) and (c) G(r) for samples with two different thicknesses, 234 Å and 471 Å.

Table 2.
Influence of specimen thickness on (a) positions and (b) heights of the eRDF peaks.
3.2. Influence of Precession Angle
PED was measured with precession angles from 0° to 3° for samples of both thicknesses and the resulting and for both 234 Å and 471 Å samples are shown in Figure 5. The main parameters are given in Table 3. These results show that only small variations are observed when comparing the data without precession (0°) to those with precession (1° to 2°). However, when the precession angle reaches 3°, data at high q (above 16 Å−1) appears larger, which leads to larger oscillations in the resulting . Furthermore, it can be seen from Table 3 that the peak positions differ very little when the precession angles vary from 0° (no precession) to 2°, with differences being less than 0.02 Å. However, for the 3° precession, the third peak position decreases by 0.08 Å. The same trend is observed for the peak heights. While experiments with precession angles from 0° to 2° show small differences of around 6.3% for all peaks, the 3° precession shows larger differences of 13.3%, 13.6%, and 65.6% for the first, second and third peaks, respectively. Similar trends are observed for the peak heights for the thicker sample of 471 Å with differences of 10.9%, 18.4%, and 47.1% for the first, second and third peaks, respectively, of the sample with 3° precession. This can be understood as the principle that applying large precession angle effectively increases the thickness of the sample. As suggested previously [31], the effect of sample thickness on the scattered intensity can be regarded as a convolution of the scattered intensity from a thin slice with itself as the electron wave propagates through a thicker sample. This results in a reduction of the amplitudes of all peaks in the total scattering intensity and, therefore, reduction in peak heights in G(r). Importantly, the large change in the peak heights has consequences for the determination of the coordination numbers from the results.
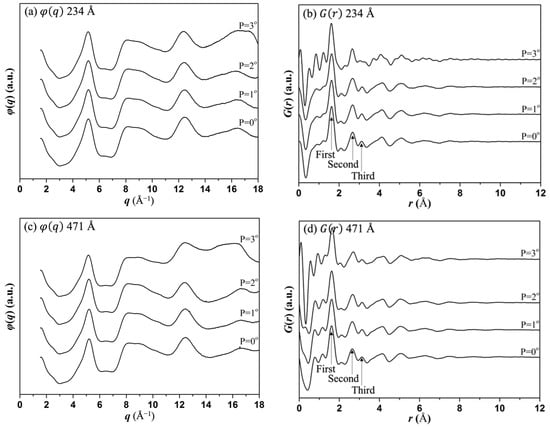
Figure 5.
Influence of precession angle on φ(q) and G(r) for (a,b) 234 Å and (c,d) 471 Å samples.

Table 3.
Influence of precession angle on (a) positions and (b) heights of the eRDF peaks for the 234 Å and 471 Å samples.
3.3. Influence of Energy Filtering on the RDF
Figure 6 shows and measured with and without energy filtering for both 234 Å and 471 Å samples. Although the overall shapes of are similar with and without energy filtering for both thicknesses, noticeable differences can be observed in curve oscillation amplitudes. The use of higher-amplitude oscillations in the in the experiments with energy filtering led to higher peaks in the corresponding curves. Measurements of the eRDF curves parameters are shown in Table 4. It can be seen that peak positions in both curves are identical, except for a small 0.01 Å difference for the first (Si-O) peak. However, the peak heights are 30.0%, 27.3%, and 56.3% smaller for the first, second and third peaks, respectively, when recorded without energy filtering. The trends for the 471 Å thick sample are similar. The difference in peak positions is small, being less than 0.02 Å, while the peak heights are 25.8%, 29.5%, and 13.8% smaller for the first, second and third peaks, respectively, without energy filtering. As the energy of the electrons defines their wavelength, the scattering of electrons of different energies will result in slightly shifted (relative to the incident beam) scattering profiles. Averaging over such scattering profiles at the detector is expected to have the effect of flattening the peaks, similar to the effects of the multiple scattering.
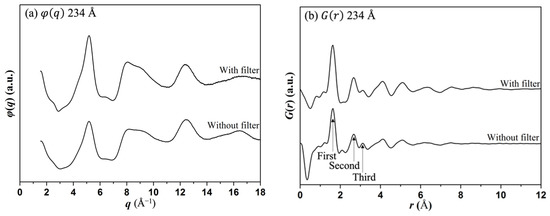
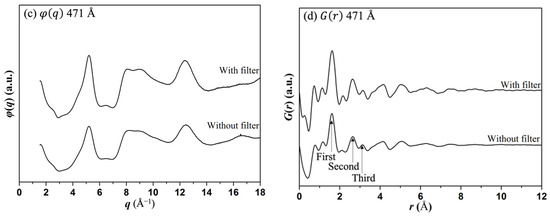
Figure 6.
Influence of energy filtering on φ(q) and G(r) for (a,b) 234 Å and (c,d) 471 Å samples.

Table 4.
Influence of energy filtering on (a) positions and (b) height of the eRDF peaks for 234 Å and 471 Å samples.
3.4. Influence of Experimental Parameters on the Refined Structure
Table 5 summarises the coordination numbers, Z, and average Si-O bond length computed from the refined models of the amorphous SiO2 films obtained under different experimental conditions, while Figure 7 shows the change in coordination numbers for various experimental conditions.

Table 5.
Influence of experimental parameters on refined coordination numbers and structural parameters of amorphous SiO2 models.
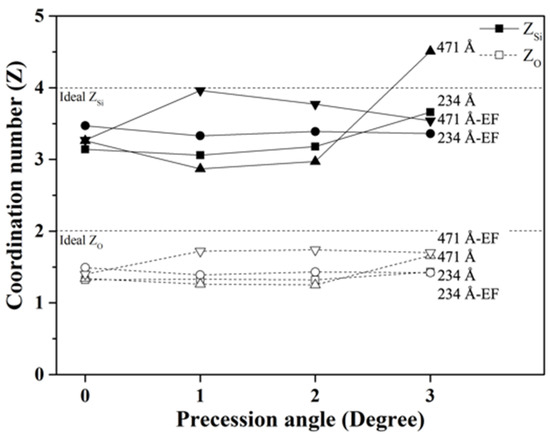
Figure 7.
Variations in coordination numbers of ZSi and ZO with sample thickness, energy filtering and precession angle obtained from structure refinements of amorphous SiO2 models.
4. Discussion
4.1. Influence of Sample Thickness
We have observed that the heights of all peaks are reduced with increasing thickness independently of precession or energy filtering, while the peak positions remain the same.
Increasing the sample thickness decreases the quality of fit, as seen in the R-factors in Table 5. This is to be expected as the contribution of inelastic and multiple scattering increases with sample thickness. This observation also agrees with earlier research showing that multiple scattering does not affect peak positions [31].
Although, the peak heights generally reduce with thickness, (Table 2) there is a less pronounced trend in the change in the coordination number obtained from the refined models (Figure 7). It can be seen, however, that the coordination number increases with thickness when energy filtering and precession are applied. Without energy filtering, the coordination number tends to be lower for the thicker sample when using smaller precession angles (Figure 7).
4.2. Influence of Precession
Smaller precession angles (1°, 2°) slightly decrease the height of the first peak as compared to data recorded without precession (Table 3), whilst a higher precession angle (3°) increases the height of the first peak considerably while notably reducing the height of the third peak. Its influence on fit quality is not straightforward. Introduction of small (1°) precession generally improves the fit quality. The improvement of fitting between model and experiment with the introduction of precession has also been seen in previous experiments with metallic nanoparticles [32]. The fit quality, however, reduces with larger precession angle. It can be suggested that larger precession angles effectively increase the sample thickness, which leads to larger contribution of inelastic scattering and, therefore, worse fit. This decrease in fit quality is notably larger for the thicker 471 Å sample (Table 5). Other possible contributing factors cannot be excluded, such as an increased probability of descanning errors.
Using higher precession angles increased the coordination numbers for the thinner sample in the present investigation. For the thicker sample, however, a high degree of precession resulted in unreasonably high coordination number (4.5 for Si), which can be attributed to the worse fit due to effective increase in sample thickness and increased contribution of inelastic scattering at higher precession.
4.3. Influence of Energy Filtering
Energy filtering, as for precession, does not affect all peaks uniformly. For example, the heights of the first and second peaks increase considerably after energy filtering, (Table 4) as compared to the third peak, which reduces for the 234 Å thin sample or increases only slightly for the 471 Å thick one.
When energy filtering is introduced, coordination numbers increase for both sample thicknesses as compared to unfiltered data, but the goodness of fit reduces slightly (Table 5). The improvement in coordination number can be attributed to the removal of the inelastic scattering contribution by the energy filter and is a consequence of increased peak heights. The slight decrease in the fitting quality may be due to some experimental error introduced by the energy filter. The magnitude of change in coordination number with introduction of energy filtering is more notable for the thicker sample, as would be expected by the removal of the larger contribution of inelastic scattering.
5. Conclusions
The study demonstrates that the peak positions in the obtained eRDF curves are generally insensitive to sample thickness, precession angle or energy filtering.
However, the studied experimental conditions influence the peak heights considerably, which results in different coordination numbers being obtained from the atomistic models.
It is shown that introducing precession and energy filtering results in higher coordination numbers, bringing them closer to the ideal theoretical values for the material when the data are obtained from a thicker sample. It is also observed that energy filtering and precession, may influence the goodness-of-fit of atomistic models to the experimental data.
Author Contributions
Conceptualization: K.B.B., A.I.K. and S.N.; methodology: S.N. and M.G.; software: K.B.B.; investigation: Y.-J.C., M.G. and P.P.D.; resources: A.I.K. and S.N.; data curation: Y.-J.C. and K.B.B.; writing—original draft preparation: Y.-J.C.; writing—review and editing: Y.-J.C. and K.B.B.; supervision: A.I.K.; funding acquisition: A.I.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by FP7-INFRASTRUCTURES grant number ESTEEM2 312483.
Data Availability Statement
The original experimental data are available from the authors upon request.
Acknowledgments
The authors are grateful to ESTEEM2 project for financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Kuo, C.-K.; Huang, H.-W.; Chen, L.-G.; Chou, Y.-J. Fabrication and characterization of freeze dried strontium-doped bioactive glasses/chitosan composite scaffolds for biomedical engineering. J. Asian Ceram. Soc. 2021, 9, 1173–1182. [Google Scholar] [CrossRef]
- Zachariasen, W.H. The atomic arrangement in glass. J. Am. Chem. Soc. 1932, 54, 3841–3851. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Raman spectroscopy of amorphous, nanostructured, diamond–like carbon, and nanodiamond. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2004, 362, 2477–2512. [Google Scholar] [CrossRef]
- Malfait, W.J.; Halter, W.E.; Morizet, Y.; Meier, B.H.; Verel, R. Structural control on bulk melt properties: Single and double quantum 29Si NMR spectroscopy on alkali-silicate glasses. Geochim. Cosmochim. Acta 2007, 71, 6002–6018. [Google Scholar] [CrossRef]
- Cockayne, D.J.H.; McKenzie, D.R. Electron diffraction analysis of polycrystalline and amorphous thin films. Acta Crystallogr. A 1988, 44, 870–878. [Google Scholar] [CrossRef]
- Cockayne, D.J.H. The Study of Nanovolumes of Amorphous Materials Using Electron Scattering. Annu. Rev. Mater. Res. 2007, 37, 159–187. [Google Scholar] [CrossRef]
- Sproul, A.; McKenzie, D.R.; Cockayne, D.J.H. Structural study of hydrogenated amorphous silicon–carbon alloys. Philos. Mag. B 1986, 54, 113–131. [Google Scholar] [CrossRef]
- Eggeman, A.S.; Barnard, J.S.; Midgley, P.A. Aberration-Corrected and Energy-Filtered Precession Electron Diffraction. Z. Kristallogr. 2013, 228, 43–50. [Google Scholar] [CrossRef]
- Vincent, R.; Midgley, P.A. Double conical beam-rocking system for measurement of integrated electron diffraction intensities. Ultramicroscopy 1994, 53, 271–282. [Google Scholar] [CrossRef]
- Gjønnes, K. On the integration of electron diffraction intensities in the Vincent-Midgley precession technique. Ultramicroscopy 1997, 69, 1–11. [Google Scholar] [CrossRef]
- Gemmi, M.; Righi, L.; Calestani, G.; Migliori, A.; Speghini, A.; Santarosa, M.; Bettinelli, M. Structure determination of φ-Bi8Pb5O17 by electron and powder X-ray diffraction. Ultramicroscopy 2000, 84, 133–142. [Google Scholar] [CrossRef]
- Abeykoon, A.M.; Hu, H.; Wu, L.; Zhu, Y.; Billinge, S.J. Calibration and data collection protocols for reliable lattice parameter values in electron pair distribution function studies. J. Appl. Crystallogr. 2015, 48, 244–251. [Google Scholar] [CrossRef]
- Abeykoon, A.M.M.; Malliakas, C.D.; Juhás, P.; Bozin, E.S.; Kanatzidis, M.G.; Billinge, S.J.L. Quantitative Nanostructure Characterization Using Atomic Pair Distribution Functions Obtained From Laboratory Electron Microscopes. Z. Kristallogr. 2012, 227, 248–256. [Google Scholar] [CrossRef]
- Kis, V.R.C.K.; Dódony, I.N.; Lábár, J.N.L. Amorphous and partly ordered structures in SiO2 rich volcanic glasses. An ED study. Eur. J. Mineral. 2006, 18, 745–752. [Google Scholar] [CrossRef]
- Petersen, T.C.; McBride, W.; McCulloch, D.G.; Snook, I.K.; Yarovsky, I. Refinements in the collection of energy filtered diffraction patterns from disordered materials. Ultramicroscopy 2005, 103, 275–283. [Google Scholar] [CrossRef]
- Ankele, J.; Mayer, J.; Lamparter, P.; Steeb, S. Quantitative Electron Diffraction Data of Amorphous Materials. Z. Für Nat. A 2005, 60, 459–468. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Courier Dover Publications: New York, NY, USA, 1969. [Google Scholar]
- Malis, T.; Cheng, S.C.; Egerton, R.F. EELS log-ratio technique for specimen-thickness measurement in the TEM. J. Electron Microsc. Tech. 1988, 8, 193–200. [Google Scholar] [CrossRef]
- Shanmugam, J.; Borisenko, K.B.; Chou, Y.-J.; Kirkland, A.I. eRDF Analyser: An interactive GUI for electron reduced density function analysis. SoftwareX 2017, 6, 185–192. [Google Scholar] [CrossRef]
- Lábár, J.L.; Das, P.P. Pattern Center and Distortion Determined from Faint, Diffuse Electron Diffraction Rings from Amorphous Materials. Microsc. Micoanal. 2017, 23, 647–660. [Google Scholar] [CrossRef]
- Tran, D.T.; Svensson, G.; Tai, C.-W. SUePDF: A program to obtain quantitative pair distribution functions from electron diffraction data. J. Appl. Crystallogr. 2017, 50, 304–312. [Google Scholar] [CrossRef]
- Shi, H.; Luo, M.; Wang, W. ePDF tools, a processing and analysis package of the atomic pair distribution function for electron diffraction. Comput. Phys. Commun. 2019, 238, 295–301. [Google Scholar] [CrossRef]
- Mitchell, D.R.G.; Petersen, T.C. RDFTools: A software tool for quantifying short-range ordering in amorphous materials. Microsc. Res. Tech. 2012, 75, 153–163. [Google Scholar] [CrossRef]
- McGreevy, R.L. Reverse Monte Carlo modelling. J. Phys. Condens. Mat. 2001, 13, R877–R913. [Google Scholar] [CrossRef]
- Borisenko, K.B.; Chen, Y.; Cockayne, D.J.H.; Song, S.A.; Jeong, H.S. Understanding atomic structures of amorphous C-doped Ge2Sb2Te5 phase-change memory materials. Acta Mater. 2011, 59, 4335–4342. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Für Krist.-Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Poulsen, H.F.; Neuefeind, J.; Neumann, H.B.; Schneider, J.R.; Zeidler, M.D. Amorphous silica studied by high energy X-ray diffraction. J. Non-Cryst. Solids 1995, 188, 63–74. [Google Scholar] [CrossRef]
- Anstis, G.R.; Liu, Z.; Lake, M. Investigation of amorphous materials by electron diffraction—The effects of multiple scattering. Ultramicroscopy 1988, 26, 65–69. [Google Scholar] [CrossRef]
- Hoque, M.M.; Vergara, S.; Das, P.P.; Ugarte, D.; Santiago, U.; Kumara, C.; Whetten, R.L.; Dass, A.; Ponce, A. Structural Analysis of Ligand-Protected Smaller Metallic Nanocrystals by Atomic Pair Distribution Function under Precession Electron Diffraction. J. Phys. Chem. C 2019, 123, 19894–19902. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).