Absolute Structure Determination of Chiral Zinc Tartrate MOFs by 3D Electron Diffraction
Abstract
:1. Introduction
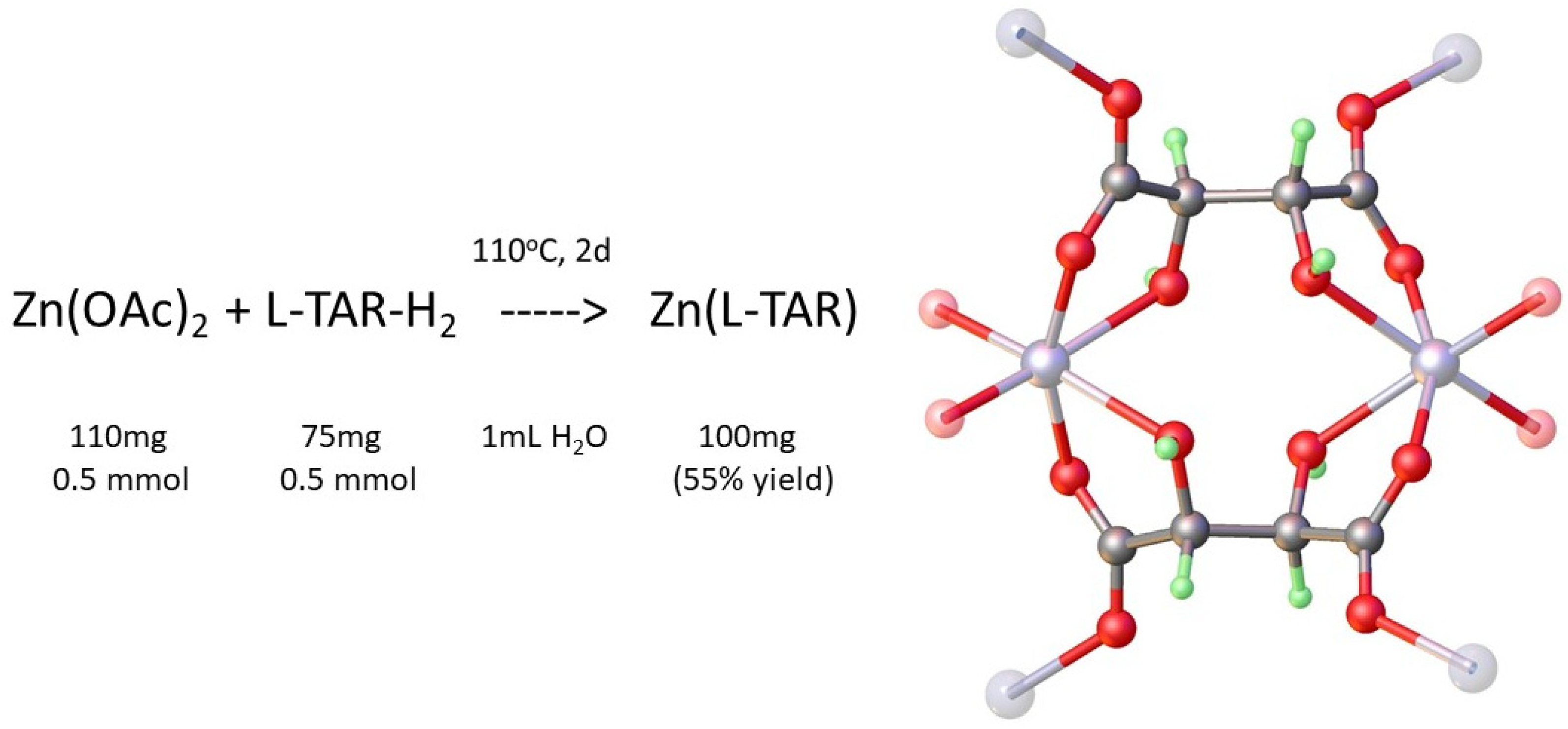
2. Materials and Methods
2.1. Preparation of Metal Tartrate Phases
2.2. X-ray Crystallography
2.3. Electron Crystallography
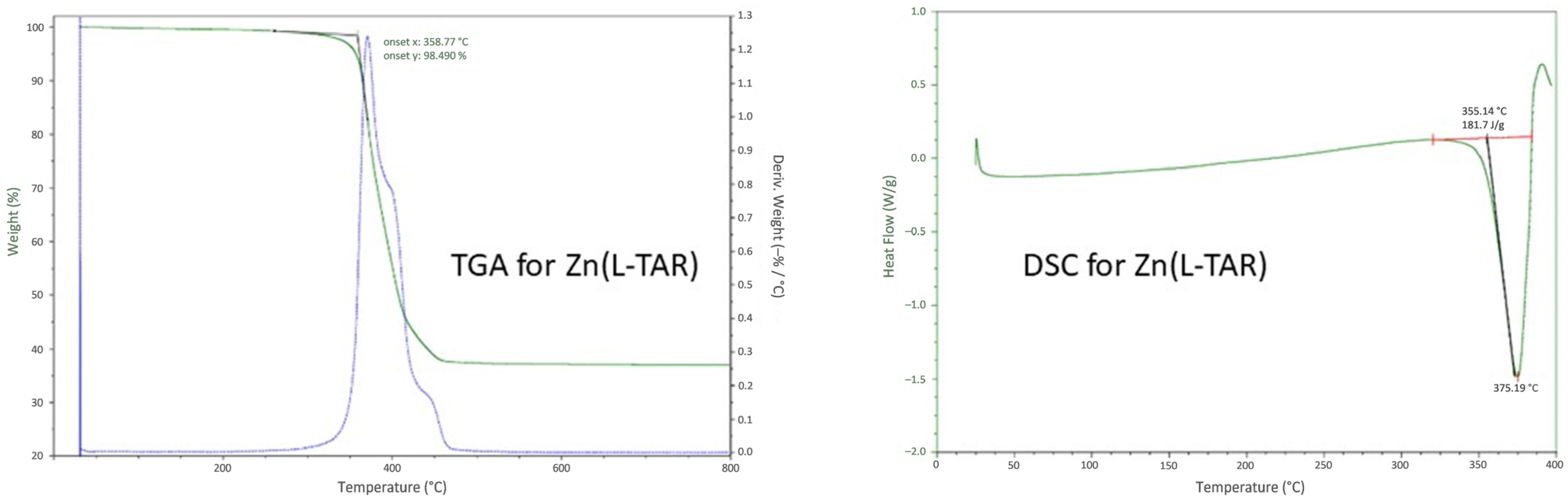
2.4. Differential Scanning Calorimetry/Thermal Gravimetric Analysis
3. Results
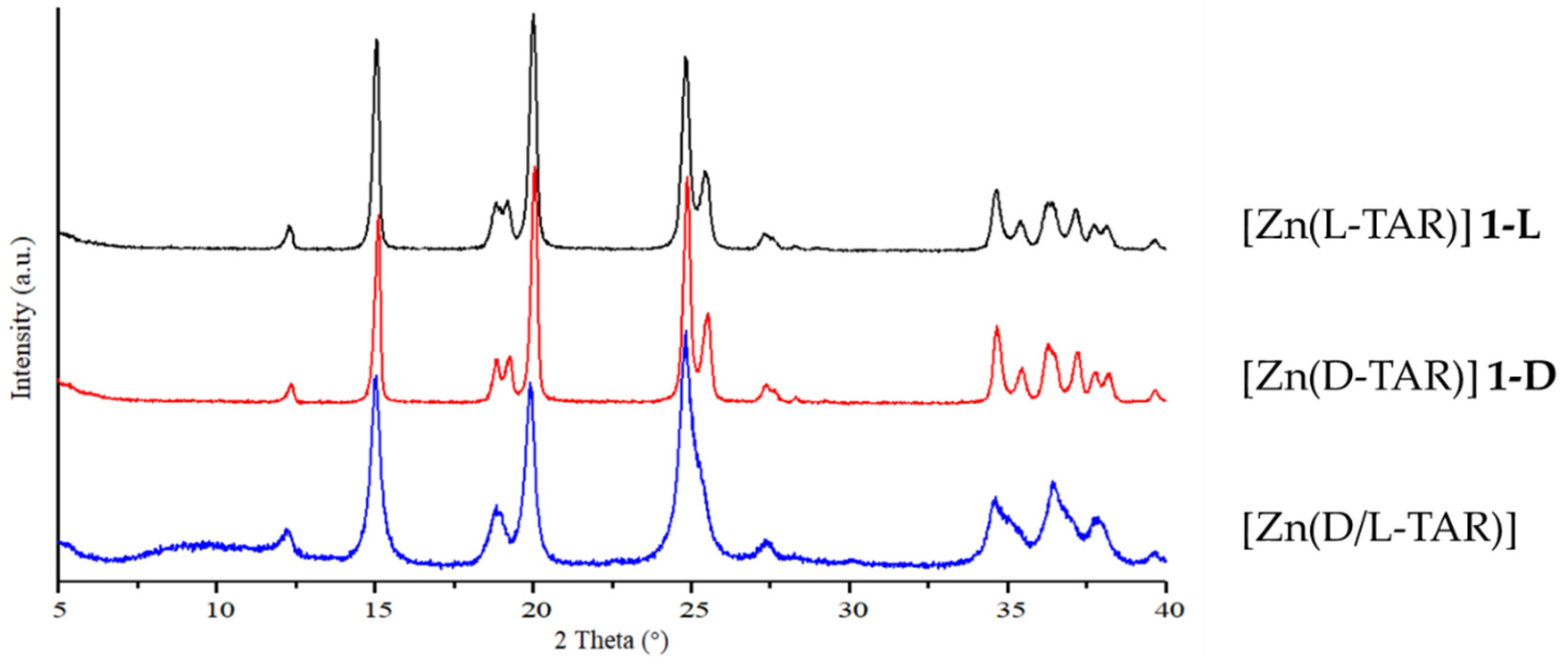
3.1. Hydrothermal Preparation of Zinc L-Tartrate and Related Phases
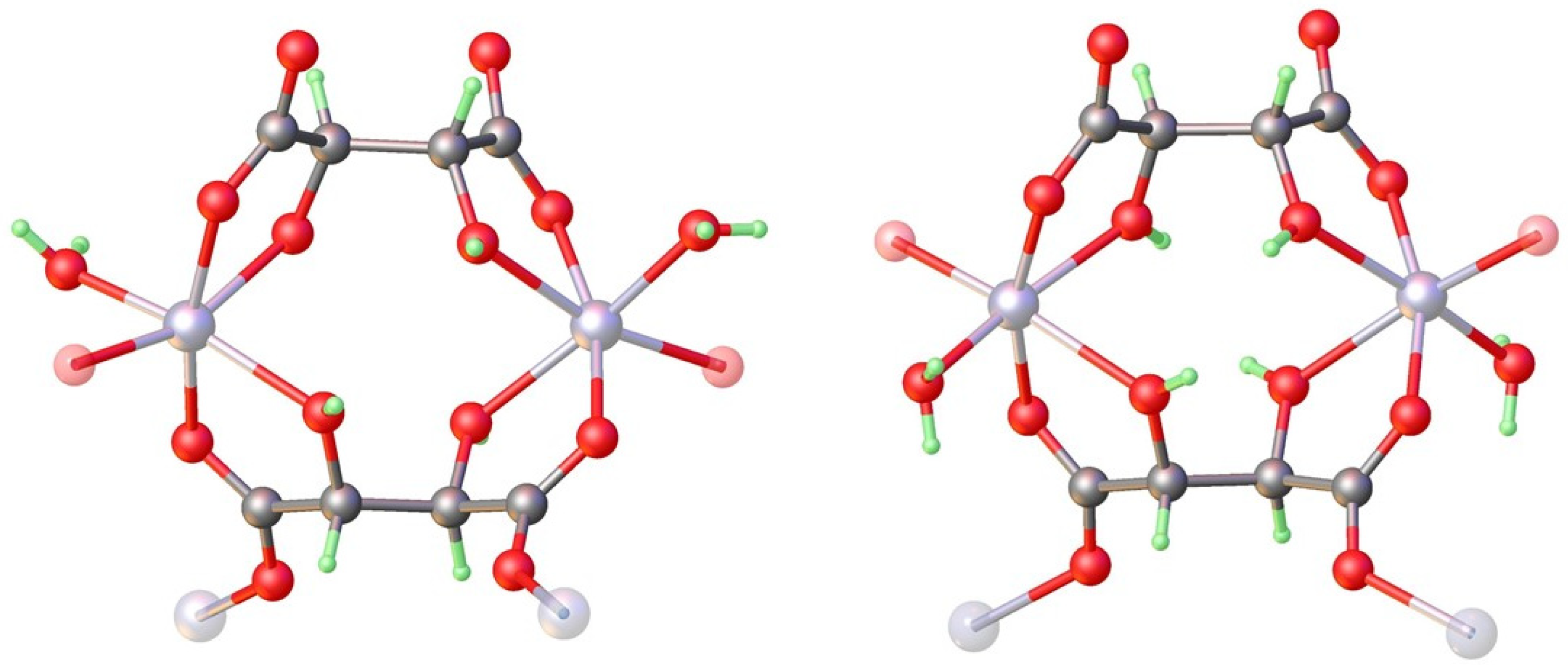
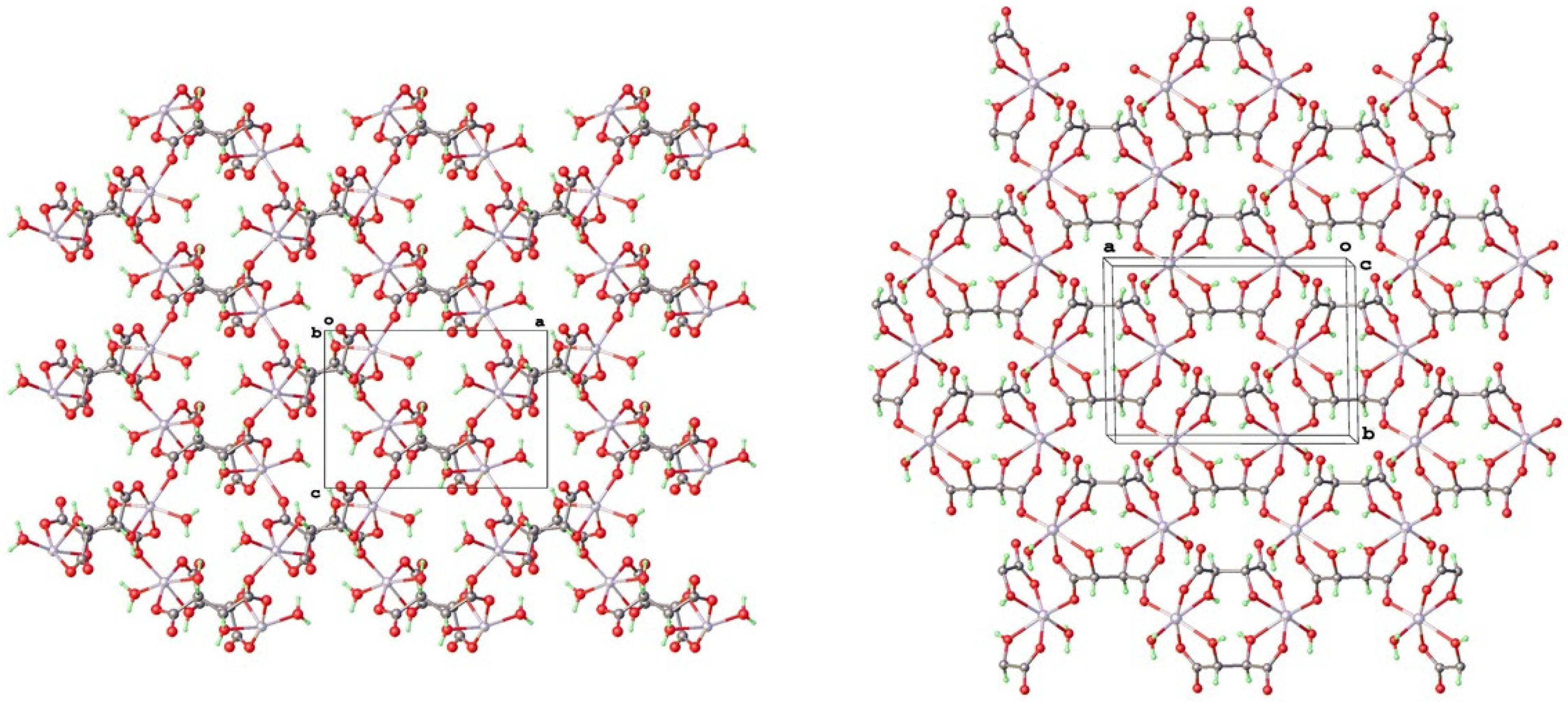
3.2. Structural Analysis of Zinc Tartrate by Electron Diffraction
3.3. Absolute Structure Determination of Zinc Tartrates by Dynamical Refinement
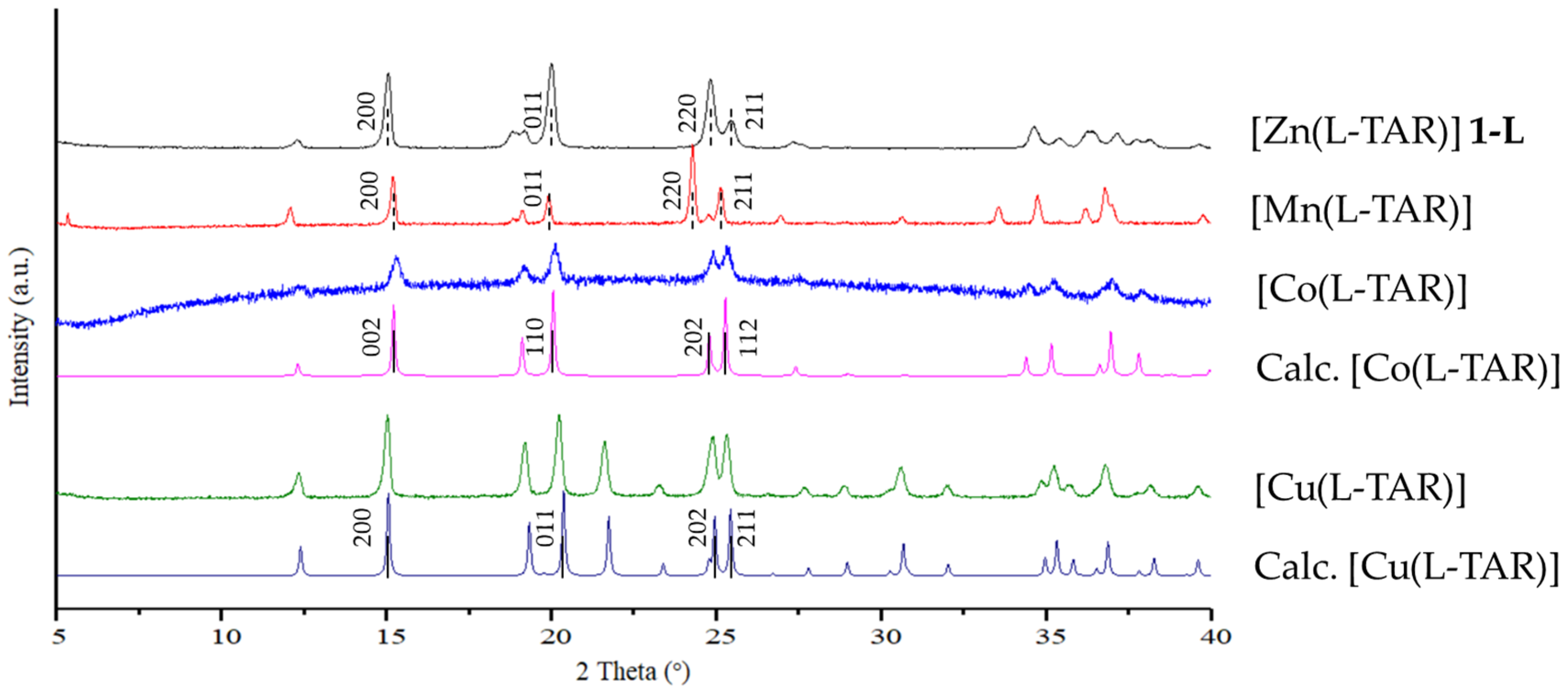
3.4. Preparation and Characterization of Related Metal Tartrate Phases
4. Discussion
4.1. Structure and Absolute Structure Determination
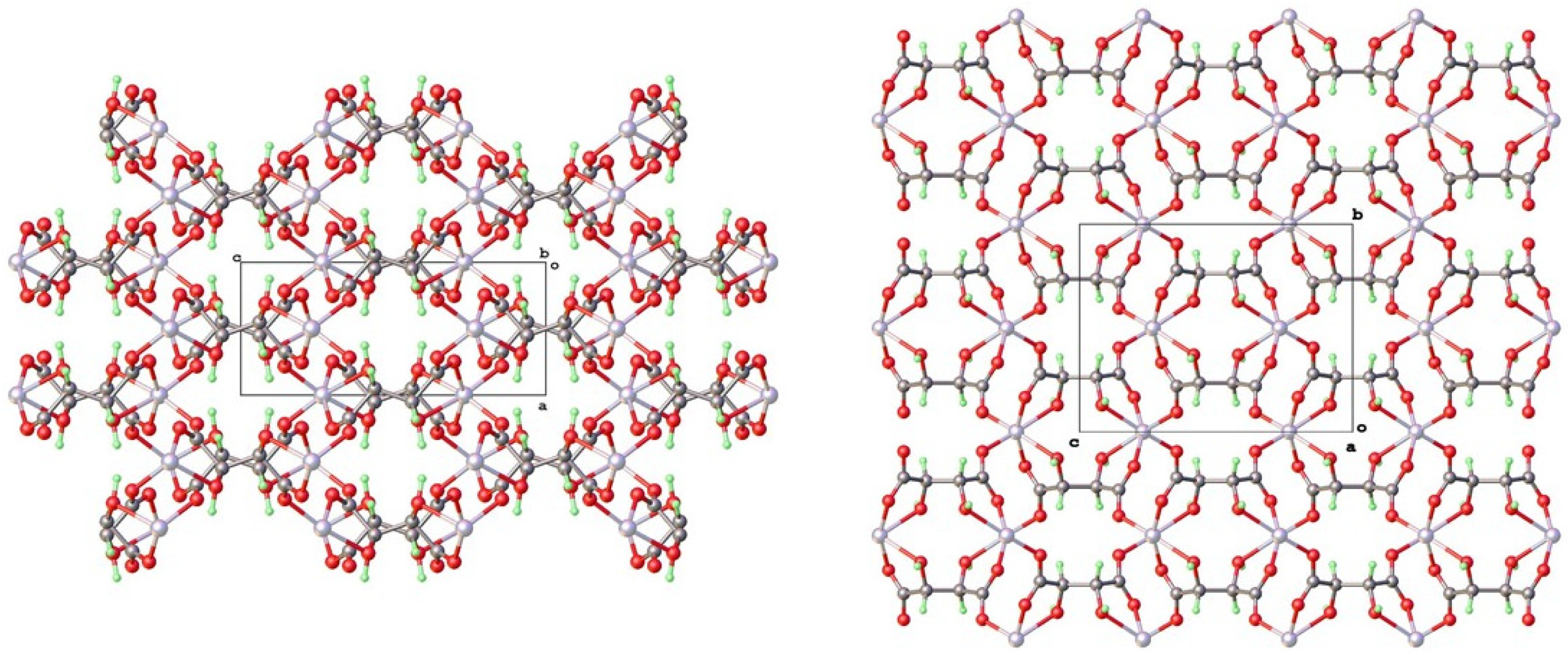
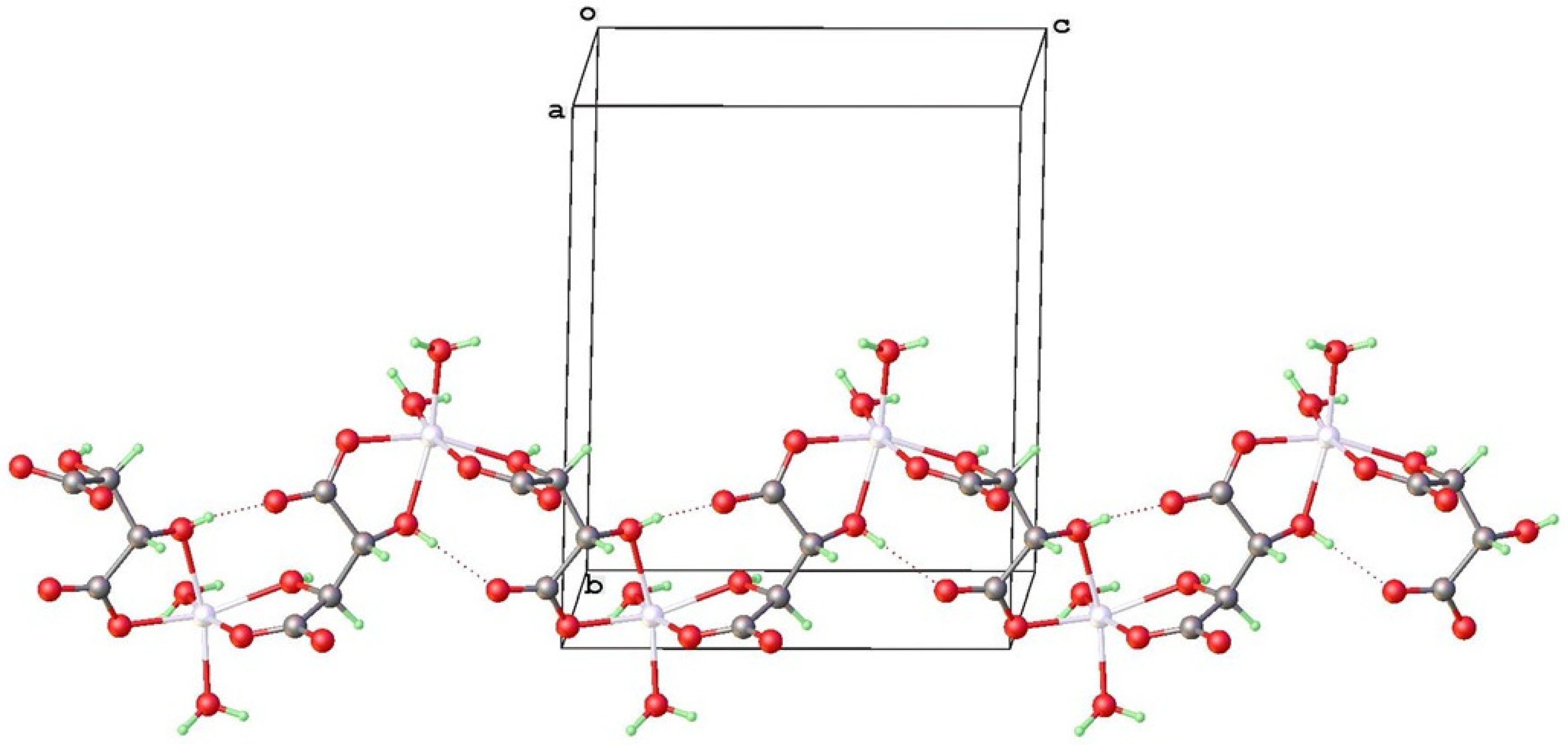
4.2. Topological Comparison of Zinc Tartrate Phases
4.3. Isostructurality with Other Bivalent Metal Tartrates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nannenga, B.L.; Gonen, T. The Cryo-EM Method Microcrystal Electron Diffraction (MicroED). Nat. Methods 2019, 16, 369–379. [Google Scholar] [CrossRef] [PubMed]
- Gruene, T.; Wennmacher, J.T.C.; Zaubitzer, C.; Holstein, J.J.; Heidler, J.; Fecteau-Lefebvre, A.; De Carlo, S.; Müller, E.; Goldie, K.N.; Regeni, I.; et al. Rapid Structure Determination of Microcrystalline Molecular Compounds Using Electron Diffraction. Angew. Chem. Int. Ed. 2018, 57, 16313–16317. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.G.; Martynowycz, M.W.; Hattne, J.; Fulton, T.J.; Stoltz, B.M.; Rodriguez, J.A.; Nelson, H.M.; Gonen, T. The CryoEM Method MicroED as a Powerful Tool for Small Molecule Structure Determination. ACS Cent. Sci. 2018, 4, 1587–1592. [Google Scholar] [CrossRef] [PubMed]
- Gruene, T.; Holstein, J.J.; Clever, G.H.; Keppler, B. Establishing Electron Diffraction in Chemical Crystallography. Nat. Rev. Chem. 2021, 5, 660–668. [Google Scholar] [CrossRef]
- Huang, Z.; Grape, E.S.; Li, J.; Inge, A.K.; Zou, X. 3D Electron Diffraction as an Important Technique for Structure Elucidation of Metal-Organic Frameworks and Covalent Organic Frameworks. Coord. Chem. Rev. 2021, 427, 213583. [Google Scholar] [CrossRef]
- Huang, Z.; Willhammar, T.; Zou, X. Three-Dimensional Electron Diffraction for Porous Crystalline Materials: Structural Determination and Beyond. Chem. Sci. 2021, 12, 1206–1219. [Google Scholar] [CrossRef]
- Samperisi, L.; Jaworski, A.; Kaur, G.; Lillerud, K.P.; Zou, X.; Huang, Z. Probing Molecular Motions in Metal–Organic Frameworks by Three-Dimensional Electron Diffraction. J. Am. Chem. Soc. 2021, 143, 17947–17952. [Google Scholar] [CrossRef]
- Hovestreydt, E. Electron Diffraction: Accelerating Drug Development. Drug Discov. Today 2022, 27, 371–373. [Google Scholar] [CrossRef]
- Au-Yeung, A.S.-F.; Sung, H.H.-Y.; Cha, J.A.K.; Siu, A.W.-H.; Chui, S.S.-Y.; Williams, I.D. Hydrothermal Synthesis of Indium Tartrates: Structures of the Chiral Polymer [In(L-TAR)3−H2O]·0.5H2O Containing the Tartrate Trianion, and a Microporous Hybrid Solid [In(OH)(D/L-TAR)2−]·2H2O. Inorg. Chem. Commun. 2006, 9, 507–511. [Google Scholar] [CrossRef]
- Thushari, S.; Cha, J.A.K.; Sung, H.H.-Y.; Chui, S.S.-Y.; Leung, A.L.-F.; Yen, Y.-F.; Williams, I.D. Microporous Chiral Metal Coordination Polymers: Hydrothermal Synthesis, Channel Engineering and Stability of Lanthanide Tartrates. Chem. Commun. 2005, 5515–5517. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, H.; Chan, J.Y.; Ou, R.; Zhu, H.; Forsyth, M.; Marijanovic, E.M.; Doherty, C.M.; Marriott, P.J.; Holl, M.M.B.; et al. Homochiral MOF–Polymer Mixed Matrix Membranes for Efficient Separation of Chiral Molecules. Angew. Chem. Int. Ed. 2019, 58, 16928–16935. [Google Scholar] [CrossRef]
- Yoon, M.; Srirambalaji, R.; Kim, K. Homochiral Metal–Organic Frameworks for Asymmetric Heterogeneous Catalysis. Chem. Rev. 2012, 112, 1196–1231. [Google Scholar] [CrossRef]
- Hu, L.; Li, K.; Shang, W.; Zhu, X.; Liu, M. Emerging Cubic Chirality in γCD-MOF for Fabricating Circularly Polarized Luminescent Crystalline Materials and the Size Effect. Angew. Chem. Int. Ed. 2020, 59, 4953–4958. [Google Scholar] [CrossRef] [PubMed]
- Templeton, L.K.; Templeton, D.H.; Zhang, D.; Zalkin, A. Structure of Di-μ-(+)-Tartrato-Bis[Aquazinc(II)] Trihydrate, [Zn2(C4H4O6)2(H2O)2]·3H2O and Anomalous Scattering by Zinc. Acta Crystallogr. Sect. C 1985, 41, 363–365. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Hu, H.-L.; Chen, B.-K.; Li, J. Synthesis and Characterization of a New Two-Dimensional Compound: {[Zn(C4H4O6)(H2O)]23H2O}n. Chin. J. Spectrosc. Lab. 2009, 26, 803–806. [Google Scholar]
- Liu, H.-T.; Lu, J.; Wang, D.-Q. Poly[[Diaqua(μ4-L-Tartrato)(μ2-L-Tartrato)Dizinc(II)] Tetrahydrate]. Acta Crystallogr. Sect. E 2010, 66, m374. [Google Scholar] [CrossRef]
- Li, M.-C.; Zhang, J.-R.; Yuan, S.-X.; Zhang, D. Crystal Structure of Catena-Poly[Diaqua-(μ2-Tartrato-κ4O,O′:O′′,O′′′)Zinc(II)], C4H8O8Zn. Z. Kristallogr.-N. Cryst. Struct. 2020, 235, 1221–1222. [Google Scholar] [CrossRef]
- Hynek, J.; Brázda, P.; Rohlíček, J.; Londesborough, M.G.S.; Demel, J. Phosphinic Acid Based Linkers: Building Blocks in Metal–Organic Framework Chemistry. Angew. Chem. Int. Ed. 2018, 57, 5016–5019. [Google Scholar] [CrossRef]
- Portolés-Gil, N.; Lanza, A.; Aliaga-Alcalde, N.; Ayllón, J.A.; Gemmi, M.; Mugnaioli, E.; López-Periago, A.M.; Domingo, C. Crystalline Curcumin BioMOF Obtained by Precipitation in Supercritical CO2 and Structural Determination by Electron Diffraction Tomography. ACS Sustain. Chem. Eng. 2018, 6, 12309–12319. [Google Scholar] [CrossRef]
- Brázda, P.; Palatinus, L.; Babor, M. Electron Diffraction Determines Molecular Absolute Configuration in a Pharmaceutical Nanocrystal. Science 2019, 364, 667–669. [Google Scholar] [CrossRef]
- Klar, P.; Krysiak, Y.; Xu, H.; Steciuk, G.; Cho, J.; Zou, X.; Palatinus, L. Chirality and Accurate Structure Models by Exploiting Dynamical Effects in Continuous-Rotation 3D ED Data. ChemRxiv 2021. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.a.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- ELDIX Software Suite, Version 0.14.0; ELDICO Scientific AG: Villigen, Switzerland, 2022.
- Apex Suite of Crystallographic Software, APEX4, Version 2022.1-1; Bruker AXS Inc.: Madison, WI, USA, 2022.
- SAINT, Version 8.40B; Bruker AXS Inc.: Madison, WI, USA, 2019.
- SADABS, Version 2016/2; Bruker AXS Inc.: Madison, WI, USA, 2016.
- Sheldrick, G.M. A Short History of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal Structure Refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Hübschle, C.B.; Sheldrick, G.M.; Dittrich, B. ShelXle: A Qt Graphical User Interface for SHELXL. J. Appl. Cryst. 2011, 44, 1281–1284. [Google Scholar] [CrossRef]
- Doyle, P.A.; Turner, P.S. Relativistic Hartree–Fock X-Ray and Electron Scattering Factors. Acta Crystallogr. Sect. A 1968, 24, 390–397. [Google Scholar] [CrossRef]
- Palatinus, L.; Brázda, P.; Jelínek, M.; Hrdá, J.; Steciuk, G.; Klementová, M. Specifics of the Data Processing of Precession Electron Diffraction Tomography Data and Their Implementation in the Program PETS2.0. Acta Crystallogr. Sect. B 2019, 75, 512–522. [Google Scholar] [CrossRef]
- Petříček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr.-Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Coronado, E.; Galán-Mascarós, J.R.; Gómez-García, C.J.; Murcia-Martínez, A. Chiral Molecular Magnets: Synthesis, Structure, and Magnetic Behavior of the Series [M(L-Tart)] (M = MnII, FeII, CoII, NiII.; L-Tart = (2R,3R)-(+)-Tartrate). Chem.–Eur. J. 2006, 12, 3484–3492. [Google Scholar] [CrossRef]
- Kam, K.C.; Young, K.L.M.; Cheetham, A.K. Chemical and Structural Diversity in Chiral Magnesium Tartrates and Their Racemic and Meso Analogues. Cryst. Growth Des. 2007, 7, 1522–1532. [Google Scholar] [CrossRef]
- Zhu, P.; Gu, W.; Zhang, L.-Z.; Liu, X.; Tian, J.-L.; Yan, S.-P. A Rare Thermally Induced Single Crystal to Single Crystal Transformation from a 2D Chiral Coordination Polymer to a 3D Chiral Coordination Polymer. Eur. J. Inorg. Chem. 2008, 2008, 2971–2974. [Google Scholar] [CrossRef]
- Liu, Y.-H.; Lee, S.-H.; Chiang, J.-C.; Chen, P.-C.; Chien, P.-H.; Yang, C.-I. Dehydration Induced 2D-to-3D Crystal-to-Crystal Network Re-Assembly and Ferromagnetism Tuning within Two Chiral Copper(II)–Tartrate Coordination Polymers. Dalton Trans. 2013, 42, 16857–16867. [Google Scholar] [CrossRef] [PubMed]
- Boultif, A.; Louer, D. Powder Pattern Indexing with the Dichotomy Method. J. Appl. Cryst. 2004, 37, 724–731. [Google Scholar] [CrossRef]
- Appelhans, L.N.; Kosa, M.; Radha, A.V.; Simoncic, P.; Navrotsky, A.; Parrinello, M.; Cheetham, A.K. Phase Selection and Energetics in Chiral Alkaline Earth Tartrates and Their Racemic and Meso Analogues: Synthetic, Structural, Computational, and Calorimetric Studies. J. Am. Chem. Soc. 2009, 131, 15375–15386. [Google Scholar] [CrossRef] [PubMed]


| [Zn(L-TAR)] | [Zn(D-TAR)] | |
|---|---|---|
| angular range [°] | −60 to +80 | −65 to +25 |
| rotation per frame [°] | 1.0 | 1.0 |
| exposure time [s] | 1.0 | 1.0 |
| total exposure [s] | 140 | 90 |
| frames collected | 140 | 90 |
| frames used | 1–80 | 1–70 |
| crystal size [µm] | 2.5 × 0.6 × 0.5 | 5.0 × 0.5 × 0.4 |
| 1-L | 1-D | |||
|---|---|---|---|---|
| kin | dyn | kin | dyn | |
| CCDC number | 2,242,890 | 2,242,892 | 2,242,891 | 2,242,894 |
| chemical formula | C4H4O6Zn | |||
| formula weight [g mol−1] | 213.46 | |||
| crystal system | orthorhombic | |||
| a [Å] | 5.14(6) | 5.16(6) | ||
| b [Å] | 8.97(10) | 9.00(10) | ||
| c [Å] | 11.82(13) | 11.78(13) | ||
| α, β, γ [°] | 90, 90, 90 | 90, 90, 90 | ||
| volume [Å3] | 545(11) | 547(11) | ||
| space group | I222 | |||
| Z | 4 | |||
| resolution [Å] | 0.79 | 0.68 | 0.79 | 0.74 |
| completeness [%] | 65 | 71 | 70 | 85 |
| Unique reflections (measured/observed) | 355/292 | 808/509 | 359/341 | 674/616 |
| parameters | 28 | 65 | 28 | 60 |
| restraints | 1 | 1 | 1 | 1 |
| Rint | 11.4 | - | 4.6 | - |
| R1(obs)/MR1(obs) 1 | 16.7 | 11.8/11.6 | 17.2 | 14.2/14.4 |
| wR2(all) | 42.6 | 22.6 | 43.7 | 27.2 |
| ΔVmin, ΔVmax | −0.29, 0.35 | −0.16, 0.20 | −0.32, 0.41 | −0.22, 0.49 |
| 1-L | 1-D | |||
|---|---|---|---|---|
| kin | dyn | kin | dyn | |
| Zn-O1 | 2.02(3) | 2.02(2) | 2.02(3) | 2.04(2) |
| Zn-O2 * | 2.00(4) | 2.03(2) | 2.06(3) | 2.00(2) |
| Zn-O3 | 2.29(4) | 2.33(2) | 2.36(4) | 2.288(19) |
| C1-O1 | 1.24(3) | 1.273(17) | 1.24(4) | 1.189(19) |
| C1-O2 | 1.29(3) | 1.260(15) | 1.21(3) | 1.27(2) |
| C1-C2 | 1.51(3) | 1.51(3) | 1.59(4) | 1.56(3) |
| C2-O3 | 1.37(3) | 1.423(18) | 1.31(4) | 1.44(2) |
| C2-C2 * | 1.55(4) | 1.54(3) | 1.52(5) | 1.55(2) |
| O1-Zn1-O3 | 74.9(10) | 75.8(7) | 74.4(11) | 74.5(7) |
| Zn1-O1-C1 | 120.5(15) | 118.6(9) | 121.3(18) | 118.9(10) |
| Zn1-O3-C2 | 110.8(16) | 110.1(9) | 109(2) | 112.8(8) |
| Zn1 *-O2-C1 | 130.4(18) | 128.3(14) | 125.2(19) | 128.5(12) |
| Sample | 1-L | 1-D | ||
|---|---|---|---|---|
| enantiomorph | L-form | D-form | L-form | D-form |
| R1(obs)/MR1(obs) | 11.8/11.6 | 14.5/15.0 | 16.1/16.3 | 14.2/14.4 |
| wR2(all) | 22.6 | 28.4 | 30.5 | 27.2 |
| z-score 1 | 4.288σ | 3.502σ | ||
| probability 1 | 99.999% | 99.977% | ||
| Mg(D-TAR) | Co(L-TAR) | Ni(L-TAR) | Cu(L-TAR) | |
|---|---|---|---|---|
| reference | [34] | [33] | [35] | [36] |
| CCDC number | 631943 | 230223 | 650895 | 927769 |
| empirical formula | C4H4O6Mg | C4H4O6Co | C4H4O6Ni | C4H4O6Cu |
| formula weight | 172.38 | 207 | 207.78 | 211.61 |
| temperature [K] | 293 | 120(2) | 113(2) | 200(2) |
| crystal system | orthorhombic | orthorhombic | orthorhombic | orthorhombic |
| space group | I222 | I222 | I222 | P21212 |
| a [Å] | 5.024(1) | 5.057(2) | 4.9740(11) | 4.9808(5) |
| b [Å] | 9.163(2) | 9.117(3) | 9.055(2) | 8.9689(11) |
| c [Å] | 11.455(2) | 11.631(3) | 11.472(2) | 11.7511(13) |
| α [°] | 90 | 90 | 90 | 90 |
| β [°] | 90 | 90 | 90 | 90 |
| γ [°] | 90 | 90 | 90 | 90 |
| volume [Å3] | 527.2(2) | 536.2(3) | 516.68(19) | 524.95(10) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jandl, C.; Steinfeld, G.; Li, K.; Pang, P.K.C.; Choi, C.L.; Wang, C.; Simoncic, P.; Williams, I.D. Absolute Structure Determination of Chiral Zinc Tartrate MOFs by 3D Electron Diffraction. Symmetry 2023, 15, 983. https://doi.org/10.3390/sym15050983
Jandl C, Steinfeld G, Li K, Pang PKC, Choi CL, Wang C, Simoncic P, Williams ID. Absolute Structure Determination of Chiral Zinc Tartrate MOFs by 3D Electron Diffraction. Symmetry. 2023; 15(5):983. https://doi.org/10.3390/sym15050983
Chicago/Turabian StyleJandl, Christian, Gunther Steinfeld, Keyao Li, Pokka Ka Chuen Pang, Chun Lung Choi, Cengan Wang, Petra Simoncic, and Ian D. Williams. 2023. "Absolute Structure Determination of Chiral Zinc Tartrate MOFs by 3D Electron Diffraction" Symmetry 15, no. 5: 983. https://doi.org/10.3390/sym15050983
APA StyleJandl, C., Steinfeld, G., Li, K., Pang, P. K. C., Choi, C. L., Wang, C., Simoncic, P., & Williams, I. D. (2023). Absolute Structure Determination of Chiral Zinc Tartrate MOFs by 3D Electron Diffraction. Symmetry, 15(5), 983. https://doi.org/10.3390/sym15050983









