Influence of Box Height on Inter-Limb Asymmetry and Box Jump Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Subjects
2.3. Procedures
3. Statistical Analyses
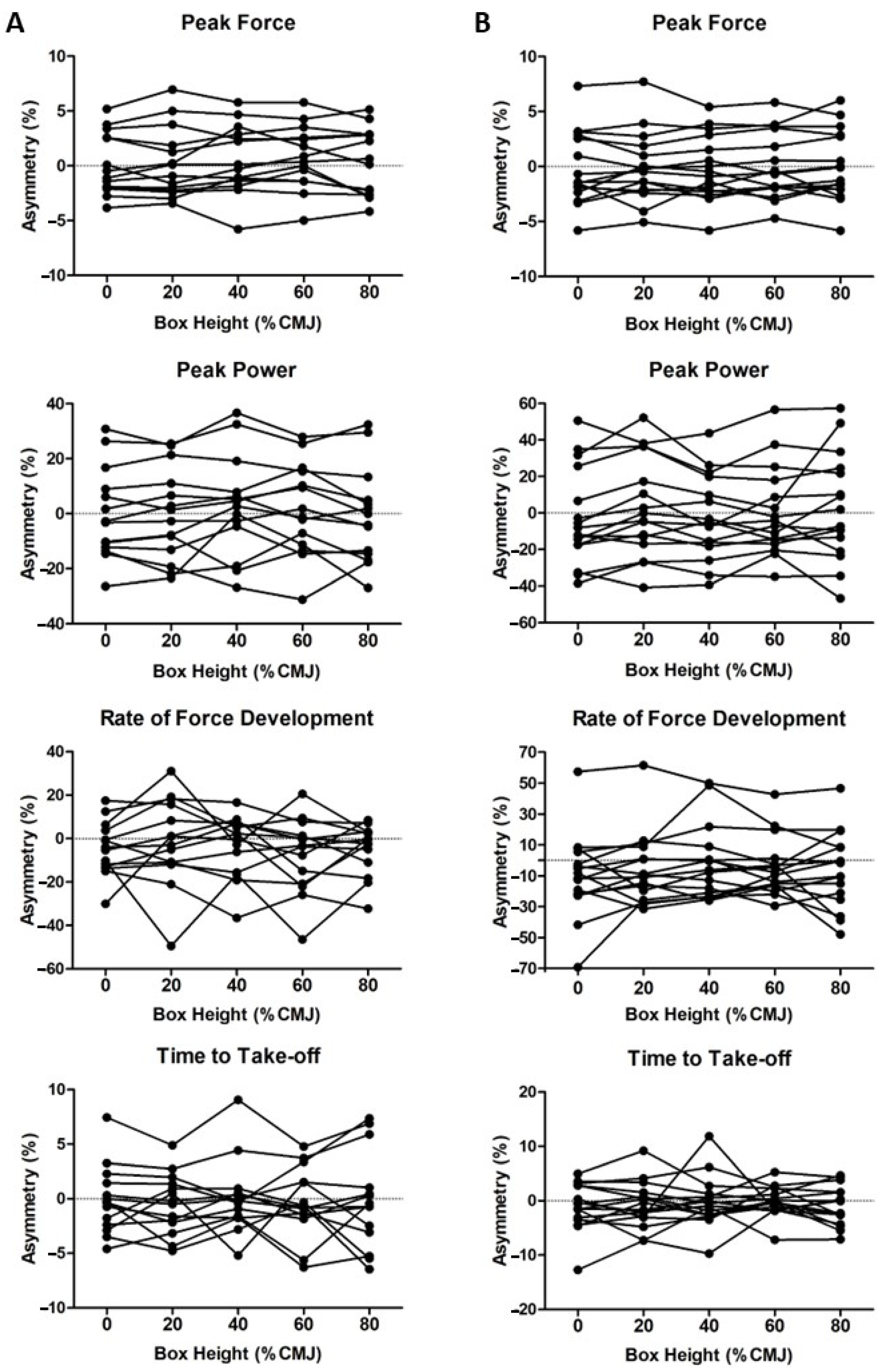
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bishop, C.; Read, P.; Chavda, S.; Turner, A. Asymmetries of the lower limb: The calculation conundrum in strength training and conditioning. Strength Cond. J. 2016, 38, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.; Turner, A.; Read, P. Effects of inter-limb asymmetries on physical and sports performance: A systematic review. J. Sport. Sci. 2018, 36, 1135–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bell, D.R.; Sanfilippo, J.L.; Binkley, N.; Heiderscheit, B.C. Lean mass asymmetry influences force and power asymmetry during jumping in collegiate athletes. J. Strength Cond. Res. 2014, 28, 884–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bishop, C.; Brashill, C.; Abbott, W.; Read, P.; Lake, J.; Turner, A. Jumping asymmetries are associated with speed, change of direction speed, and jump performance in elite academy soccer players. J. Strength Cond. Res. 2021, 35, 1841–1847. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Read, P.; McCubbine, J.; Turner, A. Vertical and horizontal asymmetries are related to slower sprinting and jump performance in elite youth female soccer players. J. Strength Cond. Res. 2021, 35, 56–63. [Google Scholar] [CrossRef] [Green Version]
- Madruga-Parera, M.; Bishop, C.; Read, P.; Lake, J.; Brazier, J.; Romero-Rodriguez, D. Jumping-based asymmetries are negatively associated with jump, change of direction, and repeated sprint performance, but not linear speed, in adolescent handball athletes. J. Hum. Kinet. 2020, 71, 47–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maloney, S.J.; Richards, J.; Nixon, D.G.; Harvey, L.J.; Fletcher, I.M. Do stiffness and asymmetries predict change of direction performance? J. Sport. Sci. 2017, 35, 547–556. [Google Scholar] [CrossRef] [Green Version]
- Lockie, R.G.; Callaghan, S.J.; Berry, S.P.; Cooke, E.R.; Jordan, C.A.; Luczo, T.M.; Jeffriess, M.D. Relationship between unilateral jumping ability and asymmetry on multidirectional speed in team-sport athletes. J. Strength Cond. Res. 2014, 28, 3557–3566. [Google Scholar] [CrossRef] [Green Version]
- Hart, N.H.; Nimphius, S.; Weber, J.; Spiteri, T.; Rantalainen, T.; Dobbin, M.; Newton, R. Musculoskeletal asymmetry in football athletes: A product of limb function over time. Med. Sci. Sport. Exerc. 2016, 48, 1379–1387. [Google Scholar] [CrossRef]
- Bazyler, C.; Bailey, C.; Chiang, C.; Sato, K.; Stone, M. The effects of strength training on isometric force production symmetry in recreationally trained males. J. Trainol. 2014, 3, 6–10. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.; Lake, J.; Loturco, I.; Papadopoulos, K.; Turner, A.; Read, P. Interlimb asymmetries: The need for an individual approach to data analysis. J. Strength Cond. Res. 2021, 35, 695–701. [Google Scholar] [CrossRef] [PubMed]
- Sands, W.A.; Wurth, J.J.; Hewit, J.K. Basics of Strength and Conditioning Manual; National Strength and Conditioning Association: Colorado Springs, CO, USA, 2012. [Google Scholar]
- Koefoed, N.; Dam, S.; Kersting, U.G. Effect of box height on box jump performance in elite female handball players. J. Strength Cond. Res. 2022, 36, 508–512. [Google Scholar] [CrossRef] [PubMed]
- Virgile, A.; Bishop, C. A narrative review of limb dominance: Task specificity and the importance of fitness testing. J. Strength Cond. Res. 2021, 35, 846–858. [Google Scholar] [CrossRef]
- Cormack, S.J.; Newton, R.U.; McGuigan, M.R.; Doyle, T.L. Reliability of measures obtained during single and repeated countermovement jumps. Int. J. Sport. Physiol. Perform. 2008, 3, 131–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- World Medical Association. World Medical Association Declaration of Helsinki: Ethical principles for medical research involving human subjects. JAMA 2013, 310, 2191–2194. [Google Scholar] [CrossRef] [Green Version]
- McMahon, J.; Suchomel, T.; Lake, J.; Comfort, P. Understanding the key phases of the countermovement jump force-time curve. Strength Cond. J. 2018, 40, 96–106. [Google Scholar] [CrossRef] [Green Version]
- Chavda, S.; Bromley, T.; Jarvis, P.; Williams, S.; Bishop, C.; Turner, A.; Lake, J.P.; Mundy, P.D. Force-time characteristics of the countermovement jump: Analyzing the curve in excel. Strength Cond. J. 2018, 40, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Kibele, A. Possibilities and limitations in the biomechanical analysis of countermovement Jumps: A methodological study. J. Appl. Biomech. 1998, 14, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Mizuguchi, S.; Sands, W.A.; Wassinger, C.A.; Lamont, H.S.; Stone, M.H. A new approach to determining net impulse and identification of its characteristics in countermovement jumping: Reliability and validity. Sport. Biomech. 2015, 14, 258–272. [Google Scholar] [CrossRef]
- Suchomel, T.J.; Bailey, C.A.; Sole, C.J.; Grazer, J.L.; Beckham, G.K. Using reactive strength index-modified as an explosive performance measurement tool in Division I athletes. J. Strength Cond. Res. 2015, 29, 899–904. [Google Scholar] [CrossRef] [Green Version]
- Owen, N.J.; Watkins, J.; Kilduff, L.P.; Bevan, H.R.; Bennett, M.A. Development of a criterion method to determine peak mechanical power output in a countermovement jump. J. Strength Cond. Res. 2014, 28, 1552–1558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McMahon, J.; Rej, S.J.E.; Comfort, P. Sex differences in countermovement jump phase characteristics. Sports 2017, 5, 8. [Google Scholar] [CrossRef] [Green Version]
- Hopkins, W.G. Measures of reliability in sports medicine and science. Sport. Med. 2000, 30, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koo, T.K.; Li, M.Y. A guideline of selecting and reporting intraclass correlation coefficients for reliability research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banyard, H.G.; Nosaka, K.; Haff, G.G. Reliability and validity of the load-velocity relationship to predict the 1RM back squat. J. Strength Cond. Res. 2017, 31, 1897–1904. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kubo, J.; Matsubayashi, T.; Matsuo, A.; Kobayashi, K.; Ishii, N. Relationship between bilateral differences in single-leg jumps and asymmetry in isokinetic knee strength. J. Appl. Biomech. 2013, 29, 61–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bishop, C.; Read, P.; Lake, J.; Chavda, S.; Turner, A. Interlimb asymmetries: Understanding how to calculate differences from bilateral and unilateral tests. Strength Cond. J. 2018, 40, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Viera, A.J.; Garrett, J.M. Understanding interobserver agreement: The kappa statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar]
- Perez-Castilla, A.; Garcia-Ramos, A.; Janicijevic, D.; Miras-Moreno, S.; De la Cruz, J.C.; Rojas, F.J.; Cepero, M. Unilateral or bilateral standing broad jumps: Which jump type provides inter-limb asymmetries with a higher reliability? J. Sport. Sci. Med. 2021, 20, 317–327. [Google Scholar] [CrossRef]
- Janicijevic, D.; Sarabon, N.; Perez-Castilla, A.; Smajla, D.; Fernandez-Revelles, A.; Garcia-Ramos, A. Single-leg mechanical performance and inter-leg asymmetries during bilateral countermovement jumps: A comparison of different calculation methods. Gait Posture 2022, 96, 47–52. [Google Scholar] [CrossRef]
- Bradshaw, E.J.; Maulder, P.S.; Keogh, J.W. Biological movement variability during the sprint start: Performance enhancement or hindrance? Sport. Biomech. 2007, 6, 246–260. [Google Scholar] [CrossRef] [PubMed]
- Moir, G.L.; Garcia, A.; Dwyer, G.B. Intersession reliability of kinematic and kinetic variables during vertical jumps in men and women. Int. J. Sport. Physiol. Perform. 2009, 4, 317–330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLellan, C.P.; Lovell, D.I.; Gass, G.C. The role of rate of force development on vertical jump performance. J. Strength Cond. Res. 2011, 25, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.L.; Cronin, J.; Gill, N.D.; Chapman, D.W.; Sheppard, J. Sources of variability in iso-inertial jump assessments. Int. J. Sport. Physiol. Perform. 2010, 5, 546–558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marques, M.C.; Izquierdo, M.; Marinho, D.A.; Barbosa, T.M.; Ferraz, R.; Gonzalez-Badillo, J.J. Association between force-time curve characteristics and vertical jump performance in trained athletes. J. Strength Cond. Res. 2015, 29, 2045–2049. [Google Scholar] [CrossRef]
- Merrigan, J.J.; Stone, J.D.; Hornsby, W.G.; Hagen, J.A. Identifying reliable and relatable force-time metrics in athletes-considerations for the isometric mid-thigh pull and countermovement jump. Sports 2020, 9, 4. [Google Scholar] [CrossRef]
| Variables | Males (n = 14) | Females (n = 16) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NDL | DL | NDL | DL | ||||||||||||
| % of CMJ | ICC (95% CI) | %CV | SEM | ICC (95% IC) | %CV | SEM | % of CMJ | ICC (95% CI) | %CV | SEM | ICC (95% IC) | %CV | SEM | ||
| Peak force (N) | 0% | 0.99 (0.98–0.99) | 2.22 | 19.5 | 0.99 (0.98–0.99) | 2.04 | 19.2 | 0% | 0.98 (0.96–0.99) | 2.46 | 17.6 | 0.98 (0.95–0.99) | 2.72 | 16.3 | |
| 20% | 0.99 (0.96–0.99) | 2.57 | 18.1 | 0.99 (0.97–0.99) | 2.28 | 18.1 | 20% | 0.98 (0.96–0.99) | 2.48 | 17.9 | 0.97 (0.94–0.99) | 2.22 | 18.2 | ||
| 40% | 0.98 (0.96–0.99) | 2.58 | 25.2 | 0.99 (0.97–0.99) | 2.54 | 18.3 | 40% | 0.97 (0.93–0.99) | 3.29 | 20.0 | 0.98 (0.95–0.99) | 2.57 | 14.3 | ||
| 60% | 0.98 (0.96–0.99) | 2.54 | 23.3 | 0.99 (0.96–0.99) | 2.37 | 16.8 | 60% | 0.99 (0.98–0.99) | 1.69 | 12.6 | 0.96 (0.92–0.99) | 2.79 | 21.3 | ||
| 80% | 0.98 (0.96–0.99) | 2.37 | 24.0 | 0.99 (0.98–0.99) | 1.88 | 17.6 | 80% | 0.98 (0.96–0.99) | 2.54 | 17.2 | 0.98 (0.95–0.99) | 2.47 | 16.1 | ||
| Peak power (W) | 0% | 0.95 (0.88–0.98) | 7.30 | 175.5 | 0.97 (0.92–0.99) | 6.15 | 128.5 | 0% | 0.96 (0.91–0.99) | 6.09 | 92.1 | 0.95 (0.86–0.98) | 10.03 | 111.5 | |
| 20% | 0.95 (0.88–0.98) | 8.41 | 168.2 | 0.93 (0.82–0.97) | 8.14 | 180.1 | 20% | 0.95 (0.88–0.98) | 9.18 | 106.8 | 0.95 (0.87–0.98) | 9.60 | 107.1 | ||
| 40% | 0.95 (0.88–0.98) | 7.76 | 168.2 | 0.96 (0.89–0.98) | 6.89 | 148.1 | 40% | 0.87 (0.69–0.95) | 10.09 | 150.1 | 0.92 (0.81–0.97) | 9.22 | 124.9 | ||
| 60% | 0.97 (0.93–0.99) | 6.29 | 122.6 | 0.96 (0.91–0.99) | 5.86 | 130.6 | 60% | 0.93 (0.83–0.97) | 9.01 | 114.3 | 0.91 (0.80–0.97) | 11.70 | 147.7 | ||
| 80% | 0.96 (0.89–0.98) | 7.19 | 141.5 | 0.97 (0.92–0.99) | 5.94 | 123.7 | 80% | 0.93 (0.83–0.97) | 10.55 | 126.9 | 0.92 (0.83–0.97) | 10.00 | 153.5 | ||
| RFD (N·s–1) | 0% | 0.97 (0.92–0.99) | 12.76 | 244.2 | 0.93 (0.82–0.98) | 14.89 | 323.5 | 0% | 0.79 (0.52–0.92) | 13.76 | 432.1 | 0.77 (0.47–0.91) | 12.48 | 271.8 | |
| 20% | 0.93 (0.83–0.98) | 10.99 | 251.7 | 0.90 (0.76–0.97) | 14.77 | 304.5 | 20% | 0.76 (0.44–0.91) | 14.65 | 530.9 | 0.85 (0.60–0.95) | 14.98 | 175.4 | ||
| 40% | 0.87 (0.69–0.96) | 11.95 | 313.9 | 0.85 (0.63–0.95) | 12.75 | 380.8 | 40% | 0.92 (0.82–0.97) | 13.26 | 263.1 | 0.87 (0.63–0.96) | 16.52 | 142.6 | ||
| 60% | 0.93 (0.82–0.98) | 12.33 | 279.7 | 0.91 (0.78–0.97) | 10.80 | 343.1 | 60% | 0.93 (0.84–0.97) | 16.43 | 258.5 | 0.89 (0.74–0.96) | 14.47 | 214.3 | ||
| 80% | 0.90 (0.77–0.97) | 11.55 | 290.0 | 0.94 (0.86–0.98) | 11.28 | 256.4 | 80% | 0.91 (0.76–0.97) | 15.11 | 284.6 | 0.75 (0.43–0.90) | 15.03 | 341.7 | ||
| TToff (s) | 0% | 0.90 (0.77–0.97) | 4.39 | 0.03 | 0.83 (0.60–0.94) | 6.44 | 0.05 | 0% | 0.89 (0.75–0.96) | 6.86 | 0.05 | 0.92 (0.82–0.97) | 6.89 | 0.05 | |
| 20% | 0.92 (0.81–0.97) | 4.79 | 0.03 | 0.94 (0.85–0.98) | 4.05 | 0.03 | 20% | 0.89 (0.74–0.96) | 6.29 | 0.05 | 0.85 (0.64–0.94) | 6.69 | 0.07 | ||
| 40% | 0.91 (0.79–0.97) | 4.03 | 0.03 | 0.91 (0.79–0.97) | 4.44 | 0.04 | 40% | 0.77 (0.45–0.92) | 6.56 | 0.05 | 0.88 (0.73–0.95) | 5.55 | 0.04 | ||
| 60% | 0.88 (0.70–0.96) | 4.83 | 0.05 | 0.94 (0.84–0.98) | 5.35 | 0.04 | 60% | 0.94 (0.86–0.98) | 4.93 | 0.03 | 0.91 (0.79–0.97) | 6.39 | 0.05 | ||
| 80% | 0.92 (0.81–0.97) | 4.27 | 0.03 | 0.95 (0.87–0.98) | 3.84 | 0.03 | 80% | 0.89 (0.75–0.96) | 6.43 | 0.05 | 0.84 (0.64–0.94) | 8.85 | 0.07 | ||
| Variable | Males (n = 14) | Females (n = 16) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| % of CMJ | NDL | DL | IA (%) | % of CMJ | NDL | DL | IA (%) | ||
| PF (N) | 0% | 1055.9 ± 195.3 | 1057.1 ± 192.3 | 0.15 ± 2.81 | 0% | 747.3 ± 124.2 | 729.6 ± 115.2 | −0.37 ± 3.44 | |
| 20% | 1033.0 ± 181.4 | 1039.7 ± 181.4 | 0.26 ± 3.16 | 20% | 742.2 ± 126.3 | 724.7 ± 104.8 | −0.20 ± 3.34 | ||
| 40% | 1063.9 ± 178.1 | 1074.4 ± 182.5 | 0.59 ± 3.14 | 40% | 739.8 ± 115.6 | 728.5 ± 100.9 | −0.22 ± 3.02 | ||
| 60% | 1059.9 ± 164.9 | 1067.6 ± 167.8 | 0.78 ± 2.87 | 60% | 755.6 ± 125.6 | 743.2 ± 106.6 | −0.26 ± 3.17 | ||
| 80% | 1053.9 ± 169.6 | 1061.1 ± 175.8 | 0.31 ± 3.08 | 80% | 766.9 ± 121.8 | 760.9 ± 113.5 * | 0.08 ± 3.30 | ||
| PP (W) | 0% | 2553.8 ± 784.8 | 2653.9 ± 742.0 | −0.18 ± 16.7 | 0% | 1532.5 ± 460.5 | 1419.5 ± 498.6 | −2.02 ± 27.9 | |
| 20% | 2520.1 ± 752.3 | 2576.4 ± 680.6 | −0.19 ± 16.7 | 20% | 1465.5 ± 477.6 | 1440.5 ± 478.8 | 2.28 ± 29.7 | ||
| 40% | 2529.2 ± 752.3 | 2667.9 ± 740.5 | 2.93 ± 18.3 | 40% | 1517.8 ± 416.2 | 1405.6 ± 441.7 | −3.62 ± 25.5 | ||
| 60% | 2444.0 ± 708.1 | 2646.8 ± 653.1 | 1.86 ± 16.7 | 60% | 1533.3 ± 431.9 | 1466.3 ± 492.4 | 0.14 ± 26.5 | ||
| 80% | 2527.3 ± 707.4 | 2574.2 ± 714.2 | −0.90 ± 17.3 | 80% | 1548.4 ± 479.6 | 1509.1 ± 542.7 | 1.59 ± 31.0 | ||
| RFD (N·s−1) | 0% | 2333.4 ± 1409.9 | 2215.5 ± 1222.6 | −4.60 ± 12.4 | 0% | 1840.2 ± 943.0 | 1314.1 ± 566.7 | −8.70 ± 27.2 | |
| 20% | 2088.8 ± 951.3 | 2082.6 ± 962.9 | −1.28 ± 20.1 | 20% | 1849.6 ± 1083.7 | 1261.4 ± 453.0 | −5.21 ± 24.2 | ||
| 40% | 2108.1 ± 870.6 | 2028.2 ± 983.1 | −3.46 ± 14.1 | 40% | 1629.2 ± 930.2 | 1255.0 ± 395.4 | −1.96 ± 24.2 | ||
| 60% | 2310.8 ± 1057.2 | 2139.6 ± 1143.5 | −7.57 ± 17.2 | 60% | 1737.1 ± 977.1 | 1452.2 ± 646.2 | −2.32 ± 19.7 | ||
| 80% | 2388.9 ± 917.2 | 2191.2 ± 1046.6 | −4.88 ± 11.6 | 80% | 2072.8 ± 948.7 | 1535.2 ± 683.3 | −9.02 ± 24.5 | ||
| TToff (s) | 0% | 0.93 ± 0.11 | 0.94 ± 0.13 | −0.12 ± 3.09 | 0% | 0.86 ± 0.15 | 0.85 ± 0.16 | −0.85 ± 4.63 | |
| 20% | 0.93 ± 0.12 | 0.94 ± 0.13 | −0.45 ± 2.76 | 20% | 0.88 ± 0.16 | 0.87 ± 0.17 | −0.27 ± 4.31 | ||
| 40% | 0.89 ± 0.10 | 0.91 ± 0.12 | 0.06 ± 3.37 | 40% | 0.88 ± 0.11 | 0.90 ± 0.11 | 0.07 ± 5.10 | ||
| 60% | 0.91 ± 0.13 | 0.92 ± 0.15 | −0.31 ± 3.18 | 60% | 0.86 ± 0.13 | 0.86 ± 0.15 | −0.34 ± 4.07 | ||
| 80% | 0.90 ± 0.11 | 0.92 ± 0.13 | −0.19 ± 4.41 | 80% | 0.88 ± 0.15 | 0.88 ± 0.18 | −0.29 ± 3.78 | ||
| 0% CMJ | 20% CMJ | 40% CMJ | 60% CMJ | 80% CMJ | ||
|---|---|---|---|---|---|---|
| Peak Force | 0% CMJ | 1 | 0.73 | 0.87 | 1 | 0.87 |
| 20% CMJ | 0.57 | 1 | 0.61 | 0.73 | 0.61 | |
| 40% CMJ | 0.57 | 1 | 1 | 0.87 | 0.75 | |
| 60% CMJ | 0.72 | 0.86 | 0.86 | 1 | 0.87 | |
| 80% CMJ | 0.72 | 0.86 | 0.86 | 1 | 1 | |
| Peak Power | 0% CMJ | 1 | 0.87 | 1 | 0.87 | 0.75 |
| 20% CMJ | 0.86 | 1 | 0.87 | 1 | 0.88 | |
| 40% CMJ | 0.72 | 0.86 | 1 | 0.87 | 0.75 | |
| 60% CMJ | 0.86 | 0.71 | 0.57 | 1 | 0.88 | |
| 80% CMJ | 0.71 | 0.86 | 0.72 | 0.57 | 1 | |
| RFD | 0% CMJ | 1 | 0.59 | 0.59 | 0.59 | 0.85 |
| 20% CMJ | 0.57 | 1 | 1 | 0.47 | 0.43 | |
| 40% CMJ | 0.29 | 0.43 | 1 | 0.47 | 0.43 | |
| 60% CMJ | 0.51 | 0.43 | 0.43 | 1 | 0.43 | |
| 80% CMJ | 0.51 | 0.43 | 0.14 | 0.38 | 1 | |
| TToff | 0% CMJ | 1 | 0.63 | 0.24 | 0.75 | 0.24 |
| 20% CMJ | 0.55 | 1 | 0.38 | 0.63 | 0.13 | |
| 40% CMJ | 0.38 | 0.26 | 1 | 0.51 | 0.49 | |
| 60% CMJ | 0.38 | 0.55 | 0.10 | 1 | 0.51 | |
| 80% CMJ | 0.55 | 0.71 | 0.10 | 0.55 | 1 |
| Variable | Males (n = 14) | Females (n = 16) | |||||
|---|---|---|---|---|---|---|---|
| ICC | p | ηp2 | ICC | p | ηp2 | ||
| Peak force (N) | 0.98 (0.96–0.99) | 0.33 | 0.08 | 0.99 (0.97–0.99) | 0.60 | 0.04 | |
| Peak power (W) | 0.98 (0.96–0.99) | 0.28 | 0.09 | 0.98 (0.96–0.99) | 0.25 | 0.09 | |
| RFD (N·s−1) | 0.86 (0.70–0.95) | 0.60 | 0.05 | 0.94 (0.88–0.98) | 0.29 | 0.08 | |
| TToff (s) | 0.91 (0.80–0.97) | 0.97 | 0.01 | 0.83 (0.65–0.93) | 0.95 | 0.01 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos, M.L.; Berton, R.; Shields, J.; Bishop, C.; Dinyer-McNeely, T.; Anderson, O.; Dawes, J. Influence of Box Height on Inter-Limb Asymmetry and Box Jump Performance. Symmetry 2023, 15, 1359. https://doi.org/10.3390/sym15071359
dos Santos ML, Berton R, Shields J, Bishop C, Dinyer-McNeely T, Anderson O, Dawes J. Influence of Box Height on Inter-Limb Asymmetry and Box Jump Performance. Symmetry. 2023; 15(7):1359. https://doi.org/10.3390/sym15071359
Chicago/Turabian Styledos Santos, Marcel Lopes, Ricardo Berton, JoCarol Shields, Chris Bishop, Taylor Dinyer-McNeely, Olivia Anderson, and Jay Dawes. 2023. "Influence of Box Height on Inter-Limb Asymmetry and Box Jump Performance" Symmetry 15, no. 7: 1359. https://doi.org/10.3390/sym15071359
APA Styledos Santos, M. L., Berton, R., Shields, J., Bishop, C., Dinyer-McNeely, T., Anderson, O., & Dawes, J. (2023). Influence of Box Height on Inter-Limb Asymmetry and Box Jump Performance. Symmetry, 15(7), 1359. https://doi.org/10.3390/sym15071359








