Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci
Abstract
:1. Introduction
2. The Tariffs and Characteristics of the Triangular Fibonacci Symmetrical Functions
3. Materials and Methods
4. The Fibonacci Riccati Method
- When , (13) has its own solution ,
- When , (13) possesses the given solution ,
- When , (13) has its own solutions
- When , (13) possesses its own solutions
- When and , (13) has its own solution
- When and , (13) has the solution .
- When and , (13) has the solutions .
- When , (13) possesses its own solution .
- When and , (13) possesses a solution
- When and , (13) has its own solution .
5. Separation Variable Solutions of the Burgers Model in (3+1)-Dimension
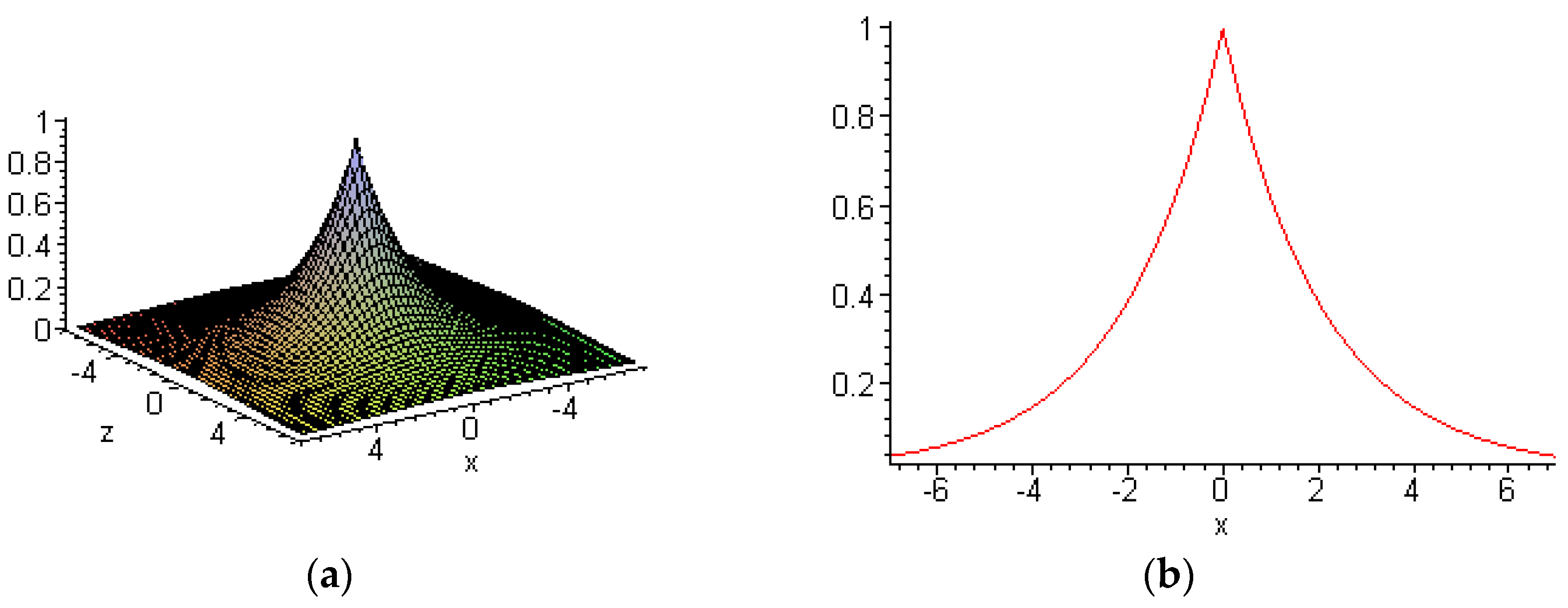
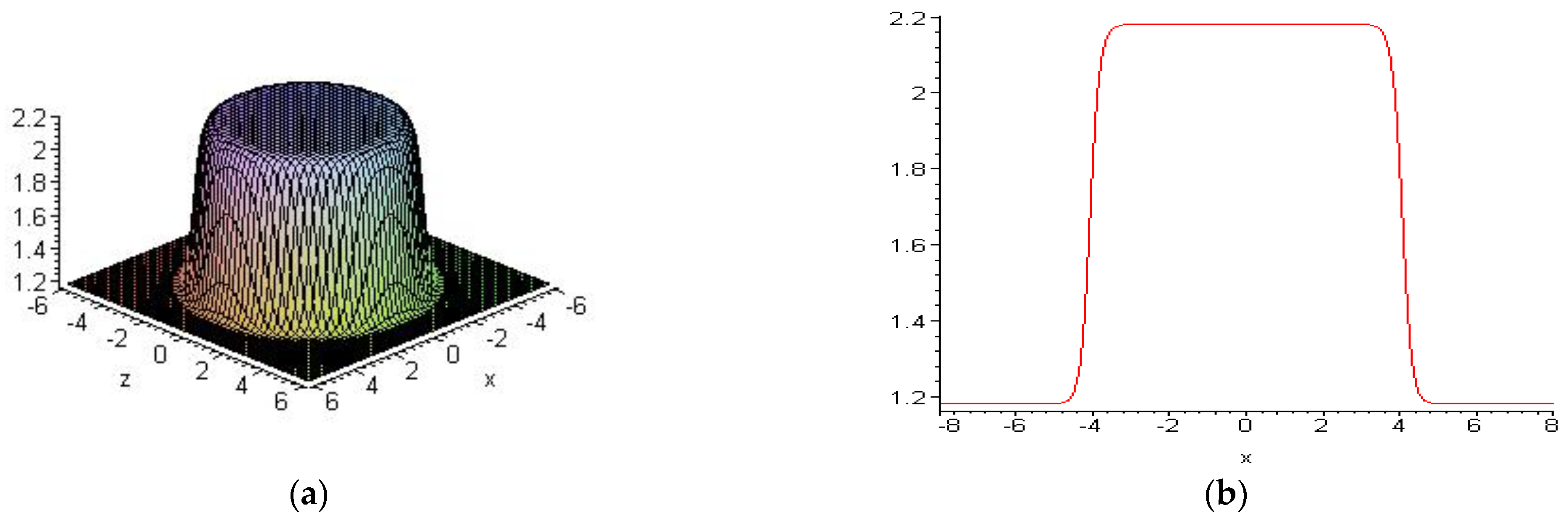
6. Novel Localized Excitements of the Burgers System in (3+1)-Dimension
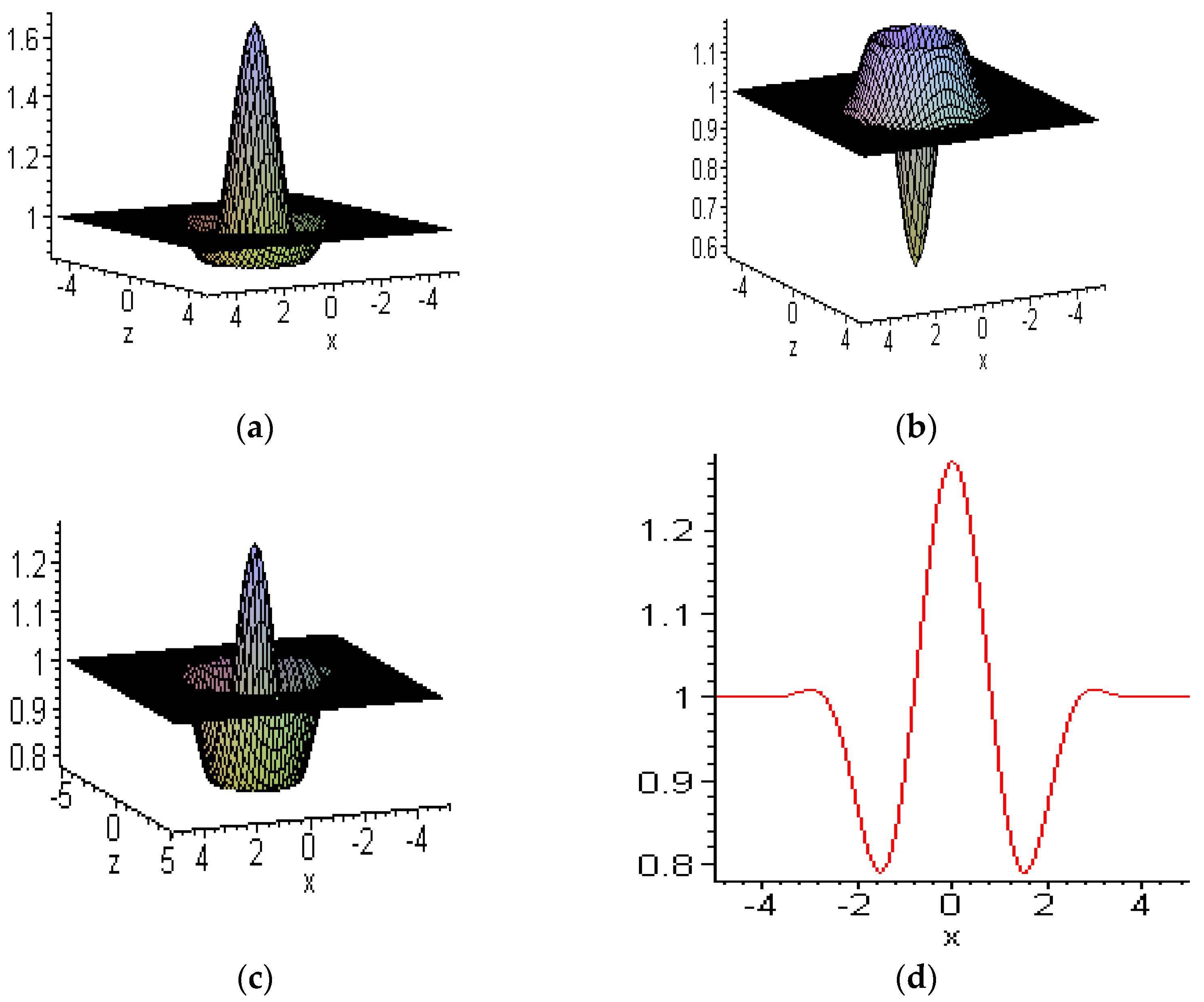
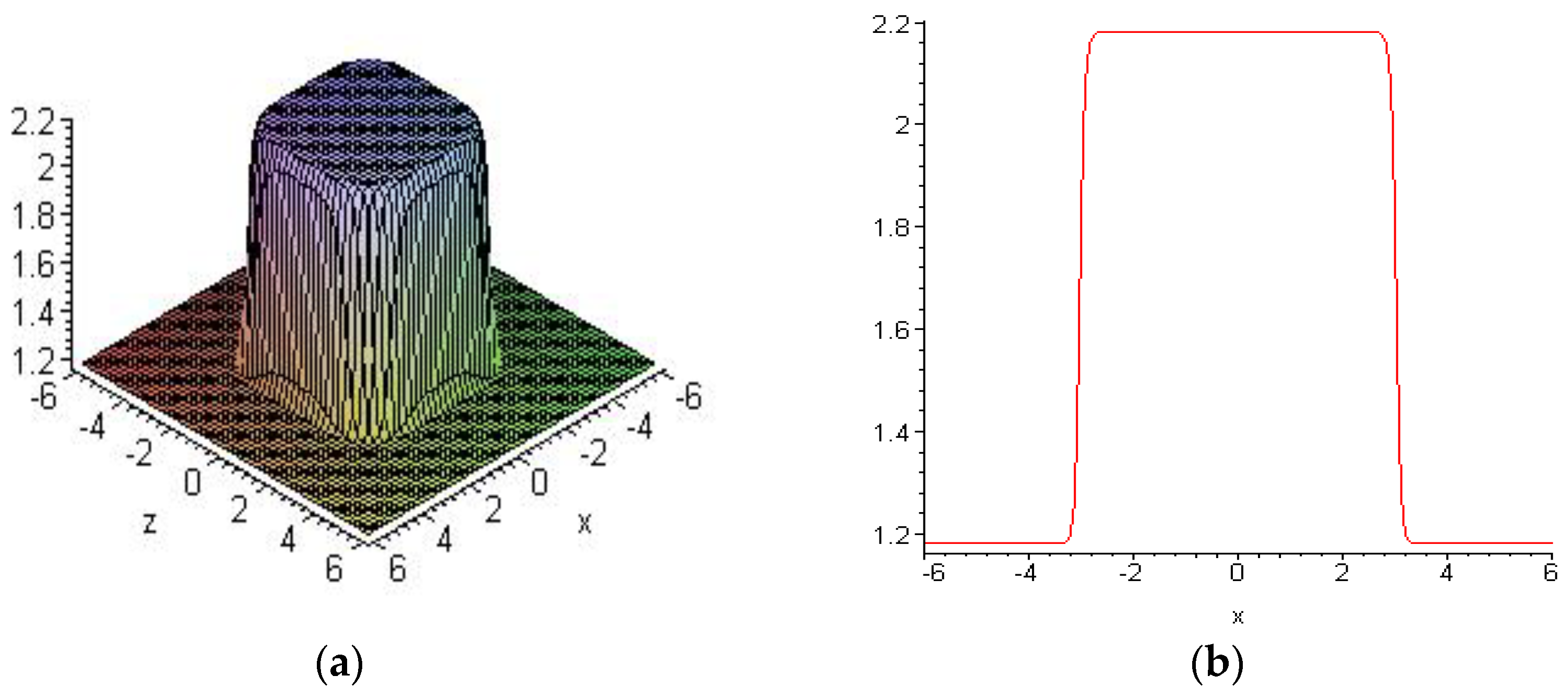
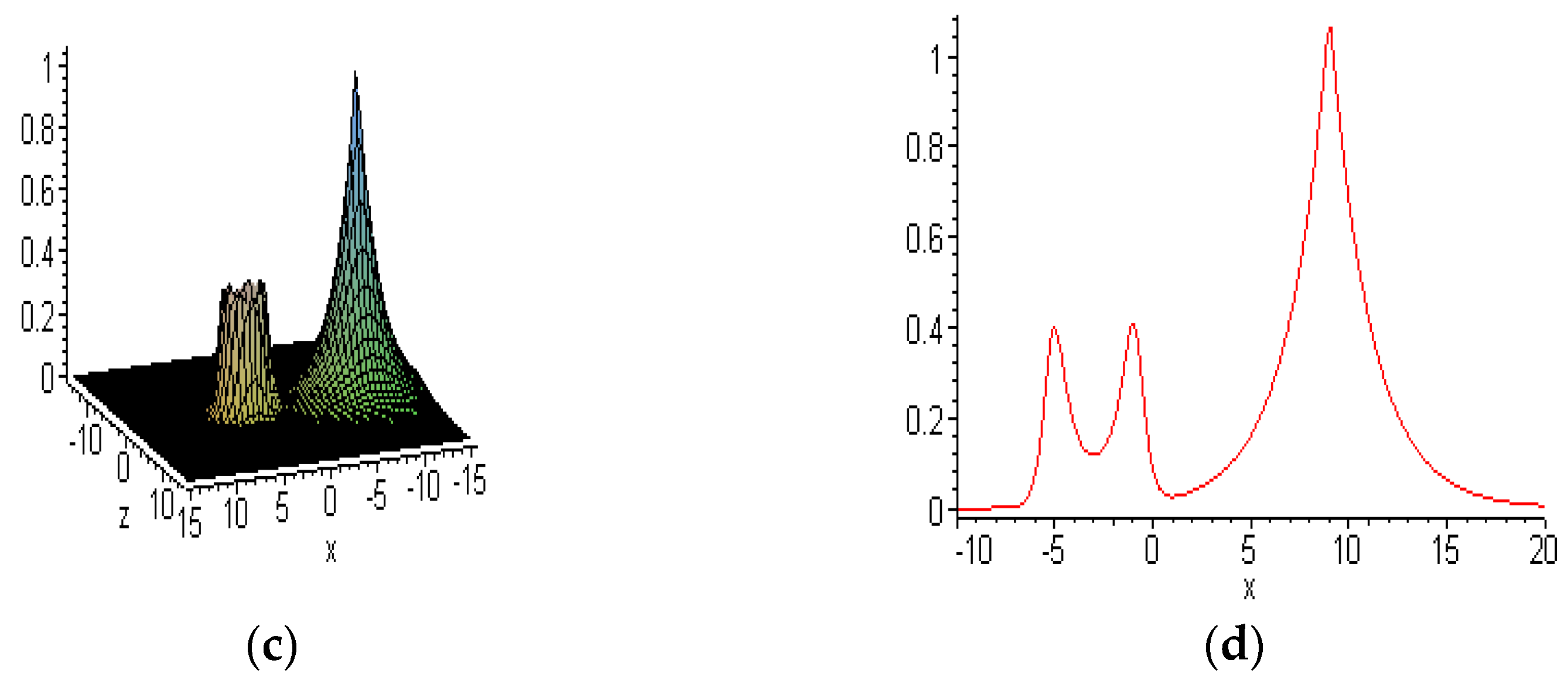
6.1. Embed-Solitons
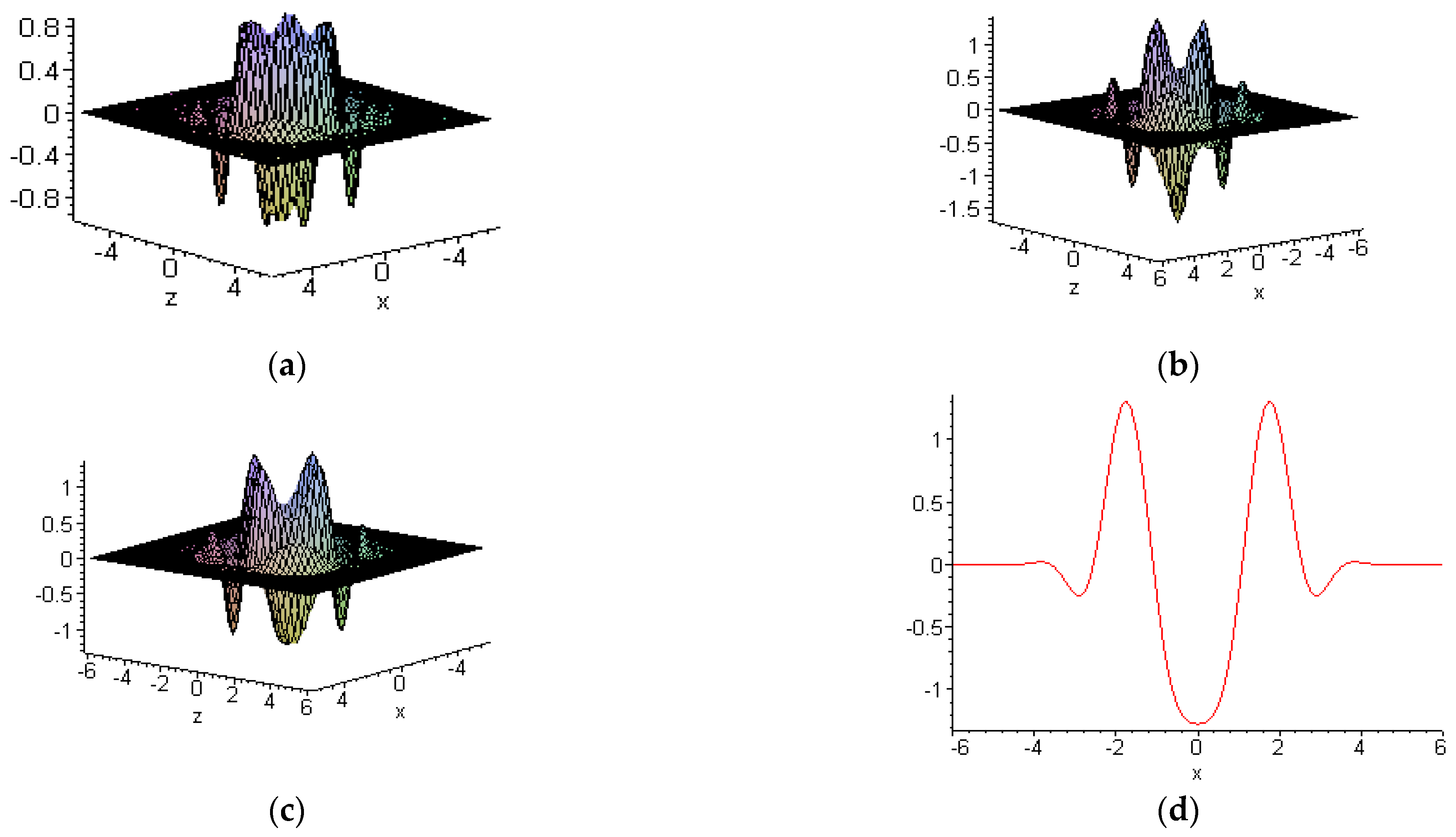
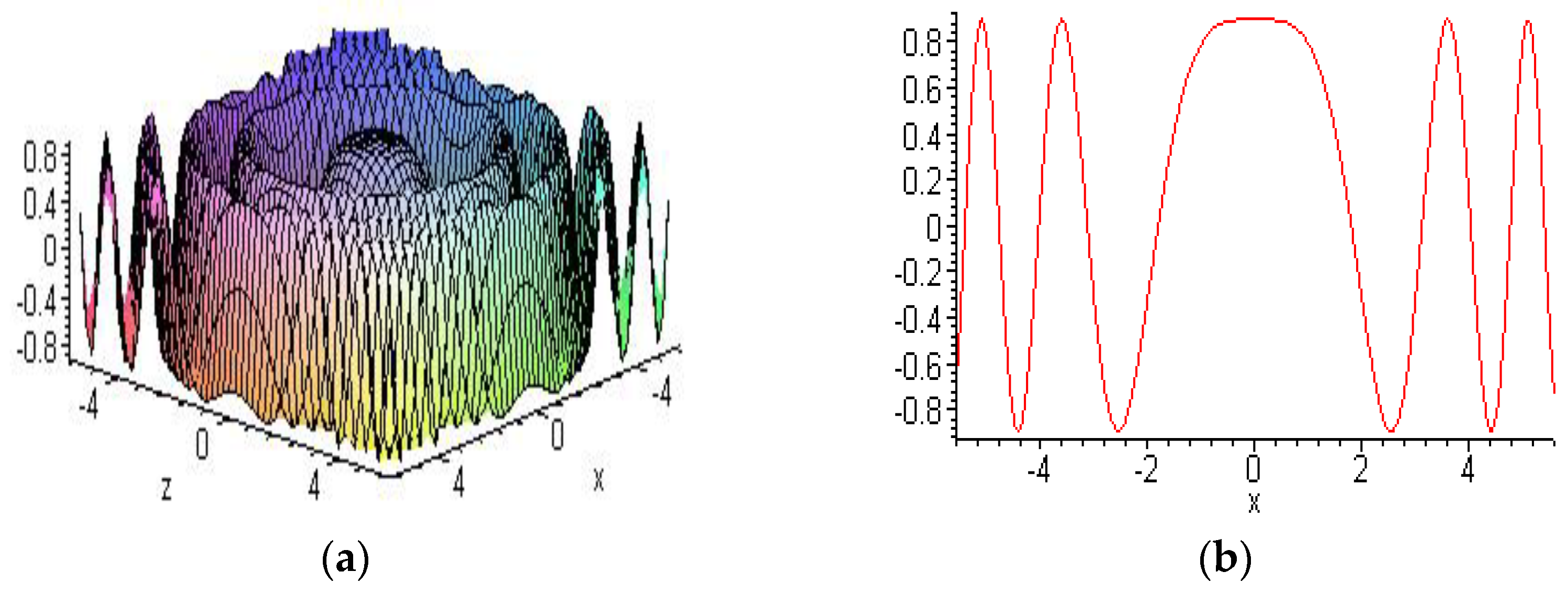
6.2. Other New Solitons
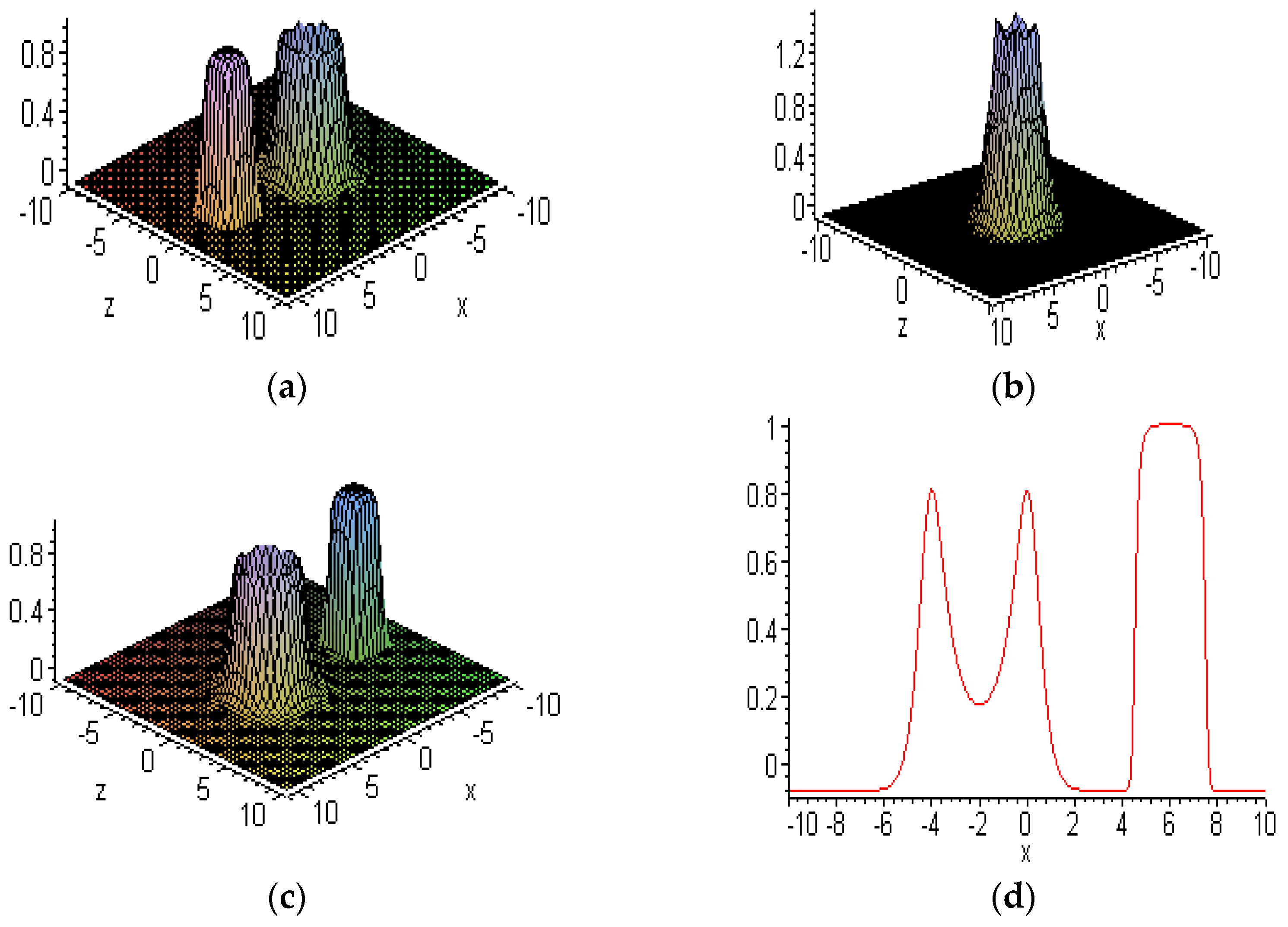
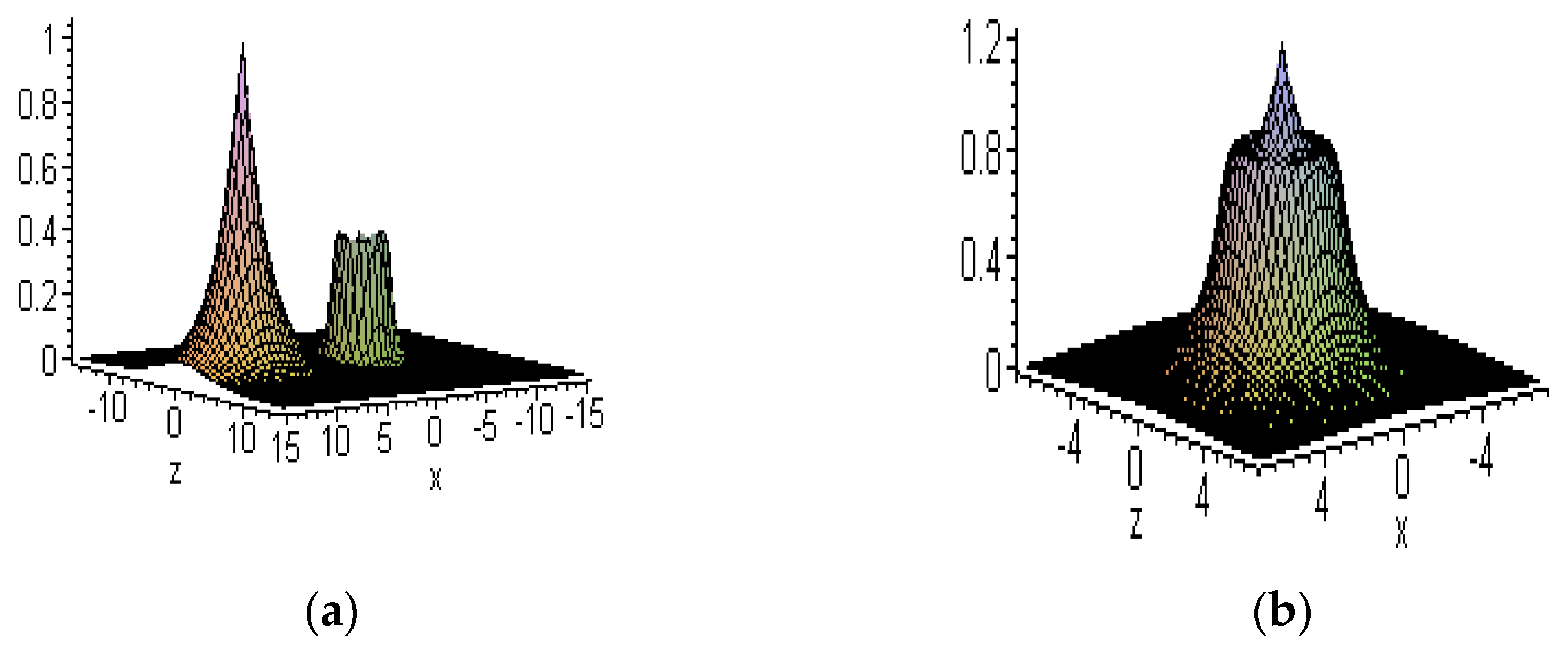
6.3. Interactions between Embedded and other Solitons
7. Summary and Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, Z.; Kong, L.; Cao, Y.; Liu, A.; Li, Z.; Wu, Q.; Huang, J.; Gao, L.; Zhu, T. Real-time dynamics of optical controlling for bound states of mode-locked fiber laser with short-range interaction. Opt. Laser Technol. 2022, 149, 107859. [Google Scholar] [CrossRef]
- Wang, X.; Xing, Y.; Chen, G.; Lin, X.; Zhang, Z.; Zhu, Q.; Peng, J.; Li, H.; Dai, N.; Li, J. Temporal optical rogue waves in high power short-cavity Yb-doped random fiber laser. Opt. Laser Technol. 2022, 149, 107797. [Google Scholar] [CrossRef]
- Pakzad, H.R.; Nobahar, D. Dust-ion acoustic solitons in superthermal dusty plasmas. New Astron. 2022, 93, 101752. [Google Scholar] [CrossRef]
- Shen, M.; Li, X.; Zhang, Y.; Yang, X.; Chen, S. Effects of the interfacial Dzyaloshinskii-Moriya interaction on magnetic dynamics. J. Phys. D Appl. Phys. 2022, 55, 213002. [Google Scholar] [CrossRef]
- Younas, U.; Bilal, M.; Ren, J. Diversity of exact solutions and solitary waves with the influence of damping effect in ferrites materials. J. Magn. Magn. Mater. 2022, 549, 168995. [Google Scholar] [CrossRef]
- Islam, M.N.; Ilhan, O.A.; Akbar, M.A.; Benli, F.B.; Soybaş, D. Wave propagation behavior in nonlinear media and resonant nonlinear interactions. Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106242. [Google Scholar] [CrossRef]
- Kengne, E.; Liu, W. Modulational instability and sister chirped femtosecond modulated waves in a nonlinear Schrodinger equation with self-steepening and self-frequency shift. Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106240. [Google Scholar] [CrossRef]
- Dong, J.; Ling, L.; Zhang, X. Kadomtsev-Petviashvili equation: One-constraint method and lump pattern. Phys. D Nonlinear Phenom. 2022, 432, 133152. [Google Scholar] [CrossRef]
- Weng, W.; Zhang, G.; Zhang, M.; Zhou, Z.; Yan, Z. Semi-rational vector rogon-soliton solutions and asymptotic analysis for any n-component nonlinear Schrodinger equation with mixed boundary conditions. Phys. D Nonlinear Phenom. 2022, 432, 133150. [Google Scholar] [CrossRef]
- Sheng, H.H.; Yu, G.F. Solitons, breathers and rational solutions for a (2+1)-dimensional dispersive longwave system. Phys. D Nonlinear Phenom. 2022, 432, 133140. [Google Scholar] [CrossRef]
- Didenkulova, E. Mixed turbulence of breathers and narrowband irregular waves: mKdV framework. Phys. D Nonlinear Phenom. 2022, 432, 133130. [Google Scholar] [CrossRef]
- Wang, X.; Wang, L.; Liu, C.; Guo, B.; Wei, J. Rogue waves, semirational rogue waves and W-shaped solitons in the three-level coupled Maxwell-Bloch equations. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106172. [Google Scholar] [CrossRef]
- Sun, Y.L.; Chen, J.; Ma, W.X.; Yu, J.P.; Khalique, C.M. Further study of the localized solutions of the (2+1)-dimensional B-Kadomtsev-Petviashvili equation. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106131. [Google Scholar] [CrossRef]
- Tian, H.Y.; Tian, B.; Sun, Y.; Zhang, C.R. Three-component coupled nonlinear Schrodinger system in a multimode optical fiber: Darboux transformation induced via a rank-two projection matrix. Commun. Nonlinear Sci. Numer. Simul. 2022, 107, 106097. [Google Scholar] [CrossRef]
- Dikande, A.M. On a Model for Nerve Impulse Generation Mediated by Electromechanical Processes. Braz. J. Phys. 2022, 52, 41. [Google Scholar] [CrossRef]
- Lavanya, C. Propagation and Soliton Collision of Positron Acoustic Waves in Four-component 208 Space Plasmas. Braz. J. Phys. 2022, 52, 38. [Google Scholar] [CrossRef]
- Kumar, S.; Dhiman, S.K. Lie symmetry analysis, optimal system, exact solutions and dynamics of solitons of a (3+1)-dimensional generalised BKP–Boussinesq equation. Pramana 2022, 96, 31. [Google Scholar] [CrossRef]
- Nisar, K.S.; Inc, M.; Jhangeer, A.; Muddassar, M.; Infal, B. New soliton solutions of Heisenberg ferromagnetic spin chain model. Pramana 2022, 96, 28. [Google Scholar] [CrossRef]
- Houwe, A.; Rezazadeh, H.; Bekir, A.; Doka, S.Y. Traveling-wave solutions of the Klein–Gordon equations with M-fractional derivative. Pramana 2022, 96, 26. [Google Scholar] [CrossRef]
- Alam, M.S.; Talukder, M.R. Characteristic behaviour of N-order ion acoustic rogue waves solution in electron-positron-ion plasmas. Plasma Res. Express 2022, 4, 015001. [Google Scholar] [CrossRef]
- Cisneros-Ake, L.A. Stability of multi-hump localized solutions in the Holstein model for linear acoustic and soft nonlinear optical interactions. Phys. D Nonlinear Phenom. 2022, 431, 133138. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Bright and dark solitons in a nonlinear saturable medium. Phys. Lett. A 2022, 427, 127913. [Google Scholar] [CrossRef]
- Chandramouli, S.; Farhat, A.; H Musslimani, Z. Time-dependent Duhamel renormalization method with multiple conservation and dissipation laws. Nonlinearity 2022, 35, 1286–1310. [Google Scholar] [CrossRef]
- Sudhakar, S.; Vignesh Raja, S.; Govindarajan, A.; Batri, K.; Lakshmanan, M. Low-power optical bistability in PT-symmetric chirped Bragg gratings with four-wave mixing. J. Opt. Soc. Am. B Opt. Phys. 2022, 39, 643. [Google Scholar] [CrossRef]
- Perna, S.; Bruckner, F.; Serpico, C.; Suess, D.; d’Aquino, M. Computational micromagnetics based on normal modes: Bridging the gap between macrospin and full spatial discretization. J. Magn. Magn. Mater. 2022, 546, 168683. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Mustafa, B.; Ali, K.; Althubiti, S. Chirped periodic waves for an cubic-quintic nonlinear Schrodinger equation with self steepening and higher order nonlinearities. Chaos Solitons Fractals 2022, 156, 111804. [Google Scholar] [CrossRef]
- Velasco-Juan, M.; Fujioka, J. Lagrangian nonlocal nonlinear Schrodinger equations. Chaos Solitons Fractals 2022, 156, 111798. [Google Scholar] [CrossRef]
- Sugati, T.G.; Seadawy, A.R.; Alharbey, R.A.; Albarakati, W. Nonlinear physical complex hirota dynamical system: Construction of chirp free optical dromions and numerical wave solutions. Chaos Solitons Fractals 2022, 156, 111788. [Google Scholar] [CrossRef]
- Li, Q.; Shan, W.; Wang, P.; Cui, H. Breather, lump and N-soliton wave solutions of the (2+1)-dimensional coupled nonlinear partial differential equation with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 2022, 106, 106098. [Google Scholar] [CrossRef]
- Evslin, J.; Halcrow, C.; Romanczukiewicz, T.; Wereszczynski, A. Spectral Walls at One Loop. arXiv 2022, arXiv:2202.08249. [Google Scholar] [CrossRef]
- Sreedharan, A.; Kuriyattil, S.; Wuster, S. Hyper-entangling mesoscopic bound states. arXiv 2022, arXiv:2202.06120. [Google Scholar]
- Evslin, J. Moving Kinks and Their Wave Packets. arXiv 2022, arXiv:2202.04905. [Google Scholar] [CrossRef]
- He, Y.; Slunyaev, A.; Mori, N.; Chabchoub, A. Experimental evidence of nonlinear focusing in standing water waves. arXiv 2022, arXiv:2202.04775. [Google Scholar] [CrossRef] [PubMed]
- Muller-Hoissen, F. Binary Darboux transformation of the first member of the nega- tive part of the AKNS hierarchy and solitons. arXiv 2022, arXiv:2202.04512. [Google Scholar]
- Zabolotnykh, A.A. Plasma solitons in gated two-dimensional electron systems: Exactly solvable analytical model for the regime beyond weak non-linearity. arXiv 2022, arXiv:2202.04503. [Google Scholar] [CrossRef]
- Lei, Z.; Ren, X.; Yang, Z. Radiation of the energy-critical wave equation with compact support. arXiv 2022, arXiv:2202.02045. [Google Scholar]
- Jin, H.-Y.; Wang, Z.-A.; Wu, L. Global dynamics of a three-species spatial food chain model. J. Differ. Equ. 2022, 333, 144–183. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Ruan, S. Global dynamics and bifurcations in a four-dimensional replicator system. Discret. Contin. Dyn. Syst.-B 2013, 18, 259–271. [Google Scholar] [CrossRef]
- Jin, H.-Y.; Wang, Z.-A. Global stabilization of the full attraction-repulsion Keller-Segel system. Discret. Contin. Dyn. Syst. 2020, 40, 3509–3527. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.-K.; Lin, H.; Tan, X.; Du, S. H∞ Consensus for Multiagent-Based Supply Chain Systems under Switching Topology and Uncertain Demands. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4905–4918. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y. Stock intelligent investment strategy based on support vector machine parameter optimization algorithm. Neural Comput. Appl. 2020, 32, 1765–1775. [Google Scholar] [CrossRef]
- Shao, Z.; Zhai, Q.; Han, Z.; Guan, X. A linear AC unit commitment formulation: An application of data-driven linear power flow model. Int. J. Electr. Power Energy Syst. 2023, 145, 108673. [Google Scholar] [CrossRef]
- Cai, Y.-J.; Wu, J.-W.; Lin, J. Nondegenerate N-soliton solutions for Manakov system. Chaos Solitons Fractals 2022, 164, 112657. [Google Scholar] [CrossRef]
- Liu, Y.; Ren, B.; Wang, D.-S. Localised Nonlinear Wave Interaction in the Generalised Kadomtsev-Petviashvili Equation. East Asian J. Appl. Math. 2021, 11, 301–325. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, L. Some novel physical structures of a (2+1)-dimensional variable-coefficient Korteweg–de Vries system. Chaos Solitons Fractals 2023, 171, 113430. [Google Scholar] [CrossRef]
- Saleh, M.H.; Altwaty, A.A. Optical solitons of the extended Gerdjikov-Ivanov Equation in DWDM system by extended simplest equation method. Appl. Math. Inf. Sci. 2020, 14, 901–907. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Eslami, M.; Bhrawy, A.H.; Ahmed, B. Biswas, Anjan, Solitons and other solutions to Complex-Valued Klein-Gordon equation in ϕ-4 field theory. Appl. Math. Inf. Sci. 2015, 9, 2793–2801. [Google Scholar]
- Zhu, H.-P.; Zheng, C.-L. Embed-Solitons and their evolutional behaviors of (3+1)-dimensional Burgers System. Commun. Theor. Phys. 2007, 48, 57–62. [Google Scholar] [CrossRef]
- Abdel-Salam, E.A.-B. Quasi-periodic structures based on symmetrical lucas Function of (2+1)-dimensional modified dispersive water-wave system. Commun. Theor. Phys. 2009, 52, 1004. [Google Scholar] [CrossRef]
- Friedman, I.; Riano, O.; Roudenko, S.; Son, D.; Yang, K. Well-posedness and dynamics of solutions to the generalized KdV with low power nonlinearity. arXiv 2022, arXiv:2202.01130. [Google Scholar] [CrossRef]
- Ali, U.; Ahmad, H.; Baili, J.; Botmart, T.; Aldahlan, M.A. Exact analytical wave solutions for space-time variable-order fractional modified equal width equation. Results Phys. 2022, 33, 105216. [Google Scholar] [CrossRef]
- Bilal, M.; Ahmad, J. A variety of exact optical soliton solutions to the generalized (2+1)-dimensional dynamical conformable fractional Schrodinger model. Results Phys. 2022, 33, 105198. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ali, K.K.; Inc, M.; Mehanna, M.S.; Rezazadeh, H.; Akinyemi, L. New solutions for the generalized resonant nonlinear Schrodinger equation. Results Phys. 2022, 33, 105153. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef] [Green Version]
- Vitanov, N.K.; Dimitrova, Z.I.; Kantz, H. Modified method of simplest equation and its application to nonlinear PDEs. Appl. Math. Comput. 2010, 216, 2587–2595. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Youssif, M.Y.; Helal, K.A.A.; Juma, M.Y.A.; Elhag, A.E.; Elamin, A.E.A.M.A.; Aiyashi, M.A.; Abo-Dahab, S.M. Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci. Symmetry 2023, 15, 1473. https://doi.org/10.3390/sym15081473
Youssif MY, Helal KAA, Juma MYA, Elhag AE, Elamin AEAMA, Aiyashi MA, Abo-Dahab SM. Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci. Symmetry. 2023; 15(8):1473. https://doi.org/10.3390/sym15081473
Chicago/Turabian StyleYoussif, Mokhtar. Y., Khadeeja A. A. Helal, Manal Yagoub Ahmed Juma, Amna E. Elhag, Abd Elmotaleb A. M. A. Elamin, Mohammed A. Aiyashi, and Sayed M. Abo-Dahab. 2023. "Embed-Solitons in the Context of Functions of Symmetric Hyperbolic Fibonacci" Symmetry 15, no. 8: 1473. https://doi.org/10.3390/sym15081473







