Linear Layer Architecture Based on Cyclic Shift and XOR

Abstract

One of the nodes of a block symmetric encryption algorithm is represented by a linear layer, the purpose of which is to distribute the mutual influence of bits within the processed data block. Several methods exist for constructing a linear layer, the most common of which are matrix multiplication operations and the permutation of bits. Both approaches have high computational complexity and are not equally effective for both hardware and software implementations. This paper presents an approach for constructing linear functions for block symmetric encryption algorithms utilizing cyclic shift, and bitwise addition operations are formulated. We provide a preliminary assessment of certain properties of such functions, including the branch number. This linear operation can accommodate binary words of any length, allowing for the design of an optimal linear layer for software or hardware architectures with any word size. Furthermore, the developed architecture allows for balancing the laboriousness of linear operations and related branch numbers. The proposed novel linear layer architecture facilitates the creation of fast lightweight encryption algorithms as well as robust classical algorithms with a high level of cryptographic strength. For efficient implementation on software and hardware platforms, no additional optimizations are required, as the proposed linear layer allows for achieving high performance in both cases.

1. Introduction

The linear diffusion layer in both classical and lightweight encryption algorithms often represents the slowest and most resource-intensive component. Maximum Distance Separable (MDS) codes have been widely used to perform linear transformations in a variety of encryption algorithms, including AES [1], due to their high branch number [2]. However, alternative functions can be considered that may not have the highest branch number but still offer favorable cryptographic properties with significantly improved performance.

Schemes utilizing a cyclic shift XOR on words of varying lengths are commonly employed in lightweight encryption algorithms [3,4] in order to mix bits of the internal state of the algorithm. These linear transformations may not require reversibility and can incorporate additional operations. As an example, the ARX (Add-Rotate-XOR) architecture involves a modular addition with a modulus $2^y$ where y represents the word length.

Algorithms also exist for constructing transformations equivalent to multiplication on MDR matrices using cyclic shift and bitwise addition operations. Refs. [5,6] provide a theoretical foundation for obtaining such operations analytically, without resorting to brute force, for a block of four words. The resulting linear operation thus constructed has a branch number of five, which is the maximum achievable for an operation involving four sub-blocks. To our knowledge, further research has not explored the generation of matrices of larger sizes with higher branch numbers.

Various studies have focused on optimizing operations in this field. For instance, ref. [7] proposes an optimization for the MixColumns operation in the AES algorithm, in which a linear transformation is performed using 92 XOR operations over individual bits. While this operation significantly accelerates hardware implementations of the algorithm, it is not suitable for software tools.

This paper introduces an architecture of a linear function that facilitates the design of a linear layer within the encryption algorithm. The experimental linear functions obtained exhibit a high branching index with improved speed. It is also possible to achieve a balance between these indicators, such as generating a highly efficient function with a low branch index or a computationally intensive function with a high branch index. The proposed architecture can be utilized in the development of new encryption algorithms, as an alternative to the conventional MDS codes.

2. Purpose and Methods

The purpose of this study was to show the possibility of constructing a linear layer of a block encryption algorithm using cyclic shift and bitwise XOR operations with sufficiently high efficiency of such a linear layer. Efficiency in this case meant low computational complexity, small memory requirements, and degree of influence of a linear operation on the general cryptographic strength of the algorithm. The latter figure is the most important and can be expressed as a value of the avalanche effect [8] as well as in the form of a branch number [2]. The avalanche effect is the average number of changed bits of the output of some function (for example, several rounds of an encryption algorithm) when one or more bits of the input are changed. This value depends not only on the linear operation of the algorithm and in general does not always reflect the cryptographic strength of the algorithm. Branch number is a more precise indicator regarding the efficiency of linear transformation, so it will be further presented in more details.

The concept of a branch number was introduced in [2], where the authors applied the “wide trail” approach to analyze the linear layer of ciphers, which later became one of the basic theories for the development and analysis of block symmetric encryption algorithms. The “wide trail” strategy was developed for a family of block symmetric encryption algorithms consisting of identical consecutive rounds, each containing a round key addition, a nonlinear transformation applied to sub-blocks of the processed block, and a linear transformation. In such a case, each transformation performed a different role, which was, respectively, to introduce key entropy, create non-linear relationships between the bits of the processed data, and mix the bits among themselves. Usually, key operation was represented by the addition modulo 2 (exclusive OR) and as a non-linear operation substitution according to a predetermined substitution table is used.

3. Linear Layer Efficiency

3.1. Cryptographic Properties

The general approach in the construction of a linear layer for a strong encryption algorithm consists of providing some minimal number of active sub-blocks of processed data block at output of linear operation, even with a minimal number of active sub-blocks at its input. As sub-blocks, groups of bits fed to the input of the substitution tables are taken. Minimal sum of number of active sub-blocks at input and output of linear operation is called differential branch number of linear operation and is crucial for encryption algorithm resistance to differential cryptanalysis processes due to the fact that a large number of links between sub-blocks complicates construction of multiround differentials.

A stricter definition of the branch number can be given after introducing the following notations:

-

Let the size of the processed block be n bits;

-

The size of the input and output of nonlinear transformation is m bits, with m dividing n, so to perform the nonlinear transformation, the input block must be divided into s = n/m sub-blocks, each of which is subjected to substitution independently of the other sub-blocks;

-

The algorithm consists of several round transforms r, which inputs blocks of size n bits;

-

Block weight w–is the number of non-zero sub-blocks of the block;

-

The bitwise addition operation will be denoted as $⨁$.

Then, the differential branch number $B$ for operation $r$ is defined in [2] as:

$$B\left(r\right)={min}_{a,b\ne a}\{w\left(a⨁b\right)+w(r\left(a\right)⨁r\left(b\right)\left)\right\}$$

(1)

for all pairs of different input blocks $a$ and $b$.

To provide a high branch number, linear operations based on the multiplication of one or more vectors given by the values of the processed text by a specially constructed matrix over some field extension are now widely used [1,9]. Many studies have been conducted (e.g., [10,11,12,13]) aimed at constructing matrices with optimal characteristics in terms of implementation efficiency without a loss of resistance to linear and differential cryptanalysis. In all the cited studies, the starting point is the conclusion in which it is reasonable to use matrices generating MDR codes to achieve the maximum branch number.

3.2. Effectiveness of Implementation

Bit permutations are widely used in hardware-oriented algorithms [14,15]. Obviously, programming such operations requires many actions to extract and process individual bits and then pack them into resulting words. In general, a bit permutation requires 2n operations of shifts and 2n XORs relative to an n-bit block of data.

Operations in the field are more convenient but not ideal for programmatic implementation. When implementing this kind of transformation in software, it is possible to solve the problem with the naive method, i.e., to perform multiplication and addition operations in the field with modulo-conversion, but it is very costly in terms of the number of computational operations. Thus, in [11], it is proven that the lower limit of the number of XOR operations for implementing multiplication with an MDR matrix of size $4\times 4$ is 35 and already 67 for matrices of the size $8\times 8$.

Alternatively, one can use precalculated values to speed up multiplication in the field, which requires additional memory. This also leads to limitation of processed word size since, for example, modulo product of 16-bit values can already require up to 15 bitwise addition operations and storing one table for precalculated values will require 32 kilobytes of memory. In practice, however, either operations on small vectors of 8-bit words are limited, as is done in the AES algorithm [1], thus strongly limiting the achievable branch number, or performing a very costly multiplication on a matrix of size $s\times s$ bytes, as in the Kuznechik algorithm [9]. Multipliers in matrix elements are also chosen small to optimize multiplication.

When implementing operations in the field for hardware solutions, similar problems arise, resulting in cumbersome logical nodes with long critical paths, which are also quite difficult to optimize [16,17].

Moving away from the classic MDR matrices multiplications to simpler operations will eliminate time-consuming modulo conversions or table substitutions, thus lowering the number of operations or memory requirements for linear layer.

4. Proposed Solution

4.1. Formal Definition of an Algorithm

Consider an encryption algorithm as a mapping of a set of plaintexts represented as a set of all possible $n$-bit vectors $V_n$ into the same set of ciphertexts depending on the key $K$. 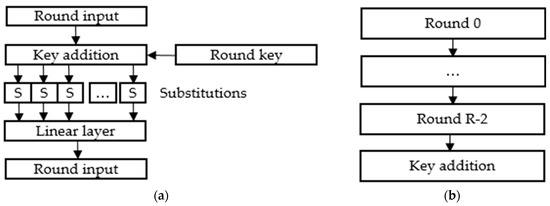The basic transformation $E$ of the algorithm consists of successively applied round transformations $r^{\left(i\right)}, i=0..R$, for each of the round keys $k^{\left(i\right)}$ from the key $K$, which are expanded and presented in Figure 1:

$$E\left(K\right)=r^{\left(0\right)}\left(k^{\left(0\right)}\right)\circ r^{\left(1\right)}\left(k^{\left(1\right)}\right)\circ \dots \circ r^{\left(R\right)}\left(k^{\left(R\right)}\right)$$

(2)

The last round of encryption is a key addition operation only. The remaining rounds also contain a non-linear operation, which is a byte substitution, and a linear operation, which will be described later:

$$r^{\left(i\right)}=s\circ l\circ x,i\ne 0$$

(3)

The algorithm can be depicted as follows:

Since substitution generation is beyond the scope of this study, let us assume that it has the best cryptographic properties [18,19]. The most interesting of these are the maximum of the differential table equal to 4, the absence of fixed points, and the avalanche effect close to 0.5, which in practice translates into the inability to reliably predict the bit change at the substitution output after inverting one input bit with an unknown value of the round key. The table according to which the substitution $t:V_8⟶V_8$ is performed is fixed, and the same for all bytes of the processed data block.

Round key addition is performed by bitwise addition to the processed data block. In each round, the whole block of data is processed. Thus, the size of the round key is equal to the block length.

4.2. Basic Linear Function

Consider a primitive that performs a bitwise addition of several words of the processed text $a=\{a_0,\dots ,a_{u-1}\}$, shifted cyclically by the number of bits given by the constants $C$, of the form:

$$g_j:a^{(n+1)}=g_j\left(a^{\left(n\right)}\right)\iff a_k^{(n+1)}=\begin{array}{c}{⨁}_{i=0}^{u-1}\left(a_{i+jmodu}^{\left(n\right)}⋘C_i\right),k=j\\ a_k^{\left(n\right)},k\ne j\end{array}$$

(4)

The computational complexity of a function can be measured in various ways. As shown in work [20], one of the optimal methods is to count the number of XOR operations required to execute the function. In this case, the function $\left(4\right)$ requires $u-2$ XOR operations and $u-1$ rotation operations.

To construct a linear operation that affects all words of the processed text, one must apply it to each word. To preserve the reversibility of the transformation, the operation (4) should be applied to words one by one, i.e., already changed values of other words should be used while changing the next word. Consequently, the linear transformation will look like this:

$$f\left(a\right)=g_{\left(0\right)}\left(a\right)\circ \dots \circ g_{(u-1)}\left(a\right)$$

(5)

Here, one word $a$ of the processed text is updated after each operation $g$.

This function requires $u\ast (u-2)$ XOR operations. The function can also be extended by increasing the number of operations (4) to m, in which case its computational complexity will be $m\ast (u-2)$ XOR operations.

Function (4) is a bijective, inverse function:

$$g_j^{-1}:a^{\left(n\right)}=g_j\left(a^{\left(n+1\right)}\right)\iff a_k^{\left(n\right)}=\begin{array}{c}{⨁}_{i=1}^{u-1}\left(a_{i+jmodu}^{\left(n+1\right)}⋘C_i\right)⋙C_0,k=j\\ a_k^{\left(n+1\right)},k\ne j\end{array}$$

(6)

Consider the properties of the operation (5) that affect the propagation of active bits.

Considering that the bitwise addition operation works for all bits independently of each other, it is possible to calculate the trajectories of individual bits as they shift and overlap with bits of other words in the processed text also independently of each other. The effect of several input bits will be linearly combined on the output.

For the same reason, the effect of an active input bit should not be considered by finding the difference between some binary vectors. Instead, it is possible to perform a linear operation on an input block containing a single 1 at a certain position. Considering the output of the operation, the activated bits will be 1.

The next property concerns the propagation of bit activation. Given a block length $n$ and the word size $v$, the number of words is $u=n/v$. Let us set the block state $a$ of $u$ words $a_0\dots a_{u-1}$, which is considered input of the linear function as $a=\sum _{i=0}^{u-1}{a}_i\ast 2^{v\ast i}$. The case when the shift values are 0 is trivial: considering the output of expression (4), it is simply the sum of all words. Consider the case with a single nonzero shift value. Let $c_{u-1}=d$ and $c_i=0$ for $i=0\dots u-2$. Let us consider the position of the active bit as $b$.

Let the active bit be at the position $b$ of one of the state words, i.e., the set of active bit numbers of this word is $\left\{b\right\}$, and for other words, it is empty. After shifting the word, the numbers of all its active bits increase by $d$ modulo $v$; let us denote the new number by $b+d$.

Obviously, in the case of splitting the processed text into two words, changing a single input bit can achieve two active output bits. If initially the active bit is at the position $b$ in the word $a_0$, the first step of the linear function will not change the position of active bits, and after the second step in the word $a_1$, there will be an active bit at the position of $b+d$. If, on the other hand, the active bit is initially located at the position $b$ in the word $a_1$, the bit at the position $b+d$ in the first word will be activated after the first step of the linear operation. After the second step of the operation in the second word, the set of numbers of the activated bits will be equal to $\{b,b+2d\}$. For brevity, these transformations can be depicted step by step as follows:

$$\begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\to \begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\to \begin{array}{c}b\\ b+d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\to \begin{array}{c}b+d\\ b\end{array}\to \begin{array}{c}b+d\\ b,b+2d\end{array}\end{array}$$

(7)

Consider the case of block division into 4 words. This division seems the most promising, considering that initially, the vast majority of block algorithms have a block size equal to degree of two; second, the linear operation will consist of only four steps; and third, it will activate significantly more bits than in the case of two words.

Depending on the word in which the active bit was located, four-bit activation scenarios are possible. The options for spreading the difference in the four steps of a linear operation, and the number of activated bits is listed below:

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b+d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b+d\end{array}\\ \begin{array}{c}b,b+d\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b+d\end{array}\\ \begin{array}{c}b,b+d\\ b,b+3d\end{array}\end{array}-6 \mathrm{active} \mathrm{bits};\\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}b,b+d,b+2d\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}b,b+d,b+2d\\ b+2d,b+3d\end{array}\end{array}-8 \mathrm{bits};\\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}b+d,b+2d\\ \mathrm{\varnothing }\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}b+d,b+2d\\ b+d,b+2d,b+3d\end{array}\end{array}-8 \mathrm{bits};\\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b+d\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b+d\\ b,b+2d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b+d\\ b,b+2d\end{array}\\ \begin{array}{c}b,b+3d\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b+d\\ b,b+2d\end{array}\\ \begin{array}{c}b,b+3d\\ b+2d,b+4d\end{array}\end{array}-7 \mathrm{bits}.\end{array}$$

(8)

If the shift value is chosen correctly, at least six bits of the processed data block can be activated with a single active input bit. If the bitwise addition of two active bits did not destroy them, then the branch number of such a linear operation would be limited to seven from below. However, there is a way to construct input blocks for which the sum of the numbers of active bytes at the input and output of a linear function with a single shift will not exceed three. Considering the described single shift function, an example of such a block is:

$$\begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ b,b+d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ b,b+d\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ b\end{array}\end{array}\to \begin{array}{c}\begin{array}{c}b\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}$$

(9)

If, on the other hand, a linear operation (5) is performed twice, the branch number of the function at some shift values can reach five. There is no analytical proof of this fact, but by full enumeration of all possible values of each triplet of input bytes, it is possible to see that a function with a single shift of six bits produces at least two active bytes at the output stage. A complete enumeration of all possible combinations of four active bytes would require about $2^{55}$ operations, so it has not yet been possible to perform it completely.

4.3. Bit Activation in the Full Function

In the previous section, a linear function with only one shift at each step was considered. Naturally, this reduced the efficiency of byte activation.

Considering a linear function implementing four shifts $\{a,b,c,d\}$, the distribution of the active bit after one and two iterations of the linear operation (5), denoted by $\Rrightarrow$, will look as follows depending on the word in which the active bit was considered:

$$\begin{array}{c}\hfill \begin{array}{c}\begin{array}{c}0\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}a\\ a+d\end{array}\\ \begin{array}{c}a+c,a+2d\\ a+b,a+3d\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}2a,a+2c,a+c+2d,a+4d\\ a+b+2d,a+2c+d,a+5d\end{array}\\ \begin{array}{c}2a+2d,a+2b,a+3c,a+c+4d,a+6d\\ a+2b+d,a+b+2c,a+b+4d,a+7d\end{array}\end{array}\hfill \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ 0\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}b\\ a,b+d\end{array}\\ \begin{array}{c}a+d,b+c,b+2d\\ a+c,a+2d,2b,b+3d\end{array}\end{array}\Rrightarrow \hfill \\ \Rrightarrow \begin{array}{c}\begin{array}{c}a+3d,b+2c,b+c+2d,b+4d\\ 2a,a+2c,a+c+2d,a+4d,2b+2d,b+2c+d,b+5d\end{array}\\ \begin{array}{c}a+2c+d,a+5d,3b,b+3c,b+c+4d,b+6d\\ 2a+2d,a+2b,a+3c,a+c+4d,a+6d,3b+d,2b+2c,2b+4d,b+7d\end{array}\end{array}\hfill \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}0\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}c\\ b,c+d\end{array}\\ \begin{array}{c}a,b+d,2c,c+2d\\ a+d,b+2d,c+3d\end{array}\end{array}\Rrightarrow \hfill \\ \Rrightarrow \begin{array}{c}\begin{array}{c}a+2d,2b,b+3d,3c,2c+2d,c+4d\\ a+3d,b+2c,b+4d,3c+d,c+5d\end{array}\\ \begin{array}{c}2a,a+2c,a+4d,2b+c,2b+2d,b+2c+d,b+5d,4c,2c+4d,c+6d\\ a+2c+d,a+5d,3b,2b+c+d,b+6d,c+7d\end{array}\end{array}\hfill \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ 0\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}d\\ c,2d\end{array}\\ \begin{array}{c}b,3d\\ a,2c,c+2d,4d\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}b+2d,2c+d,5d\\ a+2d,2b,3c,c+4d,6d\end{array}\\ \begin{array}{c}2b+d,b+2c,b+4d,7d\\ 2a,a+2c,a+4d,2b+c,4c,2c+4d,c+6d,8d\end{array}\end{array}\hfill \end{array}$$

(10)

4.4. Practical Check of a Linear Function

Presently, there is no fast way to select the shift values that provide activation for the maximum number of bits as well as an analytical method for determining the branch number depending on the value of the shift values. For this reason, it is a nontrivial task to select shift values to practically test the properties of the linear function under study.

Considering that, presently, one of the most popular encryption algorithms is AES, the new linear function has to compete with the ShiftRows and MixColumns operations of the AES-256 algorithm in terms of speed and branch number, which is five for AES [2].

By choosing different sets of shift values to test the hypothesis about the branch number of functions like (5), a linear function is generated, in which a 128-bit input block is divided into four words of 32 bits, which then undergo the described transformation with shift values $\{0, 1, 7, 14\}$. Values of the shifts have been selected with a full search method, considering the maximal avalanche effect of obtained function is obtained at its double repetition. Block size was chosen as the most popular in modern block symmetric encryption algorithms. The word size of 32 bits is supported on many processor architectures and allows us to enumerate all variants of shift values over $2^{15}$ test of shifts operations, each of which contains $2^7$ operations to calculate the avalanche effect of a function.

According to the expression (10), the activation scenarios for the bits of different words will occur as follows:

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}0\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}0\\ 14\end{array}\\ \begin{array}{c}7,28\\ 1,10\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}0,3,14,24\\ 6,28,29\end{array}\\ \begin{array}{c}2,20,21,28,31\\ 2,15,16,25\end{array}\end{array}\\ \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ 0\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}1\\ 0,15\end{array}\\ \begin{array}{c}8,14,29\\ 2,7,11,28\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}4,10,15,25\\ 0,3,7,14,24,29,30\end{array}\\ \begin{array}{c}0,3,6,21,22,28\\ 2,3,16,17,20,21,26,28,31\end{array}\end{array}\\ \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}0\\ \mathrm{\varnothing }\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}7\\ 1,21\end{array}\\ \begin{array}{c}0,3,14,15\\ 14,17,29\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}2,10,11,21,28,31\\ 3,10,13,15,25\end{array}\\ \begin{array}{c}0,6,7,9,14,24,27,28,29,30\\ 3,6,9,21,23,28\end{array}\end{array}\\ \\ \begin{array}{c}\begin{array}{c}\mathrm{\varnothing }\\ \mathrm{\varnothing }\end{array}\\ \begin{array}{c}\mathrm{\varnothing }\\ 0\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}14\\ 7,28\end{array}\\ \begin{array}{c}1,10\\ 0,3,14,24\end{array}\end{array}\Rrightarrow \begin{array}{c}\begin{array}{c}6,28,29\\ 2,20,21,28,31\end{array}\\ \begin{array}{c}2,15,16,25\\ 0,6,9,14,16,24,27,28\end{array}\end{array}\end{array}$$

(11)

The easiest way to find the input block that gives the minimum number of active bytes in the output of a linear operation is to enumerate the blocks with the minimum weight and feed them as input to the inverse linear function $f^{-1}:f^{-1}\left(f\left(a\right)\right)=a\forall a\in V_n$.

By going through all possible values of $k$ sub-blocks from $u$ at the input of the function $f$ and its inverse function $f^{-1}$ and not reaching the output blocks without active bits, it can be stated that the lower bound of the branch number of such function is $k+1$.

To check the branch number, a validation software application was developed, which goes through all values of $k$ of 16 bytes for $k=1...3$. In addition, some ranges of the sets of blocks containing four active bytes were partially searched. The minimum sum of the numbers of active input and output bytes of this function was five.

Some examples of minimum values (in hexadecimal form) for a linear function with shifts $\{0, 1, 7, 14\}$ are presented in

Table 1. Examples of input and output blocks with the lowest total number of active bytes.

	Input with 3 Active Bytes
Function input:	84 00 00 00 02 00 00 00 01 00 00 00 00 00 00 00	$w=3$
Function output:	00 00 00 00 00 00 00 00 01 00 00 00 00 40 00 00	$w=2$
	Input with 3 Active Bytes
Function input:	01 10 00 00 00 10 00 00 40 00 00 00 00 00 00 00	$w=4$
Function output:	00 00 00 00 00 00 00 00 00 00 00 00 01 00 00 00	$w=1$

.

$w=3$$w=2$$w=4$$w=1$ Thus, it can be assumed that the branch number of linear function of type (5) with some special shift values can reach five.

4.5. Experimental Validation

A comparison of the efficiency of the linear function was carried out using the AES algorithm as an example. Thus, the AES-256 algorithm is implemented in the C language using the Microsoft Visual Studio environment with some optimizations that do not require a large amount of additional memory. In particular, the SubBytes and ShiftRows operations are combined, and the MixColumns operation is accelerated using lookup tables, which contains the result of multiplication by 2 and by 3 modulo ${11b}_{16}$.

In this case, the optimization parameters/Ox (Favor Speed), /Oi (Enable Intrinsic Functions), and/Ot (Favor Fast Code) were used. A compilation was carried out in the Release configuration for the x86 architecture since, first, this is the target architecture for the AES algorithm according to the conditions of the AES contest, and second, the compared linear function operates with 32-bit words. The performance time was measured using the QueryPerformanceCounter function, which allows for measuring time intervals with high accuracy [21].

To evaluate the effectiveness of the new linear function, a modification of the AES-256-LF algorithm was developed, in which the combination of the ShiftRows and MixColumns transformations were replaced by the above linear function (5) with shift values {0, 1, 7, 14}. During the last round of AES-256, the original ShiftRows function was left to ensure the purity of the experiment.

A similar experiment was carried out for the Rijndael algorithm with a block length of 256 bits and a key length of 256 bits. The linear layer of the algorithm was replaced by a linear function of the form (5) over 64-bit words with shift values {0, 8, 9, 11}. The analysis is presented in

Table 2. Results of measuring the speed of novel linear function.

No.	Algorithm (128 Bit Block)	Time for 10 Million Runs, ms	Ratio
1	AES-256	249.4	1.216
2	AES-256-LF	205.1	0.822
No.	Algorithm (128 Bit Block)	Time for 10 Million Runs, ms	Ratio
3	Rijndael-256/256	474.5	1.107
4	Rijndael-256/256-LF	428.7	0.903

.

There is also an approach concerning the optimization of the AES algorithm using a $V_8\to V_{32}$ substitution, which implements the MixColumns operation simultaneously with SubBytes and ShiftRows [22]. For example, OpenSSH library uses this method related to the AES implementation [23]. In this case, the round is reduced to the key addition and 16 XOR operations. The linear function presented in this paper cannot be optimized in this way. However, in the case of larger words, it will be more advantageous to implement such a model [24]. It is difficult to determine the block lengths for which it will become faster than AES MixColumns since it depends on the nuances of the implementation of relevant operations on the processor.

4.6. Advantages and Disadvantages of the Resulting Function

The estimated branch number for the generated function is presumably five. With the use of new generation methods, it will be possible to obtain functions of similar architecture with higher branch number while keeping their high performance.

Considering that the function contains very simple operations, it does not require optimization and is not difficult to implement in software and hardware. At the same time, it keeps the performance at the level of the optimized AES linear transformation.

To increase the branch number, one can extend the function by adding one or more operations (4) up to twice the number of steps of the linear function. This can be useful when designing algorithms with a small number of rounds or with higher requirements for protection against differential analysis.

Another way to increase the branch number could be to increase the number of words the function handles while decreasing the length of each word. This will also increase the computational intensity of the function.

There may be shift values that can speed up a linear operation, but the theoretical apparatus for their precise determination has not been specified yet.

Since the properties of the linear function are valid for words of any length, a similar function can be used to construct an algorithm with a block size greater than the currently standard value of 128 bits. The function also allows us to use a block size other than a degree of two, although it is unlikely to find widespread practical application in this case.

The one-pass function activates the bits irregularly, and the first word of the block usually contains fewer active bits.

There is no way to prove the optimality of choosing a certain set of shift values. No method for generating values for a linear function with a given branch number has been found yet.

It is not proved that, in the case of doubled functions, the lower bound of branch number lies above four because of high computational complexity pertaining to the full enumeration of input and output values and the absence of analytical ways to determine the branch number. Considering all tested combinations of input and output blocks with activation up to and including four bytes, the sum of the numbers of input and output active bytes for some combinations of shift values was at least 10.

Considering a function consisting of a single pass over four words, it is assumed possible to have shift values that allow to reach the branch number value of five.

5. Conclusions

This paper presents a novel linear layer architecture for block symmetric encryption algorithms, which uses only cyclic shift and XOR operations. The architecture combines high efficiency in the form of the avalanche effect and (presumably) branch number, high speed, simple implementation, and the ability to balance computational complexity and cryptographic performance. Based on the proposed architecture, it is possible to create linear functions operating with words of any length. The function does not require additional memory or any optimizations.

As an example, the parameters of a function that is not inferior to the linear layer of the AES algorithm while requiring no additional memory and having less computational complexity are provided. At present, it is planned to use it for processing the candidate for the national encryption standards of the Republic of Kazakhstan, the Qalqan algorithm.

Considering the potential future developments, it makes sense to continue the research for optimal methods, which construct linear functions based on shift and XOR operations as well as methods for the analytical determination of their branch number.