Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Time-Varying Delays and Random Disturbances
Abstract
:1. Introduction
- Using the Gronwall–Bellman lemma and inequality methods, the upper bound of a CDN subject to both delays and random noise intensity is obtained. By calculating the transcendental equations, The allowable ESy range of a CDN with both delay and external noise is estimated.
- In the systems discussed in this paper, the parameter configuration matrices without delay and with delay are not necessarily symmetric.
- In [39], the robustness of neural network stability was thoroughly studied. Unlike the aforementioned paper, we investigate the robustness of ESy in CDNs with time-varying delays and random disturbances.
2. Problem Statement and Model
2.1. Notation
2.2. Problem Formulation
3. Main Results
3.1. Effect of Time Delays on CDN Synchronization
3.1.1. The Linear Controller
3.1.2. The Nonlinear Controller
3.2. Effect of Time Delays and Random Disturbances on CDN Synchronization
3.2.1. The Linear Controller
3.2.2. The Nonlinear Controller
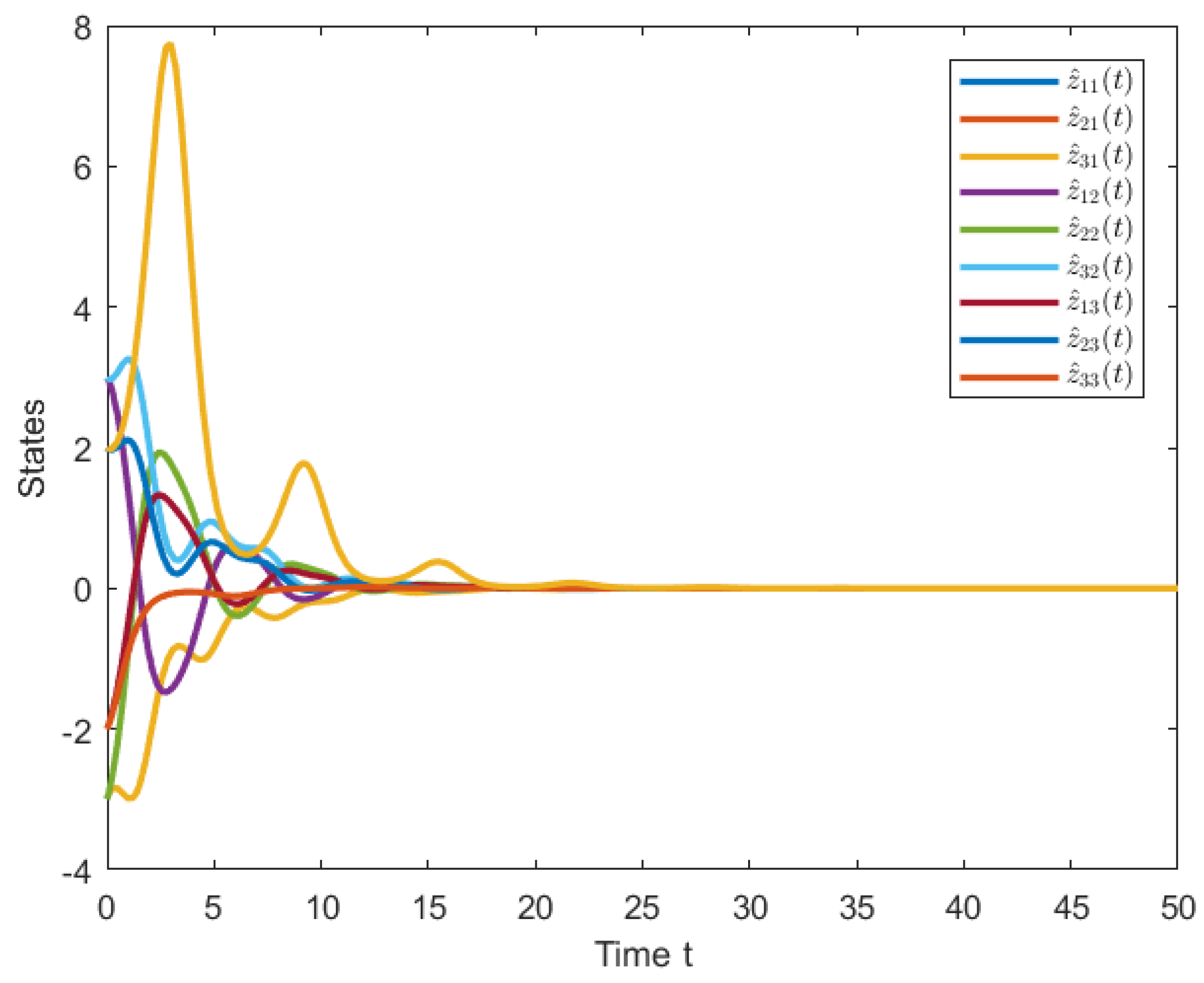
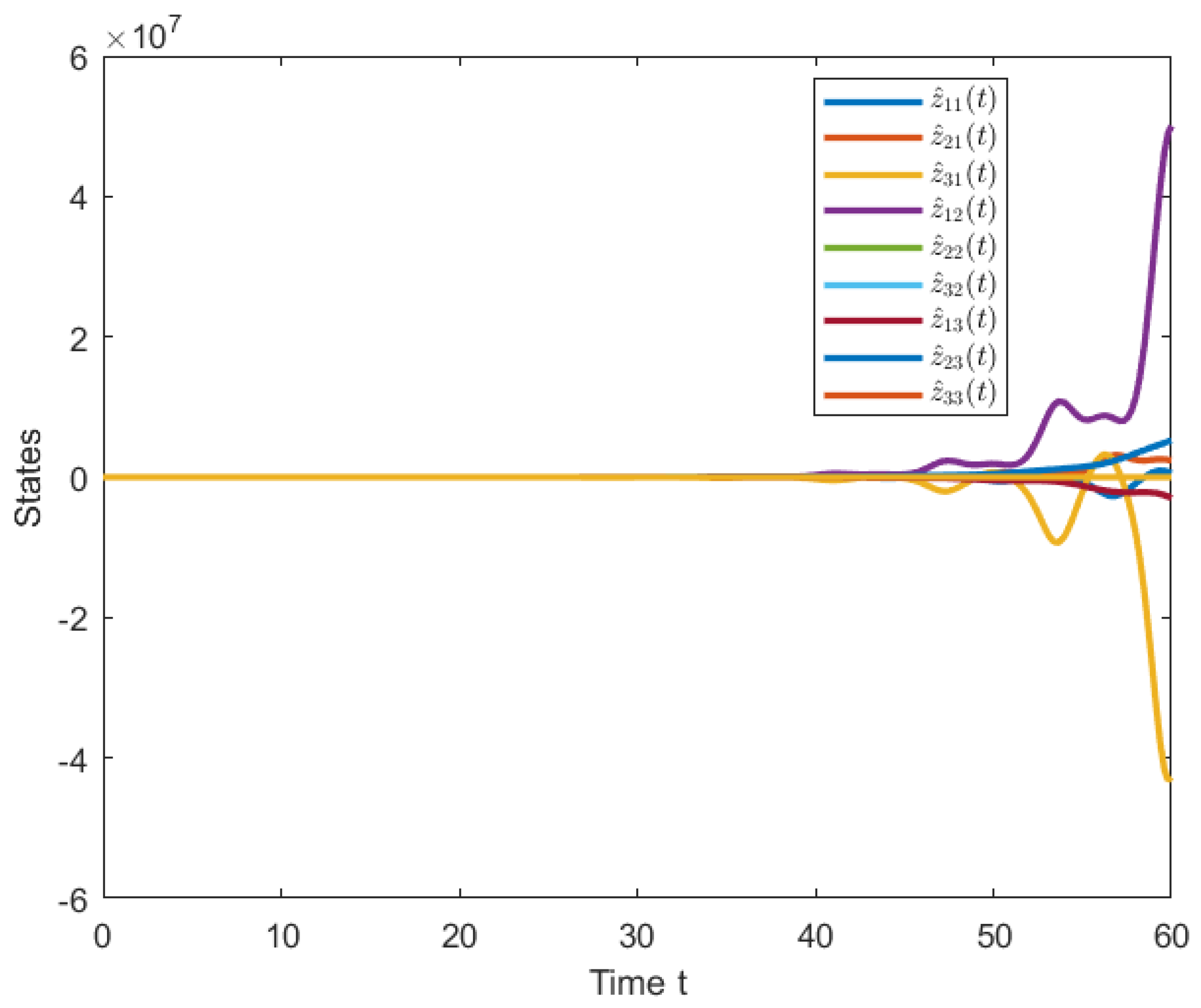
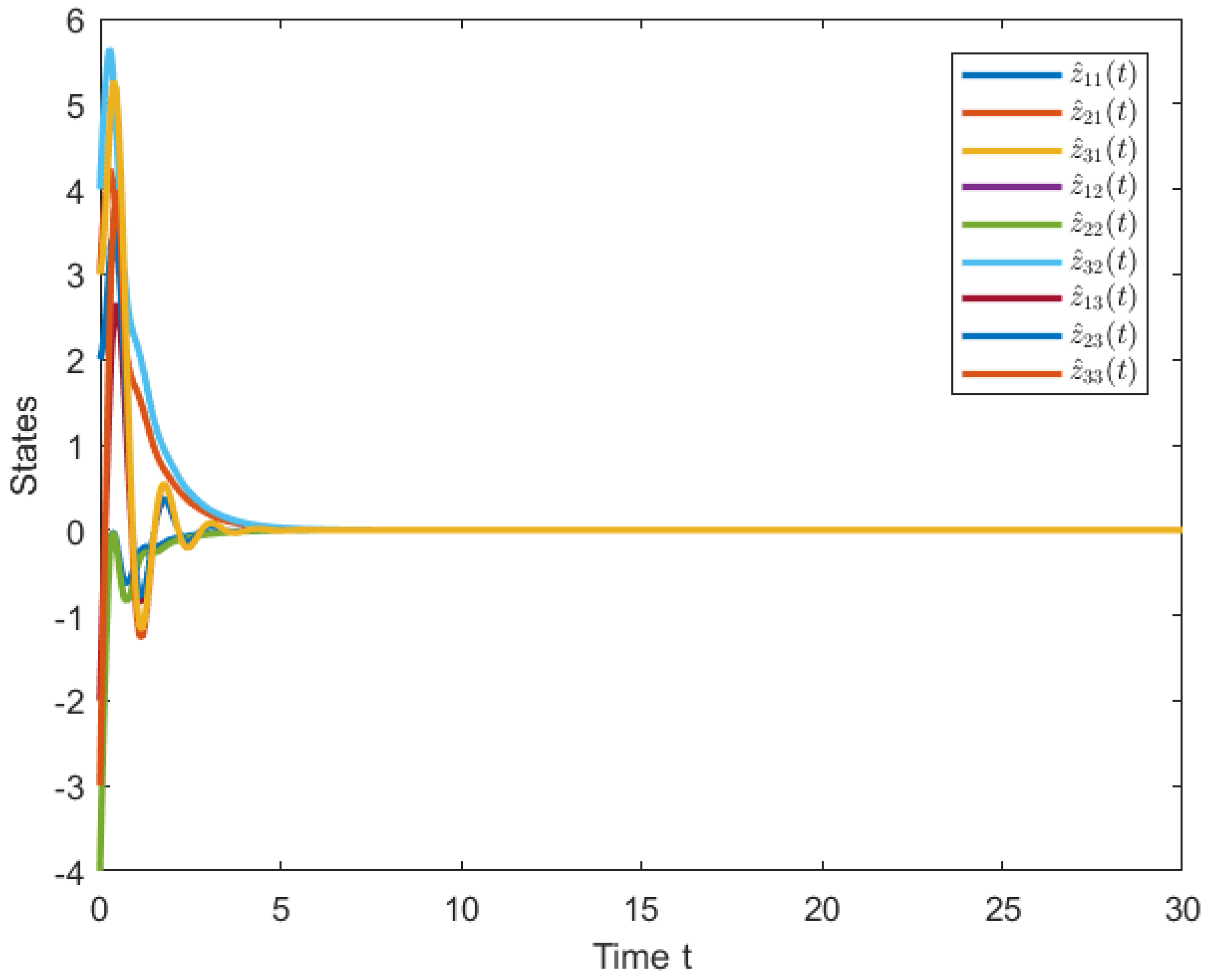
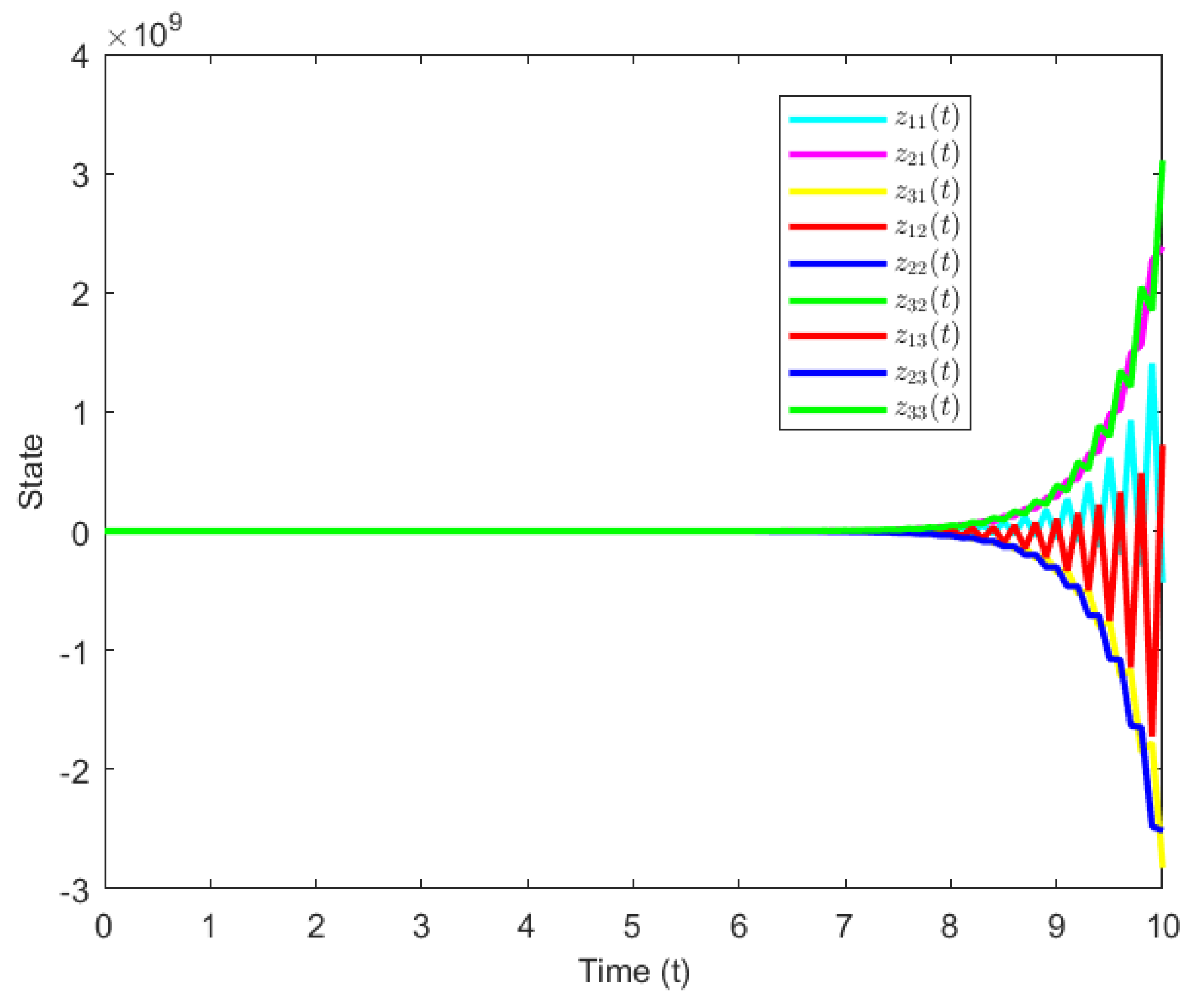
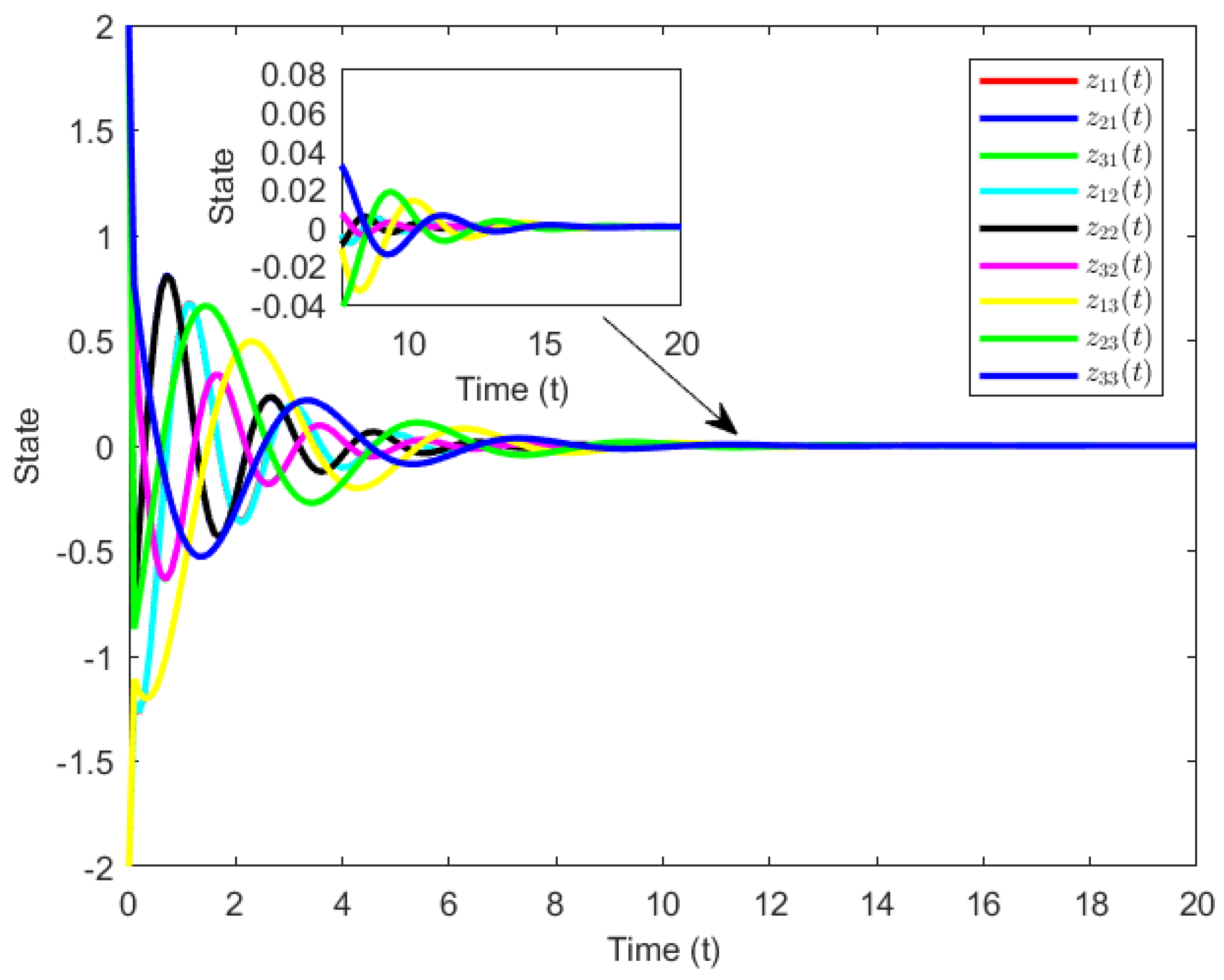
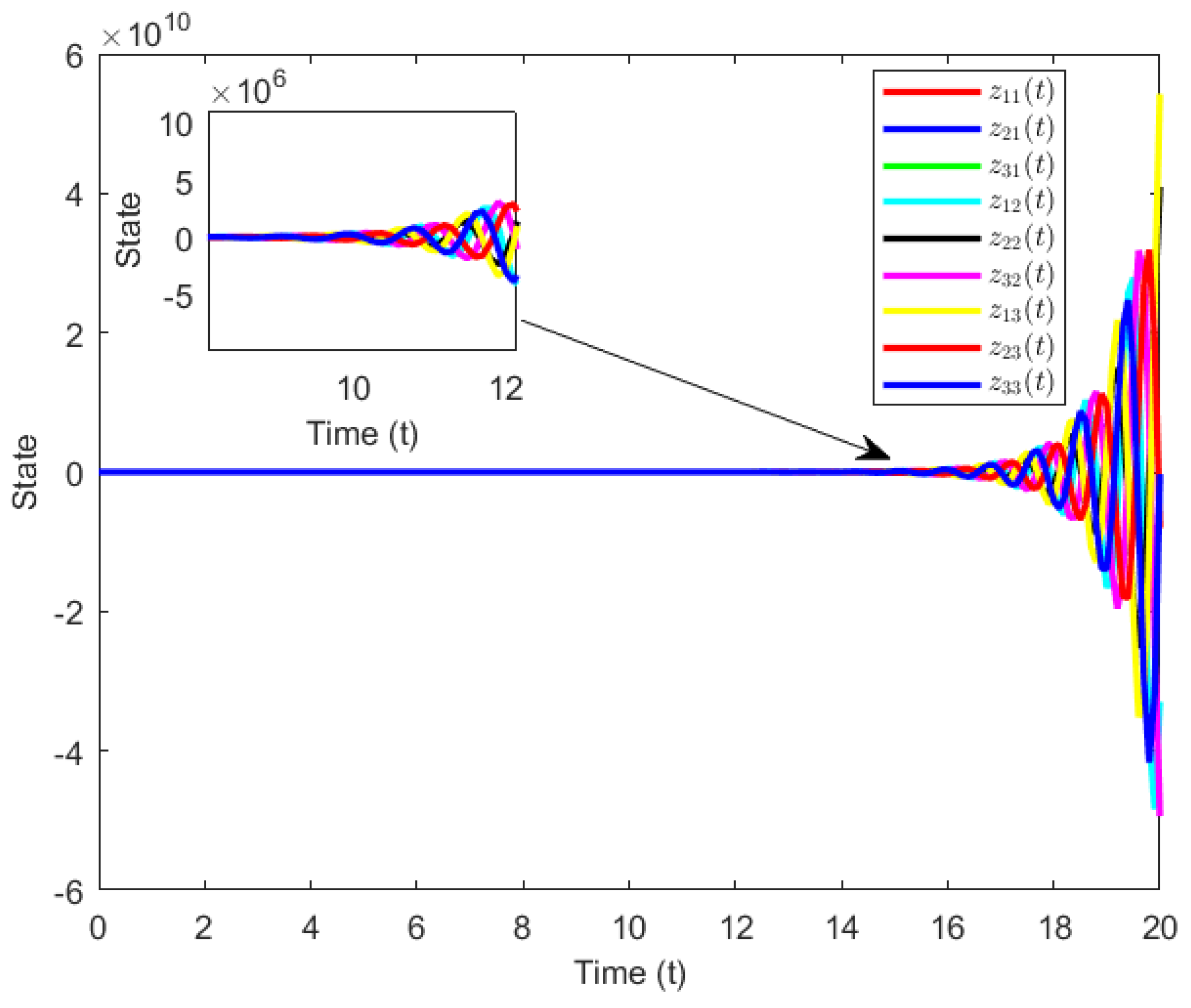
4. Numerical
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pocock, M.J.; Evans, D.M.; Memmott, J. The robustness and restoration of a network of ecological networks. Science 2012, 335, 973–977. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.L.; HLi, L.; Kao, Y.G.; Zhang, L.; Jiang, H.J. Global mittag-leffler synchronization of discrete-time fractional-order neural networks with time delays. Appl. Math. Comput. 2022, 43, 127417. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Modern Phys. 2002, 74, 47. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.F.; Chen, G.R. Complex networks: Small-world, scale-free and beyond. IEEE Circuits Syst. Mag. 2003, 3, 6–20. [Google Scholar] [CrossRef] [Green Version]
- Blekhman, I. The problem of synchronization of dynamical systems. J. Appl. Math. Mech. 1964, 28, 239–265. [Google Scholar] [CrossRef]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef] [Green Version]
- Huygens, C.; Oscillatorium, H. The pendulum clock. In Trans RJ Blackwell; The Iowa State University Press: Ames, IA, USA, 1986. [Google Scholar]
- Zhou, J.; Lu, J.A.; Lu, J.H. Adaptive synchronization of an uncertain complex dynamical network. IEEE Trans. Automat. Control. 2006, 51, 652–656. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Zhong, S.; Zhong, Q.S.; Shi, K.B.; Wang, X. Lag exponential synchronization of delayed memristor-based neural networks via robust analysis. IEEE Access 2018, 7, 173–182. [Google Scholar] [CrossRef]
- Wong, W.K.; Li, H.; Leung, S. Robust synchronization of fractional-order complex dynamical networks with parametric uncertainties. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4877–4890. [Google Scholar] [CrossRef]
- Cheng, R.R.; Peng, M.S.; Yu, W.B. Pinning synchronization of delayed complex dynamical networks with nonlinear coupling. Phys. A Stat. Mech. Its Appl. 2014, 413, 426–431. [Google Scholar] [CrossRef]
- Shen, W.W.; Zeng, Z.G.; Wen, S.P. Synchronization of complex dynamical network with piecewise constant argument of generalized type. Neurocomputing 2016, 173, 671–675. [Google Scholar] [CrossRef]
- Shi, C.X.; Yang, G.H.; Li, X.J. Event-triggered output feedback synchronization control of complex dynamical networks. Neurocomputing 2018, 275, 29–39. [Google Scholar] [CrossRef]
- Liu, S.X.; Yu, Y.G.; Zhang, S. Robust synchronization of memristor-based fractional-order hopfield neural networks with parameter uncertainties. Neural Comput. Appl. 2019, 31, 3533–3542. [Google Scholar] [CrossRef]
- Dong, Q.; Shi, S.L.; Ma, Y.C. Non-fragile synchronization of complex dynamical networks with hybrid delays and stochastic disturbance via sampled-data control. ISA Trans. 2020, 105, 174–189. [Google Scholar] [CrossRef]
- Wang, Y.; Li, T.Z. Synchronization of fractional order complex dynamical networks. Phys. A Stat. Mech. Its Appl. 2015, 428, 1–12. [Google Scholar] [CrossRef]
- Liang, S.; Wu, R.C.; Chen, L.P. Adaptive pinning synchronization in fractional-order uncertain complex dynamical networks with delay. Phys. A Stat. Mech. Its Appl. 2016, 444, 49–62. [Google Scholar] [CrossRef]
- Du, L.; Yang, Y.; Lei, Y.M. Synchronization in a fractional-order dynamic network with uncertain parameters using an adaptive control strategy. Appl. Math. Mech. 2018, 39, 353–364. [Google Scholar] [CrossRef]
- Zhang, Q.J.; Chen, G.R.; Wan, L. Exponential synchronization of discrete-time impulsive dynamical networks with time-varying delays and stochastic disturbances. Neurocomputing 2018, 309, 62–69. [Google Scholar] [CrossRef]
- Popa, C.A.; Kaslik, E. Finite-time mittag-leffler synchronization of neutral-type fractional-order neural networks with leakage delay and time-varying delays. Mathematics 2020, 8, 1146. [Google Scholar] [CrossRef]
- Zhou, J.; Bao, H.B. Fixed-time synchronization for competitive neural networks with gaussian-wavelet-type activation functions and discrete delays. J. Appl. Math. Comput. 2020, 64, 103–118. [Google Scholar] [CrossRef]
- Wang, Z.C.; Chen, G.L.; Ning, Z.P.; Xia, J.W. Stability analysis of impulsive switched nonlinear systems with double state-dependent delays. J. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 5014–5018. [Google Scholar] [CrossRef]
- Zhou, W.N.; Wang, T.B.; Mou, J.P. Mean square exponential synchronization in lagrange sense for uncertain complex dynamical networks. J. Frankl. Inst. 2012, 349, 1267–1282. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Gu, D.W.; Xu, S.Y. Global exponential adaptive synchronization of complex dynamical networks with neutral-type neural network nodes and stochastic disturbances. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2709–2718. [Google Scholar] [CrossRef]
- Wang, Y.N.; Ma, Y.C.; Chen, A.H. Exponential synchronization of markovian jump complex dynamical networks with partially uncertain transition rates and stochastic disturbances. Neurocomputing 2018, 304, 30–46. [Google Scholar] [CrossRef]
- Sipahi, R.; Niculescu, S.I.; Abdallah, C.T.; Michiels, W.; Gu, K. Stability and stabilization of systems with time delay. IEEE Control Syst. Mag. 2011, 31, 38–65. [Google Scholar]
- Mao, X.R. Stabilization of continuous-time hybrid stochastic differential equations by discrete-time feedback control. Automatica 2013, 49, 3677–3681. [Google Scholar] [CrossRef] [Green Version]
- Samidurai, R.; Sriraman, R. Non-fragile sampled-data stabilization analysis for linear systems with probabilistic time-varying delays. J. Frankl. Inst. 2019, 356, 4335–4357. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Zhu, S. Stability and dissipativity analysis for uncertain markovian jump systems with random delays via new approach. Int. J. Syst. Sci. 2019, 50, 1609–1625. [Google Scholar] [CrossRef]
- Samidurai, R.; Sriraman, R.; Cao, J.; Tu, Z. Nonfragile stabilization for uncertain system with interval time-varying delays via a new double integral inequality. Math. Methods Appl. Sci. 2018, 41, 6272–6287. [Google Scholar] [CrossRef]
- Kaviarasan, B.; Kwon, O.M.; Park, M.J.; Sakthivel, R. Composite synchronization control for delayed coupling complex dynamical networks via a disturbance observer-based method. Nonlinear Dynam. 2020, 99, 1601–1619. [Google Scholar] [CrossRef]
- Zhu, J.W.; Yang, G.H. Robust H∞ dynamic output feedback synchronization for complex dynamical networks with disturbances. Neurocomputing 2016, 175, 287–292. [Google Scholar] [CrossRef]
- Qin, Z.; Wang, J.L.; Huang, Y.L.; Ren, S.Y. Analysis and adaptive control for robust synchronization and H∞ synchronization of complex dynamical networks with multiple time-delays. Neurocomputing 2018, 289, 241–251. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J. Robustness analysis of global exponential stability of recurrent neural networks in the presence of time delays and random disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2011, 23, 87–96. [Google Scholar] [CrossRef]
- Si, W.X.; Xie, T.; Li, B.W. Robustness analysis of exponential stability of neutral-type nonlinear systems with multi-interference. IEEE Access 2021, 9, 116015–116032. [Google Scholar] [CrossRef]
- Lia, B.W.; Huang, J.J.; Wang, D.L. Robustness analysis of control laws in complex dynamical networks evoked by deviating argument. Discrete Dyn. Nat. Soc. 2022, 2022. [Google Scholar] [CrossRef]
- Zhang, Q.K.; Fang, W.X.; Xie, T. Robustness analysis of exponential synchronization in complex dynamic networks with random perturbations. AIMS Math. 2023, 8, 20487–20509. [Google Scholar] [CrossRef]
- Mao, X.R. Stochastic Differential Equations and Applications, 2nd ed.; Publishing House—Woodhead Publishing: Sawston, UK, 2008. [Google Scholar]
- Li, N.; Sun, H.Y.; Jing, X.; Zhang, Q.L. Exponential synchronisation of united complex dynamical networks with multi-links via adaptive periodically intermittent control. IET Control Theory Appl. 2013, 7, 1725–1736. [Google Scholar] [CrossRef]






| Full Name | Abbreviation |
|---|---|
| Exponential stability | ESt |
| Mean-square exponential stability (synchronization) | MSESt (MSESy) |
| Almost surely exponential stability (synchronization) | ASESt (ASESy) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, T.; Zhang, Q.; Xiong, X. Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Time-Varying Delays and Random Disturbances. Symmetry 2023, 15, 1510. https://doi.org/10.3390/sym15081510
Xie T, Zhang Q, Xiong X. Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Time-Varying Delays and Random Disturbances. Symmetry. 2023; 15(8):1510. https://doi.org/10.3390/sym15081510
Chicago/Turabian StyleXie, Tao, Qike Zhang, and Xing Xiong. 2023. "Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Time-Varying Delays and Random Disturbances" Symmetry 15, no. 8: 1510. https://doi.org/10.3390/sym15081510
APA StyleXie, T., Zhang, Q., & Xiong, X. (2023). Robustness Analysis of Exponential Synchronization in Complex Dynamic Networks with Time-Varying Delays and Random Disturbances. Symmetry, 15(8), 1510. https://doi.org/10.3390/sym15081510






