Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise
Abstract
:1. Introduction
- (i)
- A machine learning algorithm for the localization of a source of interest within a multi-source and noisy environment is proposed. The model training, validation, and testing are conducted on realistic data generated from a noisy environment;
- (ii)
- A signal improvement pipeline that mixes the source localization with array beamforming is developed. The pipeline is tested on the real data;
- (iii)
- The developed model and the pipeline are compared against two machine learning methods and popular parametric methods, such as SRP-PHAT and MUSIC.
2. Mathematical Formulation of Problem
3. Signal Model
3.1. DoA Estimation
3.2. Beamforming
4. Dataset Generation and Numerical Analysis
- (A)
- Dataset
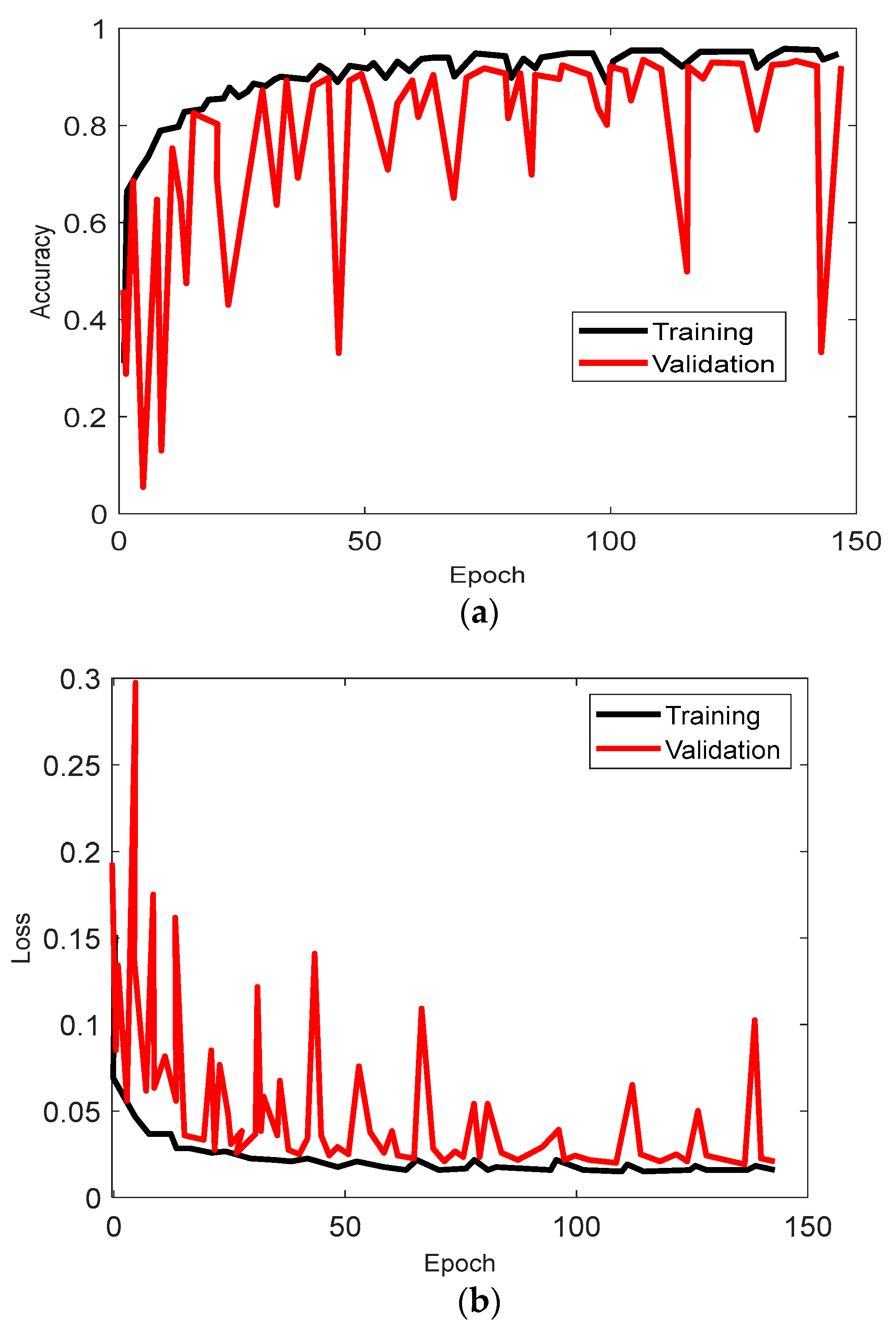
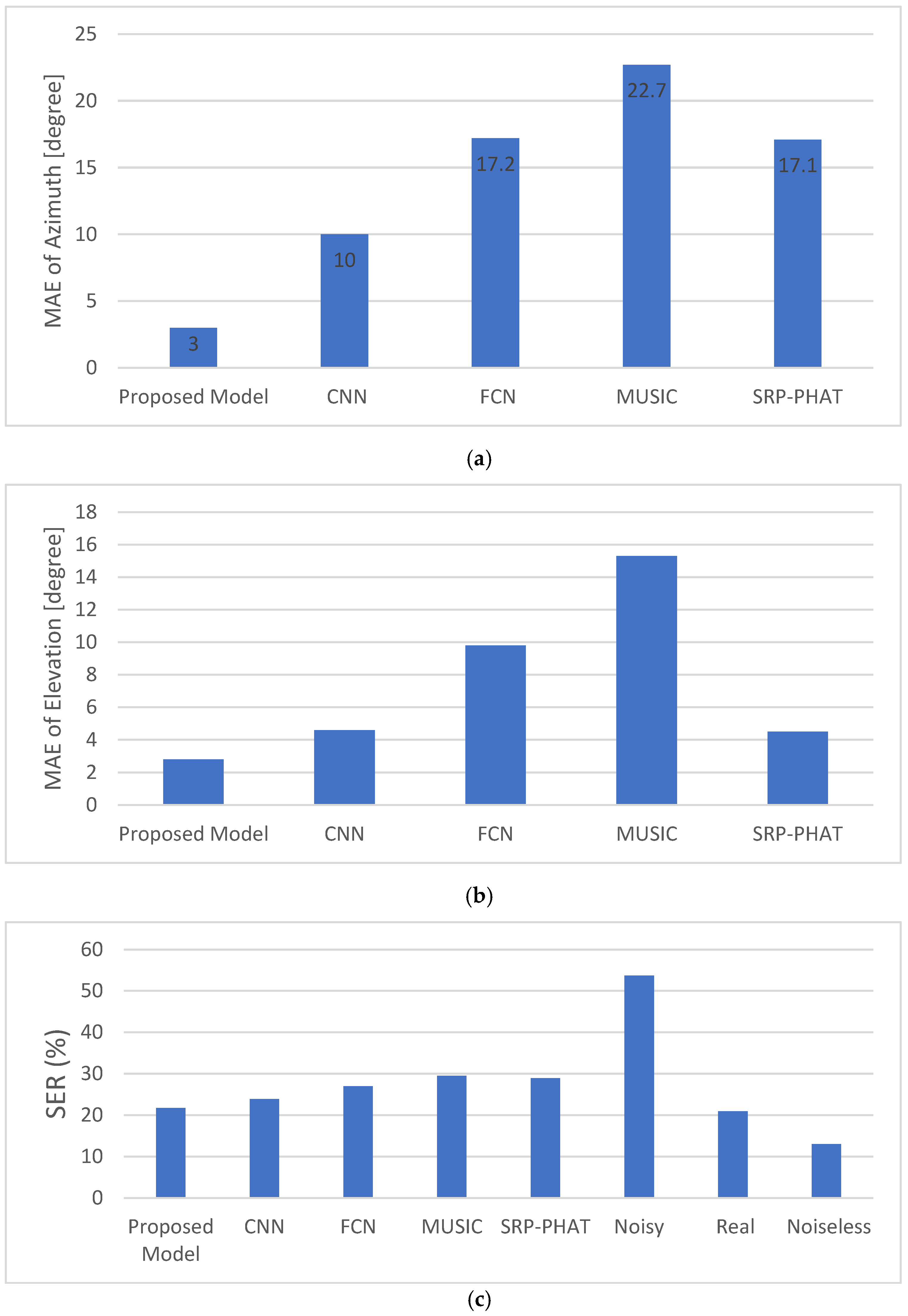
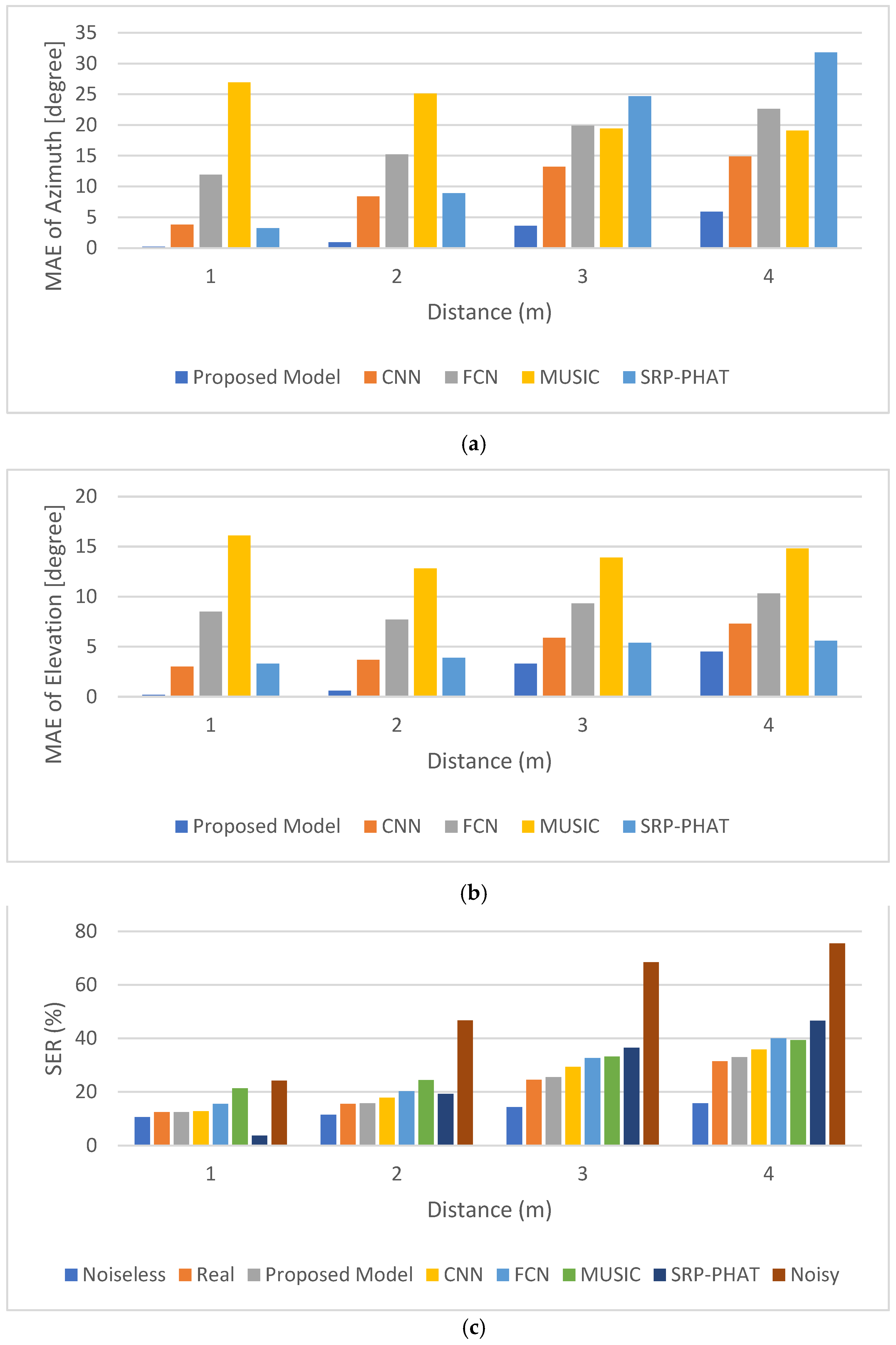
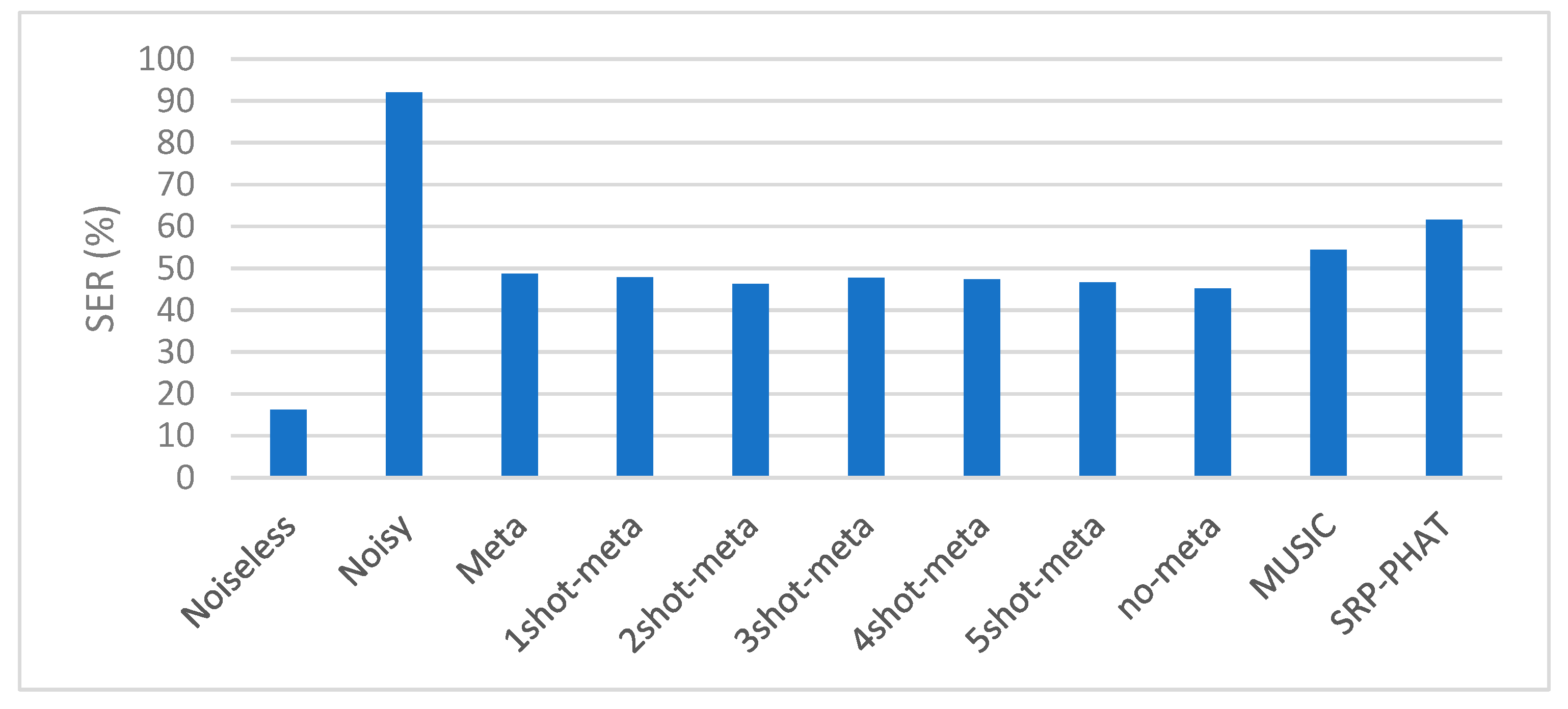
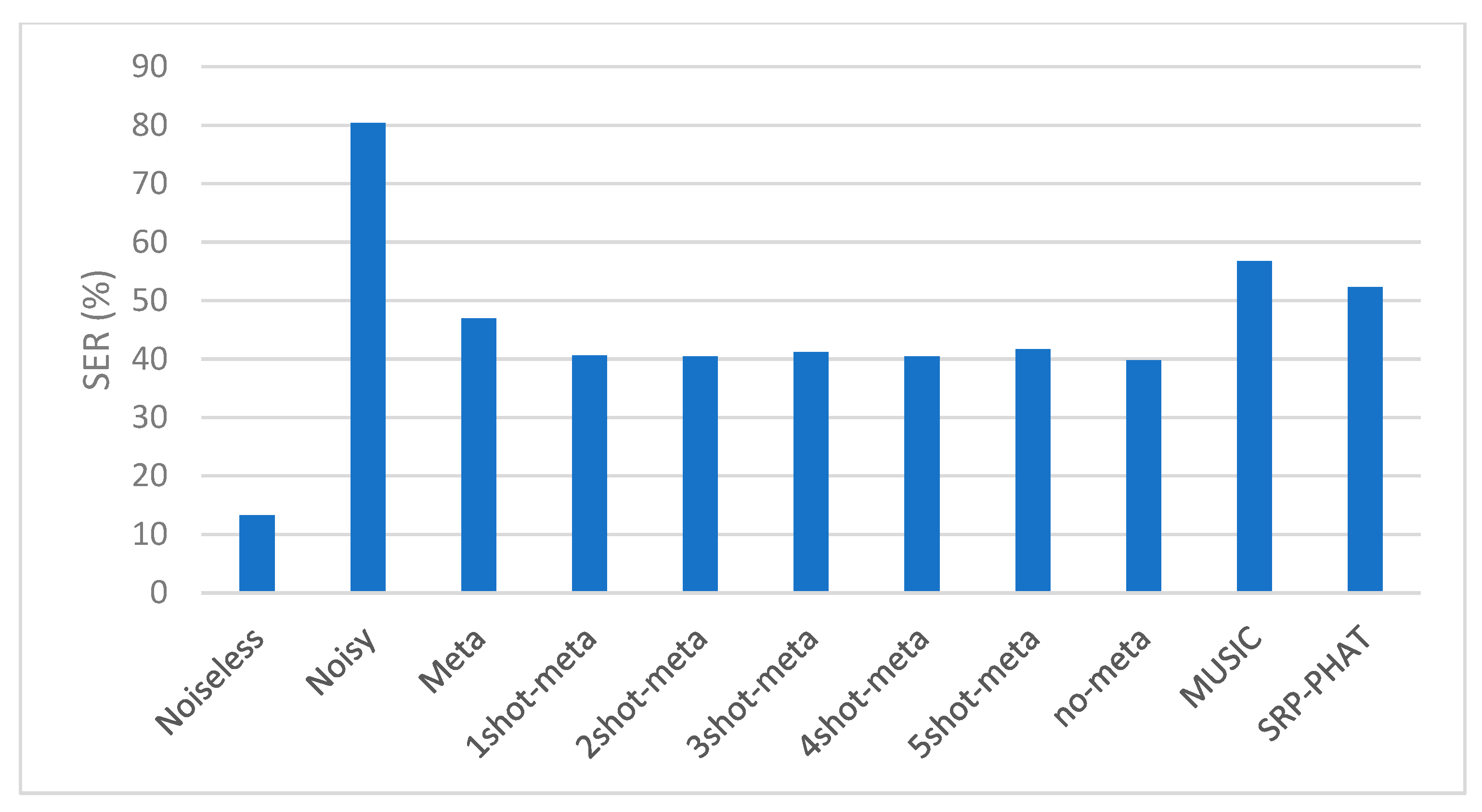
- (B) Numerical Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Famoriji, O.J.; Shongwe, T. Critical review of basic methods on DoA estimation of EM waves impinging a spherical antenna array. Electronics 2022, 11, 208. [Google Scholar] [CrossRef]
- Mostajabi, A.; Karami, H.; Azadifar, M.; Ghasemi, A.; Rubinstein, M.; Rachidi, F. Single-sensor source localization using electromagnetic time reversal and deep transfer learning: Application to lightning. Sci. Rep. 2019, 9, 17372. [Google Scholar] [PubMed] [Green Version]
- Toma, A.; Cecchinato, N.; Drioli, C.; Foresti, G.L.; Ferrin, G. CNN-based processing of radio frequency signals for augmenting acoustic source localization and enhancement in UAV security applications. In Proceedings of the 2021 International Conference on Military Communication and Information Systems (ICMCIS), The Hague, The Netherlands, 4–5 May 2021; pp. 1–5. [Google Scholar]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [PubMed]
- Ma, W.; Bao, H.; Zhang, C.; Liu, X. Beamforming of phased microphone array for rotating sound source localization. J. Sound Vibrat. 2020, 467, 115064. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Subspace Pseudointensity Vectors Approach for DoA Estimation Using Spherical Antenna Array in the Presence of Unknown Mutual Coupling. Appl. Sci. 2022, 12, 10099. [Google Scholar] [CrossRef]
- Adavanne, S.; Politis, A.; Nikunen, J.; Virtanen, T. Sound event localization and detection of overlapping sources using convolutional recurrent neural networks. IEEE J. Sel. Top. Signal Process. 2019, 13, 34–48. [Google Scholar] [CrossRef] [Green Version]
- Famoriji, O.J.; Shongwe, T. Source localization of EM waves in the near-field of spherical antenna array in the presence of unknown mutual coupling. Wirel. Commun. Mob. Comput. 2021, 2021, 3237219. [Google Scholar] [CrossRef]
- Chakrabarty, S.; Habets, E.A.P. Multi-speaker DOA estimation using deep convolutional networks trained with noise signals. IEEE J. Sel. Top. Signal Process. 2019, 13, 8–21. [Google Scholar] [CrossRef] [Green Version]
- Famoriji, O.J.; Ogundepo, O.Y.; Qi, X. An intelligent deep learning-based direction-of-arrival estimation scheme using spherical antenna array with unknown mutual coupling. IEEE Access 2020, 8, 179259–179271. [Google Scholar] [CrossRef]
- Yiwere, M.; Rhee, E.J. Distance estimation and localization of sound sources in reverberant conditions using deep neural networks. Int. J. Appl. Eng. Res. 2017, 12, 12384–12389. [Google Scholar]
- Zhuang, L.; Xu, A.; Wang, X.L. A prognostic driven predictive maintenance framework based on Bayesian deep learning. Reliab. Eng. Syst. Saf. 2023, 234, 109181. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Direction-of-arrival estimation of electromagnetic wave impinging on spherical antenna array in the presence of mutual coupling using a multiple signal classification method. Electronics 2021, 10, 2651. [Google Scholar] [CrossRef]
- He, W.; Motlicek, P.; Odobez, J.-M. Deep neural networks for multiple speaker detection and localization. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 74–79. [Google Scholar]
- Zhou, S.; Xu, A.; Tang, Y.; Shen, L. Fast Bayesian inference of reparameterized gamma process with random effects. IEEE Trans. Reliab. 2023; in press. [Google Scholar] [CrossRef]
- Ferguson, E.L.; Williams, S.B.; Jin, C.T. Sound source localization in a multipath environment using convolutional neural networks. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2386–2390. [Google Scholar]
- Vesperini, F.; Vecchiotti, P.; Principi, E.; Squartini, S.; Piazza, F. A neural network based algorithm for speaker localization in a multi-room environment. In Proceedings of the 2016 IEEE 26th International Workshop on Machine Learning for Signal Processing (MLSP), Vietri sul Mare, Italy, 13–16 September 2016; pp. 1–6. [Google Scholar]
- Sun, Y.; Chen, J.; Yuen, C.; Rahardja, S. Indoor sound source localization with probabilistic neural network. IEEE Trans. Ind. Electron. 2018, 65, 6403–6413. [Google Scholar] [CrossRef] [Green Version]
- Guirguis, K.; Schorn, C.; Guntoro, A.; Abdulatif, S.; Yang, B. SELD-TCN: Sound event localization and detection via temporal convolutional networks. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 16–20. [Google Scholar]
- Johnson, D.H.; Dudgeon, D.E. Array Signal Processing: Concepts and Techniques; Simon & Schuster, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Frost, O.L. An algorithm for linearly constrained adaptive array processing. Proc. IEEE 1972, 60, 926–935. [Google Scholar] [CrossRef]
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Vilalta, R.; Drissi, Y. A perspective view and survey of meta-learning. Artif. Intell. Rev. 2002, 18, 77–95. [Google Scholar] [CrossRef]
- Ravi, S.; Larochelle, H. Optimization as a model for few-shot learning. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese neural networks for one-shot image recognition. In Proceedings of the ICML Deep Learning Workshop, Lille, France, 6–11 July 2015; Volume 2, pp. 1–8. [Google Scholar]
- Yu, M.; Guo, X.; Yi, J.; Chang, S.; Potdar, S.; Cheng, Y.; Tesauro, G.; Wang, H.; Zhou, B. Diverse few-shot text classification with multiple metrics. In Proceedings of the 2018 Conference of the North American Chapter Association for Computational Linguistics: Human Language Technologies, New Orleans, LA, USA, 1–6 June 2018; pp. 1206–1215. [Google Scholar]
- Johnson, R.; Tong, Z. Supervised and semi-supervised text categorization using LSTM for region embeddings. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; pp. 526–534. [Google Scholar]
- Chou, S.-Y.; Cheng, K.-H.; Jang, J.-S.R.; Yang, Y.-H. Learning to match transient sound events using attentional similarity for few-shot sound recognition. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 26–30. [Google Scholar]
- Shi, B.; Sun, M.; Puvvada, K.C.; Kao, C.-C.; Matsoukas, S.; Wang, C. Few-shot acoustic event detection via meta learning. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 76–80. [Google Scholar]
- Vinyals, O.; Blundell, C.; Lillicrap, T.; Wierstra, D. Matching networks for one shot learning. Adv. Neural Inf. Process. Syst. 2016, 29, 3637–3645. [Google Scholar]
- Snell, J.; Swersky, K.; Zemel, R. Prototypical networks for few-shot learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4080–4090. [Google Scholar]
- Mishra, N.; Rohaninejad, M.; Chen, X.; Abbeel, P. A simple neural attentive meta-learner. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Munkhdalai, T.; Yu, H. Meta networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 2554–2563. [Google Scholar]
- Finn, C.; Abbeel, P.; Levine, S. Model-agnostic meta-learning for fast adaptation of deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 1126–1135. [Google Scholar]
- Nair, G.E.; Hinton, V. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6 July–11 July 2015; pp. 448–456. [Google Scholar]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Hussain, S. Efficient Ray-Tracing Algorithms for Radio Wave Propagation in Urban Environments. Doctoral Dissertation, School of Electronic Engineering, Dublin City University, Dublin, Ireland, 2017. [Google Scholar]
- Hussain, S.; Brennan, C. An efficient ray tracing method for propagation prediction along a mobile route in urban environments. Radio Sci. 2017, 52, 862–873. [Google Scholar] [CrossRef]
- Hussain, S.; Brennan, C. Efficient preprocessed ray tracing for 5G mobile transmitter scenarios in urban microcellular environments. IEEE Trans. Antennas Propag. 2019, 67, 3323–3333. [Google Scholar] [CrossRef]
- Hussain, S.; Brennan, C. A visibility matching technique for efficient millimeter-wave vehicular channel modeling. IEEE Trans. Antennas Propag. 2022; early access. [Google Scholar] [CrossRef]
- Ahmed, K.; Hussain, S. Machine learning approaches for radio propagation modeling in urban vehicle channels. IEEE Access 2022, 10, 113690–113698. [Google Scholar] [CrossRef]
- Famoriji, O.J.; Shongwe, T. Electromagnetic machine learning for estimation and mitigation of mutual coupling in strongly coupled arrays. ICT Express 2021, 9, 8–15. [Google Scholar] [CrossRef]
- Kabal, P. TSP Speech Database, Database Version; McGill University: Montréal, QC, Canada, 2002; Volume 1, pp. 02–09. [Google Scholar]
- Morris, A.C.; Maier, V.; Green, P. From WER and RIL to MER and WIL: Improved evaluation measures for connected speech recognition. In Proceedings of the Eighth International Conference on Spoken Language Processing, Jeju Island, Republic of Korea, 4–8 October 2004; pp. 2765–2768. [Google Scholar]




| Parameter | Value |
|---|---|
| Reflections | 4 |
| Diffraction | 1 |
| Transmission power | 15 dB |
| Frequency | 6 GHz |
| Antenna | Omnidirectional |
| ) | 3.75 |
| ) | 0.137 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Famoriji, O.J.; Shongwe, T. Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise. Symmetry 2023, 15, 1534. https://doi.org/10.3390/sym15081534
Famoriji OJ, Shongwe T. Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise. Symmetry. 2023; 15(8):1534. https://doi.org/10.3390/sym15081534
Chicago/Turabian StyleFamoriji, Oluwole John, and Thokozani Shongwe. 2023. "Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise" Symmetry 15, no. 8: 1534. https://doi.org/10.3390/sym15081534
APA StyleFamoriji, O. J., & Shongwe, T. (2023). Deep Learning Approach to Source Localization of Electromagnetic Waves in the Presence of Various Sources and Noise. Symmetry, 15(8), 1534. https://doi.org/10.3390/sym15081534







