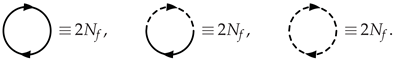Critical Properties of Three-Dimensional Many-Flavor QEDs
Abstract
:1. Introduction
1.1. Fermionic and Bosonic QEDs
1.2. Supersymmetric QEDs
1.3. Reduced QEDs
1.4. Outline of the Review
2. General QED Model and Conventions
2.1. The General gQED Model
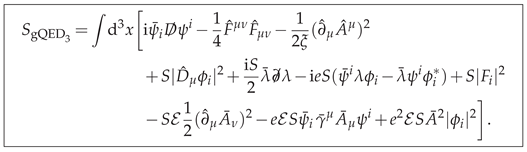
2.2. Feynman Rules
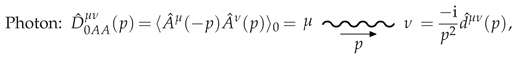
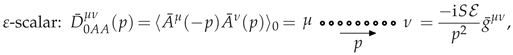
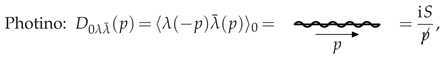
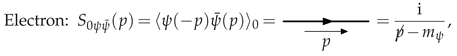
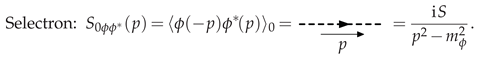
- Each matter-field loop ( and field charge flow) gives a factor of , i.e., graphically
- Each fermion loop ( and field fermion flow) gives a factor and a trace over the spinorial indices, i.e., graphically
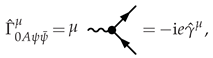
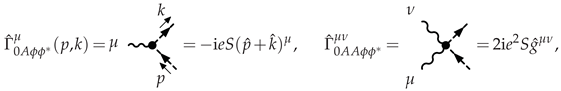
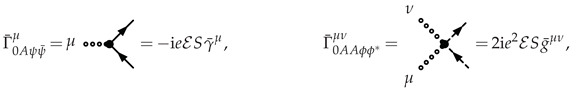


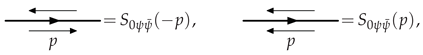
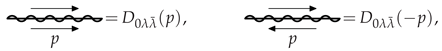


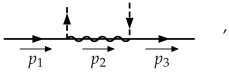
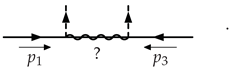
2.3. Numerator Algebra
2.4. Renormalization Setup
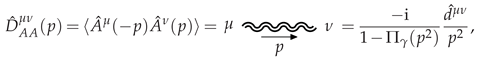
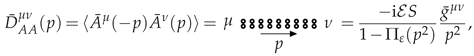



2.5. The Large- Expansion

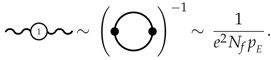
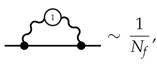

 , in the IR limit, which allows computing NLO corrections to the electron self-energy at , etc. So, the strategy goes as follows. At leading order (LO):
, in the IR limit, which allows computing NLO corrections to the electron self-energy at , etc. So, the strategy goes as follows. At leading order (LO):- (1)
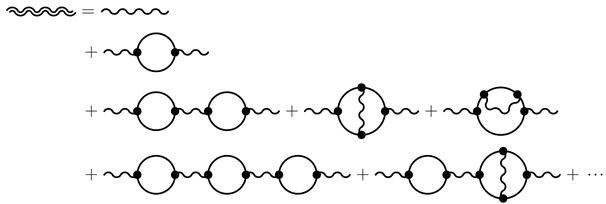
- Compute the one-loop polarization using bare Feynman rules and compute the LO-softened photon by resumming the one-loop polarization.
- (2)
- Compute the other diagrams of the theory at using the LO-softened photon only.
- (3)
- Compute the two-loop polarizations using the LO-softened photon propagator and compute the new NLO-softened photon propagator by resumming the two-loop polarization.
- (4)
- Compute the other diagrams of the theory at NLO, i.e., using both the LO and NLO-softened photon propagators.
3. Perturbative Calculations up to NLO in gQED
3.1. Gauge-Multiplet Polarizations at LO
3.1.1. Photon Polarization at LO

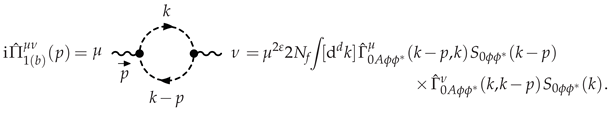
3.1.2. -Scalar Polarization at LO
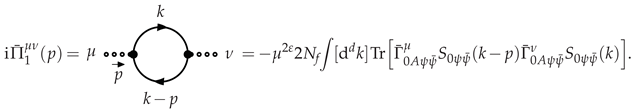
3.1.3. Photino Polarization at LO
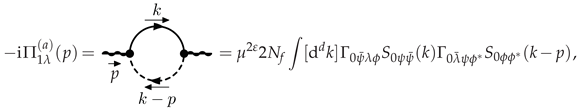
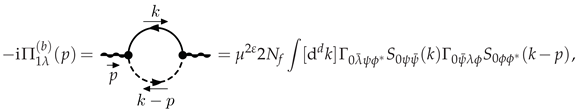
3.1.4. IR-Softened Gauge Multiplet at LO
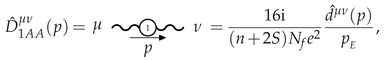
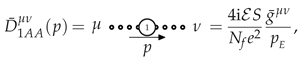

3.2. Matter-Multiplet Self-Energies at LO
3.2.1. Electron Self-Energy at LO
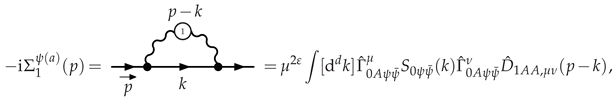
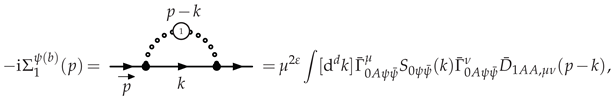
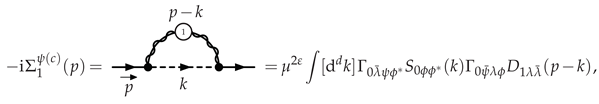
3.2.2. Selectron Self-Energy at LO
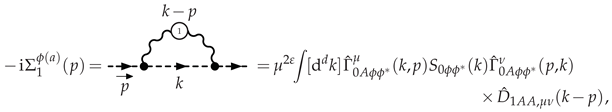

3.3. Vanishing Contributions and Generalized Furry Theorem
3.4. Gauge-Multiplet Polarizations at NLO
3.4.1. Photon Polarization at NLO
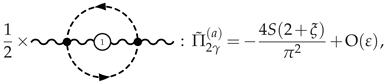
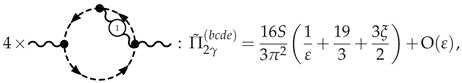
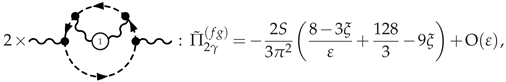
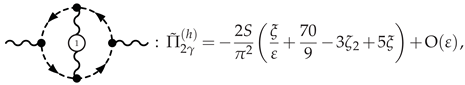
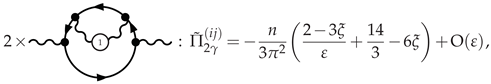
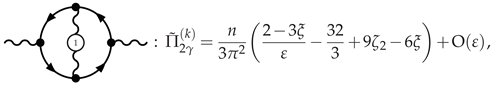
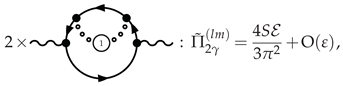
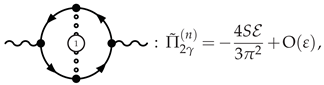

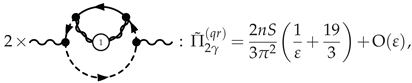
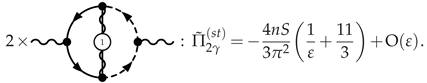
3.4.2. -Scalar Polarization at NLO
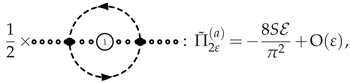
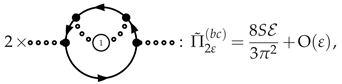
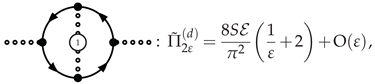
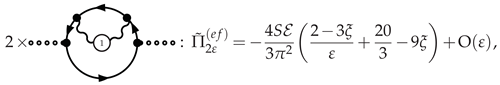
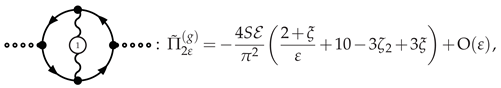
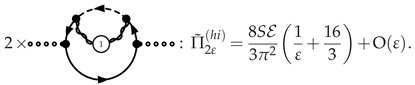
3.4.3. Photino Polarization at NLO
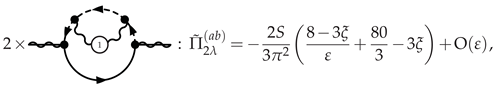

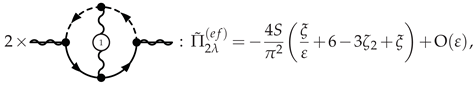
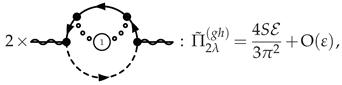
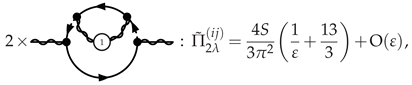
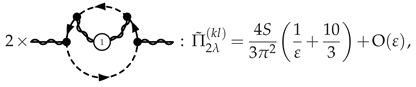
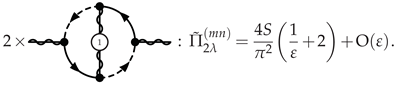
3.4.4. IR-Softened Gauge Multiplet at NLO
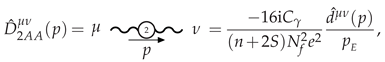


3.5. Matter-Multiplet Self-Energies at NLO
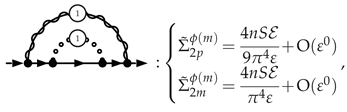
3.5.1. Electron Self-Energy at NLO
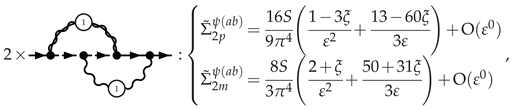
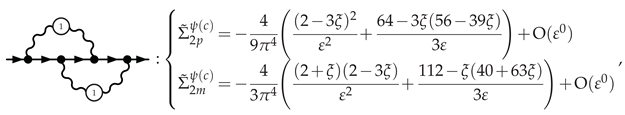
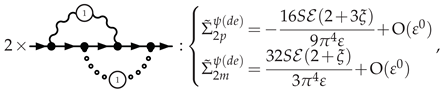
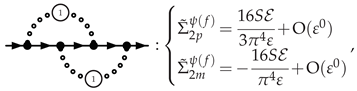
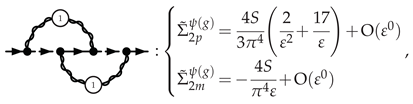
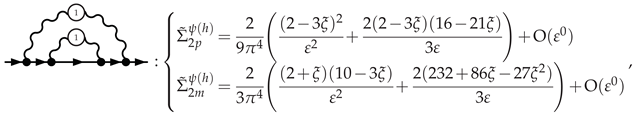
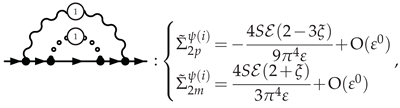


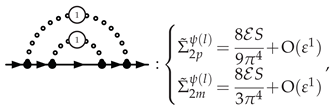
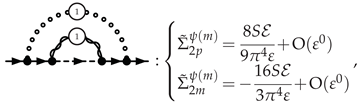
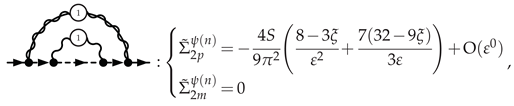
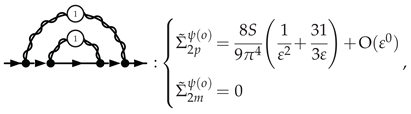
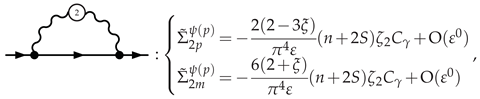
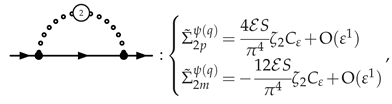
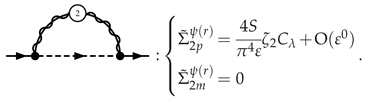
3.5.2. Selectron Self-Energy at NLO
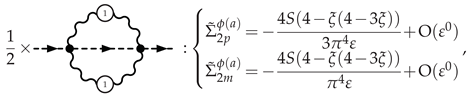
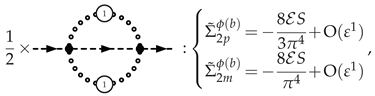
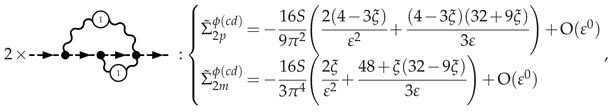

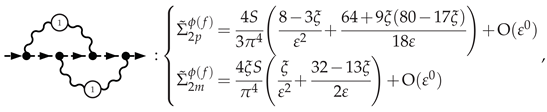
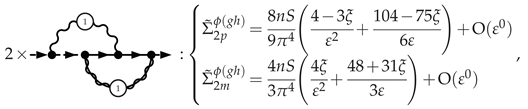
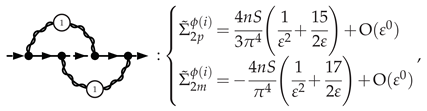
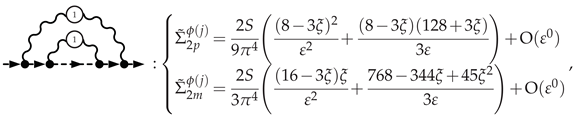
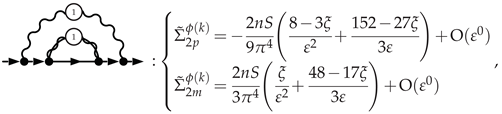
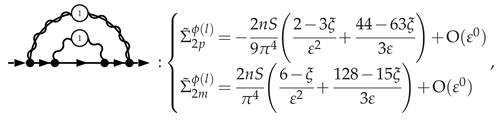
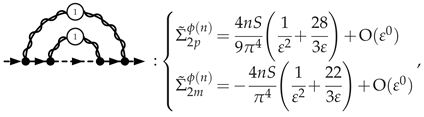
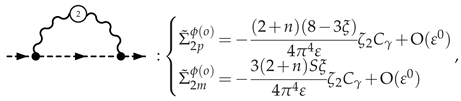
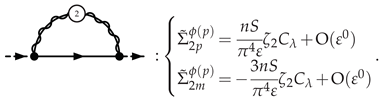
4. Critical Exponents and Observables
4.1. Results for Fermionic QED
 | (114a) |
| (114b) | |
| (114c) | |
| (114d) |
4.2. Results for SQED
 | (116a) |
| (116b) | |
| (116c) | |
| (116d) | |
| (116e) | |
| (116f) |
4.3. Results for Bosonic QED
 | (119a) |
| (119b) | |
| (119c) | |
| (119d) |
4.4. Results for Reduced QED (Graphene)
 | (124a) |
| (124b) | |
| (124c) | |
| (124d) |
4.5. Results for Reduced SQED (Super-Graphene)
 | (136a) |
| (136b) | |
| (136c) | |
| (136d) | |
| (136e) | |
| (136f) |
4.6. Stability of the IR Fixed Point
5. Dynamical (Matter) Mass Generation

5.1. The (Semi-Phenomenological) Gap Equation
5.2. Results for (S)QED
5.3. Results for (S)QED (Graphene and Super-Graphene)
5.4. Meta-Analysis of the Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Appendix on Multiloop Massless Techniques
Appendix A.1. One Loop
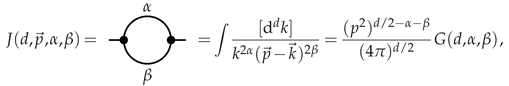
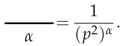
Appendix A.2. Two Loop
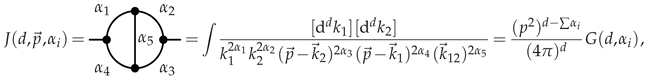




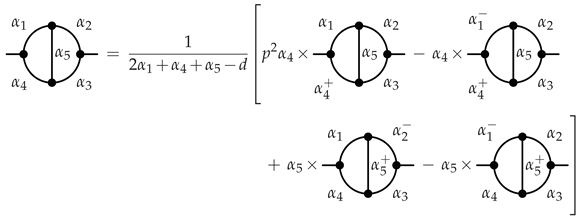
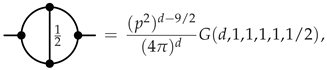
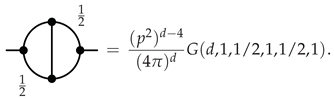
References
- Appelquist, T.; Pisarski, R.D. High-Temperature Yang–Mills Theories and Three-Dimensional Quantum Chromodynamics. Phys. Rev. D 1981, 23, 2305. [Google Scholar] [CrossRef]
- Appelquist, T.; Heinz, U.W. Three-dimensional O(N) theories at large distances. Phys. Rev. D 1981, 24, 2169. [Google Scholar] [CrossRef]
- Pisarski, R.D. Chiral Symmetry Breaking in Three-Dimensional Electrodynamics. Phys. Rev. 1984, D29, 2423. [Google Scholar] [CrossRef]
- Appelquist, T.W.; Bowick, M.J.; Karabali, D.; Wijewardhana, L. Spontaneous Chiral Symmetry Breaking in Three-Dimensional QED. Phys. Rev. D 1986, 33, 3704. [Google Scholar] [CrossRef]
- Appelquist, T.; Nash, D.; Wijewardhana, L.C.R. Critical Behavior in (2+1)-Dimensional QED. Phys. Rev. Lett. 1988, 60, 2575. [Google Scholar] [CrossRef] [PubMed]
- Nash, D. Higher Order Corrections in (2+1)-Dimensional QED. Phys. Rev. Lett. 1989, 62, 3024. [Google Scholar] [CrossRef]
- Atkinson, D.; Johnson, P.W.; Maris, P. Dynamical Mass Generation in QED in Three-dimensions: Improved Vertex Function. Phys. Rev. 1990, D42, 602–609. [Google Scholar] [CrossRef]
- Pennington, M.R.; Walsh, D. Masses from nothing: A Nonperturbative study of QED in three-dimensions. Phys. Lett. 1991, B253, 246–251. [Google Scholar] [CrossRef]
- Kotikov, A.V. Critical behavior of 3D electrodynamics. JETP Lett. 1993, 58, 731–735. [Google Scholar]
- Kotikov, A.V. On the Critical Behavior of (2+1)-Dimensional QED. Phys. Atom. Nucl. 2012, 75, 890–892. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Hams, A.H.; Reenders, M. (2+1)-dimensional QED with dynamically massive fermions in the vacuum polarization. Phys. Rev. 1996, D53, 2227–2235. [Google Scholar] [CrossRef] [PubMed]
- Maris, P. The Influence of the full vertex and vacuum polarization on the fermion propagator in QED in three-dimensions. Phys. Rev. 1996, D54, 4049–4058. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Reenders, M. Infrared cutoff dependence of the critical flavor number in QED(3). Phys. Rev. 2003, D68, 025017. [Google Scholar] [CrossRef]
- Fischer, C.S.; Alkofer, R.; Dahm, T.; Maris, P. Dynamical chiral symmetry breaking in unquenched QED(3). Phys. Rev. 2004, D70, 073007. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Pyatkovskiy, P.K. Critical number of fermions in three-dimensional QED. Phys. Rev. 2016, D94, 125009. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Shilin, V.I.; Teber, S. Critical behavior of (2+1)-dimensional QED: 1/Nf corrections in the Landau gauge. Phys. Rev. 2016, D94, 056009, Erratum in Phys. Rev. 2019, D99, 119901. [Google Scholar] [CrossRef]
- Kotikov, A.; Teber, S. Critical behavior of (2+1)-dimensional QED: 1/Nf corrections in an arbitrary nonlocal gauge. Phys. Rev. D 2016, 94, 114011, Addendum in Phys. Rev. D 2019, 99, 059902. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. Numerical determination of monopole scaling dimension in parity-invariant three-dimensional noncompact QED. Phys. Rev. 2019, D100, 054514. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Critical Behavior of (2+1)-Dimensional QED: 1/N Expansion. Particles 2020, 3, 345–354. [Google Scholar] [CrossRef]
- Kovner, A.; Rosenstein, B. Kosterlitz-Thouless mechanism of two-dimensional superconductivity. Phys. Rev. B 1990, 42, 4748–4751. [Google Scholar] [CrossRef]
- Dorey, N.; Mavromatos, N.E. QED in three-dimension and two-dimensional superconductivity without parity violation. Nucl. Phys. 1992, B386, 614–680. [Google Scholar] [CrossRef]
- Franz, M.; Tesanovic, Z. Algebraic Fermi Liquid from Phase Fluctuations: ’Topological’ Fermions, Vortex ’Berryons, ’ and QE D-3 Theory of Cuprate Superconductors. Phys. Rev. Lett. 2001, 87, 257003. [Google Scholar] [CrossRef]
- Herbut, I.F. QED(3) theory of underdoped high temperature superconductors. Phys. Rev. 2002, B66, 094504. [Google Scholar] [CrossRef]
- Farakos, K.; Mavromatos, N.E. Gauge theory approach to planar doped antiferromagnetics and external magnetic fields. Int. J. Mod. Phys. 1997, B12, 809. [Google Scholar] [CrossRef]
- Semenoff, G.W. Condensed Matter Simulation of a Three-dimensional Anomaly. Phys. Rev. Lett. 1984, 53, 2449. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: From tight-binding model to 2+1-dimensional quantum electrodynamics. Int. J. Mod. Phys. 2007, B21, 4611–4658. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Kotov, V.N.; Uchoa, B.; Pereira, V.M.; Neto, A.H.C.; Guinea, F. Electron-Electron Interactions in Graphene: Current Status and Perspectives. Rev. Mod. Phys. 2012, 84, 1067. [Google Scholar] [CrossRef]
- Teber, S. Field Theoretic Study of Electron-Electron Interaction Effects in Dirac Liquids. Habilitation Thesis, Sorbonne Université, Paris, France, 2017. [Google Scholar] [CrossRef]
- Benvenuti, S.; Khachatryan, H. QED’s in 2+1 dimensions: Complex fixed points and dualities. arXiv 2018, arXiv:1812.01544. [Google Scholar]
- Khachatryan, H. Higher Derivative Gauge theory in d=6 and the CP(Nf-1) NLSM. JHEP 2019, 12, 144. [Google Scholar] [CrossRef]
- Khachatryan, H. Exploring the Space of Many-Flavor QED’s in 2 < d < 6. Doctoral Thesis, SISSA, Trieste, Italy, 2019. Available online: https://www.sissa.it/tpp/phdsection/AlumniThesis/Hrachya%20Khachatryan.pdf (accessed on 24 July 2023).
- Gracey, J.A. Large Nf quantum field theory. Int. J. Mod. Phys. A 2019, 33, 1830032. [Google Scholar] [CrossRef]
- Gracey, J. Computation of critical exponent eta at O(1/N(f)**2) in quantum electrodynamics in arbitrary dimensions. Nucl. Phys. B 1994, 414, 614–648. [Google Scholar] [CrossRef]
- Gracey, J.A. Electron mass anomalous dimension at O(1/(Nf(2)) in quantum electrodynamics. Phys. Lett. 1993, B317, 415–420. [Google Scholar] [CrossRef]
- Jackiw, R.; Templeton, S. How Superrenormalizable Interactions Cure their Infrared Divergences. Phys. Rev. D 1981, 23, 2291. [Google Scholar] [CrossRef]
- Templeton, S. Summation of Coupling Constant Logarithms in QED in Three-dimensions. Phys. Rev. 1981, D24, 3134. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Radulovic, Z.M. Infrared Divergences in Three-dimensional Gauge Theories. Phys. Rev. 1984, D30, 1338. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Radulovic, Z.M. Loop Expansion in Massless QED in three-dimensions. Phys. Rev. 1983, D27, 357–365. [Google Scholar] [CrossRef]
- King, I.D.; Thompson, G. Non-Perturbative Analysis of Leading Logarithms in Three-Dimensional QED. Phys. Rev. 1985, D31, 2148–2150. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. Flavor and topological current correlators in parity-invariant three-dimensional QED. Phys. Rev. 2017, D96, 054509. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Kotikov, A.V.; Teber, S. Landau-Khalatnikov-Fradkin transformation in three-dimensional quenched QED. Phys. Rev. 2020, D102, 025013. [Google Scholar] [CrossRef]
- Pikelner, A.F.; Gusynin, V.P.; Kotikov, A.V.; Teber, S. Four-loop singularities of the massless fermion propagator in quenched three-dimensional QED. Phys. Rev. D 2020, 102, 105012. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Consequences of anomalous Ward identities. Phys. Lett. B 1971, 37, 95–97. [Google Scholar] [CrossRef]
- Koopmans, M.; Steringa, J.J. Dynamical Mass Generation in Supersymmetric QED in Three-dimensions. Phys. Lett. 1989, B226, 309–312. [Google Scholar] [CrossRef]
- Benvenuti, S.; Khachatryan, H. Easy-plane QED3’s in the large Nf limit. JHEP 2019, 5, 214. [Google Scholar] [CrossRef]
- Clark, T.E.; Love, S.T. Supersymmetric Quantum Electrodynamics and Dynamical Chiral Symmetry Breaking. Nucl. Phys. B 1988, 310, 371–386. [Google Scholar] [CrossRef]
- Walker, M.; Burden, C. Chiral symmetry in supersymmetric three-dimensional quantum electrodynamics. Phys. Rev. D 1999, 59, 125013. [Google Scholar] [CrossRef]
- Campbell-Smith, A.; Mavromatos, N. On dynamical mass generation in three dimensional supersymmetric U(1) gauge field theory. Phys. Rev. D 1999, 60, 105011. [Google Scholar] [CrossRef]
- Campbell-Smith, A.; Mavromatos, N.; Papavassiliou, J. Gauge coupling instability and dynamical mass generation in N = 1 supersymmetric QED(3). Phys. Rev. D 1999, 60, 085002. [Google Scholar] [CrossRef]
- Gremm, M.; Katz, E. Mirror symmetry for N=1 QED in three-dimensions. JHEP 2000, 2, 008. [Google Scholar] [CrossRef]
- Gukov, S.; Tong, D. D-brane probes of special holonomy manifolds, and dynamics of N = 1 three-dimensional gauge theories. JHEP 2002, 4, 050. [Google Scholar] [CrossRef]
- Bashmakov, V.; Gomis, J.; Komargodski, Z.; Sharon, A. Phases of N=1 theories in 2 + 1 dimensions. JHEP 2018, 7, 123. [Google Scholar] [CrossRef]
- Benini, F.; Benvenuti, S. N = 1 dualities in 2+1 dimensions. JHEP 2018, 11, 197. [Google Scholar] [CrossRef]
- Gaiotto, D.; Komargodski, Z.; Wu, J. Curious Aspects of Three-Dimensional N=1 SCFTs. JHEP 2018, 8, 004. [Google Scholar] [CrossRef]
- Benini, F.; Benvenuti, S. N=1 QED in 2+1 dimensions: Dualities and enhanced symmetries. arXiv 2018, arXiv:1804.05707. [Google Scholar] [CrossRef]
- Lee, S.S. Emergence of supersymmetry at a critical point of a lattice model. Phys. Rev. B 2007, 76, 075103. [Google Scholar] [CrossRef]
- Roy, B.; Juričić, V.; Herbut, I.F. Quantum superconducting criticality in graphene and topological insulators. Phys. Rev. B 2013, 87, 041401. [Google Scholar] [CrossRef]
- Grover, T.; Sheng, D.N.; Vishwanath, A. Emergent Space-Time Supersymmetry at the Boundary of a Topological Phase. Science 2014, 344, 280–283. [Google Scholar] [CrossRef] [PubMed]
- Ponte, P.; Lee, S.S. Emergence of supersymmetry on the surface of three dimensional topological insulators. New J. Phys. 2014, 16, 013044. [Google Scholar] [CrossRef]
- Jian, S.K.; Jiang, Y.F.; Yao, H. Emergent Spacetime Supersymmetry in 3D Weyl Semimetals and 2D Dirac Semimetals. Phys. Rev. Lett. 2015, 114, 237001. [Google Scholar] [CrossRef] [PubMed]
- Witczak-Krempa, W.; Maciejko, J. Optical conductivity of topological surface states with emergent supersymmetry. Phys. Rev. Lett. 2016, 116, 100402, Addendum in Phys. Rev. Lett. 2016, 117, 149903.. [Google Scholar] [CrossRef]
- Jian, S.K.; Lin, C.H.; Maciejko, J.; Yao, H. Emergence of supersymmetric quantum electrodynamics. Phys. Rev. Lett. 2017, 118, 166802. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Lee, J.; Moon, E.G. Lattice vibration as a knob for novel quantum criticality: Emergence of supersymmetry from spin-lattice coupling. arXiv 2019, arXiv:1911.01435. [Google Scholar]
- Zhao, P.L.; Liu, G.Z. Absence of emergent supersymmetry at superconducting quantum critical points in Dirac and Weyl semimetals. Materials 2019, 4, 37. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Gusynin, V.P.; Miransky, V.A. Dynamical chiral symmetry breaking on a brane in reduced QED. Phys. Rev. D 2001, 64, 105028. [Google Scholar] [CrossRef]
- Teber, S. Electromagnetic current correlations in reduced quantum electrodynamics. Phys. Rev. 2012, D86, 025005. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Two-loop fermion self-energy in reduced quantum electrodynamics and application to the ultrarelativistic limit of graphene. Phys. Rev. D 2014, 89, 065038. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Lee, J.W.; Son, D.T.; Stephanov, M.A. Conformality Lost. Phys. Rev. D 2009, 80, 125005. [Google Scholar] [CrossRef]
- Marino, E.C. Quantum electrodynamics of particles on a plane and the Chern-Simons theory. Nucl. Phys. B 1993, 408, 551–564. [Google Scholar] [CrossRef]
- Son, D.T. Is the Composite Fermion a Dirac Particle? Phys. Rev. X 2015, 5, 031027. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Gusynin, V.P.; Miransky, V.A.; Shovkovy, I.A. Magnetic field driven metal insulator phase transition in planar systems. Phys. Rev. B 2002, 66, 045108. [Google Scholar] [CrossRef]
- Gonzalez, J.; Guinea, F.; Vozmediano, M.A.H. NonFermi liquid behavior of electrons in the half filled honeycomb lattice (A Renormalization group approach). Nucl. Phys. B 1994, 424, 595–618. [Google Scholar] [CrossRef]
- Kotikov, A.; Teber, S. Critical behaviour of reduced QED4,3 and dynamical fermion gap generation in graphene. Phys. Rev. D 2016, 94, 114010, Erratum in Phys. Rev. D 2019, 99, 119902. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Note on an application of the method of uniqueness to reduced quantum electrodynamics. Phys. Rev. D 2013, 87, 087701. [Google Scholar] [CrossRef]
- Herbut, I.F.; Mastropietro, V. Universal conductivity of graphene in the ultrarelativistic regime. Phys. Rev. B 2013, 87, 205445. [Google Scholar] [CrossRef]
- Valenzuela, D.; Hernández-Ortiz, S.; Loewe, M.; Raya, A. Graphene transparency in weak magnetic fields. J. Phys. A 2015, 48, 065402. [Google Scholar] [CrossRef]
- Hernández-Ortiz, S.; Valenzuela, D.; Raya, A.; Sánchez-Madrigal, S. Light absorption in distorted graphene. Int. J. Mod. Phys. 2016, 30, 1650084. [Google Scholar] [CrossRef]
- Teber, S.; Kotikov, A.V. Field theoretic renormalization study of reduced quantum electrodynamics and applications to the ultrarelativistic limit of Dirac liquids. Phys. Rev. 2018, D97, 074004. [Google Scholar] [CrossRef]
- Marino, E.C.; Nascimento, L.O.; Alves, V.S.; Smith, C.M. Interaction Induced Quantum Valley Hall Effect in Graphene. Phys. Rev. X 2015, 5, 011040. [Google Scholar] [CrossRef]
- Sérgio Alves, V.; Junior, R.O.C.; Marino, E.C.; Nascimento, L.O. Dynamical Mass Generation in Pseudo Quantum Electrodynamics with Four–Fermion Interactions. arXiv 2017, arXiv:1704.00381. [Google Scholar] [CrossRef]
- Marino, E.C.; Nascimento, L.O.; Alves, V.S.; Smith, C.M. Unitarity of theories containing fractional powers of the d’Alembertian operator. Phys. Rev. D 2014, 90, 105003. [Google Scholar] [CrossRef]
- Ahmad, A.; Cobos-Martínez, J.J.; Concha-Sánchez, Y.; Raya, A. Landau-Khalatnikov-Fradkin transformations in Reduced Quantum Electrodynamics. Phys. Rev. D 2016, 93, 094035. [Google Scholar] [CrossRef]
- James, A.; Kotikov, A.V.; Teber, S. Landau-Khalatnikov-Fradkin transformation of the fermion propagator in massless reduced QED. Phys. Rev. D 2020, 101, 045011. [Google Scholar] [CrossRef]
- Hsiao, W.H.; Son, D.T. Duality and universal transport in mixed-dimension electrodynamics. Phys. Rev. B 2017, 96, 075127. [Google Scholar] [CrossRef]
- Herzog, C.P.; Huang, K.W. Boundary Conformal Field Theory and a Boundary Central Charge. JHEP 2017, 10, 189. [Google Scholar] [CrossRef]
- Bashmakov, V.; Bertolini, M.; Raj, H. On non-supersymmetric conformal manifolds: Field theory and holography. JHEP 2017, 11, 167. [Google Scholar] [CrossRef]
- Karch, A.; Sato, Y. Conformal Manifolds with Boundaries or Defects. JHEP 2018, 7, 156. [Google Scholar] [CrossRef]
- Dudal, D.; Mizher, A.J.; Pais, P. Exact quantum scale invariance of three-dimensional reduced QED theories. Phys. Rev. D 2019, 99, 045017. [Google Scholar] [CrossRef]
- Di Pietro, L.; Gaiotto, D.; Lauria, E.; Wu, J. 3d Abelian Gauge Theories at the Boundary. JHEP 2019, 05, 091. [Google Scholar] [CrossRef]
- Giombi, S.; Khanchandani, H. O(N) models with boundary interactions and their long range generalizations. JHEP 2020, 8, 010. [Google Scholar] [CrossRef]
- Herzog, C.P.; Huang, K.W.; Shamir, I.; Virrueta, J. Superconformal Models for Graphene and Boundary Central Charges. JHEP 2018, 9, 161. [Google Scholar] [CrossRef]
- Kumar Gupta, R.; Herzog, C.P.; Jeon, I. Duality and Transport for Supersymmetric Graphene from the Hemisphere Partition Function. JHEP 2020, 5, 023. [Google Scholar] [CrossRef]
- Metayer, S.; Teber, S. Electron mass anomalous dimension at O(1/Nf2) in three-dimensional N = 1 supersymmetric QED. Phys. Lett. B 2023, 838, 137729. [Google Scholar] [CrossRef]
- Siegel, W. Supersymmetric Dimensional Regularization via Dimensional Reduction. Phys. Lett. B 1979, 84, 193–196. [Google Scholar] [CrossRef]
- Siegel, W. Inconsistency of Supersymmetric Dimensional Regularization. Phys. Lett. B 1980, 94, 37–40. [Google Scholar] [CrossRef]
- Capper, D.; Jones, D.; van Nieuwenhuizen, P. Regularization by Dimensional Reduction of Supersymmetric and Nonsupersymmetric Gauge Theories. Nucl. Phys. B 1980, 167, 479–499. [Google Scholar] [CrossRef]
- Jack, I.; Jones, D. Regularization of supersymmetric theories. In Perspectives on Supersymmetry II; Kane, G.L., Ed.; World Scientific Publishing Company: Singapore, 2010; Volume 21, pp. 494–513. [Google Scholar] [CrossRef]
- Mihaila, L. Precision Calculations in Supersymmetric Theories. Adv. High Energy Phys. 2013, 2013, 607807. [Google Scholar] [CrossRef]
- Kotikov, A.V.; Teber, S. Multi-loop techniques for massless Feynman diagram calculations. Phys. Part. Nucl. 2019, 50, 1–41. [Google Scholar] [CrossRef]
- Denner, A.; Eck, H.; Hahn, O.; Kublbeck, J. Compact Feynman rules for Majorana fermions. Phys. Lett. B 1992, 291, 278–280. [Google Scholar] [CrossRef]
- Denner, A.; Eck, H.; Hahn, O.; Kublbeck, J. Feynman rules for fermion number violating interactions. Nucl. Phys. B 1992, 387, 467–481. [Google Scholar] [CrossRef]
- Nogueira, P. Automatic Feynman Graph Generation. J. Comput. Phys. 1993, 105, 279–289. [Google Scholar] [CrossRef]
- Nogueira, P. Feynman graph generation and propagator mixing, I. Comput. Phys. Commun. 2021, 269, 108103. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Supergauge Invariant Extension of Quantum Electrodynamics. Nucl. Phys. B 1974, 78, 1–13. [Google Scholar] [CrossRef]
- Zumino, B. Gauge properties of propagators in quantum electrodynamics. J. Math. Phys. 1960, 1, 1–7. [Google Scholar] [CrossRef]
- Walker, M. A Completely invariant SUSY transform of supersymmetric QED. J. Phys. G 2004, 30, 1219–1224. [Google Scholar] [CrossRef]
- Furry, W.H. A Symmetry Theorem in the Positron Theory. Phys. Rev. 1937, 51, 125–129. [Google Scholar] [CrossRef]
- Kazakov, D.I. Multiloop Calculations: Method of Uniqueness and Functional Equations. Teor. Mat. Fiz. 1984, 62, 127–135. [Google Scholar] [CrossRef]
- Kotikov, A.V. The Gegenbauer Polynomial technique: The evaluation of a class of Feynman diagrams. Phys. Lett. B 1996, 375, 240–248. [Google Scholar] [CrossRef]
- Gusynin, V.; Hams, A.; Reenders, M. Nonperturbative infrared dynamics of three-dimensional QED with four fermion interaction. Phys. Rev. D 2001, 63, 045025. [Google Scholar] [CrossRef]
- Hollik, W.; Kraus, E.; Stockinger, D. Renormalization and symmetry conditions in supersymmetric QED. Eur. Phys. J. C 1999, 11, 365–381. [Google Scholar] [CrossRef]
- Rupp, C.; Scharf, R.; Sibold, K. Susy Ward identity and its use in SQED. Nucl. Phys. B Proc. Suppl. 2000, 89, 272–276. [Google Scholar] [CrossRef]
- Metayer, S.; Teber, S. Two-loop mass anomalous dimension in reduced quantum electrodynamics and application to dynamical fermion mass generation. JHEP 2021, 09, 107. [Google Scholar] [CrossRef]
- Peres, N.M.R. Colloquium: The Transport properties of graphene: An Introduction. Rev. Mod. Phys. 2010, 82, 2673–2700. [Google Scholar] [CrossRef]
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Universal Dynamic Conductivity and Quantized Visible Opacity of Suspended Graphene. arXiv 2008, arXiv:0803.3718. [Google Scholar] [CrossRef]
- Appelquist, T.; Bowick, M.J.; Karabali, D.; Wijewardhana, L. Spontaneous Breaking of Parity in (2+1)-dimensional QED. Phys. Rev. D 1986, 33, 3774. [Google Scholar] [CrossRef]
- Rembiesa, P. Gauge independent bifurcation to the chiral symmetry breaking solution of the Dyson-Schwinger equation in continuum QED. Phys. Rev. D 1990, 41, 2009–2014. [Google Scholar] [CrossRef]
- Atkinson, D.; Bloch, J.C.R.; Gusynin, V.P.; Pennington, M.R.; Reenders, M. Strong QED with weak gauge dependence: Critical coupling and anomalous dimension. Phys. Lett. B 1994, 329, 117–122. [Google Scholar] [CrossRef]
- Bloch, J.C.R. Numerical Investigation of Fermion Mass Generation in QED. Doctoral Thesis, University of Durham, Durham, UK, 1995. [Google Scholar]
- Bardeen, W.A.; Leung, C.N.; Love, S.T. The Dilaton and Chiral Symmetry Breaking. Phys. Rev. Lett. 1986, 56, 1230. [Google Scholar] [CrossRef]
- Leung, C.N.; Love, S.; Bardeen, W.A. Spontaneous Symmetry Breaking in Scale Invariant Quantum Electrodynamics. Nucl. Phys. B 1986, 273, 649–662. [Google Scholar] [CrossRef]
- Miransky, V.A.; Yamawaki, K. On Gauge Theories with Additional Four Fermion Interaction. Mod. Phys. Lett. A 1989, 4, 129–135. [Google Scholar] [CrossRef]
- Leung, C.N.; Love, S.T.; Bardeen, W.A. Aspects of Dynamical Symmetry Breaking in Gauge Field Theories. Nucl. Phys. B 1989, 323, 493–512. [Google Scholar] [CrossRef]
- Kondo, K.I.; Tanabashi, M.; Yamawaki, K. Renormalization in the gauged Nambu-Jona-Lasinio model. Prog. Theor. Phys. 1993, 89, 1249–1302. [Google Scholar] [CrossRef]
- Ihrig, B.; Zerf, N.; Marquard, P.; Herbut, I.F.; Scherer, M.M. Abelian Higgs model at four loops, fixed-point collision and deconfined criticality. Phys. Rev. B 2019, 100, 134507. [Google Scholar] [CrossRef]
- Dagotto, E.; Kocic, A.; Kogut, J.B. Collapse of the wave function, anomalous dimensions and continuum limits in model scalar field theories. Phys. Lett. B 1990, 237, 268–273. [Google Scholar] [CrossRef]
- Shamir, Y. Chiral symmetry breaking in supersymmetric QCD. Phys. Rev. Lett. 1991, 66, 3101–3104. [Google Scholar] [CrossRef] [PubMed]
- Shamir, Y. Supersymmetric QCD chiral symmetry breaking in the ladder approximation. Nucl. Phys. B 1991, 352, 469–488. [Google Scholar] [CrossRef]
- Appelquist, T.; Nyffeler, A.; Selipsky, S.B. Analyzing chiral symmetry breaking in supersymmetric gauge theories. Phys. Lett. B 1998, 425, 300–308. [Google Scholar] [CrossRef]
- Curtis, D.; Pennington, M.; Walsh, D. Dynamical mass generation in QED3 and the 1/N expansion. Phys. Lett. 1992, 295, 313–319. [Google Scholar] [CrossRef]
- Pisarski, R.D. Fermion mass in three dimensions and the renormalization group. Phys. Rev. D 1991, 44, 1866–1872. [Google Scholar] [CrossRef] [PubMed]
- Azcoiti, V.; Luo, X.Q. (2+1)-dimensional compact QED with dynamical fermions. Nucl. Phys. Proc. Suppl. 1993, 30, 741–744. [Google Scholar] [CrossRef]
- Azcoiti, V.; Laliena, V.; Luo, X.Q. Investigation of spontaneous symmetry breaking from a nonstandard approach. Nucl. Phys. B Proc. Suppl. 1996, 47, 565–568. [Google Scholar] [CrossRef]
- Giombi, S.; Klebanov, I.R.; Tarnopolsky, G. Conformal QEDd, F-Theorem and the α Expansion. J. Phys. A 2016, 49, 135403. [Google Scholar] [CrossRef]
- Janssen, L. Spontaneous breaking of Lorentz symmetry in (2+ε)-dimensional QED. Phys. Rev. D 2016, 94, 094013. [Google Scholar] [CrossRef]
- Braun, J.; Gies, H.; Janssen, L.; Roscher, D. Phase structure of many-flavor QED3. Phys. Rev. D 2014, 90, 036002. [Google Scholar] [CrossRef]
- Kubota, K.I.; Terao, H. Dynamical symmetry breaking in QED(3) from the Wilson RG point of view. Prog. Theor. Phys. 2001, 105, 809–825. [Google Scholar] [CrossRef]
- Dagotto, E.; Kogut, J.B.; Kocic, A. A Computer Simulation of Chiral Symmetry Breaking in (2+1)-Dimensional QED with N Flavors. Phys. Rev. Lett. 1989, 62, 1083. [Google Scholar] [CrossRef] [PubMed]
- Dagotto, E.; Kocic, A.; Kogut, J.B. Chiral Symmetry Breaking in Three-dimensional QED With N(f) Flavors. Nucl. Phys. B 1990, 334, 279–301. [Google Scholar] [CrossRef]
- Herbut, I.F. Chiral symmetry breaking in three-dimensional quantum electrodynamics as fixed point annihilation. Phys. Rev. D 2016, 94, 025036. [Google Scholar] [CrossRef]
- Giombi, S.; Tarnopolsky, G.; Klebanov, I.R. On CJ and CT in Conformal QED. JHEP 2016, 08, 156. [Google Scholar] [CrossRef]
- Di Pietro, L.; Komargodski, Z.; Shamir, I.; Stamou, E. Quantum Electrodynamics in d = 3 from the ε Expansion. Phys. Rev. Lett. 2016, 116, 131601. [Google Scholar] [CrossRef] [PubMed]
- Appelquist, T.; Cohen, A.G.; Schmaltz, M. A New constraint on strongly coupled gauge theories. Phys. Rev. D 1999, 60, 045003. [Google Scholar] [CrossRef]
- Hands, S.J.; Kogut, J.B.; Scorzato, L.; Strouthos, C.G. Non-compact QED(3) with N(f) = 1 and N(f) = 4. Phys. Rev. B 2004, 70, 104501. [Google Scholar] [CrossRef]
- Strouthos, C.; Kogut, J.B. The Phases of Non-Compact QED(3). PoS 2007, 42, 278. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. No evidence for bilinear condensate in parity-invariant three-dimensional QED with massless fermions. Phys. Rev. D 2016, 93, 045020. [Google Scholar] [CrossRef]
- Karthik, N.; Narayanan, R. Scale-invariance of parity-invariant three-dimensional QED. Phys. Rev. D 2016, 94, 065026. [Google Scholar] [CrossRef]
- Vasiliev, A.N.; Pismak, Y.M.; Khonkonen, Y.R. 1/n Expansion: Calculation of the exponents η and ν in the order 1/n2 for arbitrary number of dimensions. Theor. Math. Phys. 1981, 47, 465–475. [Google Scholar] [CrossRef]
- Chetyrkin, K.G.; Tkachov, F.V. Integration by parts: The algorithm to calculate β-functions in 4 loops. Nucl. Phys. 1981, 192, 159–204. [Google Scholar] [CrossRef]
- Tkachov, F. A theorem on analytical calculability of 4-loop renormalization group functions. Phys. Lett. B 1981, 100, 65–68. [Google Scholar] [CrossRef]
- Lee, R.N. Presenting LiteRed: A tool for the Loop InTEgrals REDuction. arXiv 2012, arXiv:1212.2685. [Google Scholar]
- Lee, R.N. LiteRed 1.4: A powerful tool for reduction of multiloop integrals. J. Phys. Conf. Ser. 2014, 523, 012059. [Google Scholar] [CrossRef]
- Huber, T.; Maître, D. HypExp, a Mathematica package for expanding hypergeometric functions around integer-valued parameters. Comput. Phys. Commun. 2006, 175, 122–144. [Google Scholar] [CrossRef]
- Huber, T.; Maître, D. HypExp 2, Expanding hypergeometric functions about half-integer parameters. Comput. Phys. Commun. 2008, 178, 755–776. [Google Scholar] [CrossRef]
- Smirnov, A.V.; Tentyukov, M.N. Feynman Integral Evaluation by a Sector decomposiTion Approach (FIESTA). Comput. Phys. Commun. 2009, 180, 735–746. [Google Scholar] [CrossRef]
- Smirnov, A.V.; Tentyukov, M. FIESTA 2: Parallelizeable multiloop numerical calculations. Comput. Phys. Commun. 2011, 182, 790–803. [Google Scholar] [CrossRef]
- Smirnov, A.V. FIESTA 3: Cluster-parallelizable multiloop numerical calculations in physical regions. Comput. Phys. Commun. 2014, 185, 2090–2100. [Google Scholar] [CrossRef]
- Ferguson, H.R.P.; Bailey, D.H.; Arno, S. Analysis of PSLQ, an integer relation finding algorithm. Math. Comput. 1999, 68, 351–369. [Google Scholar] [CrossRef]

| Model | S | n | |
|---|---|---|---|
| SQED | 1 | 2 | 1 |
| Bosonic QED | 1 | 0 | 0 |
| Fermionic QED | 0 | 2 | 0 |
| fQED | |
| SQED | |
| bQED |
| in fQED | Method | Year |
|---|---|---|
| ∞ | Schwinger–Dyson (LO) | 1984 [3] |
| ∞ | Schwinger–Dyson (non-pert., Landau gauge) | 1990, 1992 [8,134] |
| ∞ | RG study | 1991 [135] |
| ∞ | Lattice simulations | 1993, 1996 [136,137] |
| F-theorem | 2015 [138] | |
| Schwinger–Dyson (LO, resum.) | 1989 [6] | |
| RG study (one loop) () | 2016 [139] | |
| 4 | Functional RG () | 2014 [140] |
| RG study | 2001 [141] | |
| Lattice simulations | 1988, 1989 [142,143] | |
| Schwinger–Dyson (NLO, Landau gauge) | 1993 [9,10] | |
| Schwinger–Dyson (NLO, Landau gauge) | 2016 [16] | |
| Schwinger–Dyson (LO, Landau gauge) | 1988 [5] | |
| 3.0084–3.0844 | Schwinger–Dyson (NLO, resum.) | 2016 [17] |
| RG study (one loop) | 2016 [144] | |
| Schwinger–Dyson (NLO, resummation, ) | 2016 [15,17] | |
| F-theorem | 2016 [145] | |
| Effective gap equation (NLO, , double resum.) | 2022 [115] | |
| RG study (one loop) | 2015 [146] | |
| Free energy constraint | 1999 [147] | |
| Lattice simulations | 2004, 2008 [148,149] | |
| 0 | Schwinger–Dyson (non-pert., Landau gauge) | 1990 [7] |
| 0 | Lattice simulations | 2015, 2016 [150,151] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Metayer, S.; Teber, S. Critical Properties of Three-Dimensional Many-Flavor QEDs. Symmetry 2023, 15, 1806. https://doi.org/10.3390/sym15091806
Metayer S, Teber S. Critical Properties of Three-Dimensional Many-Flavor QEDs. Symmetry. 2023; 15(9):1806. https://doi.org/10.3390/sym15091806
Chicago/Turabian StyleMetayer, Simon, and Sofian Teber. 2023. "Critical Properties of Three-Dimensional Many-Flavor QEDs" Symmetry 15, no. 9: 1806. https://doi.org/10.3390/sym15091806
APA StyleMetayer, S., & Teber, S. (2023). Critical Properties of Three-Dimensional Many-Flavor QEDs. Symmetry, 15(9), 1806. https://doi.org/10.3390/sym15091806