Charged Particles Orbiting Charged Black-Bounce Black Holes
Abstract
:1. Introduction
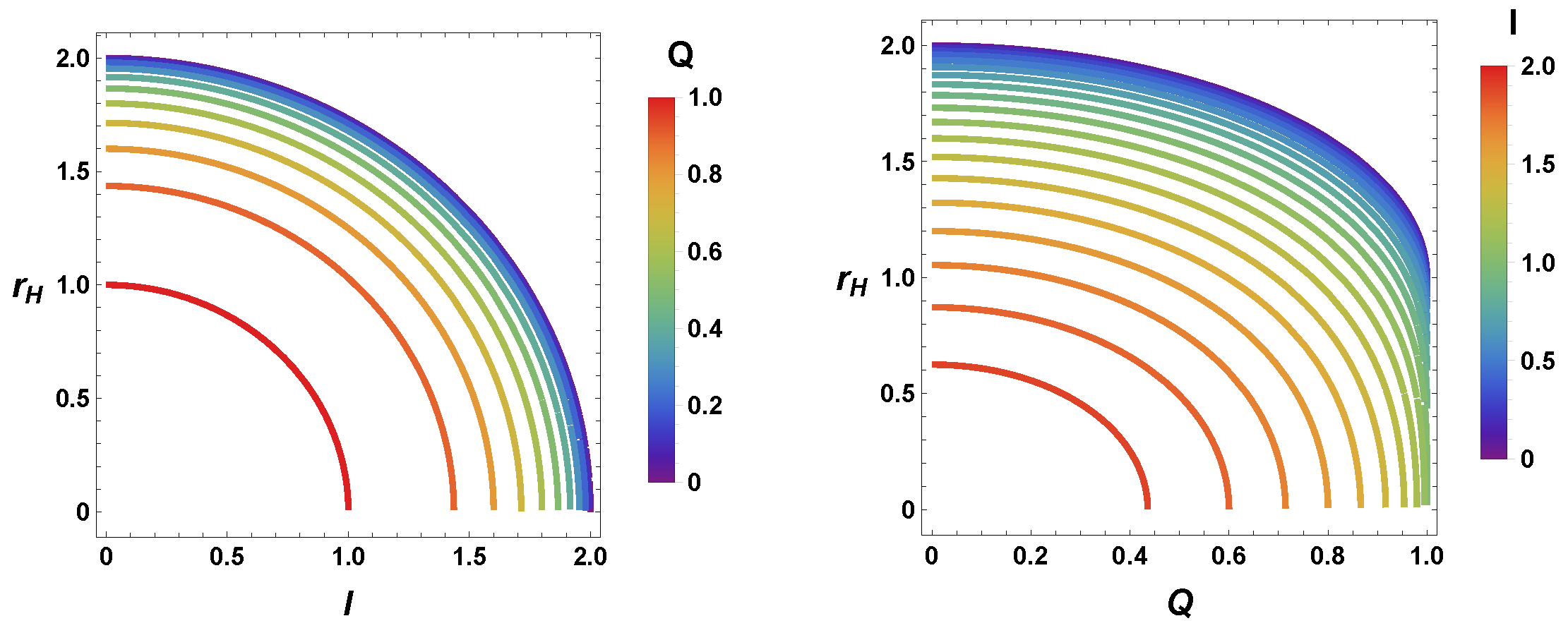
2. Charged Black-Bounce Black holes
3. Charged-Particle Motion
3.1. Equations of Motion for Charged Particles
3.2. Circular Orbits
- a.
- Since is always positive, must be found for any specific charge q and for ;
- b.
- When , then must be satisfied for large values of the particle’s charge.
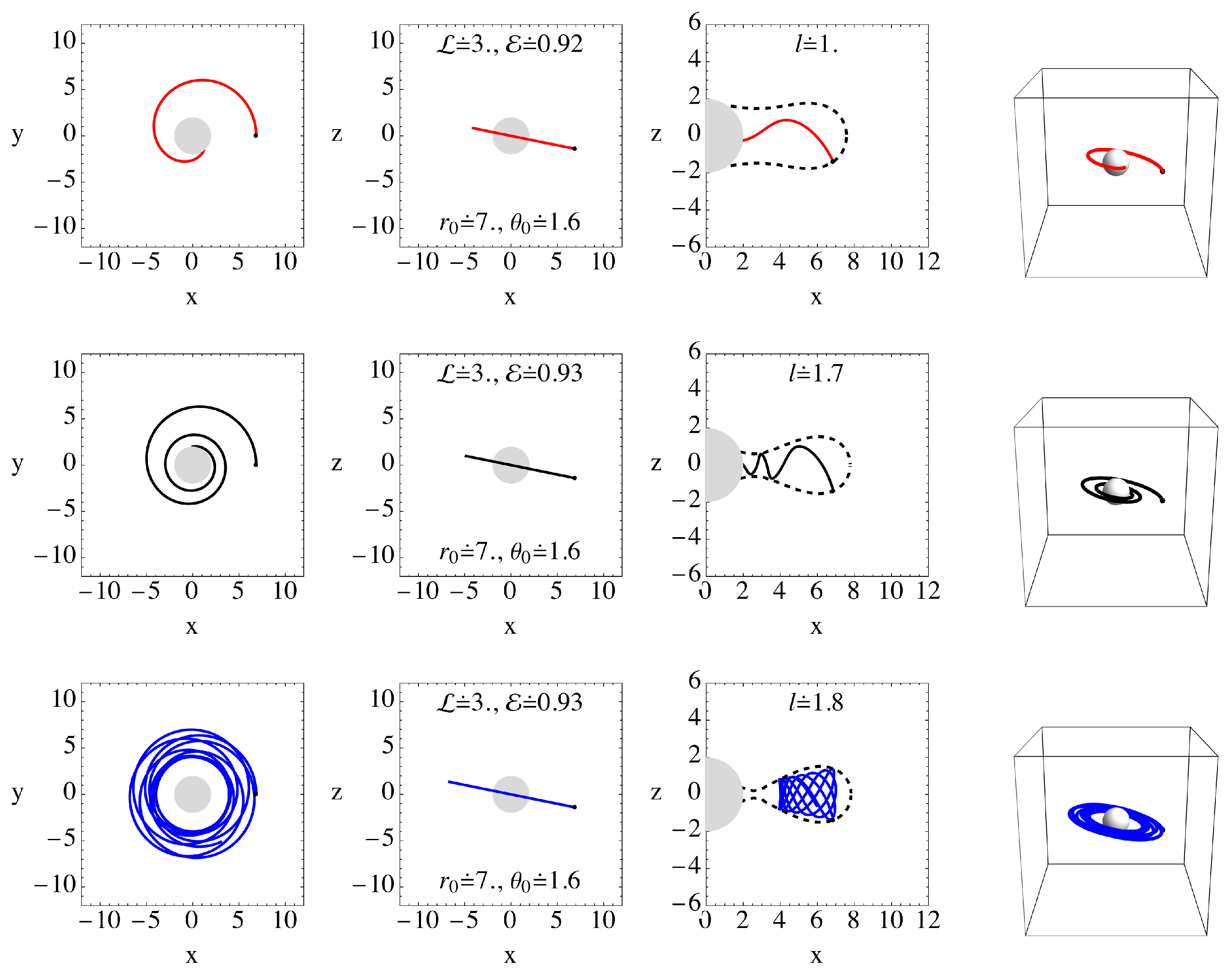
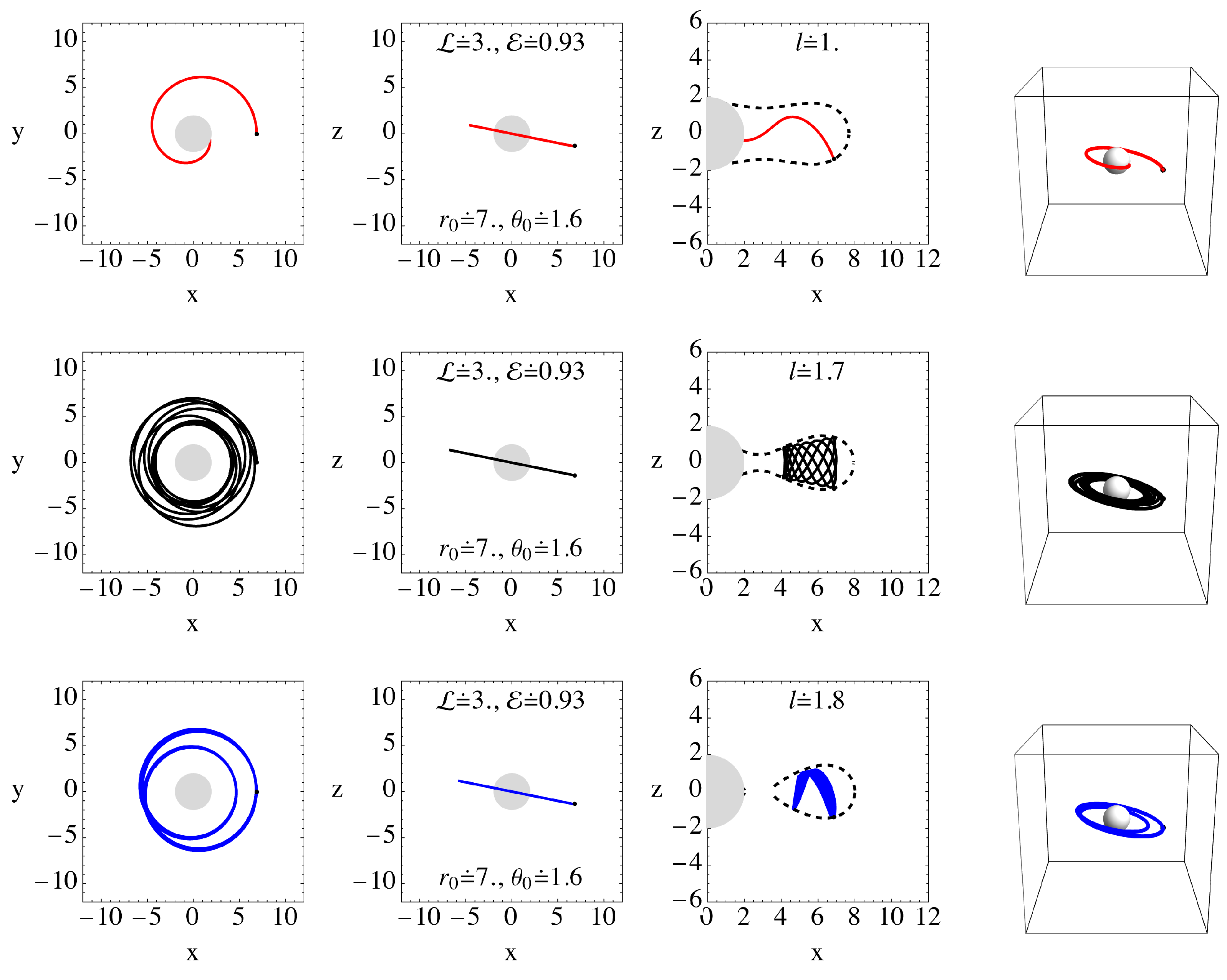
3.3. Charged-Particle Trajectories
3.4. The ISCO Radius
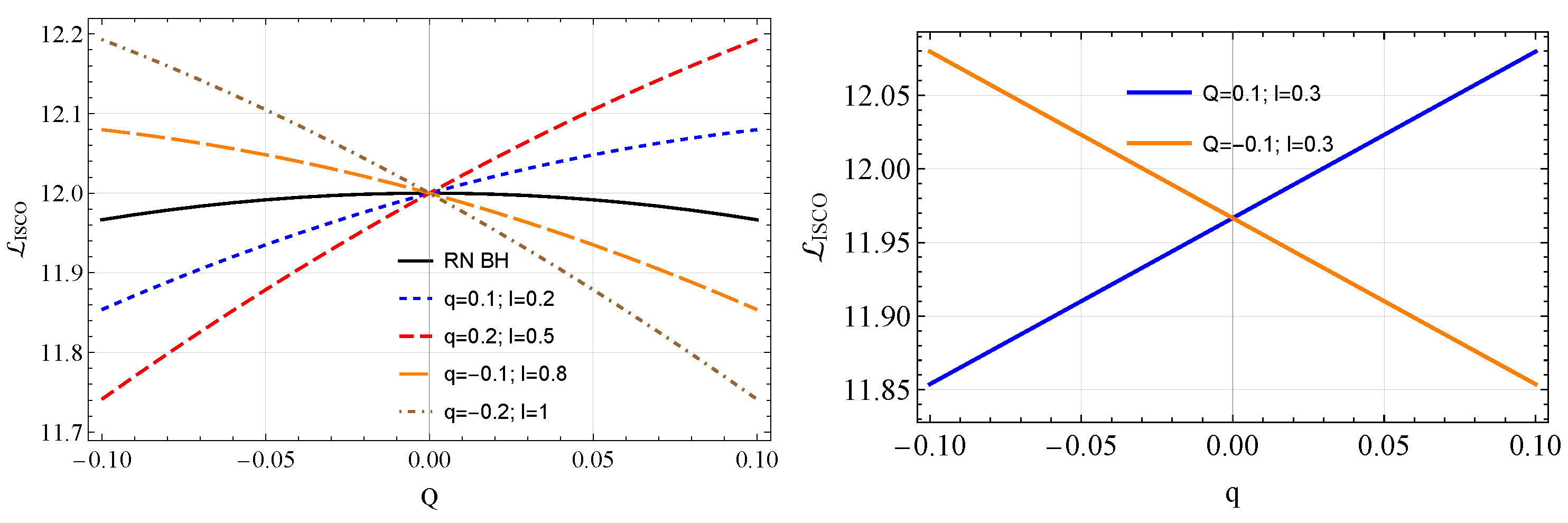
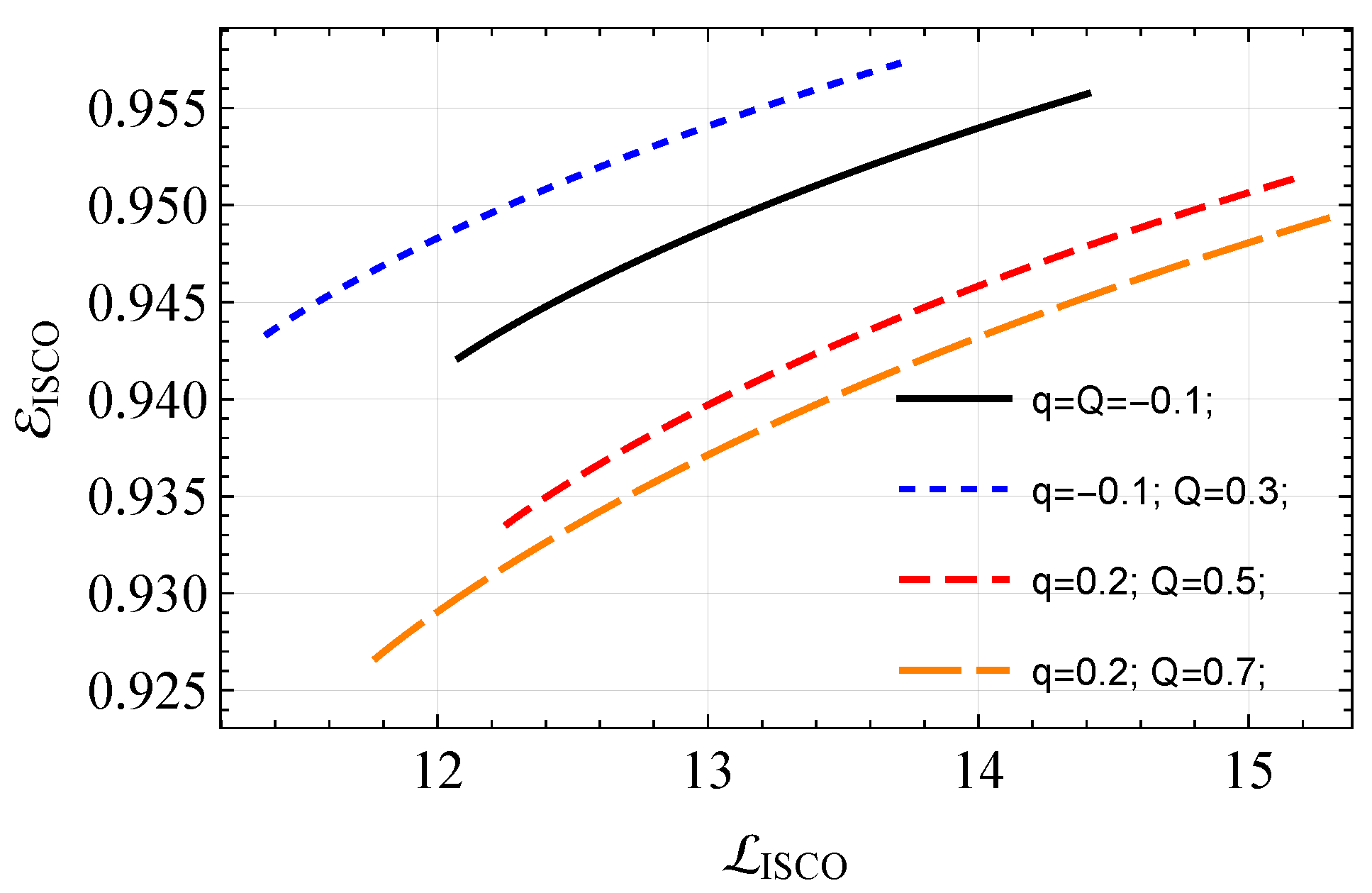
3.5. Angular Momentum at ISCO
3.6. Energy at ISCO
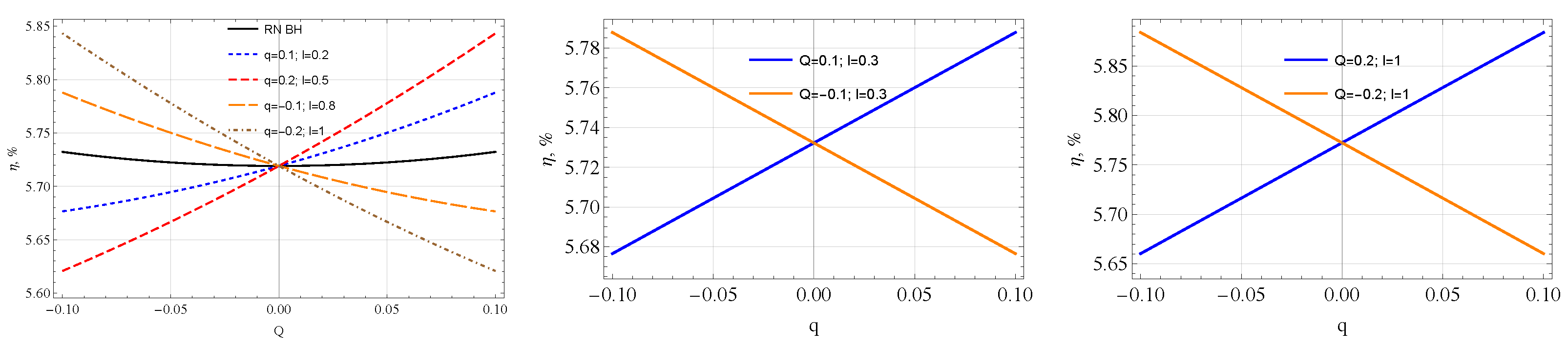
4. The Energy Efficiency
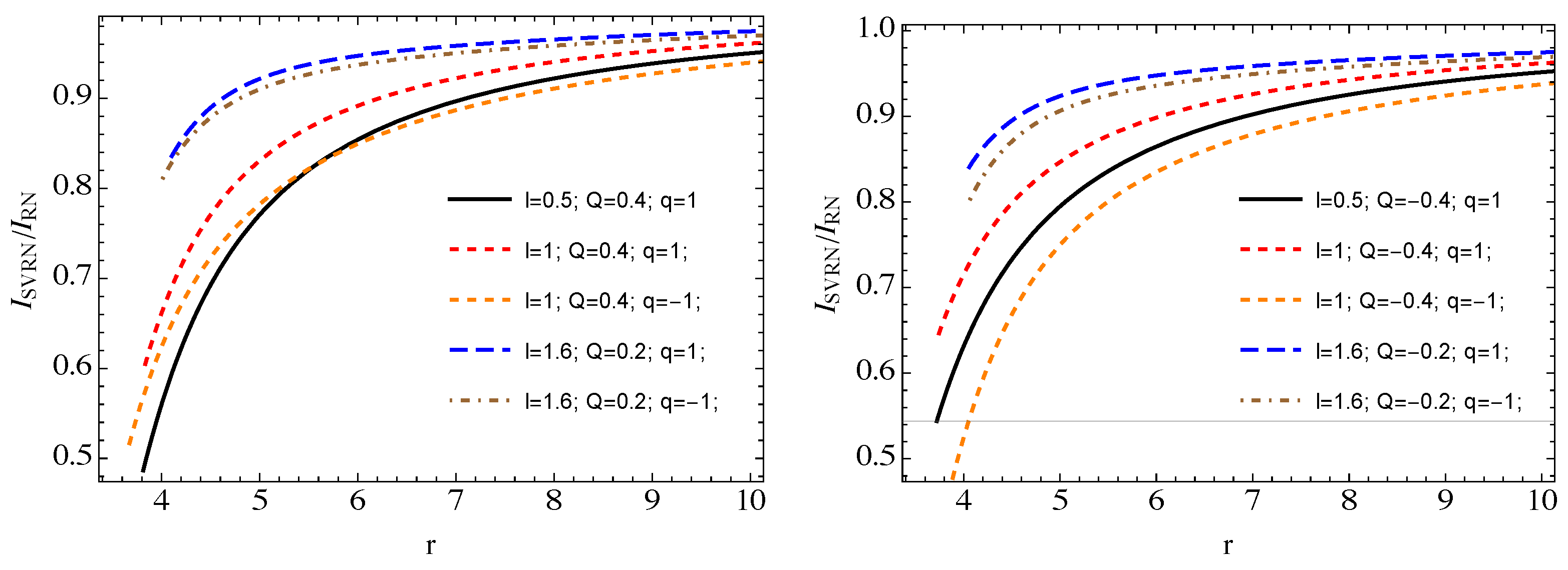
5. Intensity of Electromagnetic Radiation by Accelerated Charged Particle
5.1. Acceleration of Charged Particles in Stable Circular Orbits
5.2. Acceleration of Falling Charged Particles into Central Black Hole
6. Conclusions
- First, we have analyzed the effective potential for circular orbits and found that the gravitational effect of the RN black hole’s charge increases the maximum of the effective potential. However, for positive values of the coupling and the l parameter, the maximum decreases, while, for , the effective potential increases.
- Also, we have studied the circular orbits of charged particles and shown that both the gravitational influence of the black-hole charge and the Coulomb forces contribute to a reduction in the values of angular momentum and energy corresponding to circular orbits. Similarly, the impact of the parameter l also leads to a decrease in both quantities.
- It is also shown that there is a symmetrical behavior in ISCO profiles when q is replaced by and is replaced by Q, i.e., . For (), a minimum in the ISCO values is observed at for (), and when , the ISCO minimum changes to at . The increase in l leads to a decrease in the ISCO radius, ultimately reaching zero at a critical value of l that defines the wormhole spacetime.
- Our performed analyses have shown that the angular momentum () for electrically neutral particles slightly decreases for both negative and positive values of Q. Conversely, in the case of , the angular momentum increases (decreases) for positively (negatively) charged particles.
- In a similar scenario, for , the energy increases, while for , it decreases in a (quasi)linear fashion. It is worth noting that even small variations in the values of q and Q lead to significant changes in both and . Furthermore, a marginal increase in l results in a slight reduction in both the energy and angular momentum.
- In the case of the radiation from orbiting charged particles, the intensity of the radiation decreases with increasing l, as well as in the case of . However, it increases in cases.
- In the case of falling charged particles, the effect of the l parameter is long-lasting at far distances. The intensity rates are almost the same at higher values of l and lower values of . However, for a smaller l and a bigger , the intensity is slightly larger in the case than in the one.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Phys. 1916, 355, 106–120. [Google Scholar] [CrossRef]
- Nordström, G. On the Energy of the Gravitation field in Einstein’s Theory. K. Ned. Akad. Wet. Proc. Ser. Phys. Sci. 1918, 20, 1238–1245. [Google Scholar]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the 5th International Conference on Gravitation and the Theory of Relativity, Tbilisi, Georgia, 9–16 September 1968; DeWitt, C., DeWitt, B., Eds.; Gordon and Breach: Tbilisi, Georgia, 1968; p. 174. [Google Scholar]
- Ayón-Beato, E.; García, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Ayon-Beato, E. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25–29. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Non-Singular Charged Black Hole Solution for Non-Linear Source. Gen. Relativ. Gravit. 1999, 31, 629. [Google Scholar] [CrossRef]
- Bronnikov, K.A. Regular magnetic black holes and monopoles from nonlinear electrodynamics. Phys. Rev. D 2001, 63, 044005. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2019, 042. [Google Scholar] [CrossRef]
- Cañate, P. Black bounces as magnetically charged phantom regular black holes in Einstein-nonlinear electrodynamics gravity coupled to a self-interacting scalar field. Phys. Rev. D 2022, 106, 024031. [Google Scholar] [CrossRef]
- Franzin, E.; Liberati, S.; Mazza, J.; Simpson, A.; Visser, M. Charged black-bounce spacetimes. J. Cosmol. Astropart. Phys. 2021, 2021, 036. [Google Scholar] [CrossRef]
- Bokulić, A.; Smolić, I.; Jurić, T. Constraints on singularity resolution by nonlinear electrodynamics. Phys. Rev. D 2022, 106, 064020. [Google Scholar] [CrossRef]
- Mazza, J.; Franzin, E.; Liberati, S. A novel family of rotating black hole mimickers. J. Cosmol. Astropart. Phys. 2021, 2021, 082. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Rodrigues, M.E.; Silva, M.V.d.S.; Simpson, A.; Visser, M. Novel black-bounce spacetimes: Wormholes, regularity, energy conditions, and causal structure. Phys. Rev. D 2021, 103, 084052. [Google Scholar] [CrossRef]
- Xu, Z.; Tang, M. Rotating spacetime: Black-bounces and quantum deformed black hole. Eur. Phys. J. C 2021, 81, 863. [Google Scholar] [CrossRef]
- Churilova, M.S. Quasinormal modes of the Dirac field in the novel 4D Einstein-Gauss-Bonnet gravity. arXiv 2020, arXiv:2004.00513. [Google Scholar]
- Bronnikov, K.A. Black bounces, wormholes, and partly phantom scalar fields. Phys. Rev. D 2022, 106, 064029. [Google Scholar] [CrossRef]
- Fu, Q.M.; Zhang, X. Gravitational lensing by a black hole in effective loop quantum gravity. Phys. Rev. D 2022, 105, 064020. [Google Scholar] [CrossRef]
- Pal, K.; Pal, K.; Sarkar, T. Analogue Metric in a Black-Bounce Background. Universe 2022, 8, 197. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, D.; Övgün, A.; Long, Z.W.; Lambiase, G. Rotating black bounces surrounded by the string cloud. arXiv 2023, arXiv:2307.09344. [Google Scholar] [CrossRef]
- Vrba, J.; Rayimbaev, J.; Stuchlik, Z.; Ahmedov, B. Charged particles motion and quasiperiodic oscillation in Simpson-Visser spacetime in the presence of external magnetic fields. Eur. Phys. J. C 2023, 83, 854. [Google Scholar] [CrossRef]
- Shaikh, R. Testing black hole mimickers with the Event Horizon Telescope image of Sagittarius A*. Mon. Not. R. Astron. Soc. 2023, 523, 375–384. [Google Scholar] [CrossRef]
- Guo, Y.; Lan, C.; Miao, Y.G. Bounce corrections to gravitational lensing, quasinormal spectral stability and gray-body factors of Reissner-Nordström black holes. arXiv 2022, arXiv:2201.02971. [Google Scholar] [CrossRef]
- Tsukamoto, N. Retrolensing by two photon spheres of a black-bounce spacetime. Phys. Rev. D 2022, 105, 084036. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Gravitational lensing by a black-bounce-Reissner-Nordström spacetime. Eur. Phys. J. C 2022, 82, 471. [Google Scholar] [CrossRef]
- Tsukamoto, N. Gravitational lensing by two photon spheres in a black-bounce spacetime in strong deflection limits. Phys. Rev. D 2021, 104, 064022. [Google Scholar] [CrossRef]
- Islam, S.U.; Kumar, J.; Ghosh, S.G. Strong gravitational lensing by rotating Simpson-Visser black holes. J. Cosmol. Astropart. Phys. 2021, 2021, 013. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Probing a black-bounce-Reissner-Nordström spacetime with precessing and periodic motion. Eur. Phys. J. C 2022, 82, 854. [Google Scholar] [CrossRef]
- Sharp, N.A. Geodesics in black hole space-time. Gen. Relativ. Gravit. 1979, 10, 659–670. [Google Scholar] [CrossRef]
- Frolov, V.P.; Novikov, I.D. Black Hole Physics, Basic Concepts and New Developments; Kluwer Academic Publishers: Dordrecth, The Netherlands, 1998. [Google Scholar]
- Jawad, A.; Ali, F.; Jamil, M.; Debnath, U. Dynamics of Particles Around a Regular Black Hole with Nonlinear Electrodynamics. Commun. Theor. Phys. 2016, 66, 509. [Google Scholar] [CrossRef]
- Hussain, S.; Jamil, M. Timelike geodesics of a modified gravity black hole immersed in an axially symmetric magnetic field. Phys. Rev. D 2015, 92, 043008. [Google Scholar] [CrossRef]
- Jamil, M.; Hussain, S.; Majeed, B. Dynamics of particles around a Schwarzschild-like black hole in the presence of quintessence and magnetic field. Eur. Phys. J. C 2015, 75, 24. [Google Scholar] [CrossRef]
- Hussain, S.; Hussain, I.; Jamil, M. Dynamics of a charged particle around a slowly rotating Kerr black hole immersed in magnetic field. Eur. Phys. J. C 2014, 74, 210. [Google Scholar] [CrossRef]
- Babar, G.Z.; Jamil, M.; Lim, Y.K. Dynamics of a charged particle around a weakly magnetized naked singularity. Int. J. Mod. Phys. D 2016, 25, 1650024. [Google Scholar] [CrossRef]
- Bañados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef] [PubMed]
- Majeed, B.; Jamil, M. Dynamics and center of mass energy of colliding particles around black hole in f(R) gravity. Int. J. Mod. Phys. D 2017, 26, 1741017. [Google Scholar] [CrossRef]
- Zakria, A.; Jamil, M. Center of mass energy of the collision for two general geodesic particles around a Kerr-Newman-Taub-NUT black hole. J. High Energy Phys. 2015, 2015, 147. [Google Scholar] [CrossRef]
- Brevik, I.; Jamil, M. Black holes in the turbulence phase of viscous rip cosmology. Int. J. Geom. Methods Mod. Phys. 2019, 16, 1950030. [Google Scholar] [CrossRef]
- De Laurentis, M.; Younsi, Z.; Porth, O.; Mizuno, Y.; Rezzolla, L. Test-particle dynamics in general spherically symmetric black hole spacetimes. Phys. Rev. D 2018, 97, 104024. [Google Scholar] [CrossRef]
- Pugliese, D.; Valiente Kroon, J.A. On the evolution equations for ideal magnetohydrodynamics in curved spacetime. Gen. Relativ. Gravit. 2012, 44, 2785–2810. [Google Scholar] [CrossRef]
- Pugliese, D.; Valiente Kroon, J.A. On the locally rotationally symmetric Einstein-Maxwell perfect fluid. Gen. Relativ. Gravit. 2016, 48, 74. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Rueda, H.J.A.; Ruffini, R. Charged boson stars. Phys. Rev. D 2013, 88, 024053. [Google Scholar] [CrossRef]
- Belvedere, R.; Pugliese, D.; Rueda, J.A.; Ruffini, R.; Xue, S.S. Neutron star equilibrium configurations within a fully relativistic theory with strong, weak, electromagnetic, and gravitational interactions. Nucl. Phys. A 2012, 883, 1–24. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M.; Kovář, J.; Slaný, P.; Tursunov, A. Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes. Universe 2020, 6, 26. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Wald, R.M. Black hole in a uniform magnetic field. Phys. Rev. D. 1974, 10, 1680–1685. [Google Scholar] [CrossRef]
- Aliev, A.N.; Galtsov, D.V.; Petukhov, V.I. Negative absorption near a magnetized black hole - Black hole masers. Astrophys. Space Sci. 1986, 124, 137–157. [Google Scholar] [CrossRef]
- Aliev, A.N.; Gal’tsov, D.V. Reviews of topical problems: “Magnetized” black holes. Sov. Phys. Uspekhi 1989, 32, 75–92. [Google Scholar] [CrossRef]
- Aliev, A.N.; Özdemir, N. Motion of charged particles around a rotating black hole in a magnetic field. Mon. Not. R. Astron. Soc. 2002, 336, 241–248. [Google Scholar] [CrossRef]
- Bicak, J.; Suchlik, Z.; Balek, V. The motion of charged particles in the field of rotating charged black holes and naked singularities. Bull. Astron. Institutes Czechoslov. 1989, 40, 65–92. [Google Scholar]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; CRC Press: Boca Raton, FL, USA, 1973; pp. 343–450. [Google Scholar]
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Pringle, J.E. Accretion discs in astrophysics. Annu. Rev. Astron. Astrophys. 1981, 19, 137–162. [Google Scholar] [CrossRef]
- Bian, W.H.; Zhao, Y.H. Accretion Rates and the Accretion Efficiency in AGNs. Publ. Astron. Soc. Jpn. 2003, 55, 599–603. [Google Scholar] [CrossRef]
- Miller, J.M.; Raymond, J.; Fabian, A.; Steeghs, D.; Homan, J.; Reynolds, C.; van der Klis, M.; Wijnands, R. The magnetic nature of disk accretion onto black holes. Nature 2006, 441, 953–955. [Google Scholar] [CrossRef]
- Khan, S.U.; Chen, Z.M. Charged particle dynamics in black hole split monopole magnetosphere. Eur. Phys. J. C 2023, 83, 704. [Google Scholar] [CrossRef]
- Zaslavskii, O.B. General properties of the Penrose process with neutral particles in the equatorial plane. Phys. Rev. D 2023, 108, 084022. [Google Scholar] [CrossRef]
- Landau, L.D. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2. [Google Scholar]
- Reynolds, C.S.; Fabian, A.C. Broad Iron-Kα Emission Lines as a Diagnostic of Black Hole Spin. Astrophys. J. 2008, 675, 1048–1056. [Google Scholar] [CrossRef]
- Wilkins, D.R.; Reynolds, C.S.; Fabian, A.C. Venturing beyond the ISCO: Detecting X-ray emission from the plunging regions around black holes. Mon. Not. R. Astron. Soc. 2020, 493, 5532–5550. [Google Scholar] [CrossRef]
- Reynolds, C.S. Observing black holes spin. Nat. Astron. 2019, 3, 41–47. [Google Scholar] [CrossRef]
- Turimov, B.; Boboqambarova, M.; Ahmedov, B.; Stuchlík, Z. Distinguishable feature of electric and magnetic charged black hole. Eur. Phys. J. Plus 2022, 137, 222. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murodov, S.; Badalov, K.; Rayimbaev, J.; Ahmedov, B.; Stuchlík, Z. Charged Particles Orbiting Charged Black-Bounce Black Holes. Symmetry 2024, 16, 109. https://doi.org/10.3390/sym16010109
Murodov S, Badalov K, Rayimbaev J, Ahmedov B, Stuchlík Z. Charged Particles Orbiting Charged Black-Bounce Black Holes. Symmetry. 2024; 16(1):109. https://doi.org/10.3390/sym16010109
Chicago/Turabian StyleMurodov, Sardor, Kodir Badalov, Javlon Rayimbaev, Bobomurat Ahmedov, and Zdeněk Stuchlík. 2024. "Charged Particles Orbiting Charged Black-Bounce Black Holes" Symmetry 16, no. 1: 109. https://doi.org/10.3390/sym16010109
APA StyleMurodov, S., Badalov, K., Rayimbaev, J., Ahmedov, B., & Stuchlík, Z. (2024). Charged Particles Orbiting Charged Black-Bounce Black Holes. Symmetry, 16(1), 109. https://doi.org/10.3390/sym16010109








