1. Introduction
Recently, research into the theory of geometric functions related to the nephroid and leminscate domains has gained prominence [
1,
2,
3,
4,
5,
6]. Here, the leminscate domain refers to the image of
by the function
, while the image of
by the function
is known as nephroid domain. Two other interesting domains are the image of
by
, and
. In this article, we mainly consider
and
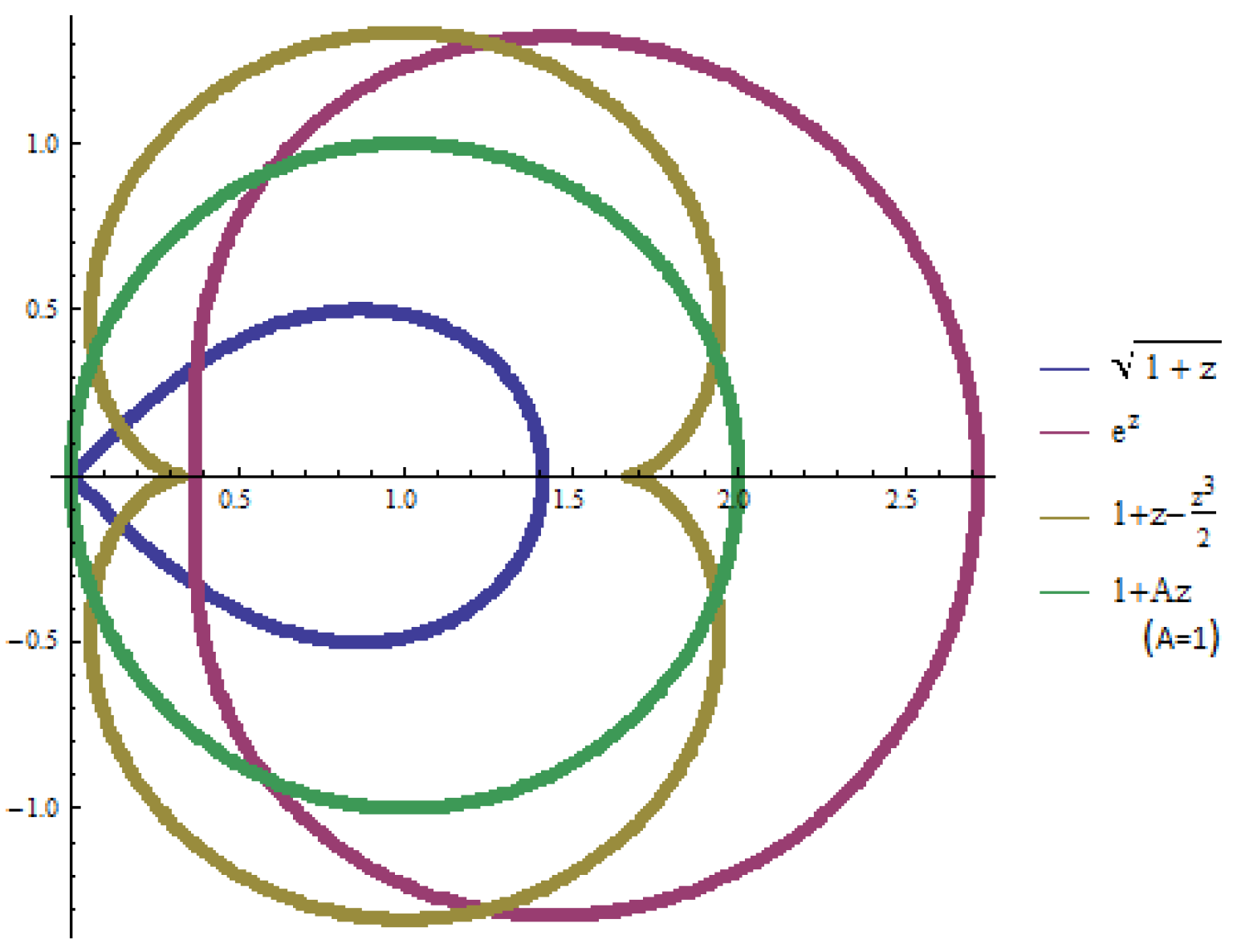
. The images of
through the four above functions can be seen in
Figure 1 below:
Now, we recall a few basic concepts of the geometric function theory. The class of functions
f defined on the open unit disk
, and normalized by the conditions
, is denoted by
. We say
if
is the normalized condition. Generally,
possess power series
while
have the power series
Subordination [
7] is one of the important concepts of geometric function theory that is useful in studying the geometric properties of analytic functions. If
and
are two analytic mappings in
, then
is said to be subordinate to
, denoted by
or
, when there an analytic self-map
of
satisfying
and
exists such that
,
. In particular, if
with univalent
, then
.
Indicate the important sub-classes of that comprise univalent starlike and convex functions by and , respectively. For and , if the line lies completely in , then ; on the other hand, if is a convex domain, then . The Cárath}eodory class includes analytic functions p that satisfy and in . These sub-classes are related to each other. In analytical terms, if , and if .
If
is within the region bounded by the right half of the lemniscate of Bernoulli, denoted by
, then the function
is known as the lemniscate convex. This is equivalent to subordination
. In an analogous way, if
, then the function
f is lemniscate starlike. Moreover, if
, then the function
is lemniscate Carathéodory. It is evident that the lemniscate Carathéodory function is univalent since it is a Carathéodory function. More details about geometric properties associated with leminiscate can be seen in [
5,
8,
9].
For the purpose of studying different classes of analytical functions, the principle of differential subordination [
10,
11] is helpful. Lemma 1, which is derived by applying the principle of differential subordination, is useful in sequence when studying geometric properties associated with the lemniscate.
Lemma 1 ([
5])
. Let with and . Let , and satisfywhenever and for , ,If for , then in . In this article, we study the geometric nature of the solution of two differential equations
where
,
, and
are analytic functions defined on the unit disc. We find the solution of the following two problems.
Problem 1. Find the condition(s) on , , and , such that the solution of the differential Equations (3) and (4), which are normalized by , is subordinated by . A few studies [
1,
2,
3,
4,
12] in the literature have examined Problem 1, taking account of special
,
, and
. Nonetheless, in this investigation we first present and evaluate a broad interpretation of the findings in
Section 2, and then we present examples in
Section 3. Below, we provides some background information:
Confluent hypergeometric function (CHF): This is a solution of the differential Equation (
3) when
,
, and
. There are several articles in the literature that studied CHF in the context of geometric function theory [
10,
13]. We note here that to the best of our knowledge, there is no CHF result related to Problem 1. We established some connection between CHF and Problem 1 in the Example 1 where we also provide a detailed literature review on CHF and its connection with geometric function theory.
Generalized Bessel function (GBF): By taking
,
, and
, in the differential Equation (4), we will obtain the GBF. Here,
and
. More details about GBF and its significance in the geometric functions theory are given in Example 5. A closed form of results related to Problem 1 involving GBF is given in [
12].
Generalized Struve functions (GSF): This function is a solution of the differential Equation (4) when , , and . Moreover, details about these notations, and the connection between GSF and Problem 1, are presented in Example 6.
Generalized Bessel–Sturve functions: For the construction details about this function, we refer the interested reader to [
4]. A Connection of Problem 1 with this function is also studied in [
4]. In Example 7, we show that the result of [
4] is a special case of our main result presented in
Section 2.
Other functions: In addition, we can consider other functions that are the solution of differential Equations (
3) and (
4), like the associated Laguerre polynomial (ALP) (Example 2), the regular Coulomb wave function (Example 8), generalized hypergeometric functions (Example 3), and modified Bessel functions (Example 4).
In the context of other similar geometric properties such as leminiscate starlike and convexity, we refer interested readers to [
1,
5,
8,
9,
12,
14] and the reference therein.
Using the solution of Problem 1, we aim to obtain the answer to the following problem.
Problem 2. Using the solution of Problem 1, construct functions g such that .
We answer Problem 2 through various examples in
Section 4.1. For this purpose, we consider the following result from [
6].
Lemma 2 ([
6])
. Let be analytic such that . Then, the following subordinations imply :- (i)
for ,
- (ii)
for
We also construct function
f, which is subordinated by
by the direct definition of subordination and then build a connection with
. Those results are presented in
Section 4.2.
In the conclusion
Section 5, we raised an open problem based on the examples constructed in
Section 4.
3. Examples Involving Special Functions
In this section, we are going to construct examples based on the theorems that are stated and proved in the previous section. The examples consist of several well-know special functions such as the Bessel, Struve, confluent hypergeometric, and generalized Bessel functions. The Laguerre polynomial and regular Coulomb wave functions are also covered. We refer to [
15,
16,
17] for additional information regarding special functions.
Example 1 (Involving confluent hypergeometric functions).
Let us consider the differential equation The differential Equation (18) is a well known confluent hypergeometric differential equation, and the solution of this equation is known as confluent hypergeometric functions (CHF) [15,17]. We denote the solution of (18) by . It is also denoted as and has the series representationHere In [10], Miller and Mocanu proved that in for real α and β satisfying either and , or and . Sufficient conditions for , are obtained by Ponnusamy and Vuorinen ([13] Theorem 1.9, p. 77). They also determined conditions that ensure is close-to-convex of the positive order with respect to the identity function. Additionally, they derived the conditions for the close-to-convexity of with respect to the starlike function , as well as the close-to-convexity of with respect to the starlike function . Constraints on a and c so that is convex of the positive order are also found in ([13] Theorem 5.1, p. 88). Now, we are going to implement Theorem 1 in the solution of differential Equation (18). Note that , and . We consider the case where and Now,Thus, condition (6) holds and we have the following result from Theorem 1: Theorem 3. For , the confluent hypergeometric function for Example 2 (Involving the Laguerre polynomial).
The associated Laguerre polynomial (ALP) denoted by is the solution of the differential equation The function can be represented by the serieswhere represents the confluent hypergeometric function, and denotes the familiar Pochhammer symbol defined as We refer to [15] for further information on this function. Consider the normalized functionThe function satisfies the normalization condition . Thus, from Theorem 3, it follows thatprovided . It is to be noted here that this result is the main result of the article ([2] Theorem 1). The result ([2] Theorem 1) obtained by considering the differential equationwhich follows from (20) by multiplying z on both sides. Thus, the result can also be obtained from Theorem 2. Before introducing the next example, we first recall generalized hypergeometric functions denoted by
with series representation
where
are positive. The series (
25) converges if
- (i)
Any of are non-positive.
- (ii)
, the series converges for any finite value of z and hence entirely.
Let
and
; then, the generalized hypergeometric function
is known as confluent hypergeometric finite functions, and this function is closely related to the Bessel function as follows:
Next, we provide an example involving the generalized hypergeometric function.
Example 3 (Involving generalized hypergeometric functions)
. Clearly, . By taking the differentiation on both sides, we haveThe relationimpliessimilarly, Again, the recurrence relationimpliesand this leads to the fact that is a solution of the differential equation Now, to implement Theorem 1, let us considerSince , we have and . Trivially, . Finally, a calculation yieldsThis means that , , and satisfy the requirement of Theorem 1; hence, we conclude that . Example 4 (Involving classical modified Bessel functions)
. Here, is a well-known modified Bessel function that is the solution of the differential equationand have the series representationclearly,Thus, Our objective here is to find the corresponding differential equation of . Various well-known recurrence relations of modified Bessel functions help us to establish the differential equation. We recall the following recurrence relations of :A calculation from (27) and (28) yieldsFor , the recurrence relation (27) gives Further, the recurrence relations (28) and (29) leads toUsing above relation and several adjustment, one can obtainand Now, a combination of (26), (30), and (31) leads toThus, is the solution of the differential equationTakingit follows thatFinally, from Theorem 1, one can conclude that . Example 5 (Involving generalized Bessel functions)
. In the literature on geometric functions theory, one of the most important functions is the generalized and normalized Bessel functions of the formwhich satisfies the second-order differential equation The function yields the Spherical Bessel function for , and reduces to the normalized classical Bessel (modified) Bessel functions of order p when ().
There is an extensive amount of research on the inclusion of in different subclasses of univalent functions theory [12,18,19,20,21,22] and some references therein. In [12], the lemniscate convexity and additional properties of are examined in detail. The lemniscate starlikeness of is discussed in [1]. From the differential Equation (33), it follows that , , and . The condition (14) is equivalent to Thus, we have the following result.
Theorem 4. If , then .
Baricz [18] proved that the following recurrence relation is satisfied by as follows: Lemma 3 ([
18])
. If and , then the function satisfies the relation for all . Now, Theorem 4 and Lemma 3 together imply that for and ,The subordination in (34) is established in [12] with the condition Example 6 (Involving Generalized Struve functions)
. For , consider the function The function is well known as the Struve function of order p, and it is a particular solution of the non-homogeneous differential equationA slightly modified differential equationhas a particular solution of the formThe function is known as a modified Struve function of order p. The notion of generalized Struve functions is given in [23]. The starlikeness and convexity properties of generalized Struve functions also studied in [24]. Now, let us consider the second-order non-homogeneous linear differential equation.where . If we choose and , then we obtain (35), and if we choose and , then we obtain (36). So, this generalizes (35) and (36). Hence, the study based on (37) helps us to study the Struve and modified Struve functions together. Now, the particular solution of the differential Equation (37) is known as a generalized Struve function of order p and denoted by . The generalized struve function is represented by the following series:While this series converges everywhere, the function typically is not univalent within . Now, let us examine the function defined by the transformationBy using the Pochhammer symbol, which is defined in relation to Euler’s gamma functions, by , we obtain for the function in the following form:where .This function is analytic on and satisfies the second-order non-homogeneous differential equation From differential Equation (39), it follows that , and . Now, to satisfy the condition (14), we have to showSince , a simplification of right hand side of (40) gives Thus, the inequality (40) holds if , and by this we have the conclusion . Example 7 (Involving the generalized Bessel–Sturve function)
. The concept of the generalized Bessel–Sturve function is introduced in [4], building upon the concepts of the generalized Struve function from [23] and the generalized Bessel function from article [18]. By denoting the generalized Bessel–Sturve functions as , it is shown in [4] that for , the generalized Bessel–Sturve functions exhibit a power series of the form:Further, it is established in ([4] Proposition 2) that is a solution of the differential equationwhere and . Now, to apply Theorem 2, setThe condition (14) is equivalent toSince , it follows thatSubstituting the expression for , it follows that Finally, the condition (43) holds ifThe inequality (44) help us to conclude that . A similar result is also obtained in [4]. Example 8 (Involving the regular Coulomb wave function)
. The regular Coulomb wave function , defined across the complex plane, is an entire function linked to the classical Bessel function. The Coulomb differential equation is a secound-order differential equation of the formclaiming two distinct solutions: the regular and irregular Coulomb wave functions. The regular Coulomb wave function is expressed in terms of the Kummer confluent hypergeometric function as follows:In this case, and For our requirement, we consider the following normal form:By a calculation, it can be shown from (45) that satisfies the differential equationFor condition (14), the conclusion of this results follows ifNow, due to the fact that and , we haveprovided , and due to this inequality it is always true that . Now, from Theorem 2, it follows that . We remark here that this result is obtained in ([3] Theorem 1). 4. Connections with Nephroid Domain
In this section, we investigate the functions that map the unit disk to a domain confined by the nephroid curve. We are going to generate appropriate cases in two ways: first, by employing some of the examples established in
Section 3, and second, by taking into consideration the idea of subordination. Suppose that
such that
and
. Define
and assume that the integration on the right-hand side is convergent. From (
48), it follows by the fundamental theorem of calculus that
From Lemma 2 (i), it follows that
, for
.
Denote
. A logarithmic differentiation of
h yields
Again by Lemma 2 (ii), it follows that
for
.
Lemma 4. If , then the following two subordinations are true: Now, we can construct the functions
g in two ways. In the first method, we can consider constructed functions
f in various examples in
Section 3 and calculate the integration (
48), while in the second method, we will directly construct a function
using the definition of subordination. Before constructing more examples in this direction, we state the following theorem, which directly follows from the relationship between (
49) and Theorems 1 and 2. We omit the proof.
Theorem 5. Consider the analytic functions , and defined on such that the conditions of Theorems 1 and 2 holds. Then, for , where g is the solution of any of the following two differential equations: 4.1. Examples Based on Section 3
To construct examples in connection with
, we first revisit
Section 3 where the connections with
are presented.
Example 9. In Example 5, we prove that for , the generalized Bessel function . Now, from the series (32) of , it follows that DefineThen, we have for provided integration (50) exists. Our next aim is to find the closed form of .This concludes the following subordination: for ,
for .
Example 10. In Example 4, we prove that 4.2. Examples Using Definition of Subordination
The next few examples are constructed directly using the definition of subordination.
Example 11. For and , consider the function To establish the subordination, consider the function with . Then, clearly , and for , . By the definition of subordination, the relation implies
For and , definewith . The solution of the integration in (52) can be easily established using computational software, but here we solve the problem to achieve the completeness of the result. First, we consider the following indefinite integration: Next, substitute . Then, The integration I reduces to Finally, the integration (52) has the closed formFrom Lemma 4, it follows thatfor . Example 12. In this example, we show that for the functionLet us consider the functionClearly, and for Further, we haveUsing the definition of differential subordination, we conclude thatNow, if we definethen by Lemma 4, we can conclude that for . It remains to find a closed form of that is subject to the existence of the integration in (56). To check this, first we consider the indefinite integrationwhich can be further separated into two parts as follows:Taking in (53), we have the solution of the first integration in asBy a routine calculation, the second integration in leads toThis finally leads to the closed form of as follows:This completes the verification. Example 13. In this example, we show that for , the function To establish this, we consider the following two functions:Clearly, andFurther, a computation yieldsThis gives us required subordination Similarly to the earlier examples, let us defineSincethe integration in (59) can be evaluated as follows:The conclusion follows from Lemma 4. 5. Conclusions
In this article, we state and prove two results that gave conditions on the analytic coefficient of the second-order differential equation by which the solution of the differential equation maps the unit disk to a domain subordinate to the leminscate
and the nephroid curve
. In consequence, several examples involving special functions such as Bessel, Struve, Bessel–Sturve, the confluent, and generalized hypergeometric functions are presented. Based on the construction pattern of
,
in
Section 4.2, we have the following open problem:
Problem 3. For a fixed , construct a sequence and define the polynomial , and for . Find the exact range of a, such thatFurther, for , the functionprovided the integration converge. We note that
- (i)
Example 11: , and ,
- (ii)
Example 12: , and
- (iii)
Example 13: , and .
Thus, Examples 11–13 partially answer Problem 3. Now, from the pattern of the above three examples and Problem 3, we can observe the following specific problem:
Problem 4. For a fixed , define the polynomial Then, some exist such that