Mechanical Behavior of Large Symmetric Fiber Reinforced Polymer-Reactive Powder Concrete Composite Tanks with Floating Tops
Abstract
:1. Introduction
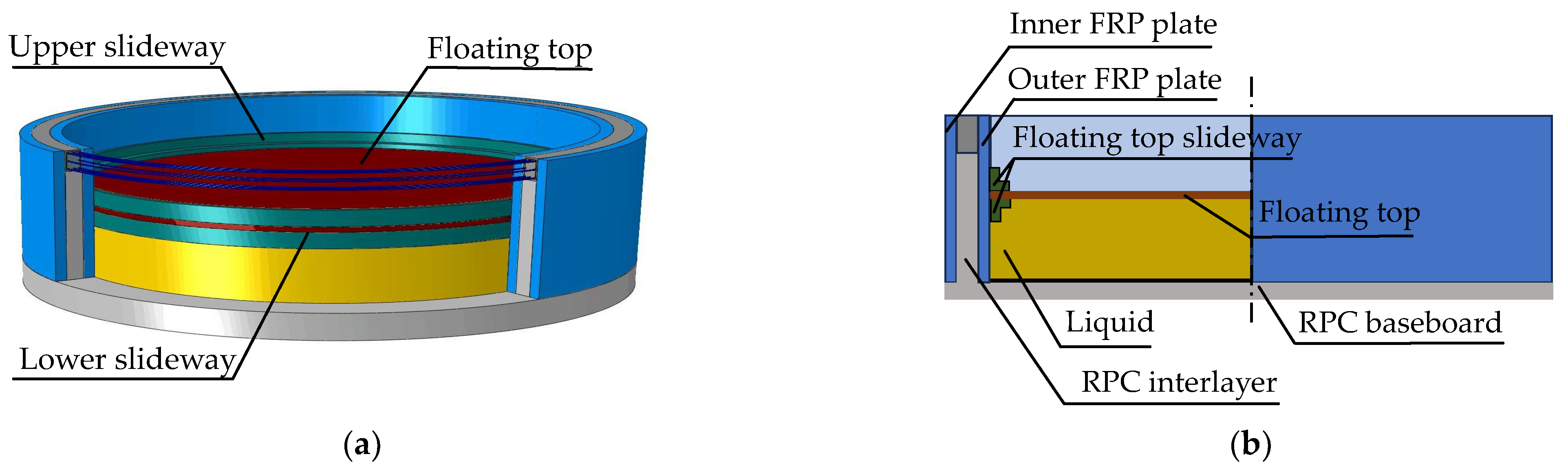
2. Specimen Design
3. Finite Element Models (FEMs)
3.1. Simplified Mechanical Model of the FRPCTs
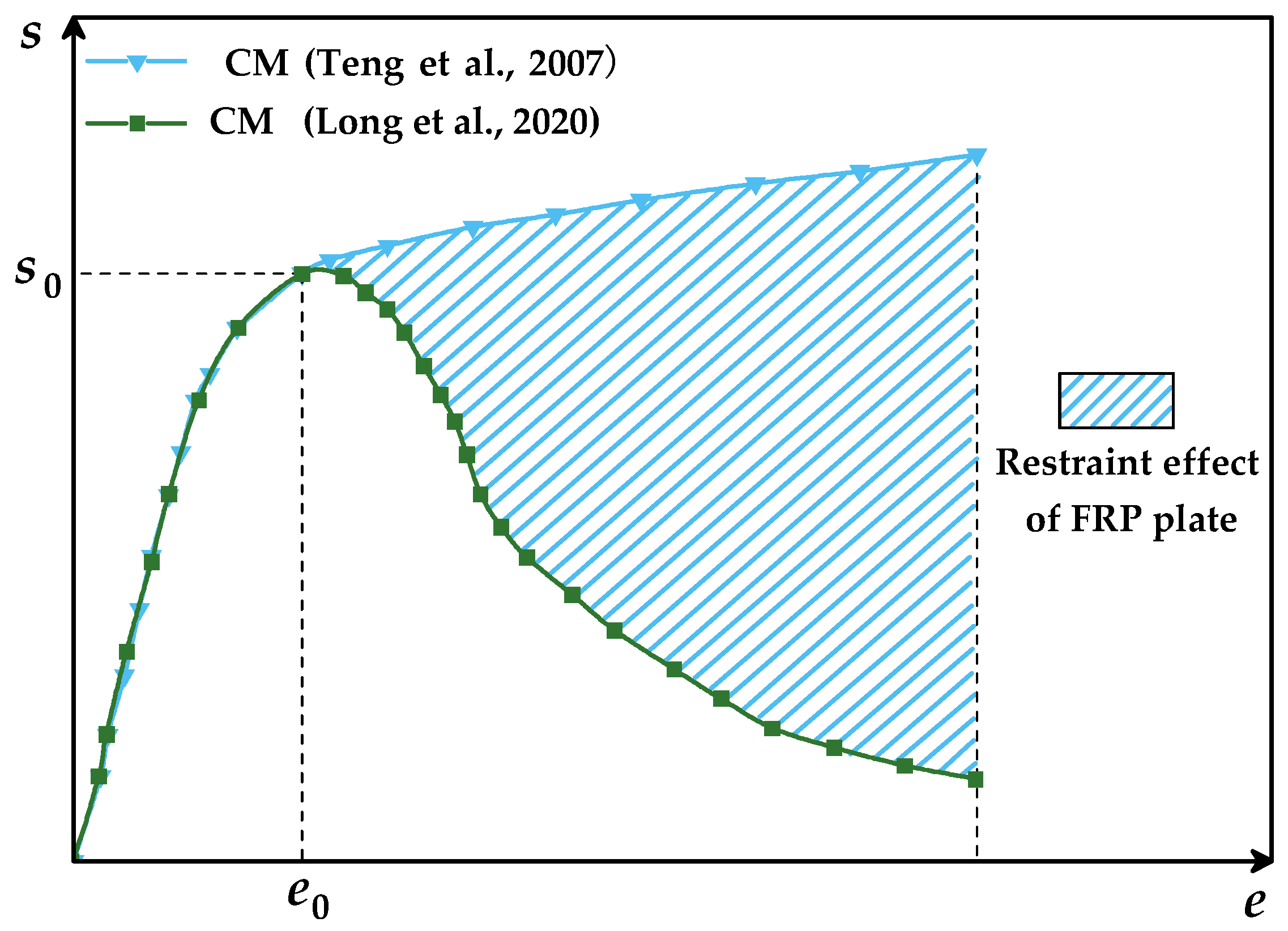
3.2. Constitutive Models of Materials
3.2.1. Constitutive Models of FRP
3.2.2. Constitutive Models of the RPC
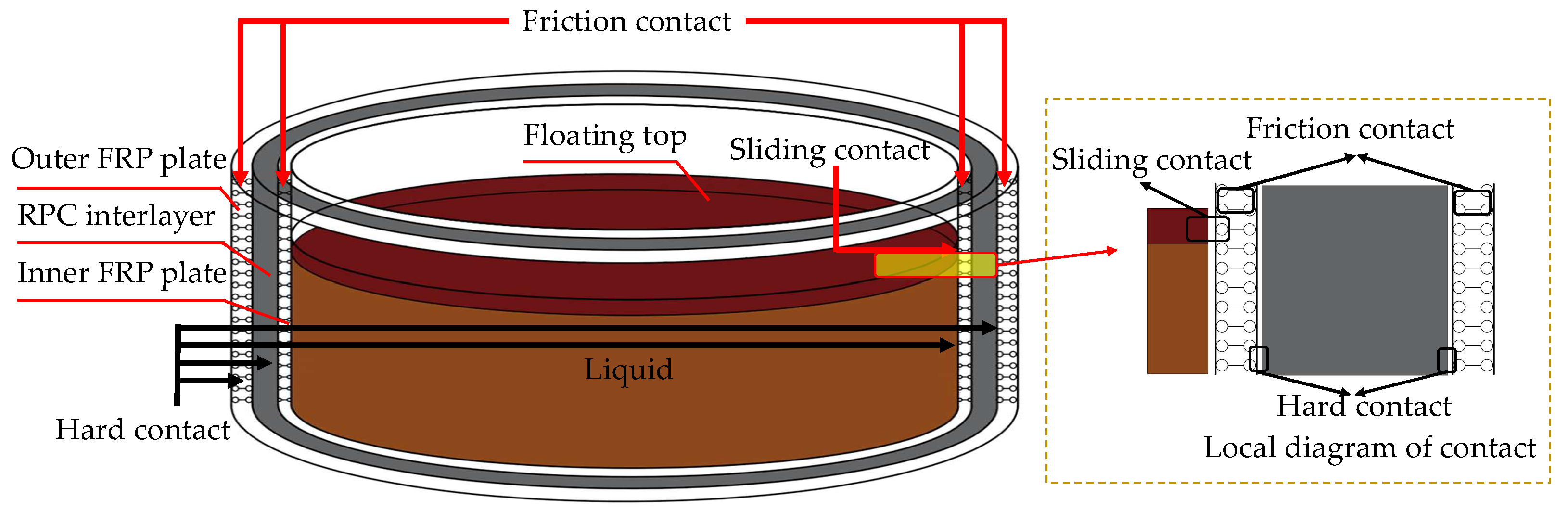
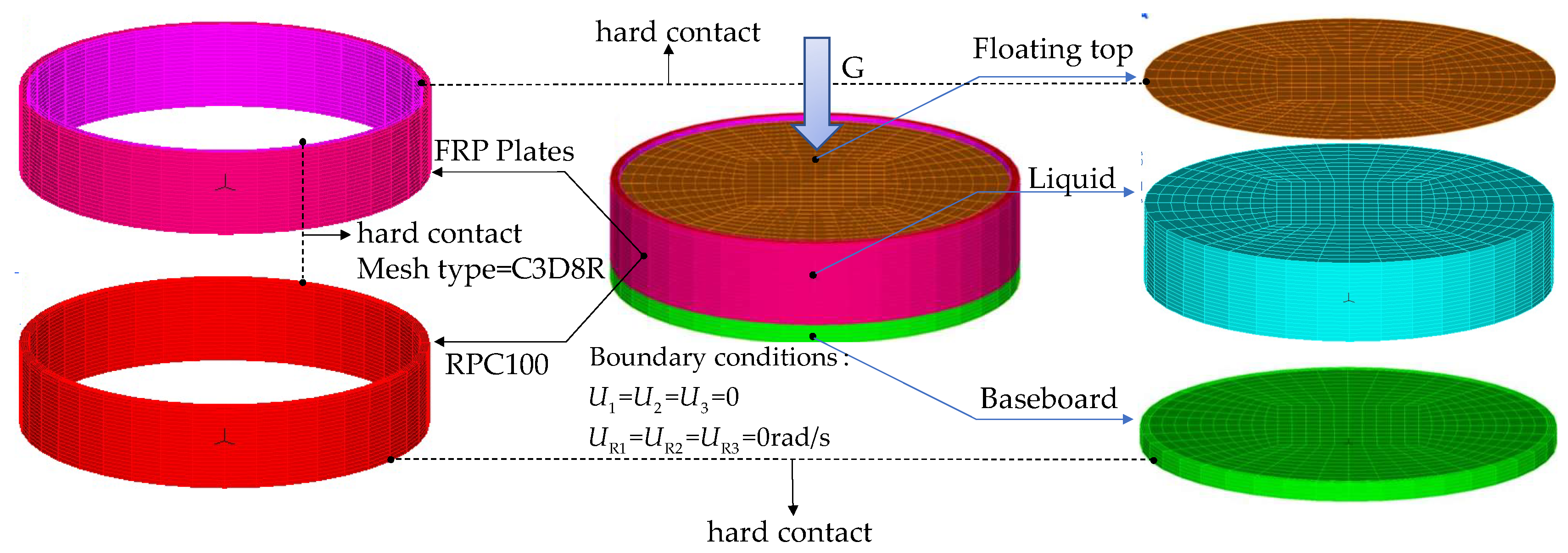
3.3. Element Selection and Contact
3.4. Boundary Conditions and Mesh
4. FEM Verification
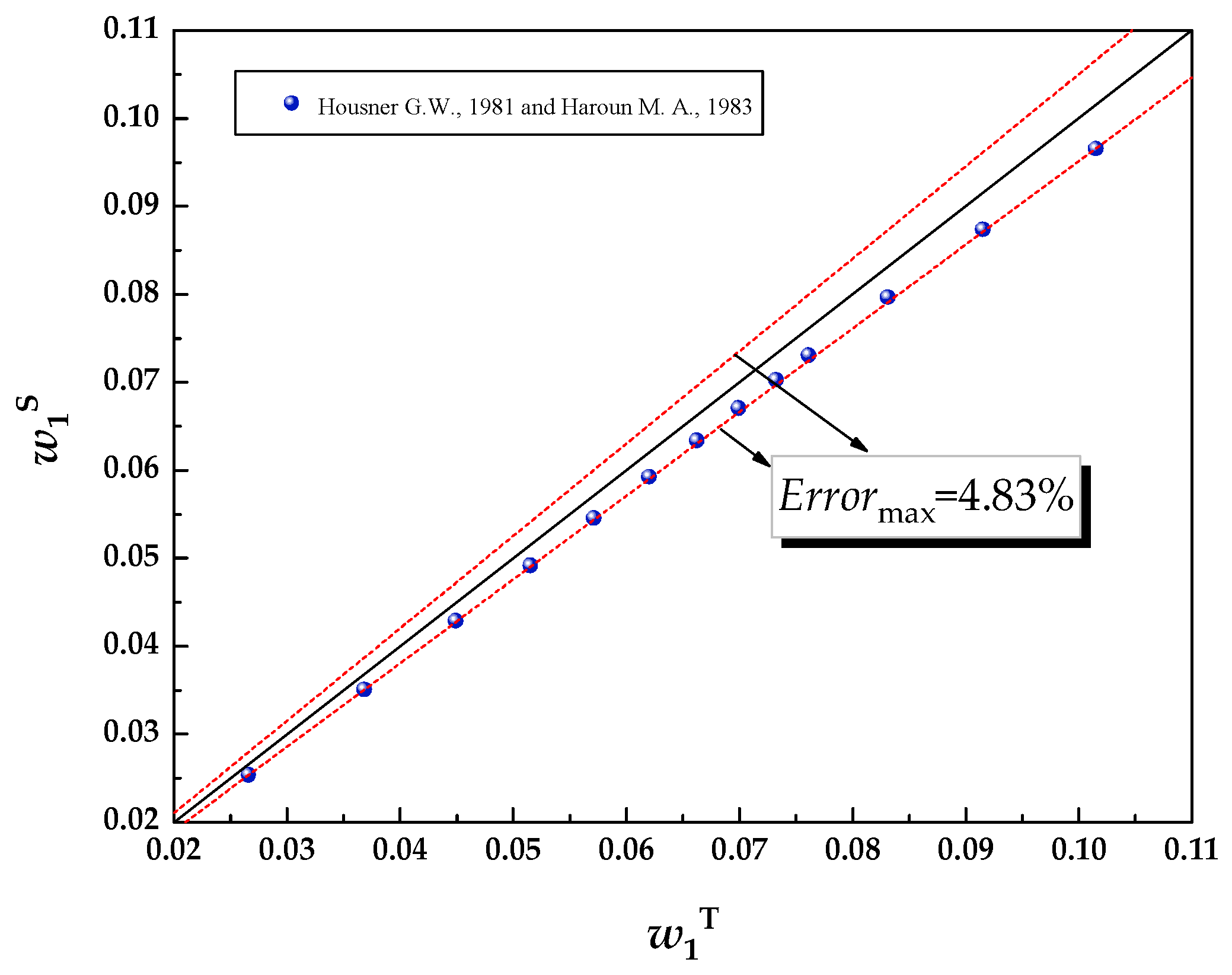
4.1. The Theoretical Verification of the FRPCTs without a Floating Top
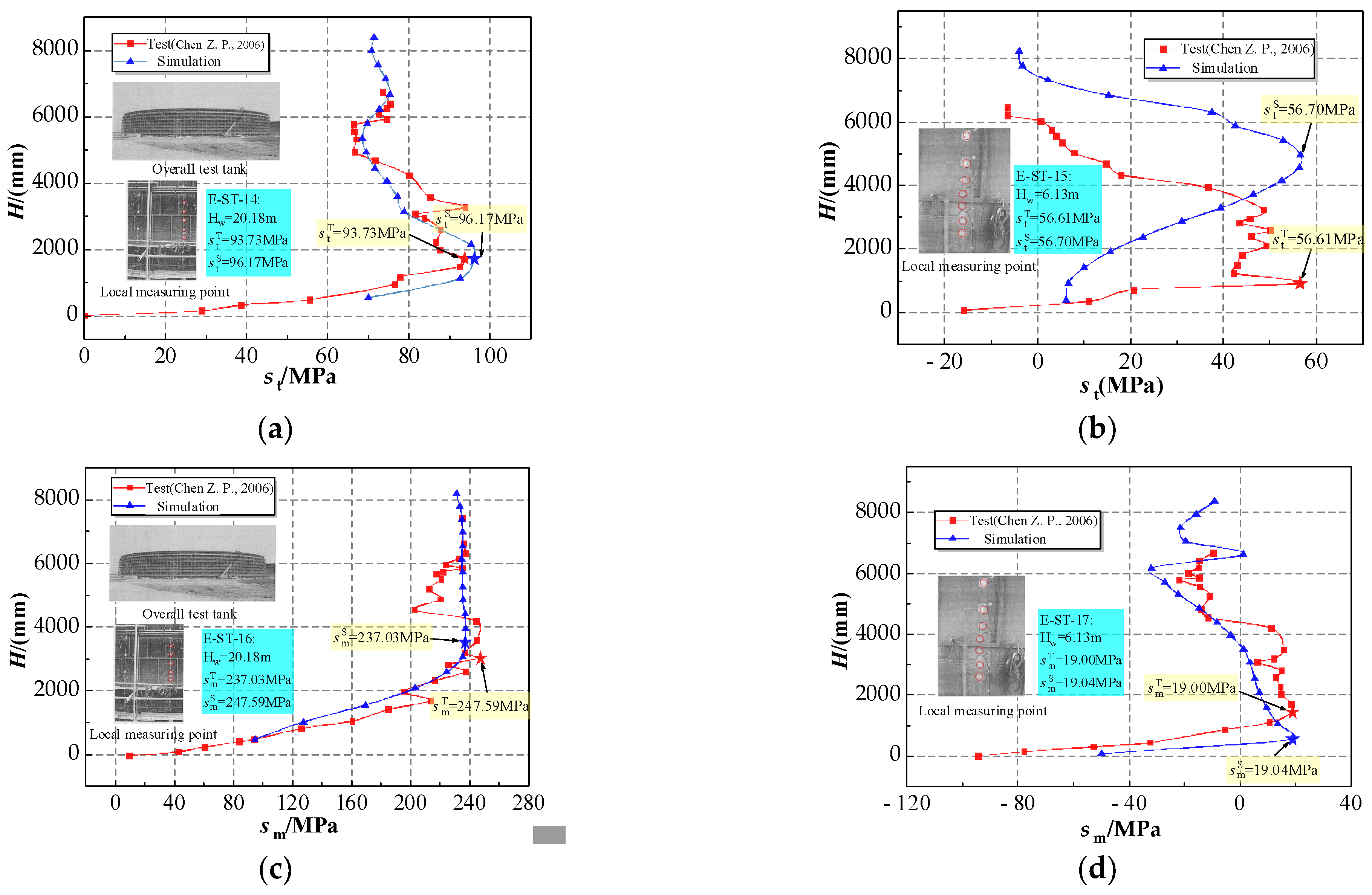
4.2. The Test Validation of the LNG Storage Tank with a Floating Top
5. Parametrical Investigation
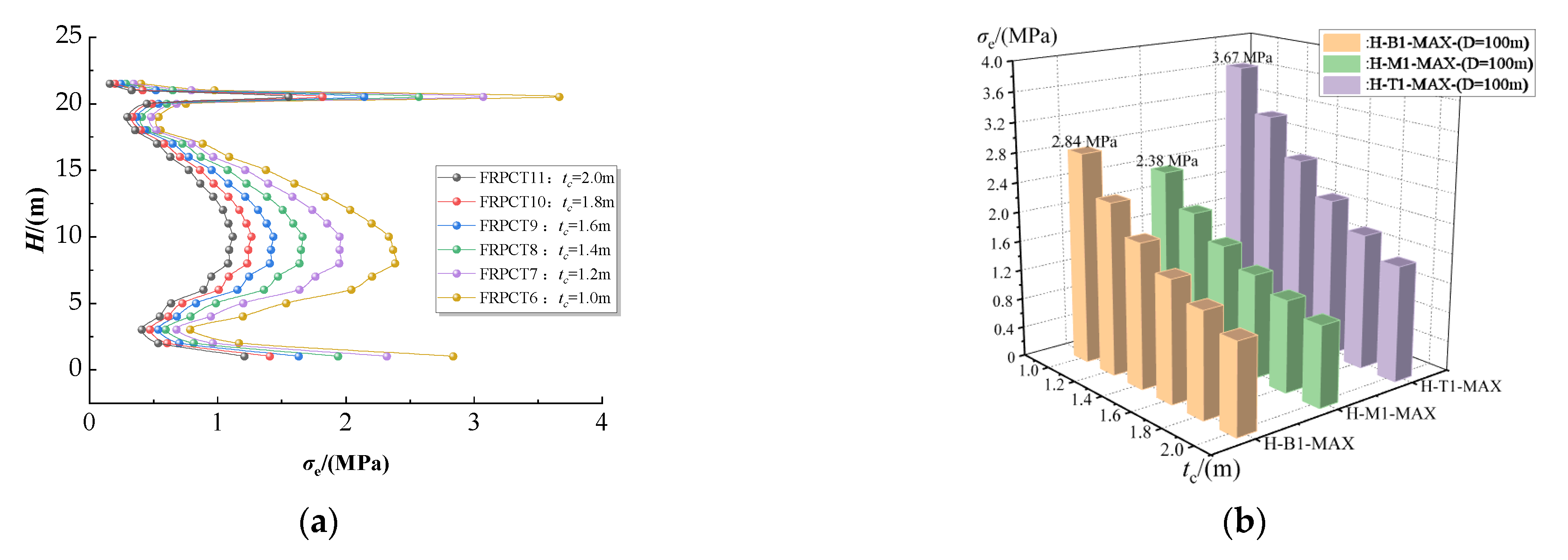
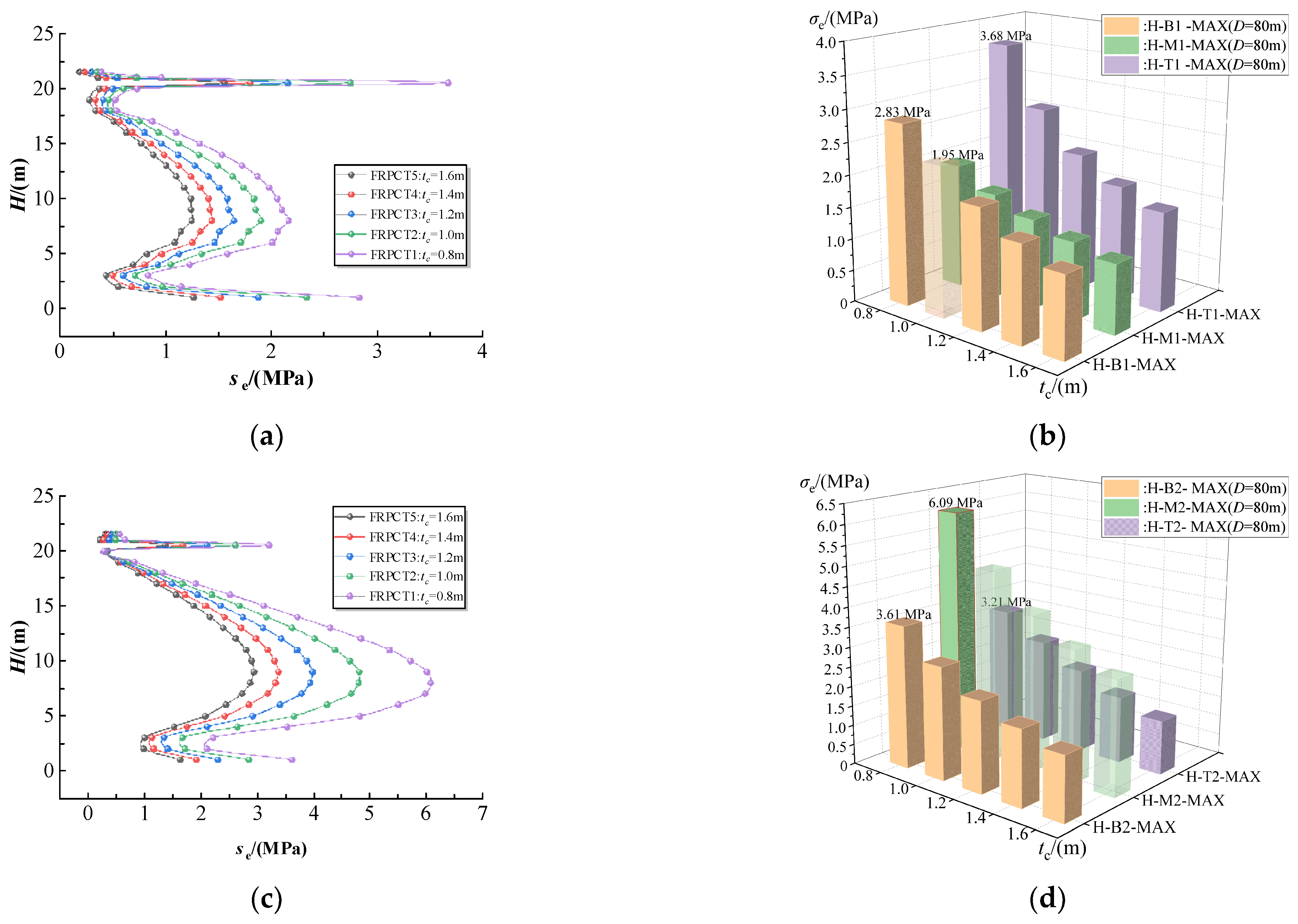
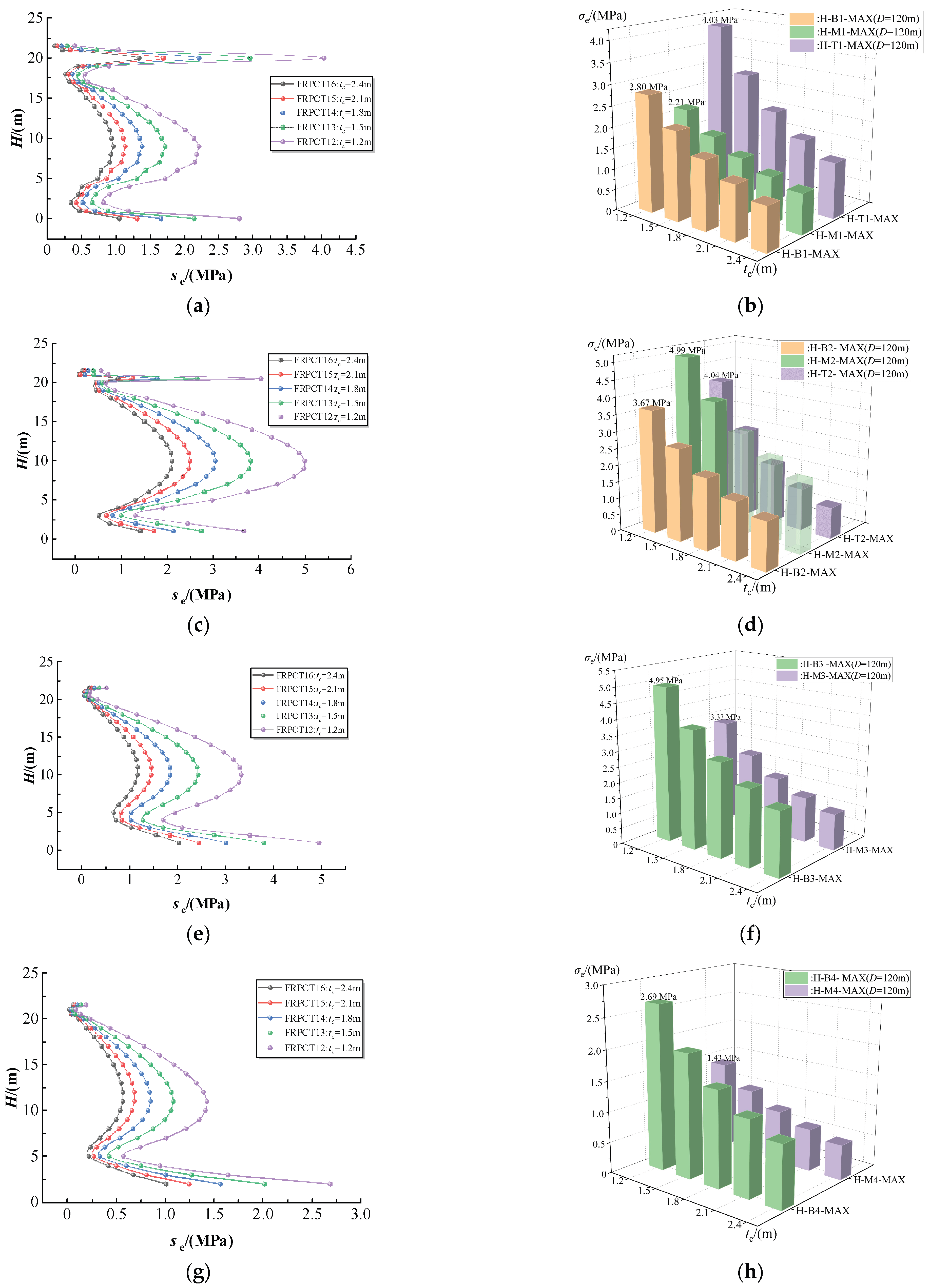
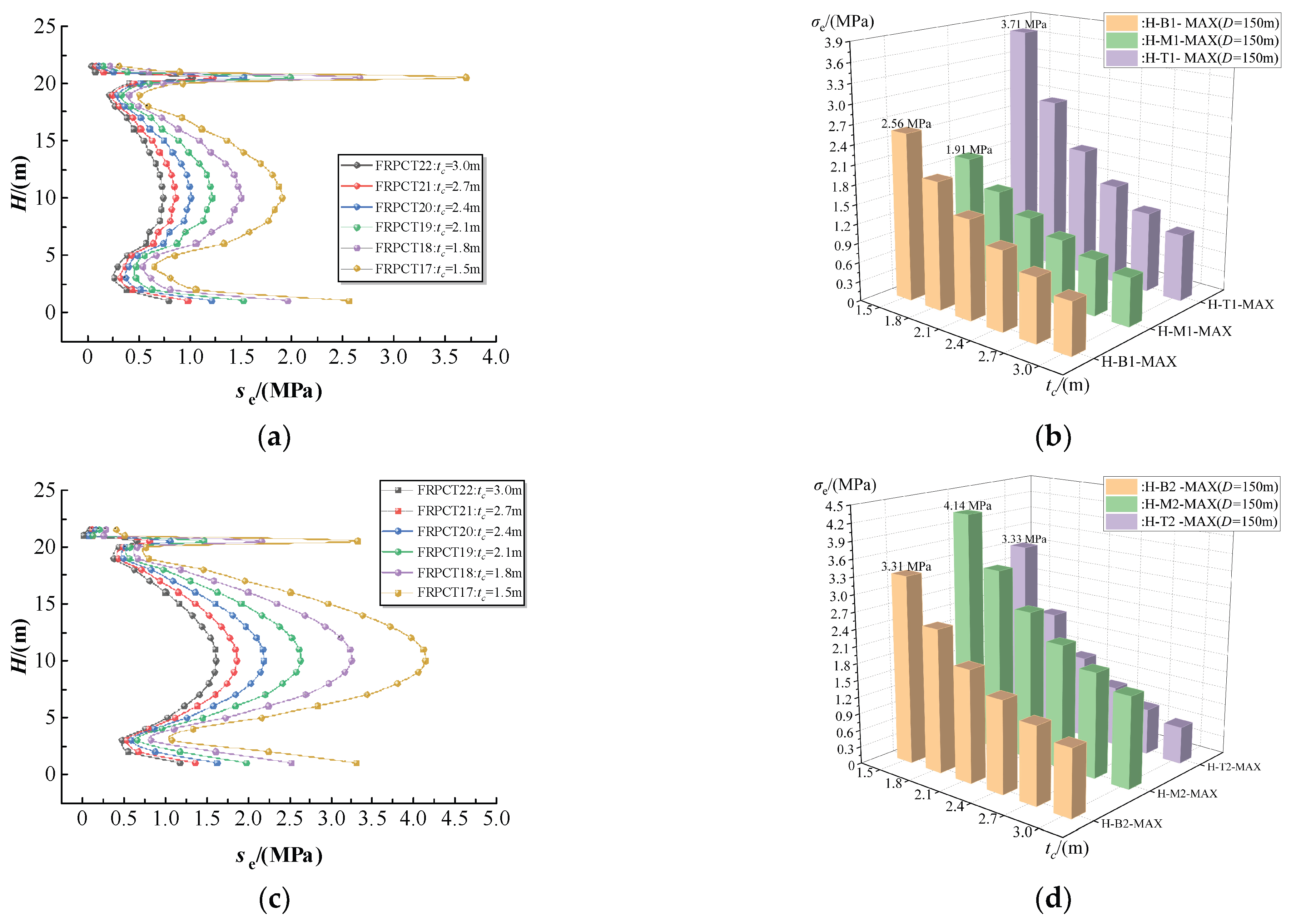
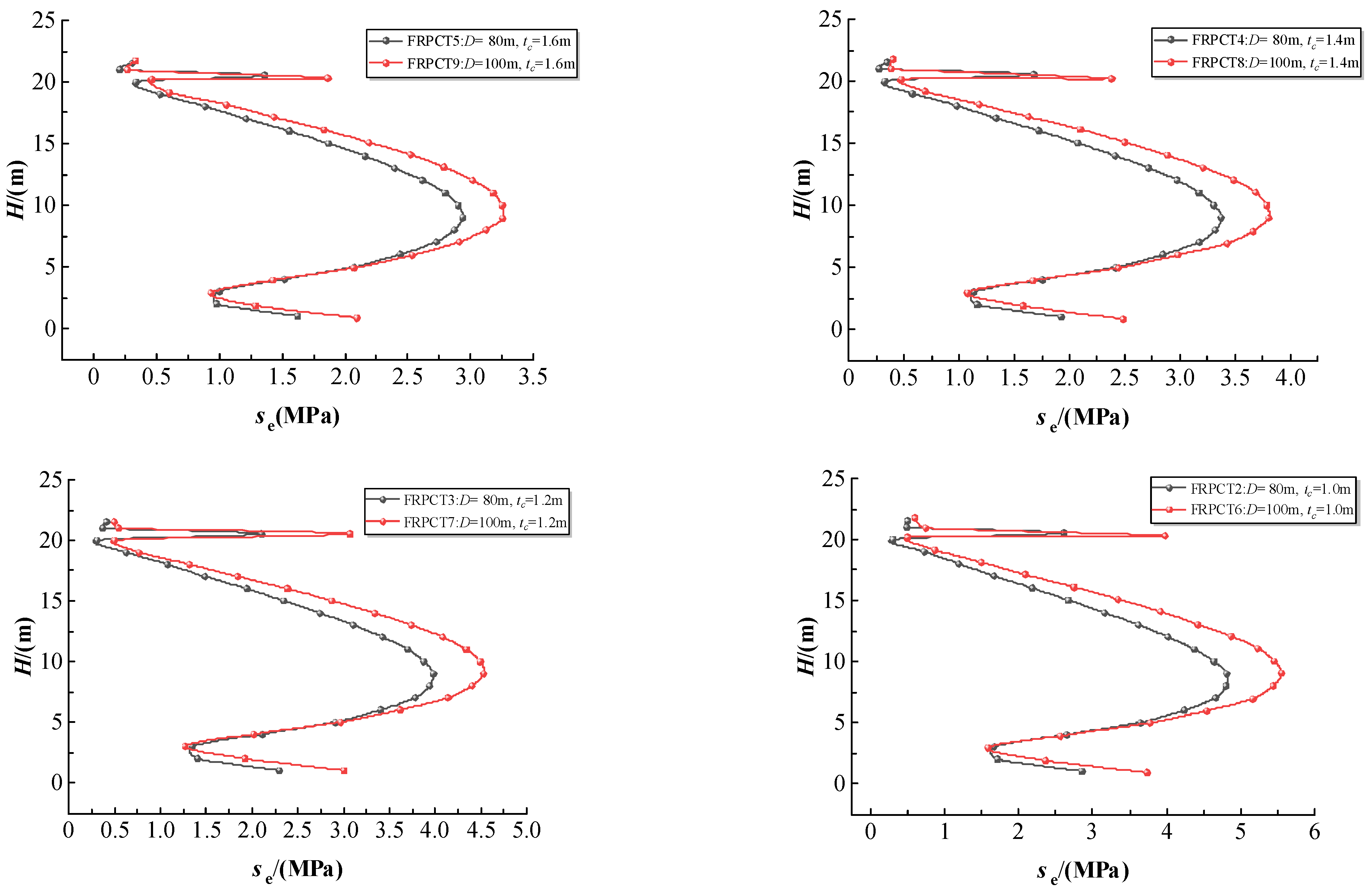
5.1. Influence of the Thickness of RPC (tc) on the Equivalent Stress
5.1.1. Influence of the Thickness of RPC (tc) on the Equivalent Stress with an Inner Diameter of the Storage Tank (D) of 100 m
5.1.2. Influence of the Thickness of RPC (tc) on the Equivalent Stress with an Inner Diameter of the Storage Tank (D) of 80 m
5.1.3. Influence of the Thickness of the RPC (tc) on the Equivalent Stress with an Inner Diameter (D) of 120 m
5.1.4. Influence of the Thickness of RPC (tc) on the Equivalent Stress with an Inner Diameter of the Storage Tank (D) of 150 m
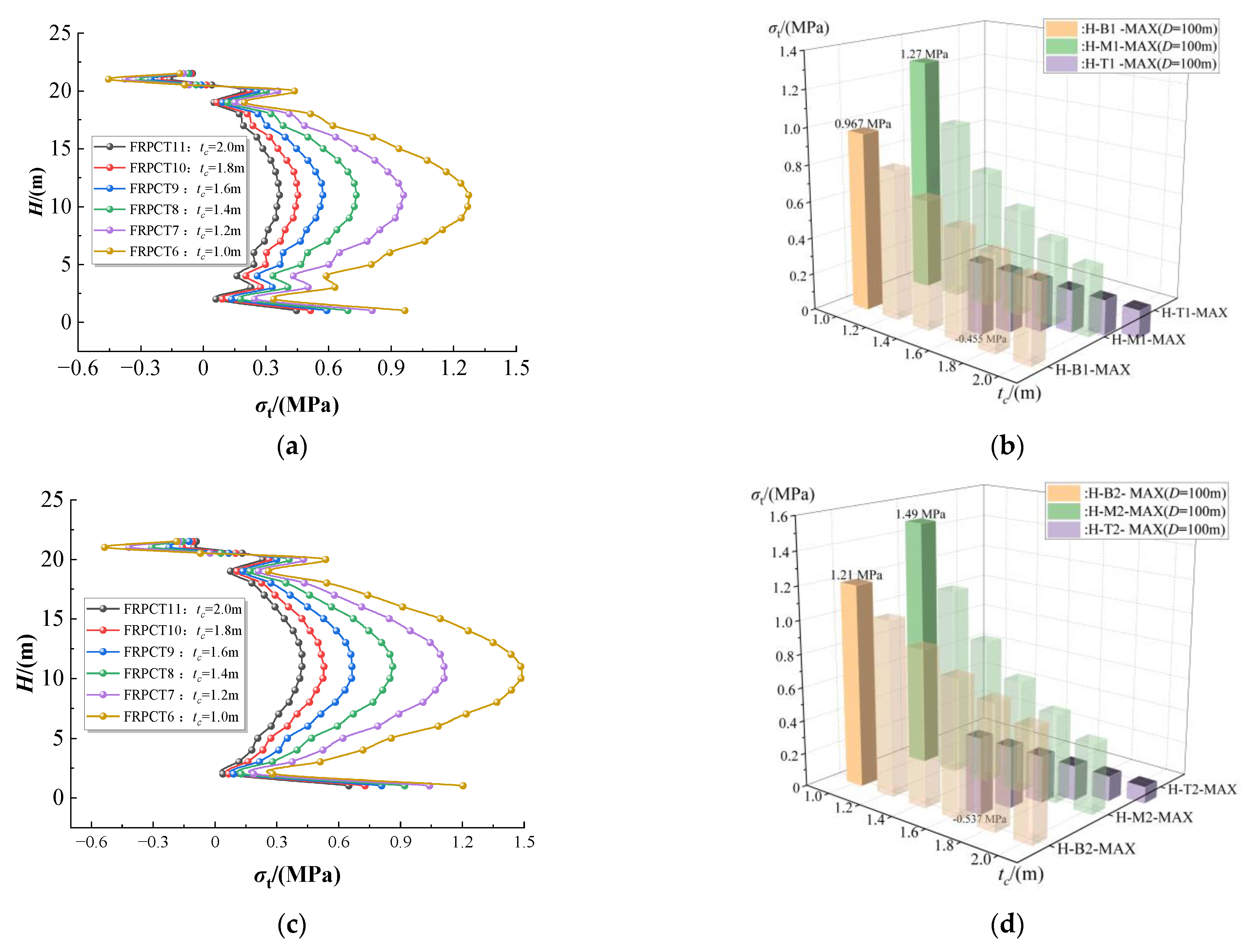
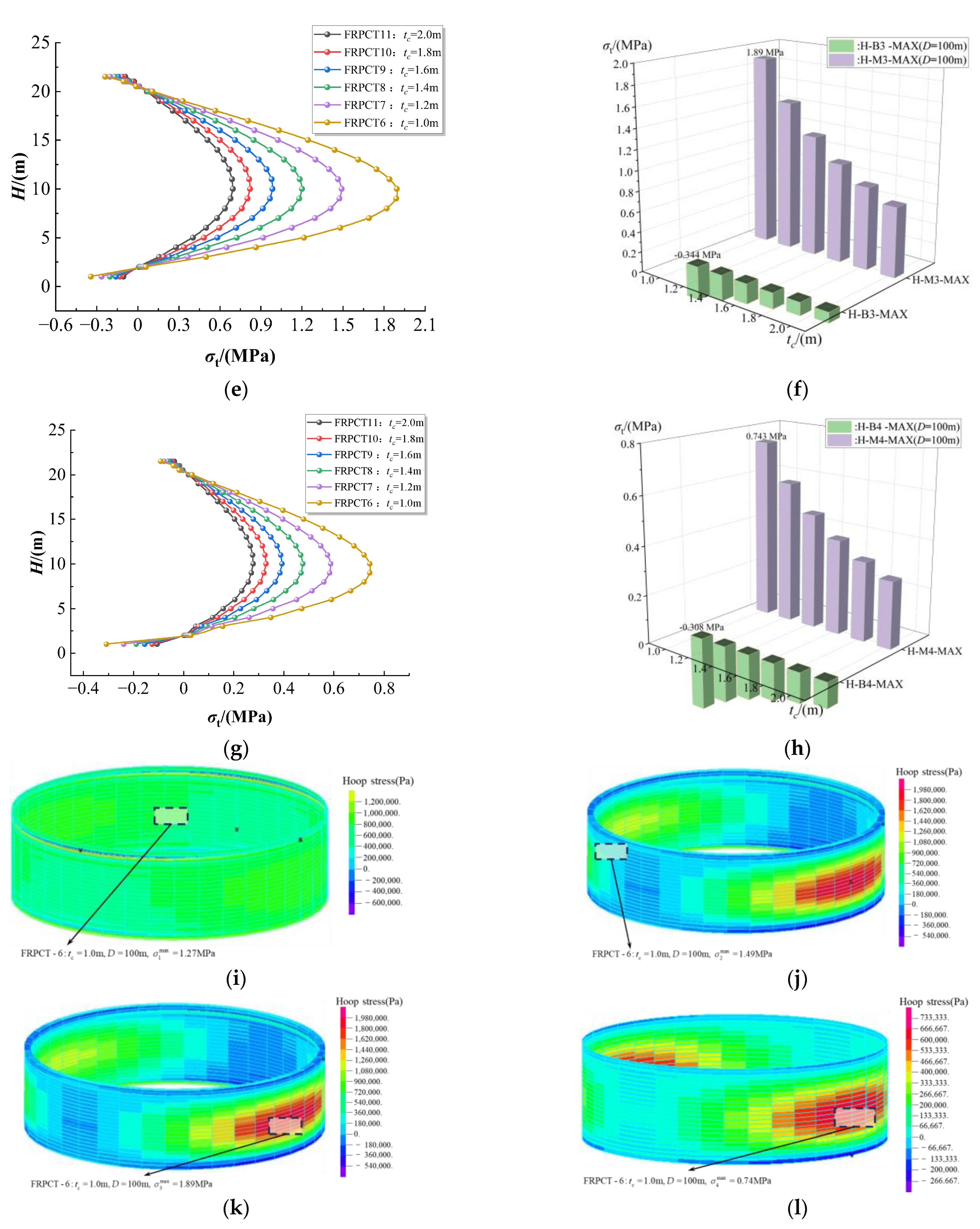
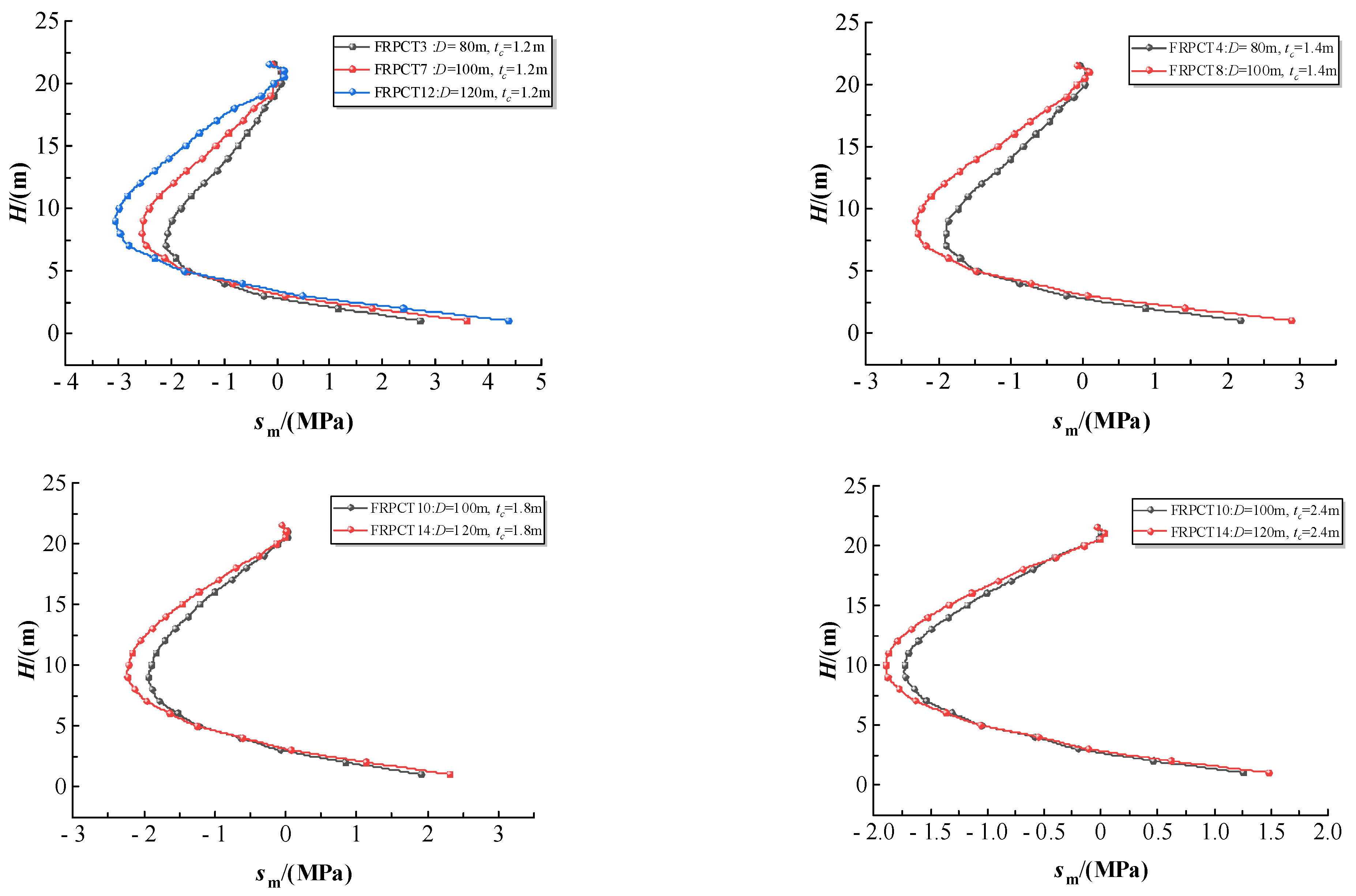
5.2. Influence of the Thickness of RPC (tc) on the Hoop Stress
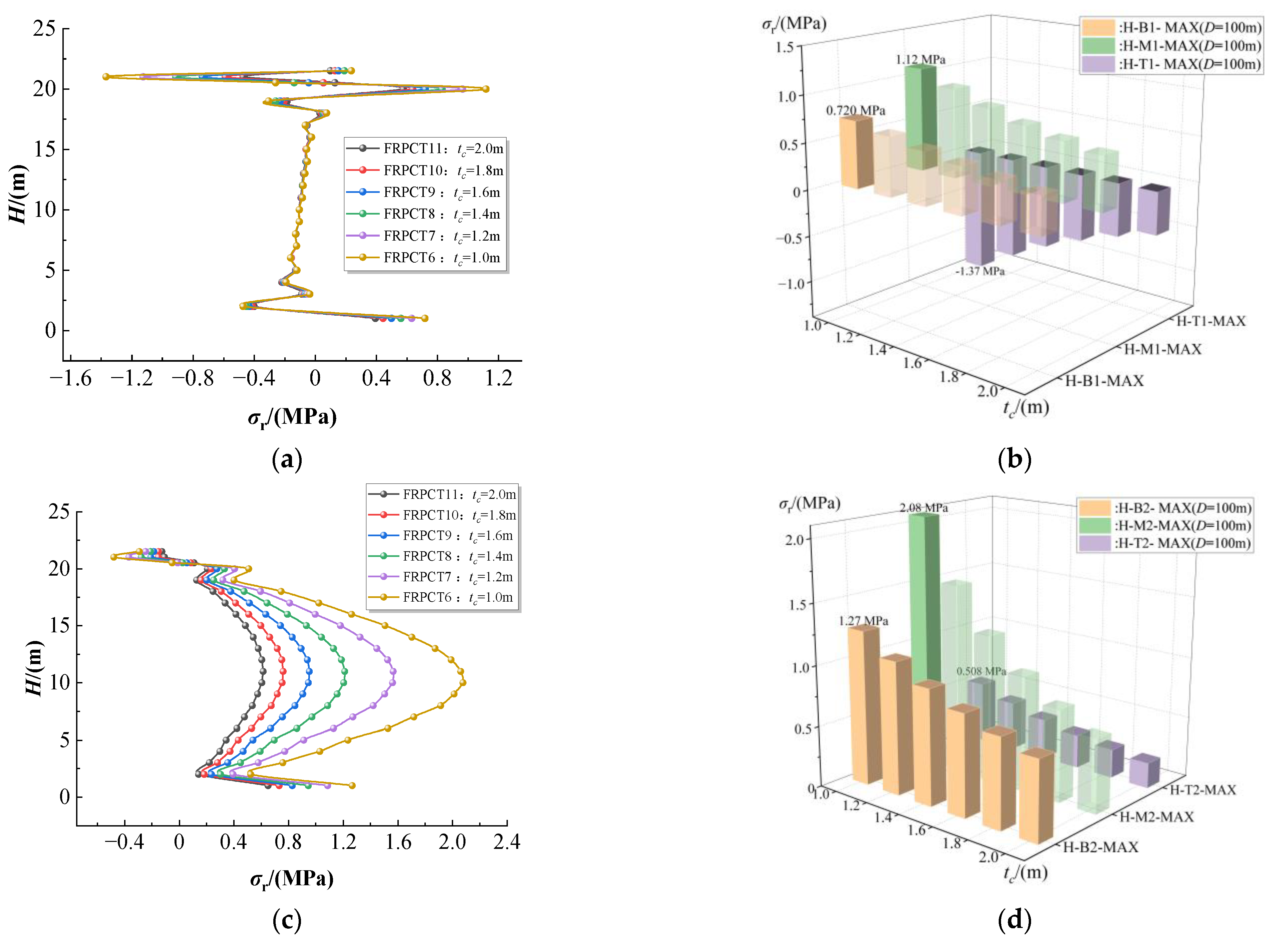
5.3. Influence of the Thickness of RPC (tc) on the Radial Stress
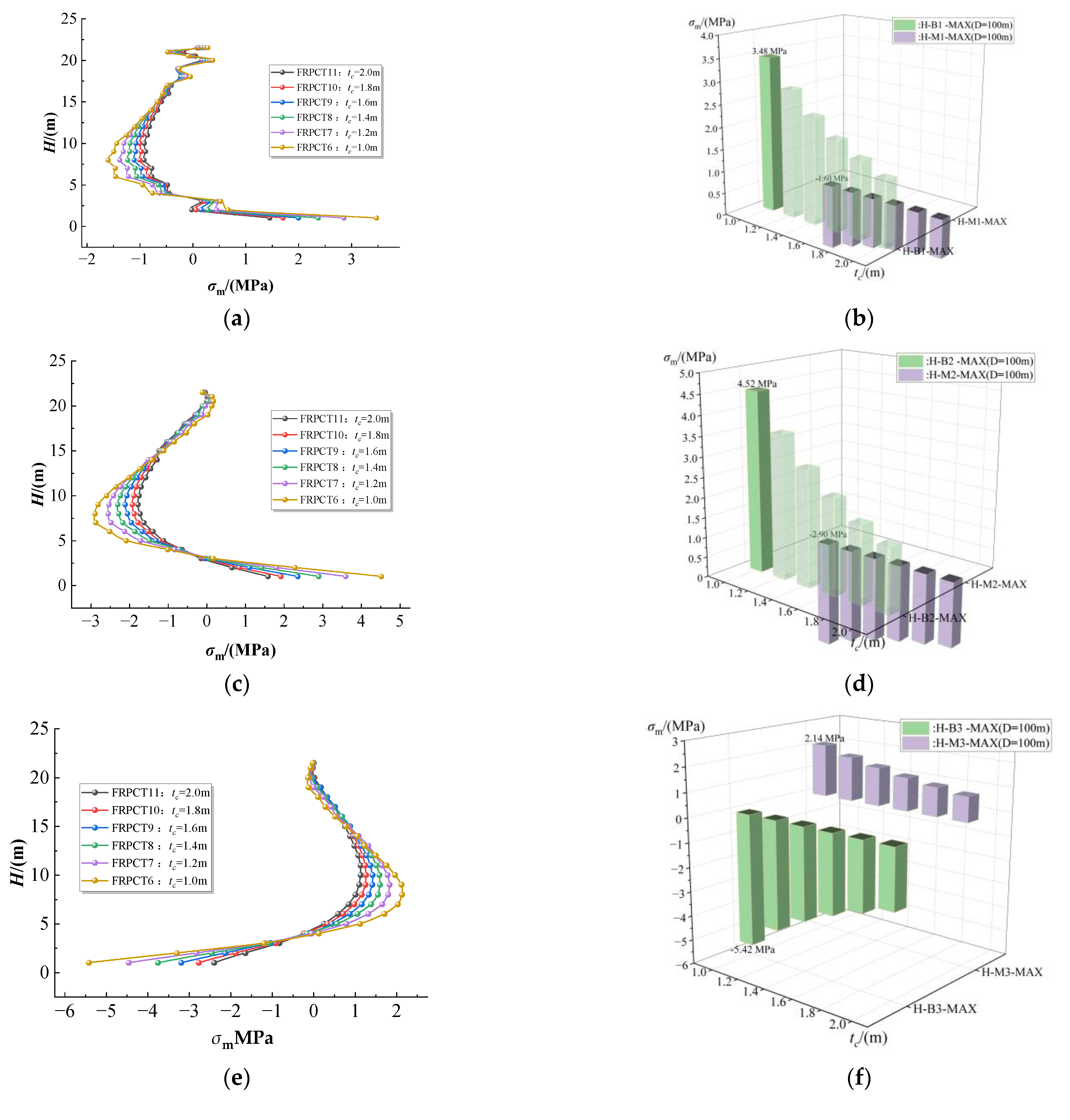
5.4. Influence of the Thickness of RPC (tc) on the Axial Stress
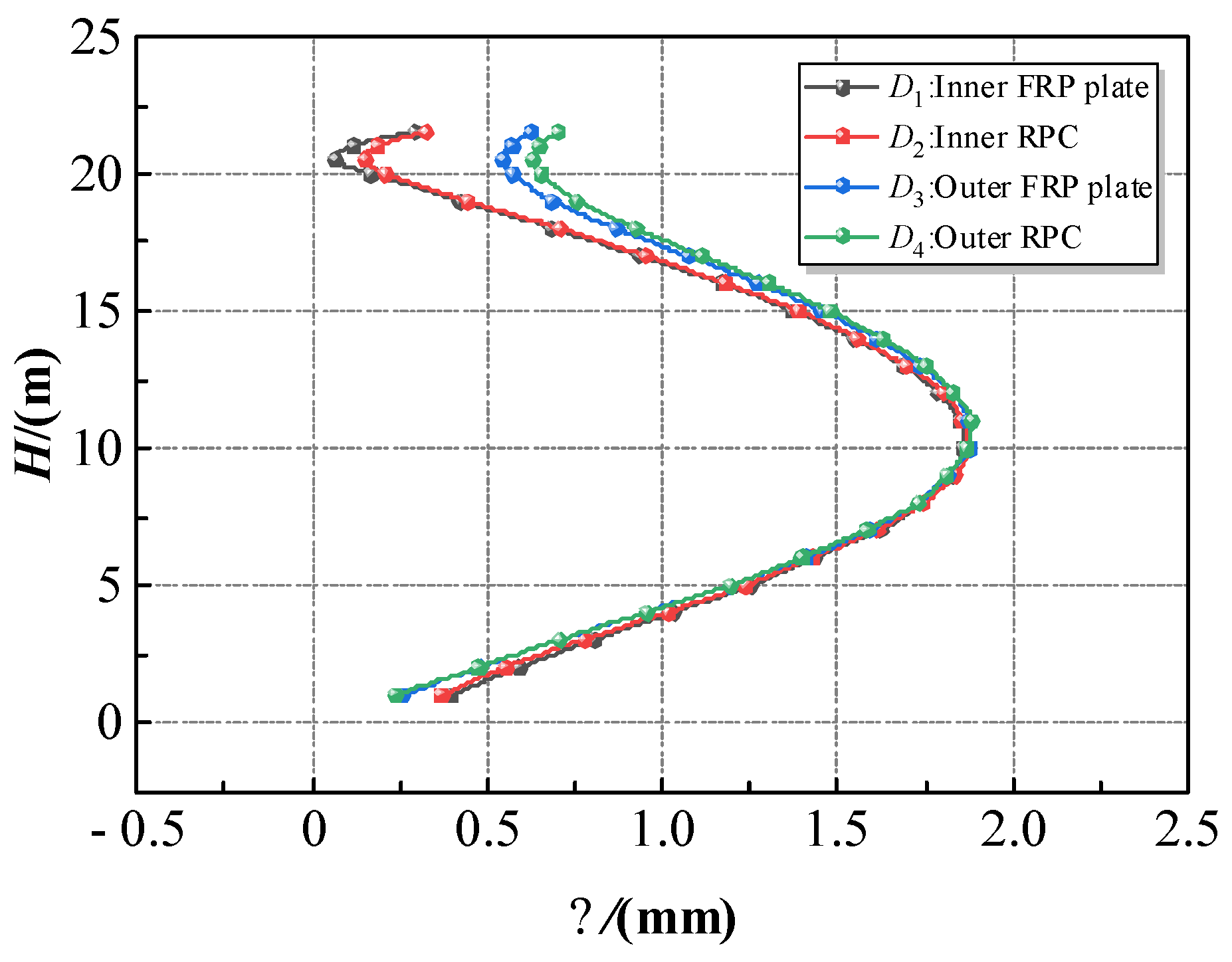
5.5. Displacement Analysis on the FRPCTs
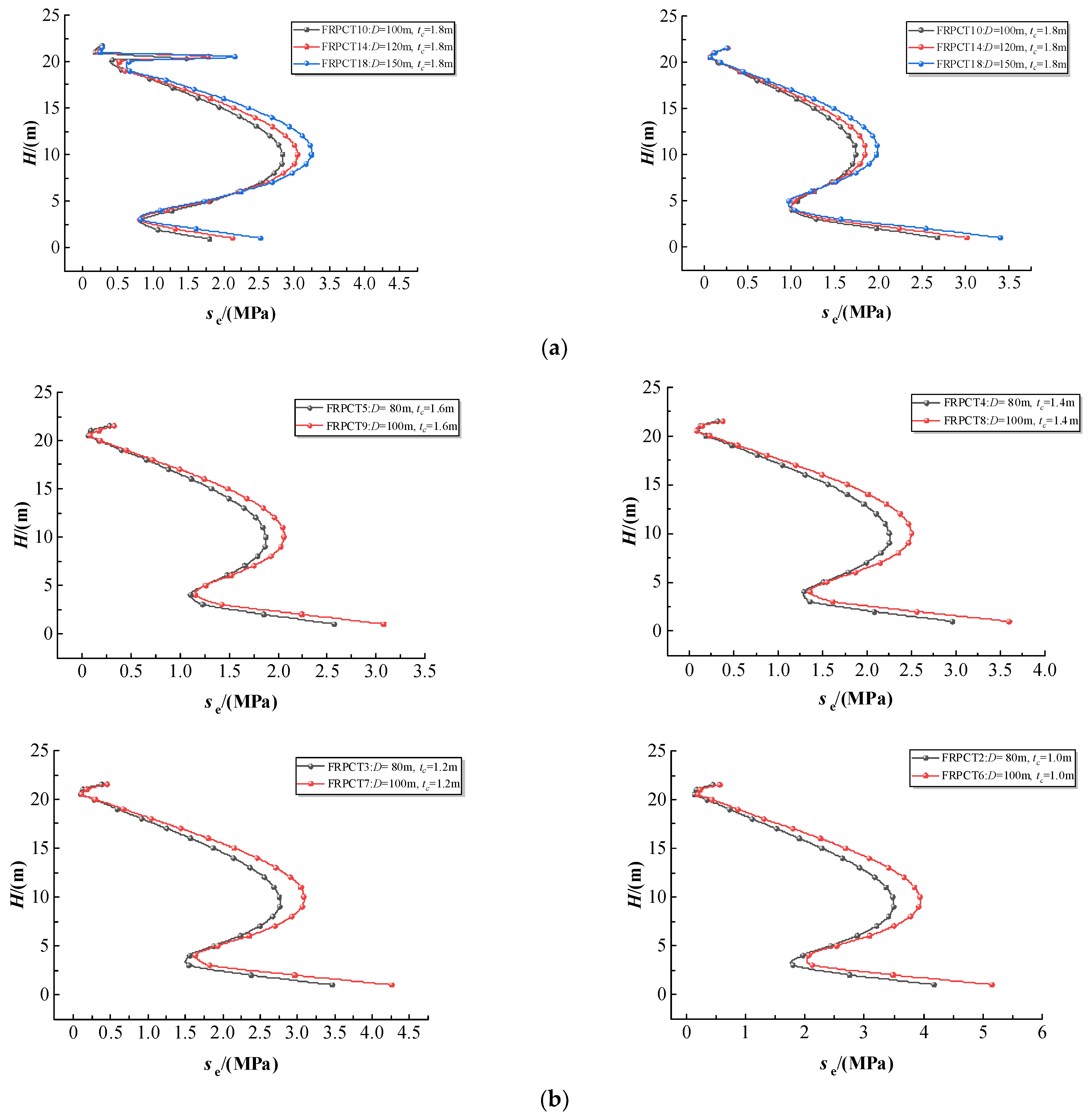
5.6. Influence of the Inner Diameter of the Storage Tank (D) on the Equivalent Stress
5.7. Influence of the Inner Diameter of the Storage Tank (D) on the Axial Stress
6. Discussion
6.1. Force Mechanism
6.2. Theoretical Formula of the Tank Wall Composition
6.3. Design and Construction Suggestion for FRPCTs
- (1)
- To solve the design problem of wall thickness, the calculation formula for the variation regularity of the tc is developed with the different D in this paper. The appropriate wall thickness can ensure the material utilization and safety of FRPCTs.
- (2)
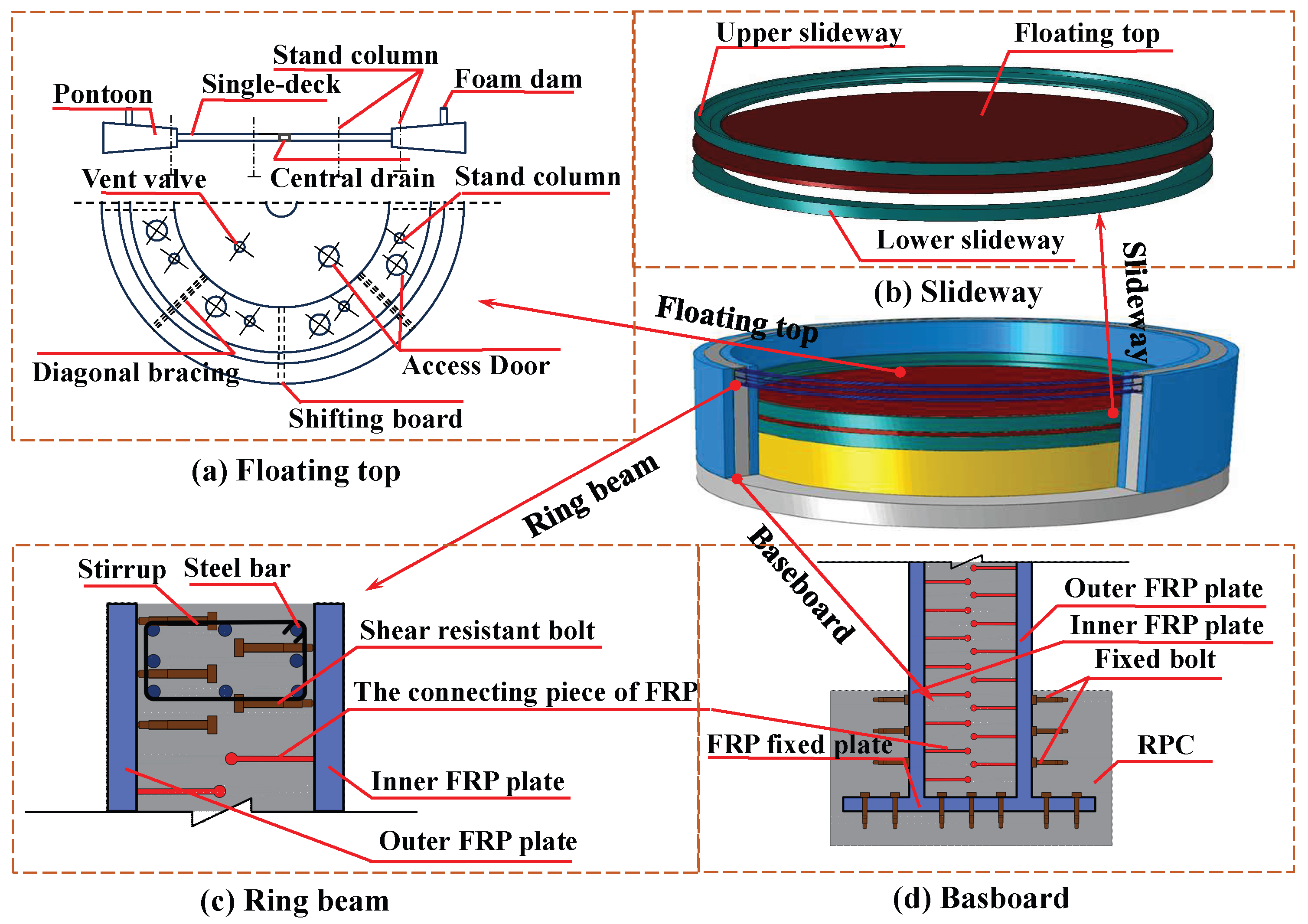
- In order to ensure the stiffness of the baseboard, it is suggested that the baseboard be poured with reinforced reactive powder concrete [40]. The influence of uneven settlement of the foundation on the baseboard is a severe problem, which is the main reason for structural failure. In the future, the form of the baseboard of the storage tank can be carried out to enrich the study of the storage tank. Due to the rounding effect, the internal pressure of the storage tank is specific to the bolt tension. In order to achieve the overall stability of the tank wall and the baseboard, the M64 bolt is adopted in Figure 21c,d.
- (3)
- The floating top is connected with the tank wall by the sealing rubber trap, which is placed in the groove of the floating top, and the upper slideway and the lower slideway are fixed at the design-in location to ensure gas tightness. The floating top slides into the tank, and the reserve vent removes gas below the floating top. The sketch of the floating top is shown in Figure 21a,b.
- (4)
- The layered construction method was used to construct the tank walls. First, the FRP precast plates are spliced through rivets, and the connection for the FRP plate is bonded along the circumference between the inner FRP plate and the outer FRP plate. Then, the RPC is poured between the inner FRP plate and the outer FRP plate, and one layer is completed to construct the next layer until the tank wall of the FRPCTs is finished. At last, the ring beam is built to improve the overall stability of the storage tank.
7. Conclusions
- In the case of the full tank, the equivalent stress of the inner FRP plate and the inner RPC occurs stress mutation at the top and bottom of the tank. The equivalent stress of the inner FRP plate reaches a peak value at the top of the tank. The equivalent stress of the inner FRP plate, inner RPC, outer RPC, and outer FRP plate uniformly changes at the middle of FRPCTs, and the equivalent stress of outer RPC and outer FRP plate reaches the peak equivalent stress at the bottom of FRPCTs. The distribution of equivalent stress of FRPCT is horizontal W-shaped, and the peak equivalent stress of inner RPC appears in the middle of FRPCTs.
- Due to the influence of the floating top, the hoop stress, radial stress, and axial stress exhibit complexity of stress distribution at the top of FRPCTs. Among them, the radial stress of the inner FRP plate causes mutation at the top of FRPCTs. Compared with traditional steel storage tanks, due to the FRP characteristic of high tensile strength, the deformation of FRPCTs is less prone to buckling at the top of the storage tank.
- The equivalent stress, hoop stress, radial stress, and axial stress of FRPCT decrease with an increase in tc. Furthermore, the tc positively affects the stress mutation, and with an increase in tc, the magnitude of the stress change is significantly reduced. Especially, the radial stress mutation of the inner FRP plate is improved obviously with the increase in tc. By comparison of the stress distribution of inner RPC with different D, the equivalent stress and axial stress increase with an increase in D. However, the effect of D on the axial stress of the FRPCTs is slight.
- The displacement of the inner FRP plate, inner RPC, outer FRP plate, and outer RPC have a good agreement. In the case of the full tank, there is no obvious dislocation between the FRP and RPC. Therefore, the bond–slip between the FRP and RPC can be neglected. The concentric double-layer FRP plate can be used as a template to pour concrete, which has economic efficiency.
- Based on the stress distribution acquired through the static analysis of FRPCTs, the calculation formula for the variation regularity of the tc is developed, and the design suggestion for this kind of novel tank is proposed correspondingly. The findings of the numerical simulation results agree with the calculation formula for the variation regularity of the tc obtained by polynomial fitting, indicating that the calculation formula for the variation regularity of the tc is reasonable and feasible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pouyakian, M.; Jafari, M.J.; Laal, F.; Nourai, F.; Zarei, E. A comprehensive approach to analyze the risk of floating roof storage tanks. Process Saf. Environ. Prot. 2021, 146, 811–836. [Google Scholar] [CrossRef]
- Yasunaga, J.; Uematsu, Y. Dynamic buckling of cylindrical storage tanks under fluctuating wind loading. Thin-Walled Struct. 2020, 150, 106677. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H.N.; Zhang, S.C.; Mercan, O.; Zhang, C.Y. Seismic analysis of a large LNG tank considering different site conditions. Appl. Sci. 2020, 10, 8121. [Google Scholar] [CrossRef]
- Cortes, G.; Prinz, G.S. Seismic fragility analysis of large unanchored steel tanks considering local instability and fatigue damage. Bull. Earthq. Eng. 2017, 15, 1279–1295. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, Y.; Huang, B. Corrosion analysis and remaining useful life prediction for storage tank bottom. Int. J. Adv. Robot. Syst. 2019, 16, 172988141987705. [Google Scholar] [CrossRef]
- Cwirzen, A.; Penttala, V.; Vornanen, C. Reactive powder based concretes: Mechanical properties, durability and hybrid use with OPC. Cem. Concr. Res. 2008, 38, 1217–1226. [Google Scholar] [CrossRef]
- Lee, P.N.; Fry, J.S.; Forey, B.A. A review of the evidence on smoking bans and incidence of heart disease. Regul. Toxicol. Pharmacol. 2014, 70, 7–23. [Google Scholar] [CrossRef]
- Soupionis, G.; Georgiou, P.; Zoumpoulakis, L. Polymer composite materials fiber-reinforced for the reinforcement/repair of concrete structures. Polymers 2020, 12, 2058. [Google Scholar] [CrossRef]
- Saleem, S.; Pimanmas, A.; Rattanapitikon, W. Lateral response of PET FRP-confined concrete. Constr. Build. Mater. 2018, 159, 390–407. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Ur Rahman Dogar, A.; Liu, Y.; Manalo, A.; Thambiratnam David, P. Performance and design of steel structures reinforced with FRP composites: A state-of-the-art review. Eng. Fail. Anal. 2022, 138, 106371. [Google Scholar] [CrossRef]
- Sanjuán M, Á.; Andrade, C. Reactive powder concrete: Durability and applications. Appl. Sci. 2021, 11, 5629. [Google Scholar] [CrossRef]
- Venkatasudhahar, M.; Velu, R.; Dilip Raja, N.; Logesh, K. Experimental investigation on natural fibre composite for thermal insulation performance enhancement. Int. J. Ambient Energy 2020, 41, 1304–1307. [Google Scholar] [CrossRef]
- Beaufait, F.W.; Ioannides, S.A.; Gerlein, M.A. Analysis of shell walls of circular tanks under axisymmetrical pressure. Comput. Struct. 1979, 10, 531–538. [Google Scholar] [CrossRef]
- Balendra, T.; Ang, K.K.; Paramasivam, P.; Lee, S.L. Seismic design of flexible cylindrical liquid storage tanks. Earthq. Eng. Struct. Dyn. 1982, 10, 477–496. [Google Scholar] [CrossRef]
- API Standard 650; Welded Tanks for Oil Storage. 12th ed. American Petroleum Institute: Washington, DC, USA, 2013.
- Azzuni, E.; Guzey, S. Comparison of the shell design methods for cylindrical liquid storage tanks. Eng. Struct. 2015, 101, 621–630. [Google Scholar] [CrossRef]
- Malhotra, P.K.; Wenk, T.; Wieland, M. Simple procedure for seismic analysis of liquid-storage tanks. Struct. Eng. Int. 2000, 10, 197–201. [Google Scholar] [CrossRef]
- Huang, M.; Chen, G.; Yang, P.; Hu, K.; Zhou, L.X.; Men, J.K.; Zhao, J. Multi-hazard coupling vulnerability analysis for buckling failure of vertical storage tank: Floods and hurricanes. Process Saf. Environ. Prot. 2022, 161, 528–541. [Google Scholar] [CrossRef]
- Jhung, M.J.; Kang, S.-S. Fluid effect on the modal characteristics of a square tank. Nucl. Eng. Technol. 2019, 51, 1117–1131. [Google Scholar] [CrossRef]
- Wang, L.L.; Fu, S.B.; Qiao, H.Y. Simplified finite element model for static analysis of vertical storage tank. Oil Gas Storage Transp. 2021, 40, 51–57. [Google Scholar]
- De Angelis, M.; Giannini, R.; Paolacci, F. Experimental investigation on the seismic response of a steel liquid storage tank equipped with floating roof by shaking table tests. Earthq. Eng. Struct. Dyn. 2009, 39, 377–396. [Google Scholar] [CrossRef]
- Luo, D.Y.; Liu, C.G.; Sun, J.G.; Cui, L.F.; Wang, Z. Sloshing effect analysis of liquid storage tank under seismic excitation. Structures 2022, 43, 40–58. [Google Scholar] [CrossRef]
- Wang, M.Z.; Sun, Z.G.; Sun, J.G.; Cui, L.F.; Wu, Y.J. Probabilistic seismic fragility assessment of vertical storage tank with a floating roof. Structures 2023, 48, 318–330. [Google Scholar] [CrossRef]
- Li, K.N. The Nonlinear Analysis on Underground Reinforced Concrete Oil Tank; Beijing University of Aeronautics and Astronautics: Beijing, China, 2011. [Google Scholar]
- Du, Y.K. Dynamic Characteristics and Seismic Behavior of Large Inground Liquid Storage Tanks; Beijing University of Aeronautics and Astronautics: Beijing, China, 2006. [Google Scholar]
- Long, P.H.; Huang, L.Y.; Qiao, H.; Song, H.; Li, F. RPC constitutive relation and ultimate flexural capacity of rectangular RPC beams. China Concr. Cem. Prod. 2020, 10, 55–60. [Google Scholar]
- Teng, J.G.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical model for fiber-reinforced polymer-confined concrete. J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Zhao DZhang JG Liu FF Zhao GL Gu CZhang WC Song, H.Y. Experimental study of the behavior under axial compression of steel tube confined concrete with a circular hollow section (STCC-CHS). Ocean Eng. 2023, 285, 115267. [Google Scholar]
- Lin, H.W.; Zeng, H.X.; Feng, P.; Jiang Cheng, J.; Zhang, Y.Q. Bond behavior of FRP-concrete wet-bonding interface under lateral confinement. Eng. Struct. 2023, 292, 116536. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, L.; Yang, F.; Zhang, B.C.; Huang, H. Static analysis of 160000 cubic meters LNG storage tank. Port Eng. Technol. 2020, 57, 85–90. [Google Scholar]
- Ji, J.; He, L.J.; Jiang, L.Q.; Zhang, Y.F.; Liu, Y.C.; Li, Y.H.; Zhang, Z.B. Numerical study on the axial compression behavior of composite columns with steel tube SHCC flanges and honeycombed steel web. Eng. Struct. 2023, 283, 115883. [Google Scholar] [CrossRef]
- Haroun, G.W.; Housner, M.A. Earquake response of deformable liquid storage tanks. Trans. ASME 1981, 48, 411–418. [Google Scholar] [CrossRef]
- Haroun, M.A. Vibration studies and tests of liquid storage tanks. Earthq. Eng. Struct. Dyn. 1983, 11, 179–206. [Google Scholar] [CrossRef]
- Chen, Z.P. Stress Analysis and Aseismatic Resarch of Large Unanchored Oil Storage Tanks; Zhejiang University: Hangzhou, China, 2006. [Google Scholar]
- Ji, J.; Zhang, Z.B.; Lin, M.F.; Li, L.Z.; Jiang, L.Q.; Ding, Y.; Yu, K.Q. Structural application of engineered cementitious composites (ECC): A state-of-the-art review. Constr. Build. Mater. 2023, 406, 133289. [Google Scholar] [CrossRef]
- Liu, Y.C.; He, Z.W.; Zhang, W.F.; Ji, J.; Liu, Y.C.; Zhang, Z.Z.; Wang, R.L.; Yang, K.L.; Zhang, Z.C. Lateral-torsional buckling analysis for doubly symmetric tubular flange composite beams with lateral bracing under concentrated load. Symmetry 2021, 13, 2328. [Google Scholar] [CrossRef]
- Ji, J.; Li, Y.H.; Jiang, L.Q.; Zhang, Y.F.; Liu, Y.C.; He, L.J.; Zhang, Z.B.; Wang, Y. Axial compression behavior of strength-gradient composite stub columns encased CFST with small diameter: Experimental and numerical investigation. Structures 2023, 47, 282–298. [Google Scholar] [CrossRef]
- Li, Y.M.; Yang, P. Anti-Quake Architectural Structure Design; Chongqing University: Chongqing, China, 2011. [Google Scholar]
- Wang, Q.W.; Shi, Q.X.; Tao, Y.; Wang, Z.W. Compressive mechanical properties and indexes of reactive powder concrete. J. Build. Mater. 2020, 23, 1381–1389. [Google Scholar]
- Ji, J.; Zeng, W.; Jiang, L.Q.; Bai, W.; Ren, H.G.; Chai, Q.R.; Zhang, L.; Wang, H.T.; Li, Y.H.; He, L.J. Hysteretic behavior on asymmetrical composite joints with concrete-filled steel tube columns and unequal high steel beams. Symmetry 2021, 13, 2381. [Google Scholar] [CrossRef]
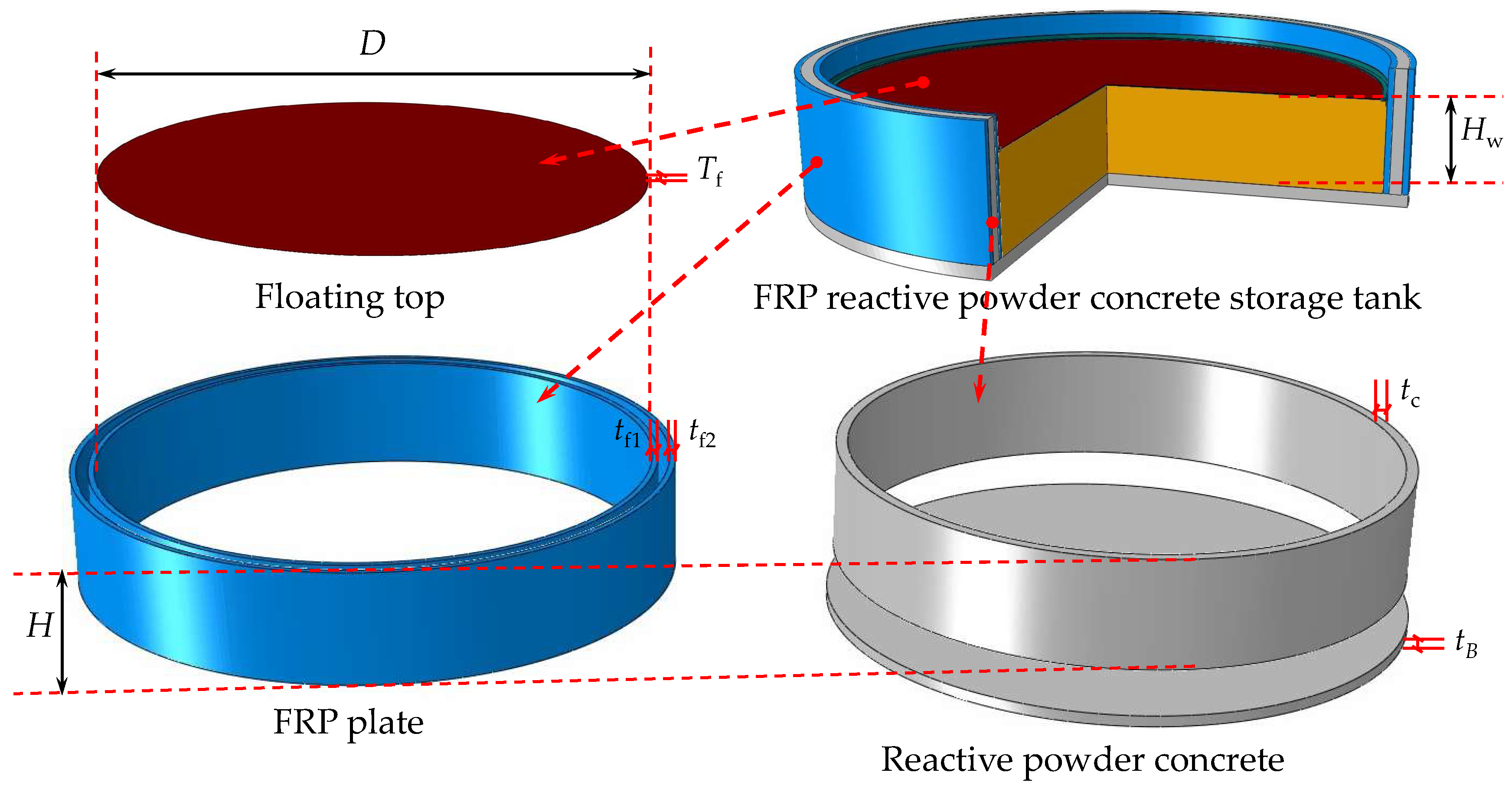








| Specimens | D(m) | H(m) | tf1(m) | tf2(m) | tc(m) | tB(m) | Tf(m) | Hw(m) |
|---|---|---|---|---|---|---|---|---|
| FRPCT1 | 80 | 21.7 | 0.1 | 0.1 | 0.8 | 5.0 | 0.1 | 20.18 |
| FRPCT2 | 80 | 21.7 | 0.1 | 0.1 | 1.0 | 5.0 | 0.1 | 20.18 |
| FRPCT3 | 80 | 21.7 | 0.1 | 0.1 | 1.2 | 5.0 | 0.1 | 20.18 |
| FRPCT4 | 80 | 21.7 | 0.1 | 0.1 | 1.4 | 5.0 | 0.1 | 20.18 |
| FRPCT5 | 80 | 21.7 | 0.1 | 0.1 | 1.6 | 5.0 | 0.1 | 20.18 |
| FRPCT6 | 100 | 21.7 | 0.1 | 0.1 | 1.0 | 5.0 | 0.1 | 20.18 |
| FRPCT7 | 100 | 21.7 | 0.1 | 0.1 | 1.2 | 5.0 | 0.1 | 20.18 |
| FRPCT8 | 100 | 21.7 | 0.1 | 0.1 | 1.4 | 5.0 | 0.1 | 20.18 |
| FRPCT9 | 100 | 21.7 | 0.1 | 0.1 | 1.6 | 5.0 | 0.1 | 20.18 |
| FRPCT10 | 100 | 21.7 | 0.1 | 0.1 | 1.8 | 5.0 | 0.1 | 20.18 |
| FRPCT11 | 100 | 21.7 | 0.1 | 0.1 | 2.0 | 5.0 | 0.1 | 20.18 |
| FRPCT12 | 120 | 21.7 | 0.1 | 0.1 | 1.2 | 5.0 | 0.1 | 20.18 |
| FRPCT13 | 120 | 21.7 | 0.1 | 0.1 | 1.5 | 5.0 | 0.1 | 20.18 |
| FRPCT14 | 120 | 21.7 | 0.1 | 0.1 | 1.8 | 5.0 | 0.1 | 20.18 |
| FRPCT15 | 120 | 21.7 | 0.1 | 0.1 | 2.1 | 5.0 | 0.1 | 20.18 |
| FRPCT16 | 120 | 21.7 | 0.1 | 0.1 | 2.4 | 5.0 | 0.1 | 20.18 |
| FRPCT17 | 150 | 21.7 | 0.1 | 0.1 | 1.5 | 5.0 | 0.1 | 20.18 |
| FRPCT18 | 150 | 21.7 | 0.1 | 0.1 | 1.8 | 5.0 | 0.1 | 20.18 |
| FRPCT19 | 150 | 21.7 | 0.1 | 0.1 | 2.1 | 5.0 | 0.1 | 20.18 |
| FRPCT20 | 150 | 21.7 | 0.1 | 0.1 | 2.4 | 5.0 | 0.1 | 20.18 |
| FRPCT21 | 150 | 21.7 | 0.1 | 0.1 | 2.7 | 5.0 | 0.1 | 20.18 |
| FRPCT22 | 150 | 21.7 | 0.1 | 0.1 | 3.0 | 5.0 | 0.1 | 20.18 |
| Dilation Angle/° | Eccentric Ratio | fb0/fc0 | K | Viscosity Parameter |
|---|---|---|---|---|
| 36 | 0.1 | 1.16 | 0.667 | 0.0005 |
| E1 /MPa | E2 /MPa | v12 | G12 /MPa | Xt /MPa | Xc /MPa | Yt /MPa | Yc /MPa | θ /° | tr /mm |
|---|---|---|---|---|---|---|---|---|---|
| 52,000 | 8000 | 0.32 | 3000 | 584 | 203 | 43 | 187 | ±80 | 0.5 |
| Specimens | D (m) | Hw (m) | tf1 (m) | tf2 (m) | tc (m) | tB (m) | Tf (m) | w1T (Hz) | w1S (Hz) | w1T−w1S/w1T (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| T-FRPCT1 | 52.2 | 2.018 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0266 | 0.0254 | 4.51 |
| T-FRPCT2 | 52.2 | 4.036 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0368 | 0.0351 | 4.62 |
| T-FRPCT3 | 52.2 | 6.054 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0449 | 0.0429 | 4.45 |
| T-FRPCT4 | 52.2 | 8.072 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0515 | 0.0492 | 4.47 |
| T-FRPCT5 | 52.2 | 10.090 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0571 | 0.0546 | 4.38 |
| T-FRPCT6 | 52.2 | 12.108 | 0.1 | 0.1 | 2 | 5 | 0 | 0.062 | 0.0593 | 4.35 |
| T-FRPCT7 | 52.2 | 14.126 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0662 | 0.0634 | 4.23 |
| T-FRPCT8 | 52.2 | 16.144 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0699 | 0.0671 | 4.01 |
| T-FRPCT9 | 52.2 | 18.162 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0732 | 0.0703 | 3.96 |
| T-FRPCT10 | 37.2 | 20.180 | 0.1 | 0.1 | 2 | 5 | 0 | 0.1015 | 0.0966 | 4.83 |
| T-FRPCT11 | 42.2 | 20.180 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0915 | 0.0874 | 4.48 |
| T-FRPCT12 | 47.2 | 20.180 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0831 | 0.0797 | 4.09 |
| T-FRPCT13 | 52.2 | 20.180 | 0.1 | 0.1 | 2 | 5 | 0 | 0.0761 | 0.0731 | 3.94 |
| Chen Z. P. [34] | Specimens | Hw (mm) | σtT (MPa) | σtS (MPa) | |σtT−σtS|/σtT (%) |
| T-ST-14 | 20.18 | 93.73 | 96.17 | 2.55 | |
| T-ST-15 | 6.13 | 56.70 | 56.61 | 0.16 | |
| Chen Z. P. [34] | Specimens | Hw (mm) | σmT (MPa) | σmS (MPa) | |σmT−σmS|/σmT (%) |
| T-ST-16 | 20.18 | 247.59 | 237.03 | 4.27 | |
| T-ST-17 | 6.13 | 19.00 | 19.04 | 0.21 |
| Specimens | D (m) | tc (m) | σ1max (MPa) | σ2max (MPa) | σ3max (MPa) | σ4max (MPa) |
|---|---|---|---|---|---|---|
| FRPCT1 | 80 | 0.8 | 3.68 | 6.08 | 4.54 | 2.88 |
| FRPCT2 | 80 | 1.0 | 2.75 | 4.81 | 3.48 | 2.27 |
| FRPCT3 | 80 | 1.2 | 2.15 | 3.98 | 2.76 | 1.86 |
| FRPCT4 | 80 | 1.4 | 1.80 | 3.3785 | 2.25 | 1.56 |
| FRPCT5 | 80 | 1.6 | 1.56 | 2.94 | 1.88 | 1.33 |
| FRPCT6 | 100 | 1.0 | 3.67 | 5.56 | 2.83 | 5.15 |
| FRPCT7 | 100 | 1.2 | 3.07 | 4.53 | 2.29 | 4.26 |
| FRPCT8 | 100 | 1.4 | 2.57 | 3.81 | 1.92 | 3.60 |
| FRPCT9 | 100 | 1.6 | 2.15 | 3.25 | 1.61 | 3.08 |
| FRPCT10 | 100 | 1.8 | 1.82 | 2.83 | 1.38 | 2.68 |
| FRPCT11 | 100 | 2.0 | 1.55 | 2.50 | 1.19 | 2.34 |
| FRPCT12 | 120 | 1.2 | 4.03 | 4.99 | 4.95 | 2.69 |
| FRPCT13 | 120 | 1.5 | 2.96 | 3.82 | 3.80 | 2.02 |
| FRPCT14 | 120 | 1.8 | 2.21 | 3.05 | 3.01 | 1.56 |
| FRPCT15 | 120 | 2.1 | 1.69 | 2.49 | 2.44 | 1.24 |
| FRPCT16 | 120 | 2.4 | 1.33 | 2.10 | 2.04 | 1.01 |
| FRPCT17 | 150 | 1.5 | 3.71 | 4.14 | 4.39 | 2.34 |
| FRPCT18 | 150 | 1.8 | 2.67 | 3.25 | 3.4 | 1.77 |
| FRPCT19 | 150 | 2.1 | 1.98 | 2.63 | 2.71 | 1.39 |
| FRPCT20 | 150 | 2.4 | 1.53 | 2.19 | 2.22 | 1.11 |
| FRPCT21 | 150 | 2.7 | 1.23 | 1.86 | 1.86 | 0.94 |
| FRPCT22 | 150 | 3.0 | 1.02 | 1.61 | 1.58 | 0.76 |
| Specimens | D (m) | tf1(m) | tf2(m) | tc(m) | σesmax (MPa) | σesmax’ (MPa) | σasmax’ (MPa) |
|---|---|---|---|---|---|---|---|
| FRPCT1 | 80 | 0.1 | 0.1 | 0.8 | 6.07 | 5.15 | 4.39 |
| FRPCT2 | 80 | 0.1 | 0.1 | 1.0 | 4.80 | 4.18 | 3.41 |
| FRPCT3 | 80 | 0.1 | 0.1 | 1.2 | 3.97 | 3.491 | 2.70 |
| FRPCT4 | 80 | 0.1 | 0.1 | 1.4 | 3.37 | 2.97 | 2.17 |
| FRPCT5 | 80 | 0.1 | 0.1 | 1.6 | 2.92 | 2.58 | 1.76 |
| FRPCT6 | 100 | 0.1 | 0.1 | 1.0 | 5.76 | 5.14 | 4.50 |
| FRPCT7 | 100 | 0.1 | 0.1 | 1.2 | 4.54 | 4.25 | 3.58 |
| FRPCT8 | 100 | 0.1 | 0.1 | 1.4 | 3.81 | 3.59 | 2.89 |
| FRPCT9 | 100 | 0.1 | 0.1 | 1.6 | 3.26 | 3.08 | 2.35 |
| FRPCT10 | 100 | 0.1 | 0.1 | 1.8 | 2.84 | 2.67 | 1.92 |
| FRPCT11 | 100 | 0.1 | 0.1 | 2.0 | 2.51 | 2.34 | 1.57 |
| FRPCT12 | 120 | 0.1 | 0.1 | 1.2 | 4.99 | 4.95 | 4.39 |
| FRPCT13 | 120 | 0.1 | 0.1 | 1.5 | 3.83 | 3.80 | 3.17 |
| FRPCT14 | 120 | 0.1 | 0.1 | 1.8 | 3.05 | 3.01 | 2.33 |
| FRPCT15 | 120 | 0.1 | 0.1 | 2.1 | 2.51 | 2.34 | 1.57 |
| FRPCT16 | 120 | 0.1 | 0.1 | 2.4 | 4.99 | 4.95 | 4.39 |
| FRPCT17 | 150 | 0.1 | 0.1 | 1.5 | 3.83 | 3.80 | 3.17 |
| FRPCT18 | 150 | 0.1 | 0.1 | 1.8 | 3.05 | 3.01 | 2.33 |
| FRPCT19 | 150 | 0.1 | 0.1 | 2.1 | 2.51 | 2.44 | 1.71 |
| FRPCT20 | 150 | 0.1 | 0.1 | 2.4 | 2.11 | 2.03 | 1.26 |
| FRPCT21 | 150 | 0.1 | 0.1 | 2.7 | 1.86 | 1.85 | 1.09 |
| FRPCT22 | 150 | 0.1 | 0.1 | 3.0 | 1.61 | 1.58 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.; Yu, K.; Jiang, L.; Liu, Y.; Zhang, Z.; Chu, X.; Li, J.; Zhang, H. Mechanical Behavior of Large Symmetric Fiber Reinforced Polymer-Reactive Powder Concrete Composite Tanks with Floating Tops. Symmetry 2024, 16, 51. https://doi.org/10.3390/sym16010051
Ji J, Yu K, Jiang L, Liu Y, Zhang Z, Chu X, Li J, Zhang H. Mechanical Behavior of Large Symmetric Fiber Reinforced Polymer-Reactive Powder Concrete Composite Tanks with Floating Tops. Symmetry. 2024; 16(1):51. https://doi.org/10.3390/sym16010051
Chicago/Turabian StyleJi, Jing, Kexin Yu, Liangqin Jiang, Yingchun Liu, Zhanbin Zhang, Xuan Chu, Jiaqi Li, and Huiling Zhang. 2024. "Mechanical Behavior of Large Symmetric Fiber Reinforced Polymer-Reactive Powder Concrete Composite Tanks with Floating Tops" Symmetry 16, no. 1: 51. https://doi.org/10.3390/sym16010051
APA StyleJi, J., Yu, K., Jiang, L., Liu, Y., Zhang, Z., Chu, X., Li, J., & Zhang, H. (2024). Mechanical Behavior of Large Symmetric Fiber Reinforced Polymer-Reactive Powder Concrete Composite Tanks with Floating Tops. Symmetry, 16(1), 51. https://doi.org/10.3390/sym16010051