Abstract
Pattern formation in biological aggregations is a topic of great interest, due to the complex spatial structure of various aggregations of cells/bacteria/animals that can be observed in nature. While many such aggregations look similar at the macroscopic level, they might differ in their microscopic spatial structure. However, the complexity of the non-linear and sometimes non-local interactions among individuals inside these aggregations makes it difficult to investigate these spatial structures. In this study, we investigate numerically the transitions between different spatial patterns of animal aggregations with various symmetries (even, odd or no symmetry) that characterise the microscopic distribution of individuals inside these aggregations. To this end, we construct a bifurcation diagram starting with perturbations of spatially homogeneous solutions with low, medium, and high amplitudes. For perturbations with low amplitudes, the bifurcating structures show transitions among even-symmetric, odd-symmetric, and non-symmetric solutions. For perturbations with large amplitudes, there are wide parameter regions with non-convergent solutions, characterised by oscillatory transitions between different relatively similar solutions. These numerical results emphasize: (i) the effect of nonlinear and non-local interactions on the microscopically different symmetric/non-symmetric structures of macroscopically similar ecological aggregations; (ii) the difficulty of developing continuation algorithms for this class of non-local models.
Keywords:
localised solutions; even and odd symmetries; biological aggregations; nonlocal hyperbolic models; numerical bifurcations MSC:
35; 37; 45; 65; 68; 92
1. Introduction
Pattern formation in biological/ecological aggregations has been a subject of interest for millennia [1]. During the last century, the collection of data on such biological/ecological aggregations and the development of new approaches to investigate this kind of data has led to a resurgence of the interest in these aggregations: from aggregations of cells during morphogenesis, tissue repair or cancer [2]; to aggregations of bacteria during biofilm formation [3]; or aggregations of locusts [4], birds [5], fish [6], etc. While many of these aggregations look similar at the macroscopic level (e.g., round 2D shapes in stationary animal groups, elongated 2D shapes in travelling animal groups; see [7]), their microscopic structure can be different, as it depends on the spatial distribution of individuals inside these aggregations; see also Figure 1. This spatial distribution could be determined by (i) the local/non-local interactions of individuals with their neighbours inside these aggregations, or by (ii) the interactions of these individuals with a heterogeneous environment (e.g., which could have more food in some areas and less food in other areas).
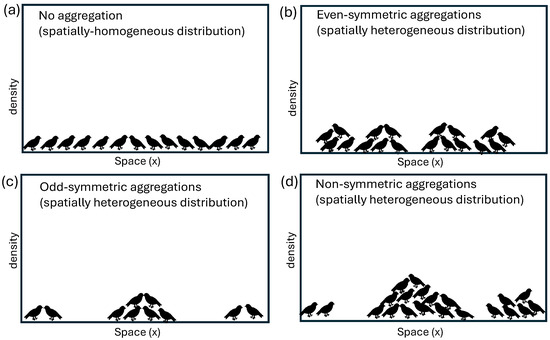
Figure 1.
Caricature description of different types of possible animal aggregation patterns in 1D. For illustrating purposes, we show a population of birds (left-facing and right-facing in a 1D domain). Horizontal axis shows the spatial domain, while vertical axis describes the density of individuals. (a) No spatial aggregation, as the animal density is given by a spatially-homogeneous state; (b) Even-symmetric aggregation patterns, described by four aggregating groups with similar densities and spatial distributions; (c) Odd-symmetric aggregation patterns, described by three aggregating groups; (d) Non-symmetric aggregation patterns.
An interesting observation is that while in vivo cellular aggregations are usually part of domain covering patterns (i.e., aggregations of cells inside tissues formed of other cells [8]; although in vitro experiments can have also clusters of cells cultured on gel substrate [9]), the majority of ecological aggregations are described by localised patterns (e.g., the aggregation of animals inside specific spatial regions of the domain [7], the aggregation of vegetation in different types of soil and environments [10]). In fairness, we need to mention the localised spiking activity of cortical neurons in the context of biological/medical applications [11]. However, such localised patterns are not specific to ecology/biology/medicine, but they are quite common in physics and chemistry (e.g., Newtonian fluids, colloidal suspensions, liquid crystals) [12], and in fact these domains have been the main drivers of the research on localised patterns over the past three decades.
Returning to biological/ecological applications, since the complex social interactions taking place inside the self-organised biological/ecological aggregations cannot be fully understood through experiments, mathematical and computational studies have been used intensively over the past three decades to propose and test hypotheses related to the mechanisms behind the formation of various spatial and spatiotemporal aggregation patterns; see, for example, [5,7,13,14,15,16] and references therein. The mathematical models derived to investigate self-organised aggregations can be generally classified as discrete individual-based models (where the position and velocity of each cell/individual is tracked through time) [15,16], and continuum models (where the densities of individuals distributed over a spatial domain are changing with respect to time) [13]. These discrete models are either lattice-based (where individuals are moving on a spatial grid, and interact with neighbours according to specified rules), or off-lattice models (where the changes in the position and velocity of individuals are given by ordinary differential equations (ODEs)). The continuum models are described by partial differential equations (PDEs) that describe the changes in the distribution of individuals.
In this study, we focus on continuum models for self-organised biological aggregations, as they have been shown to exhibit a large variety of spatial and spatiotemporal patterns [17]. The mechanisms behind the formation of these patterns, as well as the transitions (bifurcations) between different patterns can be investigated using either analytical or numerical approaches. Classical analytical approaches for the investigation of patterns in local/non-local partial differential equations focus on linear stability analysis, combined with weakly nonlinear analysis [13], central manifold reduction [18], or Lyapunov–Schmidt reduction [18]. However, all these approaches usually lead to normal form equations that are valid near bifurcation points and do not allow us to understand the transitions between different types of aggregating patterns as we move away from these points. Note, that the normal form equations used to describe the amplitude of the solution branches usually include terms up to cubic order; adding higher order terms could allow for the description of the solution branches further away from the bifurcating points, but this is analytically and computationally very expensive [17,19]. In such cases, numerical continuation algorithms are usually employed. While continuation algorithms (and software) are classical for analysing the behaviour of dynamical systems described by ODEs [20,21], in the case of PDEs the situation is more complex as these equations can change their structure when we vary model parameters. Therefore, different numerical approaches might need to be implemented to track numerically the various solution branches as parameters are varied. Thus, even if continuation algorithms are still developed for PDEs, these depend on a case-by-case problem (see, for example, [22,23,24,25], and references therein).
Another aspect that needs to be emphasised here is the challenge associated with understanding the mechanisms behind the emergence of localised patterns (in contrast to more classical domain-covering patterns that generally emerge from pattern-forming/Turing instabilities) [12]. Such localised patterns have been investigated mainly in 1D and mainly computationally via numerical continuation approaches [12] (that have their own limitations, as seen above). Moreover, the equations exhibiting such localised patterns are usually described by local PDEs (e.g., the Swift–Hohenberg equation [26] or the plane Couette flow equation [27]), or non-local integrodifferential equations (e.g., the neural field equations [11]). To our knowledge, there are not many non-local integro-partial differential equations that exhibit such localised patterns, apart from the studies in [17,28,29,30] derived in the context of 1D ecological aggregations, and which are the focus of this current investigation.
In this study, we consider a non-local hyperbolic system for ecological aggregations that was initially introduced in [28,29]. Previous analytical and numerical studies [17,28,30,31,32] have shown that this particular hyperbolic system can exhibit a variety of spatial and spatiotemporal patterns describing different types of stationary and moving biological aggregations: from stationary pulses to travelling trains, breathers, zigzags, etc. [28]. However, this current study does not focus on these general patterns, but rather on understanding the details of a particular type of stationary pattern (representing stationary biological aggregations) described by localised solutions: i.e., spatially heterogeneous solutions that are non-zero only inside a region of the spatial domain. In Figure 2 we show these localised patterns which can be obtained by changing one parameter, i.e., the magnitude of attractive interactions: (a) a spatially homogeneous state (describing all individuals in a population equally spread over the domain) which, following perturbations, can lead to spatially heterogeneous solutions; (b) a spatially heterogeneous localised state with even spatial symmetry (see the even symmetry of the peaks with respect to the centre of mass of the aggregation localised at ); (c) a spatially-heterogeneous localised state with odd spatial symmetry (see the odd symmetry of the peaks with respect to ); (d) a spatially-heterogeneous localised state with no symmetry (the peaks of both sides of do not have the same amplitude).
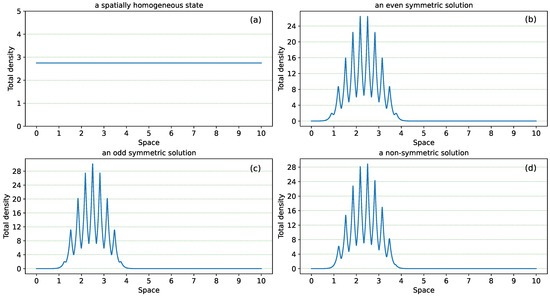
Figure 2.
Examples of four types of patterns displayed by model (1) [13,32]. (a): a spatially homogeneous state, with density uniformly distributed over the whole spatial domain; (b–d): localised spatial patterns with different symmetries. (b) an even-symmetric pattern, (c) an odd-symmetric pattern, and (d) an asymmetric pattern.
From an ecological perspective, these localised patterns with different symmetries could describe animal aggregations with symmetric and asymmetric interactions that lead to macroscopically similar animal aggregations but which have different microscopic characteristics (i.e., similar/different animal densities at various spatial positions inside the aggregating collective of animals).
In [31], the authors used weakly nonlinear analysis and numerical simulations to show that such localised patterns can arise through a real bifurcation from the spatially homogeneous steady state, and this bifurcation is subcritical (i.e., the low-amplitude bifurcating branch is unstable; the solutions eventually approach a stable high-amplitude branch formed of these localised patterns). In [32] we investigated the numerical problems that could arise when trying to construct continuation algorithms to investigate the bifurcation structure of the spatial and spatiotemporal solutions observed in [28]. In particular, we have shown non-convergence of solutions to a spatially-homogeneous state or a spatially-heterogeneous localised patterns (see Figure 4b that will be discussed later), which complicates the development of a continuation algorithm to approximate the computed solutions.
The goal of this study is to take forward the results in [32], by constructing the bifurcating structure of a particular class of localised solutions (obtained for a particular parameter set), which describe spatial aggregations of animals with/without spatial symmetry. We focus on the transitions between different types of solutions (with even, odd, or no symmetry) as we move further away from the bifurcation point, and therefore, we are outside the range of validity of linear or weakly nonlinear stability analyses. The construction of such a bifurcating diagram could allow us to understand better the effect of nonlinear and non-local social interactions inside ecological aggregations (that become important away from the bifurcation points), and how such interactions impact the spatial micro-structure of the aggregations.
2. Model Description
In this study, we consider the following one-dimensional non-local hyperbolic model that was initially introduced in [28,29] to describe the movement inside a 1D domain (approximating a domain that is much longer than wide) of a generic population that could describe cells, animals, etc. The changes in the densities of right-moving () and left-moving () individuals, as a result of interactions with neighbours positioned nearby, as well as neighbours positioned further away, is given by the following equations [29]:
As in [29], we assume that the left-moving and right-moving populations travel at a constant speed . Moreover, the turning rates, , have a random component described by the constant , and a biased component described by the term [13,29]:
Also as in [29], the turning function h is assumed to be a positive, increasing, and bounded functional that depends on the signals perceived from right-moving/left-moving neighbors located at different positions in space. In [28,29] this function was chosen to be described by
where the constant was such that for , the value of would be determined only by (i.e., random turning when no neighbours are perceived: ).
The terms describe the social interactions between a reference individual at x and its neighbours at [29]: repulsion (with strength ) from neighbours located nearby; alignment (with strength ) with those at intermediate distances; attractions (with strength ) towards those neighbours positioned further away:
In the above equation, describes the total population density at time t and position x. The interaction kernels are described by [13,28]:
where define the spatial regions for repulsive, alignment, and attractive interactions, while define the width of these regions. The constants are chosen such that the support of more than of the mass of the kernels is inside the domain; see [13,28].
To complete the description of model (1) we need to specify an initial condition (which will be defined later in the context of numerical simulations):
Moreover, to ensure that the domain boundaries do not have any impact on the patterns observed, we assume that the 1D spatial domain () has periodic boundary conditions [28]:
Because of these boundary conditions, the integrals can wrap around the domain (if , with , is close to either one of the two domain boundaries).
Remark 1.
We note that model (1), initially introduced in [28,29], was further developed in various other studies to investigate the impact of stochastic turning terms on collective patterns [30], the role of leader vs. follower behaviours on collective patterns [33], the role of avoidance and learning behaviours on the formation and movement of patterns [34], or the role of different communication mechanisms on the formation of patterns [35,36]. All these studies have identified various types of stationary and moving localised patterns, which are not the focus of this study and are still open to investigation.
- Steady states.
We note that model (1) can exhibit various spatially-homogeneous steady states (which depend on model parameters) that represent individuals equally spread over the whole domain [28,29]. Denoting by the total population density (which is constant since the system is density-preserving), then we can easily show that these spatially-homogeneous steady-states are the solutions of the following equation
To simplify the discussion, throughout this study, we focus only on the case , which leads to a unique spatially-homogeneous steady state . The stability of this state is influenced by various model parameters, among which we mention (the strength of attractive interactions with neighbours). In Figure 3 we show numerically the transition between different stable solutions (with different amplitudes, as recorded by ), as we vary (i.e., for each value we run simulations starting with initial conditions that are small-amplitude perturbations of the spatially-homogeneous steady state ). For , we obtain spatially-homogeneous solutions with zero amplitudes (depicted in Figure 3 by blue stars; see also Figure 2a), and for we obtain spatially-heterogeneous even-symmetric solutions with high amplitudes (depicted in Figure 3 by red stars; see also Figure 2b). Therefore, is a bifurcation point: as increased above , the spatially-homogeneous state loses its stability, and the solution trajectories approach a spatially-heterogeneous state characterised by strictly positive amplitudes. In fact, as investigated in [31] through a weakly nonlinear analysis, these two stable solution branches are connected by another unstable solution branch that bifurcates sub-critically to the left at . However, the exact structure of this bifurcation, is not fully understood, especially when we move away from .
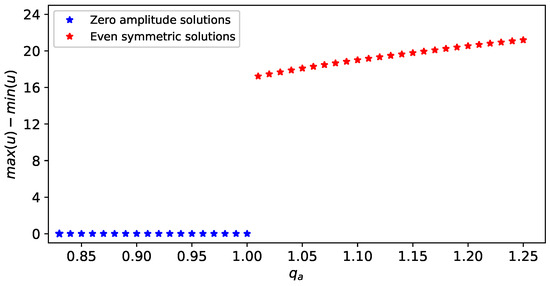
Figure 3.
A numerical transition from spatially-homogeneous solutions (obtained for ) to spatially-heterogeneous solutions (obtained for ). The initial conditions for the simulations are very small perturbations (with amplitude close to zero) applied to the spatially homogeneous state . This implies that for the spatially-homogeneous state is stable, while for it is unstable and the solution trajectories approach a stable spatially-heterogeneous state. The parameter values for the simulations are shown in Table 1.
As mentioned before, the goal of this study is to investigate the role of non-linear and non-local social interactions incorporated into the individual turning rates , on the micro-structure of the localised aggregations exhibited by this model (1). To this end, we reconstruct numerically the structure of the bifurcation (and the transition between the different types of spatial patterns) in the parameter region where and . Here, we do not focus only on the parameter region near the bifurcation point (where the linear and weakly nonlinear stability analyses performed in [31] were valid); but we also focus further away from this bifurcation point. This allows us to see the impact of the non-linear terms (that are usually ignored in the linear and weakly nonlinear analysis) on the dynamics of this model and on the transitions between the different types of spatial localised patterns with different symmetries (see Figure 2).
3. Results
Since we consider a numerical approach to investigate the bifurcation of patterns nearby and further away from , in Section 3.1 we present the numerical method used for the discretisation of model (1). Then, in Section 3.2 we discuss some of the numerical details and further challenges we encountered during simulations. Finally, in Section 3.3 we show the bifurcation diagrams we constructed using the approaches presented in the previous subsections. We conclude the paper with a discussion of the results in Section 4.
3.1. Numerical Method
To discretise model (1) we introduce a uniform space mesh of width and a time step of . We define the discrete mesh point with and , where
Let us now consider the finite volumes (or cells) . We denote by , and the averages of , and on these finite volumes :
We also use the notations and to denote the averages over these cells of the right-hand-side terms (i.e., source terms) in the equations for and of model (1). Finally, to approximate the integrals in (4) we use the composite Simpson’s 1/3 rule.
To calculate the numerical steady-state solutions for model (1), we use the Quasi-Steady Wave-Propagation Algorithm introduced in [37], aimed at preserving steady states in which the flux gradients are non-zero and balanced by source terms. Note that in [32], this algorithm showed faster convergence compared to algorithms such as upwind, MacCormack, or the Fractional Step Method. To this end, we combine this high-resolution method with the centered slope limiter (see [38], Chapter 6). The fundamental concept of this algorithm applied to the general problem is to introduce a new discontinuity at the center of each grid cell at the beginning of each time step, with a value on the left half of the cell and a value on the right half. These values are chosen so that
and also that
Condition (11) ensures that the average value on this cell remains unchanged by the introduction of this discontinuity. Condition (12) is a discrete version of , and this implies that the waves resulting from solving the Riemann problem at this new discontinuity will cancel the effect of the source term in this cell, and hence the application of the source term is no longer unnecessary. Therefore, we can apply Godunov’s method to compute the value of at the next time step as follows
where the flux is determined by the values and , and hence the high-resolution methods can be applied directly. For our problem, one of the possible choices that satisfy (11) and (12) is:
with
Applying the above algorithm, we obtain the following numerical scheme:
with the centred slope limiter
This is equivalent to
We observe that the above scheme is equivalent to applying Fromm’s method (see [38], Chapter 6) to the homogeneous problem, but with a 4-point approximation for the source term also included. Note that our scheme is second-order accurate, and satisfies the CFL condition:
For the detailed description of this particular numerical scheme and comparison with other numerical schemes, we refer the reader to [32].
3.2. Computational Details and Challenges
This subsection presents several computational details (e.g., initial conditions, time and space steps) and some computational challenges (some of them presented in [32]) encountered when trying to construct bifurcation diagrams for the non-local hyperbolic system (1).
- Initial conditions. In this study, we use initial conditions that are perturbations of the spatially homogeneous steady state . Here, these conditions arewhere denotes the amplitude of the initial perturbation (see, for example, Figure 4a where ). Note, that the shape of the numerical solutions obtained with initial data in the form of or is identical. However, the aggregations of peaks forming the solution corresponding to the initial data given in terms of lie in the middle of the domain, making them easier to visualise.
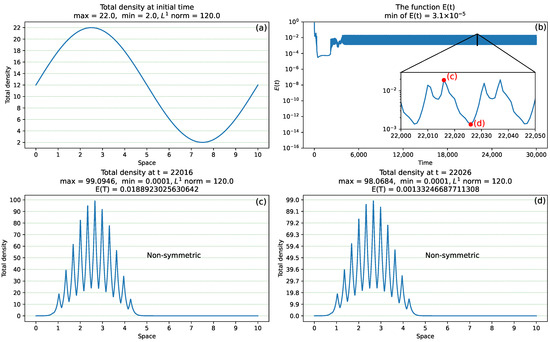 Figure 4. An example of non-convergence of numerical scheme when and . (a) initial data , with the perturbation amplitude ; (b) the error function ; the inset shows a zoom-in sub-figure for [22,000; 22,050]; (c) a non-symmetric total density at time with . (d) a non-symmetric total density at time t = 22,026 with . Note that for cases (c,d), the norm of the total density u is the same (i.e., ), while the error between the values of the total densities at the last two calculated time steps are different, suggesting that there is a change in the spatial distribution of individuals inside these localised aggregations. Note that the aggregations in (c,d) have no spatial symmetry.
Figure 4. An example of non-convergence of numerical scheme when and . (a) initial data , with the perturbation amplitude ; (b) the error function ; the inset shows a zoom-in sub-figure for [22,000; 22,050]; (c) a non-symmetric total density at time with . (d) a non-symmetric total density at time t = 22,026 with . Note that for cases (c,d), the norm of the total density u is the same (i.e., ), while the error between the values of the total densities at the last two calculated time steps are different, suggesting that there is a change in the spatial distribution of individuals inside these localised aggregations. Note that the aggregations in (c,d) have no spatial symmetry. - Time and space steps. In this study, we fix and , which strikes a balance between the smoothness of the spatial grid (containing 1281 points) and maintaining an acceptable computation time. These time and space steps satisfy the CFL condition (16) (for given in Table 1). As noted before in [32], choosing different time-space steps might lead to localised numerical patterns with different symmetries.
 Table 1. Summary of the model parameters used during simulations (note that these values are the same as in [31]). Most of the parameters are kept fixed at the values listed here, except which will be varied within the range .
Table 1. Summary of the model parameters used during simulations (note that these values are the same as in [31]). Most of the parameters are kept fixed at the values listed here, except which will be varied within the range . - Numerical classification of even-symmetric, odd-symmetric and non-symmetric patterns. To identify the spatial symmetry of a numerical solution, we start by finding the local maximum values of . We denote by these maximum values, which occur at points for , where M is the number of local maximum points. After that, let if M is even or if M is odd. We say that the numerical solution is non-symmetric if there exists such thatorOtherwise, the numerical solution is symmetric. It is even-symmetric if M is even, or odd-symmetric if M is odd.
- Estimating convergence via function. To investigate the convergence of the numerical solution from the initial data towards a (spatially homogeneous or heterogeneous) steady-state solution, we first define the discrete norm:Then, we define the error to be the norm of the difference between the total population densities at two adjacent time steps, and , with :
- Numerical steady-state solutions. A steady-state solution is a solution that does not depend on time. Numerically, this means that the error approaches zero as time becomes sufficiently large. If the steady state is stable, then the error stays near zero indefinitely. For our simulations, we choose an acceptable level of error (tolerance) of 10−14. We say that a numerical solution at time is a numerical steady state if and does not change significantly for , i.e., , .
- Non-convergence of the numerical scheme for some cases. When the initial perturbation amplitude is large enough (typically ), the non-convergence of the numerical scheme can occur (see also [32]). This means that the error does not approach zero but instead undergoes oscillations within a narrow range, typically in . For example, Figure 4 shows an example of such non-convergence of the numerical scheme when (the simulations are run until the final time T = 30,000 and with initial data described in sub-panel (a), where the amplitude of the sinusoidal perturbation is ). In this case, for , the error oscillates within the range , as shown in sub-panel (b). The inset in sub-panel (b) shows a zoom-in of for time [22,000; 22,050], to help us better visualize the variation in this error function. Sub-panels (c) and (d) show the spatial distributions of the total densities u at times t = 22,016 and t = 22,026, respectively. These total densities have similar values of the norm, but different values for the error function that estimates the differences between the densities calculated at the last two recorded time steps. This result suggests that while the total population density is preserved, there are variations in the spatial distribution of individuals inside aggregations (i.e., densities of peaks inside those aggregations fluctuate between two consecutive time steps, as individuals move to adjacent spatial positions).
- Different solution branches when starting with different . To construct numerically a solution branch, we can fix the initial value of our parameter of interest, , and the amplitude of the sinusoidal perturbation applied to the spatially homogeneous steady state (see Equation (17)). The numerical solution obtained after a long simulation time (to try to reach a steady state) is then used as initial data for the next simulation with . We keep repeating this process (i.e., run simulations for a long time, record the obtained solution as the new initial condition, increase , and run again the long-term simulations) until we reach a defined upper value for parameter .Figure 5 shows what can happen with the high-amplitude localised solutions when we start the numerical simulations with three different values (depicted by ★), and then we incrementally increase or decrease . Thus, Figure 5a shows a solution branch where simulations start from . This branch includes all three symmetry types: even-symmetric solutions for and ; odd-symmetric solutions for and non-symmetric solutions for . Figure 5b shows a solution branch when simulations start from (all other parameters are the same as in (a)); this branch contains even-symmetric solutions for ; non-symmetric solutions for . Figure 5c shows a solution branch when simulations start from : this branch contains even-symmetric solutions for ; odd-symmetric solutions for . Finally, Figure 5d shows the superimposed three solution branches given above, and we can conclude that: (i) the solution branches in sub-panels (a–c) have the same amplitude (as given by ); (ii) the symmetry of the solutions on this “common branch” might depend on the value from where we start the numerical simulations (see for example, the region where odd-symmetric and even-symmetric solutions overlap; or the region where odd-symmetric and non-symmetric solutions overlap). It seems that small perturbations triggered by slightly different initial values can cause different symmetries in these localised stationary solutions (i.e., have an impact on the micro-structure of these localised aggregations). This result poses a significant challenge to the development of continuation algorithms to explore the detailed structure of the bifurcations exhibited by model (1).
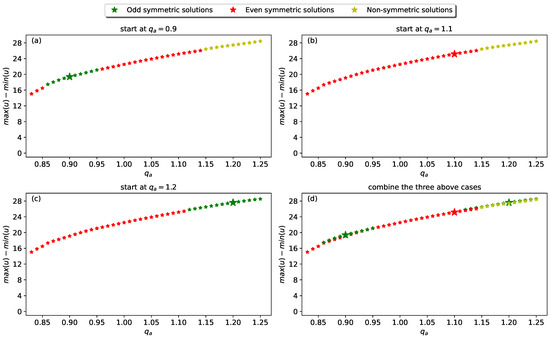 Figure 5. Sub-panels (a–c): solution branches obtained with simulations starting with different (all remaining parameters are the same, including ): (a) ; (b) ; (c) . The big stars “★” show the initial values of for each of these simulations. Sub-panel (d) shows the superimposed three solution branches discussed above, to emphasise that their amplitude (i.e., ) is almost the same, irrespective of where we start the simulations; however, the symmetry of the localised patterns on these solution branches depends on the value of .
Figure 5. Sub-panels (a–c): solution branches obtained with simulations starting with different (all remaining parameters are the same, including ): (a) ; (b) ; (c) . The big stars “★” show the initial values of for each of these simulations. Sub-panel (d) shows the superimposed three solution branches discussed above, to emphasise that their amplitude (i.e., ) is almost the same, irrespective of where we start the simulations; however, the symmetry of the localised patterns on these solution branches depends on the value of . - Manual investigation of the bifurcation structure. Since numerical problems can arise when trying to construct numerical continuation algorithms (as mentioned above, and discussed in more detail in [32]), in this study we construct the bifurcation diagram step-by-step. We start with and increase the value of from to with a step of ; for each value of we perform 361 simulations with different initial amplitudes which belong to the set (where ). These initial perturbation amplitudes correspond to the norm of the densities u within the range . Further, to display the continuous norm of the total density u in our bifurcation figures, we assume that the solution obtained with the initial amplitude is actually an average of solutions with initial amplitudes in the interval .
- Total execution time. The extensive execution time required for each simulation, coupled with the large number of simulations (over 30,000 simulations) needed to manually construct the bifurcation structure, presented a significant challenge. To address this issue, we had to select an appropriate final time for each simulation (so the final simulation time was different for different cases) and to make good choices regarding the programming language and tools used.
- -
- The final simulation time T. In [32] we showed the presence of two distinct types of numerical solutions (with different symmetries), that exhibit very small errors (in some cases these errors are less than the tolerance), which might initially suggest that a steady-state solution has been reached, but this was not the case. Hence, the simulations in this study do not stop when errors fall below the chosen tolerance, and additional time is essential to be considered to guarantee that the numerical solutions are indeed steady-state solutions. To end this, we start with a large initial final time T (usually T = 500,000), and after that, in the iteration process, we identify a time that is the first time which satisfies . The simulation continues until it reaches the new final time , where the additional time depends on the initial amplitude ( = 14,000 if , = 10,000 if , if and if , which are chosen from our experiences obtained via many simulations). We conclude that the numerical solution is at the steady-state and stop the simulations, if the error at this new final time is still less than the tolerance, i.e., . If not, we continue the simulation and repeat the above process for the next time that satisfies . To address the non-convergence case, based on our experiences, we terminate the simulation at the stop time = 30,000 if the error never falls below .
- -
- Programming language. Here, we employ C++, a low-level programming language, that offers better control over memory management and execution speed compared to higher-level languages. We also implement both shared-memory parallel techniques (OpenMP) and Message Passing Interface techniques (MPI). Moreover, the majority of simulations are conducted on the supercomputer facilities of the Mésocentre de calcul de Franche-Comté. Besides, for visualisation, we use Python (version 3.0.0 or later), a high-level programming language.
Remark 2.
In addition to the above information regarding the execution time, we need to emphasise that despite of code parallelisation, the average CPU time for each simulation was about 13.19 h (on the supercomputing facilities of the Mésocentre de calcul de Franche-Comté). Given that the construction of the bifurcation diagram shown below (see Figure 6) required more than 30,000 simulations, this amounted to approx. 400,000 CPU h. This large simulation time is prohibitive to creating such bifurcation diagrams for all types of localised patterns that can be exhibited by these non-local hyperbolic models (see [13,19,28]).
3.3. Diagrams for the Transitions between Different Localised Solutions
Using the numerical approaches described above, we obtain the bifurcation diagrams shown in Figure 6, when we vary (top sub-figure) and (bottom sub-figure). Recall that is a bifurcation point at which the spatially-homogeneous steady state loses its stability and becomes unstable to small perturbations (as discussed in Section 2 above and proven analytically in [31]).
To present the results in Figure 6, we start by focusing on the spatially-homogeneous steady states depicted by the dark blue colour. For (top sub-figure), small-amplitude perturbations of decay and the solution trajectories return to this stable homogeneous steady state. Note, that the smallest amplitude perturbation we apply is , which corresponds to a norm for u of . Close to the blue region is very narrow, while further away from (i.e., outside the range of validity of linear and weakly nonlinear stability results [31]) this blue region becomes wider. Finally, for (bottom sub-figure), small-amplitude perturbations of grow and give rise to localised spatially-heterogeneous patterns.
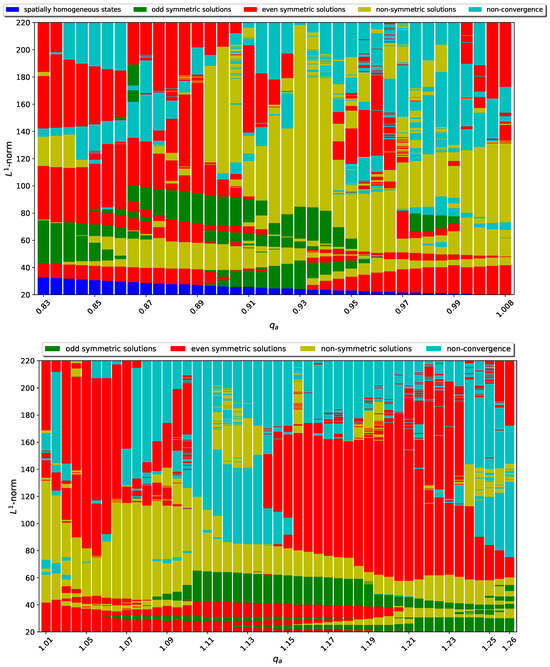
Figure 6.
Transitions between regions with different types of spatially-homogeneous states and spatially-heterogeneous states as we vary: (top) (≤), and (bottom) (≥). The vertical axis shows the norm of the total density of solutions (which increases as we apply perturbations with higher amplitudes to the spatially-homogeneous states). The colours (in the online version) denote the following types of solutions: “blue” = spatially homogeneous states; “green” = spatially-heterogeneous states with odd symmetries; “red” = spatially-heterogeneous states with even symmetries; “yellow” = spatially heterogeneous states with no symmetries (i.e., asymmetric); “light blue” = non-convergence of the numerical scheme.
The transition between this dark blue region (depicting stable homogeneous states) and red/green/yellow regions (depicting stable heterogeneous states with different symmetries) represents an unstable bifurcation curve, which bifurcates subcritically at as we decrease .
We note that near the critical point (i.e., for ), the spatially-heterogeneous solutions that emerge following small perturbations of spatially-homogeneous states have all even symmetries (here depicted by the red regions). Further away from this critical point (i.e., and ) there are larger regions of odd-symmetric solutions. This suggests that non-local and non-linear interactions among individuals (which have an effect further away from the critical point ) might favourise odd-symmetric aggregations.
As we increase the amplitude of the perturbations (and so we increase the norm ), there is a sequence of rather chaotic transitions between red regions (stable even-symmetric heterogeneous patterns), green regions (stable odd-symmetric heterogeneous patterns), and yellow regions (stable non-symmetric heterogeneous patterns). Higher-amplitude perturbations also lead to a larger number of yellow regions.
Remark 3.
The coloured red, green and yellow regions are actually the regions of attraction of the stable spatially-heterogeneous states with even symmetries, odd symmetries and no symmetries, respectively. These red, green, and yellow regions are separated by unstable solution curves, which are not shown here because this numerical approach records only the regions with stable states. The stable solution curves (depicting each of these types of localised patterns) are inside the corresponding coloured regions.
For very high amplitude perturbations (which lead to high norms), we see large regions of non-convergence towards a spatially-heterogeneous state (depicted by the light-blue colour). These regions are very few and exist only for large-amplitude perturbations when is very low (here, ), but they are very frequent for very large.
Since for large and large initial perturbations, the non-convergent areas are inter-spread with areas with even-symmetric patterns (in red) and non-symmetric patterns (in yellow), it is possible that these non-convergent patterns might be formed only of such localised solution (with either even symmetry or no symmetry—as seen in Figure 4).
Remark 4.
Note, that non-symmetric patterns are mainly observed closer to , while further away from (where the non-linear terms become important) the dynamics seem dominated by even-symmetric patterns.

Table 2.
Summary of the dominant spatially-homogeneous and spatially-heterogeneous patterns observed in Figure 6. “Homog.” means “spatially-homogeneous” patterns; “Heter.” means “spatially-heterogeneous” patterns; “ES” means “even-symmetric”, “OS” means “odd-symmetric”, “NS” means “non-symmetric”, and “NC” means “non-convergent”.
4. Discussion
The goal of this study was to advance the knowledge related to localised patterns exhibited by non-local PDEs of the hyperbolic type and thus create a detailed bifurcation diagram for the transitions between different spatially-homogeneous and spatially-heterogeneous patterns, in the enlarged neighbourhood of a steady-state bifurcation point for the non-local hyperbolic models (1). With the help of this bifurcation diagram, we aimed to investigate the role of nonlinear and non-local interactions on the formation of spatial aggregation patterns with (i) even symmetry, (ii) odd symmetry, and (iii) no symmetry, which are characterising the microscale dynamics of these aggregations (at macroscale level the localized aggregations look similar).
We started the paper with a detailed discussion of the methodology used to address this question (i.e., numerical scheme, initial conditions, performed numerical tests), and the numerical challenges posed by these non-local transport models (1)—in particular, the lack of convergence of the solution to a steady state, which impacts the development of specific numerical continuation algorithms for these types of non-local PDEs of hyperbolic type [22,32]. Note, that apart from the study in [22] which also has its own limitations, we are not aware of any other continuation algorithms developed to study the evolution of and the transitions between localised patterns in non-local hyperbolic PDEs of type (1). Bifurcation diagrams for these kinds of non-local PDEs were created in [18,19,39] to study the transitions between patterns nearby bifurcation points. But since they were obtained mainly via weakly nonlinear analysis and centre manifold reduction that led to cubic-order amplitude equations, the bifurcation diagrams were valid only near the bifurcation points. Here, we aimed to investigate such transitions further away from the bifurcation points.
The main results of this study are presented in the two sub-panels in Figure 6: the top sub-panel focuses on the patterns obtained for , while the bottom sub-panel focuses on the patterns obtained for (where is the critical point at which the spatially homogeneous steady state loses its stability). We can summarise these results as follows:
- For small-amplitude spatio-temporal perturbations: around the critical point (where linear stability analysis is valid), we can see mainly even-symmetric localised aggregation patterns. This corresponds to two similar high-density groups positioned in the middle of the animal aggregation, surrounded by smaller sub-groups symmetrically distributed around the two main groups (see also Figure 1b). Further away from this critical point (where nonlinear and non-local terms have a significant effect), we can see the formation of odd-symmetric aggregations, formed of a single-centred high-density group surrounded by smaller sub-groups symmetrically distributed around the main group (see also Figure 1c).
- For medium/large-amplitude spatio-temporal perturbations: near the critical point we have a large region of non-symmetric patterns (where individuals are randomly distributed inside the aggregation sub-groups). However, for the small inter-individual attraction, i.e., , the aggregation patterns are mainly even-symmetric. For large inter-individual attraction (i.e., ), there are large regions where the aggregation patterns vary in time and do not stabilize (i.e., non-convergence areas). It is possible to have a type of periodic individual movement inside these aggregations (that are not at steady state).
We can conclude from here that the nonlinear and non-local terms (that have a bigger impact away from the critical point ) seem to induce some symmetry in the aggregation patterns. This symmetry is mainly even symmetry (although there are also regions of non-convergent patterns that are usually formed of non-symmetric aggregations).
An open question of this study focuses on the mathematical and biological mechanisms responsible for those “non-convergent” patterns that appear very often when we perturb the homogeneous states with high amplitudes. Given that in this case the error has oscillatory dynamics (and since is calculated as the difference in densities at specific spatial points; see (19)) we suspect that there is a periodic spatial movement of individuals inside these aggregations, which is too small to be detected macroscopically. These localised aggregation patterns are unstable, and they might be part of a heteroclinic cycle. However, this is just a hypothesis, that needs to be investigated more rigorously.
In addition, we are aware that the bifurcation results in Figure 6 (and, in particular, the symmetry of these aggregations) might be dependent on the time and step sizes of the numerical discretisation chosen here, on the numerical scheme chosen here, on the parameter value used as the initial condition (even if we keep all other parameters fixed) [32]. This makes it very difficult to construct general numerical continuation algorithms for this class of non-local hyperbolic models (1).
As discussed in Remark 2, the large amount of CPU time required for the numerical simulations involved in the construction of the bifurcation diagrams presented here prohibits us from investigating all types of localised patterns exhibited by the non-local hyperbolic models (1) (see the patterns presented in [13,19,28,35,36,39], that include breathers, zigzags, travelling trains, etc.). The investigation of these other types of localised patterns (with or without symmetry) remains an open problem in the field.
To conclude this study, we note that other studies in the literature (focused on discrete models) have started looking into the impact of symmetric and asymmetric interactions between animals and groups, on overall group behaviour [40]. In [28] the authors developed four different mathematical models that include four different directional/omnidirectional communication mechanisms possible between the individuals in a self-organised collective, in the future, we plan to create such bifurcation diagrams for all four models introduced in [28]. This will allow us to investigate in these continuum models the impact of symmetric/non-symmetric animal communication mechanisms on the structure of bifurcations for similar localised patterns.
Author Contributions
Conceptualization, T.T.L. and R.E.; software, T.T.L.; writing—original draft preparation, T.T.L. and R.E.; writing—review and editing, T.T.L. and R.E.; project administration, R.E.; funding acquisition, R.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a Region Bourgogne Franche-Comté “Accueil de Nouvelle Équipe de Recherche (ANER) 2022” grant number FC22070.LMB.CL.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All codes for the numerical simulations in this study can be found at (accessed on 1 September 2024). https://github.com/ThanhTrungLe-mathematician/Different-spatial-symmetries-in-non-local-hyperbolic-models.
Acknowledgments
Computations have been performed on the supercomputer facilities of the Mésocentre de calcul de Franche-Comté and on the computation server of Laboratoire de Mathématiques de Besançon.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Pliny the Elder. The Natural History. Book X; Bostock, J., Riley, H.T., Eds.; Taylor and Francis: London, UK, 1855. [Google Scholar]
- Friedl, P.; Gilmour, D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009, 10, 445–457. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Hurley, A.; Hu, W.; Warrick, J.; Lozano, G.; Ayuso, J.; Pan, W.; Handelsman, J.; Beebe, D. Social motility of biofilm-like microcolonies in a gliding bacterium. Nat. Commun. 2021, 12, 5700. [Google Scholar] [CrossRef]
- Ariel, G.; Ayali, A. Locust collective motion and its modeling. PLoS Comput. Biol. 2015, 11, e1004522. [Google Scholar] [CrossRef] [PubMed]
- Ballerini, M.; Cabibbo, N.; Candelier, R.; Cavana, A.; Cisbani, E.; Giardina, I.; Lecomte, V.; Orlandi, A.; Parisi, G.; Procaccini, A.; et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proc. Natl. Acad. Sci. USA 2008, 105, 1232–1237. [Google Scholar] [CrossRef]
- Lopez, U.; Gautrais, J.; Couzin, I.; Theraulaz, G. From behavioral analyses to models of collective motion in fish schools. Interface Focus 2012, 2, 693–707. [Google Scholar] [CrossRef] [PubMed]
- Parrish, J.K.; Edelstein-Keshet, L. Complexity, Pattern, and Evolutionary Trade-Offs in Animal Aggregation. Science 1999, 284, 99–101. [Google Scholar] [CrossRef]
- Dive, A.; Bodhade, A.; Mishra, M.; Upadhyaya, N. Histological patterns of head and neck tumours: An insight to tumour histology. J. Oral Maxillofac. Pathol. 2014, 18, 58–68. [Google Scholar] [PubMed]
- Mendes, R.; Santos, A.; Martins, M.; Vilela, M. Cluster size distribution of cell aggregates in culture. Phys. A Stat. Mech. Its Appl. 2001, 298, 471–487. [Google Scholar] [CrossRef]
- Jaibi, O.; Doelman, M.; Chirilus-Bruckner, M.; Meron, E. The existence of localized vegetation patterns in systematically reduced model for dryland vegetation. Phys. D Nonlinear Phenom. 2020, 412, 132637. [Google Scholar] [CrossRef]
- Rankin, J.; Avitabile, D.; Baladron, J.; Faye, G.; lloyd, D. Continuation of localised coherent structures in nonlocal neural field equations. SIAM J. Sci. Comput. 2014, 36, 870–893. [Google Scholar] [CrossRef]
- Hill, D.; Lioyd, D. Approximate localised multi-dimensional patterns. SIAM News 2024, 57. Available online: https://www.siam.org/publications/siam-news/articles/approximate-localized-multidimensional-patterns/ (accessed on 3 June 2024).
- Eftimie, R. Hyperbolic and kinetic models for self-organized biological aggregations and movement: A brief review. J. Math. Biol. 2012, 65, 35–75. [Google Scholar] [CrossRef] [PubMed]
- Jolles, J.; King, A.; Killen, S. The role of individual heterogeneity in collective animal behaviour. Trends Ecol. Evol. 2020, 35, 278–291. [Google Scholar] [CrossRef] [PubMed]
- Couzin, I.D.; Krause, J.; James, R.; Ruxton, G.D.; Franks, N.R. Collective memory and spatial sorting in animal groups. J. Theoret. Biol. 2002, 218, 1–11. [Google Scholar] [CrossRef]
- Vicsek, T.; Czirók, A.; Ben-Jacob, E.; Cohen, I.; Shochet, O. Novel Type of Phase Transition in a System of Self-Driven Particles. Phys. Rev. Lett. 1995, 75, 1226–1229. [Google Scholar] [CrossRef]
- Eftimie, R. Hyperbolic and Kinetic Models for Self-Organised Biological Aggregations. A Modelling and Pattern Formation Approach; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Buono, P.L.; Eftimie, R. Lyapunov–Schmidt and Centre Manifold Reduction Methods for Nonlocal PDEs Modelling Animal Aggregations. In Mathematical Sciences with Multidisciplinary Applications; Springer: Cham, Switzerland, 2016; pp. 29–59. [Google Scholar]
- Buono, P.L.; Eftimie, R. Codimension-two bifurcations in animal aggregation models with symmetry. SIAM J. Appl. Dyn. Syst. 2014, 13, 1542–1582. [Google Scholar] [CrossRef]
- Ermentrout, B. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Dankowicz, H.; Schilder, F. Recipes for Continuation; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Buono, P.L.; Eftimie, R.; Kovacic, M.; Veen, L.V. Kinetic models for pattern formation in animal aggregations: A symmetry and bifurcation approach. In Active Particles. Volume 2; Springer International Publishing: Cham, Switzerland, 2019; pp. 39–64. [Google Scholar]
- Burke, J.; Knobloch, E. Localized states in the generalized Swift-Hohenberg equation. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2006, 73, 056211. [Google Scholar] [CrossRef]
- Kuehn, C. Efficient gluing of numerical continuation and a multiple solution method for elliptic PDEs. Appl. Math. Comput. 2015, 266, 656–674. [Google Scholar] [CrossRef]
- Uecker, H. Numerical Continuation and Bifurcation in Nonlinear PDEs; SIAM: Philadelphia, PA, USA, 2021. [Google Scholar]
- Bentley, D.; Rucklidge, A. Localized patterns in a generalized Swift–Hohenberg equation with a quartic marginal stability curve. IMA J. Appl. Math. 2021, 86, 944–983. [Google Scholar] [CrossRef]
- Schneider, T.; Gibson, J.; Burke, J. Snakes and ladders: Localised solutions of plane Couette flow. Phys. Rev. Lett. 2010, 104, 104501. [Google Scholar] [CrossRef]
- Eftimie, R.; de Vries, G.; Lewis, M.A. Complex spatial group patterns result from different animal communication mechanisms. Proc. Natl. Acad. Sci. USA 2007, 104, 6974–6979. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; de Vries, G.; Lewis, M.A.; Lutscher, F. Modeling group formation and activity patterns in self-organizing collectives of individuals. Bull. Math. Biol. 2007, 69, 1537–1565. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R. The impact of environmental noise on animal communication: Pattern formation in a class of deterministic and stochastic hyperbolic models for self-organised biological aggregations. Biomath 2018, 7, 1–18. [Google Scholar] [CrossRef]
- Eftimie, R.; de Vries, G.; Lewis, M.A. Weakly nonlinear analysis of a hyperbolic model for animal group formation. J. Math. Biol. 2009, 59, 37–74. [Google Scholar] [CrossRef] [PubMed]
- Le, T.T.; Eftimie, R. Numerical challenges for the understanding of localised solutions with different symmetries in non-local hyperbolic systems. Comput. Math. Appl. 2024, 169, 112–131. [Google Scholar] [CrossRef]
- Bernardi, S.; Eftimie, R.; Painter, K.J. Leadership through influence: What mechanisms allow leaders to steer a swarm? Bull. Math. Biol. 2021, 83, 69. [Google Scholar] [CrossRef]
- Eftimie, R.; Coulier, A. The role of avoidance and learning behaviours on the formation and movement of biological aggregations. Math. Model. Nat. Phenom. 2015, 10, 27–44. [Google Scholar] [CrossRef][Green Version]
- Eftimie, R. The effect of different communication mechanisms on the movement and structure of self-organised aggregations. Math. Model. Nat. Phenom. 2013, 8, 5–24. [Google Scholar] [CrossRef]
- Eftimie, R. The evolution of communication mechanisms in self-organised ecological aggregations: Impact on pattern formation. Math. Model. Methods Appl. Sci. 2020, 30, 1917–1934. [Google Scholar] [CrossRef]
- LeVeque, R.J. Balancing source terms and flux gradients in high-resolution Godunov methods: The quasi-steady wave-propagation algorithm. J. Comput. Phys. 1998, 146, 346–365. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2002; pp. xx+558. [Google Scholar] [CrossRef]
- Buono, P.L.; Eftimie, R. Analysis of Hopf/Hopf bifurcations in nonlocal hyperbolic models for self-organised aggregations. Math. Model. Methods Appl. Sci. 2014, 24, 327–357. [Google Scholar] [CrossRef]
- Hollingdale, E.; Pérez-Barbería, F.; Walker, D.M. Inferring symmetric and asymmetric interactions between animals and groups from positional data. PLoS ONE 2018, 13, e0208202. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).