Influence of Spiral Stiffeners’ Symmetric and Asymmetric Angles on Nonlinear Vibration Responses of Multilayer FG Cylindrical Shells
Abstract
:1. Introduction
2. Basic Formulations
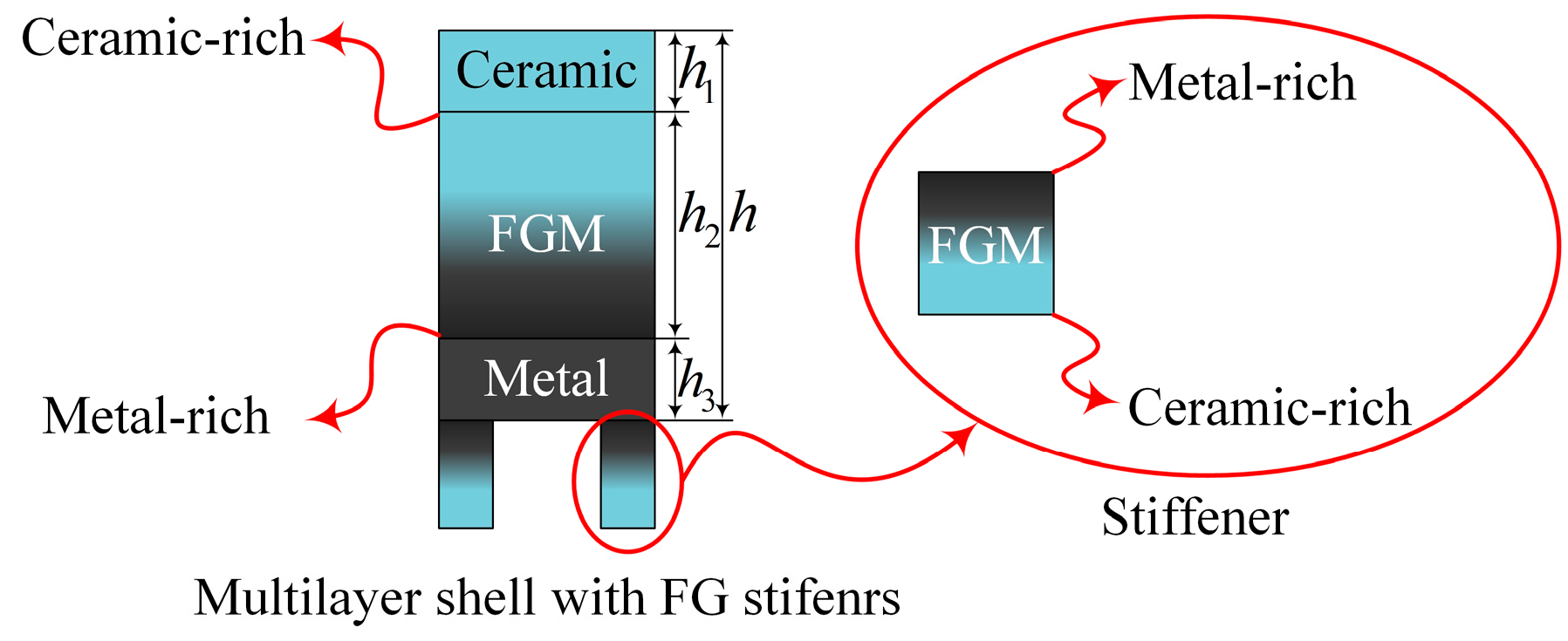
2.1. MFG Cylindrical Shells Reinforced by FGSSs
2.2. Governing Equation
- MFG cylindrical shells:
- FG spiral stiffeners:
2.3. Semi-Analytical Solutions
2.4. Addressing the Nonlinear Equation with the MMSs
3. Numerical Results
3.1. Validation of the Current Results
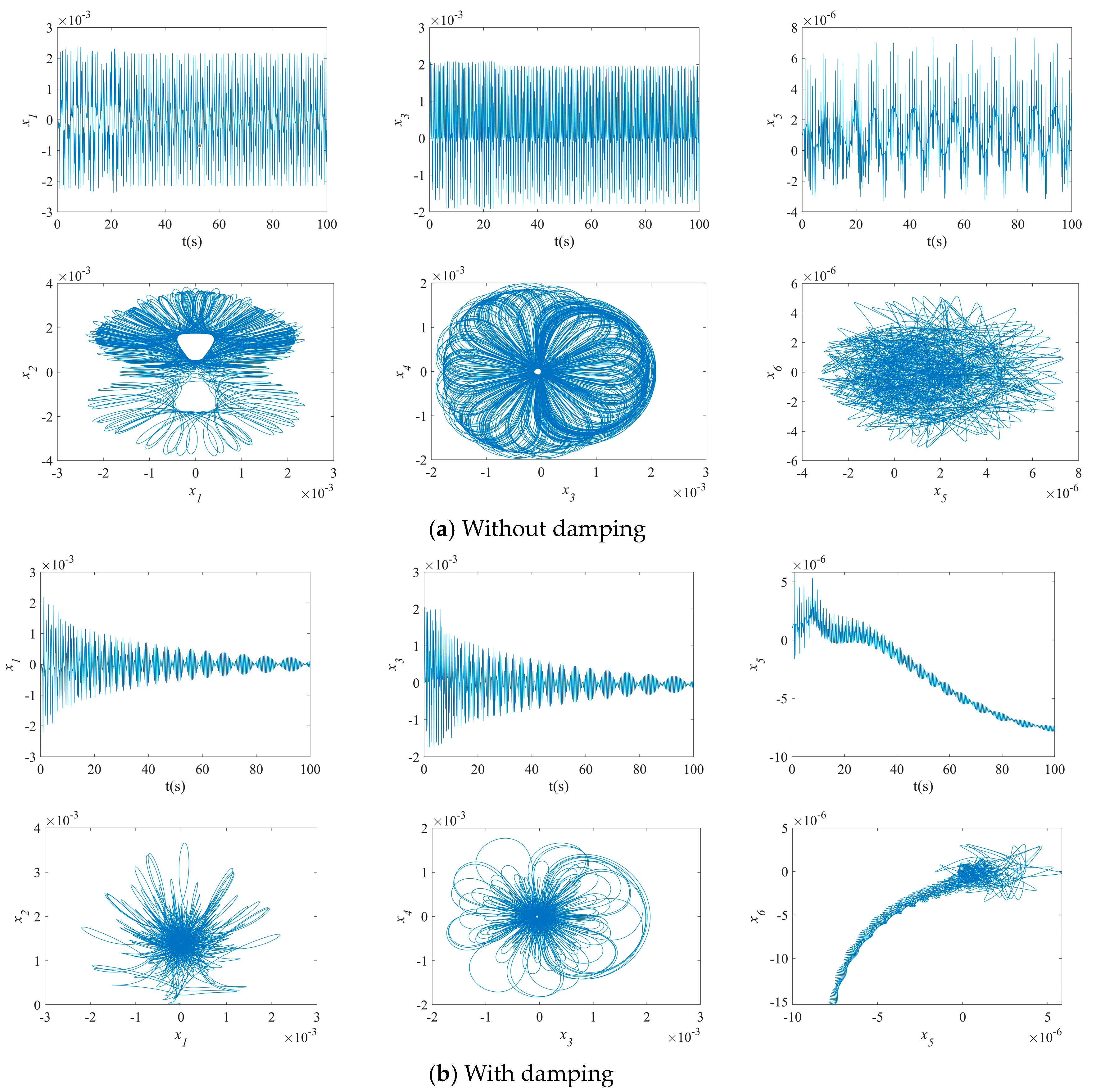
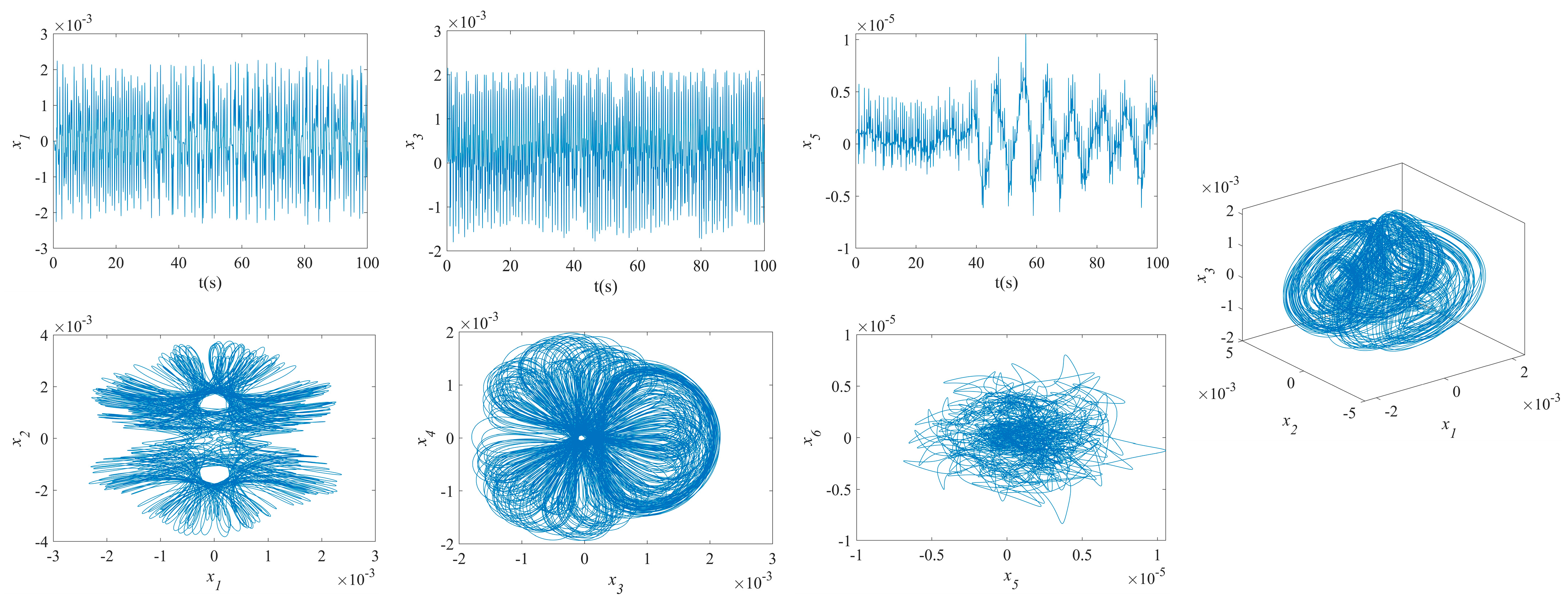
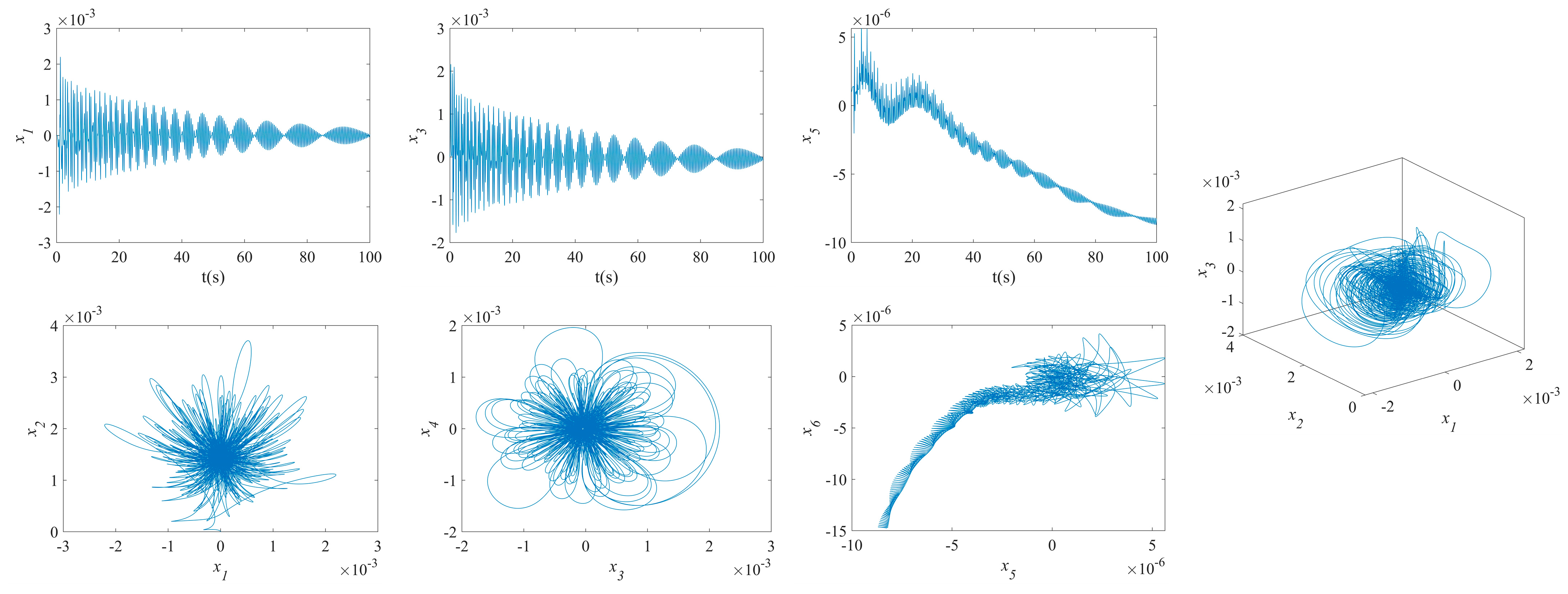
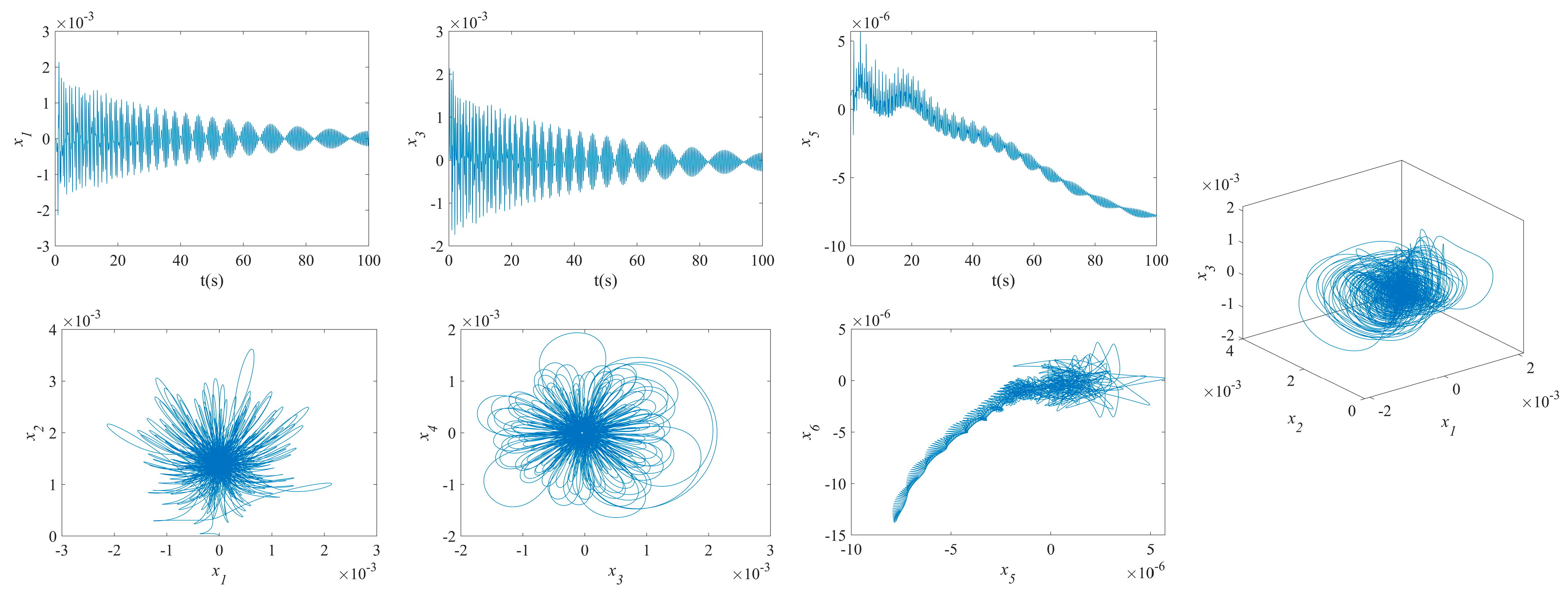
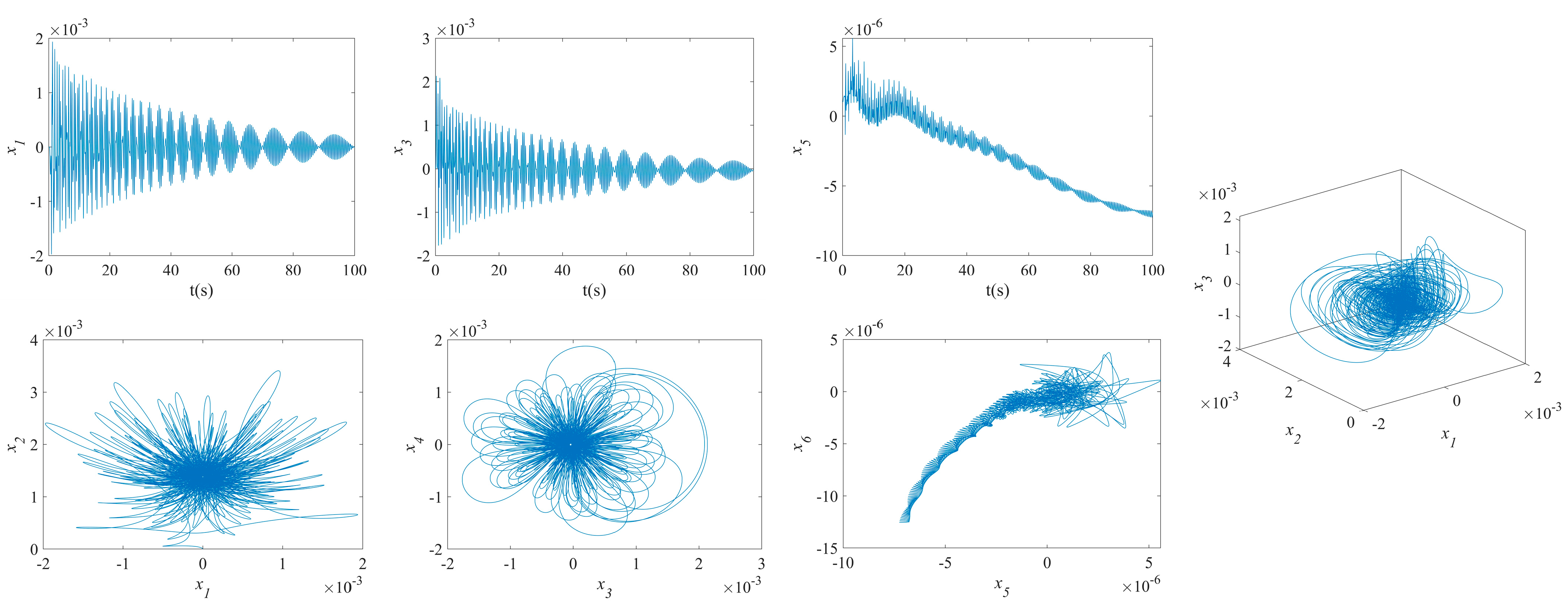
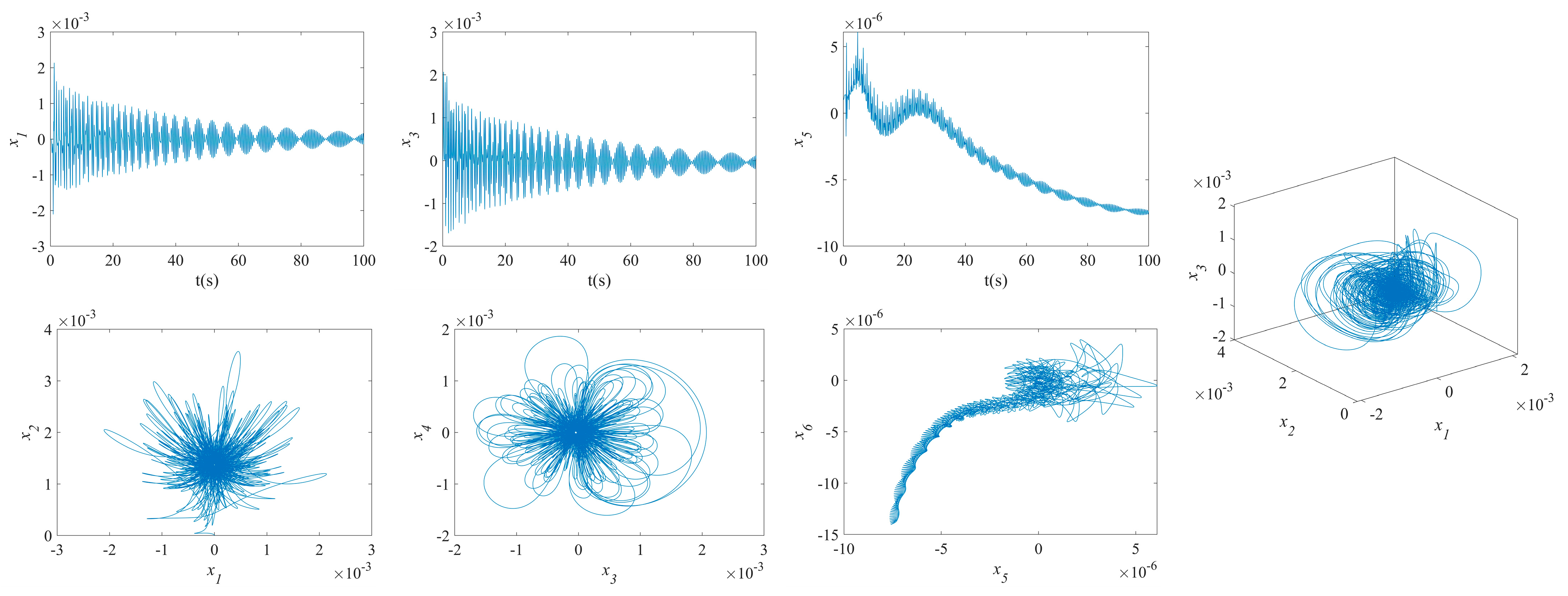
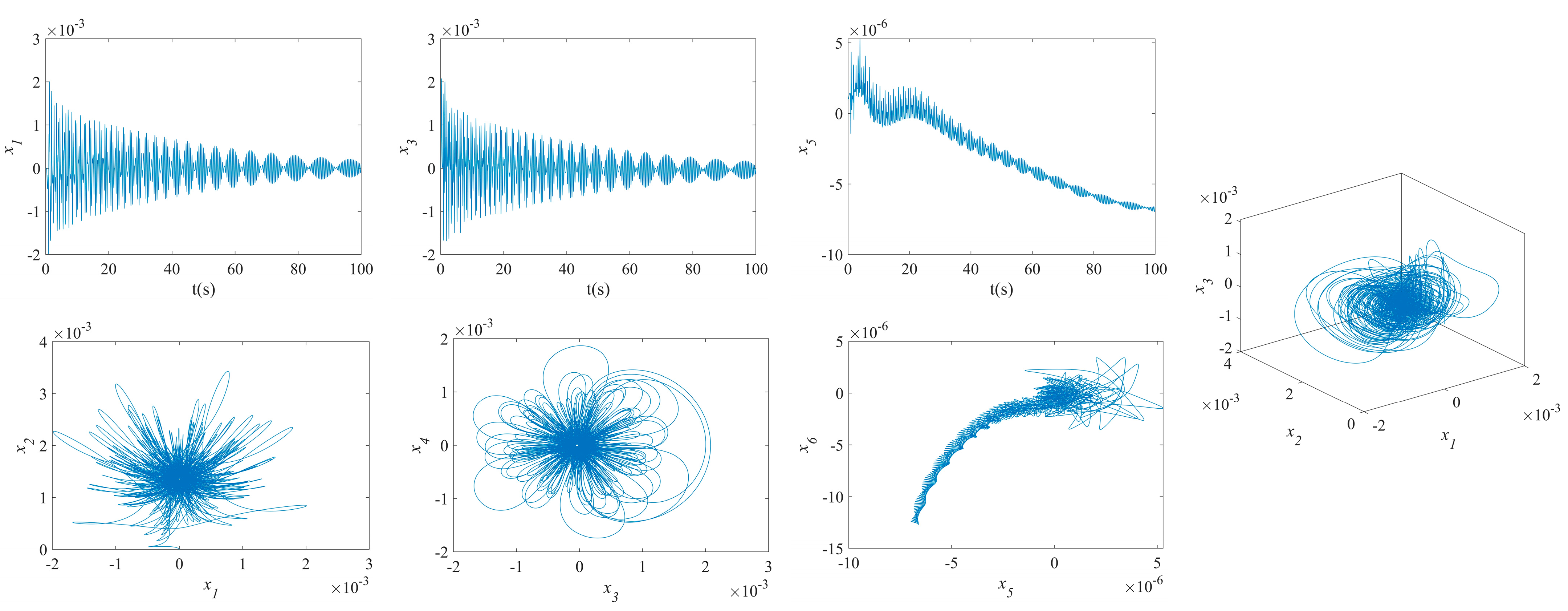
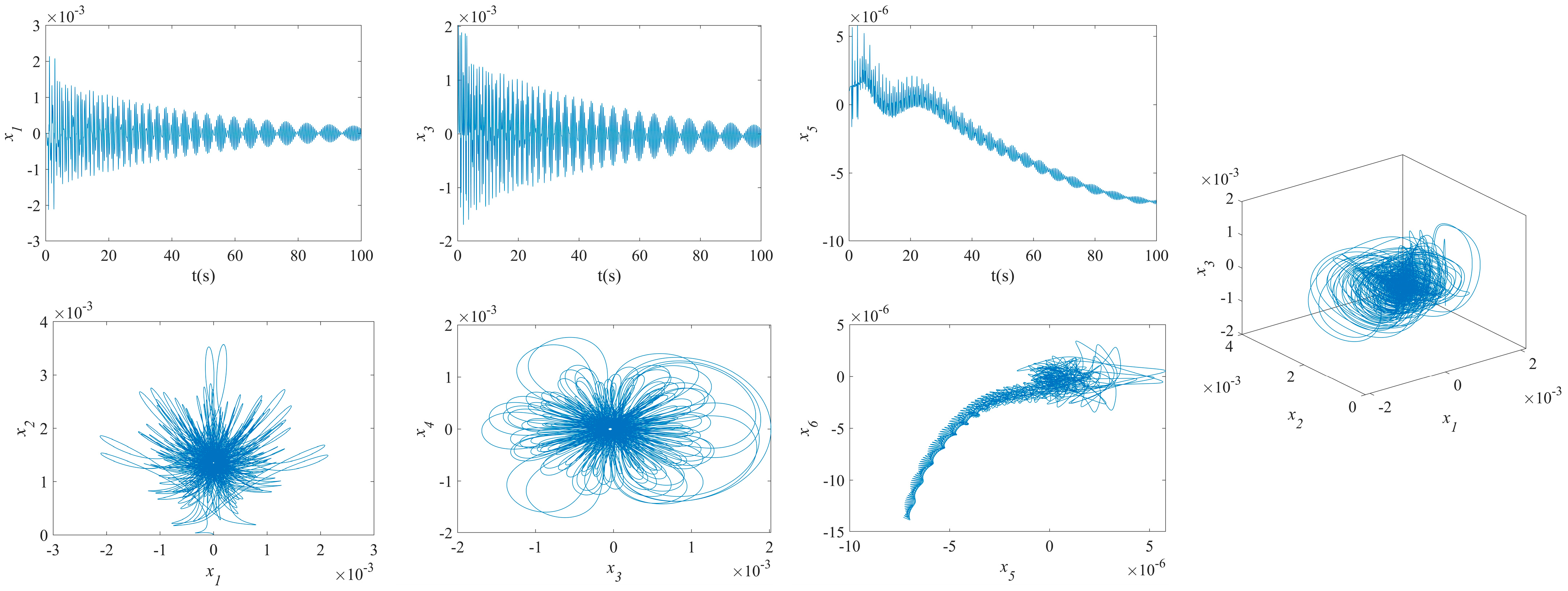
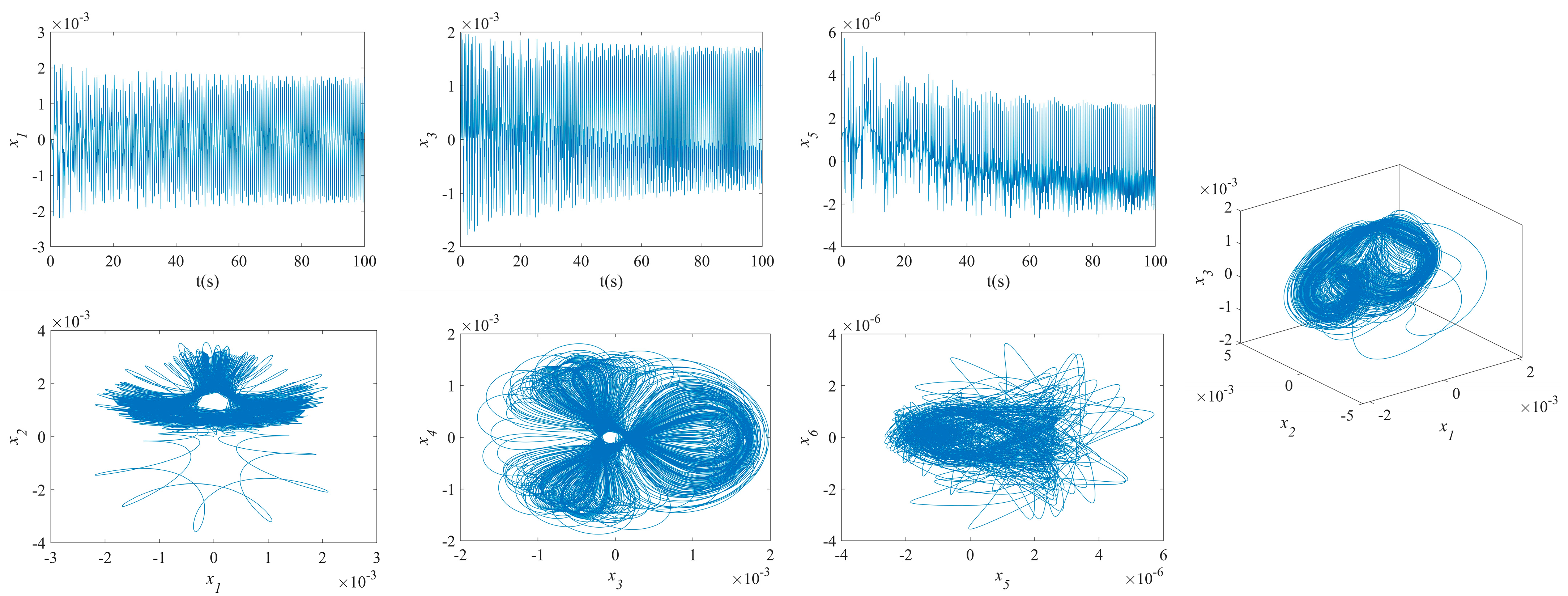
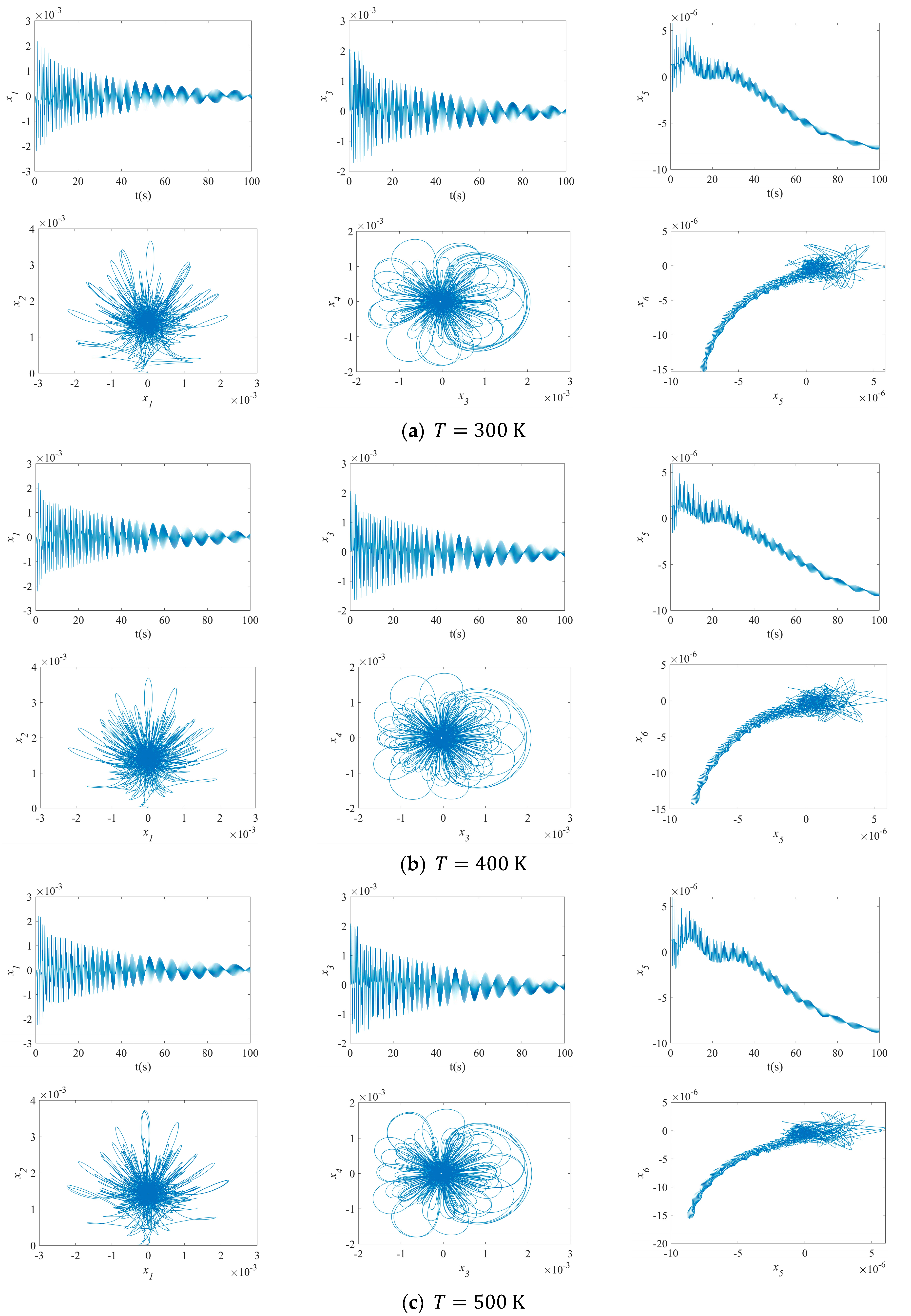
3.2. Results of NVs for MFG Cylindrical Shells Reinforced by FGSS
4. Conclusions
- The velocity of MFG cylindrical shells reinforced by FGSSs is lower in the modes () with stiffener angles and , in the modes () with stiffener angles and or , and in the modes () with stiffener angles and or or , compared to other configurations.
- The phase plane of the vibration of the MFG cylindrical shells, reinforced by FGSSs with modes () and stiffener angles and , tends towards a limit cycle quickly. Consequently, the NVs of the system are stabilized rapidly.
- By increasing the temperatures, the disorder on the maximum deflection versus velocity curve of the MFG cylindrical shells reinforced by FGSSs with the modes () and the modes () increases. Conversely, the vibration amplitude of the system with the modes () decreases slightly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Zhang, Y.; Zhang, W.; Yao, Z. Analysis on nonlinear vibrations near internal resonances of a composite laminated piezoelectric rectangular plate. Eng. Struct. 2018, 173, 89–106. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z. Nonlinear vibrations of moving functionally graded plates containing porosities and contacting with liquid: Internal resonance. Nonlinear Dynam. 2017, 90, 1461–1480. [Google Scholar] [CrossRef]
- Permoon, M.; Haddadpour, H.; Javadi, M. Nonlinear vibration of fractional viscoelastic plate: Primary, subharmonic, and superharmonic response. Int. J. Nonlinear Mech. 2018, 99, 154–164. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Nonlinear primary resonance of third-order shear deformable functionally graded nanocomposite rectangular plates reinforced by carbon nanotubes. Compos. Struct. 2016, 54, 707–723. [Google Scholar] [CrossRef]
- Wang, Y. Electro-mechanical vibration analysis of functionally graded piezoelectric porous plates in the translation state. Acta. Astronaut. 2018, 143, 263–271. [Google Scholar] [CrossRef]
- Mahmoudkhani, S.; Navazi, H.M.; Haddadpour, H. An analytical study of the non-linear vibrations of cylindrical shells. Int. J. Nonlinear Mech. 2011, 46, 1361–1372. [Google Scholar] [CrossRef]
- Rodrigues, L.; Gonçalves, P.B.; Silva, F.M.A. Internal resonances in a transversally excited imperfect circular cylindrical shell. Pro. Eng. 2017, 199, 838–843. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Guo, X. Internal resonance of axially moving laminated circular cylindrical shells. J. Sound Vib. 2013, 332, 6434–6450. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, T.; Xi, A.; Wang, Y. Resonant responses and chaotic dynamics of composite laminated circular cylindrical shell with membranes. J. Sound Vib. 2018, 423, 65–99. [Google Scholar] [CrossRef]
- Abe, A.; Kobayashi, Y.; Yamada, G. Nonlinear dynamic behaviors of clamped laminated shallow shells with one-to-one internal resonance. J. Sound Vib. 2007, 304, 957–968. [Google Scholar] [CrossRef]
- Li, F.; Yao, G. 1/3 Subharmonic resonance of a nonlinear composite laminated cylindrical shell in subsonic air flow. Compos. Struct. 2013, 100, 249–256. [Google Scholar] [CrossRef]
- Li, X. Parametric resonances of rotating composite laminated nonlinear cylindrical shells under periodic axial loads and hygrothermal environment. Compos. Struct. 2021, 255, 112887. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Large amplitude vibration of FGM orthotropic cylindrical shells interacting with the nonlinear Winkler elastic foundation. Compos. Part B Eng. 2016, 98, 141–150. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Hui, D.; Haciyev, V.C.; Erdem, H.; Yuan, G.Q.; Schnack, E.; Guldal, V. The nonlinear vibration of orthotropic functionally graded cylindrical shells surrounded by an elastic foundation within first order shear deformation theory. Compos. Part B Eng. 2017, 116, 170–185. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M.; Bakhtiari-Nejad, F. On the accuracy of the multiple scales method for non-linear vibrations of doubly curved shallow shells. Int. J. Nonlinear Mech. 2011, 46, 170–179. [Google Scholar] [CrossRef]
- Li, X.; Du, C.; Li, Y. Parametric resonance of a FG cylindrical thin shell with periodic rotating angular speeds in thermal environment. Appl. Math. Model. 2018, 59, 393–409. [Google Scholar] [CrossRef]
- Du, C.; Li, Y. Nonlinear resonance behavior of functionally graded cylindrical shells in thermal environments. Compos. Struct. 2013, 102, 164–174. [Google Scholar] [CrossRef]
- Sheng, G.; Wang, X. The dynamic stability and nonlinear vibration analysis of stiffened functionally graded cylindrical shells. Appl. Math. Model. 2018, 56, 389–403. [Google Scholar] [CrossRef]
- Gao, K.; Gao, W.; Wu, B.; Wu, D.; Song, C. Nonlinear primary resonance of functionally graded porous cylindrical shells using the method of multiple scales. Thin Wall. Struct. 2018, 125, 281–293. [Google Scholar] [CrossRef]
- Foroutan, K.; Dai, L.; Zhao, H. Combination resonances of porous FG shallow shells reinforced with oblique stiffeners subjected to a two-term excitation. Steel Compos. Struct. 2024, 51, 391. [Google Scholar]
- Foroutan, K.; Ahmadi, H. Nonlinear vibration of SSMFG cylindrical shells with internal resonances resting on the nonlinear viscoelastic foundation. Struct. Eng. Mech. 2022, 84, 767–782. [Google Scholar]
- Foroutan, K.; Ahmadi, H. Nonlinear parametric vibration of imperfect SSMFG cylindrical shells in thermal environment including internal and subharmonic resonances. Mech. Adv. Mater. Struct. 2022, 29, 3499–3522. [Google Scholar] [CrossRef]
- Dai, L.; Foroutan, K. Sub-harmonic and super-harmonic resonances of spiral stiffened FG cylindrical panels of variable thickness embedded within a nonlinear elastic foundation. J. Vib. Control 2024, 10775463231226344. [Google Scholar] [CrossRef]
- Duc, N.D.; Nguyen, P.D.; Khoa, N.D. Nonlinear dynamic analysis and vibration of eccentrically stiffened S-FGM elliptical cylindrical shells surrounded on elastic foundations in thermal environments. Thin-Walled Struct. 2017, 117, 178–189. [Google Scholar]
- Dong, Y.; Li, X.; Gao, K.; Li, Y.; Yang, J. Harmonic resonances of graphene-reinforced nonlinear cylindrical shells: Effects of spinning motion and thermal environment. Nonlinear Dynam. 2020, 99, 981–1000. [Google Scholar] [CrossRef]
- Brush, D.O.; Almroth, B.O. Buckling of Bars, Plates and Shells; Mc Graw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Duc, N.D.; Thang, P.T. Nonlinear dynamic response and vibration of shear deformable imperfect eccentrically stiffened S-FGM circular cylindrical shells surrounded on elastic foundations. Aerosp. Sci. Technol. 2015, 40, 115–127. [Google Scholar] [CrossRef]
- Paliwal, D.; Pandey, R.K.; Nath, T. Free vibrations of circular cylindrical shell on Winkler and Pasternak foundations. Int. J. Pres. Ves. Pip. 1996, 69, 79–89. [Google Scholar] [CrossRef]
- Sofiyev, A.; Avcar, M.; Ozyigit, P.; Adigozel, S. The Free Vibration of non-homogeneous truncated conical shells on a winkler foundation. Int. J. Eng. Appl. Sci. 2009, 1, 34–41. [Google Scholar]
- Zhang, X.; Liu, G.; Lam, K. Vibration analysis of thin cylindrical shells using wave propagation approach. J. Sound Vib. 2001, 239, 397–403. [Google Scholar] [CrossRef]
- Song, Z.; Li, F. Aerothermoelastic analysis and active flutter control of supersonic composite laminated cylindrical shells. Compos. Struct. 2013, 106, 653–660. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, W.; Mao, J. Nonlinear vibrations of carbon fiber reinforced polymer laminated cylindrical shell under non-normal boundary conditions with 1:2 internal resonance. Eur. J. Mech.-A/Solids 2019, 74, 317–336. [Google Scholar] [CrossRef]




| Present | Zhang et al. [30] | Song et al. [31] | Yang et al. [32] | ||||
|---|---|---|---|---|---|---|---|
| Discrepancy | Discrepancy | Discrepancy | |||||
| 0.0151266 | 0.0161065 | 6.10 | 0.0161299 | 6.20 | 0.0151185 | 0.05 | |
| 0.1097431 | 0.1098113 | 0.06 | 0.1097653 | 0.02 | 0.1096523 | 0.08 | |
| 0.0161008 | 0.0161011 | 0.002 | 0.0161011 | 0.002 | 0.0161003 | 0.003 | |
| 0.0050421 | 0.0050418 | 0.006 | 0.0050424 | 0.006 | 0.0050423 | 0.004 | |
| Material | Properties | |||||
|---|---|---|---|---|---|---|
(Ceramic) | 3.48 × 1011 | 0 | −3.07 × 10−4 | 2.16 × 10−7 | −8.95 × 10−11 | |
| 2370 | 0 | 0 | 0 | 0 | ||
| 5.87 × 10−6 | 0 | 9.10 × 10−4 | 0 | 0 | ||
| 13.723 | 0 | 0 | 0 | 0 | ||
(Metal) | 2.01 × 1011 | 0 | 3.08 × 10−4 | −6.53 × 10−7 | 0 | |
| 8166 | 0 | 0 | 0 | 0 | ||
| 1.23 × 10−5 | 0 | 8.09 × 10−4 | 0 | 0 | ||
| 15.379 | 0 | 0 | 0 | 0 |
| R (m) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.01 | 2.5 | 40 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foroutan, K.; Torabi, F. Influence of Spiral Stiffeners’ Symmetric and Asymmetric Angles on Nonlinear Vibration Responses of Multilayer FG Cylindrical Shells. Symmetry 2024, 16, 1318. https://doi.org/10.3390/sym16101318
Foroutan K, Torabi F. Influence of Spiral Stiffeners’ Symmetric and Asymmetric Angles on Nonlinear Vibration Responses of Multilayer FG Cylindrical Shells. Symmetry. 2024; 16(10):1318. https://doi.org/10.3390/sym16101318
Chicago/Turabian StyleForoutan, Kamran, and Farshid Torabi. 2024. "Influence of Spiral Stiffeners’ Symmetric and Asymmetric Angles on Nonlinear Vibration Responses of Multilayer FG Cylindrical Shells" Symmetry 16, no. 10: 1318. https://doi.org/10.3390/sym16101318





