Symmetrical Convergence Rates and Asymptotic Properties of Estimators in a Semi-Parametric Errors-in-Variables Model with Strong Mixing Errors and Missing Responses

Abstract

This paper considers a semi-parametric errors-in-variables (EV) model, ${\eta }_i=x_i\beta +g({\tau }_i)+{ϵ}_i$, ${\xi }_i=x_i+{\delta }_i$, $1⩽i⩽n$. The properties of estimators are investigated under conditions of missing data and strong mixing errors. Three approaches are used to handle missing data: direct deletion, imputation, and the regression surrogate. Furthermore, estimators for the coefficient $\beta$ and the nonparametric function $g(·)$ are obtained. Notably, both estimators achieve strong consistency at a rate of $o(n^{-1/4})$, exhibiting a symmetry in their convergence rates, and they also demonstrate asymptotic normality. Additionally, the validity of our theoretical results is supported by simulations demonstrating the finite sample behaviour of these estimators.

1. Introduction

We examine the semi-parametric EV model given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\eta }_i& =x_i\beta +g({\tau }_i)+{ϵ}_i,{\xi }_i=x_i+{\delta }_i.\hfill \end{array}\end{array}$$

(1)

where the response variables ${\eta }_i$ are determined by a linear combination of the known design point $(x_i,{\tau }_i)$, unobservable latent variables $x_i$, an unknown function $g({\tau }_i)$, and random errors ${ϵ}_i$ with a mean of zero. Additionally, observations of $x_i$, denoted as ${\xi }_i$, are subject to measurement errors ${\delta }_i$ that also have a mean of zero. The estimation of the unknown real parameter $\beta$ is required, and the unknown function $g({\tau }_i)$ is defined on the closed interval $[0,1]$. Furthermore, a known function $f(·)$ is defined on the same interval and relates to the latent variables $x_i$ through the following equation:

$$\begin{array}{c}\hfill x_i=f({\tau }_i)+u_i.\end{array}$$

(2)

Here, $u_i$ represents design points related to $x_i$.

The practicality of Model (1) has garnered increasing scholarly attention. In the case where $x_i$ is observed without a measurement error, the model simplifies to the standard semi-parametric regression model, as initially proposed by Engle and his colleagues [1] for examining the relationship between climatic conditions and electricity usage. In recent years, numerous other scholars have conducted research on this topic. For instance, Roozbeh et al. [2] proposed a robust estimator for semi-parametric models, proven to outperform traditional estimators in terms of asymptotic normality and consistency under certain conditions through simulations and real data analysis. Ding and co-authors [3] analyzed the long-run behavior of wavelet-based estimators applied to semi-parametric models with varying error variances and randomness. Wei et al. [4] explored variance estimation in partial linear variable-coefficient semi-parametric models, introducing a ridge estimator to enhance the least squares method. Fu et al. [5] examined a generalized semi-parametric model, developing a difference-based M-estimator for its parametric component. They proved the asymptotic normality of this estimator and evaluated the convergence behavior of a wavelet-based estimator for the model’s nonparametric function. These outcomes were subsequently applied to models exhibiting dependent errors.

Measurement errors in covariates present a significant challenge to statistical analyses, underscoring the importance of model (1). In cases where $g(·)$ is identically zero, model (1) reduces to the basic linear errors-in-variables (EV) regression model, which Deaton [6] effectively used to mitigate the impacts of sampling error. Chen et al. [7] established pivotal results on convergence and the strong law of large numbers for sums of i.i.d. random variables, providing valuable insights into the strong consistency and convergence rates of nonparametric regression and least squares estimators in linear EV models. Research has since expanded into semi-parametric EV models with independent errors and complete data. For instance, Zhou et al. [8] investigated a semi-parametric partially linear model for panel data, introducing heteroscedasticity detection methods and an efficient weighted least squares estimator. Zhang et al. [9] addressed heteroscedastic partially linear EV models, defining Berry–Esseen bounds for estimators and evaluating their performance under independent errors. Emami [10] examined ridge and restricted ridge estimation in semi-parametric EV models in the presence of covariate measurement errors and unstable covariance matrices, establishing conditions and regions of optimality through simulations based on quadratic risks. Further relevant discussions can be found in the works of Miao and colleagues [11], Hu et al. [12], Zhang et al. [13], and others.

While semi-parametric regression and errors-in-variables models have traditionally relied on complete data, real-world applications frequently face the challenge of incomplete data due to missing observations or data losses. Recognizing the critical need for advanced methodologies, recent studies have made noteworthy contributions. Zou et al. [14] developed methods for estimation and inference in partial functional linear models with measurement error and incomplete data, demonstrating their asymptotic validity and practical utility through simulations and real data analysis. Similarly, Xiao et al. [15] proposed two estimation techniques for varying-coefficient models, showing the superior accuracy and convergence of the imputation-based method through simulations and real-world applications. Additionally, Zou et al. [16] introduced novel approaches for analyzing heteroscedastic partially linear varying-coefficient models with right-censored and randomly missing data. Through the integration of regression calibration, imputation techniques, and inverse probability weighting, they improved estimators for parameters and coefficient functions, demonstrating their asymptotic properties. These efforts underscore the evolving strategies to address data incompleteness, enriching the toolset for statistical analysis in the presence of incomplete information.

It is crucial to recognize that error independence is not consistently a valid assumption in practical applications, especially when dealing with economic data collected sequentially. Such data frequently exhibit significant error dependence. A variety of correlation structures have been identified, including autoregressive series, negatively associated sequences, $\rho$-mixing sequences, $\alpha$-mixing sequences, and moving average series. There has been substantial interest among researchers in exploring models characterized by $\alpha$-mixing errors. For example, Xi et al. [17] demonstrated the asymptotic properties of $\beta$, g, and f under conditions of $\alpha$-mixing errors. Zhang et al. [18] examined the asymptotic performance of estimators in a semi-parametric EV model where errors are negatively associated (NA) and data are incomplete. Similarly, Zhang and Yang [19] analyzed the asymptotic behavior of estimators in a semi-parametric EV model with linear process sequence errors under incomplete data.

In conclusion, there exists a significant gap in the research: no theoretical foundation has been established for semi-parametric EV models with strong mixing errors under incomplete data. Our study fills this gap, focusing on such a model and addressing both strong mixing errors and the challenge of missing data. This effort is driven by curiosity and a desire to shed light on the unknown.

This paper unfolds in several key parts. Section 2 lays out our assumptions. In Section 3, we explore three methodologies for estimating $\beta$ and $g(·)$ while addressing incomplete responses. In this section, we also unveil strong consistency rates and the asymptotic normality of our estimators. In Section 4, we dedicate our focus to a simulation study, delving into the behavior of our suggested estimators under limited sample sizes. In Section 5, we present some propositions. The justifications for the outcomes and propositions are detailed in Section 6 and Section 7. Finally, Section 8 concludes this paper, summarizing the key findings.

2. Assumptions

In this study, we analyze incomplete datasets denoted by $\left\{({\eta }_i,{\rho }_i,{\xi }_i,{\tau }_i)\right\}$ that are derived from model (1). Here, ${\rho }_i$ indicates the presence of data, with ${\rho }_i=0$ representing instances where the values of ${\eta }_i$ are randomly missing, and ${\rho }_i=1$ indicating observed values. Additionally, ${ϵ}_i$ are strong mixing errors. It is crucial to distinguish between different types of missing data mechanisms, as these influence the validity of statistical methods applied to incomplete data:

• Missing Completely at Random (MCAR): The probability of missingness is independent of both the observed and unobserved data values.
• Missing at Random (MAR): The probability of missingness depends on the observed values, but not on the unobserved (missing) values themselves.
• Not Missing at Random (NMAR): Missingness depends on the unobserved (missing) values themselves.

In this work, we assume a Missing at Random (MAR) mechanism, as it aligns with the methods employed to handle incomplete data, including direct deletion, imputation, and regression surrogate techniques. Next, we will present several assumptions, which will serve to substantiate the principal results outlined below.

Definition 1.

In a probability space $\left(\Gamma ,\mathcal{B},Q\right)$, consider a sequence of real-valued random variables $\left\{Y_i:i\in X\right\}$. Let ${\mathcal{G}}_p^n$ denote the σ-algebra generated by the collection of random variables $\left\{Y_i:p⩽i⩽n\right\}$. Set

$$\alpha \left(n\right)=sup\left\{\left|Q\left(CD\right)-Q\left(C\right)Q\left(D\right)\right|:C\in {\mathcal{G}}_{-\infty }^n,D\in {\mathcal{G}}_{p+n}^{\infty }\right\}$$

The sequence $\left\{Y_i\right\}$ is termed strongly mixing when $\alpha \left(n\right)$ approaches zero as n tends to infinity.

(H0)

Consider the sequence ${\left\{{ϵ}_i\right\}}_{i=1}^n$ of random variables which are both stationary and exhibit strong mixing properties with mixing coefficients $\left\{\alpha \left(n\right)\right\}$. Additionally, consider the sequence ${\left\{{\delta }_i\right\}}_{i=1}^n$ of independent random variables that satisfy the following:

(i)

$E{ϵ}_i=0$, $E{ϵ}_i^2=1$, $E{\delta }_i=0$, $E{\delta }_i^2={\Xi }_{\delta }^2>0$;

(ii)

${sup}_{i}E{\left|{ϵ}_i\right|}^{4+2\eta }<\infty$, ${sup}_{i}E{\left|{\delta }_i\right|}^{4+2\eta }<\infty$ for some $\eta ⩾0$;

(iii)

The sequences ${\left\{{ϵ}_i\right\}}_{i=1}^n$ and ${\left\{{\delta }_i\right\}}_{i=1}^n$ are mutually independent.

(H1)

Let ${\left\{{\mu }_i\right\}}_{i=1}^n$ be a sequence as defined in (2) satisfying the following:

(i)

As $n\to \infty$, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\mu }_i^2\to {\Lambda }_0$, ${\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\rho }_i{\mu }_i^2\to {\Lambda }_1$ where $\left(0<{\Lambda }_0,{\Lambda }_1<\infty \right)$.

(ii)

As $n\to \infty$, ${sup}_n{\displaystyle \frac{{max}_{1\le m\le n}|{\sum }_{i=1}^m{\mu }_{k_i}|}{\sqrt{n}logn}}<\infty$, $\{k_1,k_2,\dots ,k_n\}$ denotes any order of 1 to n.

(H2)

On $[0,1]$, both $g(·)$ and $f(·)$ are continuous and Lipschitz continuous of order one.

(H3)

For each integer k with $1⩽k⩽n$, there exists a weight function $V_{nk}^c\left(\tau \right)$ that is confined to the domain [0, 1] and satisfies the following:

(i)

Let $S_{nk}\left({\tau }_i\right)={\sum }_{i=1}^n{\rho }_k{V}_{nk}^c({\tau }_i)$. Then, ${\displaystyle \underset{1\le k\le n}{max}}{S}_{nk}\left({\tau }_i\right)=O(1)$.

(ii)

Assume for all $a>0$: ${sup}_{\tau }{\sum }_{j=1}^n{\rho }_j{V}_{nk}^c\left(\tau \right)I\left(|\tau -{\tau }_k|>a{n}^{-1/4}\right)=O\left(n^{-\frac{1}{4}}\right)$.

(iii)

${sup}_{\tau }{V}_{nk}^c\left(\tau \right)=o\left({\displaystyle \frac{1}{\sqrt{n}logn}}\right)$.

(H4)

Let $V_{nk}\left(\tau \right)$, for $1⩽k⩽n$, denote the probability weight functions defined over the interval $[0,1]$, which are subject to the following conditions:

(i)

Let $T_{nk}\left({\tau }_i\right)={\sum }_{i=1}^n{\rho }_k{V}_{nk}({\tau }_i)$. Then, ${\displaystyle \underset{1\le k\le n}{max}}{T}_{nk}\left({\tau }_i\right)=O(1)$.

(ii)

Assume for all $a>0$: ${sup}_{\tau }{\sum }_{k=1}^n{V}_{nk}\left(\tau \right)I\left(|\tau -{\tau }_k|>a·n^{-\frac{1}{4}}\right)=o\left(n^{-\frac{1}{4}}\right)$.

(iii)

${sup}_{\tau }\left({\displaystyle \underset{k}{max}}{V}_{nk}(\tau )\right)=o\left({\displaystyle \frac{1}{\sqrt{n}logn}}\right).$

(H5)

(i)

Given $b>0$, it holds that ${sup}_{\tau }{\sum }_{k=1}^n{\rho }_k{V}_{nk}^c\left(\tau \right)I\left(|\tau -{\tau }_k|>b·n^{-\frac{1}{2}}\right)=o\left(n^{-\frac{1}{2}}\right)$.

(ii)

Given $b>0$, it holds that ${sup}_{\tau }{\sum }_{k=1}^n{V}_{nk}\left(\tau \right)I\left(|\tau -{\tau }_k|>b·n^{-\frac{1}{2}}\right)=o\left(n^{-\frac{1}{2}}\right)$.

(H6)

(i)

${\sum }_{k=1}^n{\left[V_{nk}^c(\tau )\right]}^2=O(n^{-3/5})$ for any $0⩽\tau ⩽1$.

(ii)

${\sum }_{k=1}^n{\left[V_{nk}(\tau )\right]}^2=O(n^{-3/5})$ for any $0⩽\tau ⩽1$.

(H7)

Positive integers $r:=r\left(n\right)$ and $s:=s\left(n\right)$ exist, satisfying the following:

(i)

$r+s⩽n$, $r\to \infty$, $s\to \infty$, ${\displaystyle \frac{s}{r}}\to 0$, $r^2=O\left(ns\right)$.

(ii)

Let ${\mu }_{\max }={max}_{1⩽i⩽n}\left|{\mu }_i\right|$; it follows that $\sqrt{{\displaystyle \frac{s}{r}}}{\mu }_{\max }\to 0$ as $n\to \infty$.

Remark 1.

Assumptions (H0) to (H5) are commonly accepted conditions that are frequently cited in scholarly articles, including works by Zhang et al. [9] and Liang et al. [20].

Remark 2.

Meeting assumption (H7) is relatively effortless. For instance, one can choose $r=n^{1/3}$ and $s=logn$, and ensure that ${max}_{1⩽i⩽n}\left|{\mu }_i\right|=o\left(n^{1/6}\right)$.

3. Main Results

3.1. Building Estimators: Methods and Techniques

3.1.1. Direct Deletion Method

In model (1), the direct deletion method simplifies the model by excluding missing data and using only complete observations. This results in the following simplified model: ${\rho }_i{\eta }_i={\rho }_i{x}_i\beta +{\rho }_{i}g({\tau }_i)+{\rho }_i{ϵ}_i$ When $x_i$ is observable (i.e., ${\rho }_i=1$), the least squares estimation (LSE) method can be used to estimate the parameter $\beta$. Given a known $\beta$, the estimator for $g(·)$ is constructed using the complete data, which consist of the observed triplets ${\left\{({\rho }_i{\eta }_i,{\rho }_i{\xi }_i,{\rho }_i{\tau }_i)\right\}}_{i=1}^n$. Specifically, the estimator $g_n^{*}(\tau ,\beta )$ is given by

$$g_n^{*}(\tau ,\beta )=\sum _{k=1}^n{V}_{nk}^c(\tau )\left({\rho }_k{\eta }_k-{\rho }_k{\xi }_k\beta \right),$$

where $V_{nk}^c(t)$ are weight functions that satisfy assumption (H3).

Computational Complexity: The computational complexity of the direct deletion method is $O(n)$, as it only requires performing least squares regression on the complete data. This method is suitable when the proportion of missing data is small, but it may introduce bias if the missing data are not missing at random.

3.1.2. Modified Least Squares Estimation (LSE)

Liang et al. [21] proposed a standard LSE method for parameter estimation in partial linear models. However, their method does not fully account for missing data or incomplete observations. To address this, we modify their LSE approach by incorporating an additional term that utilizes weighted information from the available data, thereby reducing bias caused by missing values. The modified estimator ${\widehat{\beta }}_c$ is obtained by minimizing the following loss function:

$$SS(\beta )=\sum _{i=1}^n{\rho }_i\left[{\left({\eta }_i-{\xi }_i\beta -g_n^{*}({\tau }_i,\beta )\right)}^2-{\Xi }_{\delta }^2{\beta }^2\right]=min.$$

This modification incorporates the function $g_n^{*}({\tau }_i,\beta )$, which accounts for missing data, by using weights derived from available data. The resulting modified estimator for $\beta$ is

$$\begin{array}{c}\hfill {\widehat{\beta }}_c={\left[\sum _{i=1}^n({\rho }_i{\widetilde{{\xi }_i^c}}^2-{\rho }_i{\Xi }_{\delta }^2)\right]}^{-1}\sum _{i=1}^n{\rho }_i\widetilde{{\xi }_i^c}\widetilde{{\eta }_i^c},\end{array}$$

(3)

Substituting ${\widehat{\beta }}_c$ into $g_n^{*}(\tau ,\beta )$ gives the estimator for $g(·)$:

$$\begin{array}{c}\hfill {\widehat{g}}_n^c\left(\tau \right)=\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left(\tau \right)({\eta }_k-{\xi }_k{\widehat{\beta }}_c).\end{array}$$

(4)

Computational Complexity: The computational complexity of the modified LSE is $O(n^2)$ due to the need to perform weighted least squares regression across all available data points. This method takes advantage of all available data, making it more robust in the presence of missing values, though it requires more computational resources.

3.1.3. Imputation Method

To fully utilize the incomplete data, the imputation method fills in the missing values. Following the approach proposed by Wang and Sun [22], the imputed value $U_i^{\left[I\right]}$ is given by

$$\begin{array}{c}\hfill U_i^{\left[I\right]}={\rho }_i{\eta }_i+(1-{\rho }_i)[{\xi }_i{\widehat{\beta }}_c+{\widehat{g}}_n^c({\tau }_i)].\end{array}$$

(5)

After imputation, the complete dataset ${\left\{(U_i^{\left[I\right]},{\xi }_i,{\tau }_i)\right\}}_{i=1}^n$ is used to construct the estimators ${\widehat{\beta }}_I$ and ${\widehat{g}}_n^{\left[I\right]}(\tau )$:

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_I& =& {\left[\sum _{i=1}^n\left({\tilde{\xi }}_i^2-{\rho }_i{\Xi }_{\delta }^2\right)\right]}^{-1}\sum _{i=1}^n{\tilde{\xi }}_i{\tilde{U}}_i^{\left[I\right]},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\widehat{g}}_n^{\left[I\right]}\left(\tau \right)& =& \sum _{k=1}^n{V}_{nk}\left(\tau \right)(U_k^{\left[I\right]}-{\xi }_k{\widehat{\beta }}_I).\hfill \end{array}$$

(7)

Computational Complexity: The computational complexity of the imputation method is $O(n^2)$, as it involves the iterative imputation of missing values and the performance of regression analysis for each iteration. While the computational cost is higher, this method allows for a better utilization of the incomplete data and can reduce bias compared to methods that discard missing observations.

3.1.4. Regression Substitution Method

The regression substitution method replaces missing values with predicted values using a regression model. The imputed value $U_i^{\left[R\right]}$ is given by

$$\begin{array}{c}\hfill U_i^{\left[R\right]}={\xi }_i{\widehat{\beta }}_c+{\widehat{g}}_n^c({\tau }_i).\end{array}$$

(8)

After imputation, the complete dataset ${\left\{(U_i^{\left[R\right]},{\xi }_i,{\tau }_i)\right\}}_{i=1}^n$ is used to estimate ${\widehat{\beta }}_R$ and ${\widehat{g}}_n^{\left[R\right]}(\tau )$:

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_R& =& {\left(\sum _{i=1}^n{\tilde{\xi }}_i^2\right)}^{-1}\sum _{i=1}^n{\tilde{\xi }}_i{\tilde{U}}_i^{\left[R\right]},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\widehat{g}}_n^{\left[R\right]}\left(\tau \right)& =& \sum _{k=1}^n{V}_{nk}\left(\tau \right)(U_k^{\left[R\right]}-{\xi }_k{\widehat{\beta }}_R).\hfill \end{array}$$

(10)

Computational Complexity: The computational complexity of the regression substitution method is also $O(n^2)$ due to the regression imputation and subsequent updates. Similar to the imputation method, this method benefits from the complete use of available data but at the cost of increased computational time.

3.1.5. Summary of Computational Complexities

The direct deletion method, with its computational complexity of $O(n)$, is efficient and suitable for cases with minimal missing data. However, it may introduce bias if data are not Missing at Random. In contrast, the imputation and regression substitution methods, which operate at $O(n^2)$, effectively utilize incomplete data and reduce bias but require significantly more computational resources due to their iterative nature.

In practical decision-making scenarios, such as policy formulation or resource allocation, data constraints and resource limitations are common. In these contexts, selecting the appropriate estimation method is crucial. Practitioners should consider the extent of missing data and the available computational resources when making this choice. For example, when the proportion of missing data is low, the direct deletion method provides a quick and low-cost solution. However, when missing data is more substantial, imputation and regression substitution methods, though computationally more demanding, offer more accurate estimates and help ensure that decisions are based on more reliable data.

In cases of large datasets or limited computational resources, it is advisable to set an upper limit on the number of iterations or to use the direct deletion method for initial estimates. Techniques like early stopping or gradually reducing the sample size can help manage computational load when convergence is slow. These strategies allow for efficient decision-making even under data and resource constraints, ensuring that robust decisions can still be made without overburdening computational resources.

3.2. Strong Consistency in Estimator Behavior

Our focus in this part of the paper is on studying the strong consistency of the two estimators, $\beta$ and $g\left(·\right)$, assuming that the missingness of ${\eta }_i$ is random. We emphasize that strong consistency is a critical criterion for evaluating estimator quality, allowing us to distinguish effective estimators from ineffective ones based on their consistency rates. Below, we present three theorems that exhibit symmetrical structures.

Theorem 1.

Assume that (H0)–(H3), (H6) and ${sup}_{i}E{\left|{ϵ}_i\right|}^{10}<\infty$ are fulfilled. Given τ in $[0,1]$, it holds that

(a) 

${\widehat{\beta }}_c-\beta =o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

(b) 

${\widehat{g}}_n^c(\tau )-g(\tau )=o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

Theorem 2.

Assume that (H0)–(H4), (H6) and ${sup}_{i}E{\left|{ϵ}_i\right|}^{10}<\infty$ are fulfilled. Given τ in $[0,1]$, it holds that

(a) 

${\widehat{\beta }}_I-\beta =o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

(b) 

${\widehat{g}}_n^{\left[I\right]}(\tau )-g(\tau )=o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

Theorem 3.

Assume that (H0)–(H4), (H6) and ${sup}_{i}E{\left|{ϵ}_i\right|}^{10}<\infty$ are fulfilled. Given τ in $[0,1]$, it holds that

(a) 

${\widehat{\beta }}_R-\beta =o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

(b) 

${\widehat{g}}_n^{\left[R\right]}(\tau )-g(\tau )=o(n^{-{\displaystyle \frac{1}{4}}})a.s.$

3.3. Asymptotic Normality in Estimator Behavior

Normal distribution occupies a central position not only in mathematics but also in physics, engineering, and numerous other fields of study. Its significance extends to the realm of asymptotic normality of estimators, which is essential for constructing confidence bands for these estimators. Our further analysis delves into the asymptotic normality behavior of the $\beta$ and $g\left(·\right)$ estimators.

To begin, we shall review key terms that will hold significant importance in the subsequent conclusions and demonstrations:

$$\begin{array}{c}{\tilde{x}}_i^c=x_i-\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right)x_k,{\tilde{\delta }}_i^c={\delta }_i-\sum _{k=1}^n{\delta }_k{V}_{nk}^c\left({\tau }_i\right){\delta }_k,{\tilde{g}}_i^c=g\left({\tau }_i\right)-\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right)g\left({\tau }_k\right),\hfill \\ {\widetilde{ϵ}}_i^c={ϵ}_i-\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){ϵ}_k,{\tilde{x}}_i=x_i-\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)x_k,{\tilde{\delta }}_i={\delta }_i-\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k,{\chi }_i={ϵ}_i-{\delta }_i\beta ,\hfill \\ {\tilde{g}}_i=g\left({\tau }_i\right)-\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)g\left({\tau }_k\right),{\widetilde{ϵ}}_i={ϵ}_i-\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){ϵ}_k,R_n^2=\sum _{i=1}^n{\tilde{x}}_i^2,R_{1n}^2=\sum _{i=1}^n\left({\rho }_i{\tilde{\xi }}_i^2-{\rho }_i{\Xi }_{\delta }^2\right),\hfill \\ R_{2n}^2=\sum _{i=1}^n\left({\tilde{\xi }}_i^2-{\Xi }_{\delta }^2\right),R_{3n}^2=\sum _{i=1}^n{\tilde{\xi }}_i^2,{\Theta }_{1n}^2=Var\left[\sum _{i=1}^n{\rho }_i({\tilde{x}}_i^c+{\delta }_i)\left({ϵ}_i-{\delta }_i\beta \right)\right],\hfill \\ {\Lambda }_{1n}^2\left(\tau \right)=Var[\left(\sum _{k=1}^n{V}_{nk}^c\left(\tau \right){\rho }_k+\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)\sum _{i=1}^n{V}_{ni}^c({\tau }_k){\rho }_i)\left({ϵ}_k-{\delta }_k\beta \right)\right],\Omega ={\displaystyle \frac{{\sum }_{i=1}^n\left(1-{\rho }_i\right){\Xi }_{\delta }^2}{R_{1n}^2}},\hfill \\ \Phi ={\displaystyle \frac{{\sum }_{i=1}^n{\tilde{x}}_i^2\left(1-{\rho }_i\right)}{R_{1n}^2}},{\Theta }_{2n}^2=Var\left[\sum _{i=1}^n{\rho }_i({\tilde{x}}_i+\left(\Omega +\Phi \right){\tilde{x}}_i^c+\left(1+\Omega +\Phi \right){\delta }_i)\left({ϵ}_i-{\delta }_i\beta \right)\right],\hfill \\ M={\displaystyle \frac{R_{3n}^2}{R_{1n}^2}}\sum _{i=1}^n\widetilde{x_i^2},N={\displaystyle \frac{R_{3n}^2}{R_{1n}^2}}E{\delta }_i^2,{\Theta }_{3n}^2=Var\left[\left(M+N\right)\sum _{i=1}^n{\rho }_i({\tilde{x}}_i^c+{\delta }_i)\left({ϵ}_i-{\delta }_i\beta \right)\right],\hfill \\ {\Lambda }_{2n}^2\left(\tau \right)=Var\left[\sum _{k=1}^n{V}_{nk}\left(\tau \right){\rho }_k\left({ϵ}_k-{\delta }_k\beta \right)\right],{\Lambda }_{3n}^2\left(\tau \right)=Var\left[\sum _{k=1}^n{V}_{nk}\left(\tau \right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_k\right){\rho }_i\left({ϵ}_i-{\delta }_i\beta \right)\right].\hfill \end{array}$$

Theorem 4.

Assume that (H0)–(H3), (H5) and (H7) are fulfilled. Given τ in $[0,1]$,

(a) 

Given ${\Theta }_{1n}^2\ge Cn$, it follows that $R_{1n}^2({\widehat{\beta }}_c-\beta )/{\Theta }_{1n}\stackrel{D}{\to }\mathcal{N}(0,1).$

(b) 

Under the condition $n{\Lambda }_{1n}^2(\tau )\to \infty$ as $n\to \infty$, it holds that ${\widehat{g}}_n^c(\tau )-g(\tau )/{\Lambda }_{1n}(\tau )\stackrel{D}{\to }\mathcal{N}(0,1).$

Theorem 5.

Assume that (H0)–(H5) and (H7) are fulfilled. Given τ in $[0,1]$,

(a) 

Given ${\Theta }_{2n}^2\ge Cn$, it follows that $R_{2n}^2({\widehat{\beta }}_I-\beta )/{\Theta }_{2n}\stackrel{D}{\to }\mathcal{N}(0,1).$

(b) 

Under the condition $n{\Lambda }_{2n}^2(\tau )\to \infty$ as $n\to \infty$, it holds that ${\widehat{g}}_n^{\left[I\right]}(\tau )-g(\tau )/{\Lambda }_{2n}(t)\stackrel{D}{\to }\mathcal{N}(0,1).$

Theorem 6.

Assume that (H0)–(H5) and (H7) are fulfilled. Given τ in $[0,1]$,

(a) 

Given ${\Theta }_{1n}^2\ge Cn$, it follows that $R_{3n}^2({\widehat{\beta }}_R-\beta )/{\Theta }_{3n}\stackrel{D}{\to }\mathcal{N}(0,1).$

(b) 

Under the condition $n{\Lambda }_{3n}^2(\tau )\to \infty$ as $n\to \infty$, it holds that ${\widehat{g}}_n^{\left[R\right]}(\tau )-g(\tau )/{\Lambda }_{3n}(\tau )\stackrel{D}{\to }\mathcal{N}(0,1).$

4. Simulation Study

The main focus of this investigation is to assess how well the proposed estimators perform when dealing with finite samples using simulated data. Specifically, our investigation focuses on the following two aspects:

(i)

To evaluate the efficacy of three estimators for $\beta$ $\left({\widehat{\beta }}_c,{\widehat{\beta }}_I,{\widehat{\beta }}_R\right)$ and three estimators for $g(·)$ $\left({\widehat{g}}_n^c(\tau ),{\widehat{g}}_n^{\left[I\right]}(\tau ),{\widehat{g}}_n^{\left[R\right]}(\tau )\right)$. For the $\beta$ estimators, the performance metric utilized in this study is the MSE. For the estimators of $g(·)$, the assessment is carried out using the GMSE as the evaluation criterion.

(ii)

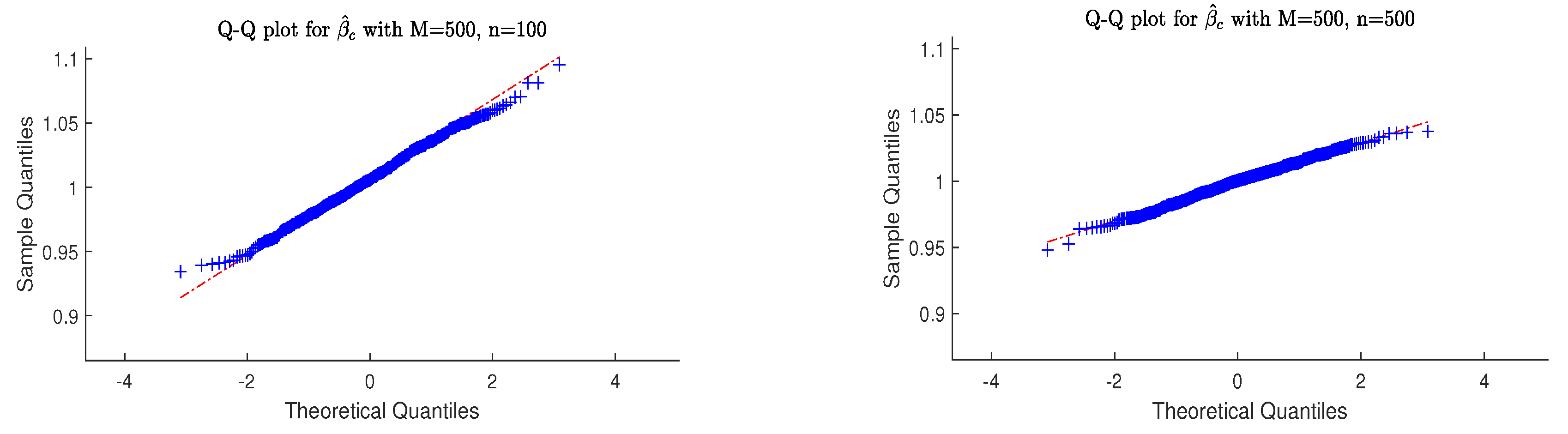
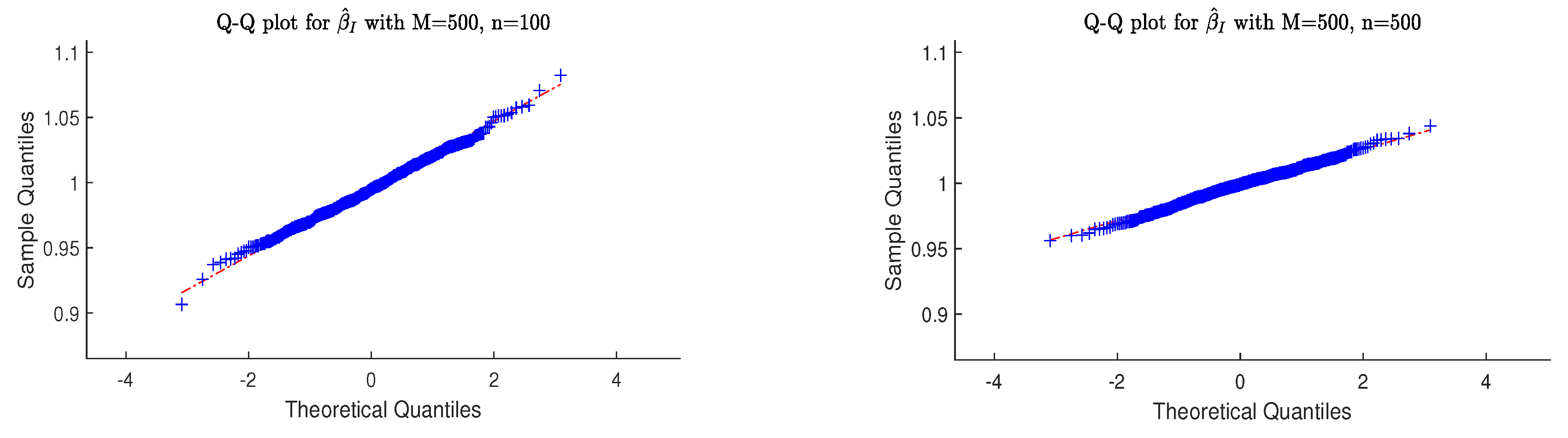
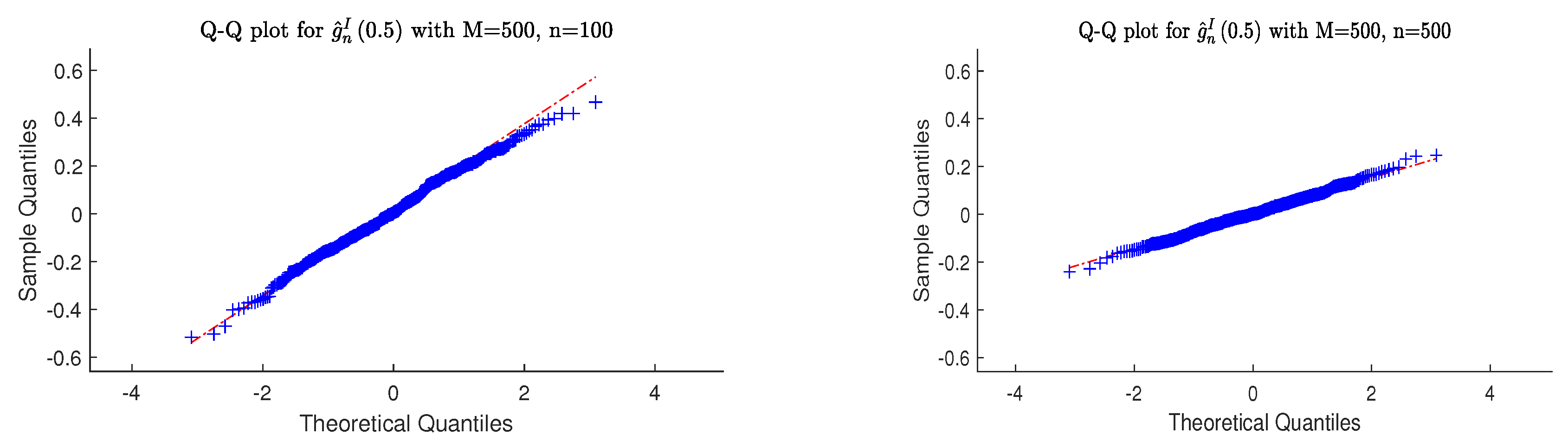
Q-Q plots are utilized to graphically represent and compare the distributional properties of the three estimators for $\beta$ and $g(·)$ are presented.

To conduct the simulation study, we designed the following data generation process for the observation $i=1,2,\cdots ,n$. The variables ${\eta }_i$ and ${\xi }_i$ are generated as follows:

$${\eta }_i=x_i+sin\left(2\pi {\tau }_i\right)+{\epsilon }_i,{\xi }_i=x_i+{\delta }_i$$

Simply put, we have $\beta =1$, ${\tau }_i={\displaystyle \frac{i-0.5}{n}}$, $x_i={\tau }_i^2+{\mu }_i$ with ${\mu }_i={\displaystyle \frac{sin\left(i\right)}{n^{1/3}}}$ for $1⩽i⩽n$. The sequence ${\left\{{\mu }_i\right\}}_{i=1}^n$ consists of independent and identically distributed random variables, all adhering to a normal distribution $N(0,0.2^2)$. Additionally, ${\left\{{ϵ}_i\right\}}_{i=1}^n$ represents a strong mixing sequence. Assume that the sequence ${\left\{{ϵ}_i\right\}}_{i=1}^n$ is governed by a multivariate normal distribution with expected values $E\left({ϵ}_1,\cdots ,{ϵ}_n\right)=\left(0,\cdots ,0\right)$, covariance $Cov\left({ϵ}_i,{ϵ}_j\right)=0.3^{2}exp(-\alpha \left|j-i\right|)$ for $i\ne j$ and variance $Var\left({ϵ}_i\right)=0.3^2$ for $1⩽i⩽n$. The decay function in the covariance decreases exponentially with the absolute difference in indices $\left|j-i\right|$, and is controlled by the parameter $\alpha$. The following are the specified weight functions for the estimators we propose:

$$V_{nk}^c\left(\tau \right)={\displaystyle \frac{Q\left(\frac{\tau -{\tau }_i}{a_n}\right)}{{\sum }_{k=1}^n{\rho }_{k}Q\left(\frac{\tau -{\tau }_k}{a_n}\right)}},V_{nk}\left(\tau \right)={\displaystyle \frac{T\left(\frac{\tau -{\tau }_i}{d_n}\right)}{{\sum }_{k=1}^{n}T\left(\frac{\tau -{\tau }_k}{d_n}\right)}}.$$

Here, $Q(·)$ and $T(·)$ refer to Gaussian kernels, $a_n$ and $d_n$ are defined as the corresponding bandwidths.

4.1. MSE/GMSE Evaluation for $\beta$ and $g(·)$ Estimators

In this section, datasets were generated with the sample size sets $n=100$, $n=300$, and $n=500$. We assumed that the response variables had missing probabilities of $p=0.1$, 0.25, and 0.5 based on $M=500$ replications. For the estimation of $\beta$ and the function $g\left(·\right)$, the corresponding MSE and GMSE of the estimators are

$$\mathrm{MSE}\left(\widehat{\beta }\right)={\displaystyle \frac{1}{M}}\sum _{l=1}^M{[\widehat{\beta }\left(l\right)-\beta ]}^2,\mathrm{GMSE}\left(\widehat{g}\left(·\right)\right)={\displaystyle \frac{1}{Mn}}\sum _{l=1}^M\sum _{k=1}^n{\left[\widehat{g}\left({\tau }_k,l\right)-g\left({\tau }_k\right)\right]}^2$$

For each estimator, we compute the Mean Squared Error (MSE) or Generalized Mean Squared Error (GMSE) using $M=500$ replications. The bandwidth grids, denoted as $a_n$ and $d_n$, range from 0 to 1 and are discretized into 20 points with a step size of 0.05. We then proceed to select the bandwidths that yield the smallest MSE or GMSE. The results for the smallest MSE and GMSE obtained with $\alpha =0.1$ and $\alpha =0.3$ are presented below, respectively.

By referring to

Table 1. The MSE comparison for three estimators of $\beta$ with $\alpha =0.1$ and $\alpha =0.3$.

n	p	${\widehat{\mathit{\beta }}}_{\mathit{c}}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{\beta }}}_{\mathit{c}}(\mathit{\alpha }=\mathbf{0.3})$	${\widehat{\mathit{\beta }}}_{\mathit{I}}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{\beta }}}_{\mathit{I}}(\mathit{\alpha }=\mathbf{0.3})$	${\widehat{\mathit{\beta }}}_{\mathit{R}}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{\beta }}}_{\mathit{R}}(\mathit{\alpha }=\mathbf{0.3})$
100	0.1	$5.2900\times {10}^{-4}$	$7.8500\times {10}^{-4}$	$4.2470\times {10}^{-4}$	$5.9300\times {10}^{-4}$	$3.7200\times {10}^{-4}$	$5.0100\times {10}^{-4}$
300	0.1	$3.5000\times {10}^{-4}$	$4.3800\times {10}^{-4}$	$2.9600\times {10}^{-4}$	$3.7300\times {10}^{-4}$	$2.6800\times {10}^{-4}$	$3.5500\times {10}^{-4}$
500	0.1	$1.4100\times {10}^{-4}$	$2.4100\times {10}^{-4}$	$1.3690\times {10}^{-4}$	$2.0900\times {10}^{-4}$	$1.1590\times {10}^{-4}$	$1.9900\times {10}^{-4}$
100	0.25	$8.4900\times {10}^{-4}$	$1.6000\times {10}^{-3}$	$7.4200\times {10}^{-4}$	$1.4200\times {10}^{-3}$	$7.0100\times {10}^{-4}$	$1.3000\times {10}^{-3}$
300	0.25	$5.9000\times {10}^{-4}$	$6.5200\times {10}^{-4}$	$3.1800\times {10}^{-4}$	$4.0790\times {10}^{-4}$	$4.2300\times {10}^{-4}$	$3.9400\times {10}^{-4}$
500	0.25	$2.2800\times {10}^{-4}$	$3.3790\times {10}^{-4}$	$1.8000\times {10}^{-4}$	$2.2760\times {10}^{-4}$	$2.6700\times {10}^{-4}$	$2.9500\times {10}^{-4}$
100	0.5	$1.7300\times {10}^{-3}$	$1.8300\times {10}^{-3}$	$1.2000\times {10}^{-3}$	$1.500\times {10}^{-3}$	$1.2400\times {10}^{-3}$	$1.6000\times {10}^{-3}$
300	0.5	$3.8500\times {10}^{-4}$	$8.2600\times {10}^{-4}$	$3.3200\times {10}^{-4}$	$6.1200\times {10}^{-4}$	$3.3900\times {10}^{-4}$	$6.4500\times {10}^{-4}$
500	0.5	$3.8300\times {10}^{-4}$	$4.2000\times {10}^{-4}$	$2.5000\times {10}^{-4}$	$3.3700\times {10}^{-4}$	$3.1000\times {10}^{-4}$	$3.3500\times {10}^{-4}$

and

Table 2. The MSE comparison for three estimators of $g(\tau )$ with $\alpha =0.1$ and $\alpha =0.3$.

n	p	${\widehat{\mathit{g}}}_{\mathit{n}}^{\mathit{c}}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{g}}}_{\mathit{n}}^{\mathit{c}}(\mathit{\alpha }=\mathbf{0.3})$	${\widehat{\mathit{g}}}_{\mathit{n}}^{\left[\mathit{I}\right]}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{g}}}_{\mathit{n}}^{\left[\mathit{I}\right]}(\mathit{\alpha }=\mathbf{0.3})$	${\widehat{\mathit{g}}}_{\mathit{n}}^{\left[\mathit{R}\right]}(\mathit{\alpha }=\mathbf{0.1})$	${\widehat{\mathit{g}}}_{\mathit{n}}^{\left[\mathit{R}\right]}(\mathit{\alpha }=\mathbf{0.3})$
100	0.1	$2.6900\times {10}^{-2}$	$3.5800\times {10}^{-2}$	$2.4400\times {10}^{-2}$	$3.4700\times {10}^{-2}$	$2.6200\times {10}^{-2}$	$3.4500\times {10}^{-2}$
300	0.1	$3.4700\times {10}^{-3}$	$1.9800\times {10}^{-2}$	$3.3200\times {10}^{-3}$	$1.6100\times {10}^{-2}$	$3.2700\times {10}^{-3}$	$1.6100\times {10}^{-2}$
500	0.1	$2.6100\times {10}^{-3}$	$1.5100\times {10}^{-2}$	$2.3700\times {10}^{-3}$	$1.1700\times {10}^{-2}$	$2.3500\times {10}^{-3}$	$1.1500\times {10}^{-2}$
100	0.25	$2.9000\times {10}^{-2}$	$3.9500\times {10}^{-2}$	$2.6600\times {10}^{-2}$	$3.5300\times {10}^{-2}$	$2.8300\times {10}^{-2}$	$3.6200\times {10}^{-2}$
300	0.25	$3.6500\times {10}^{-3}$	$2.1100\times {10}^{-2}$	$3.3400\times {10}^{-3}$	$1.7700\times {10}^{-2}$	$3.3300\times {10}^{-3}$	$1.8200\times {10}^{-2}$
500	0.25	$2.7200\times {10}^{-3}$	$1.7700\times {10}^{-2}$	$2.4400\times {10}^{-3}$	$1.3100\times {10}^{-2}$	$2.4000\times {10}^{-3}$	$1.2500\times {10}^{-2}$
100	0.5	$3.1300\times {10}^{-2}$	$4.3400\times {10}^{-2}$	$2.7500\times {10}^{-2}$	$4.0000\times {10}^{-2}$	$2.9400\times {10}^{-2}$	$4.1000\times {10}^{-2}$
300	0.5	$3.8500\times {10}^{-3}$	$2.3800\times {10}^{-2}$	$3.3500\times {10}^{-3}$	$2.0800\times {10}^{-2}$	$3.3900\times {10}^{-3}$	$2.0500\times {10}^{-2}$
500	0.5	$2.8300\times {10}^{-3}$	$1.8700\times {10}^{-2}$	$2.5000\times {10}^{-3}$	$1.7400\times {10}^{-2}$	$2.6500\times {10}^{-3}$	$1.8200\times {10}^{-2}$

, one can observe the following:

(i)

All estimators demonstrated notably strong consistency.

(ii)

For every fixed n, a higher missing probability led to an increased MSE or GMSE for every estimator considered.

(iii)

For every fixed p, a larger sample size n brought about a reduction in both the MSE and GMSE for every estimator considered.

(iv)

Compared to $\alpha =0.1$, almost all estimators showed a rise in both MSE and GMSE when $\alpha =0.3$.

(v)

In comparison to ${\widehat{\beta }}_c$, the estimated values of ${\widehat{\beta }}_I$ and ${\widehat{\beta }}_R$ exhibited a greater proximity to the real value, suggesting that addressing incomplete data is indeed beneficial. A similar result was observed for the estimators of $g\left(·\right)$.

4.2. Simulation Evidence for Asymptotic Normality

Below, we focus on this subsection, where we have developed quantile–quantile plots to illustrate the behavior of $\beta$ and $g\left(·\right)$, using the parameter $\alpha$ = 0.3. We investigate the performance of all estimators for $\beta$ and $g(·)$ under the conditions $p=0.25$ with sample sizes of $n=100,500$. In Figure 1, Figure 2 and Figure 3, Q-Q plots are showcased for the estimators ${\widehat{\beta }}_c$, ${\widehat{\beta }}_I$, and ${\widehat{\beta }}_R$ with sample sizes of 100 and 500. Additionally, in Figure 4, Figure 5 and Figure 6, Q-Q plots are presented for the estimators ${\widehat{g}}_n^c\left(0.5\right)$, ${\widehat{g}}_n^{\left[I\right]}(0.5)$, and ${\widehat{g}}_n^{\left[R\right]}\left(0.5\right)$ with sample sizes of 100 and 500, respectively. In all Q-Q plots, the blue points represent the sample quantiles, and the red dashed line indicates the theoretical normal distribution for comparison. This visualization helps to evaluate how closely the estimated values follow a normal distribution.

By examining Figure 1 through Figure 6, the following become evident:

(i)

Derived from a sample size of 500, the estimated values for $\beta$ and $g\left(0.5\right)$ closely resemble a normal distribution, indicating asymptotic normality.

(ii)

As sample size increases from 100 to 500, all estimators’ sample variances decrease, reflecting improved precision and stability in larger datasets.

(iii)

The simulation outcomes corroborated the findings predicted by our theory.

5. Preliminary Lemmas

In the following section, we use the notation $C,C_1,\dots$ to represent various finite positive constants, each assigned a distinct value based on the specific context. We then present several essential lemmas vital for proving our main results. Consider a sequence of random variables, denoted as ${\left\{Y_i\right\}}_{i=1}^n$, which exhibit strong mixing properties with associated mixing coefficients given by $\left\{\alpha \left(n\right)\right\}$.

Lemma 1

(Härdle et al. [23], Lemma A.3). Consider a sequence of n independent random variables $X_1,\cdots ,X_n$, each having zero mean, finite variance and s-th moments uniformly bounded for some $s>2$. Given a sequence $\{b_{kj},k,j=1,\cdots ,n\}$ satisfying ${sup}_{1⩽j,k⩽n}|b_{kj}|=O\left(n^{-q_1}\right)$ with $0<q_1<1$ and ${\sum }_{i=1}^n{b}_{ij}=O\left(n^{q_2}\right)$ for $q_2⩾max\left(0,2/s-q_1\right)$. Then,

$${\displaystyle \underset{1⩽j⩽n}{max}}|\sum _{k=1}^n{b}_{kj}{X}_k|=O\left(n^{-\left(q_1-q_2\right)/2}logn\right)a.s.$$

Lemma 2

(Xu Bing [24]). Consider a sequence of strongly mixing random variables $\left\{Y_i\right\}$, such that $E{Y}_i=0$ and $su{p}_{i⩾1}E{\left|Y_i\right|}^q<\infty$ for $q>2$. Suppose that the mixing coefficients $\alpha \left(n\right)$ and the real-valued sequences $\{b_{ni}{\}}_{i=1}^n$ satisfy the conditions:

$$\sum _{n=1}^{\infty }{\left(\sum _{i=1}^n{b}_{ni}^{2}logn\right)}^{q/2}<\infty$$

$$\sum _{n=1}^{\infty }\alpha {\left(n\right)}^{\left(q-2\right)/q}<\infty .$$

Under these assumptions, it follows that

$$\sum _{i=1}^{\infty }{b}_{ni}{Y}_i=o\left(1\right)a.s.$$

Lemma 3

(Volkonskii and Rozanov [25]). Consider a collection of strongly mixing random variables $\{Y_1,\cdots ,Y_m\}$, each associated with a distinct σ-algebra ${\mathcal{F}}_{r_j}^{s_j}$ that satisfies the conditions $1\le r_1<s_1<\cdots <s_m\le N$ and $r_{j+1}-s_j\ge \gamma \ge 1$. Assume that each $Y_j$ satisfies the inequality $-1\le Y_j\le 1$. Then,

$$\left|\mathbb{E}\left(\prod _{j=1}^m{Y}_j\right)-\prod _{j=1}^m\mathbb{E}{Y}_j\right|\le 16(m-1)\rho (\gamma ),$$

where $\rho (\gamma )$ represents the mixing coefficient associated with the gap γ, and ${\mathcal{F}}_{r_j}^{s_j}$ denotes the σ-algebra generated by the random variables $\{Y_i:r_j\le i\le s_j\}$.

Lemma 4

(Hall and Heyde [26]). Suppose we have two random variables, denoted as U and V, which fulfill the conditions that ${E|U|}^r<\infty$, ${E|V|}^s<\infty$, where $r,s>1$ are such that $r^{-1}+s^{-1}<1$. Thus,

$$|EUV-EUEV|⩽{8\parallel U\parallel }_r{\parallel V\parallel }_s{\left\{\underset{C\in \sigma (U),D\in \sigma (V)}{sup}|P(CD)-P(C)P(D)|\right\}}^{1-r^{-1}-s^{-1}}.$$

Lemma 5

(Yang [27], Therorem 2.2).

(a) 

Given $v>2$, $\gamma >0$, the assumptions $\mathbb{E}\left[Y_i\right]=0$ and $\mathbb{E}[|Y_i{|}^{v+\gamma }]<\infty$ as well as $\lambda >{\displaystyle \frac{v(v+\gamma )}{2\gamma }}$ and $\alpha (n)=O(n^{-\lambda })$, it follows that for any arbitrarily small positive number η, a constant $(C)$ exists, which is dependent on $(\eta ,v,\gamma ,\lambda )$, such that the following inequality holds:

$$\mathbb{E}\left[\underset{1\le m\le n}{max}{\left|\sum _{i=1}^m{Y}_i\right|}^s\right]\le C\left\{n^{\eta }\sum _{i=1}^n\mathbb{E}[|Y_i{|}^r]+{\left(\sum _{i=1}^n{\parallel Y_i\parallel }_{v+\gamma }^2\right)}^{{\displaystyle \frac{s}{2}}}\right\}.$$

(b) 

Assume that $\mathbb{E}\left[Y_i\right]=0$ and $\mathbb{E}[|Y_i{|}^{2+\gamma }]<\infty$ when $\gamma >0$, we have

$$\mathbb{E}\left[{\left(\sum _{i=1}^n{Y}_i\right)}^2\right]\le \left[1+16\sum _{l=1}^n{\alpha }^{{\displaystyle \frac{\gamma }{2+\gamma }}}(l)\right]\sum _{i=1}^n{\parallel Y_i\parallel }_{2+\gamma }^2.$$

In this case, by setting $r=v=2+\gamma$, the proof for (b) is directly obtainable from the Lemma 4.

Lemma 6.

Let $\left\{Y_i\right\}$ be stationary with $E{Y}_i=0$ and $E|Y_1{|}^p<\infty$ for a certain $p>2$. Suppose further that $\alpha (n)$ decreases at a rate of $O\left(n^{-\lambda }\right)$ for some positive λ. Consider an array of real numbers $\left\{b_{ni},1⩽i⩽n,n⩾1\right\}$ which satisfies the conditions that ${max}_{1⩽i⩽n}\left|b_{ni}\right|=O\left(n^{-u}\right)$ for some $u>0$ and ${\sum }_{i=1}^n\left|b_{ni}\right|=O\left(1\right)$. Let $p=4+2\rho$ for some $\rho >0$. If $\lambda >v\left(v+\rho \right)/2\rho$ for some $v>p$. ${max}_{1⩽i⩽n}\left|b_{ni}\right|=O\left(n^{-u}{L}_1(n)\right)$ and $\left|{\sum }_{i=1}^m{b}_{ni}^2\right|=O\left(n^{-\tau }\right)$ for a positive τ, then

$$\left|\sum _{i=1}^n{b}_{ni}{Y}_i\right|=o_p\left(n^{-\psi }\right)$$

for $\psi <min\{1-1/p,u,u-1/p+\left(\tau -2u+1\right)/v,\tau /2-1/p-\rho /\left[v\left(v+\rho \right)\right]+{\displaystyle \frac{1}{v}}\}$.

Here, $L_1\left(x\right)$ is a positive slowly varying function as $n\to \infty$.

Lemma 7

(Zhang et al. [28]).

(a) 

Let ${\tilde{L}}_i=L({\tau }_i)-{\sum }_{k=1}^n{V}_{nk}({\tau }_i)L({\tau }_k)$, where $L(·)$ can be eithor $g(·)$ or $f(·)$. Let ${\tilde{L}}_i^c=L({\tau }_i)-{\sum }_{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i)L({\tau }_k)$, where $L(·)=g(·)$ or $f(·)$. According to conditions (H0)–(H4), it follows that $\underset{1\le i\le n}{max}|{\tilde{L}}_i|=o\left(n^{-1/4}\right)$ and ${\displaystyle \underset{1\le i\le n}{max}}|{\tilde{L}}_i^c|=o\left(n^{-1/4}\right)$.

(b) 

Based on (H0)–(H4), we conclude that $n^{-1}{\sum }_{i=1}^n{\tilde{x}}_i^2\to {\Delta }_0$, $n^{-1}{\sum }_{i=1}^n{\rho }_i{({\tilde{x}}_i^c)}^2\to {\Delta }_1$, ${\sum }_{i=1}^n|{\tilde{x}}_i|⩽C_{1}n$, and ${\sum }_{i=1}^n|{\rho }_i{\tilde{x}}_i^c|⩽C_{2}n$.

6. Proof of Main Results

6.1. Proof of Strong Consistency

Proof of Theorem 1(a).

Taking into account (3), we may conclude that

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_c-\beta & =& R_{1n}^{-2}\{\sum _{i=1}^n{\rho }_i{\widetilde{{\xi }_i}}^c({\widetilde{{\eta }_i}}^c-{\widetilde{{\xi }_i}}^c\beta )+\sum _{i=1}^n{\rho }_i{\Xi }_{\delta }^2\beta \}\hfill \\ & =& R_{1n}^{-2}\left\{\sum _{i=1}^n\left[{\rho }_i({\tilde{x}}_i^c+{\tilde{\delta }}_i^c)({\widetilde{ϵ}}_i^c-{\tilde{\delta }}_i^c\beta )+{\rho }_i{\Xi }_{\delta }^2\beta \right]+\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c{\tilde{g}}_i^c+\sum _{i=1}^n{\rho }_i{\tilde{\delta }}_i^c{\tilde{g}}_i^c\right\}\hfill \\ & =& R_{1n}^{-2}\{\sum _{i=1}^n\left[{\rho }_i({\tilde{x}}_i^c+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+{\rho }_i{\Xi }_{\delta }^2\beta \right]+\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c{\tilde{g}}_i^c+\sum _{i=1}^n{\rho }_i{\tilde{\delta }}_i^c{\tilde{g}}_i^c\hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{\rho }_i{\rho }_k{V}_{nk}^c({\tau }_i){\tilde{x}}_i^c{ϵ}_k+\sum _{i=1}^n\sum _{k=1}^n{\rho }_i{\rho }_k{V}_{nk}^c({\tau }_i){\tilde{x}}_i^c{\delta }_k\beta \hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{\rho }_i{\rho }_k{V}_{nk}^c({\tau }_i){ϵ}_i{\delta }_k-\sum _{i=1}^n\sum _{k=1}^n{\rho }_i{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_i{ϵ}_k+\sum _{i=1}^n\sum _{k=1}^n\sum _{j=1}^n{\rho }_i{\rho }_k{\rho }_j{V}_{nk}^c({\tau }_i)V_{nj}^c({\tau }_i){\delta }_k{ϵ}_j\hfill \\ & & +2\sum _{i=1}^n\sum _{k=1}^n{\rho }_i{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_i{\delta }_k\beta -\sum _{i=1}^n\sum _{k=1}^n\sum _{j=1}^n{\rho }_i{\rho }_k{\rho }_j{V}_{nk}^c({\tau }_i)V_{nj}^c({\tau }_i){\delta }_k{\delta }_j\beta \}\hfill \\ & :=& R_{1n}^{-2}\sum _{k=1}^{10}{A}_n.\hfill \end{array}$$

(11)

Therefore, in order to verify Theorem 1(a), we firstly deduce, almost surely, based on (11), $R_{1n}^{-2}-R_n^{-2}\to 0$. Furthermore, for each l in the set $\{1,2,\cdots ,10\}$, we show that $n^{-1}{A}_{ln}=o(n^{-{\displaystyle \frac{1}{4}}})$, almost surely.

Stage 1. We demonstrate that $R_{1n}^{-2}-R_n^{-2}\to 0\mathrm{a}.\mathrm{s}.$ Also, keep in mind that

$$\begin{array}{ccc}\hfill R_{1n}^2& =& \sum _{i=1}^n\left[{\rho }_i{({\tilde{x}}_i^c+{\tilde{\delta }}_i^c)}^2-{\rho }_i{\Xi }_{\delta }^2\right]\hfill \\ & =& \sum _{i=1}^n{\rho }_i{({\tilde{x}}_i^c)}^2+\sum _{i=1}^n{\rho }_i\left[{\left({\tilde{\delta }}_i^c\right)}^2-{\Xi }_{\delta }^2\right]+2\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c{\tilde{\delta }}_i^c\hfill \\ & =& \sum _{i=1}^n{\rho }_i{({\tilde{x}}_i^c)}^2+\sum _{i=1}^n{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)+2\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c{\delta }_i\hfill \\ & & +\sum _{i=1}^n{\rho }_i{\left[\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){\delta }_k\right]}^2-2\sum _{i=1}^n{\rho }_i{\delta }_i\sum _{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_k-2\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c\sum _{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_k\hfill \\ & :=& R_n^2+R_{11n}+2R_{12n}+R_{13n}-2R_{14n}-2R_{15n}.\hfill \end{array}$$

Using Lemma 7(b), one can determine that $n^{-1}{R}_n^2\to {\Delta }_1$. Therefore, it is enough to confirm that $R_{1kn}=o(n)$ a.s. over the range $k=1$ to 5. Let $s=2+\delta$, $q_1=0$, and $q_2=1$ in Lemma 1. By applying assumption (H0), we have that $R_{11n}=o(n)$ a.s. Next, by choosing $s=4+2\delta$, $q_1=1/4$, and $q_2=1/4$ in Lemma 1 and applying assumption (H0), (H1), and (H3), it can be concluded that

$$\begin{array}{c}\hfill |R_{12n}|=n^{{\displaystyle \frac{3}{4}}}·|\sum _{i=1}^n{n}^{-{\displaystyle \frac{3}{4}}}{\rho }_i{\tilde{x}}_i^c{\delta }_i|=o(n)\mathrm{a}.\mathrm{s}.\end{array}$$

(12)

similarly to (12). With the help of Lemma 1 and the assumption (H0)(i) and (H3)(i)(iii), it is obvious that

$$\begin{array}{c}\hfill \underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){\delta }_k|=O\left(n^{-{\displaystyle \frac{1}{4}}}logn\right)\mathrm{a}.\mathrm{s}.,\sum _{i=1}^n(|{\delta }_i|-E|{\delta }_i|)=o(n)\mathrm{a}.\mathrm{s}.\end{array}$$

(13)

By referring to Lemma 7(b) and considering assumption (H0)(i), (H3)(i)(ii)(iii), as well as (13). One can determine that

$$\begin{array}{ccc}\hfill |R_{13n}|& ⩽& \sum _{i=1}^n|{\rho }_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_k{|}^2=O(n^{1/2}{log}^{2}n)=o(n)\mathrm{a}.\mathrm{s}.\hfill \\ \hfill |R_{14n}|& ⩽& 2\left[\sum _{i=1}^{n}E|{\rho }_i{\delta }_i|+\sum _{i=1}^n(|{\rho }_i{\delta }_i|-E|{\rho }_i{\delta }_i|)\right]·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_k|=o(n)\mathrm{a}.\mathrm{s}.\hfill \\ \hfill |R_{15n}|& ⩽& 2\sum _{i=1}^n|{\rho }_i{\tilde{x}}_i^c|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c({\tau }_i){\delta }_k|=o(n)\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

Therefore, one can deduce that $R_{1n}^2=R_n^2+o(n)=R_n^2+o(R_n^2)\mathrm{a}.\mathrm{s}.$, which yields $R_{1n}^{-2}⩽C{n}^{-1}\mathrm{a}.\mathrm{s}.$

Stage 2. Note the following:

$$\begin{array}{ccc}\hfill A_{1n}& =& \sum _{i=1}^n{\rho }_i({\tilde{x}}_i^c+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+\sum _{i=1}^n{\rho }_i{\Xi }_{\delta }^2\beta \hfill \\ & =& \sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c({ϵ}_i-{\delta }_i\beta )+\sum _{i=1}^n{\rho }_i{\delta }_i{ϵ}_i-\sum _{i=1}^n{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)\beta \hfill \\ & :=& A_{11n}+A_{12n}+A_{13n}\hfill \end{array}$$

Based on (H0), the sequence ${\{{\chi }_i={ϵ}_i-{\delta }_i\beta \}}_{i=1}^n$ exhibits strong mixing and has a mean of zero, where $p=4+2\rho$. We can take $\rho >0$, $u=1/2$, $\tau =1$, and $v=4+3\rho$ in Lemma 6. Consequently,

$$\begin{array}{c}\hfill n^{-1}{A}_{11n}=n^{-1}\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c({ϵ}_i-{\delta }_i\beta ):=\sum _{i=1}^n{\rho }_i{Q}_{in}{\chi }_i,\\ \hfill \underset{1⩽i⩽n}{max}|Q_{in}|⩽n^{-1}\underset{1⩽i⩽n}{max}|{\tilde{x}}_i^c|=o(n^{-1/2})\\ \hfill \sum _{i=1}^n{Q}_{in}^2=n^{-2}\sum _{i=1}^n{\tilde{x}}_i^{c^2}=O\left(n^{-1}\right)\end{array}$$

Then,

$$\begin{array}{c}\hfill n^{-1}{A}_{11n}=n^{-1}\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c({ϵ}_i-{\delta }_i\beta )=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\end{array}$$

(14)

The sequence ${\left\{{\delta }_i{ϵ}_i\right\}}_{i=1}^n$ consists of strongly mixing random variables. Let $q=4+2\eta >2$ and $b_{ni}=n^{-3/4}$ in Lemma 2. We then obtain that ${\sum }_{n=1}^{\infty }{({\sum }_{i=1}^{\infty }(b_{ni}^{2}logn)}^{q/2}<\infty$ and ${\sum }_{n=1}^{\infty }\alpha {(n)}^{(q-2)/q}<\infty$; therefore,

$$\begin{array}{c}\hfill n^{-1}{A}_{12n}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\delta }_i{ϵ}_i=n^{-{\displaystyle \frac{1}{4}}}·n^{-3/4}\sum _{i=1}^n{\delta }_i{ϵ}_i=o(n^{-{\displaystyle \frac{1}{4}}})\mathrm{a}.\mathrm{s}.\end{array}$$

(15)

From (H0) to (H3) and let $q_1=1$ and $q_2=0$ in Lemma 1, we obtain

$$\begin{array}{ccc}\hfill n^{-1}{A}_{13n}& ⩽& {\displaystyle \frac{C}{n}}|\sum _{i=1}^n{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)\beta |=O(n^{-{\displaystyle \frac{1}{4}}})\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

(16)

Hence, from (14) to (16), one can deduce that $n^{-1}{A}_{1n}=o(n^{-1/4})\mathrm{a}.\mathrm{s}.$

Stage 3. The results indicate that $n^{-1}{A}_{kn}=o(n^{-1/4})\mathrm{a}.\mathrm{s}.$ over the range $k=2$ to 10. Using the conditions of Theorem 1, and let $u=1/2$, $\tau =3/5$, $\rho =2$, and $v=10$ in Lemma 6 and (H6), this results in

$$\begin{array}{c}\hfill |\sum _{k=1}^n{V}_{nk}^c(\tau ){\rho }_k{ϵ}_k|=o(n^{-1/4})a.s.,|\sum _{k=1}^n{V}_{nk}(\tau ){\rho }_k{ϵ}_k|=o(n^{-1/4})a.s.\end{array}$$

(17)

Thus, by Lemma 7, (13), (17), (H0)–(H3), and Abel’s inequality [23], we prove that

$$\begin{array}{ccc}\hfill n^{-1}{A}_{2n}& ⩽& {\displaystyle \frac{C}{n}}|\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c{\tilde{g}}_i^c|⩽{\displaystyle \frac{C}{n}}\left[\sum _{i=1}^n|{\rho }_i{\tilde{x}}_i^c|·\underset{1⩽i⩽n}{max}|{\tilde{g}}_i^c|\right]=o(n^{-1/4})\hfill \\ \hfill n^{-1}{A}_{3n}& ⩽& {\displaystyle \frac{C}{n}}|\sum _{i=1}^n{\rho }_i{\tilde{\delta }}_i^c{\tilde{g}}_i^c|⩽{\displaystyle \frac{C}{n}}\left[\sum _{i=1}^n|{\delta }_i|·|{\rho }_i{\tilde{g}}_i^c|+\sum _{i=1}^n|{\rho }_i{\tilde{g}}_i^c|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){\delta }_k|\right]\hfill \\ & ⩽& {\displaystyle \frac{C}{n}}·\left(\sum _{i=1}^n(|{\delta }_i|-E|{\delta }_i|)+\sum _{i=1}^{n}E|{\delta }_i|\right)·\underset{1⩽i⩽n}{max}|{\rho }_i{\tilde{g}}_i^c|+o(n^{-{\displaystyle \frac{1}{2}}}logn)=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{A}_{4n}& ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n{\rho }_i(\widetilde{f_i}+{\mu }_i-\sum _{j=1}^n{V}_{nj}\left({\tau }_i\right){\mu }_j)\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){ϵ}_k\hfill \\ & ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n{\delta }_i|\widetilde{f_i}|·\underset{1⩽i⩽n}{max}|\sum _{j=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){ϵ}_k|\hfill \\ & +& {\displaystyle \frac{C}{n}}·\underset{1⩽i⩽n}{max}|\sum _{j=1}^m{\mu }_{j_i}|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){ϵ}_k|+o(n^{-1/2}logn)\hfill \\ & & =(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{A}_{5n}& ⩽& {\displaystyle \frac{C}{n}}|\sum _{i=1}^n{\rho }_i{\tilde{x}}_i^c\beta |·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}^c\left({\tau }_i\right){\delta }_k|=O(n^{-1/4}logn)\hfill \\ \hfill n^{-1}{A}_{6n}& ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n|{\rho }_i{ϵ}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}^c\left({\tau }_i\right){\rho }_k{\delta }_k|=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

Similarly, we can demonstrate that $n^{-1}{A}_{kn}=o(n^{-1/4})$ almost surely when $k=7,8,9,10$. As a result, we have proven Theorem 1(a). □

Proof of Theorem 2(a).

Based on Equations (5) and (6), one can write the following:

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_I-\beta & =& R_{2n}^{-2}\{\sum _{i=1}^n{\tilde{x}}_i(x_i+{\delta }_i)(1-{\rho }_i)({\widehat{\beta }}_c-\beta )+\sum _{i=1}^n(1-{\rho }_i){\tilde{\delta }}_i(x_i+{\delta }_i)({\widehat{\beta }}_c-\beta )\hfill \\ & & -\sum _{i=1}^n(1-{\rho }_i){\tilde{x}}_i[g({\tau }_i)-{\widehat{g}}_n^c({\tau }_i)]-\sum _{i=1}^n(1-{\rho }_i){\tilde{\delta }}_i[g({\tau }_i)-{\widehat{g}}_n^c({\tau }_i)]\hfill \\ & & +\sum _{i=1}^n{\rho }_i{\tilde{x}}_i({ϵ}_i-{\delta }_i\beta )-\sum _{i=1}^n{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)\beta +\sum _{i=1}^n{\tilde{\delta }}_i{\tilde{g}}_i^c+\sum _{i=1}^n{\tilde{x}}_i{\tilde{g}}_i^c.\hfill \\ & & +\sum _{i=1}^n{\rho }_i{\delta }_i{ϵ}_i-\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{x}}_i(x_k+{\delta }_k)({\widehat{\beta }}_c-\beta ).\hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{\delta }}_i(x_k+{\delta }_k)({\widehat{\beta }}_c-\beta )\hfill \\ & & +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{x}}_i[g({\tau }_k)-{\widehat{g}}_n^c({\tau }_k)]\hfill \\ & & +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{\delta }}_i[g({\tau }_k)-{\widehat{g}}_n^c({\tau }_k)]\hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\tilde{x}}_i{ϵ}_k+\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\tilde{x}}_i{\delta }_k\beta \hfill \\ & & +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_i{\delta }_i{\delta }_k\beta +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\delta }_i{\delta }_k\beta \hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n\sum _{j=1}^n{V}_{nk}({\tau }_i)V_{nj}({\tau }_i){\rho }_k{\delta }_k{\delta }_j\beta -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_i{\delta }_k{ϵ}_i\hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\delta }_i{ϵ}_k+\sum _{j=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)V_{nj}({\tau }_i){\rho }_k{\delta }_j{ϵ}_k\}\hfill \\ & :=& R_{2n}^{-2}\sum _{k=1}^{21}{D}_{kn}\hfill \end{array}$$

Similar to $S_{1n}^{-2}⩽C{n}^{-1}\mathrm{a}.\mathrm{s}.$ in the proof of Theorem 1(a), we can establish that $S_{2n}^{-2}⩽C{n}^{-1}\mathrm{a}.\mathrm{s}.$ Hence, it is sufficient to confirm that $n^{-1}{D}_{kn}=o(n^{-1/4})$ a.s. over the range $k=1$ to 21. Utilizing (H0)–(H4), Lemmas 1, 2, and 7, as well as Theorem 1(a) and Equations (12)–(17), we derive that

$$\begin{array}{ccc}\hfill n^{-1}{D}_{1n}& =& n^{-1}\sum _{i=1}^n{\tilde{x}}_i^2\left(1-{\rho }_i\right)({\widehat{\beta }}_c-\beta )+n^{-1}\sum _{i=1}^n|{\tilde{x}}_i\left(1-{\rho }_i\right)|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)x_k|({\widehat{\beta }}_c-\beta )\hfill \\ & & +n^{-1}|\sum _{i=1}^n{\tilde{x}}_i{\delta }_i(1-{\rho }_i)|({\widehat{\beta }}_c-\beta )=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{2n}& =& n^{-1}\sum _{i=1}^n{\tilde{\delta }}_i(1-{\rho }_i)(x_i+{\delta }_i)({\widehat{\beta }}_c-\beta )⩽n^{-1}|\sum _{i=1}^n(1-{\rho }_i)x_i{\delta }_i|·|{\widehat{\beta }}_c-\beta |\hfill \\ & & +n^{-1}|\sum _{i=1}^n(1-{\rho }_i)({\delta }_i^2-{\Xi }_{\delta }^2)|·|{\widehat{\beta }}_c-\beta |+{\displaystyle \frac{C}{n}}\sum _{i=1}^n(1-{\rho }_i)·|{\widehat{\beta }}_c-\beta |\hfill \\ & & +n^{-1}|\sum _{i=1}^n{x}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i){\delta }_k|·|{\widehat{\beta }}_c-\beta |\hfill \\ & & +n^{-1}|\sum _{i=1}^n{\delta }_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i){\delta }_k|·|{\widehat{\beta }}_c-\beta |=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{3n}& ⩽& n^{-1}\left[\sum _{i=1}^n|(1-{\rho }_i){\tilde{x}}_i|·\underset{1⩽i⩽n}{max}|g({\tau }_i)-{\widehat{g}}_n^c({\tau }_i)|\right]=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{5n}& =& n^{-1}\sum _{i=1}^n{\rho }_i{\tilde{x}}_i({ϵ}_i-{\delta }_i\beta )=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{10n}& =& n^{-1}\sum _{i=1}^n|{\tilde{x}}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i)|·\underset{1⩽k⩽n}{max}|f({\tau }_k)+{\mu }_k|·|{\widehat{\beta }}_c-\beta |\hfill \\ & & +n^{-1}\sum _{i=1}^n|{\tilde{x}}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\delta }_k|·|{\widehat{\beta }}_c-\beta |=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{11n}& =& n^{-1}\sum _{i=1}^n|{\tilde{\delta }}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i)|·\underset{1⩽k⩽n}{max}|f({\tau }_k)+{\mu }_k|·|{\widehat{\beta }}_c-\beta |\hfill \\ & & +n^{-1}\sum _{i=1}^n|{\tilde{\delta }}_i|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\delta }_k|·|{\widehat{\beta }}_c-\beta |\hfill \\ & ⩽& n^{-1}\left[\sum _{i=1}^n\left(|{\delta }_i|-E|{\delta }_i|\right)+\sum _{i=1}^{n}E|{\delta }_i|-\sum _{i=1}^n|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k|\right]·o(n^{-{\displaystyle \frac{1}{4}}})+o(n^{-{\displaystyle \frac{1}{4}}})=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{13n}& ⩽& n^{-1}\sum _{i=1}^n\left|{\tilde{\delta }}_i\right|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n\left(1-{\rho }_k\right)V_{nk}\left({\tau }_i\right)|·\underset{1⩽i⩽n}{max}\left|g\left({\tau }_i\right)-{\widehat{g}}_n^c\left({\tau }_i\right)\right|\hfill \\ & ⩽& n^{-1}\left[\sum _{i=1}^n\left(|{\delta }_i|-E|{\delta }_i|\right)+\sum _{i=1}^{n}E|{\delta }_i|-\sum _{i=1}^n|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k|\right]·o(n^{-1/4})=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill n^{-1}{D}_{14n}& ⩽& n^{-1}\sum _{i=1}^n(\widetilde{f_i}+{\mu }_i-\sum _{j=1}^n{V}_{nj}\left({\tau }_i\right){\mu }_j)·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{\rho }_k{V}_{nk}({\tau }_i){ϵ}_k|=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

The almost sure convergence of $n^{-1}{D}_{kn}=o\left(n^{-1/4}\right)$ for $n=4,6,\cdots ,9,12,15,\cdots ,21$ is completely similar. Hence, we have concluded Theorem 2(a). □

Proof of Theorem 2(b).

Based on (5)–(7), it is possible to state that

$$\begin{array}{ccc}\hfill {\widehat{g}}_n^{\left[I\right]}(\tau )-g(\tau )& =& \sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)x_k({\widehat{\beta }}_c-\beta )+\sum _{k=1}^n{V}_{nk}(\tau )x_k(\beta -{\widehat{\beta }}_I)-\sum _{k=1}^n{V}_{nk}(\tau ){\delta }_k(\beta -{\widehat{\beta }}_c)\hfill \\ & & +\sum _{k=1}^n{V}_{nk}(\tau ){\delta }_k(\beta -{\widehat{\beta }}_I)-\sum _{k=1}^n{V}_{nk}(\tau ){\rho }_k{\delta }_k{\widehat{\beta }}_c+\sum _{k=1}^n{V}_{nk}(\tau ){\rho }_k{ϵ}_k\hfill \\ & & +\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)[{\widehat{g}}_n^c({\tau }_k)-g({\tau }_k)]+\sum _{k=1}^n{V}_{nk}(\tau )[g({\tau }_k)-g(\tau )]\hfill \\ & :=& \sum _{k=1}^8{I}_{kn}\hfill \end{array}$$

Thus, it is sufficient to demonstrate that $I_{kn}(\tau )=o(n^{-{\displaystyle \frac{1}{4}}})$ a.s. over the range $k=1$ to 8. Using (H0)–(H4), Lemma 7, Equation (13), and Theorem 1 and Theorem 2(a), we find that

$$\begin{array}{ccc}\hfill I_{1n}(\tau )& ⩽& |\beta -{\widehat{\beta }}_c|·|\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)x_k|⩽|\beta -{\widehat{\beta }}_c|·|\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)[f\left({\tau }_k\right)+{\mu }_k]|\hfill \\ & ⩽& o(n^{-1/4})·\left[|\sum _{k=1}^n{V}_{nk}(\tau )|+\underset{1⩽k⩽n}{max}|V_{nk}(\tau )(1-{\rho }_k)|·\underset{1⩽m⩽n}{max}|\sum _{j=1}^m{\mu }_{k_j}|\right]=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill I_{7n}(\tau )& ⩽& \underset{1⩽k⩽n}{max}|g({\tau }_k)-{\widehat{g}}_n^c({\tau }_k)|·|\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)|=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \\ \hfill I_{8n}(\tau )& ⩽& |\sum _{k=1}^n{V}_{nk}(\tau )(g({\tau }_k)-g(\tau ))|⩽|\sum _{k=1}^n{V}_{nk}(\tau )[g({\tau }_k)-g(\tau )]·I\left(|{\tau }_k-\tau |>a·n^{-1/4}\right)|\hfill \\ & & +|\sum _{k=1}^n{V}_{nk}(\tau )[g({\tau }_k)-g(\tau )]·I\left(|{\tau }_k-\tau |<a·n^{-1/4}\right)|=o(n^{-1/4})\mathrm{a}.\mathrm{s}.\hfill \end{array}$$

By utilizing (17), we demonstrate that $n^{-1}{I}_{kn}\left(\tau \right)=o\left(n^{-1/4}\right)$, which holds almost surely for k values ranging from 2 to 6, is analogous. Therefore, the demonstration of Theorem 2(b) has been finalized. □

Proof of Theorem 1(b).

To establish Theorem 1(b), we employ a proof strategy analogous to that used in our derivation of Theorem 2(b). □

Proof of Theorem 3.

To establish Theorem 3, we employ a proof strategy analogous to that used in our derivation of Theorem 2. □

6.2. Proof of Asymptotic Normality

Proof of Theorem 5(a).

The demonstration of Theorem 4(a) follows a comparable pattern. Next, we proceed to prove Theorem 5(a). Based on (6), it is feasible to express that

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_I-\beta & =& R_{2n}^{-2}\{\sum _{i=1}^n{\rho }_i\left[({\tilde{x}}_i+\left(\Omega +\Phi \right){\tilde{x}}_i^c+\left(1+\Omega +\Phi \right){\delta }_i)\left({ϵ}_i-{\delta }_i\beta \right)+\left(1+\Omega +\Phi \right){\Xi }_{\delta }^2\beta \right].\hfill \\ & & +\left(\Omega +\Phi \right)\sum _{k=4}^{10}{A}_{kn}+\left[\sum _{i=1}^n\sum _{k=1}^n{\tilde{x}}_i\left(1-{\rho }_i\right)V_{nk}\left({\tau }_i\right)x_k.+\sum _{i=1}^n{\tilde{x}}_i\left(1-{\rho }_i\right){\delta }_i\right]({\widehat{\beta }}_c-\beta )\hfill \\ & & +[\sum _{i=1}^n\left(1-{\rho }_i\right)\left({\delta }_i^2-E{\delta }_i^2\right)+\sum _{i=1}^n\left(1-{\rho }_i\right)x_i{\delta }_i-\sum _{i=1}^n\left(1-{\rho }_i\right)x_i\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k.\hfill \\ & & .-\sum _{i=1}^n\left(1-{\rho }_i\right){\delta }_i\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k]({\widehat{\beta }}_c-\beta )-\sum _{i=1}^n\left(1-{\rho }_i\right){\tilde{x}}_i\left(g\left({\tau }_i\right)-{\widehat{g}}_n^c\left({\tau }_i\right)\right)+\sum _{i=1}^n{\tilde{\delta }}_i{\tilde{g}}_i^c+\sum _{i=1}^n{\tilde{x}}_i{\tilde{g}}_i^c\hfill \\ & & -\sum _{i=1}^n\left(1-{\rho }_i\right){\tilde{\delta }}_i\left(g\left({\tau }_i\right)-{\widehat{g}}_n^c\left({\tau }_i\right)\right)-\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{x}}_i(x_k+{\delta }_k)({\widehat{\beta }}_c-\beta ).\hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{\delta }}_i(x_k+{\delta }_k)({\widehat{\beta }}_c-\beta )+\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{x}}_i[g({\tau }_k)-{\widehat{g}}_n^c({\tau }_k)]\hfill \\ & & +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)(1-{\rho }_k){\tilde{\delta }}_i[g({\tau }_k)-{\widehat{g}}_n^c({\tau }_k)]-\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\tilde{x}}_i{ϵ}_k+\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\tilde{x}}_i{\delta }_k\beta \hfill \\ & & +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_i{\delta }_i{\delta }_k\beta +\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\delta }_i{\delta }_k\beta -\sum _{i=1}^n\sum _{k=1}^n\sum _{j=1}^n{V}_{nk}({\tau }_i)V_{nj}({\tau }_i){\rho }_k{\delta }_k{\delta }_j\beta \hfill \\ & & -\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_i{\delta }_k{ϵ}_i-\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i){\rho }_k{\delta }_i{ϵ}_k+\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}({\tau }_i)V_{nj}({\tau }_i){\rho }_k{\delta }_j{ϵ}_k\}\hfill \\ & :=& R_{2n}^{-2}\sum _{k=1}^{20}{D}_{kn}\hfill \end{array}$$

Set ${\omega }_i={\rho }_i\left[({\tilde{x}}_i+\left(\Omega +\Phi \right){\tilde{x}}_i^c+\left(1+\Omega +\Phi \right){\delta }_i)\left({ϵ}_i-{\delta }_i\beta \right)+\left(1+\Omega +\Phi \right){\Xi }_{\delta }^2\beta \right]$, $Z_{ni}={\omega }_i/{\Theta }_{2n}$. With $E{Z}_{ni}=0$, $Var\left({\sum }_{i=1}^n{Z}_{ni}\right)=1$, $E{\left|Z_{ni}\right|}^{2+\delta }<\infty$, based on (H0) and Lemma 7 along with the condition ${\Theta }_{2n}^2⩾Cn$, we utilize Bernstein’s big-block and small-block technique. Setting $k=\left[n/\left(s+r\right)\right]$, we proceed as follows:

$$y_{nb}=\sum _{i=k_b}^{k_b+s-1}{Z}_{ni},y_{nb}^{\prime }=\sum _{i=l_b}^{l_b+r-1}{Z}_{ni},y_{nk+1}^{\prime }=\sum _{i=k\left(s+r\right)+1}^n{Z}_{ni},$$

where $k_b=\left(b+1\right)\left(s+r\right)+1$, $l_b=\left(b+1\right)\left(s+r\right)+s+1$, b ranges from 1 to k. Consequently,

$${\displaystyle \frac{D_{1n}}{{\Theta }_{2n}}}=\sum _{i=1}^n{Z}_{ni}=\sum _{b=1}^k{y}_{nb}+\sum _{b=1}^k{y}_{nb}^{\prime }+y_{nk+1}^{\prime }:=D_n^{\prime }+D_n^{″}+D_n^{‴}$$

To establish that $R_{2n}^2({\widehat{\beta }}_I-\beta )/{\Theta }_{2n}\stackrel{D}{\to }N(0,1)$, it is enough to demonstrate that

$$D_n^{\prime }\stackrel{D}{\to }N\left(0,1\right),E{(D_n^{″})}^2\to 0,E{(D_n^{‴})}^2\to 0,{\displaystyle \frac{D_{kn}}{{\Theta }_{2n}}}\stackrel{P}{\to }0fork=2,\cdots ,20.$$

Stage 1. We demonstrate that $E{(D_n^{″})}^2\to 0$, $E{(D_n^{‴})}^2\to 0$ and $D_n^{\prime }\stackrel{D}{\to }N\left(0,1\right)$. Applying Lemma 5(b), from (H0) to (H3) and (H7), accordingly, we verify that

$$\begin{array}{ccc}\hfill E{(D_n^{″})}^2& ⩽& {\displaystyle \frac{C}{n}}·E[\sum _{b=1}^k\sum _{i=l_b}^{l_b+r-1}{\rho }_i\left[({\tilde{x}}_i+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+{\Xi }_{\delta }^2\beta \right]\hfill \\ & & +\left(\Omega +\Phi \right)\left[\sum _{i=1}^n\sum _{i=l_b}^{l_b+r-1}{\rho }_i\left[({\tilde{x}}_i^c+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+{\Xi }_{\delta }^2\beta \right]\right]{]}^2\hfill \\ & ⩽& {\displaystyle \frac{C_1}{n}}·E{\left[\sum _{b=1}^k\sum _{i=l_b}^{l_b+r-1}{\rho }_i{\tilde{x}}_i{ϵ}_i-{\rho }_i{\tilde{x}}_i{\delta }_i\beta +{\rho }_i{\delta }_i{ϵ}_i-{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)\beta \right]}^2\hfill \\ & & +{\displaystyle \frac{C_2}{n}}·E{\left[\sum _{b=1}^k\sum _{i=l_b}^{l_b+r-1}{\rho }_i{\tilde{x}}_i^c{ϵ}_i-{\rho }_i{\tilde{x}}_i^c{\delta }_i\beta +{\rho }_i{\delta }_i{ϵ}_i-{\rho }_i({\delta }_i^2-{\Xi }_{\delta }^2)\beta \right]}^2\hfill \\ & ⩽& {\displaystyle \frac{C_{1}q}{p}}·\underset{1⩽i⩽n}{max}|{\tilde{x}}_i{|}^2+{\displaystyle \frac{C_{2}s}{r}}·\underset{1⩽i⩽n}{max}{|{\tilde{x}}_i^c|}^2+{\displaystyle \frac{C_{2}kr}{n}}=o(1)\hfill \end{array}$$

(18)

$$\begin{array}{ccc}\hfill E{(D_n^{‴})}^2& ⩽& {\displaystyle \frac{C_1}{n}}·E[{\sum _{i=k(s+r)+1}^n{\rho }_i\left[({\tilde{x}}_i+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+{\Xi }_{\delta }^2\beta \right]}^2\hfill \\ & & +{\displaystyle \frac{C_2}{n}}·E[{\sum _{i=k(s+r)+1}^n{\rho }_i\left[({\tilde{x}}_i^c+{\delta }_i)({ϵ}_i-{\delta }_i\beta )+{\Xi }_{\delta }^2\beta \right]}^2\hfill \\ & ⩽& {\displaystyle \frac{C_{1}s}{n}}·\underset{1⩽i⩽n}{max}|{\tilde{x}}_i{|}^2+{\displaystyle \frac{C_{2}s}{n}}·\underset{1⩽i⩽n}{max}{|{\tilde{x}}_i^c|}^2+{\displaystyle \frac{C_{2}s}{n}}=o(1)\hfill \end{array}$$

(19)

Next, we verify that $D_n^{\prime }\stackrel{D}{\to }N(0,1)$. It is enough to demonstrate that

$$\begin{array}{c}Var(D_n^{\prime })\to 1\end{array}$$

(20)

$$\begin{array}{c}|Eexp(it{\sum }_{b=1}^k{y}_{nb})-{\prod }_{b=1}^{k}Eexp(it{y}_{nb})|\to 0\end{array}$$

(21)

$$\begin{array}{c}{U}_n(\omega )={\sum }_{b=1}^{k}E{y}_{nb}^{2}I\left(\left|y_{nb}\right|>\omega \right)\to 0,\forall \omega >0\end{array}$$

(22)

It is apparent that $E{\left(D_n^{\prime }+D_n^{″}+D_n^{‴}\right)}^2=1$ and

$$E{\left(D_n^{\prime }+D_n^{″}+D_n^{‴}\right)}^2=E{\left(D_n^{\prime }\right)}^2+E{\left(D_n^{″}\right)}^2+E{\left(D_n^{‴}\right)}^2+2E{\left(D_n^{\prime }{D}_n^{″}\right)}^2+2E{\left(D_n^{″}{D}_n^{‴}\right)}^2+E{\left(D_n^{\prime }{D}_n^{‴}\right)}^2$$

From the given definition of $D_n^{\prime }$, one can hence straightforwardly confirm that $E{\left(D_n^{\prime }\right)}^2<\infty$ by referring to Equations (18) and (19).

It is straightforward to verify

$$\begin{array}{ccc}\hfill \left|Var\left(D_n^{\prime }\right)-1\right|& ⩽& E{(D_n^{″}+D_n^{‴})}^2+2\left|E(D_n{D}_n^{″})\right|+2\left|E(D_n{D}_n^{‴})\right|\hfill \\ & ⩽& 2\left[E{(D_n^{″})}^2+E{(D_n^{‴})}^2\right]+2{\left[E{(D_n^{″})}^2\right]}^{{\displaystyle \frac{1}{2}}}+2{\left[E{(D_n^{‴})}^2\right]}^{{\displaystyle \frac{1}{2}}}=o(1)\hfill \end{array}$$

This results in (20). For (21), by applying Lemma 3 and (H7), we obtain

$$|Eexp(it\sum _{b=1}^k{y}_{nb})-\prod _{b=1}^{k}Eexp(it{y}_{nb})|\to 0$$

We thus need to verify (22). Suppose that $\lambda >\left(2+\gamma \right)/\gamma$. Set $v=2\left(1+t\right)$ and $\eta =\left(\gamma -2t\right)$, where $0<t<{\displaystyle \frac{\gamma }{2}}$. We then select t in such a way that

$${\displaystyle \frac{2+\gamma }{\gamma }}<{\displaystyle \frac{\left(2+\gamma \right)\left(1+t\right)}{\gamma -2t}}={\displaystyle \frac{v\left(v+\eta \right)}{2\eta }}<\lambda$$

Obviously, $v+\eta =2+\gamma$, by applying Lemmas 5 and 7 from (H0) to (H7) and ${\Theta }_{2n}^2⩾Cn$. For small values of $ϵ$ where $0<\epsilon <t$, we discover that

$$\begin{array}{ccc}\hfill U_n(\omega )& ⩽& C\sum _{b=1}^{k}E{\left|y_{nb}\right|}^v=C\sum _{b=1}^{k}E|\sum _{i=k_b}^{k_b+s-1}{Z}_{ni}{|}^v\hfill \\ & ⩽& C{n}^{-{\displaystyle \frac{v}{2}}}\sum _{b=1}^k\left[s^{\epsilon }\sum _{i=k_b}^{k_b+s-1}E{\left|{\omega }_i\right|}^v+{\left(\sum _{i=k_b}^{k_b+s-1}{\parallel {\omega }_i\parallel }_{2+\gamma }^2\right)}^{{\displaystyle \frac{v}{2}}}\right]\hfill \\ & ⩽& C{n}^{-\left(1+t\right)}\{s^{\epsilon }\sum _{b=1}^k\sum _{i=k_b}^{k_b+s-1}|{\tilde{x}}_i^c{|}^{2(1+t)}+{|{\tilde{x}}_i|}^{2(1+t)}+O(1)\hfill \\ & & +\sum _{b=1}^k[\sum _{i=k_b}^{k_b+s-1}|{\tilde{x}}_i^c{|}^2+|{\tilde{x}}_i{|}^2+O(1)){]}^{1+t}\}\hfill \\ & ⩽& C{n}^{-\left(1+t\right)}[n{s}^{\epsilon }·(\underset{1⩽i⩽n}{max}|{\tilde{x}}_i^c{|)}^{2t}+n{s}^{\epsilon }·(\underset{1⩽i⩽n}{max}|{\tilde{x}}_i{|)}^{2t}\hfill \\ & & +n{s}^t·(\underset{1⩽i⩽n}{max}|{\tilde{x}}_i^c{|)}^{2t}+n{p}^t·(\underset{1⩽i⩽n}{max}|{\tilde{x}}_i{|)}^{2t}+C_{1}n{s}^t]=o(1)\hfill \end{array}$$

Thus, we know that $D_{1n}/{\Theta }_{2n}\stackrel{D}{\to }N(0,1)$.

Stage 2. We demonstrate that $D_{kn}/{\Theta }_{2n}\stackrel{P}{\to }0,k=2,\cdots ,20$.

$$\begin{array}{ccc}\hfill D_{3n}& =& \left(P_{1n}+P_{2n}\right)({\widehat{\beta }}_c-\beta )\hfill \\ \hfill \left|{\displaystyle \frac{P_{1n}}{{\Theta }_{2n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}·\sum _{i=1}^n|\left[{\tilde{f}}_i+{\mu }_i-\sum _{j=1}^n{V}_{nj}\left({\tau }_i\right){\mu }_j\right]|·\underset{1⩽i⩽n}{max}\left|\left(1-{\rho }_i\right)\right|\hfill \\ & & ·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)\left[f\left({\tau }_k\right)+{\mu }_k\right]|\hfill \\ & =& o(n^{1/2})\hfill \\ \hfill \left|{\displaystyle \frac{P_{2n}}{{\Theta }_{2n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}|\sum _{i=1}^n{\tilde{x}}_i\left(1-{\rho }_i\right){\delta }_i|=O(n^{1/4}logn)\hfill \\ \hfill \left|{\displaystyle \frac{D_{5n}}{{\Theta }_{2n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}\{\underset{1⩽i⩽n}{max}|1-{\rho }_i|[n·\underset{1⩽i⩽n}{max}|{\tilde{f}}_i|·\underset{1⩽i⩽n}{max}|{\widehat{g}}_n^c\left({\tau }_i\right)-g\left({\tau }_i\right)|+\underset{1⩽m⩽n}{max}|\sum _{i=1}^m{\mu }_{j_i}|·\underset{1⩽i⩽n}{max}|{\widehat{g}}_n^c\left({\tau }_i\right)-g\left({\tau }_i\right)|\hfill \\ & & +\underset{1⩽i⩽n}{max}|\sum _{j=1}^n{V}_{nk}({\tau }_i)|·\underset{1⩽i⩽n}{max}|{\widehat{g}}_n^c\left({\tau }_i\right)-g\left({\tau }_i\right)|·\underset{1⩽m⩽n}{max}|\sum _{i=1}^m{\mu }_{j_k}|\left]\right\}=o(1)\mathrm{a}.\mathrm{s}.\hfill \\ \hfill E{\left({\displaystyle \frac{D_{6n}}{{\Theta }_{2n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}\left[E{\left(\sum _{i=1}^n{\delta }_i{\tilde{g}}_i^c\right)}^2+E{\left(\sum _{i=1}^n{\tilde{g}}_i^c\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k\right)}^2\right]=o(n^{-1/2})\hfill \\ \hfill \left|{\displaystyle \frac{D_{7n}}{{\Theta }_{2n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}|\sum _{i=1}^n{\tilde{x}}_i{\tilde{g}}_i^c|⩽{\displaystyle \frac{C}{\sqrt{n}}}\left\{|\sum _{i=1}^n{\tilde{f}}_i{\tilde{g}}_i^c|+|\sum _{i=1}^n{\mu }_i{\tilde{g}}_i^c|+|\sum _{i=1}^n\left[\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\mu }_k\right]{\tilde{g}}_i^c|\right\}\hfill \\ & ⩽& {\displaystyle \frac{C}{\sqrt{n}}}[n·\underset{1⩽i⩽n}{max}|{\tilde{f}}_i|·\underset{1⩽i⩽n}{max}|{\tilde{g}}_i^c|+\underset{1⩽m⩽n}{max}|\sum _{i=1}^m{\mu }_{j_i}|·\underset{1⩽i⩽n}{max}|{\tilde{g}}_i^c|\hfill \\ & & +\underset{1⩽k⩽n}{max}|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)|·\underset{1⩽i⩽n}{max}|{\tilde{g}}_i^c|·\underset{1⩽m⩽n}{max}|\sum _{k=1}^m{\mu }_{j_k}|]\hfill \\ & =& o(1)\hfill \\ \hfill D_{9n}& =& \left[\sum _{i=1}^n\widetilde{x_i}\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)\left(1-{\rho }_j\right)x_k+\sum _{i=1}^n\widetilde{x_i}\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)\left(1-{\rho }_k\right){\delta }_k\right]\left({\widehat{\beta }}_c-\beta \right)\hfill \\ & :=& \left(T_{1n}+T_{2n}\right)({\widehat{\beta }}_c-\beta )\hfill \\ \hfill \left|{\displaystyle \frac{T_{1n}}{{\Theta }_{2n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}\sum _{i=1}^n|\left[{\tilde{f}}_i+{\mu }_i-\sum _{j=1}^n{V}_{nj}\left({\tau }_i\right){\mu }_j\right]|·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right)\left(1-{\rho }_i\right)x_k|\hfill \\ & & =O(n^{1/2})\hfill \\ \hfill E{\left({\displaystyle \frac{T_{2n}}{{\Theta }_{1n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n{\left[\sum _{k=1}^n\widetilde{x_i}{V}_{nk}\left({\tau }_i\right)(1-{\rho }_k)\right]}^2{\Xi }_{\delta }^2=O(1)\hfill \\ \hfill D_{14n}& =& \sum _{i=1}^n\widetilde{f_i}\sum _{k=1}^n{\rho }_k{V}_{nk}\left({\tau }_i\right){\delta }_k\beta +\sum _{i=1}^n{\mu }_i\sum _{k=1}^n{\rho }_k{V}_{nk}\left({\tau }_i\right){\delta }_k\beta -\sum _{i=1}^n\sum _{s=1}^n{V}_{ns}\left({\tau }_i\right){\mu }_s\sum _{k=1}^n{\delta }_k{V}_{nk}\left({\tau }_i\right){\delta }_k\beta \hfill \\ & :=& Q_{1n}+Q_{2n}+Q_{3n}\hfill \\ \hfill E{\left({\displaystyle \frac{Q_{1n}}{{\Theta }_{2n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}\sum _{k=1}^n{\left[\sum _{i=1}^n{V}_{nk}\left({\tau }_i\right)\widetilde{f_i}\right]}^2\hfill \\ & ⩽& C·\underset{1⩽i⩽n}{max}|\widetilde{f_i}{|}^2·\underset{1⩽k⩽n}{max}|\sum _{i=1}^n{V}_{nk}({\tau }_i){|}^2=o(n^{-1/2})\hfill \\ \hfill E{\left({\displaystyle \frac{Q_{2n}}{{\Theta }_{2n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}\sum _{k=1}^n{\left[\sum _{i=1}^n{V}_{nk}\left({\tau }_i\right){\mu }_i\right]}^2⩽C·\underset{1⩽m⩽n}{max}|\sum _{i=1}^m{\mu }_{ji}{|}^2·\underset{1⩽i,k⩽n}{max}{V}_{nk}^2\left({\tau }_i\right)=o(1)\hfill \\ \hfill \left|{\displaystyle \frac{Q_{3n}}{{\Theta }_{3n}}}\right|& ⩽& {\displaystyle \frac{C}{\sqrt{n}}}·\underset{1⩽m⩽n}{max}|\sum _{s=1}^m{v}_{js}|·\underset{1⩽s⩽n}{max}\sum _{i=1}^n{V}_{ns}\left({\tau }_i\right)·\underset{1⩽i⩽n}{max}|\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k|=o_p(1)\hfill \\ \hfill E{\left({\displaystyle \frac{D_{16n}}{{\Theta }_{2n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}\sum _{i_1=1}^n\sum _{i_2=1}^n\sum _{k_1=1}^n\sum _{k_2=1}^n{V}_{n{k}_1}\left({\tau }_{i_1}\right)V_{n{k}_2}\left({\tau }_{i_2}\right)E\left({\delta }_{i_1}{\delta }_{i_2}{\delta }_{k_1}{\delta }_{k_2}\right)\hfill \\ & ⩽& {\displaystyle \frac{C}{n}}\left[\sum _{i=1}^n\sum _{k=1}^n{V}_{n{k}_1}^2\left({\tau }_i\right)E\left({\delta }_i^2{\delta }_k^2\right)+\sum _{i_1=1}^n\sum _{i_2=1}^n{V}_{n{i}_1}\left({\tau }_{i_1}\right)V_{n{i}_2}\left({\tau }_{i_2}\right)E\left({\delta }_{i_1}^2{\delta }_{i_2}^2\right)\right]\hfill \\ & & =O(n^{-1})\hfill \\ \hfill E{\left({\displaystyle \frac{D_{18n}}{{\Theta }_{2n}}}\right)}^2& ⩽& {\displaystyle \frac{C}{n}}·E{\left[\sum _{i=1}^n\sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){ϵ}_i{\delta }_k\right]}^2\hfill \\ & ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n{\parallel \sum _{k=1}^n{V}_{nk}\left({\tau }_i\right){\delta }_k\parallel }_{2+\eta }^2·{\parallel {ϵ}_i\parallel }_{2+\eta }^2\hfill \\ & ⩽& {\displaystyle \frac{C}{n}}\sum _{i=1}^n{\left\{\sum _{k=1}^n{\left[V_{nk}\left({\tau }_i\right)\right]}^{2+\eta }+{\left[\sum _{k=1}^n{V}_{nk}^2\left({\tau }_i\right)\right]}^{(2+\eta )/2}\right\}}^{2/(2+\eta )}\hfill \\ & & =o(n^{-1/2}{log}^{-1}n).\hfill \end{array}$$

The demonstration that $D_{kn}=o_p\left(1\right)$ for $k=2,4,8,10,11,12,13,15,17,19,20$ proceeds in a similar manner. Thus, Theorem 5(a) is thereby proven. □

Proof of Theorem 5(b).

Based on (7), we have that

$$\begin{array}{ccc}\hfill {\widehat{g}}_n^{\left[I\right]}\left(\tau \right)-g\left(\tau \right)& =& \left[\sum _{k=1}^n{V}_{nk}(\tau ){\rho }_k+\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)\sum _{i=1}^n{V}_{ni}^c({\tau }_k){\rho }_i\right]\left({ϵ}_k-{\delta }_k\beta \right)\hfill \\ & & +[\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)x_k+\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k){\delta }_k\hfill \\ & & -\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)\sum _{i=1}^n{V}_{ni}^c({\tau }_k){\rho }_i{\delta }_k-\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)\sum _{i=1}^n{V}_{ni}^c({\tau }_k){\rho }_i{x}_k]\left({\widehat{\beta }}_c-\beta \right)\hfill \\ & & +\left[\sum _{k=1}^n{V}_{nk}(\tau )x_k+\sum _{k=1}^n{V}_{nk}(\tau ){\delta }_k\right]\left(\beta -{\widehat{\beta }}_I\right)\hfill \\ & & +\left[\sum _{k=1}^n{V}_{nk}(\tau )(1-{\rho }_k)\sum _{i=1}^n{V}_{ni}^c({\tau }_k){\rho }_i+\sum _{k=1}^n{V}_{nk}(\tau ){\delta }_k\right](g\left({\tau }_k\right)-g\left(\tau \right))\hfill \\ & :=& U_{1n}(\tau )+[U_{2n}(\tau )+U_{3n}(\tau )+U_{4n}(\tau )+U_{5n}(\tau )]\left({\widehat{\beta }}_c-\beta \right)\hfill \\ & & +[U_{6n}(\tau )+U_{7n}(\tau )]\left(\beta -{\widehat{\beta }}_I\right)+(U_{8n}(\tau )+U_{9n}(\tau ))\hfill \end{array}$$

Analogous to the proof of 4(a) and 5(a). One can verify that $U_{1n}\left(\tau \right)/{\Lambda }_{2n}\left(\tau \right)\stackrel{D}{\to }N\left(0,1\right)$. Observe that $n{\Lambda }_{2n}^2\left(\tau \right)\to \infty$ as $n\to \infty$. According to Theorems 4 and 5, we can obtain $\beta -{\widehat{\beta }}_c=O_p(n^{-1/2})$ and $\beta -{\widehat{\beta }}_I=O_p(n^{-1/2})$. Thus, it is adequate to demonstrate that $U_{kn}\left(\tau \right)=O(n^{-1/2})$ for $k=8,9$. $U_{sn}\left(\tau \right)=O_p(1)$ for $s=2,\cdots ,7$. For $\forall b>0$,

$$\begin{array}{ccc}\hfill \left|U_{2n}\left(\tau \right)\right|& ⩽& |\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)x_k|⩽|\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\left[f\left({\tau }_k\right)+{\mu }_k\right]|\hfill \\ & ⩽& \underset{1⩽k⩽n}{max}|f\left({\tau }_k\right)|·|\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)|+\underset{1⩽k⩽n}{max}|V_{nk}\left(\tau \right)\left(1-{\rho }_k\right)|·\underset{1⩽m⩽n}{max}|\sum _{k=1}^m{\mu }_{j_k}|=O\left(1\right)\hfill \\ \hfill E{\left(U_{3n}\left(\tau \right)\right)}^2& ⩽& \sum _{k=1}^n{\left[V_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\right]}^2{\Xi }_{\delta }^2=O(n^{-1/2}{log}^{-1}n)\hfill \\ \hfill E{\left(U_{4n}\left(\tau \right)\right)}^2& ⩽& \sum _{k=1}^n{\left[V_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_k\right){\rho }_i\right]}^2{\Xi }_{\delta }^2=O(n^{-1/2}{log}^{-1}n)\hfill \\ \hfill \left|U_{5n}\left(\tau \right)\right|& ⩽& |\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left(\tau \right){\rho }_i{x}_k|⩽|\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_i\right){\rho }_k\left[f\left({\tau }_k\right)+{\mu }_k\right]|\hfill \\ & ⩽& \underset{1⩽j⩽n}{max}|f\left({\tau }_k\right)|·|\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_k\right){\rho }_i|\hfill \\ & & +\underset{1⩽k⩽n}{max}|V_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{nk}^c\left(\tau \right){\rho }_i|·\underset{1⩽m⩽n}{max}|\sum _{k=1}^m{\mu }_{j_k}|=O\left(1\right)\hfill \\ \hfill U_{8n}\left(\tau \right)& ⩽& \left[\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_k\right){\rho }_i\right]\left[g\left({\tau }_k\right)-g\left(\tau \right)\right]·I\left(|{\tau }_k-\tau |>b·n^{-1/2}\right)\hfill \\ & & +\left[\sum _{k=1}^n{V}_{nk}\left(\tau \right)\left(1-{\rho }_k\right)\sum _{i=1}^n{V}_{ni}^c\left({\tau }_k\right){\rho }_i\right]\left[g\left({\tau }_k\right)-g\left(\tau \right)\right]·I\left(|{\tau }_k-\tau |⩽b·n^{-1/2}\right)=O\left(n^{-1/2}\right)\hfill \end{array}$$

The argument for showing $U_{kn}=O_p\left(1\right)$ for $k=6,7,9$ follows in a similar manner. Therefore, Theorem 5(b) is proven. □

Proof of Theorem 6.

The proof of Theorem 6 bears a resemblance to the previous one. □

7. Appendix Proofs of Lemmas

Proof of Lemma 6. Set ${\upsilon }_{ni}=Y_{i}I(|Y_i|⩽n^{1/p})$, ${\upsilon }_{ni}^{\prime }=Y_{i}I(|Y_i|>n^{1/p})$. Then,

$$\left|\sum _{i=1}^n{b}_{ni}{Y}_i\right|⩽\left|\sum _{i=1}^n{b}_{ni}{\upsilon }_{ni}\right|+\left|\sum _{i=1}^n{b}_{ni}{\upsilon }_{ni}^{\prime }\right|:=G_{1n}+G_{2n}$$

Simply put, if $E|Y_1{|}^p<\infty$, it follows that ${\sum }_{i=1}^{\infty }P(|Y_i|>i^{1/p})<\infty$. This implies that ${\sum }_{i=1}^n|Y_i|I(|Y_i|>i^{1/p})<\infty$ a.s. Consequently,

$$G_{2n}=O(n^{-u})\sum _{i=1}^n|Y_i|I(|Y_i|>n^{1/p})=o_p(n^{-\psi }{L}_1(n))by\psi <u.$$

(23)

From the conditions $E{Y}_i=0$, $E|Y_i{|}^p<\infty$ and $\psi ⩽1-1/p$, we can deduce that

$$|\sum _{i=1}^n{b}_{ni}E{\upsilon }_{ni}|=|\sum _{i=1}^n{b}_{ni}E{Y}_{i}I(|Y_i|>n^{1/p})|⩽CE|Y_1|I(|Y_1|>n^{1/p})=O(n^{{\displaystyle \frac{1-p}{p}}})=o(n^{-\psi }logn).$$

(24)

Next, we prove that $G_{1n}=o_p(n^{-\psi })$. Based on (23), we establish that

$$P\left(|\sum _{i=1}^n{b}_{ni}\left({\upsilon }_{ni}-E{\upsilon }_{ni}\right)|>\tau n^{-\psi }\right)\to 0forany\tau >0.$$

(25)

Drawing upon Lemma 5(a), by selecting a sufficiently large value for $v>p$ and a sufficiently small value for $\eta >0$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}& P\left(|\sum _{i=1}^n{b}_{ni}({\upsilon }_{ni}-E{\upsilon }_{ni})|>\tau n^{-\psi }\right)\hfill \\ & ⩽{(\tau n^{-\psi })}^{-v}E|\sum _{i=1}^n{b}_{ni}({\upsilon }_{ni}-E{\upsilon }_{ni}){|}^v\hfill \\ & ⩽C{n}^{\psi v}·\left\{n^{\eta }\sum _{=1}^{n}E|b_{ni}({\upsilon }_{ni}-E{\upsilon }_{ni}){|}^v+{\left(\sum _{i=1}^n\parallel b_{ni}({\upsilon }_{ni}-E{\upsilon }_{ni}){\parallel }_{v+\rho }^2\right)}^{{\displaystyle \frac{v}{2}}}\right\}\hfill \\ & ⩽C{n}^{\psi v}·\left\{n^{\eta }\sum _{i=1}^n|b_{ni}{|}^v·E{|Y_1|}^{r}I(|Y_1|⩽n^{1/p})+{\left(\sum _{i=1}^n{b}_{ni}^2\right)}^{{\displaystyle \frac{v}{2}}}{\left[E|Y_1{|}^{r+\rho }I(|Y_1|⩽n^{1/p})\right]}^{{\displaystyle \frac{v}{v+\rho }}}\right\}\hfill \\ & ⩽C{n}^{\psi v}·n^{\eta }·n^{-u(v-2)}·n^{-\tau }·n^{{\displaystyle \frac{v-p}{p}}}·{\left[L_1(n)\right]}^{v-2}+C{n}^{\psi v}·n^{-{\displaystyle \frac{\tau v}{2}}}·n^{{\displaystyle \frac{v+\rho -p}{p}}·{\displaystyle \frac{v}{v+\rho }}}\hfill \\ & ⩽C\left\{n^{\eta +\psi v-uv+2u-\tau +v/p-1}{\left[L_1(n)\right]}^{v-2}+n^{\psi v-\tau v/2+v/p+\rho /(v+\rho )-1}\right\}\hfill \end{array}\end{array}$$

Let $I_1=\psi v-uv+2u-\tau +v/p-1$ and $I_2=\psi v-\tau v/2+v/p+\rho /(r+\rho )-1$. According to the premises in Lemma 6, it is shown that $I_1<0$ and $I_2<0$, resulting in (25). Hence, the proof of Lemma 6 is finished.

8. Conclusions

This study presents robust methods for handling incomplete data with strong mixing errors, focusing on estimating $\beta$ and $g(·)$ under the Missing at Random (MAR) assumption. We establish the strong consistency and asymptotic normality of the proposed estimators, demonstrating their effectiveness in addressing data uncertainty. Among these approaches, the imputation estimator ${\widehat{g}}_n^{\left[I\right]}(\tau )$ and ${\widehat{\beta }}_I$ provide the most accurate estimates by leveraging both observed and imputed data. These results suggest that the imputation method is the most effective for managing incomplete data in the context of the semi-parametric EV model. In practical applications, such as policy formulation and resource allocation, where incomplete data are common, the imputed estimator is a reliable and efficient tool. By utilizing available information, it ensures more accurate parameter estimates, which are crucial for making informed decisions under data uncertainty.