Abstract
Due to its critical importance in engineering applications, this study is motivated by the essential need to understand natural convection over a vertical cylinder with combined heat and mass transfer. Lie group symmetry transformations are used to analyze the thermal and velocity boundary layers of steady, naturally convective laminar fluid flow over the surface of a vertical cylinder. The one-parameter Lie group symmetry technique converts the system of governing equations into ordinary differential equations, which are then solved numerically using the implicit Runge–Kutta method. The effect of the Prandtl number, Schmidt number, and combined buoyancy ratio parameter on axial velocity, temperature, and concentration profiles are illustrated graphically. A specific range of parameter values was chosen to compare the obtained results with previous studies, demonstrating the accuracy of this method relative to others. The average Nusselt number and average Sherwood number are computed for various values of the Prandtl number Pr and Schmidt number Sc and presented in tables. It was found that the time required to reach a steady state for velocity and concentration profiles decreases as the Schmidt number Sc increases. Additionally, both temperature and concentration profiles decrease with an increase in the combined buoyancy ratio parameter N. Flow reversal and temperature defect with varying Prandtl numbers are also shown and discussed in detail.
1. Introduction
Fluid mechanics is considered one of the oldest branches of applied mathematics and the foundation for understanding different aspects of science and engineering. Key concepts in fluid mechanics encompass fluid dynamics, which examines the governing fluid flow principles including velocity profiles, temperature distribution, and the impacts of energy and mass transfer. Studying in-depth fluid dynamics is essential for creating efficient systems such as pipelines, aircraft, and pumps. The interaction of fluids with different shapes is an area of great interest as the shape of an object significantly influences the flow over a body affecting heat and mass transfer characteristics. In this present study, we are interested in studying steady natural convective laminar fluid flow in a vertical circular cylinder. The flow past a cylinder is a classic fluid dynamics problem exhibiting interesting and complex behavior. Understanding fluid flow over a cylinder is crucial in diverse engineering applications, including designing structures, vehicles and pipelines.
The flow past a cylinder has been the main topic of several studies. Reddy et al. [] applied Bejan’s heat function concept to study the effect of Prandtl number on fluid flow over a uniformly heated vertical cylinder. Rani et al. [] investigated the unsteady natural convective flow over a semi-infinite vertical cylinder considering the impact of a homogeneous first-order chemical reaction. Kumar and Rizvi [] studied unsteady flow characteristics involving a viscous, incompressible, and electrically conductive fluid passing over a vertically oriented cylinder initiated with an impulsive start. The system includes temperature and mass diffusion variations and operates in a uniform chemical reaction and magnetic field occurring transversely. The governing equations, which are expressed in a non-dimensional form within the flow model, were numerically solved using the Crank–Nicolson method. Chamkha et al. [] analyzed the behavior of a free unsteady convection boundary layer flow of a nanofluid surrounding a vertical cylinder. The equations governing this flow were solved using an implicit finite-difference method. Javaid et al. [] explored the second-grade fluid flow and its natural convection heat transfer characteristics. They applied the integral transform technique to obtain precise solutions. Gholinia et al. [] examined the incompressible viscous nanofluid passed into a vertical circular cylinder with added consideration for electric conductivity. This analysis was conducted without the influence of an inductive and electromagnetic field while also accounting for both homogeneous and heterogeneous reactions. In [], experiments were performed numerically to examine the average Nusselt numbers associated with laminar isothermal vertical cylinders undergoing natural convection.
In the present work, we applied the Lie group symmetry method to study the governing equations for laminar natural convection fluid flow past a vertical cylinder. This method is a powerful technique with straightforward steps and minimal assumptions, capable of solving nonlinear partial differential equations or systems of equations. Lie symmetry analysis generates exact solutions for nonlinear partial differential equations by reducing the number of independent variables, yielding simpler equivalent equations. Lie point symmetries and their corresponding reduced differential equations are used to construct a broad range of exact solutions [,,,,,,,].
In a previous study, we employed the Lie group method to investigate unsteady natural free convection flow past a vertical plate, as presented in Abd-el-Malek et al. []. The governing equations of the boundary layer flow are represented by a system of partial differential equations, which are typically difficult to solve using classical methods. Thus, a one-parameter Lie group transformation was used to reduce the number of variables in the system, converting it into ordinary differential equations. This approach has proven effective for studying these types of nonlinear systems.
Obtaining an accurate solution for the present problem is challenging, making it suitable for practical applications. The effects of the Prandtl number, Schmidt number, and combined buoyancy ratio parameter on axial velocity, thermal boundary layer, and concentration profiles are presented graphically. The rates of heat and mass transfer are also illustrated to demonstrate the respective impacts of the Prandtl and Schmidt numbers. The average Nusselt number and Sherwood number are calculated for different values of the Prandtl and Schmidt numbers. Finally, the present work is compared with previous studies to verify the accuracy of the obtained results.
2. Formulation of the Physical Model
Consider the laminar fluid flow over a vertical circular cylinder of radius ro in an open-air, quiescent environment with temperature and concentration . The cylinder surface is kept at a constant temperature and concentration . In Figure 1, the coodinate r starts from the middle of the vertical cylinder and the coordinate z starts vertically upward from the lower cylinder edge. This problem can be modeled as two-dimensional due to its geometric and thermal symmetry.
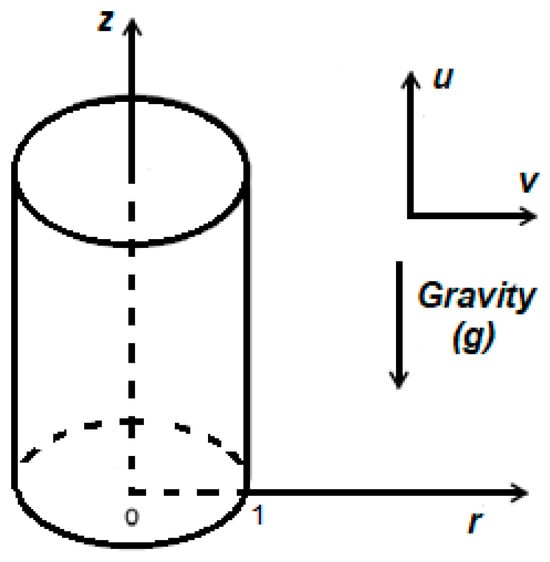
Figure 1.
Schematic diagram of the physical model.
Applying the Boussinesq and boundary-layer approximations, the fluid flow motion-governing equations for laminar natural convection over an outer surface of a vertical cylinder, in cylindrical coordinates form, are represented by the equations:
Conservation of mass
Conservation of momentum in z direction
Conservation of energy
Navier–Stokes approximation for concentration
where the dimensionless parameters are defined as:
u and ʋ are dimensionless axial and radial velocity components, respectively, T represents dimensionless temperature, and C represents dimensionless concentration. D is the mass diffusion coefficient, Gr is the thermal Grashof coefficient, Gr* is the mass Grashof number for mass diffusion, g is the acceleration due to gravity, Pr is the Prandtl number, Sc is the Schmidt number, N is the combined buoyancy ratio parameter, is the volumetric coefficient of thermal expansion, is the thermal diffusivity, is the volumetric coefficient of expansion, and is the kinematic viscosity.
Given the following boundary conditions for dimensionless quantities,
Due to the complexity of these equations, analytical solutions are often challenging and numerical methods become crucial for obtaining accurate results. Here, we apply the Lie group analysis method to obtain an acceptable solution for the previous system of equations.
3. Application of Lie Group Transformation Method
The similarity solutions are derived by applying the classical Lie group scaling transformation defined , where ɛ is the infinitesimal parameter and X is the infinitesimal vector, defined as:
The symmetry Lie group transformations of (z, r; u, ʋ, T, c) leaving (1)–(4) invariant are given by:
Equations (1)–(4) are written in the form:
where
An infinitesimal vector field X is defined as a Lie symmetry generator vector field for Equations (1)–(4) if
And represents the second prolongation as
According to Equation (12), applying Equations (13) to Equations (8)–(10) and (11) gives the following differential equations system:
where
And k stands for (z, r) in addition to:
Substituting from Equations (15) and (16) into Equation (14) gives four large expressions which lead to a group of determining Equations; solving these equations leads to:
Then, the vector (6) is a combination of
X1 and X3 contradict the given boundary conditions. Thus, X2 is the only accepted generator according to the conditions in (5).
4. Reduction to the Ordinary Differential System
For the obtained vector field generator , the characteristic equation is
Then,
The original system (1)–(4) is reduced into an ordinary differential system as follows:
From the introduced conditions (5), the appropriate new conditions for the ODE system are given by:
5. Results and Discussion
The system of ordinary differential Equations (21)–(24) with the boundary conditions (25) has been solved numerically using the Lobatto IIIA formula (implicit Runge–Kutta). Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 present the impact of various parameters on the velocity and thermal boundary layer, in addition to the concentration profile.
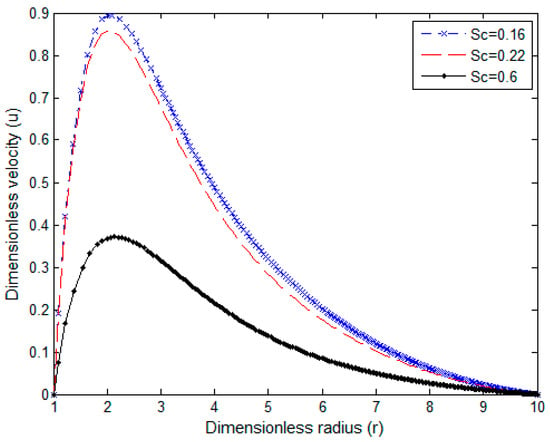
Figure 2.
Velocity profile for Pr = 0.7 and N = 2.
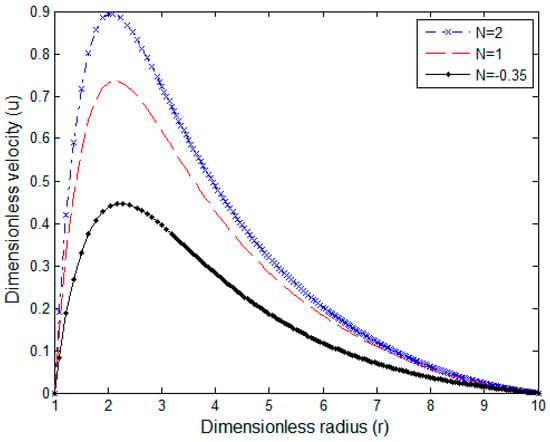
Figure 3.
Velocity profile for Pr = 0.7 and Sc = 0.16.
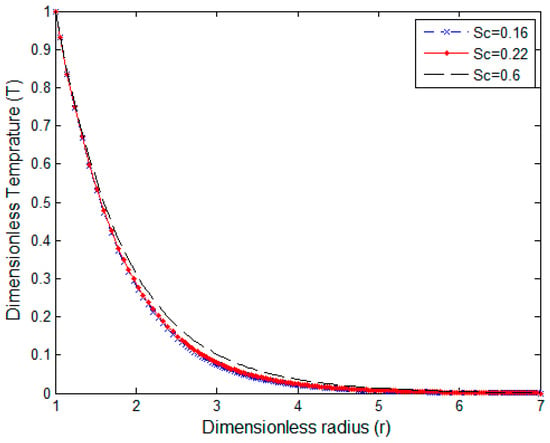
Figure 4.
Temperature profile for Pr = 0.7 and N = 2.
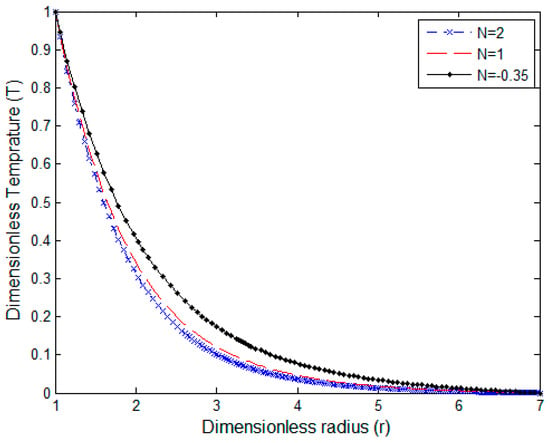
Figure 5.
Temperature profile for Pr = 0.7 and Sc = 0.16.
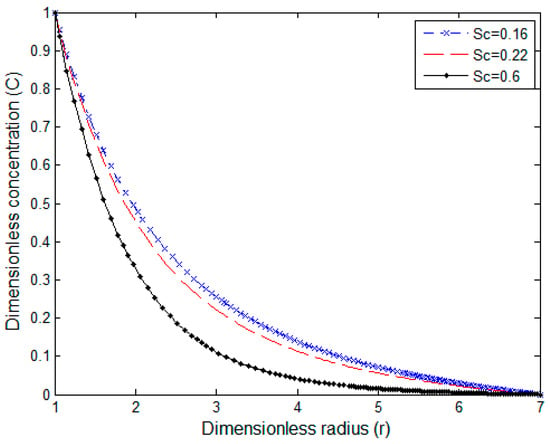
Figure 6.
Concentration profile for Pr = 0.7 and N = 2.
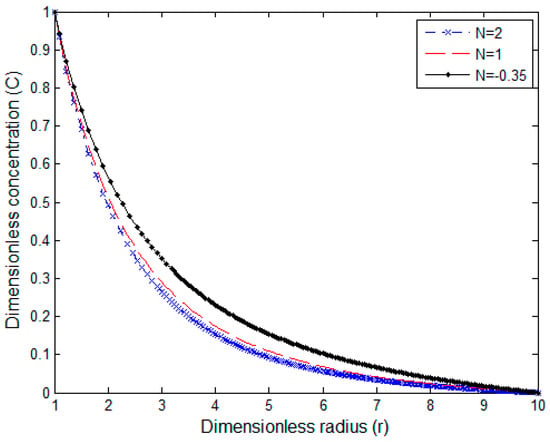
Figure 7.
Concentration profile for Pr = 0.7 and Sc = 0.16.
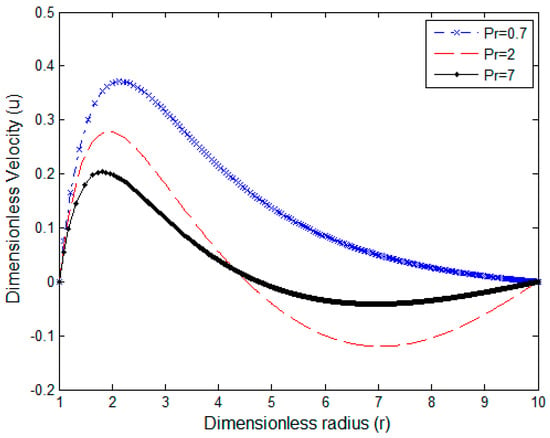
Figure 8.
Velocity profile for N = −0.35 and Sc = 0. 6.
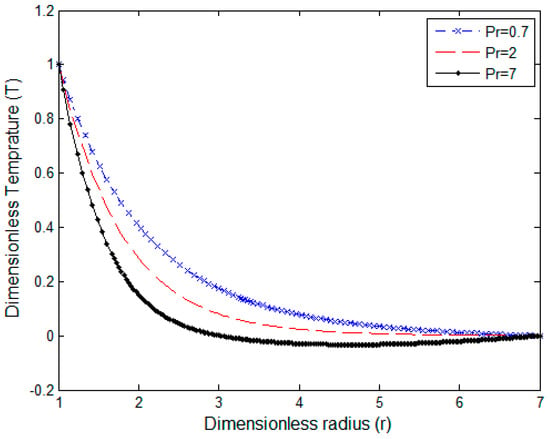
Figure 9.
Temperature profile for N = −0.35 and Sc = 0.6.
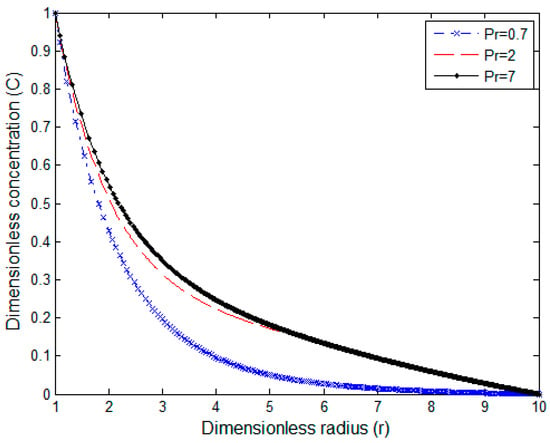
Figure 10.
Concentration profile for N = −0.35 and Sc = 0.16.
To enable fair comparisons with findings from other studies, we selected specific ranges for key parameters. The Prandtl number Pr values span a broad range to capture effects on both velocity and temperature fields, particularly highlighting phenomena such as fluid reversal and temperature defects within the boundary layer. The Schmidt number Sc is varied from 0.16 to 0.6, and the combined buoyancy ratio parameter N is adjusted from −0.35 to 2. This range allows us to observe their influence on flow behavior, temperature distribution, and species concentration.
The rate of heat transfer and mass transfer with the Prandtl number and the Schmidt number have been illustrated in Figure 11 and Figure 12.
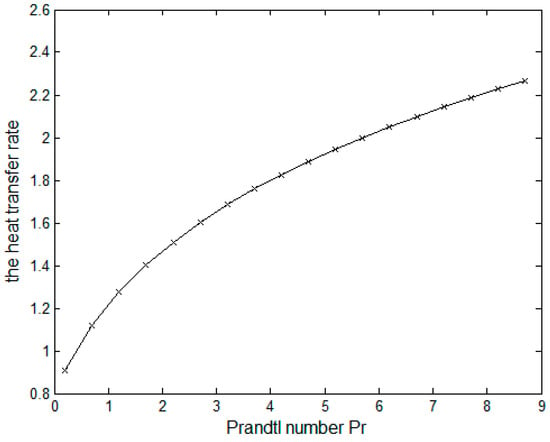
Figure 11.
Heat transfer rate versus Pr.
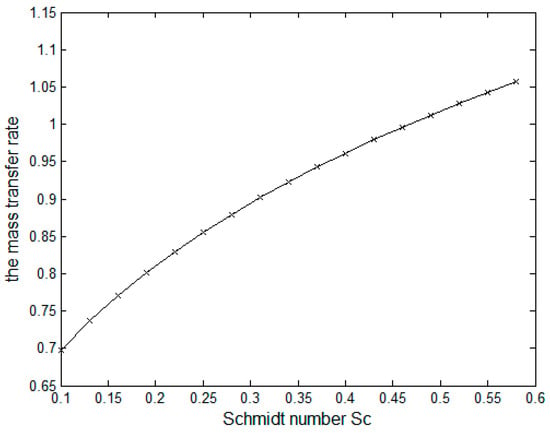
Figure 12.
Mass transfer rate versus Sc.
The impact of Schmidt number Sc and parameter N on the velocity profile is illustrated in Figure 2 and Figure 3. In Figure 2, the rising Schmidt number value decreases the velocity magnitude due to the increase of viscosity, which increases the fluid thickness and hence reduces its velocity. The increment of the combined buoyancy ratio N leads to a rise in the combined buoyancy force compared to the gravity force; then, the velocity profile peak rises near the surface, as indicated in Figure 3.
Temperature profiles are represented for various Schmidt number Sc and parameter N in Figure 4 and Figure 5. In Figure 4, temperature slightly increases with Schmidt number Sc due to a decrease in the heat transfer of high viscous fluids with an increment of Sc. When N decreases, the thermal buoyancy force overcomes the combined buoyancy, then the temperature profile rises as indicated in Figure 5. Figure 4 and Figure 5 show that temperature profiles reach the steady state faster with decreasing Sc and increasing N.
In Figure 6 and Figure 7, concentration profiles are shown for various Schmidt numbers and combined buoyancy ratio parameters with Pr = 0.7. Concentration distribution reaches a saturation state faster with increasing Sc and N. As Sc increases (e.g., in liquids), momentum diffuses faster than mass. This creates a thinner concentration boundary layer and the profile shifts closer to the surface. This means it reaches a steady state faster but with a sharper gradient. For high N, the concentration profile typically decreases because the influence of concentration buoyancy is greater than thermal buoyancy, often leading to a decrease in concentration distribution in the boundary layer. A good agreement is found when the previously presented results are compared with the introduced results in the study represented by Ganesan and Rani [].
The change in the boundary layer characteristics with the Prandtl number is highlighted in Figure 8, Figure 9 and Figure 10. The axial component of the velocity profiles for different values of Pr is illustrated in Figure 8. The maximum value of the velocity appears near the surface of the cylinder, then it returns to zero far away from it. The peak of velocity distribution decreases with the rise of the Pr value due to higher viscosity and small thermal conductivity. Figure 8 also indicates the flow reversal phenomenon which takes place at a higher Prandtl number Pr far from the surface of the cylinder due to the low values of buoyancy. It is shown that the magnitude of the flow reversal decreases with the increase of the Pr. Figure 9 indicates the temperature versus the Pr number. The temperature of the fluid reduces faster with the increment of the Pr number. The same figure shows the slight reverse in the sign of temperature in a certain range of the temperature profiles for values of Pr, which is known as temperature defect. These results agree with the velocity profiles introduced by Abd-el-Malek and Badran []. Unlike velocity and temperature distributions, concentration distribution increases with increasing of the Prandtl number, as shown in Figure 10.
Figure 11 indicates the relation between the cylinder surface heat transfer and the Prandtl number Pr. The figure shows that the increment of the Pr number increases the heat transfer rate. The rate of mass transfer has a similar attitude as the rate of heat transfer concerning Sc as in Figure 12.
The values of average Nusselt number and average Sherwood number for different values of Prandtl number Pr and Schmidt number Sc are calculated in Table 1 and Table 2. In Table 1, increasing the Prandtl number leads to a higher average Nusselt number and a lower average Sherwood number. This behavior is just the opposite in Table 2, as the average Nusselt number decreases and the average Sherwood number increases with the increment of Sc.

Table 1.
Computing the values of the average Nusselt number and average Sherwood number for different values of Pr.

Table 2.
Computing the values of the average Nusselt number and average Sherwood number for different values of Sc.
6. Conclusions
In the present work, the governing system of equations for natural convection laminar fluid flow over the surface of a vertical cylinder has been analyzed using the one-parameter Lie group scaling transformation method, a powerful technique for solving nonlinear systems of partial differential equations. The system is successfully reduced to ordinary differential equations and solved numerically under appropriate boundary conditions. The impact of various parameters, specifically Prandtl number Pr, Schmidt number Sc, and combined buoyancy ratio parameter N, on velocity, thermal boundary layers, and concentration distribution is presented graphically in detail. The average Nusselt number and average Sherwood number for different Prandtl and Schmidt values are also calculated and presented in tables.
The results from this study were compared with previous research. In [], an implicit finite difference scheme was applied, requiring multiple time steps and approximation formulas to evaluate derivatives, while [] employed the group method, which, although effective in variable reduction, involves numerous assumptions and complex procedures. The comparison demonstrates good agreement, supporting the efficiency of the classical Lie group scaling transformation with simple steps and assumptions used in this study.
Author Contributions
A.M.H. was responsible for calculations, software, and manuscript writing. M.B.A.-e.-M. was responsible for validating the calculation, checking the accuracy of plotted results, and editing the writing. N.A.B. was accountable for writing, reviewing, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to express their gratitude to the reviewers for their valuable and insightful comments, which significantly improved the quality of this paper to the present form.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reddy, G.J.; Hiremath, A.; Kumar, M. Computational modeling of unsteady third-grade fluid flow over a vertical cylinder: A study of heat transfer visualization. Results Phys. 2018, 8, 671–682. [Google Scholar] [CrossRef]
- Rani, H.P.; Reddy, G.J.; Kim, C.N. Transient analysis of diffusive chemical reactive species for couple stress fluid flow over vertical cylinder. Appl. Math. Mech. 2013, 34, 985–1000. [Google Scholar] [CrossRef]
- Kumar, G.; Rizvi, S.M.K. Casson fluid flow past on vertical cylinder in the presence of chemical reaction and magnetic field. Appl. Appl. Math. Int. J. (AAM) 2021, 16, 28. [Google Scholar]
- Chamkha, A.J.; Rashad, A.M.; Aly, A.M. Transient natural convection flow of a nanofluid over a vertical cylinder. Meccanica 2013, 48, 71–81. [Google Scholar] [CrossRef]
- Javaid, M.; Imran, M.; Imran, M.A.; Khan, I.; Nisar, K.S. Natural convection flow of a second grade fluid in an infinite vertical cylinder. Sci. Rep. 2020, 10, 8327. [Google Scholar] [CrossRef] [PubMed]
- Gholinia, M.; Gholinia, S.; Hosseinzadeh, K.; Ganji, D.D. Investigation on ethylene glycol nanofluid flow over a vertical permeable circular cylinder under effect of magnetic field. Results Phys. 2018, 9, 1525–1533. [Google Scholar] [CrossRef]
- Day, J.C.; Zemler, M.K.; Traum, M.J.; Boetcher, S.K. Laminar natural convection from isothermal vertical cylinders: Revisiting a classical subject. J. Heat Transf. 2013, 135, 022505. [Google Scholar] [CrossRef]
- Steeb, W.H. Invertible Point Transformations and Nonlinear Differential Equations, 1st ed.; World Scientific: London, UK, 1993. [Google Scholar]
- Hill, J.M. Solutions of Differential Equations by Means of One-Parameter Groups; Pitman: London, UK, 1982; Volume 63. [Google Scholar]
- Hydon, P.E. Symmetry Methods for Differential Equations; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations: Vol. II. Applications in Engineering and Physical Sciences; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Stephani, H. Differential Equations: Their Solution Using Symmetries; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Abd-el-Malek, M.B.; Badran, N.A.; Amin, A.M.; Hanafy, A.M. Lie Symmetry Group for Unsteady Free Convection Boundary-Layer Flow over a Vertical Surface. Symmetry 2021, 13, 175. [Google Scholar] [CrossRef]
- Ganesan, P.; Rani, H. Transient natural convection along vertical cylinder with Heat and Mass transfer. Heat Mass Transf. 1998, 33, 449–455. [Google Scholar] [CrossRef]
- Abd-el-Malek, M.B.; Badran, N.A. Group method analysis of steady free-convective laminar boundary-layer flow on a nonisothermal vertical circular cylinder. J. Comput. Appl. Math. 1991, 36, 227–238. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).