FGeo-SSS: A Search-Based Symbolic Solver for Human-like Automated Geometric Reasoning

Abstract

Geometric problem solving (GPS) has always been a long-standing challenge in the fields of automated reasoning. Its problem representation and solution process embody rich symmetry. This paper is the second in a series of our works. Based on the Geometry Formalization Theory and the FormalGeo geometric formal system, we have developed the Formal Geometric Problem Solver (FGPS) in Python 3.10, which can serve as an interactive assistant or as an automated problem solver. FGPS is capable of executing geometric predicate logic and performing relational reasoning and algebraic computation, ultimately achieving readable, traceable, and verifiable automated solutions for geometric problems. We observed that symmetry phenomena exist at various levels within FGPS and utilized these symmetries to further refine the system’s design. FGPS employs symbols to represent geometric shapes and transforms various geometric patterns into a set of symbolic operation rules. This maintains symmetry in basic transformations, shape constructions, and the application of theorems. Moreover, we also have annotated the formalgeo7k dataset, which contains 6981 geometry problems with detailed formal language descriptions and solutions. Experiments on formalgeo7k validate the correctness and utility of the FGPS. The forward search method with random strategy achieved a 39.71% problem-solving success rate.

1. Introduction

Symmetry refers to the property of an object remaining invariant under a certain transformation, which is widely present in various aspects of the real world, such as the periodic repetition of musical notes [1], the time/space translational symmetry of physical properties [2], and the bilateral symmetry of organisms [3]. This article designs a formal symbolic solver for the formal representation and automated solution of planar geometric problems and explores the symmetry involved in various aspects of geometric problem solving (GPS). GPS has always been a long-standing challenge [4,5,6] in the fields of mathematical reasoning and Artificial Intelligence (AI), owing to the cross-modal forms of knowledge and the absence of automated solving methods. As depicted in Figure 1, a geometry problem typically consists of geometric texts and images.

Based on the Geometry Formalization Theory and the FormalGeo geometric formal system [7], we have developed the Formal Geometric Problem Solver (FGPS) in Python. We elucidate the symmetry phenomena present in FGPS and how these symmetries can be utilized to improve solver design:

• Geometric shapes consist of several points, and when performing basic transformations such as rotation and scaling on the shapes, the relative positional information among the points does not change; that is, the shape’s topological structure information is symmetrical with respect to basic transformations. A complex geometric shape is often composed of several basic shapes, and the order of combination of the basic shapes does not change the final complex shape constructed; that is, the construction result is symmetrical relative to the construction order. We have implemented the above formal representation methods and construction methods, transforming the symmetry and asymmetry into a series of rules for symbolic operations. The implementation of these symmetries helps to ensure the comprehensiveness and correctness of the FGPS design.
• The process of GPS can be seen as the application of theorems, where each application derives new conditions, ultimately leading to the derivation of the solution objective. The application order of geometric theorems can form a directed acyclic graph (DAG), and any theorem sequence obtained through its topological sorting can solve the current geometric problem. The solvability of geometric problems with respect to the topological sorting of the theorem’s DAG is symmetrical. By leveraging this symmetry, we expand the number of problems according to the process of GPS, effectively addressing issues such as high labeling costs and scarcity of datasets.
• FGPS incorporates two symmetric problem-solving algorithms: forward search, which starts from known conditions and continuously applies theorems to reach the problem’s goal, and backward search, which starts from the problem’s goal and expands it into sub-goals until all sub-goals are known conditions. We organize the process of GPS into a hypertree with conditions as hypernodes and theorems as hyperedges. The hypertrees obtained from the two algorithms are mirror-symmetrical. We designed the backward search algorithm by analyzing the symmetrical processes of forward search, and the solution generation process of backward search is also based on forward search.

Traditional methods for GPS can generally be divided into three categories [8]: synthesis methods, algebraic methods, and invariant-based point elimination methods. Synthesis methods, such as the backward search method [9], forward chaining method [10] and deductive database method [11], is essentially a search-based method. Algebraic methods are based on coordinates, such as Wu’s method [12], transforming GPS into a computational problem. Invariant-based point elimination methods [13] find that the solution methods for geometric problems are embedded in their geometric shape construction. Due to limitations in computing power and the readability of the solution process, traditional methods can solve only a limited type and difficulty of geometric problems.

The rapid development of AI has provided new ideas for GPS. New neural network architectures have given models the ability to model geometric knowledge. New learning and training methods have made it easier for people to teach computers geometric a priori knowledge. Hence, AI-assisted synthesis methods, i.e., heuristic search methods, have attracted much attention from researchers. Such works can generally be divided into two categories [14]: symbolic approaches [15] and probabilistic approaches [16]. Symbolic methods require the prior construction of a formal system, and then geometric problem texts and images are parsed into a unified formal language. The AI predictor predicts theorems that may be needed in problem solving according to the formal language. The formal reasoner applies theorems and updates the known conditions of the problem. Direct theorem prediction can be modeled as a sequence generation task, and step-by-step theorem prediction can be modeled as a multi-classification task. Probabilistic methods model GPS as a sequence generation task with multimodal inputs, directly encoding geometric problem texts and images into a unified internal representation, then learning from human examples to generate problem-solving programs. These programs are subsequently executed by an executor to obtain the solution.

Nevertheless, both symbolic and probabilistic methods focus on the study of learning methods and model structures, neglecting the study of formal systems. Existing formal systems are roughly implemented using programming languages, and defining new predicates and theorems requires changing the solver’s code, making it difficult to expand. The reasoning process cannot record process information, making the problem-solving process unreadable and unverifiable by humans. There is little research on the formal theory of geometry, and no systematic sorting of the structure and knowledge in the geometric field. These shortcomings severely limit the representational ability of formal systems, making it almost impossible to solve higher difficulty problems, such as International Mathematical Olympiad (IMO)-level geometric problems [17]. There is an urgent need for research on geometric formal systems and solvers.

Based on FormalGeo [7], we constructed a search-based symbolic solver to addresses these issues. FormalGeo is a geometric formal system built on Geometry Formalization Theory, featuring good readability. The syntax of the geometric formal language is similar to predicate logic and close to natural language, providing excellent readability and establishing a bridge for communication between humans and computers. The geometric formal language includes Geometric Definition Language (GDL) and Condition Declaration Language (CDL). FGPS parses GDL and CDL to configure the formal system and input geometric problem. FormalGeo transforms the process of GPS into a series of applications of theorems, defined using Geometric Predicate Logic (GPL). FGPS can parse and execute GPL, achieving traceable geometric relational reasoning and algebraic equation solving. The known conditions of a geometric problem are stored internally in FGPS as quintuples (condition ID, condition type, condition body, premises, and theorem). Based on the premises and theorem of conditions, we reorganize and structure them, transforming the process of GPS into a hypertree with conditions as hypernodes and theorems as hyperedges. Thus, we achieve formal language input of problems and structured output of solutions, ultimately realizing readable, traceable, and verifiable solutions for geometric problems.

FGPS can run in two modes: interactive and automated. As shown in Figure 1, in the interactive mode, an external decision-maker is required to provide the next theorem information. FGPS applies the theorem and updates the problem status. When the external decision-maker is a human, FGPS can serve as an interactive proof assistant to help humans verify the proof process; when the decision-maker is an AI, it can conveniently implement heuristic search methods. When FGPS operates in automatic mode, it can use various methods (forward search, backward search, and heuristic search) combined with various search strategies (breadth-first search, depth-first search, random search, and random beam search) to solve problems, automatically removing redundant theorems after achieving the solution goal.

Our contributions can be summarized as follows:

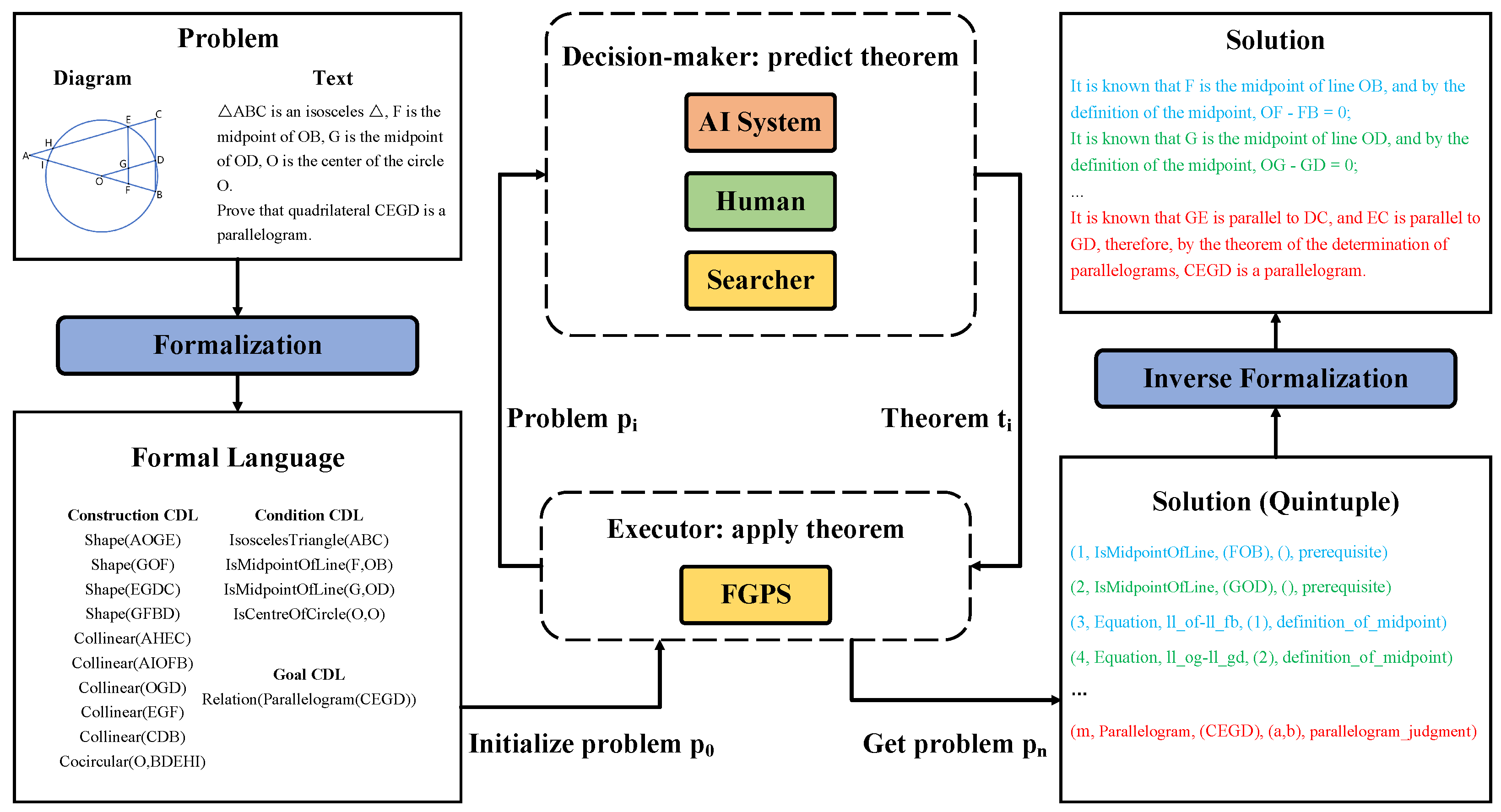
• We crafted FGPS in Python. It serves as both an interactive assistant for verifying problem-solving processes and an automated problem solver that utilizes a variable search-based method and strategy. FGPS incorporates functions such as formal statement parsing, condition validity checks, automatic diagram construction, and condition expansion. It is capable of performing readable, traceable, and verifiable algebraic equation solving and relational reasoning.
• We explored the symmetry phenomena inherent in basic geometric transformations, geometric constructions, geometric problem solving, and the design of the solving system, and utilized these symmetries to further refine the system’s design. The two symmetrical parts can verify and complement each other, making the design of FGPS more comprehensive and avoiding omissions.
• We annotated the formalgeo7k dataset, which contains 6981 (expanded to 133,818 using data augmentation method). Each problem comprises a complete natural language description, geometric shapes, formal language annotations, and theorem sequences annotations. Additionally, we have attempted to annotate 18 geometry IMO-level problems, forming the dataset formalgeo-imo.
• We conducted experiments on formalgeo7k, comparing different search methods and strategies in terms of their problem-solving success rate, search time, and search step. The forward search method combined with random search strategy achieved a 39.7% problem-solving accuracy rate.

2. Related Works

Gelernter et al. developed the pioneering automated GPS system known as the Geometry Theorem Prover [9], which employed a backward search approach to solve pre-formalized problems. Nevins pointed out that the forward chaining method [10] can also be effective by efficiently representing the known conditions of the problem and limiting the typical application of those conditions. The development of geometry problem solving has led to the emergence of various downstream tasks, including geometry problem formalization [18,19], geometric knowledge extraction [20,21,22,23,24], geometric diagram parsing [25,26,27], geometric theorem proving [28,29,30], and geometry problem solving [31,32,33,34,35,36]. Such methods are essentially a search-based method, which requires humans to predefine the search space or provide the system with a priori knowledge, namely theorems. Meanwhile, geometric problems need to be highly formalized to suit search formats. Theoretically, given a complete formal system and a priori knowledge, the search-based solver could provide solutions to any problem. However, in practice, we cannot determine if the given a priori knowledge is complete. Additionally, due to the exponential explosion characteristic of search-based methods, it is impossible to provide a correct solution within reasonable memory and time constraints.

Wen-Tsun proposed Wu’s method [12], which transforms geometric problem into a system of algebraic equations consisting of polynomials and inequalities. Then, by utilizing the properties of algebraic computation, these algebraic expressions are simplified and solved, transforming complex algebraic expressions into forms understandable by humans, and thus interpreting their geometric meanings. The study of algebraic approaches to geometry problems has given rise to a range of research achievements, such as Buchberger’s Gröbner bases method [37], numerical parallel methods [38], polynomial system triangulation elimination algorithm [39], cylindrical algebraic decomposition for solving inequalities [40], dimensionality reduction methods [41], and software tools like GEOTHER 1.0 [42]. These methods fully leverage the computational power of computers, but their problem-solving processes are not easily comprehensible to humans.

Zhang proposed the point elimination method based on geometric invariants [13]. This approach employs constructive methods to describe problems and is capable of generating concise and meaningful readable proofs for a large number of non-trivial geometric problems. Subsequently, research on machine proofs of geometric theorems based on geometric invariants rapidly advanced [43,44,45], leading to the development of practical software tools such as Geometry Explorer 1.1 [46], Geometry Expert 1.0 [47], and Java Geometry Expert 0.8 [48]. The method based on geometric invariant can also be extended to solid geometry [49] and non-Euclidean geometry [50]. Point elimination method is a mechanized method but requires a lot of effort in discovering new invariants and shape construction, and the types of geometric problems that can be solved are limited.

GPS has been gaining more attention in the natural language processing community recently. Several geometry formal systems and datasets have been constructed, such as Geometry3K [15], GeoQA [16], and GeometryQA [51]. Geometry3K [15] translates the known conditions of geometric problems into formal statements, defining theorems as a set of rules for converting between formal statements. This approach, referred to as “formal language”, is also used in GeoRE [22], which focuses on geometric relation extraction, and PGDP5k [52], which is designed for geometric image parsing; while these methods are intuitive, they lack theoretical guidance, are not comprehensive, and are not easily extensible with additional predicates and theorems. GeoQA [16] employs the formal method of the “program” approach, transforming the process of GPS into a sequence of programs consisting of variables and operators. Executing this program sequence yields the solution. Subsequent work extended the number and types of questions and rules, resulting in GeoQA+ [53], UniGeo [54], and PGPS9K [55]. These formal methods can represent algebraic and symbolic problem-solving processes, but compared to formal language methods, they are less intuitive and cannot represent traditional solutions. Additionally, adding new rules requires modifying the solver’s code, making them less extensible. GeometryQA [51] employs a formal method known as the expression tree, which transforms the problem-solving process into a solving tree composed of operators and variables. This method is similar to the program approach but is more structured. Shared benchmarks and datasets have significantly advanced research in AI-assisted GPS. Several AI systems, such as the CL-based model [56], SCA [57], GeoDRL [14], and LANS [58], have been constructed to achieve higher problem-solving success rates.

The integration of logic and neural networks has increasingly captured researchers’ interest in recent years. Early research endeavors, such as Neural Turing Machines [59], Memory Networks [60], and Neural Programmer [61], replaced discrete algorithms with end-to-end differentiable counterparts, which enable models to not only optimize via gradient descent but also to incorporate discrete computational and reasoning capabilities. Subsequent studies infused this concept into logical reasoning, proposing many neurosymbolic approaches. Notable examples include Neural Theorem Provers [62], DeepProbLog [63], Logical Tensor Networks [64], Neural Logic Machines [65], and Conditional Theorem Provers [66], which have been extensively applied in the area of knowledge graph reasoning [67,68]. In the field of automated theorem proving, simple reasoning rules are inducted as tactics, while large language models (LLMs) learn higher-level reasoning rules from experience, predicting the tactics necessary for problem solving. These tactics are then fed into a symbolic reasoner for verification. Approaches such as SCL [69], Thor [70], and HTPS [71] have been successful in solving IMO-level problems [72]. Furthermore, the reasoning capabilities of LLMs [73,74] have become a focal point of current research [75,76].

3. FGPS

In this section, we introduce the specific implementation of FGPS. FGPS is built upon Geometry Formalization Theory and the FormalGeo formal system [7].

3.1. Architecture

As illustrated in Figure 2, FGPS can be divided into five components:

• Main is the control module of FGPS, invoking other modules to enable interactive problem solving and automated problem solving. The automated solving component implements both forward search and backward search, allowing for the configuration of various search strategies and defining interfaces for AI-assisted searches.
• Engine is the core component of FGPS, responsible for parsing and executing GPL and consists of two sub-modules, GPL executor for relational reasoning and equation solver for algebraic computation.
• Parser facilitates bidirectional conversion between formal language and machine language. It consists of three sub-modules. GDL parser parses GPDL and GTDL into machine language, enabling custom configuration of the solver. CDL parser parses the formal describing of problems into machine language for subsequent reasoning. Inverse parser translates machine language back into formal language, facilitating the verification and checking of the solution process.
• Data preserves all details of the problem-solving process and comprises two sub-modules. The problem module ensures the correctness and consistency of the problem input conditions, implementing automatic diagram construction, condition auto-expansion, and validity checks. The condition module is responsible for data storage.
• AI interface defines the interface for interaction between the AI system and FGPS. Both the AI automatic formalization and the AI problem solver can be seamlessly integrated with FGPS.

Guided by Geometry Formalization Theory and modular design, FGPS boasts excellent extensibility, allowing for easy customization of the formal system and the definition of external interfaces.

3.2. GPL Executor

The process of GPS can be represented as a sequence of theorem applications and theorems are defined using GPL. As a result, the process of GPS within FGPS is essentially the execution of GPL. GPL statements can consist of multiple logical conjunction words, geometric relations, and quantitative relations nested together. The application process can be divided into three steps:

• In the GPL parsing phase, the solver expands complex GPL statements into Disjunctive Normal Form (DNF) using the distributive law. Each simple conjunction represents a branch of the theorem. This not only meets the requirements for backward reasoning and facilitates the generation of sub-goals but also speeds up theorem execution by skipping irrelevant branches.
• In the GPL ordering phase, for each branch of the theorem, the solver adjusts the positions of geometric relations and quantitative relations within simple conjunctions according to the commutative law. The guiding principles for this adjustment are as follows: 1. Transforming relation composition into geometric constraints. 2. Moving geometric constraints forward. 3. Moving algebraic constraints backward. This approach not only helps filter out geometric relation elements that do not comply with the constraints, preventing the explosion of combinatorics caused by Cartesian product operations, but also reduces the number for algebraic equation solving, thereby improving theorem application speed.
• In the GPL execution phase, the solver reads geometric and quantitative relations sequentially and performs relational reasoning in the order of their appearance.

The GPL execution process can be illustrated with an example. Suppose that we have a theorem defined as shown in Equation (1), which includes five geometric relations $R_1(v_1,v_2)$, $R_2(v_2,v_3)$, $R_3\left(v_2\right)$, $R_4(v_2,v_3)$, and $R_5\left(v_2\right)$ and one quantitative relation $R_A(v_1,v_2)$. It should be noted that the detailed definition of &, | and ∼ can be found in Geometry Formalization Theory [7].

$$R_1\&\left(R_2\right|(\sim R_3|R_A)\&R_4\&R_5)$$

(1)

During the GDL parsing phase, it is expanded into a DNF according to the distributive law, as shown in Equation (2). This DNF consists of three simple conjunctions, with each simple conjunction serving as a theorem branch.

$$R_1\&R_2|R_1\&\sim R_3\&R_4\&R_5|R_1\&R_A\&R_4\&R_5$$

(2)

In the GDL reordering phase, let us take branch $R_1\&R_A\&R_4\&R_5$ as an example. It adjusts the order of its statements according to the commutative law, resulting in the form shown in Equation (3).

$$R_1\&R_5\&R_4\&R_A$$

(3)

In the GPL execution phase, the GDL statements are read and executed in order, and the process is as shown in Equation (4).

$$R_1\&R_5\&R_4\&R_A\to R_{1,5}\&R_4\&R_A\to R_{1,5,4}\&R_A\to R_{1,5,4,A}$$

(4)

3.3. Core Engine

This subsection introduces the key methods that enable FGPS to perform geometric relational reasoning and algebraic equation solving. These methods are organized within a unified framework and constitute the core solving engine of FGPS.

3.3.1. Traceable Geometric Relational Reasoning

We transformed the execution process of GPL into its two most fundamental operations: $R_1\&R_2$ and $R_1\&R_A$. $R_1$ and $R_2$ are geometric relations, and $R_A$ is an quantitative relation. Let us assume the existing geometric relations $R_1(a,b)=\{(X,Y),(M,N)\}$, $R_2(b,c)=\left\{(Y,Z)\right\}$, quantitative constraint $R_A(a,b)$: $Equal\left(Attr\right(a),Attr(b\left)\right)$, and the known algebraic equations being $\{attr\_m-attr\_n=0\}$.

For the $R_1\&R_2$ type of operation, first, a Cartesian product operation is executed to obtain preliminary reasoning results $R^{\prime }$. Subsequently, intersection is performed on their point variables to obtain common variables, and each value of the common variables in $R^{\prime }$ is checked for correctness, filtering out the elements that meet the requirements. Then, a union of point variables is taken to reorganize the reasoning results.

Let us take $R_1(a,b)\&R_2(b,c)$ as example. First, we perform the Cartesian product operation:

$$R_1(a,b)\&R_2(b,c)=\{(X,Y,Y,Z),(M,N,Y,Z)\}$$

(5)

We filter out the elements based on common variables:

$$R^{\prime }(a,b,b,c)=\left\{(X,Y,Y,Z)\right\}$$

(6)

Remove duplicates variables:

$$R_{1,2}(a,b,c)=\left\{(X,Y,Z)\right\}$$

(7)

For the $R_1\&R_A$ type of operation, the intersection of point variables is taken to obtain common variables, and then the values of these common variables are substituted into the quantitative relation $R_A$, filtering out the elements that conform to the algebraic constraints.

Let us take $R_1(a,b)\&R_A(a,b)$ as example. First, we construct equations:

$$R_1(a,b)\&R_A(a,b)=\{attr\_a-attr\_b=0,attr\_m-attr\_n=0\}$$

(8)

We construct a system of equations based on the known algebraic equations and check whether the equations hold true.

$$R_A^{\prime }(a,b)=\{attr\_m-attr\_n=0\}$$

(9)

Filter the elements in $R_1$ based on whether the equations hold true.

$$R_{1,A}(a,b)=\left\{(M,N)\right\}$$

(10)

In the above reasoning process, the premises of the new relations are recorded synchronously, achieving traceable geometric relational reasoning.

3.3.2. Minimum Dependency Equation Constructing

The known conditions of geometric problems can be categorized into geometric and quantitative relationships. Quantitative relationships are eventually represented as a set of algebraic equations or inequalities. When performing algebraic constraint in the execution of GPL, the satisfaction of the algebraic constraint under the known algebraic equations or inequalities of the problem is checked.

Algebraic constraints can be transformed into algebraic expressions represented by a, creating the target equation $g-a$. Among the several known equations X in the problem conditions, those relevant to $g-a$ are selected to construct the target equation group G, which is subsequently solved. If $g=0$ is obtained as a solution, the algebraic constraints are satisfied. Typically, only a few equations in X are related to $g-a$, and this subset of equations is referred to as the minimum dependency equations.

The solving of equations accounts for the majority of the time spent in the entire process of solving geometric problems. Accelerating the equation solving process is crucial for enhancing the speed of geometric problem solving. To address this, we propose a method for constructing the minimum dependency equations. Without loss of generality, we examine the intermediate process of constructing G. At time t ($t=1,2,\dots$), $G_t$ contains t equations and m unknowns, with the set of unknowns denoted as $M_t$. We need to select a candidate equation $x_t$ from X to add to $G_t$ in a way that increases the likelihood of obtaining a solution for the unknown g. The set of unknowns in $x_t$ is represented as $B_t$. This process is repeated until $|M_t|=t$ or no new equations can be added.

$$|B_t\cap M_t|>0$$

(11)

$$min\left(\right|B_t-M_t\left|\right)$$

(12)

$$max\left(\right|B_t\cap M_t\left|\right)$$

(13)

The selection criteria for $x_t$ are as follows:

• $B_t$ must intersect with $M_t$, as shown in Equation (11). If they do not intersect, it implies that $x_t$ is unrelated to $G_t$.
• Under the condition of satisfying Equation (11), adding $x_t$ should introduce as few new unknown variables as possible, as depicted in Equation (12). The closer the number of t and $|M_t|$ are, the higher the likelihood of solving $G_t$. In the initial stages of constructing G, which only contains $g-a$, $M_1-1>1$. The number of added equations each time is a fixed value 1. If we aim to minimize the gap between t and $|M_t|$, we should try to introduce as few new equations when selecting $x_t$.
• Under the condition of satisfying Equations (11) and (12), the equation to be added should encompass more unknown variables, as demonstrated in Equation (13). These additional unknown variables are often associated with other equations within $G_t$, providing more choices for simplifying $G_t$. If there are multiple equations that satisfy these conditions, we can choose any of them at random.

3.4. GPS Methods

By invoking FGPS’s core modules, we have developed both an interactive solver and a search-based problem solver. Next, we will introduce the forward search algorithm and the backward search algorithm.

Forward search (FW) starts from the known conditions of the problem and continuously applies theorems to derive new conditions until the goal is achieved. The search process involves the construction of a search tree, with nodes representing sets of known conditions and edges denoting theorems, as depicted in Figure 3. The description of the forward search algorithm is provided in Algorithm 1. The function $get\_expandable\left(\right)$ traverses the search tree based on predefined strategies (BFS, DFS, RS, and RBS) and returns nodes with the EXPANDABLE state. The function $apply\_theorem\left(\right)$ applies the theorem associated with the current node and returns whether the problem solved. The function $get\_theorem\_seqs\left(\right)$ returns a list of theorems applied from the root node to the current node. The function $expand\left(\right)$, guided by the known conditions of the current node, checks the list of applicable theorems and extends new nodes.

Algorithm 1 Forward search

Input: $tree$: a tree with the known problem conditions as the root node. Output: $theorem\_seqs$: list of theorem sequences for problem solving. Initialize a list $theorem\_seqs$ $node\leftarrow tree.get\_expandable\left(\right)$ while $node$ is not $None$ do    $solved\leftarrow node.apply\_theorem\left(\right)$    if $solved$ then       $node.state\leftarrow$ SOLVED       $theorem\_seqs\leftarrow node.get\_theorem\_seqs\left(\right)$       break    end if    $node.state\leftarrow$ EXPANDED    if $node.expand\left(\right)=0$ then       $node.state\leftarrow$ FAILED    end if    $node\leftarrow tree.get\_expandable\left(\right)$ end while

The complexity of forward search is related to the size of the search space (the number of defined theorems M) and the difficulty of the problem (the length of the problem-solving theorem sequence L). We need to apply theorems to expand each node of the forward search tree. The number of theorems that can be applied varies for different types of nodes, and we take the average number, $k_{f}M$, as the number of applied theorems for each node expansion. From the beginning to the end of problem solving, the search tree expands to the M level, and we need to store all nodes of the search tree. The time complexity and space complexity are shown in Equation (14) and Equation (15), respectively.

$$T(M,L)=\sum _{l=1}^L{\left(k_{f}M\right)}^l=\frac{k_{f}M(k_f{M}^L-1)}{k_{f}M-1}=O\left(M^L\right)$$

(14)

$$S(M,L)=\sum _{l=0}^L{\left(k_{f}M\right)}^l=\frac{k_f{M}^{L+1}-1}{k_{f}M-1}=O\left(M^L\right)$$

(15)

Backward search (BW), on the other hand, begins with the problem-solving goal, expands it into multiple sub-goals, and repeats this process until all sub-goals are resolved. The search process involves the construction of a search tree, with nodes representing sub-goals, supernodes representing sets of sub-goals, and edges representing theorems, as illustrated in Figure 3. The description of the backward search algorithm is provided in Algorithm 2. The function $get\_expandable\left(\right)$ traverses the search tree based on predefined strategies, returning supernodes with the EXPANDABLE state. The function $node.check\left(\right)$ updates the state of the superNode based on the known problem conditions, while the function $super\_node.check\left(\right)$ updates its own state based on the states of its nodes. The function $expand\left(\right)$ extends the current goal into several sub-goals based on the list of theorems. The function $update\left(\right)$ propagates the state update from child nodes to parent nodes, starting from the leaves and progressing up to the root. The function $get\_theorem\_seqs\left(\right)$ provides a list of theorems applied from the current node to the root node.

Algorithm 2 Backward search

Input: $super\_tree$: a super tree with the problem goal as the root super node. Output: $theorem\_seqs$: list of theorem sequences for problem solving. Initialize a list $theorem\_seqs$ $super\_node\leftarrow super\_tree.get\_expandable\left(\right)$ while $super\_node$ is not $None$ do    for $i=1$ to $len(super\_node.nodes)$ do      $node\leftarrow super\_node.nodes\left[i\right]$      $node.check\left(\right)$      if $node.state$ is SOLVED then         continue      else if $node.state$ is FAILED then         break      else if $node.expand\left(\right)=0$ then         $node.state\leftarrow$ FAILED         break      else         $node.state\leftarrow$ EXPANDED      end if    end for    $super\_node.check\left(\right)$    $super\_tree.update\left(\right)$    if $super\_tree.solved$ then      $theorem\_seqs\leftarrow super\_tree.get\_theorem\_seqs\left(\right)$      break    end if    $super\_node\leftarrow super\_tree.get\_expandable\left(\right)$ end while

Similar to the forward search algorithm, the backward search algorithm is related to M and L. Let us assume that each node can be expanded into an average of $k_{b}M$ supernodes, and each supernode contains an average of $k_s$ nodes. In the node expansion phase, the algorithm needs to expand one node to $k_{b}M\times k_s$ nodes. In the the backpropagation phase, algorithm needs to update the state of ${\left(k_s{k}_{b}M\right)}^l$ nodes from l levels up to root node. Therefore, its overall time complexity is as shown in Equation (16). The algorithm needs to save all nodes during the running process, and its space complexity is as shown in Equation (17).

$$T(M,L)=\sum _{l=1}^L{\left(k_s{k}_{b}M\right)}^l+\sum _{l=1}^{L}l{\left(k_s{k}_{b}M\right)}^l=O\left(L{M}^L\right)$$

(16)

$$S(M,L)=\sum _{l=1}^L{\left(k_s{k}_{b}M\right)}^l=O\left(M^L\right)$$

(17)

4. Datasets

Most of the existing datasets for GPS suffer from the following issues: 1. Limited data volume or non-open source availability. 2. Lack of annotations or incomplete and low-quality annotations. 3. Absence of formalization theory support, resulting in incoherent and inconsistent formal systems. 4. Low scalability, defining new predicates and theorems require solver’s code modifications. 5. Lower difficulty level of the problems. To address the aforementioned issues, we annotated datasets formalgeo7k and formalgeo-imo. We conducted a comparative analysis with existing works, as shown in

Table 1. Comparative analysis with existing GPS datasets.

Datasets	FM	Size	Comparative Metrics
			FW	BW	IS	AS	NT	PT	ET	VC	SS
GEOS [31]	FL	186	✔		✔		✔
GEOS++ [20]	FL	1406	✔		✔		✔
Geometry3K [15]	FL	3002	✔		✔		✔
GeoQA [16]	P	5010	✔		✔		✔
GeometryQA [51]	P	1398	✔		✔		✔
GeoQA+ [53]	P	7528 (5010 from [16])	✔		✔		✔
UniGeo [54]	P	14,541 (4998 from [16])	✔		✔		✔	✔
PGPS9K [55]	P	9022 (2891 from [15])	✔		✔		✔
formalgeo7k	FL	6981 (DA to 133,818)	✔	✔	✔	✔	✔	✔	✔	✔	✔
formalgeo-imo	FL	18 (DA to 2627)	✔	✔	✔	✔	✔	✔	✔	✔	✔

✔ indicates that the dataset and its formal system have such features. FM denotes formalized methods, FL denotes formal language, P denotes program, and DA denotes data augmentation. The 9 comparative metrics are forward solving method, backward solving method, interactive solving, automatic solving, numerical target, proving target, extensible, validity check, and structured solution.

.

Our data are collected from various sources, including Geometry3k [15], GeoQA [16], GeoQA+ [53], and online resources. We carefully curated, classified, deduplicated, and standardized the problem statements. The creation of the formalgeo7k involved 16 trained master’s students over a period of around 13 weeks. The creation of the formalgeo-imo involved four trained master’s students over a period of around 1 week. Excluding the time spent on collaboration and dataset allocation, annotating datasets took approximately 1000 person-hours.

formalgeo7k comprises 6981 geometric problems that are accompanied by natural language descriptions, geometric diagrams, formal language annotations, and solution theorem sequence annotations. An annotated problem is illustrated in in Figure 1 (omitting the theorem annotations). The problem-solving process can be represented as a hypertree with conditions as hypernodes and theorems as hyperedges. The solution theorem sequence is a path from the root node (known conditions) to a leaf node (the problem-solving objective). By selecting any intermediate node along this path as the problem-solving objective, we can generate new problems, allowing us to expand the problem number to 133,818. formalgeo-imo is constructed with the same standards but with more challenging problem difficulty.

We used the length of theorem sequences required for problem solving as a rough metric for assessing problem difficulty. All annotated and expanded problems have been verified by the solver, and their average solution times varying with problem difficulty are also show in Figure 4. The number of questions with a difficulty level of 15 or higher in formalgeo7k is quite small, leading to significant fluctuations. After data augmentation, datasets exhibited a larger scale of data and a smoother difficulty curve. In general, more challenging problems require longer solving time.

5. Experiments

We conducted experiments on the formalgeo7k, comparing different search methods and strategies in terms of problem-solving success rate, solution time, and the number of steps required for problem solving.

Forward search (FW) starts from the known conditions of the problem and continuously applies theorems to derive new conditions until the goal is achieved. Backward search (BW), on the other hand, begins with the problem-solving goal, expands it into multiple sub-goals, and repeats this process until all sub-goals are resolved.

The search-based methods construct a search tree during the problem-solving process. We have the flexibility to choose various strategies to traverse the search tree and reach the goal. Breadth-first search (BFS) begins by expanding the top-level nodes of the search tree and then proceeds layer by layer into the depth. Depth-first search (DFS) recursively selects nodes from the search tree from shallow to deep and continues this process. Random search (RS) randomly selects an expandable node at each stage of expansion. Beam search (BS) selects k nodes in each stage of expansion and can be viewed as a trade-off between BFS and RS.

We conducted experiments on two Intel i9-10900X, one AMD Ryzen 9 5900X, and one AMD Ryzen 9 7950X (The Intel processors were sourced from Intel Corporation, Santa Clara, California, USA. The AMD processors were sourced from Advanced Micro Devices, Inc., Sunny vale, California, USA.), running the search algorithms using multiple processes while maintaining a CPU utilization rate of 80%. The maximum search depth was set to 15, and the beam size was set to 20. The total duration of the experiments was approximately 3 days. When the timeout for each problem was 300 s, the best success rate for problem solving was approximately 30%. When the timeout for each problem was increased to 600 s, the specific results are as follows.

An overview of search-based automated problem-solving results is presented in

Table 2. An overview of search results.

Method	Strategy	Result (%)
		Solved	Unsolved	Timeout
FW	BFS	38.86	7.42	53.72
FW	DFS	36.16	9.80	54.05
FW	RS	39.71	9.07	51.22
FW	BS	25.28	38.72	36.00
BW	BFS	35.44	2.68	61.88
BW	DFS	33.73	2.42	63.84
BW	RS	34.05	2.65	63.30
BW	BS	34.39	12.86	52.74

The bold data indicates the best results in the FW or BW methods.

. The highest problem-solving success rate was achieved by forward random search, reaching 39.708%. Most of the remaining problems were due to timeouts. As timeout settings are extended and computational resources increase, the proportion of timeout problems is expected to decrease. The number of unsolved problems using beam search was significantly higher compared to other strategies. This is because when selecting k branches, beam search occasionally discards the correct branch. Other contributing factors may include code bugs, equation solving timeouts, and the omission of theorems related to trigonometry.

In accordance with the length of the theorems required for problem solving, we roughly categorized the difficulty of the questions into six levels, denoted as $l_1(length<3)$, $l_2(3\le length\le 4)$, $l_3(5\le length\le 6)$, $l_4(7\le length\le 8)$, $l_5(9\le length\le 10)$, and $l_6(length>10)$, with corresponding problem numbers of 2407, 1898, 1247, 824, 313, and 292. The success rates for solving geometric problems of varying difficulty are presented in

Table 3. Results of success rates.

Method	Strategy	Success Rates (%)
		Total	${\mathit{l}}_{\mathbf{1}}$	${\mathit{l}}_{\mathbf{2}}$	${\mathit{l}}_{\mathbf{3}}$	${\mathit{l}}_{\mathbf{4}}$	${\mathit{l}}_{\mathbf{5}}$	${\mathit{l}}_{\mathbf{6}}$
FW	BFS	38.86	59.95	38.62	28.55	17.35	8.63	3.77
FW	DFS	36.16	55.75	40.04	22.94	12.38	7.03	4.11
FW	RS	39.71	59.24	40.04	33.68	16.38	5.43	4.79
FW	BS	25.28	46.12	22.60	13.47	5.83	2.88	0.34
BW	BFS	35.44	67.22	33.72	11.15	6.67	6.07	1.03
BW	DFS	33.73	65.93	30.82	8.90	6.55	5.11	0.68
BW	RS	34.05	66.64	31.66	8.66	5.83	4.47	0.68
BW	BS	34.39	67.10	31.35	9.46	6.31	5.75	1.03

The bold data indicates the best results in the FW and BW methods.

. As the problem difficulty increases, the success rate of problem solving rapidly declines. This phenomenon can be attributed to the fact that search-based problem-solving methods exhibit exponential growth in solving time as the length of the theorem sequence increases, often resulting in timeouts before achieving the goal. For problems of lower difficulty, backward search demonstrate a relatively higher success rate, while forward search outperforms in the case of more challenging problems.

The efficiency of the problem-solving algorithm can be measured by the search time and step. The experimental results of search-based automated problem-solving algorithms on the formalgeo7k are presented in Figure 5.

In terms of average search time, backward search is slightly better than forward search overall. For solved problems, the search time is roughly proportional to the difficulty of the problems when problems are of low difficulty. However, as the difficulty increases, the search time for both forward search and backward search decreases. On the one hand, this is because there are very few successfully solved high-difficulty problems, leading to significant statistical errors. On the other hand, when dividing the difficulty of problems, we only consider the length of the solution theorem sequence but do not consider the time required for each theorem execution. The solved high-difficulty problems are precisely those that require less solution time. For unsolved problems, the search time is roughly proportional to the difficulty of the problems.

Comparing different search strategies, it can be observed that in the forward search, BFS has a slightly lower success rate compared to the RS, but it takes the most time. BS has the lowest success rate but the least time consumption. For forward search, RS is the optimal strategy as it has the highest success rate and only slightly higher time consumption than BS that has the lowest success rate. In backward search, BFS is the optimal strategy, with the highest success rate and only slightly higher time consumption than DFS.

We observe a significant difference in the solution time of the BS strategy in backward search for solved and unsolved problems. This difference may be due to the characteristics of the backward search, where even if possible solution branches were discarded in previous steps, they may be reconstructed in later search steps. Therefore, as for BS strategy in backward search, discarding potential solution branches does not lead to solution failure but takes longer search time.

Regarding the search step, forward search statistics are based on the number of nodes, while backward search statistics are based on the number of super nodes. Hence, they cannot be directly compared. The search step length in forward search is positively correlated with the difficulty of problems, while in backward search, it is negatively correlated with problem difficulty. The results of backward search are counterintuitive, and this could be because, for higher difficulty problems, the super nodes in backward search may contain more nodes, leading to increased time spent traversing a single super node and a reduction in the total number of traversed super nodes. Additionally, it can be observed that the search step length for unsolved problems in backward search is significantly higher than the average step length for solved problems. This is because, compared to forward search, backward search is less likely to halt, and it continues searching even if it misses a potential solution branch.

Comparing different strategies, DFS has the highest search step length, BS has the lowest search step length, and RS and BFS strategies have approximately the same average step length. For forward search, RS strategy is still the optimal strategy because it has the highest success rate and its search step length is only slightly higher than BS. Backward search does not exhibit a significantly superior strategy.

6. Conclusions

Based on the Geometry Formalization Theory and the FormalGeo geometric formal system, we constructed FGPS, which can serve as an interactive assistant for verifying problem-solving processes and as an automated problem solver that utilizes variable search-based methods and strategies. Moreover, we explored the symmetry phenomena inherent in basic geometric transformations, geometric constructions, geometric problem solving, and the design of the solving system, and utilize these symmetries to further refine the system’s design. We annotated GPS datasets formalgeo7k and formalgeo-imo, the former contains 6981 geometry problems with detailed formal language descriptions and solutions. Experiments have demonstrated the correctness and efficiency of FGPS. In the future, we plan to further refine the formal system to annotate geometry problems at the IMO-level. We also plan to apply deep learning techniques to search tree pruning for the automatic solving of IMO-level geometric problems.