Modeling the Non-Hermitian Infinity-Loop Micro-Resonator over a Free Spectral Range Reveals the Characteristics for Operation at an Exceptional Point
Abstract
:1. Introduction
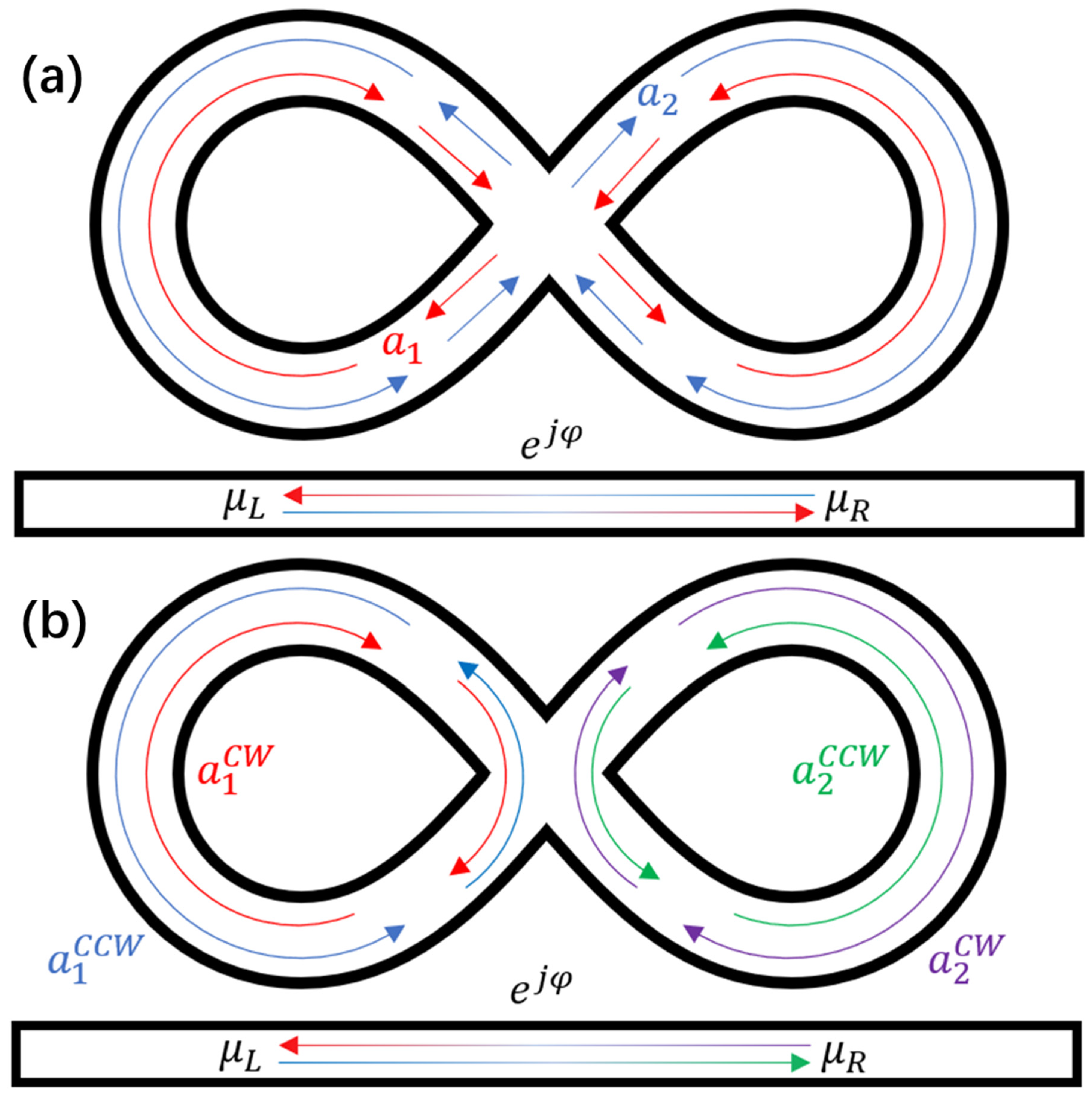
2. Temporal Coupled-Mode Theory Model
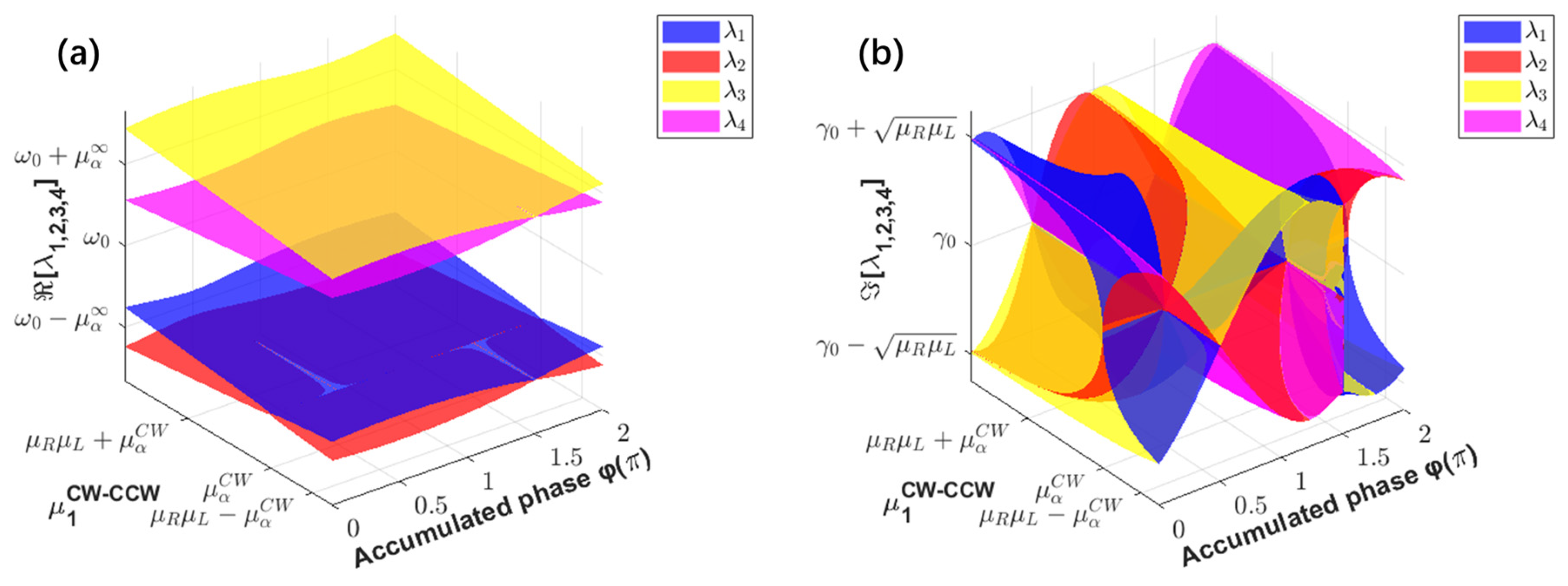
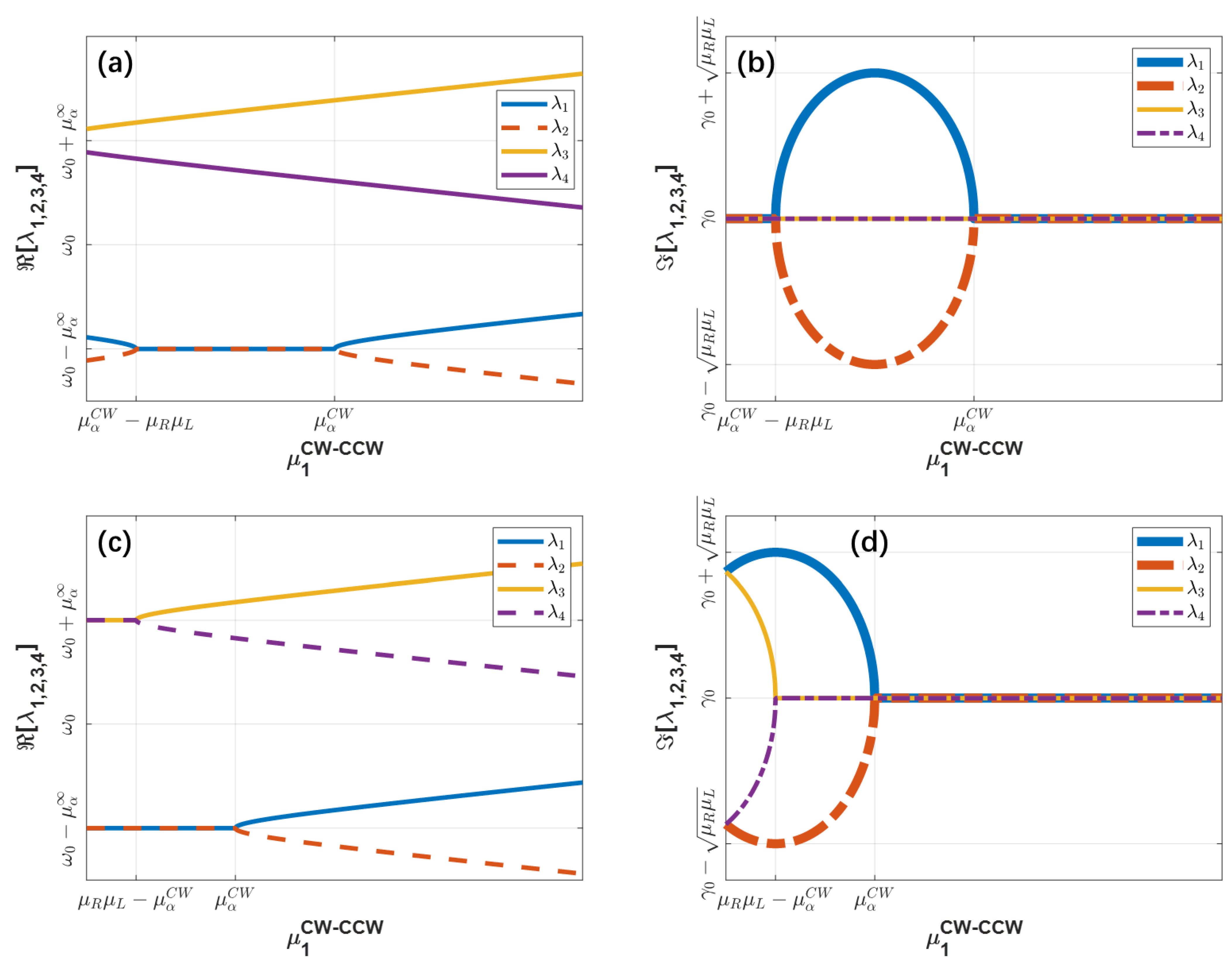
2.1. Eigenvalue Analysis
2.2. COMSOL Simulation of Coupling Coefficients between Modes
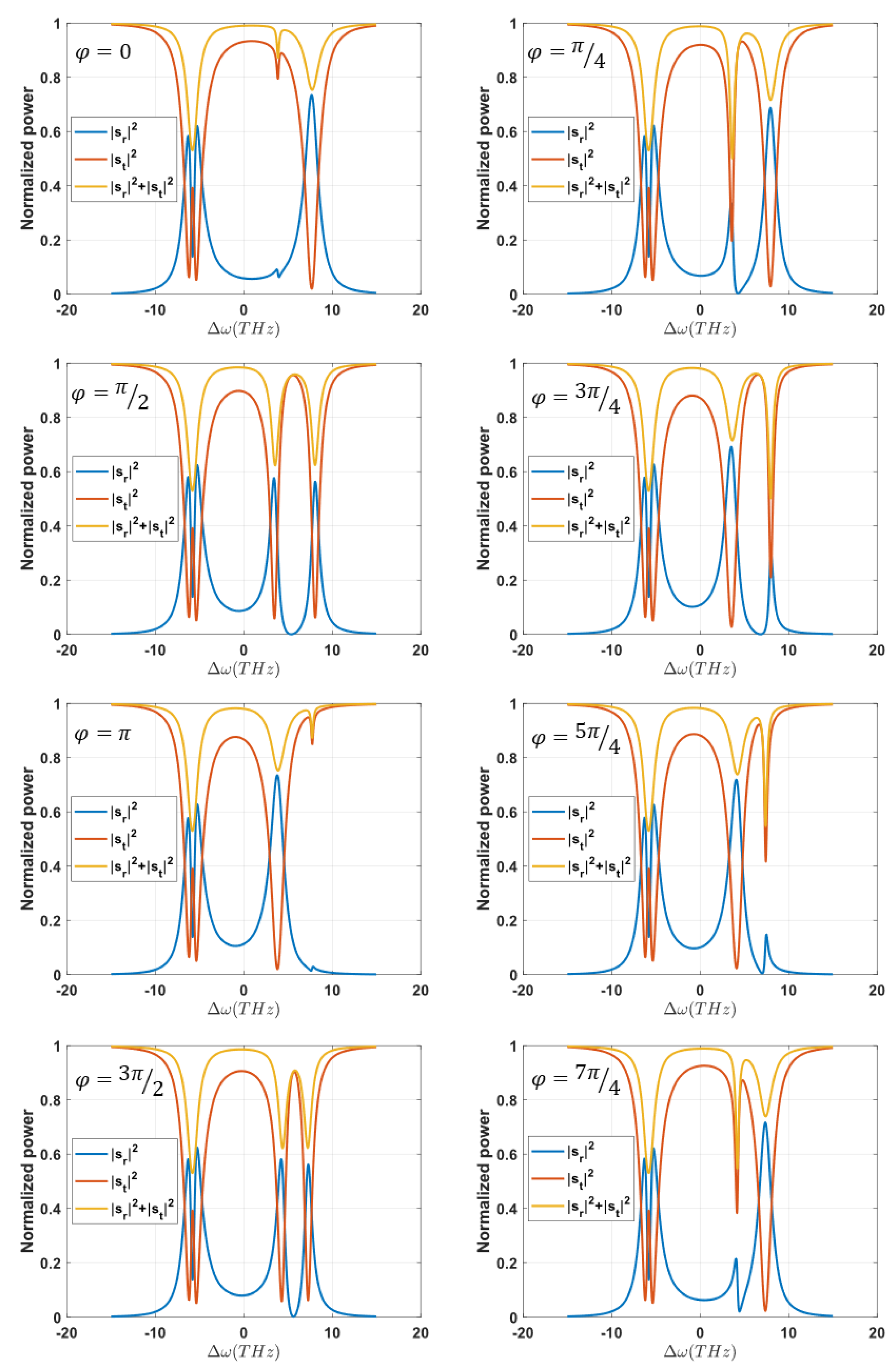
2.3. TCMT-Model-Derived Spectral Resonances
3. COMSOL-Simulation-Derived Spectral Resonances
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haus, H.; Huang, W. Coupled-mode theory. Proc. IEEE 1991, 79, 1505–1518. [Google Scholar] [CrossRef]
- Wang, T. Generalized temporal coupled-mode theory for a P T-symmetric optical resonator and Fano resonance in a P T-symmetric photonic heterostructure. Opt. Express 2022, 30, 37980–37992. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, N.; Lu, X.; Hu, Y.; Yang, Z.; Zhang, X.; Xu, J. Bandwidth Tunable Optical Bandpass Filter Based on Parity-Time Symmetry. Micromachines 2022, 13, 89. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Chen, N.; Zhang, B.; Yang, H.; Chen, Y.; Zhang, X.; Xu, J. Parity-Time Symmetry Enabled Band-Pass Filter Featuring High Bandwidth-Tunable Contrast Ratio. Photonics 2022, 9, 380. [Google Scholar] [CrossRef]
- Fan, S. 12—Photonic crystal theory: Temporal coupled-mode formalism. In Optical Fiber Telecommunications V A, 5th ed.; Kaminow, I.P., Li, T., Willner, A.E., Eds.; Optics and Photonics; Academic Press: Burlington, MA, USA, 2008; pp. 431–454. [Google Scholar] [CrossRef]
- Van, V. Optical Microring Resonators: Theory, Techniques, and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Behunin, R.O.; Otterstrom, N.T.; Rakich, P.T.; Gundavarapu, S.; Blumenthal, D.J. Fundamental noise dynamics in cascaded-order Brillouin lasers. Phys. Rev. A 2018, 98, 023832. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, M.; Zhu, D.; Sinclair, N.; Shams-Ansari, A.; Shao, L.; Holzgrafe, J.; Puma, E.; Zhang, M.; Lončar, M. On-chip electro-optic frequency shifters and beam splitters. Nature 2021, 599, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192–195. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Joglekar, Y.N.; Harter, A.K. Passive parity-time-symmetry-breaking transitions without exceptional points in dissipative photonic systems [Invited]. Photonics Res. 2018, 6, A51–A57. [Google Scholar] [CrossRef]
- Ma, J.; Wen, J.; Ding, S.; Li, S.; Hu, Y.; Jiang, X.; Jiang, L.; Xiao, M. Chip-Based Optical Isolator and Nonreciprocal Parity-Time Symmetry Induced by Stimulated Brillouin Scattering. Laser Photonics Rev. 2020, 14, 1900278. [Google Scholar] [CrossRef]
- Calabrese, A.; Ramiro-Manzano, F.; Price, H.M.; Biasi, S.; Bernard, M.; Ghulinyan, M.; Carusotto, I.; Pavesi, L. Unidirectional reflection from an integrated “taiji” microresonator. Photonics Res. 2020, 8, 1333–1341. [Google Scholar] [CrossRef]
- Biasi, S.; Franchi, R.; Mione, F.; Pavesi, L. Interferometric method to estimate the eigenvalues of a non-Hermitian two-level optical system. Photonics Res. 2022, 10, 1134–1145. [Google Scholar] [CrossRef]
- Zhong, Q.; Ren, J.; Khajavikhan, M.; Christodoulides, D.; Özdemir, Ş.K.; El-Ganainy, R. Sensing with Exceptional Surfaces in Order to Combine Sensitivity with Robustness. Phys. Rev. Lett. 2019, 122, 153902. [Google Scholar] [CrossRef]
- Franchi, R.; Biasi, S.; Piciocchi, D.; Pavesi, L. The infinity-loop microresonator: A new integrated photonic structure working on an exceptional surface. APL Photonics 2023, 8, 056111. [Google Scholar] [CrossRef]
- Dingel, B.B.; Nacpil, J.C. Multifunctional tunable band-limited optical Coupled-Ring Reflector (CRR) device using criss-crossing directional coupler. In Proceedings of the 2021 IEEE Region 10 Symposium (TENSYMP), Jeju, Republic of Korea, 23–25 August 2021; pp. 1–5. [Google Scholar] [CrossRef]



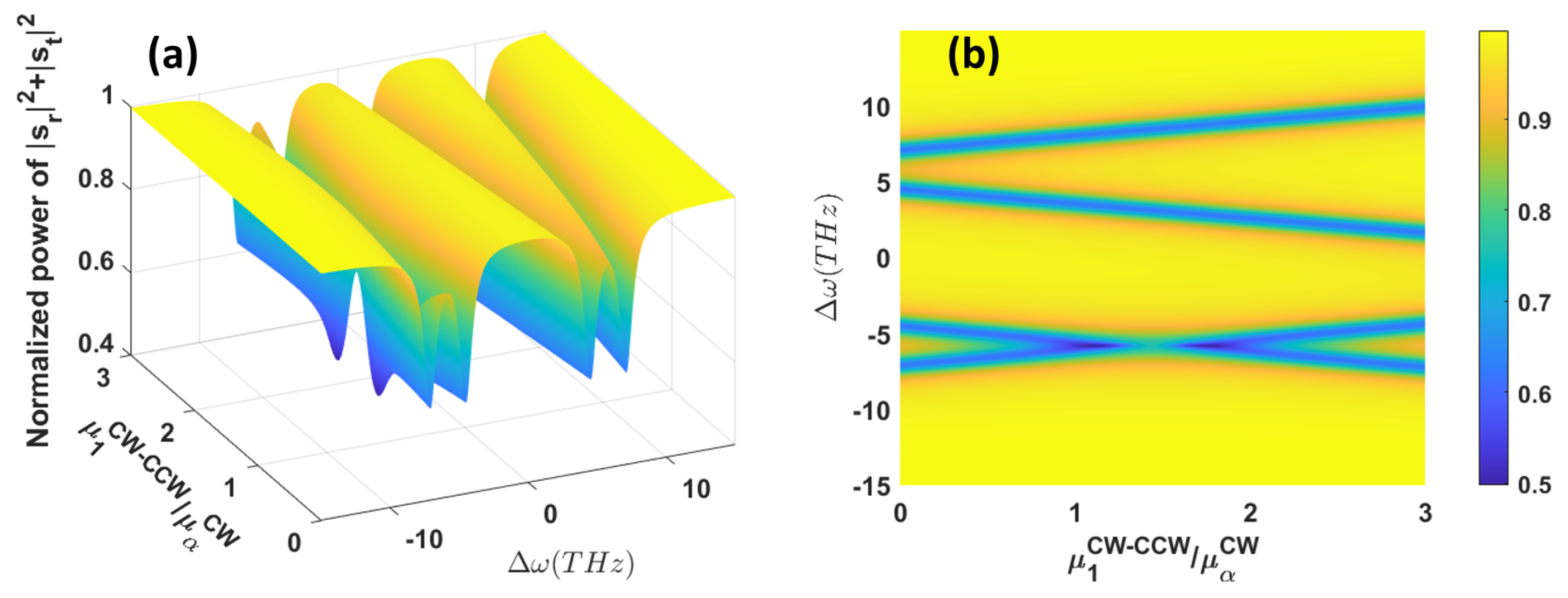
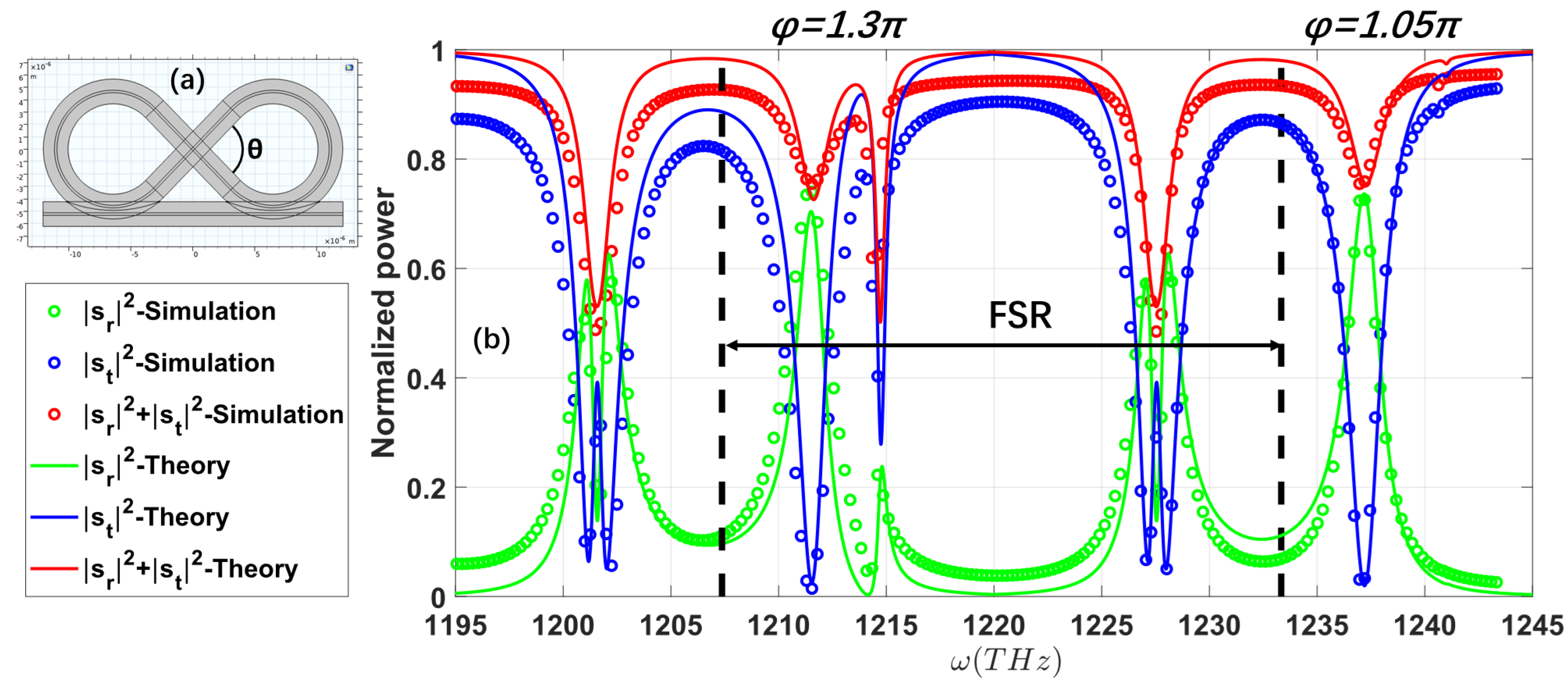
| Parameters | The Coupling/Loss Rates [THz] |
|---|---|
| 5.8037 | |
| 0.9431 | |
| 0.9431 | |
| 0.8152 | |
| 0.8152 | |
| 0.5421 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Halsall, M.P.; Crowe, I.F. Modeling the Non-Hermitian Infinity-Loop Micro-Resonator over a Free Spectral Range Reveals the Characteristics for Operation at an Exceptional Point. Symmetry 2024, 16, 430. https://doi.org/10.3390/sym16040430
Li T, Halsall MP, Crowe IF. Modeling the Non-Hermitian Infinity-Loop Micro-Resonator over a Free Spectral Range Reveals the Characteristics for Operation at an Exceptional Point. Symmetry. 2024; 16(4):430. https://doi.org/10.3390/sym16040430
Chicago/Turabian StyleLi, Tianrui, Matthew P. Halsall, and Iain F. Crowe. 2024. "Modeling the Non-Hermitian Infinity-Loop Micro-Resonator over a Free Spectral Range Reveals the Characteristics for Operation at an Exceptional Point" Symmetry 16, no. 4: 430. https://doi.org/10.3390/sym16040430
APA StyleLi, T., Halsall, M. P., & Crowe, I. F. (2024). Modeling the Non-Hermitian Infinity-Loop Micro-Resonator over a Free Spectral Range Reveals the Characteristics for Operation at an Exceptional Point. Symmetry, 16(4), 430. https://doi.org/10.3390/sym16040430






