Novel Phenomena of the Hartle–Hawking Wave Function
Abstract
:1. Introduction
- Wave packet: If we consider a wave function as a superposition of eigenstates, we obtain the following wave function:where denotes the n-th eigenstates and is the corresponding energy eigenvalue. In this wave packet, one can provide the meaning of the classicality: if a wave function is highly localized, the Ehrenfest theorem shows that the expectation value of an observable satisfies the classical equation of motion.
- Eigenstate: If we only choose one specific eigenstate, e.g., the ground state, we will only focus on with a fixed energy eigenvalue. The probability to measure at x is . In the scattering state, if the wave function is oscillatory, say , it indicates a classical propagation, while if the wave function is exponentially varied, say , it indicates a quantum regime. Here, the latter can be well approximated by the Wentzel–Kramers–Brillouin (WKB) approximation, and this can provide a tunneling or nucleation probability.
- Wave packet interpretation: If one interprets the wave function as a superposition of various states, one can define a propagating wave packet [6]. From this wave packet, one can read a classical trajectory that is consistent with the Ehrenfest theorem. If the wave function is flat along the steepest-descent while its dispersion is bounded, and hence, if the probability is not varied along the path, one can interpret that the trajectory is classical; indeed, it can satisfy the classical equation of motion [7,8]. Therefore, one can reasonably recover an arrow of time. Thus, the wave function describes the classical dynamics of the universe (although it can include non-classical effects, e.g., quantum bounces, thanks to the wave nature of the wave function).
- Eigenstate interpretation: If one interprets the wave function as a specific eigenstate, one will first interpret that the wave function has two limits, where the wave function shows exponential behaviors in the classically disallowed domain, while it shows oscillatory behaviors in the classically allowed domain [3,4,5]. Hence, at the classically disallowed domain, one will measure a specific a and , where the absolute square of the wave function is the probability to measure a and ϕ. Once one measures a specific a and , the universe will evolve along the classical path; hence, the measured a and become a set of initial conditions. If one selects this interpretation, we cannot see any subsequent classical dynamics from the wave function of the universe; this only provides a probability distribution.
2. Preliminaries
2.1. Wheeler–DeWitt Equation
2.2. Hartle–Hawking Wave Function
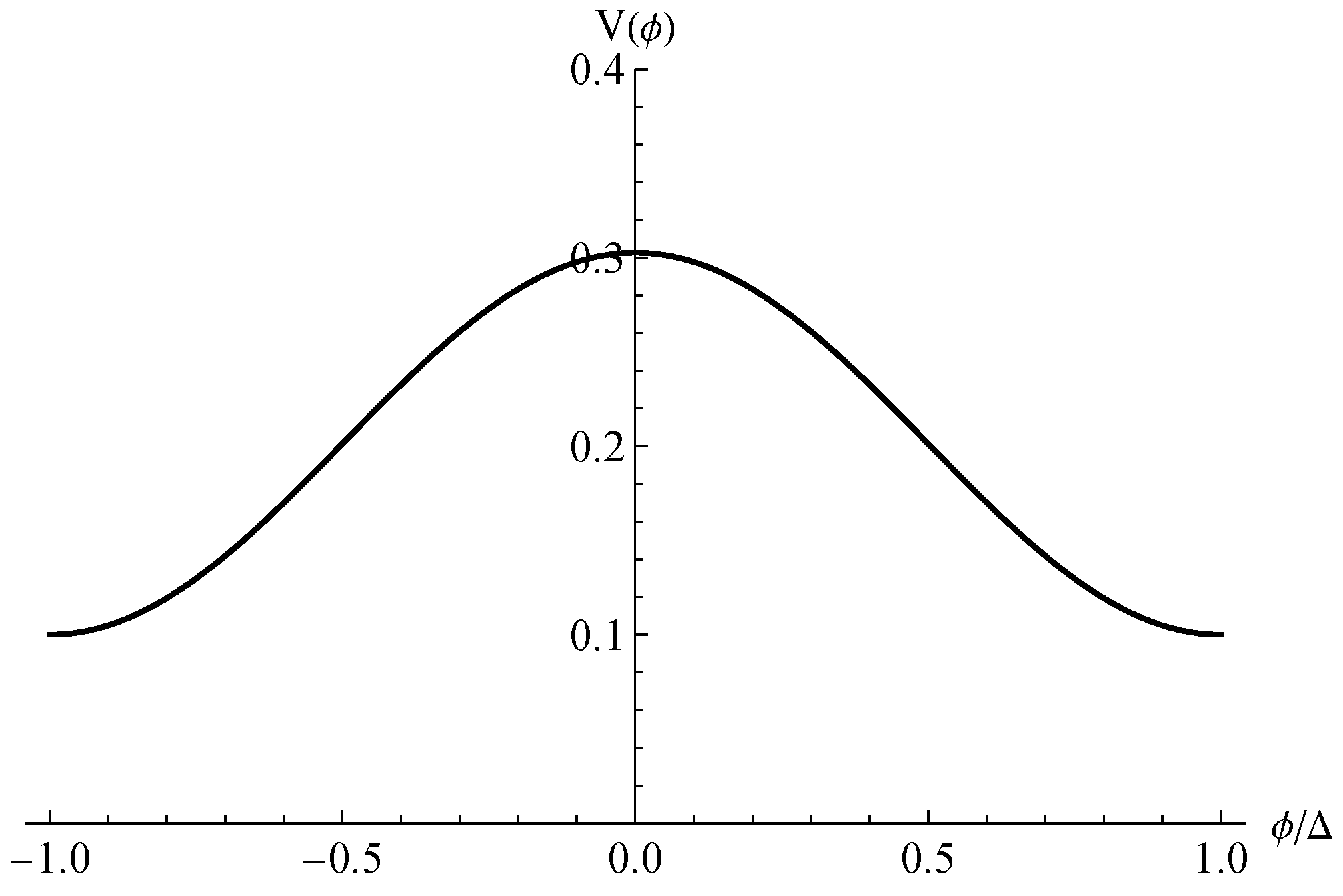
2.3. Model and Boundary Conditions
3. Novel Phenomena of the Hartle–Hawking Wave Function
3.1. Wave Function
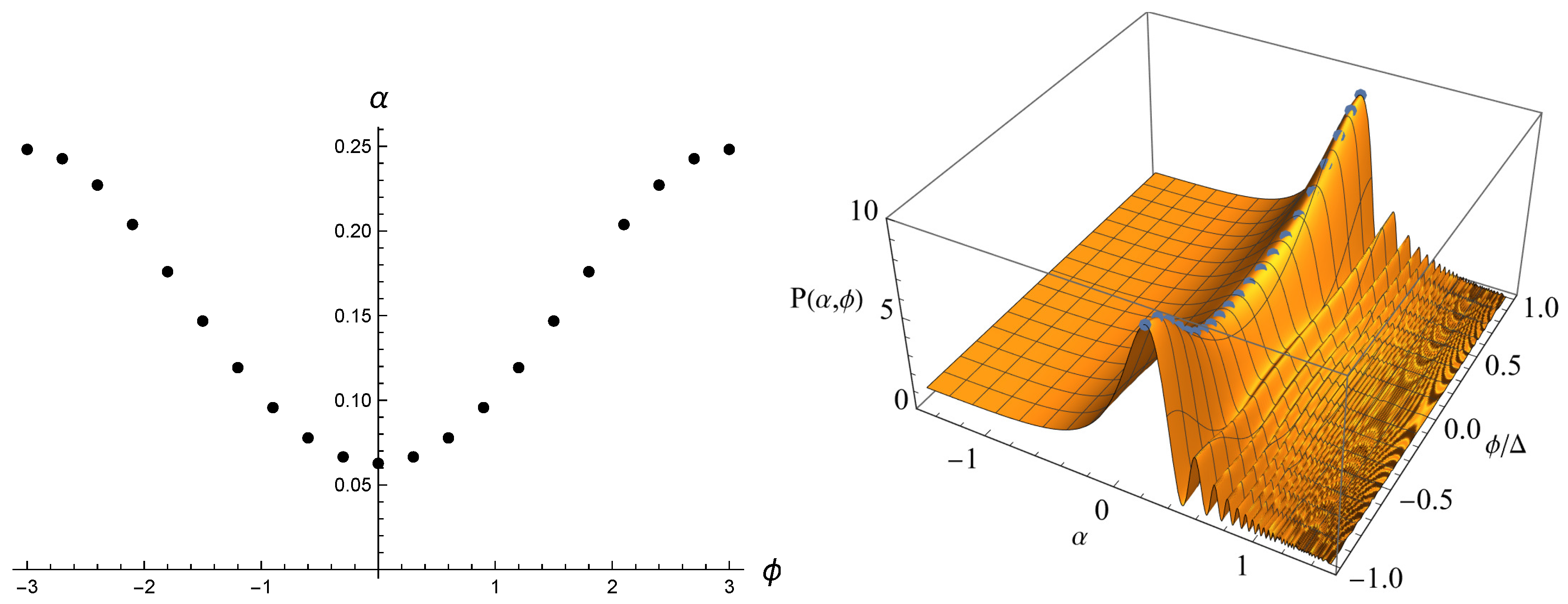
3.2. Probabilities
- 1.
- Analytic limit: Interestingly, as increases (equivalently, as the potential becomes increasingly flat, satisfying the slow-roll condition), the measure approaches to one (Figure 5). This shows that the analytic approximation is very good for ultra-slow-roll cases. Therefore, we confirm that this numerical approach is consistent with the analytic expectations.
- 2.
- Beyond Hawking–Moss instantons: On the other hand, as the slow-roll parameter increases, the bias from the analytic expectation becomes clearer. It is interesting to observe that, as the potential becomes increasingly steep, the hierarchy between the local minimum and the local maximum becomes smaller than the naive expectationwhich is known as the Hawking–Moss instantons [17], where and denote the probability at the local maximum and the local minimum, respectively. This shows that the Hawking–Moss instanton is just an approximate description and the real tunneling (thermal excitation) process depends not only on the initial and final conditions but also on the entire field space (see also [18]).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hawking, S.W.; Penrose, R. The Singularities of gravitational collapse and cosmology. Proc. R. Soc. Lond. A 1970, 314, 529–548. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory of Gravity. 1. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Vilenkin, A. Quantum Cosmology and the Initial State of the Universe. Phys. Rev. D 1988, 37, 888. [Google Scholar] [CrossRef] [PubMed]
- Vilenkin, A. The Interpretation of the Wave Function of the Universe. Phys. Rev. D 1989, 39, 1116. [Google Scholar] [CrossRef] [PubMed]
- Vilenkin, A. Approaches to quantum cosmology. Phys. Rev. D 1994, 50, 2581–2594. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, C. Wave Packets in Minisuperspace. Phys. Rev. D 1988, 38, 1761–1772. [Google Scholar] [CrossRef] [PubMed]
- Bouhmadi-López, M.; Brahma, S.; Chen, C.Y.; Chen, P.; Yeom, D. Annihilation-to-nothing: A quantum gravitational boundary condition for the Schwarzschild black hole. JCAP 2020, 11, 2. [Google Scholar] [CrossRef]
- Brahma, S.; Chen, C.Y.; Yeom, D. Annihilation-to-nothing: DeWitt boundary condition inside a black hole. Eur. Phys. J. C 2021, 82, 772. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Wave Function of the Universe. Phys. Rev. D 1983, 28, 2960–2975. [Google Scholar] [CrossRef]
- Hawking, S.W. The Quantum State of the Universe. Nucl. Phys. B 1984, 239, 257. [Google Scholar] [CrossRef]
- Halliwell, J.J.; Hartle, J.B. Integration Contours for the No Boundary Wave Function of the Universe. Phys. Rev. D 1990, 41, 1815. [Google Scholar] [CrossRef] [PubMed]
- Lehners, J.L. Review of the no-boundary wave function. Phys. Rep. 2023, 1022, 1–82. [Google Scholar] [CrossRef]
- Alexander, S.; Herczeg, G.; Magueijo, J. A generalized Hartle–Hawking wave function. Class. Quantum Gravity 2021, 38, 095011. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W.; Hertog, T. The Classical Universes of the No-Boundary Quantum State. Phys. Rev. D 2008, 77, 123537. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W.; Hertog, T. No-Boundary Measure of the Universe. Phys. Rev. Lett. 2008, 100, 201301. [Google Scholar] [CrossRef]
- Kiefer, C. Quantum Gravity; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Hawking, S.W.; Moss, I.G. Supercooled Phase Transitions in the Very Early Universe. Phys. Lett. B 1982, 110, 35–38. [Google Scholar] [CrossRef]
- Weinberg, E.J. Hawking–Moss bounces and vacuum decay rates. Phys. Rev. Lett. 2007, 98, 251303. [Google Scholar] [CrossRef]
- Yeom, D. Fuzzy Instantons in Landscape and Swampland: Review of the Hartle–Hawking Wave Function and Several Applications. Universe 2021, 7, 367. [Google Scholar] [CrossRef]
- Hwang, D.; Sahlmann, H.; Yeom, D. The No-boundary measure in scalar-tensor gravity. Class. Quantum Gravity 2012, 29, 095005. [Google Scholar] [CrossRef]
- Hwang, D.; Lee, B.H.; Sahlmann, H.; Yeom, D. The no-boundary measure in string theory: Applications to moduli stabilization, flux compactification, and cosmic landscape. Class. Quantum Gravity 2012, 29, 175001. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, S.; Park, W.-i.; Yeom, D.-h. Novel Phenomena of the Hartle–Hawking Wave Function. Symmetry 2024, 16, 444. https://doi.org/10.3390/sym16040444
Kang S, Park W-i, Yeom D-h. Novel Phenomena of the Hartle–Hawking Wave Function. Symmetry. 2024; 16(4):444. https://doi.org/10.3390/sym16040444
Chicago/Turabian StyleKang, Subeom, Wan-il Park, and Dong-han Yeom. 2024. "Novel Phenomena of the Hartle–Hawking Wave Function" Symmetry 16, no. 4: 444. https://doi.org/10.3390/sym16040444
APA StyleKang, S., Park, W. -i., & Yeom, D. -h. (2024). Novel Phenomena of the Hartle–Hawking Wave Function. Symmetry, 16(4), 444. https://doi.org/10.3390/sym16040444






