Research on Genetic Algorithm Optimization with Fusion Tabu Search Strategy and Its Application in Solving Three-Dimensional Packing Problems

Abstract

Symmetry is an important principle and characteristic that is prevalent in nature and artificial environments. In the three-dimensional packing problem, leveraging the inherent symmetry of goods and the symmetry of the packing space can enhance packing efficiency and utilization.The three-dimensional packing problem is an NP-hard combinatorial optimization problem in the field of modern logistics, with high computational complexity. This paper proposes an improved genetic algorithm by incorporating a fusion tabu search strategy to address this problem. The algorithm employs a three-dimensional loading mathematical model and utilizes a wall-building method under residual space constraints for stacking goods. Furthermore, adaptation of fitness variation strategy, chromosome adjustment, and tabu search algorithm are introduced to balance the algorithm’s global and local search capabilities, as well as to enhance population diversity and convergence speed. Through testing on benchmark cases such as Bischoff and Ratcliff, the improved algorithm demonstrates an average increase of over 3% in packing space utilization compared to traditional genetic algorithms and other heuristic algorithms, validating its feasibility and effectiveness. The proposed improved genetic algorithm provides new insights for solving three-dimensional packing problems and optimizing logistics loading schedules, offering promising prospects for various applications.

1. Introduction

The Three-Dimensional Bin Packing Problem (3D-BPP) is a class of NP-hard combinatorial optimization problems. Given a set of three-dimensional boxes to be packed and one or more fixed-size three-dimensional containers, the objective of 3D-BPP is to select the optimal subset of boxes and determine their best spatial arrangement within the container to minimize the number of required containers or to maximize space utilization. Solving 3D-BPP faces the following major challenges:

• Combinatorial Explosion: As the number and variety of boxes increase, the possible combinations grow exponentially, leading to an extremely large search space;
• Complex Constraints: Boxes come in various shapes and sizes, and containers have diverse requirements such as load-bearing capacity and stacking stability, posing difficulties in problem modeling and solving;
• Geometric Computations: Operations like rotation, translation, and nesting of boxes in three-dimensional space involve a significant number of geometric computations, imposing higher demands on algorithm design and implementation.

To address the challenges posed by the rapid expansion of solution space and escalating search complexity in the Three-Dimensional Bin Packing Problem (3D-BPP), the academic community has proposed various intelligent optimization algorithms. These algorithms can be broadly categorized into three types: exact algorithms, approximate algorithms, and heuristic algorithms.

Exact algorithms, employing methods such as mathematical programming, dynamic programming, and branch and bound, theoretically guarantee the optimal solution to the problem. However, due to the NP-hard nature of the problem, their computational complexity grows exponentially with problem size, making them impractical for real-world applications. For instance, Martello et al. [1] proposed an exact algorithm based on the branch and bound framework, achieving optimal solutions only for small-scale instances. Approximate algorithms, on the other hand, offer theoretical guarantees on the deviation of their solutions from the optimal solution. Despite these guarantees, their practical performance often falls short of expectations. For example, Miyazawa et al. [2] designed an approximate algorithm with an approximation ratio of 2, but, in instance testing, its performance showed significant deviations from the optimal solution. Heuristic algorithms, inspired by human intelligence and natural phenomena, efficiently explore and optimize solution spaces to obtain satisfactory solutions within reasonable timeframes. They have gained widespread popularity in practical applications. Among them, Genetic Algorithms (GA) have garnered significant attention from scholars in the 3D-BPP field due to their superior global search capabilities and flexible problem-modeling characteristics.

Gehring et al. [3] were among the pioneers to introduce Genetic Algorithms (GAs) into the 3D-BPP. They achieved favorable loading results at the time by designing targeted chromosome encoding, crossover, and mutation operations. Subsequently, many scholars have made improvements and innovations based on this foundation. Bortfeldt et al. [4] proposed a hybrid genetic algorithm, incorporating layer-based heuristic strategies and tree search optimization. They also designed special diploid individual representation schemes, heuristic packing methods, and several specific genetic algorithm operations, achieving excellent performance in benchmark tests such as Bischoff and Ratcliff. Gonçalves et al. [5] introduced a biased random-key genetic algorithm, which optimizes the packing sequence and parameters of boxes by combining a new placement procedure with a random-key-based genetic algorithm, effectively addressing both 2D and 3D packing problems. Kang et al. [6] combined knowledge guidance and heuristic reasoning to propose an improved grouped genetic algorithm for solving the three-dimensional packing problem. They enhanced algorithm performance by controlling gene transmission while maintaining a balance between selection pressure and population diversity.

In heterogeneous bin packing optimization, scholars have devised targeted genetic algorithm enhancements. Rajab et al. [7] employed an adaptive genetic algorithm for heterogeneous 3D bin packing, optimizing vacant volume inside containers while satisfying practical constraints. Yousaf et al. [8] proposed a genetic algorithm framework for heterogeneous 3D bin packing, considering practical constraints to optimize box packing. Kh et al. [9] introduced multi-objective hybrid genetic algorithms, utilizing metaheuristic and local search techniques to minimize box count in 2D bin packing while maintaining load balance.

Additionally, integration of genetic algorithms with other intelligent optimization methods has been explored. Rajapakshe et al. [10] combined Depth Bottom Left Fill heuristic with genetic algorithms to tackle complex 3D-BPP and knapsack problem combinations, enhancing efficiency and value of packing layouts. Soukaina et al. [11] devised a genetic algorithm based on Crow Search, merging bio-inspired heuristics to solve 2D-BPP and achieve synergistic effects. Wang et al. [12] proposed a method that united genetic algorithms with reinforcement learning for automatic design of genetic algorithms to solve the 2D-BPP, aiming to enhance efficiency by reducing computational resources.

In recent years, there have been some new research advancements in addressing online and large-scale packing problems. Zhang et al. [13] proposed an online three-dimensional packing method based on constrained deep reinforcement learning. By introducing a buffer zone to allow for multiple item action selections, they improved packing performance. Sun et al. [14] utilized reinforcement learning algorithms to optimize neural network models for the multi-bin three-dimensional packing problem. By integrating Transformer models with conditional query mechanisms and attention mechanisms, they achieved excellent packing results. Jiang et al. [15] introduced a data-driven tree search algorithm. They utilized a convolutional neural network trained on historical data to guide tree pruning, thereby accelerating the solution of large-scale 3D-BPP problems.

Genetic algorithms have also been actively researched and applied in 3D-BPP: Jia Kang [16], based on genetic algorithms, utilized a three-dimensional space-partitioning encoding approach to stack similar items together, thereby improving space utilization. Zhang Jun et al. [17] proposed a hybrid algorithm that incorporated genetic algorithms and simulated annealing, which included multiple constraints. They introduced new crossover and mutation operators to determine the optimal placement sequence. Chen Yuanwen [18] introduced a priority preservation strategy based on genetic algorithms, which enhanced loading space utilization.

In addition, some scholars have utilized other types of heuristic algorithms to solve 3D-BPPs. Zhang Defu et al. [19] proposed a combined heuristic algorithm, employing simulated annealing and human-inspired strategies. They controlled the loading of goods using point-finding methods and reference line rules. Liu Sheng et al. [20] introduced a multi-layer tree search algorithm, generating loading schemes with the order of box–slice–strip–layer–entity. Ying et al. [21] merged a differential evolution algorithm with a ternary search tree model, proposing an algorithm suitable for solving weak heterogeneous packing problems. Liu Jiaming et al. [22] presented a hybrid tabu search algorithm, combining heuristic strategies and residual space handling to generate optimal layouts for goods. Gao Peng et al. [23] combined a three-dimensional greedy stacking method with ant colony optimization, proposing a solution for solving strongly heterogeneous packing problems.

Despite advancements in 3D-BPP solving algorithms, challenges persist in terms of algorithm robustness, practicality, and adaptability to varying constraints. While many algorithms perform well in specific scenarios, they often struggle with changes in problem types and scales, necessitating improved adaptability [24,25,26]. Moreover, existing algorithms often rely on idealized assumptions, limiting their applicability to real-world packing operations. Future research should prioritize considerations such as physical attributes of goods, loading stability, and ease of loading and unloading [27].

Symmetry is widely present in nature and human-made environments as a fundamental geometric and physical principle. Properly utilizing the symmetric properties of objects themselves and the symmetry of the external environment can simplify problems and improve efficiency. In the three-dimensional packing problem, taking advantage of the symmetry of goods and packing spaces can reduce the search space and increase packing density.

Therefore, this paper proposes an enhanced genetic algorithm fused with a tabu search strategy. Building upon prior research, this approach aims to improve loading efficiency while ensuring solution robustness. By integrating tabu search with genetic algorithms, this method offers a novel solution for practical applications in three-dimensional packing optimization.

2. Materials and Methods

2.1. 3D-BPP

The Three-Dimensional Bin Packing Problem (3D-BPP) involves finding the optimal solution to maximize the utilization of container space given a set of different-sized and -shaped three-dimensional objects and a container with a specific volume. The foundation of this study assumes that both the container and three-dimensional objects are regular shapes with specific length, width, and height.

Consider a container of regular dimensions and n types of items to be loaded, where the dimensions of the container and the i-th type of item are expressed as in Equations (1) and (2), respectively. Establish a Cartesian coordinate system with the point at the left rear corner of the container denoted as the origin. Item placement begins from the origin, where the left rear point of the item (c) coincides with the origin, as illustrated in Figure 1. Both the container and items have regular dimensions.

$$C=\{L,W,H\}$$

(1)

$$c_i=\{l_i,w_i,h_i\}$$

(2)

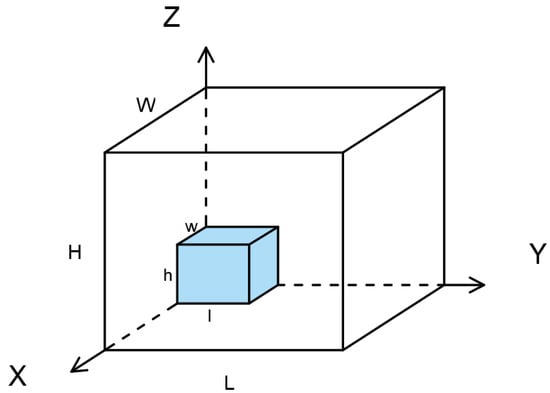
Figure 1. The schematic diagram of container and item placement.

Given the specified container and items, the loading objective is defined as follows: to find an optimal item placement strategy based on the given dimensions, maximizing the utilization of the container space. The item placement process must adhere to the following constraints:

• Items must not overlap during the loading process;
• During the loading process, items must not exceed the maximum dimensions of the container;
• When loading vertically, items must not be suspended; they must have one side in close contact with the bottom of the container or the top surface of another item.

Based on this, the objective function is defined as follows:

$$U=Max\frac{{\displaystyle \sum _{i=1}^m}{l}_i{w}_i{h}_i}{LWH}$$

(3)

In this equation, m represents the number of loaded items.

2.2. Loading Strategy

Different loading strategies result in different packing effects and affect space utilization. To minimize the generation of gaps while satisfying the above constraints, this paper adopts a loading strategy of constructing item walls.

The item wall (refer to Figure 2) is formed by stacking items of the same type in a specific orientation simultaneously, denoted as B. Its dimensions can be expressed as in Equation (4):

$$B=\{l_b,w_b,h_b\}$$

(4)

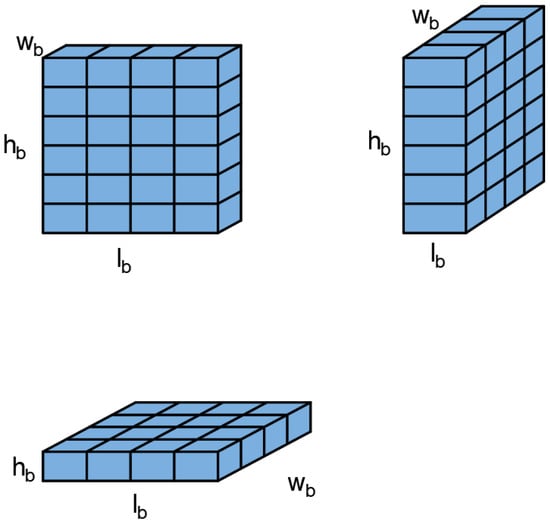
Figure 2. The schematic diagram of the item wall.

The dimensions of the item wall depend on the size of the remaining space. The remaining space (refer to Figure 3) is defined as the vacant rectangular area formed by the items before loading, and its dimensions can be expressed as in Equation (5):

$$C_R=\{L_R,W_R,H_R\}$$

(5)

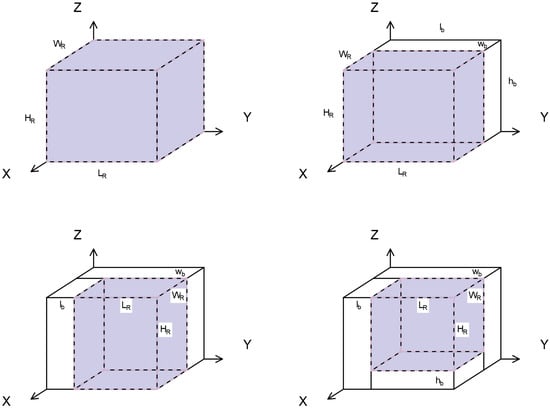
Figure 3. The schematic diagram of the remaining space.

The generation and loading of the item wall are carried out within the remaining space in the container according to specific rules. Depending on the orientation of the item wall, it can be divided into XZ wall, YZ wall, and XY wall, denoted as the set $B^{\prime }$, as shown in Equation (6):

$$B^{\prime }=\{B_{xz},B_{yz},B_{xy}\}$$

(6)

The item wall is placed adjacent to one side of the remaining space. After each placement of the item wall, the remaining space is redefined based on the boundaries of the item wall and the container, and its size changes according to Equation (7):

$$\left\{\begin{array}{cc}{L}_R=L-{\displaystyle \sum _{i=1}^x}{l}_{b_i}& l_{b_i}\in B_{yz}\\ W_R=W-{\displaystyle \sum _{j=1}^y}{w}_{b_j}& w_{b_j}\in B_{xz}\\ H_R=H-{\displaystyle \sum _{k=1}^z}{h}_{b_k}& h_{b_k}\in B_{xy}\end{array}\right.$$

(7)

In the equation, x, y and z represent the quantities of YZ walls, XZ walls and XY walls inside the container, respectively.

The dimensions of the item wall are constrained by the remaining space and must satisfy the following size constraints:

$$\left\{\begin{array}{cc}0\le l_b\le L_R\le L& l_b\in B_{yz}\cup B_{xy}\\ 0\le w_b\le W_R\le W& w_b\in B_{xz}\cup B_{xy}\\ 0\le h_b\le H_R\le H& h_b\in B_{xz}\cup B_{yz}\end{array}\right.$$

(8)

Under the constraints, the dimensions of the item wall can be determined according to the selected type of item using the following equations:

$$l_b=\left\{\begin{array}{cc}{l}_i& B_{xz}\\ ⌊\frac{L_R}{l_i}⌋•l_i& others\end{array}\right.$$

(9)

$$w_b=\left\{\begin{array}{cc}{w}_i& B_{yz}\\ ⌊\frac{W_R}{w_i}⌋•w_i& others\end{array}\right.$$

(10)

$$h_b=\left\{\begin{array}{cc}{h}_i& B_{xy}\\ ⌊\frac{H_R}{h_i}⌋•h_i& others\end{array}\right.$$

(11)

The item wall is sequentially generated and loaded into the specified position of the remaining space in the order of XZ wall, YZ wall, and XY wall. The schematic diagram is shown in Figure 4.

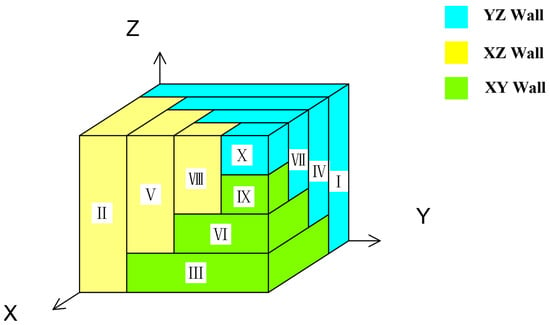
Figure 4. The schematic diagram of the sequence of item wall placement.Roman numerals I to X denote the sequence of filling the item wall.

Selecting k types of items and generating item walls according to the aforementioned method to load them into the container, let $B^{\prime }=\{B_1,B_2,B_3,\cdots ,B_n\}$ denote the set of item walls. Therefore, based on Equation (3), the objective function is modified to the following equation:

$$U=\frac{{\displaystyle \sum _{i=1}^n}{l}_{b_i}{w}_{b_i}{h}_{b_i}}{LWH}$$

(12)

2.3. Genetic Algorithm

The genetic algorithm is an optimization algorithm that simulates the process of biological evolution. It possesses strong global search capabilities and gradually improves candidate solutions by simulating operations such as natural selection, genetic crossover, and mutation, aiming to find the optimal or suboptimal solution to a problem.

2.3.1. Encoding and Decoding

In genetic algorithms, each chromosome represents a feasible solution, describing how items are arranged and placed into containers. This paper adopts sorting encoding as the encoding method for chromosomes. According to the aforementioned wall construction method, each gene on the chromosome represents a wall of items. During the decoding process, genes are expressed in the order of their sequence on the chromosome, and the walls of items are placed into containers in an orderly manner.

Each gene should contain the following information: the type of item used to construct the item wall and its orientation. Assume that there are n types of items, represented by the set E = {1, 2, 3, …, n}. As shown in Figure 5, each type of item has six orientations, represented by the set F = {a, b, c, d, e, f}. Therefore, each time a type of items and its orientation are randomly selected from sets E and F and encoded as a gene according to Equation (13). Through multiple extractions, chromosomes are formed in the order of gene generation according to Equation (14), completing the chromosome-encoding process.

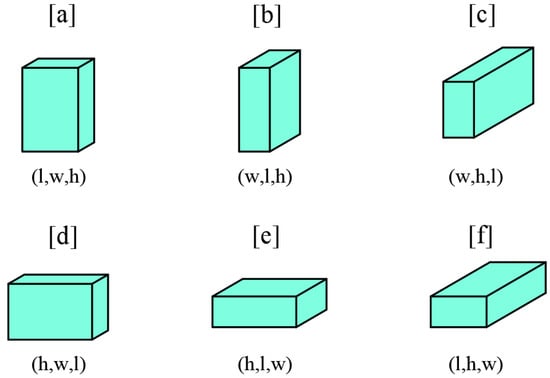
Figure 5. The schematic diagram of the orientations of item placement. (a–f) diagrams represent the six orientations of the cargo in three-dimensional space.

During the decoding process, the inverse procedure of encoding is followed. Gene codes on the chromosome are extracted one by one and decoded into corresponding item walls in the order of YZ walls, XZ walls, and XY walls, which are then filled into the container. As item walls are filled, the remaining space continuously decreases. If the size of the remaining space is insufficient to generate the item wall represented by a gene code, that gene code is skipped, and decoding operations proceed to the next gene code until the entire chromosome is decoded.

$$\begin{array}{cc}{B}_k=e_i{f}_j& e_i\in E,f_j\in F\end{array}$$

(13)

$$B^{\prime }=\{B_1,B_2,B_3,\cdots ,B_n\}$$

(14)

2.3.2. Selection

In this paper’s algorithm, roulette wheel selection is used as the selection operator. The fitness of each individual is transformed into a probability value according to the following equation, allowing individuals with higher fitness to have a greater chance of participating in crossover to produce the next generation, while individuals with lower fitness also have a certain probability of being selected. To preserve superior genes, implement an elitist retention strategy, where the top five individuals with the highest fitness proceed directly to the next generation without participating in crossover.

$$p_i=\frac{U_i}{{\displaystyle \sum _{i=1}^n}{U}_i}$$

(15)

2.3.3. Crossover

Crossover is a crucial step in genetic algorithms, where genetic information is exchanged between parents to produce offspring. Single-point crossover is chosen as the crossover operator. Parents undergo crossover with a certain probability. If no crossover occurs, the parents are considered as offspring and directly added to the new population, as shown in the following equation:

$$i_1,i_2=\left\{\begin{array}{c}\begin{array}{cc}Crossover(I_1,I_2)& rand(0,1)<CP\end{array}\\ \begin{array}{cc}{I}_1,I_2& others\end{array}\end{array}\right.$$

(16)

In the equation, $i_1$ and $i_2$ represent the new individuals, $I_1$ and $I_2$ represent the parent individuals, and $CP$ represents the crossover probability.

As illustrated in Figure 6, during single-point crossover, a random position is selected on two chromosomes as the crossover point. Subsequently, the genes to the right of the crossover point on each chromosome are exchanged, resulting in the generation of two new offspring, thereby completing the crossover process.

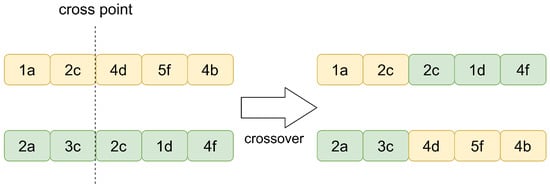
Figure 6. The schematic diagram of the process of crossover.

The offspring obtained after crossover inherit partial genetic information from the parents, resulting in alterations in the arrangement of gene codes. The validity of the offspring is not influenced by the arrangement of their own gene codes. All generated offspring are considered legitimate, as they can be mapped to a three-dimensional space according to their gene code sequence using the aforementioned decoding method.

2.3.4. Mutation

Mutation introduces randomness and diversity to help the algorithm escape local optima. Exchange mutation is selected as the mutation operator. All individuals in the population undergo mutation with a certain probability.

$$i=\left\{\begin{array}{c}\begin{array}{cc}Mutation\left(i\right)& rand(0,1)<MP\end{array}\\ \begin{array}{cc}i& others\end{array}\end{array}\right.$$

(17)

In the equation, i represents an individual in the population and $MP$ represents the mutation probability.

As illustrated in Figure 7, during exchange mutation, two genes are randomly selected on the chromosome, and their positions are swapped. This process completes the mutation.

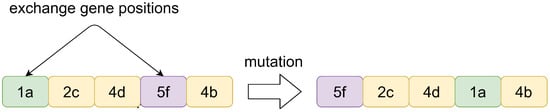
Figure 7. The schematic diagram of the process of mutation.

3. Improved Genetic Algorithm

Although genetic algorithms possess strong search capabilities, their inherent global search characteristic may cause the algorithm to occasionally become trapped in local optimum regions during the evolutionary process, thereby hindering further enhancement of solution quality. Moreover, with the increase in the number of item types, the solution space of the Three-Dimensional Bin Packing Problem grows exponentially, making it more challenging for the algorithm to find the global optimal solution within a limited number of iterations.

To address the aforementioned challenges, this paper integrates various optimization strategies into the traditional genetic algorithm, proposing an enhanced algorithm:

• Building upon Equation (12), the fitness function of the genetic algorithm is improved to simplify the computation process of the algorithm;
• Adjustments are made to the structure of chromosomes to facilitate effective exchange of information between populations, thereby accelerating convergence speed;
• During the initial population creation and evolution process, a tabu search strategy is incorporated, introducing flexible tabu criteria and unblocking mechanisms to assist the algorithm in escaping local optima.

The algorithm flowchart is shown in Figure 8.

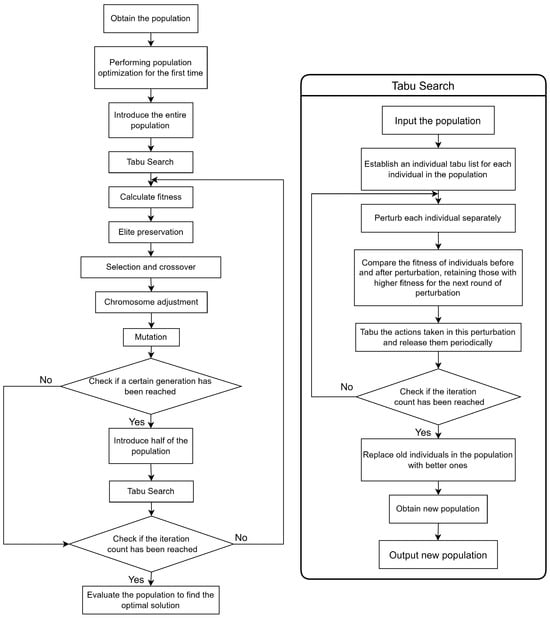
Figure 8. The schematic diagram of the flowchart of the algorithm.

Based on the above ideas, this paper presents the pseudocode of the improved genetic algorithm. The pseudocode of Algorithm 1 is shown below.

Algorithm 1 Improving Hybrid Heuristic Algorithm
Input: Cargo to be loaded $Cargos$, carriage space $Space$, and iteration count $Iter$.
Output: the optimal cargo loading strategy $Sequence$
1:	$pop\leftarrow CreatePop(Cargos,Space)$ # Randomly initialize the population
2:	$heu\_pop\leftarrow HeuristicInit(Cargos,Space)$ # Heuristic initialization of the population
3:	$pop\leftarrow pop\cup heu\_pop$ # Merge populations
4:	$best\_ind\leftarrow \varnothing$ # Initialize elite individuals
5:	for each $i\in [1,Iter]$ do
6:	$eval\_list\leftarrow Evaluation\left(pop\right)$ # Multi-objective fitness evaluation
7:	$best\_ind\leftarrow GetBest(pop,best\_ind)$ # Update elite individuals
8:	$new\_pop\leftarrow Crossover(pop,eval\_list)$ # Crossover
9:	$new\_pop\leftarrow Mutation(new\_pop)$ # Mutation
10:	if $imodinterval==0$ then
11:	# Perform tabu search every certain number of generations
12:	$tabu\_pop\leftarrow Selection(new\_pop,eval\_list)$ # Select a portion of individuals
13:	$tabu\_pop\leftarrow TabuSearch(tabu\_pop,best\_ind)$ # Tabu search
14:	$new\_pop\leftarrow new\_pop-tabu\_pop+TabuSearch(tabu\_pop)$ # Replace individuals
15:	end if
16:	$pop\leftarrow Elite(new\_pop,best\_ind)$ # Preserve elites
17:	if $Termination(pop,best\_ind,i)$ then
18:	# Check if termination condition is met
19:	break
20:	end if
21:	end for
22:	return $best\_ind$ # Return the best solution

3.1. Fitness Transformation

To accelerate computation speed, the three-dimensional space inside the container is transformed into a two-dimensional depth table. As shown in Figure 9, each point on the two-dimensional depth table represents the height available for placement at that position within the container, decreasing as item walls are filled in.

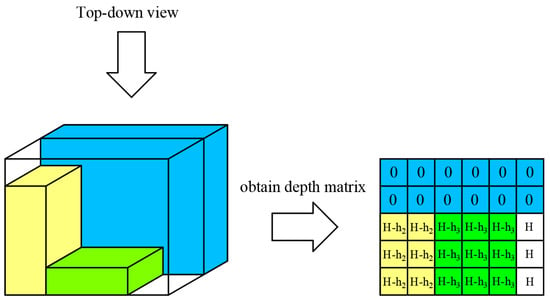
Figure 9. The schematic diagram of the depth table.

The width of the container is used as the number of rows, the length as the number of columns, and the height as the filling element to establish the depth matrix:

$$\begin{array}{cc}P={\left[\begin{array}{cccc}H& H& \cdots & H\\ H& H& \cdots & H\\ ⋮& ⋮& \ddots & ⋮\\ H& H& \cdots & H\end{array}\right]}_{m\times n}& \begin{array}{c}m=W\hfill \\ n=L\hfill \end{array}\end{array}$$

(18)

At position (0,0), which corresponds to the left rear point of the three-dimensional container, serve as the initial placement point for item walls. Each element in the matrix represents the remaining available space height at that position.

Let $(p,q)$ denote the left rear point of the item wall as the reference point for placement. The placement of the item wall must satisfy the size constraint defined in Equation (8), expressed as in Equation (19):

$$\left\{\begin{array}{c}p+w_b\le m\\ q+l_b\le n\\ P(p,q)\ge h_b\end{array}\right.$$

(19)

After each placement of an item wall, update the depth value corresponding to each point in the depth matrix according to the following equation:

$$a_{ij}=a_{ij}-h_b$$

(20)

In this equation, a represents an element of the depth matrix and $i\in [p,p+w_b]$, $j\in [q,q+l_b]$.

Based on this, the optimization objective function of the problem can be abstracted as follows:

$$U^{\prime }=1-\frac{{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^n}{a}_{ij}}{m\times n\times H_R}$$

(21)

Due to the enhanced weak heterogeneity of solutions by the wall construction method, the fitness function is modified to enrich the combination of goods in the optimal solution as much as possible. Let the number of types of goods be n and the number of used types of goods in an individual be $n^{\prime }$. Then, the fitness function is defined as follows:

$$\left\{\begin{array}{c}F={\omega }_1\times U^{\prime }+{\omega }_2\times \frac{n^{\prime }}{n}\\ {\omega }_1+{\omega }_2=1\end{array}\right.$$

(22)

3.2. Chromosome Adjustment

As the internal space of the container increases or the number of item types grows, the length of the sorting code also increases. However, excessively long chromosomes may introduce redundant information. Some segments of genes cannot be effectively expressed during the decoding process, which interferes with the effective exchange of genes among individuals to some extent, resulting in a decrease in convergence speed and a reduction in the performance of the genetic algorithm. To reduce this interference, this paper introduces a chromosome adjustment strategy.

As shown in Figure 10, the chromosome, composed of sorted encoding, consists of effective and ineffective genes. When a gene code on the chromosome representing the size of an item wall exceeds the size of the remaining space, failing to meet the size constraint defined in Equation (8), resulting in the inability to accommodate the item wall in the container, this gene is defined as an ineffective gene that cannot be expressed. Conversely, genes that can be expressed normally during the decoding process are referred to as effective genes. To reduce the interference of ineffective genes and strengthen the exchange of effective information during crossover, successfully expressed genes are extracted during the first decoding process and formed into a new sorted sequence, serving as the new chromosome for that individual.

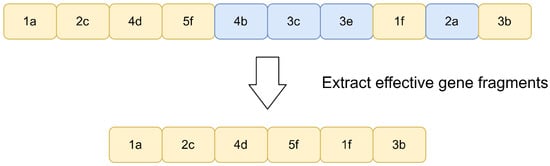
Figure 10. The schematic diagram of the process of crossover.

During the decoding process, all chromosomes are traversed and updated. The updated chromosomes are then used in other stages of the algorithm.

3.3. Local Search Algorithm

Compared to genetic algorithms, the tabu search algorithm demonstrates stronger local search capabilities, enabling exploration within the neighborhood of local optima and preventing entrapment in them by introducing a tabu list. Therefore, integrating tabu search as a local search algorithm to complement genetic algorithms as global search algorithms can enhance search diversity and facilitate rapid convergence.

The auxiliary optimization process using tabu search is as follows:

• Incorporate the population to be optimized. Embed the tabu search algorithm into two key stages of the genetic algorithm as auxiliary search algorithms to improve the performance and search effectiveness of the algorithm: (1) After creating the initial population, the entire population is introduced into the tabu search algorithm; (2) Randomly select half of the individuals from the new population generated after crossover as the population to be optimized, and then introduce them into the tabu search algorithm.
• Initialize a tabu list with the same size as the population, where each individual is independent of others.
• Calculate and save the fitness of the population before optimization, considering the current population and fitness as the best population and best fitness.
• Perturb all individuals within the neighborhood, randomly altering segments of genes on the chromosome.
• Check if this perturbation exists in the tabu list. If it does, perturb again; otherwise, add this perturbation to the corresponding tabu list of the individual. The tabu tenure is calculated as follows, and the action is automatically released after reaching the tabu tenure. In the equation, t represents the length of the chromosome.

  $$tabutenure=\sqrt{6t}$$

  (23)
• The fitness of the new population is computed, and the presence of individuals with enhanced fitness is examined. If such individuals are found, then substitute the corresponding individuals in the best population with higher fitness while updating the best fitness.
• Repeat Steps 4 to 6 until the maximum number of iterations is reached.
• Export the updated optimal population and replace the old individuals participating in tabu search in the original population with them.

4. Results

The algorithm proposed in this paper is compiled using the Python programming language and runs on a computer with a 13th Gen Intel(R) Core(TM) i5-13500H 2.60 GHz CPU. To enhance the computational speed, multiprocessing is employed for computing the fitness function. The benchmark dataset provided by Bischoff and Ratcliff [28] is utilized as the test data. Results are compared with genetic algorithms (GA [16], GA_GB [3]), simulated annealing (SA [19]), tabu search (HTS_L [22]), and the algorithm of Bischoff and Ratcliff to validate the feasibility of the proposed algorithm (Improving Hybrid Heuristic Algorithm, abbreviated as IHHA).

4.1. Parameter Settings

Before implementing the algorithm, specific parameters for the genetic algorithm and tabu search were determined, as shown in Table 1.

Table 1. Parameters involved in the algorithm.

Parameters	Value
Number of individuals	200
Number of iterations for the genetic algorithm	200
Crossover probability	0.7
Mutation probability	0.2
Number of iterations for tabu search	100
Interval between offspring	10
Weight of space utilization	0.7
Weight of goods diversity	0.3

4.2. Example Validation

The selected test data consist of five categories, BR1 to BR5, from Bischoff and Ratcliff’s instances. The types of boxes are 3, 5, 8, 10, and 12, with the dimensions of the container determined to be 587 cm × 233 cm × 220 cm, in accordance with international standards. Eight instances were randomly selected from the five categories, and each instance was tested five times. The maximum space utilization rate of the selected instances was chosen as the test result.

To enhance the visual intuitiveness of the program, different colors are used in the packing effect diagram to distinguish between different items. The obtained solutions are represented in the form of sorted codes, which include information such as the labels of the item walls and the placement order, as shown in Figure 11.

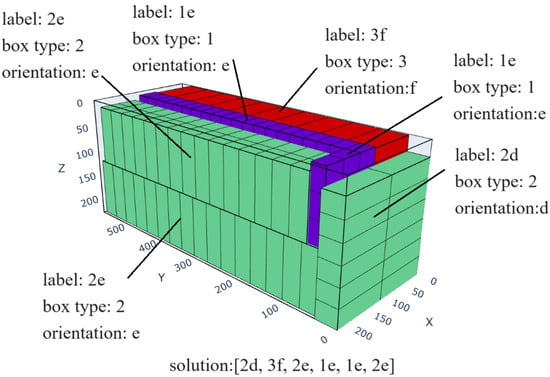
Figure 11. Explanation diagram of the solution.

The final test results are shown in Table 2, Table 3, Table 4, Table 5 and Table 6, and the packing effect diagrams are shown in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16.

Table 2. Table of BR1 test results.

Example	Optimal Solution	Maximum Space Utilization	Runtime
5	[2c,3f,3a,1b,1d,2c]	88.57%	24.50 s
12	[2e,1d,3e,2c,3e,3e]	94.43%	24.16 s
27	[2d,2f,1f,3f,1d]	88.32%	24.89 s
36	[2c,3f,2e,2e,2f]	91.22%	28.68 s
43	[2f,2f,3e,3b,3d,2e,2f,2f]	90.96%	27.13 s
64	[1b,3f,3c,3c,3c,3c]	93.40%	27.49 s
78	[3f,3a,2c,3e,3d,3c,2c,3a,2e]	89.18%	28.92 s
89	[1b,1b,3e,2e,2e,3b,2e,3b]	88.53%	22.89 s

Table 3. Table of BR2 test results.

Example	Optimal Solution	Maximum Space Utilization	Runtime
12	[2e,1d,3e,2f,1d,2c]	92.33%	23.26 s
23	[5d,3e,1f,1d,2f,3e,4d,4f]	90.12%	28.70 s
34	[3c,4f,2c,3e,2f]	91.82%	26.94 s
45	[4c,3d,2f,5e,2d]	93.60%	27.68 s
56	[3a,4d,5b,3f,1f,3e,3a,3a]	90.84%	30.41 s
67	[2e,3d,5c,4b,4f,1e]	90.18%	27.65 s
78	[2d,4d,5a,3d,4d,2a,2c,2c]	89.87%	28.73 s
89	[4d,5d,1e,5e,1b]	91.52%	23.54 s

Table 4. Table of BR3 test results.

Example	Optimal Solution	Maximum Space Utilization	Runtime
8	[5a,8c,8c,8c,8c,8c]	96.23%	25.25 s
19	[8a,8f,2c,2f,5f,3e,8a,1b,1c]	91.26%	30.26 s
30	[7f,7f,1e,2f,8d]	92.01%	28.81 s
41	[3f,6d,4e,4e,4e,4e,8c,8c,8c]	94.48%	26.50 s
54	[2f,1d,1c,5e,4b,5b,6b,5e]	90.25%	29.47 s
63	[8d,5f,5c,8b,3f,5c]	91.21%	27.57 s
76	[2d,2f,8c,8e,8d]	92.19%	27.47 s
92	[8d,4d,3c,4a,6d]	90.19%	24.64 s

Table 5. Table of BR4 test results.

Example	Optimal Solution	Maximum Space Utilization	Runtime
5	[6b,7f,7f,9c,7f]	94.34%	26.67 s
14	[8a,3d,3e,8b,3d,10a,3a,10c]	90.16%	26.31 s
37	[6f,6a,6c,3e,10d,6e]	91.80%	27.10 s
50	[10a,5d,5c,1d,2d]	93.74%	29.79 s
68	[1a,4e,2e,2e,2e,2e,2e,2e,2e]	93.12%	25.69 s
70	[4c,7d,7d,7d,7d]	95.08%	26.47 s
82	[3b,10b,6c,3b,2b,2e,1d,4f]	91.50%	29.55 s
91	[6d,1d,2c,8a,1d,8e,8e,8e]	89.60%	29.14 s

Table 6. Table of BR5 test results.

Example	Optimal Solution	Maximum Space Utilization	Runtime
7	[4d,10d,8c,10d,10d]	93.44%	27.75 s
16	[5a,5a,5f,5b,5b,5e,6e,5e]	92.21%	26.56 s
29	[3c,5a,3e,6d,1f,3e]	90.51%	28.28 s
42	[6a,5d,11e,2f,4f,11c]	93.37%	25.42 s
58	[12c,12d,12e,5c,2e,12a,12a,12a]	91.61%	28.49 s
73	[12a,2d,3e,11e,12f]	94.15%	26.80 s
85	[7e,1d,12c,9f,4d,12c]	92.07%	28.22 s
94	[1e,11f,5c,4a,11e,7c,4a,4a,11c]	90.56%	27.39 s

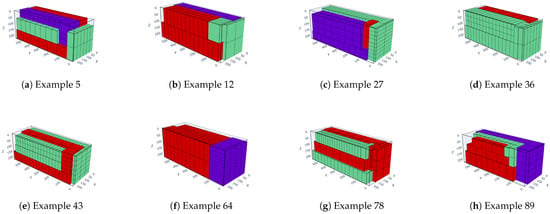
Figure 12. The packing effect diagram for instance BR1.

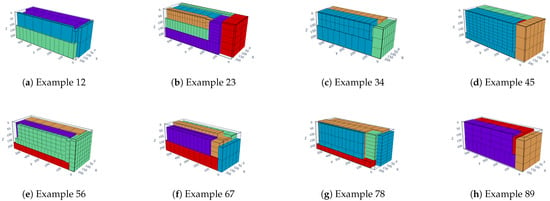
Figure 13. The packing effect diagram for instance BR2.

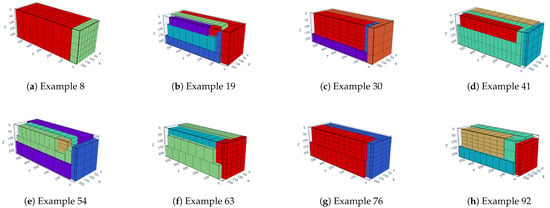
Figure 14. The packing effect diagram for instance BR3.

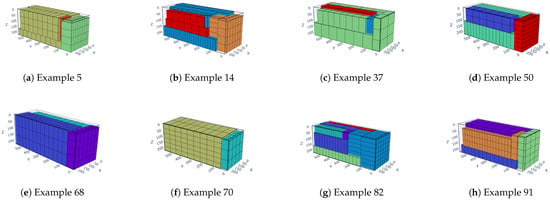
Figure 15. The packing effect diagram for instance BR4.

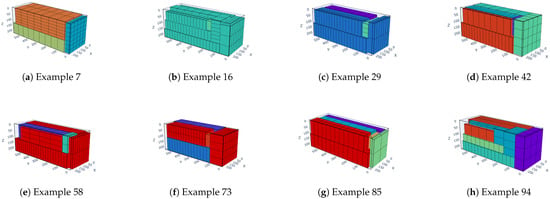
Figure 16. The packing effect diagram for instance BR5.

From the depicted graphs and presented tables, it is evident that the algorithm proposed herein effectively selects the optimal arrangement of goods from a range of goods with varying dimensions, thus maximizing cargo space utilization. The maximum space utilization rate for all instances of each test case can exceed 85%. These findings indicate that the IHHA algorithm proposed in this study performs admirably in addressing three-dimensional packing problems with fewer types of goods. However, for scenarios featuring a wider variety of goods, the algorithm tends to prioritize space utilization over goods diversity.

4.3. Algorithm Comparison

To validate the effectiveness of the IHHA algorithm proposed in this paper, the average space utilization rate across instances was calculated as the experimental result and compared with GA, GA_GB, SA, HTS_L and the algorithm of Bischoff. The experimental comparison results are presented in Table 7.

Table 7. Table of algorithm results comparison.

Algorithm	Instance
	BR1	BR2	BR3	BR4	BR5
GA	84.55%	87.02%	88.45%	88.76%	88.60%
GA_GB	85.80%	87.26%	88.10%	88.04%	87.86%
SA	89.94%	91.13%	92.09%	91.94%	91.72%
HTS_L	88.14%	89.52%	90.53%	90.75%	90.79%
Bischoff	85.4%	86.25%	85.86%	85.08%	85.21%
IHHA1	90.58%	91.29%	92.23%	92.42%	92.23%

¹ The bold text indicates the operational results of the algorithm presented in this paper.

Based on the table data, our algorithm outperforms GA, GA_GB, SA, HTS_L and the algorithm of Bischoff. Compared to other heuristic algorithms (SA, HTS_L) in the table, our algorithm demonstrates superior packing efficiency. Furthermore, compared to genetic algorithms (GA, GA_GB), our algorithm achieves further improvement in space utilization.

These findings highlight the algorithm’s strong adaptability to scenarios with fewer types of goods, allowing for the generation of optimal packing strategies and maximizing space utilization. The experimental results confirm the feasibility and effectiveness of the algorithm for such packing problems.

5. Conclusions

This paper proposes an enhanced genetic algorithm integrated with tabu search strategies to tackle the three-dimensional packing problem. It establishes a mathematical model for loading goods, ensuring stability and maximizing space utilization. The algorithm incorporates adaptive chromosome encoding, heuristic-guided operations, elite retention, and tabu search to improve search efficiency and solution quality.

Experimental validation using the Bischoff and Ratcliff test set shows significant advantages over traditional genetic algorithms and other heuristics, particularly in scenarios with fewer item types and more individual items. The algorithm achieves optimal or near-optimal solutions with increased loading utilization and reduced solving time. It demonstrates adaptability in complex scenarios but suggests further optimization in areas like item encoding and space partitioning.

Given the NP-hard nature of the problem, challenges remain, such as handling irregular items and multi-objective optimization. Future research will focus on refining mathematical modeling, exploring collaborative optimization frameworks, developing online optimization algorithms, and enhancing system integration for real-world applications.