Hawking Radiation as a Manifestation of Spontaneous Symmetry Breaking
Abstract
1. Introduction
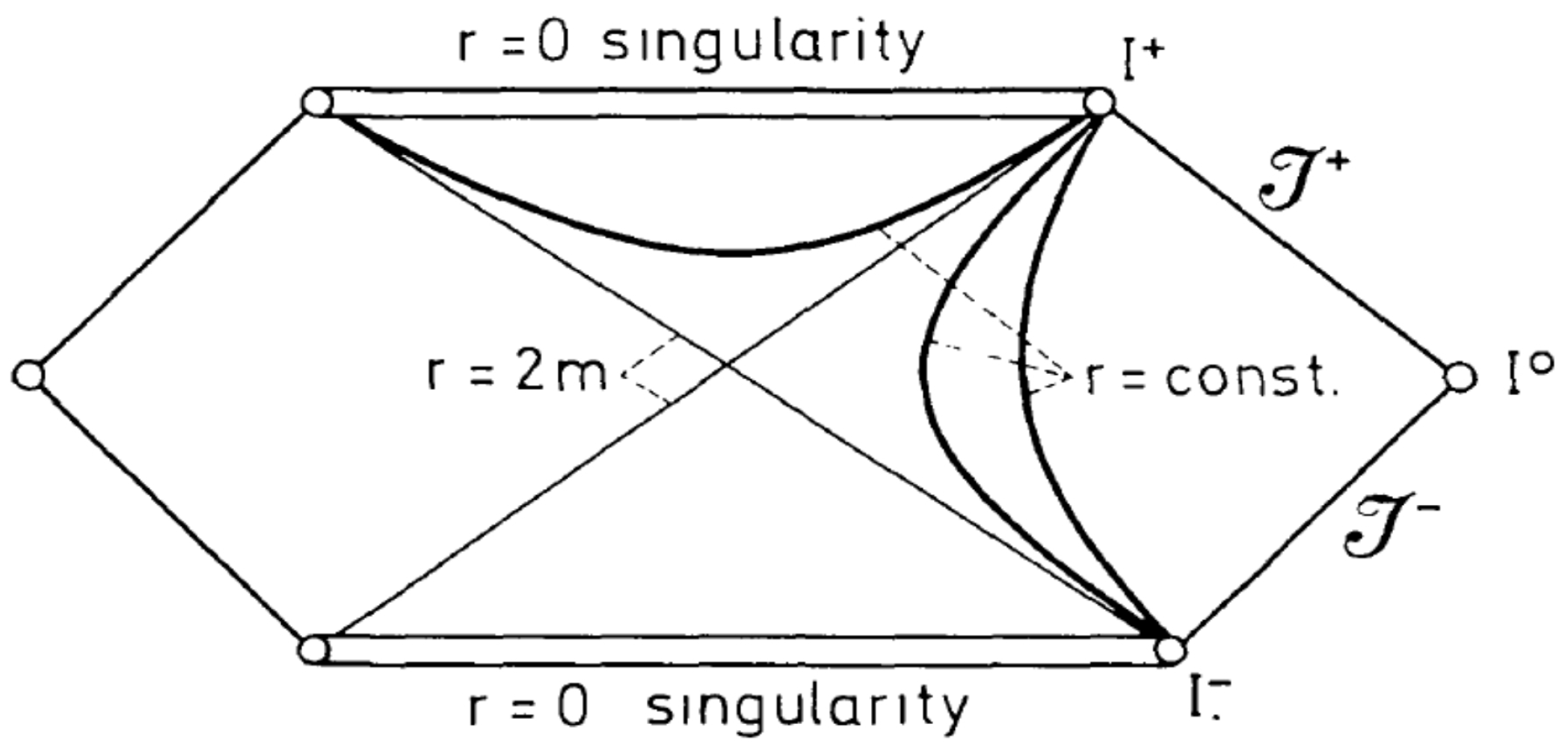
2. Standard Formulation of Black Hole Evaporation
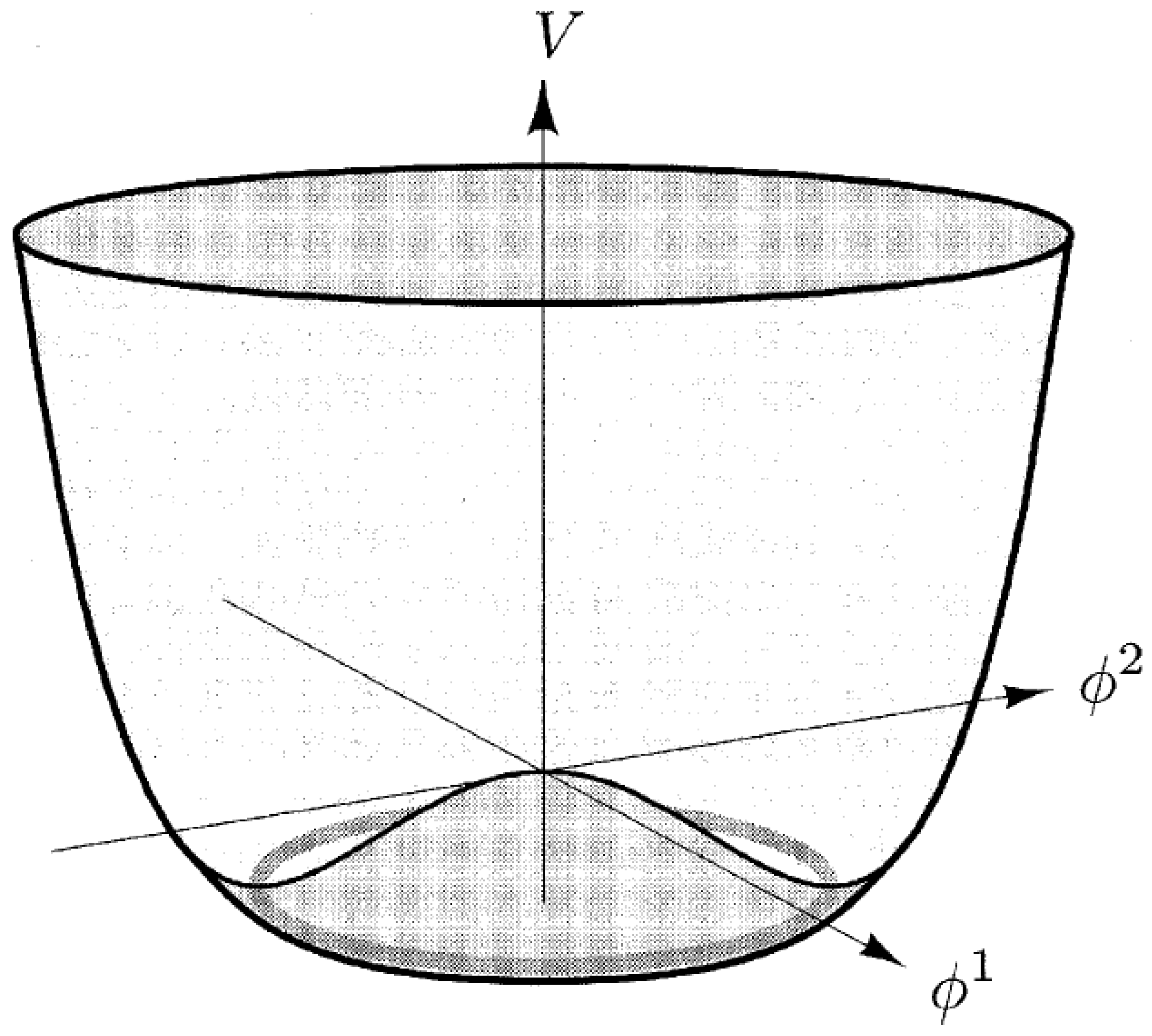
3. Spontaneous Symmetry Breaking: Basic Concepts
4. Black Hole Evaporation as a Consequence of Spontaneous Symmetry Breaking
4.1. Emission of Particles
4.2. The Connection of with the Particle Statistic
4.3. Symmetry Analysis of the Phenomena
5. Curvature Effects Appearing from the Particle Lagrangian
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carrol, S. Spacetime and Geometry: An Introduction to General Relativity; Addison-Wesley: San Francisco, CA, USA, 2004; ISBN 978-0-8053-8732-2. [Google Scholar]
- Walt, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984; ISBN 978-0-226-87033-5. [Google Scholar]
- Kerr, R.P. Gravitational Field of a Spinning Mass as an Example of Algebraically Special Metrics. Phys. Rev. Lett. 1963, 11, 237–238. [Google Scholar] [CrossRef]
- Reissner, H. Über die Eigengravitation des elektrischen Feldes nach der Einsteinschen Theorie. Ann. Phys. 1916, 50, 106–120. (In Germany) [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black Holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in Commun. Math. Phys. 1976, 46, 206. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Path-integral derivation of black-hole radiance. Phys. Rev. D 1976, 13, 2188. [Google Scholar] [CrossRef]
- Hawking, S.W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 1976, 14, 2460–2473. [Google Scholar] [CrossRef]
- Zettili, N. Quantum Mechanics: Concepts and Applications; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2009; ISBN-13 978-0470026793. [Google Scholar]
- Sakurai, S.S.; Napolitano, J. Modern Quantum Mechanics; Cambridge U. Press: Cambridge, UK, 2020; ISBN-13 978-1108473224. [Google Scholar] [CrossRef]
- Susskind, L. The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics; Little, Brown: Boston, MA, USA, 2008; p. 10. ISBN 9780316032698. [Google Scholar]
- Susskind, L.; Lindesay, J. Black Holes, Information and the String Theory Revolution; World Scientific: Singapore, 2005; pp. 69–84. ISBN 978-981-256-083-4. [Google Scholar]
- Dvali, G.; Gomez, C. Self-Completeness of Einstein Gravity. arXiv 2010, arXiv:1005.3497. [Google Scholar]
- Dvali, G.; Folkerts, S.; Germani, C. Physics of Trans-Planckian Gravity. Phys. Rev. D 2011, 84, 024039. [Google Scholar] [CrossRef]
- Arraut, I. Black-Hole evaporation and quantum-depletion in Bose–Einstein condensates. Mod. Phys. Lett. A 2021, 36, 2150006. [Google Scholar] [CrossRef]
- Arraut, I. Black-hole evaporation from the perspective of neural networks. EPL 2018, 124, 50002. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum theory of Fields; Press Syndicate of the University of Cambridge: New York, NY, USA, 1996. [Google Scholar]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345. [Google Scholar] [CrossRef]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. II. Phys. Rev. 1961, 124, 246. [Google Scholar] [CrossRef]
- Nambu, Y.J. From Yukawa’s Pion to Spontaneous Symmetry Breaking. Phys. Soc. Jpn. 2007, 76, 111002. [Google Scholar] [CrossRef]
- Arraut, I. The Quantum Yang-Baxter Conditions: The Fundamental Relations behind the Nambu-Goldstone Theorem. Symmetry 2019, 11, 803. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Ryder, L. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1985; ISBN 0521478146. [Google Scholar]
- de Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- de Rham, C.; Gabadadze, G. Generalization of the Fierz-Pauli action. Phys. Rev. D 2010, 82, 044020. [Google Scholar] [CrossRef]
- Kodama, H.; Arraut, I. Stability of the Schwarzschild–de Sitter black hole in the dRGT massive gravity theory. PTEP 2014, 2014, 023E02. [Google Scholar] [CrossRef]
- Arraut, I. Path-integral derivation of black-hole radiance inside the de-Rham–Gabadadze–Tolley formulation of massive gravity. Eur. Phys. J. C 2017, 77, 501. [Google Scholar] [CrossRef]
- Arraut, I. On the apparent loss of predictability inside the de-Rham-Gabadadze-Tolley non-linear formulation of massive gravity: The Hawking radiation effect. EPL 2015, 109, 10002. [Google Scholar] [CrossRef]
- Stückelberg, E.C.G. Die Wechselwirkungskräfte in der Elektrodynamik und in der Feldtheorie der Kräfte. Helv. Phys. Acta 1938, 11, 225. (In Germany) [Google Scholar]
- Pourhassan, B.; Dehghani, M.; Faizal, M.; Dey, S. Non-Pertubative Quantum Corrections to a Born-Infeld Black Hole and its Information Geometry. Class. Quantum Grav. 2021, 38, 105001. [Google Scholar] [CrossRef]
- Campos Delgado, R. Quantum gravitational corrected evolution equations of charged black holes. J. Hologr. Appl. Phys. 2023, 3, 39–48. [Google Scholar] [CrossRef]
- Upadhyay, S.; ul Islam, N.; Ganai, P.A. A modified thermodynamics of rotating and charged BTZ black hole. J. Hologr. Appl. Phys. 2022, 2, 25–48. [Google Scholar] [CrossRef]
- Beekman, A.; Rademaker, L.; van Wezel, J. An Introduction to Spontaneous Symmetry Breaking. SciPost Phys. Lect. Notes 2019, 11. [Google Scholar] [CrossRef]
- Moffat, J. Predictability in quantum gravity and black hole evaporation. arXiv 1993, arXiv:gr-qc/9312017. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I. Hawking Radiation as a Manifestation of Spontaneous Symmetry Breaking. Symmetry 2024, 16, 519. https://doi.org/10.3390/sym16050519
Arraut I. Hawking Radiation as a Manifestation of Spontaneous Symmetry Breaking. Symmetry. 2024; 16(5):519. https://doi.org/10.3390/sym16050519
Chicago/Turabian StyleArraut, Ivan. 2024. "Hawking Radiation as a Manifestation of Spontaneous Symmetry Breaking" Symmetry 16, no. 5: 519. https://doi.org/10.3390/sym16050519
APA StyleArraut, I. (2024). Hawking Radiation as a Manifestation of Spontaneous Symmetry Breaking. Symmetry, 16(5), 519. https://doi.org/10.3390/sym16050519




