Character Varieties and Algebraic Surfaces for the Topology of Quantum Computing
Abstract
1. Introduction
2. Prolegomena
2.1. Algebraic Surfaces
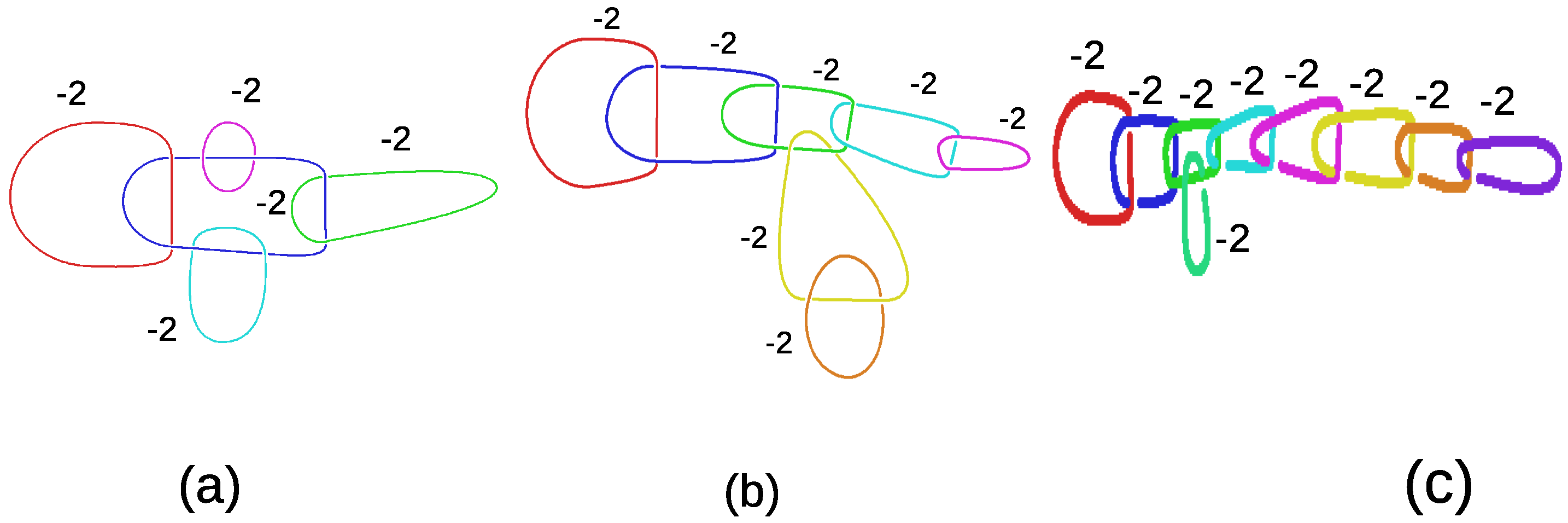
2.2. The Hopf Link
2.3. Magic State Quantum Computing
3. Character Varieties for Fundamental Groups of Three-Manifolds and the Related Algebraic Surfaces
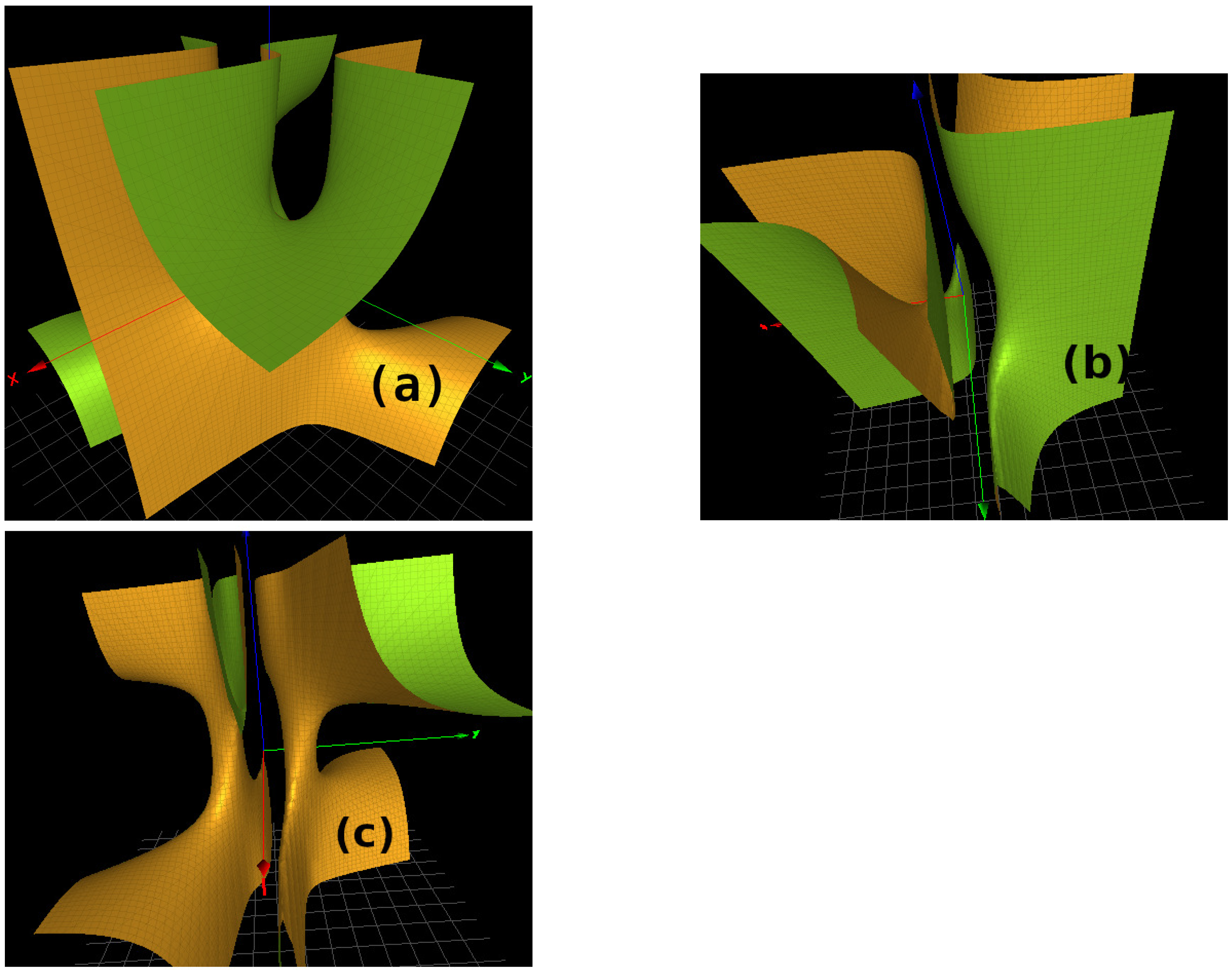
3.1. The Character Varieties of Knot Groups Whose Reducible Component Is that of the Hopf Link
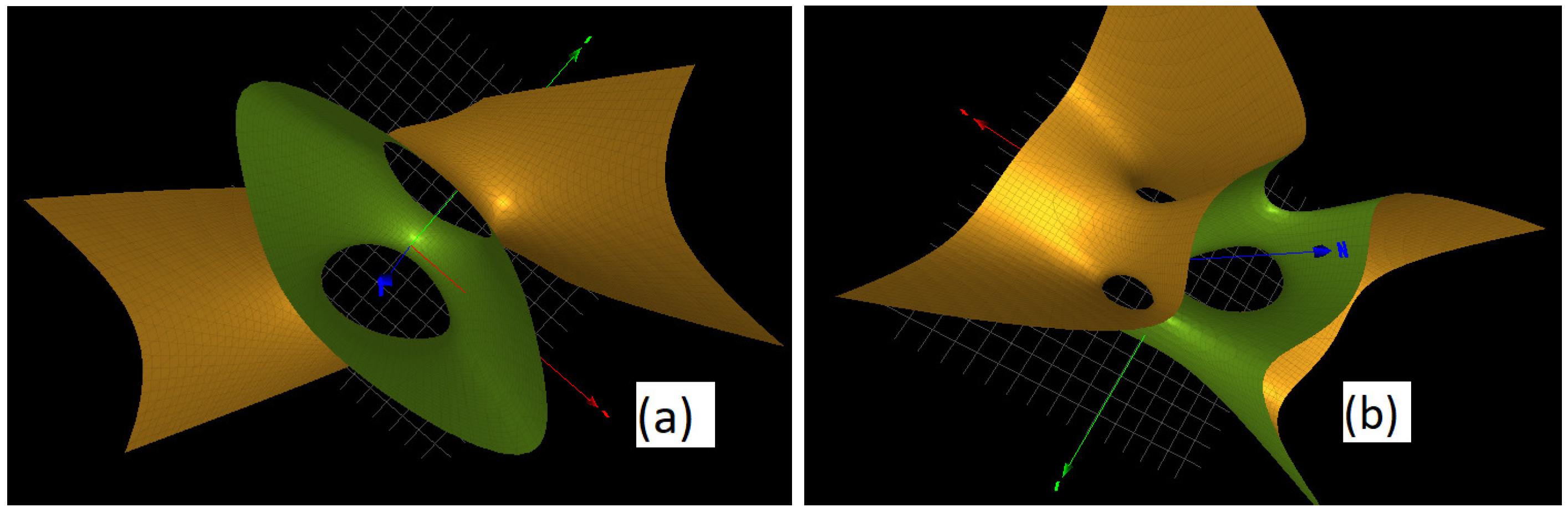
3.2. The Character Variety of Singular Fiber
3.3. The Character Variety of Singular Fiber
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Culler, M.; Shalen, P.B. Varieties of group representations and splitting of 3-manifolds. Ann. Math. 1983, 117, 109–146. [Google Scholar] [CrossRef]
- Harada, S. Canonical components of character varieties of arithmetic two-bridge link complements. arXiv 2012, arXiv:1112.3441. [Google Scholar]
- Ashley, C.; Burelle, J.P.; Lawton, S. Rank 1 character varieties of finitely presented groups. Geom. Dedicata 2018, 192, 1–19. [Google Scholar] [CrossRef]
- Python Code to Compute Character Varieties. Available online: http://math.gmu.edu/~slawton3/Main.sagews (accessed on 1 May 2021).
- Enriques–Kodaira Classification. Available online: https://en.wikipedia.org/wiki/Enriques–Kodaira_classification (accessed on 1 May 2021).
- Topological Quantum Computer. Available online: https://en.wikipedia.org/wiki/Topological_quantum_computer (accessed on 1 January 2021).
- Pachos, J.K. Introduction to Topological Quantum Computation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Wang, Z. Topological Quantum Computation; Number 112; American Mathematical Society: Providence, Rhode Island, 2010. [Google Scholar]
- Asselmeyer-Maluga,T. Topological quantum computing and 3-manifolds. Quant. Rep. 2021, 3, 9. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T. 3D topological quantum computing. Int. J. Quant. Inf. 2021, 19, 2141005. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M. Irwin, Group geometrical axioms for magic states of quantum computing. Mathematics 2019, 7, 948. [Google Scholar] [CrossRef]
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions. 2017. Available online: http://magma.maths.usyd.edu.au/magma/ (accessed on 1 January 2019).
- Liskovets, V.; Mednykh, A. On the number of connected and disconnected coverings over a manifold. Ars Math. Contemp. 2009, 2, 181–189. [Google Scholar] [CrossRef]
- Baake, M.; Grimm, U. Aperiodic Order, Vol. I: A Mathematical Invitation; Cambrige University Press: Cambridge, UK, 2013. [Google Scholar]
- Goldman, W.M. Trace coordinates on Fricke spaces of some simple hyperbolic surfaces. In Handbook of Teichmüller Theory; European Mathematical Society: Zürich, Switzerland, 2009; Volume 13, pp. 611–684. [Google Scholar]
- Asselmeyer-Maluga, T. Quantum computing and the brain: Quantum nets, dessins d’enfants and neural networks. EPI Web Conf. 2019, 198, 00014. [Google Scholar] [CrossRef][Green Version]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and nosy ancillas. Phys. Rev. 2005, A71, 022316. [Google Scholar] [CrossRef]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef]
- Planat, M. The Poincaré half-plane for informationally complete POVMs. Entropy 2018, 20, 16. [Google Scholar] [CrossRef]
- Grunewald, F.; Schwermer, J. Subgroups of Bianchi groups and arithmettic quotients of hyperbolic 3-space. Trans. Am. Math. Soc. 1993, 335, 47–78. [Google Scholar] [CrossRef][Green Version]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing with Bianchi groups. EPJ Web Conf. 2018, 2018 198, 0012. [Google Scholar]
- Culler, M.; Dunfield, N.M.; Goerner, M.; Weeks, J.R. SnapPy, a Computer Program for Studying the Geometry and Topology of three-Manifolds. Available online: http://snappy.computop.org (accessed on 1 January 2022).
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing, Seifert surfaces and singular fibers. Quantum Rep. 2019, 1, 3. [Google Scholar] [CrossRef]
- Scorpian, A. The Wild World of 4-Manifolds; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Wu, Y.-Q. Seifert fibered surgery on Montesinos knots. arXiv 2012, arXiv:1207.0154. [Google Scholar]
- Generalizations of Fibonacci Numbers. Available online: https://en.wikipedia.org/wiki/Generalizations_of_Fibonacci_numbers (accessed on 1 March 2022).
- Planat, M.; Amaral, M.M.; Fang, F.; Chester, D.; Aschheim, R.; Irwin, K. Group theory of syntactical freedom in DNA transcription and genome decoding Curr. Issues Mol. Biol. 2022, 44, 95. [Google Scholar] [CrossRef]
- Kauffman, L.H.; Lomonacco, S.J., Jr. Topological quantum information theory. Proc. Symp. Appl. Math. 2010, 68, 103–176. [Google Scholar]
- Assanioussi, M.; Bahr, B. Hopf link volume simplicity constraints in spin foam models. Class. Quant. Grav. 2020, 37, 205003. [Google Scholar] [CrossRef]
- Rovelli, C.; Vidotto, F. Covariant Loop Quantum Gravity, 1st ed.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Paluba, R. Geometry of Complex Character Varieties. Ph.D. Thesis, Université Paris-Saclay, Gif-sur-Yvette, France, 2017. Available online: https://tel.archives-ouvertes.fr/tel-01596075 (accessed on 1 March 2022).
- Boalch, P.; Paluba, R. Symmetric cubic surfaces as G2 character varieties. J. Algebr. Geom. 2016, 25, 607–631. [Google Scholar] [CrossRef]
- Planat, M.; Zainuddin, H. Zoology of atlas-groups: Dessins d’enfants, finite geometries and quantum commutation. Mathematics 2017, 5, 6. [Google Scholar] [CrossRef]
- Lévay, P.; Saniga, M.; Vrna, P. Three-qubit operators, the split Cayley hexagon of order two, and black holes Phys. Rev. D 2008, 78, 124022. [Google Scholar] [CrossRef]
- Planat, M.; Saniga, M.; Holweck, F. Distinguished three-qubit ‘magicity’ via automorphisms of the split Cayley hexagon. Quant. Inf. Proc. 2013, 12, 2535–2549. [Google Scholar] [CrossRef]
- Stacey, B.M. Sporadic SICs and the Normed Division Algebras. Found. Phys. 2017, 47, 1665. [Google Scholar] [CrossRef]

| Link L | Name | Rel(s) Link Group | Character Variety |
|---|---|---|---|
| L2a1 | Hopf | ||
| - | - | - | deg 3 Del Pezzo |
| , L7n1 | QT related | ||
| , L6a3 | 2QB related | ||
| , L5a1 | Whitehead | ||
| WL | - | conic bundle, type | |
| , L13n5885 | sister WL | ||
| - | - | deg 4 Del Pezzo, type | |
| , L6a2 | Bergé | ||
| - | - | conic bundle, general type | |
| , L6a1 | undetermined | ||
| - | - | - | |
| - | - | - | type |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Amaral, M.M.; Fang, F.; Chester, D.; Aschheim, R.; Irwin, K. Character Varieties and Algebraic Surfaces for the Topology of Quantum Computing. Symmetry 2022, 14, 915. https://doi.org/10.3390/sym14050915
Planat M, Amaral MM, Fang F, Chester D, Aschheim R, Irwin K. Character Varieties and Algebraic Surfaces for the Topology of Quantum Computing. Symmetry. 2022; 14(5):915. https://doi.org/10.3390/sym14050915
Chicago/Turabian StylePlanat, Michel, Marcelo M. Amaral, Fang Fang, David Chester, Raymond Aschheim, and Klee Irwin. 2022. "Character Varieties and Algebraic Surfaces for the Topology of Quantum Computing" Symmetry 14, no. 5: 915. https://doi.org/10.3390/sym14050915
APA StylePlanat, M., Amaral, M. M., Fang, F., Chester, D., Aschheim, R., & Irwin, K. (2022). Character Varieties and Algebraic Surfaces for the Topology of Quantum Computing. Symmetry, 14(5), 915. https://doi.org/10.3390/sym14050915







