The Thermoelastic Dynamic Response of a Rod Due to a Moving Heat Source under the Fractional-Order Thermoelasticity Theory

Abstract

In this paper, the thermoelastic behavior of a rod made of an isotropic material under the action of a moving heat source was investigated using a new theory of thermoelasticity related to fractional-order time with two relaxation times. A mathematical model of the one-dimensional thermoelasticity problem was established based on the new thermoelasticity theory. We considered the symmetry of the material, and the fractional-order thermoelasticity control equation was given. Subsequently, the control equations were solved and analyzed using the Laplace transform and its inverse transform. This study examined the effects of fractional-order parameters, time, two thermal relaxation times, and the speed of movement of the heat source on the displacement, temperature, and stress distribution patterns in the rod.

1. Introduction

The concept of symmetry is of major relevance in the area of thermoelasticity theory. The thermoelastic properties and behavior of an object are influenced by its symmetry in space, materials, loads, and other factors. The material of the rod under investigation in this paper was isotropic, which facilitated the study in question and simplified the solution process.

The thermoelasticity theory deals with the relationship between stress and strain in solid materials under the influence of heat. It is an essential tool for understanding and predicting the physical behavior of materials under the influence of temperature changes. The discipline of engineering makes extensive use of the notion of thermoelasticity, and research into it is always expanding. The conservative thermoelastic coupling theory proposed by Biot [1] in 1956 assumes an unlimited velocity of the traveling heat wave, but this is inconsistent with physical observations. In order to resolve this paradox, scholars have proposed the generalized thermoelasticity theory. Lord and Shulman [2] introduced a thermal relaxation factor and heat flow rate to the Fourier heat conduction equation, developing a generalized thermoelasticity theory (the L-S thermoelasticity theory), which resolved the paradox of an infinite wave propagation velocity that exists in the classical uncoupled thermoelasticity theory and coupled thermoelasticity theory. Green and Lindsay [3] developed a new generalized theory of thermoelasticity by taking into account the temperature change ratio in the heat transfer equation and included relaxation times in the stress and energy equations (the G-L thermoelasticity theory). Green and Naghdi [4,5,6] developed the Green–Naghdi (G-N I, II, and III) generalized thermoelasticity theory, which considers the energy balance but does not account for energy dissipation. Oskouie [7] proposed a numerical method to analyze the generalized thermo-viscoelastic coupling under the action of thermal shock based on the L-S theory of generalized thermoelasticity and the Kelvin–Voigt theory of viscoelasticity and investigated the effects of the viscoelastic parameter, the intensity of the thermal shock, and the relaxation time on the response to thermal shock. Yu and Xue [8] modified the G-L generalized thermoelastic theory by introducing the strain rate into the model. This modification avoids the displacement discontinuity present in the original G-L model. Deswal [9] employed the L-S and G-N generalized thermoelasticity theories to examine the influences of the initial stress and temperature dependence on the propagation of elastic waves in anisotropic thermoelastic media. Youssef [10] proposed a new generalized thermoelasticity model based on the linear non-Fourier heat conduction theorem and applied it to a one-dimensional thermoelastic rod problem for validation.

Scholars extensively utilize the generalized thermoelasticity theory to analyze the dynamic responses of various materials under transient loads, as well as to assess the stability and safety of structures in thermal environments. However, the traditional generalized thermoelasticity theory still exhibits limitations in addressing certain specialized thermoelasticity problems, such as the mobile heat source problem. In order to avoid these limitations, scholars have started to explore new theoretical frameworks and mathematical tools. In 1812, the Laplace transformation introduced the concept of fractional-order derivatives. While solving the problem of isochronous curves, Abel was the first to employ fractional-order operators in integral equations, introducing fractional calculus to represent the solutions of the equations. Following a protracted period of dedicated research by numerous scholars, the theory of fractional-order calculus was gradually established.

The theory of fractional-order calculus has been successfully applied to thermoelastic mechanics following extensive research by numerous scholars. The introduction of fractional-order derivatives into the field of generalized thermoelasticity offers new avenues for addressing complex dynamical problems and nonlinear systems. Povstenko [11] studied the thermal stress related to an unbounded medium with columnar cavities by introducing fractional-order derivatives into the heat transfer equation. Sherief [12] applied fractional-order calculus to the theory of generalized thermoelasticity, developing a fractional-order generalized thermoelasticity theory that degenerates into the L-S thermoelasticity theory when the fractional parameter is equal to one. Sherief and El-Latief [13] employed Sherief’s theory of fractional-order thermoelasticity to investigate the impact of fractional-order operators on half-space problems consisting of materials with variable thermal conductivity. Youssef [14] established a new fractional thermoelasticity theory, proved its uniqueness theorem, and applied it to a one-dimensional thermal shock problem. Ezzat et al. [15,16] developed a fractional thermoelasticity theory with a two-phase/three-phase lagging heat transfer equation by introducing a Taylor series into the heat transfer equation. The fractional-order thermoelasticity theory represents an extension of the generalized thermoelasticity theory. It offers a more comprehensive account of the nonlinear and nonlocal properties of materials than the integer order and is thus better suited to modeling the behavior of real materials. A great deal of research has been carried out on the fractional-order thermoelasticity theory. Hobiny [17] studied the distribution of physical field waves generated by the pulsed laser heating of the surface of an elastic medium and analyzed the effects of non-local parameters and fractional-order derivatives’ generation. Abouelregal [18] created a heat transfer model with single-phase hysteresis by introducing fractional calculus into the heat transfer equation, which differs from previous models by including two fractional parameters in the heat equation. Sherief et al. [19,20] investigated the impacts of fractional parameters on the thermoelastic behavior of anisotropic media using the integral transform method in conjunction with Sherief’s fractional thermoelasticity theory. Youssef [21] investigated how stresses and strains in unbounded media with spherical cavities were affected by fractional factors. Wang et al. [22] researched the behavior of infinite elastic media with cylindrical cavities. F. Hamza et al. [23] developed a new fractional thermoelasticity theory related to two thermal relaxation time factors using fractional-order calculus, which is characterized by the fact that all control equations in the model are affected by the time-fractional order parameter. Under three boundary conditions, Kothari [24] investigated the issue of the thermoelastic behavior of fractional-order parameters in isotropic elastic media. The thermoplasticity of inhomogeneous media with material properties in finite-length elliptical plates under the fractional-order theory was studied by Varghese [25]. Tian [26] and Shakeriaski [27] summarized the progress of research on the fundamental problem of generalized thermoelasticity and provided an outlook on the possible research directions for thermoelastic problems.

In the field of thermoelasticity, a moving heat source can be employed to model a multitude of real-world scenarios, such as the heat transfer process of a moving heat source in a material and the change in the heat source with time. By studying the effect of a mobile heat source on thermoelasticity problems, the deformation and stress distributions of materials under the action of heat can be better understood. This provides a theoretical basis for the design and application of materials. In conjunction with the generalized thermoelasticity theory, Youssef et al. [28,29,30] examined the thermoelastic behavior of several mathematical models with the existence of a mobile source of heat and examined the heat source’s impact on the physical field’s distribution. Mondal [31] incorporated memory-related derivatives into the L-S thermoelasticity model to develop a novel theoretical framework for the investigation of the transient responses of thermoelastic rods subjected to the influence of magnetic induction fields and moving heat sources. Zenkour [32] investigated the thermoelasticity of unbounded solids with cylindrical pores when a mobile source of heat was present using the dual-phase hysteretic thermoelasticity theory. Sarkar [33] investigated the thermoelastic behavior of a dual-temperature generalized thermoelastic unlimited-cavity dielectric with a columnar cavity in response to a mobile source of heat. Abbas [34] studied the distribution of the physical field of a thermoelastic solid under the influence of a moveable source of heat in a magnetic field. Abbas [35] employed a thermoelasticity model that incorporated a relaxation time in order to examine the evolution of physical fields within orthotropic anisotropic media. Ma [36] used Sherief’s fractional thermoelasticity theory to investigate the role of temperature correlation in the thermal shock in a nickel ore medium. Ma and He [37,38] investigated the dynamic reaction of functional-gradient piezoelectric rods under the action of a moveable hot source in light of the fractional thermoelasticity theory developed by Sherief. Youssef [39] formulated a new dual-temperature fractional generalized thermoelasticity model and investigated the half-space problem of a thermoelastic medium under the impact of a moveable source of heat. Al-Huniti [40] investigated the dynamic thermal and elastic behaviors of rods under the action of a moving heat source using a hyperbolic heat transfer model. He and Guo [41] used Sherief’s fractional generalized thermoelasticity theory to investigate the thermoelastic behavior of fixed rods under the action of a moveable source of heat. Xiong and Guo [42] studied the generalized magneto-thermoelasticity problem for temperature-dependent rods using the fractional-order thermoelasticity theory. Ezzat [43] set up a new fractional heat transfer model using the fractional-order time Taylor series expansion form proposed by Jumarie [44].

In the mathematical models of fractional thermoelasticity considered in references [41,42], only the energy equation takes into account the time-fractional order. Fractional-order parameters have important implications in describing the time dependence of materials, time lag effects, and non-local effect times. To enhance the model’s applicability, accuracy, and comprehensiveness, a new fractional thermoelasticity model with two relaxation times based on the G-L thermoelasticity theory and the Ezzat-type heat conduction model was used in this study. In this work, the fractional parameter and two thermal relaxation factors were considered for the study of the thermoelastic behavior of a fixed rod under the action of a moveable source of heat. Our model has a time-fractional parameter in all the control equations, which has an essential role in the model, influencing the model’s description of the material’s time dependence and non-local and time-lag effects and is crucial for an accurate description of the material’s thermoelastic behavior.

2. Basic Control Equations

In the fractional thermoelasticity theory that includes two relaxation times, the governing equations for a uniform isotropic elastomer are given below.

The equation of motion is expressed as

$${\sigma }_{ij,j}=\rho \frac{{\partial }^2{u}_i}{\partial t^2}.$$

(1)

The constitutive equation is expressed as

$${\sigma }_{ij}=\lambda e_{kk}{\delta }_{ij}+2\mu e_{ij}-\gamma \left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\theta {\delta }_{ij},$$

(2)

$$q_{i,i}+\rho T_0\frac{\partial \eta }{\partial t}=Q,$$

(3)

$$\rho \eta =\gamma u_{,j}+\frac{\rho C_E}{T_0}\left(\theta +{\tau }_1\frac{\partial \theta }{\partial t}\right).$$

(4)

The relationship between the strain and displacement is expressed as

$$e_{ij}=\frac{1}{2}\left(u_{j,i}+u_{i,j}\right),$$

(5)

$$\kappa {\theta }_{,ii}=\gamma T_0{\dot{e}}_{kk}+\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left(\rho C_E\dot{\theta }-Q\right).$$

(6)

where ${\sigma }_{ij}$ represents the stress components, $u_i$ represents the displacement components, $e_{ij}$ represents the strain components, $\eta$ is the entropy density, $e_{kk}$ represents the volume expansion rates, $\rho$ is the mass density, $\kappa$ is the thermal conductivity, ${\tau }_0$ and ${\tau }_1$ are the relaxation times, ${\delta }_{ij}$ is the Kronecker delta, and $C_E$ is the specific heat capacity. $\gamma$ is the thermal modulus, $\gamma ={\alpha }_t\left(2\mu +3\lambda \right)$, where ${\alpha }_t$ is the linear thermal expansion coefficient, and $\lambda$ and $\mu$ are Lame’s constants. $\alpha$ is a constant parameter, such that $0<\alpha \le 1$. $\theta =T-T_0$, where $T$ is the absolute temperature, $T_0$ is the reference temperature, and $Q$ is the intensity of the moveable heat source, while the subscript “,” indicates the derivation from the spatial coordinates, and the “.” In the variable indicates the derivation with respect to time. This symbol appears in the following content to represent the same meaning.

3. Formulation of the Problem

We built a coordinate system with the left end as the origin, as seen in Figure 1, and the object of investigation was a fixed rod under the action of a traveling source of heat.

For this one-dimensional problem, there is a non-zero displaced component $u_x=u(x,t)$; therefore, Equations (1), (2), and (6) are converted into:

$$\left(\lambda +2\mu \right)\frac{{\partial }^{2}u}{\partial x^2}-\gamma \left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\frac{\partial \theta }{\partial x}=\rho \frac{{\partial }^{2}u}{\partial t^2},$$

(7)

$$\sigma =\left(\lambda +2\mu \right)\frac{\partial u}{\partial x}-\gamma \left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\theta ,$$

(8)

$$\kappa \frac{{\partial }^2\theta }{\partial x^2}=\gamma T_0\frac{{\partial }^{2}u}{\partial x\partial t}+\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left(\rho C_E\dot{\theta }-Q\right).$$

(9)

To simplify the calculations, the subsequent non-dimensional variables are presented:

$$\begin{array}{l}{x}^{*}=c_0{\eta }_{0}x,u^{*}=c_0{\eta }_{0}u,{\tau }_0^{*}=c_0^2{\eta }_0{\tau }_0,{\tau }_1^{*}=c_0^2{\eta }_0{\tau }_1,t^{*}=c_0^2{\eta }_{0}t,\\ {\theta }^{*}=\frac{\theta }{T_0},{\sigma }^{*}=\frac{\sigma }{\mu },c_0^2=\frac{\lambda +2\mu }{\rho },{\eta }_0=\frac{\rho C_E}{\kappa },Q^{*}=\frac{Q}{\kappa T_0{c}_0^2{\eta }_0^2}.\end{array}$$

(10)

where $c_0$ is the elastic wave speed, and ${\eta }_0$ is the reciprocal of the thermal diffusivity.

Equations (7)–(9) are transformed into non-dimensional forms (the asterisks are removed for ease of calculation):

$$\frac{{\partial }^{2}u}{\partial x^2}-\frac{b}{{\beta }^2}\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\frac{\partial \theta }{\partial x}=\frac{{\partial }^{2}u}{\partial t^2},$$

(11)

$$\sigma ={\beta }^2\frac{\partial u}{\partial x}-b\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\theta ,$$

(12)

$$\frac{{\partial }^2\theta }{\partial x^2}=g\frac{{\partial }^{2}u}{\partial x\partial t}+\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left(\frac{\partial \theta }{\partial t}-Q\right).$$

(13)

where

$${\beta }^2=\frac{\lambda +2\mu }{\mu },b=\frac{\gamma T_0}{\mu },g=\frac{\gamma }{\rho C_E}.$$

(14)

For the sake of argument, the rod is thought to be stationary with a starting temperature of $T_0$, and the ratio of change over time is zero. The initial conditions are:

$$\theta \left(x,0\right)=\frac{\partial \theta \left(x,0\right)}{\partial t}=0,u\left(x,0\right)=\frac{\partial u\left(x,0\right)}{\partial t}=0.$$

(15)

Considering that the rod’s left end represents the coordinate origin and that its non-dimensional length is l, the boundary conditions are:

$$\frac{\partial \theta \left(0,t\right)}{\partial x}=\frac{\partial \theta \left(l,t\right)}{\partial x}=0,u\left(0,t\right)=u\left(l,t\right)=0.$$

(16)

The rod is affected by a non-dimensional moveable source of heat. In the directional $x$-axis, it is expressed as:

$$Q=Q_0\left(x-vt\right)\delta ,$$

(17)

where $Q_0$ is the non-dimensional moveable heat source’s amplitude, and $v$ is the heat source’s travel speed.

4. Laplace’s Solution

The expression for the Laplace transform equation is as follows:

$$L\left[f(t)\right]=\overline{f}\left(s\right)={\displaystyle {\int }_0^{\infty }{\mathrm{e}}^{-st}f\left(t\right)\mathrm{d}t},\mathrm{Re}(s)>0.$$

(18)

where $\mathrm{Re}$ represents the genuine component of the parameter, and $s$ is a parameter in the Laplace transform.

Combining Equation (18) yields:

$$\left(D^2-s^2\right)\overline{u}-\frac{b}{{\beta }^2}\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{s}^{\alpha }\right)D\overline{\theta }=0,$$

(19)

$$\overline{\sigma }={\beta }^{2}D\overline{u}-b\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{s}^{\alpha }\right)\overline{\theta },$$

(20)

$$D^2\overline{\theta }=gsD\overline{u}+\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}{s}^{\alpha }\right)\left(s\overline{\theta }-w{\mathrm{e}}^{-\frac{s}{v}x}\right).$$

(21)

where $D=\frac{\mathrm{d}}{\mathrm{d}x}$ and $w=\frac{Q_0}{v}$.

The boundary conditions in Equations (15) and (16) can be converted into

$$\frac{\partial \theta \left(0,s\right)}{\partial x}=\frac{\partial \theta \left(l,s\right)}{\partial x}=0,u\left(0,s\right)=u\left(l,s\right)=0.$$

(22)

Eliminating the $\overline{\theta }$ between Equations (19) and (21) obtains the equation for $\overline{u}$:

$$D^4\overline{u}-A_1{D}^2\overline{u}+A_2\overline{u}=A_3{\mathrm{e}}^{-\frac{s}{v}x}.$$

(23)

where

$$\begin{array}{l}{A}_1=\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}{s}^{\alpha }\right)s+\frac{gbs}{{\beta }^2}\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{s}^{\alpha }\right)+s^2,\\ A_2=\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}{s}^{\alpha }\right)s^3,\\ A_3=\frac{bws}{{\beta }^{2}v}\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{s}^{\alpha }\right)\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}{s}^{\alpha }\right).\end{array}$$

(24)

The common solution of Equation (23) reads as:

$$\overline{u}={\displaystyle \sum _{i=1}^4{C}_i{\mathrm{e}}^{h_{i}x}}+E{\mathrm{e}}^{-\frac{s}{v}x}.$$

(25)

where $C_i\left(i=1,2,3,4\right)$ are the factors of determination with respect to $s$, and the expression of $E$ is given by

$$E=\frac{A_3}{{\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$v$}\right.\right)}^4-A_1{\left(\raisebox{1ex}{$s$}\!\left/ \!\raisebox{-1ex}{$v$}\right.\right)}^2+A_2}.$$

(26)

$h_i$ represents the roots of Equation (27):

$$h^4-A_1{h}^2+A_2=0,$$

(27)

Then,

$$h_1=-h_2=\sqrt{\frac{A_1+\sqrt{{A_1}^2-4A_2}}{2}},h_3=-h_4=\sqrt{\frac{A_1-\sqrt{{A_1}^2-4A_2}}{2}}.$$

(28)

The elimination of $\overline{u}$ achieved by combining Equations (19) and (21) results in the equation for $\overline{\theta }$:

$$D^4\overline{\theta }-A_1{D}^2\overline{\theta }+A_2\overline{\theta }=A_4{\mathrm{e}}^{-\frac{s}{v}x},$$

(29)

where $A_4=w\left(1+\frac{{\tau }_1^{\alpha }}{\alpha !}{s}^{\alpha }\right)\left(s^2-\frac{s^2}{v^2}\right).$

The common solution of Equation (29) reads as:

$$\overline{\theta }={\displaystyle \sum _{i=1}^4{C}_{ii}{\mathrm{e}}^{h_{i}x}}+E^{\prime }{\mathrm{e}}^{-\frac{s}{v}x},$$

(30)

where $C_{ii}\left(i=1,2,3,4\right)$ are the factors to be determined with respect to $s$.

Substituting Equations (25) and (30) into Equation (19) yields

$$C_{ii}=\frac{{\beta }^2\left(h_i^2-s^2\right)}{b_1{h}_i}{C}_i,E^{\prime }=\frac{{\beta }^2\left(v^{2}s-s\right)}{b_{1}v}E.$$

(31)

where $b_1=b\left(1+\frac{{\tau }_0^{\alpha }}{\alpha !}{s}^{\alpha }\right)$.

To determine the coefficients $C_i$ and $C_{ii}$ in accordance with the boundary condition in Equation (22), the following expressions are obtained:

$$\begin{array}{l}{C}_1+C_2+C_3+C_4+E=0,\\ C_1{\mathrm{e}}^{h_{1}l}+C_2{\mathrm{e}}^{h_{2}l}+C_3{\mathrm{e}}^{h_{3}l}+C_4{\mathrm{e}}^{h_{4}l}+E{\mathrm{e}}^{-\frac{s}{v}l}=0,\\ C_{11}{h}_1+C_{22}{h}_2+C_{33}{h}_3+C_{44}{h}_4-\frac{s}{v}{E}^{\prime }=0,\\ C_{11}{h}_1{\mathrm{e}}^{h_{1}l}+C_{22}{h}_2{\mathrm{e}}^{h_{2}l}+C_{33}{h}_3{\mathrm{e}}^{h_{3}l}+C_{44}{h}_4{\mathrm{e}}^{h_{4}l}-\frac{s}{v}{E}^{\prime }{\mathrm{e}}^{-\frac{s}{v}l}=0.\end{array}$$

(32)

The calculation is derived by linking Equations (31) and (32):

$$\begin{array}{l}{C}_1=\frac{\left(h_3^2-\frac{s^2}{v^2}\right)\left({\mathrm{e}}^{h_{2}l}-{\mathrm{e}}^{-\frac{s}{v}l}\right)}{\left(h_1^2-h_3^2\right)\left({\mathrm{e}}^{h_{2}l}-{\mathrm{e}}^{h_{1}l}\right)}E,C_2=-\frac{\left(h_3^2-\frac{s^2}{v^2}\right)\left({\mathrm{e}}^{h_{1}l}-{\mathrm{e}}^{-\frac{s}{v}l}\right)}{\left(h_1^2-h_3^2\right)\left({\mathrm{e}}^{h_{2}l}-{\mathrm{e}}^{h_{1}l}\right)}E,\\ C_3=-\frac{\left(h_1^2-\frac{s^2}{v^2}\right)\left({\mathrm{e}}^{h_{4}l}-{\mathrm{e}}^{-\frac{s}{v}l}\right)}{\left(h_1^2-h_3^2\right)\left({\mathrm{e}}^{h_{4}l}-{\mathrm{e}}^{h_{3}l}\right)}E,C_4=\frac{\left(h_1^2-\frac{s^2}{v^2}\right)\left({\mathrm{e}}^{h_{3}l}-{\mathrm{e}}^{-\frac{s}{v}l}\right)}{\left(h_1^2-h_3^2\right)\left({\mathrm{e}}^{h_{4}l}-{\mathrm{e}}^{h_{3}l}\right)}E.\end{array}$$

(33)

Equation (25) can be transformed into

$$\overline{u}=C_1{\mathrm{e}}^{h_{1}x}+C_2{\mathrm{e}}^{h_{2}x}+C_3{\mathrm{e}}^{h_{3}x}+C_4{\mathrm{e}}^{h_{4}x}+E{\mathrm{e}}^{-\frac{s}{v}x}.$$

(34)

Equation (30) can be transformed into

$$\begin{array}{l}\overline{\theta }=\frac{{\beta }^2\left(h_1^2-s^2\right)}{b_1{h}_1}{C}_1{\mathrm{e}}^{h_{1}x}+\frac{{\beta }^2\left(h_2^2-s^2\right)}{b_1{h}_2}{C}_2{\mathrm{e}}^{h_{2}x}+\frac{{\beta }^2\left(h_3^2-s^2\right)}{b_1{h}_3}{C}_3{\mathrm{e}}^{h_{3}x}\\ +\frac{{\beta }^2\left(h_4^2-s^2\right)}{b_1{h}_4}{C}_4{\mathrm{e}}^{h_{4}x}+\frac{{\beta }^2\left(v^{2}s-s\right)}{b_{1}v}E{\mathrm{e}}^{-\frac{s}{v}x}.\end{array}$$

(35)

Substituting Equations (34) and (35) into Equation (20) obtains

$$\overline{\sigma }=\frac{{\beta }^2{s}^2}{h_1}{C}_1{\mathrm{e}}^{h_{1}x}+\frac{{\beta }^2{s}^2}{h_2}{C}_2{\mathrm{e}}^{h_{2}x}+\frac{{\beta }^2{s}^2}{h_3}{C}_3{\mathrm{e}}^{h_{3}x}+\frac{{\beta }^2{s}^2}{h_4}{C}_4{\mathrm{e}}^{h_{4}x}-{\beta }^{2}vsE{\mathrm{e}}^{-\frac{s}{v}x}.$$

(36)

5. Numerical Inverse Laplace Transforms

The expressions for $\overline{u}$, $\overline{\theta }$, and $\overline{\sigma }$ obtained using the Laplace transform are inverted in order to determine the distributions of the displacement, stress, and temperature in the fixed rod at both ends in response to the action of a moveable source of heat. Because the solution of the Laplace domain is so complicated, it is not feasible to obtain the inverse transformation via the analytic method. Thus, the Riemann sum [45] approach is employed to accomplish the numerical inverse transformation. With this approach, the following formula can be used to transform any Laplace-domain function $\overline{f}(x,s)$ back into the time domain:

$$f\left(x,t\right)=\frac{{\mathrm{e}}^{\beta t}}{t}\left[\frac{1}{2}\overline{f}\left(x,\beta \right)+\mathrm{Re}{\displaystyle \sum _{n=1}^N\overline{f}\left(x,\beta +\frac{\mathrm{i}n\mathsf{\pi }}{t}{(-1)}^n\right)}\right],$$

(37)

where $\mathrm{i}$ is a virtual number, and $\mathrm{Re}$ is the actual part. In order to achieve rapid convergence in numerical calculations, extensive experimental numerical calculations have indicated that the value of $\beta t\approx 4.7$ [45].

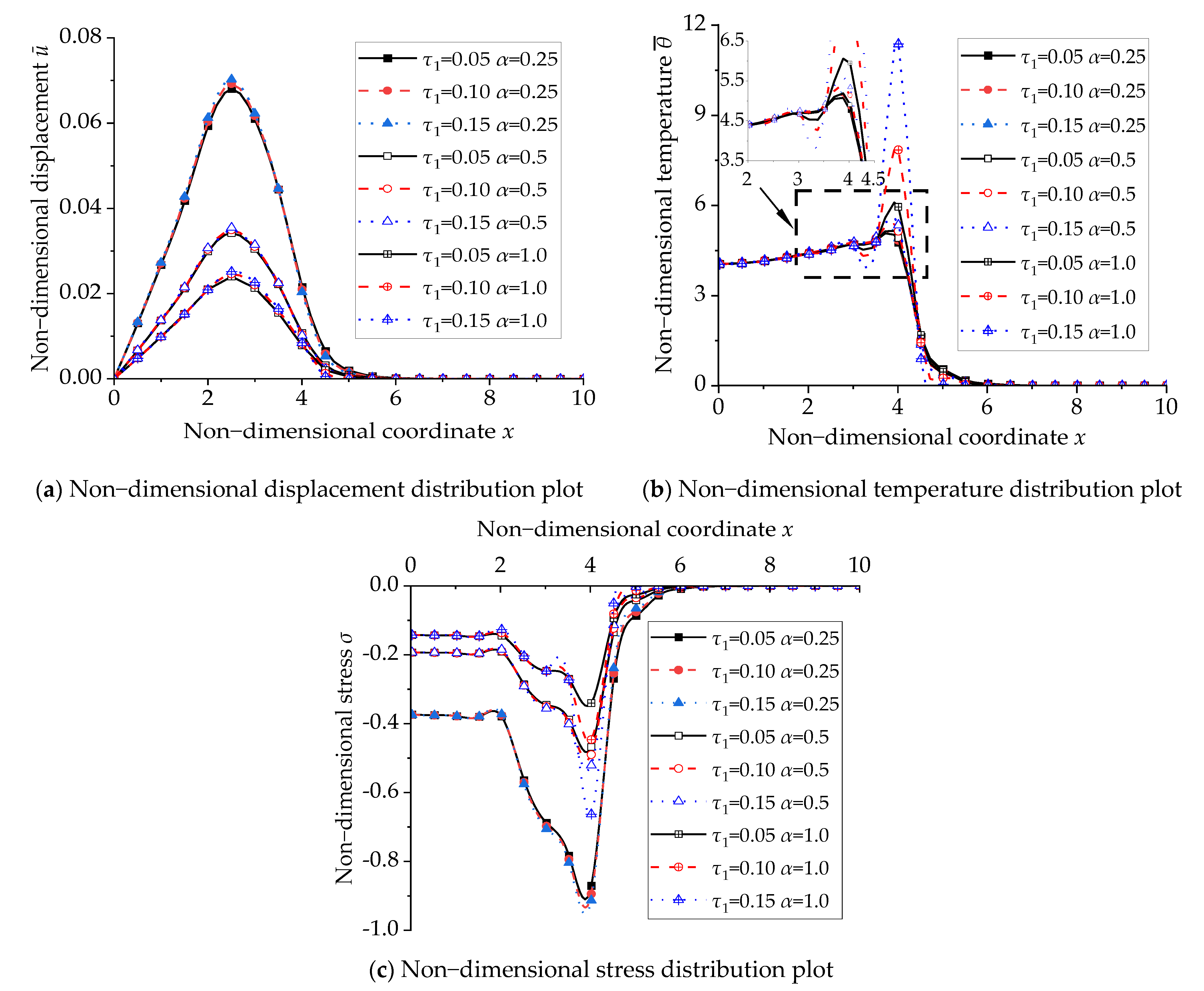
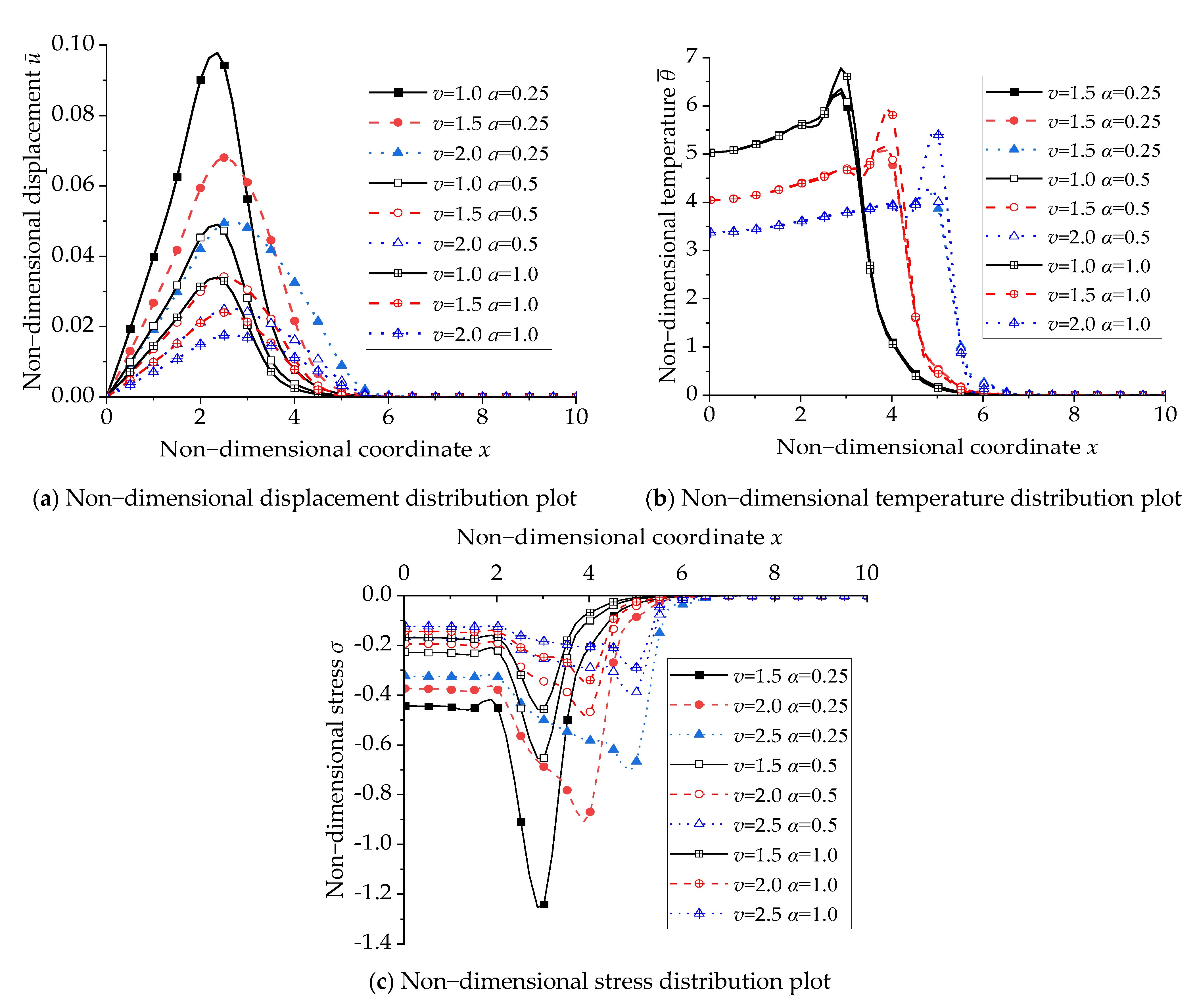
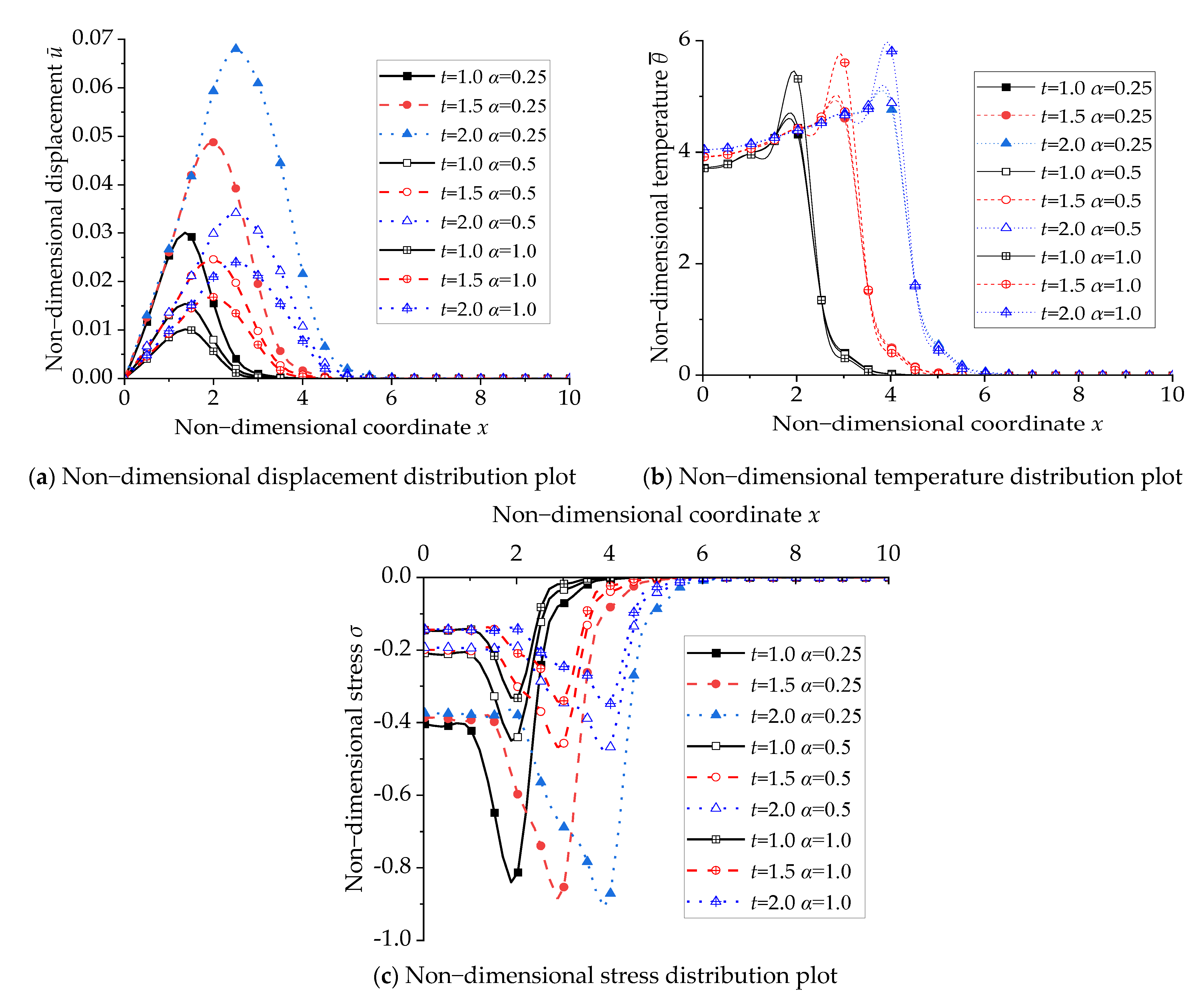
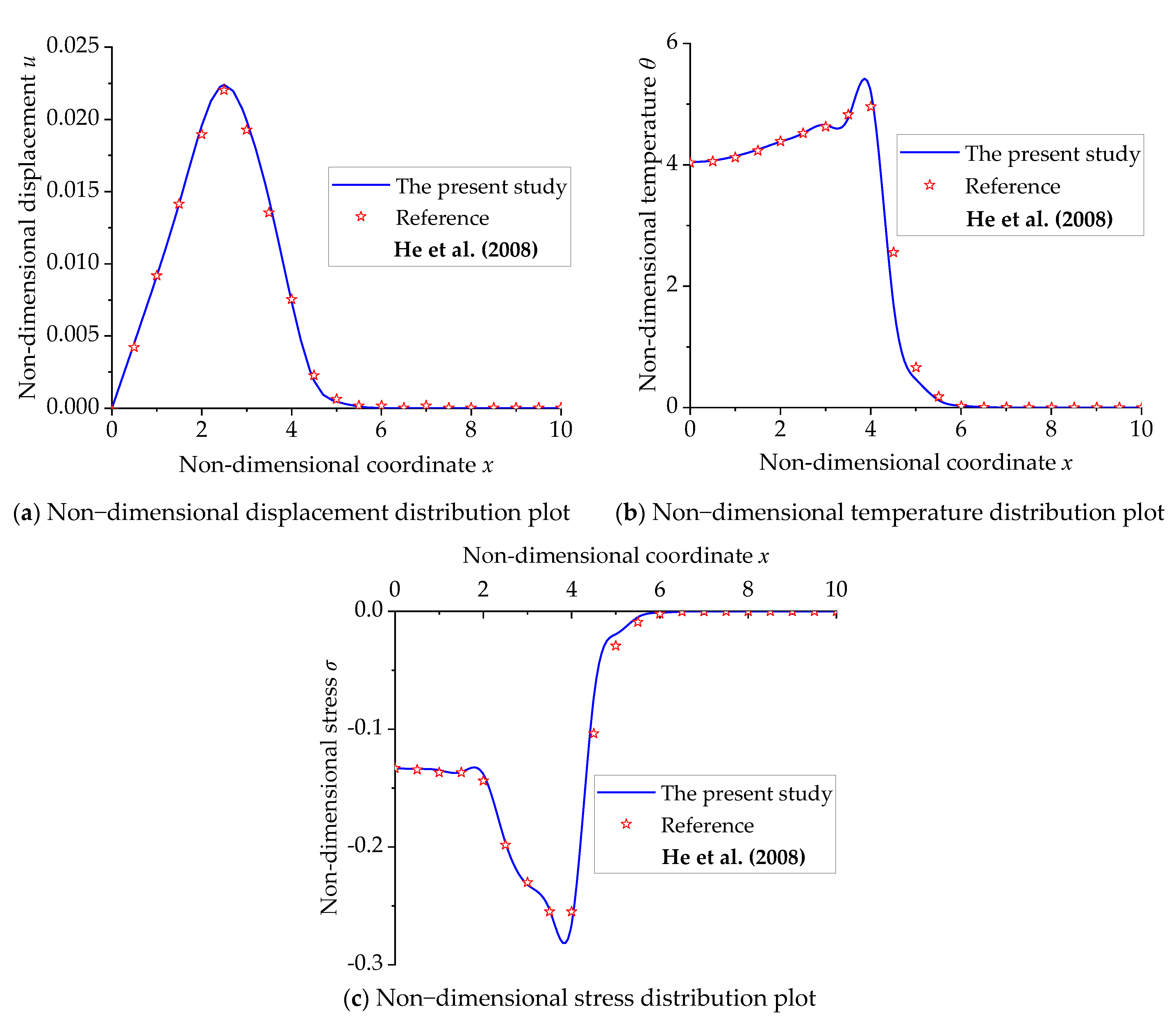
6. Analysis of Numerical Results

In addition to introducing Equation (37) for the numerical inverse transformation to obtain the non-dimensional displacement, temperature, and stress in the time domain, the following material-specific parameters need to be incorporated:

$$\begin{gathered} \lambda =7.76\times {10}^{10}\mathrm{N}\cdot {\mathrm{m}}^{-2},T_0=293\mathrm{K},\mu =3.86\times {10}^{10}\mathrm{N}\cdot {\mathrm{m}}^{-2},C_E=383.1\mathrm{kg}\cdot {\mathrm{K}}^{-1}, \\ \rho =8954\mathrm{kg}\cdot {\mathrm{m}}^{-3},\kappa =386\mathrm{N}\cdot {\mathrm{K}}^{-1}\cdot {\mathrm{s}}^{-1},{\alpha }_t=1.78\times {10}^{-5}{\mathrm{K}}^{-1},Q_0=10,l=10. \end{gathered}$$

The Laplace inverse transform is employed in order to obtain the variation curves of the non-dimensional temperature displacement and stress in the rod in the presence of a moveable source of heat. In the numerical calculations, the analysis of the distribution patterns of the physical variables is carried out, considering the impacts of the fractional coefficient $\alpha$, the two thermal relaxation factors ${\tau }_0$ and ${\tau }_1$, the heat source’s traveling speed $v$, and the time $t$. In this work, we considered four different kinds of cases: case I, altering the thermal relaxation factor ${\tau }_0$ (${\tau }_0=0.03$, ${\tau }_0=0.06$, and ${\tau }_0=0.09$) while keeping the thermal relaxation factor ${\tau }_1$, the time $t$, and the heat source’s traveling speed $v$ constant; case II, altering the thermal relaxation factor ${\tau }_1$ (${\tau }_1=0.05$, ${\tau }_1=0.10$, and ${\tau }_1=0.15$) while keeping the thermal relaxation factor ${\tau }_0$, the time $t$, and the heat source’s traveling speed $v$ constant; case III, altering the heat source’s traveling speed $v$ while keeping the thermal relaxation times ${\tau }_0$ and ${\tau }_1$ and the time $t$ constant; and case IV, altering the time $t$ while keeping the thermal relaxation times ${\tau }_0$ and ${\tau }_1$ and the heat source’s traveling speed $v$ constant. Three kinds of $\alpha$ for the above four cases were used, $\alpha =0.25$, $\alpha =0.5$, and $\alpha =1.0$. The non-dimensional displacement $\overline{u}$, temperature $\overline{\theta }$, and stress $\overline{\sigma }$ distributions were obtained. Figure 2, Figure 3, Figure 4 and Figure 5 present the distribution laws of the non-dimensional temperature, displacement, and stress.

Figure 2 illustrates the impacts of the fractional coefficient $\alpha$ and the thermal relaxation factor ${\tau }_0$ on the distributions of the non-dimensional displacement $\overline{u}$, stress $\overline{\sigma }$, and temperature $\overline{\theta }$. As shown in Figure 2, as the fractional coefficient $\alpha$ increases, the extreme values of the non-dimensional displacement and stress are then reduced. The non-dimensional temperature is not significantly affected by the fractional coefficients. The distribution of the non-dimensional displacement is shown in Figure 2a, where it is evident that the non-dimensional displacement increases as the thermal relaxation factor ${\tau }_0$ increases. In Figure 2b, it is evident that the changes in the thermal relaxation factor ${\tau }_0$ have virtually no impact on the non-dimensional temperature $\overline{\theta }$. In Figure 2c, it is evident that the non-dimensional stress $\overline{\sigma }$ increases as the thermal relaxation factor ${\tau }_0$ increases. In Equations (9)–(11), it can be found that the thermal relaxation factor ${\tau }_0$ directly affects the displacement and stress and is not directly related to the temperature, so the effect of the thermal relaxation factor ${\tau }_0$ on the non-dimensional displacement and stress is much larger than that on the non-dimensional temperature. It is also shown that as the fractional coefficient $\alpha$ increases, the thermal relaxation factor ${\tau }_0$ has a decreasing impact on the non-dimensional displacement and stress. It can be seen in Figure 2c that there is compressive stress in the rod. This is because the rod’s ends are fixed, limiting the displacement and leading to the creation of compressive stress.

Figure 2. Effects of fractional coefficient $\alpha$ and relaxation time ${\tau }_0$ on the non−dimensional displacement, temperature, and stress.

Figure 2. Effects of fractional coefficient $\alpha$ and relaxation time ${\tau }_0$ on the non−dimensional displacement, temperature, and stress.

The impacts of the thermal relaxation time ${\tau }_1$ and fractional coefficient $\alpha$ on the non-dimensional displacement $\overline{u}$, temperature $\overline{\theta }$, and stress $\overline{\sigma }$ are displayed in Figure 3. Figure 3a makes it clear that the displacement rises quickly to a peak value as the coordinate x increases, then sharply declines as the coordinate x increases further, and, ultimately, converges to zero. This indicates that the thermoelastic response of the fixed rod at both ends drastically varies at the beginning but gradually stabilizes when the heat wave propagates to a certain distance. The non-dimensional displacement and stress are not significantly impacted by the relaxation time ${\tau }_1$ parameter compared with the thermal relaxation time ${\tau }_0$, as depicted in Figure 3. However, the pole value of the non-dimensional temperature is significantly influenced by the thermal relaxation period, particularly at $\alpha =1$, where the increase rate of the pole point exceeds thirty-two percent. This is primarily determined by the properties of the delta function, where the moving source of heat releases the most heat at $x=vt$, making the temperature higher there. It is evident in Figure 3a,b that the effects of the relaxation time ${\tau }_1$ on the non-dimensional temperature and non-dimensional stress are basically the same. This is due to the fact that the thermal expansion of the rod increases with the increasing temperature, but because the rod is fixed at both ends and cannot be extended toward the ends, the stress in the rod also rises with the increasing temperature.

Figure 3. Effects of fractional coefficient $\alpha$ and relaxation time ${\tau }_1$ on the non−dimensional displacement, temperature, and stress.

Figure 3. Effects of fractional coefficient $\alpha$ and relaxation time ${\tau }_1$ on the non−dimensional displacement, temperature, and stress.

Figure 4 illustrates the impacts of the fractional coefficient $\alpha$ and heat source’s traveling speed $v$ on the non-dimensional displacement $\overline{u}$, temperature $\overline{\theta }$, and stress $\overline{\sigma }$. The extreme values of the non-dimensional displacement and stress diminish with the increasing fractional coefficients, as illustrated in Figure 4. The temperature that is non-dimensional is slightly affected by the fractional coefficients. Figure 4 makes it clear that the non-dimensional displacement, temperature, and stress all progressively reduce as the traveling velocity of the non-dimensional source of heat improves. Moreover, the peak of the curve gradually moves backward, and the range of disturbance in the rod gradually increases. For the same amount of time, the heat source releases a consistent amount of energy. As the heat source’s traveling speed increases, the density of the heat liberated by the source of heat per unit length gradually decreases, leading to a reduction in the temperature in the rod, and this leads to a cumulative reduction in the thermal expansion within the rod; therefore, the strain in the rod diminishes. The compressive stress in the rod decreases as the strain decreases because it is fixed at both ends.

Figure 4. Effects of fractional coefficient $\alpha$ and heat source’s traveling speed $v$ on the non−dimensional displacement, temperature, and stress.

Figure 4. Effects of fractional coefficient $\alpha$ and heat source’s traveling speed $v$ on the non−dimensional displacement, temperature, and stress.

Figure 5 shows the dispersion patterns of the non-dimensional displacement $\overline{u}$, temperature $\overline{\theta }$, and stress $\overline{\sigma }$ at different time instances with the fractional-order coefficient $\alpha$. The non-dimensional displacement and stress gradually decrease with the increasing fractional-order coefficient $\alpha$ while the remaining parameters remain constant. Furthermore, the fractional coefficient $\alpha$ has very little influence on the non-dimensional temperature. As shown in Figure 5, the fractional coefficient $\alpha$ remains constant, while the curves of each physical variable considerably vary at different times. As the time increases, each physical variable gradually increases, and its peak positions itself positively on the $x$-axis. The reason for this phenomenon is that the rod’s ends are fixed, and the thermal expansion and deformation of the rod gradually accumulate over time as the moveable source of heat continues to release heat. As a result, the rod’s displacement, temperature, and stress all rise with time.

Figure 5. Effects of fractional coefficient $\alpha$ and time $t$ on the non−dimensional displacement, temperature, and stress.

Figure 5. Effects of fractional coefficient $\alpha$ and time $t$ on the non−dimensional displacement, temperature, and stress.

When $\alpha =1.0$ and ${\tau }_0=0$, the model proposed in this paper can degenerate into the model described in reference [46]. We compared the computed results using the model proposed in this paper with the distribution plots of various physical variables when parameters $\tau =0.05$, $t=2$, and $v=2$ presented in reference [46]. In Figure 6, it can be observed that the computed results exhibit good agreement between the two, with minor discrepancies arising from differences in the numerical computation methods. This further validates the correctness and rationality of the model proposed in this paper.

7. Conclusions

In this paper, the thermoelastic dynamic response of an isotropic homogeneous rod under the action of a moving heat source was investigated using the fractional-order thermoelasticity theory. The effects of the fractional-order coefficient $\alpha$, the time t, two relaxation times ${\tau }_0$ and ${\tau }_1$, and the speed of movement of the heat source on the displacement, temperature, and stress distribution patterns in the rod were analyzed. The preceding discussion led to the following conclusions:

(1)

The fractional coefficient has an important impact on the thermoelastic behavior of a fixed rod within the framework of the fractional-order thermoelasticity theory. The thermoelastic reaction of the fixed rod becomes increasingly noticeable as the fractional-order coefficient declines, particularly for the displacements and stresses within the rod.

(2)

The thermal relaxation time ${\tau }_0$ has significant effects on the displacements and stresses, which gradually increase as the thermal relaxation time ${\tau }_0$ increases for the rod. The thermal relaxation time ${\tau }_0$ has no significant effect on the temperature of the rod.

(3)

The thermal relaxation time ${\tau }_1$ exerts a considerable influence on the temperature peak region within the rod, whereas its impacts on the stress and displacement within the rod are relatively modest.

(4)

The time and the heat source’s traveling speed have significant effects on the displacement, temperature, and stress in the rod. Each physical variable decreases with the increasing heat source traveling speed and increases with time.

Future research could investigate the influence of magnetic and electric fields on the thermoelastic behavior of materials. Alternatively, it could examine the impact of mechanical loading on the thermoelastic behavior of materials.