Numerical Solution for the Heat Conduction Model with a Fractional Derivative and Temperature-Dependent Parameters
Abstract
:1. Introduction
2. Mathematical Model
3. Numerical Procedure
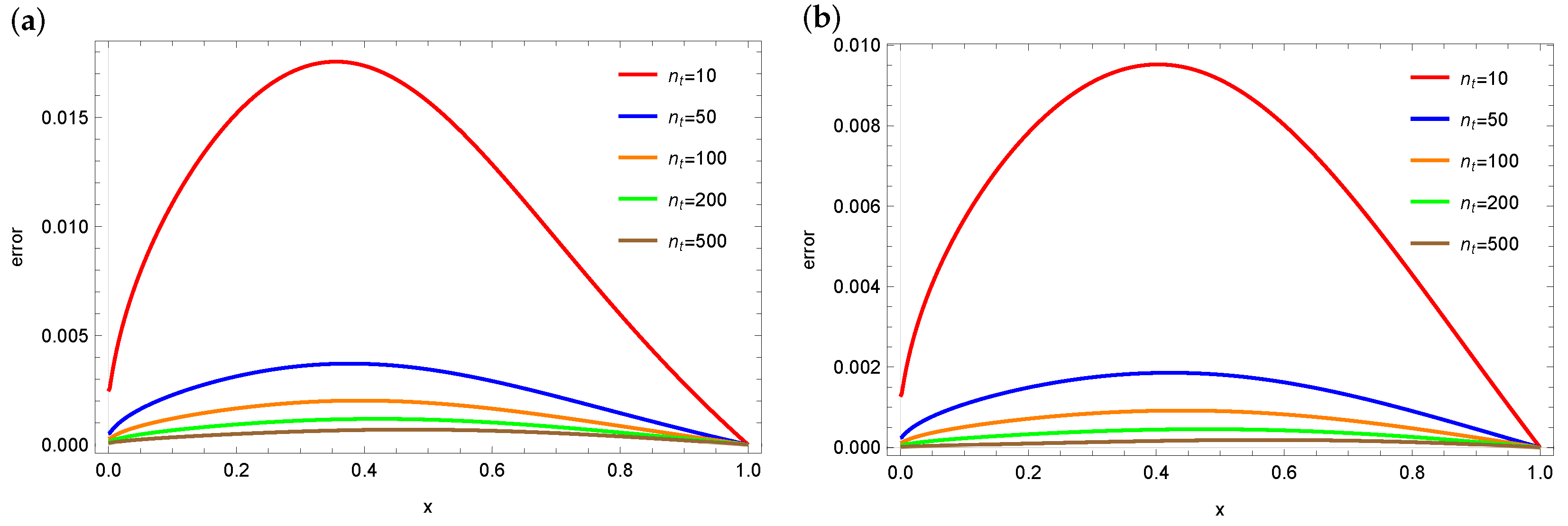
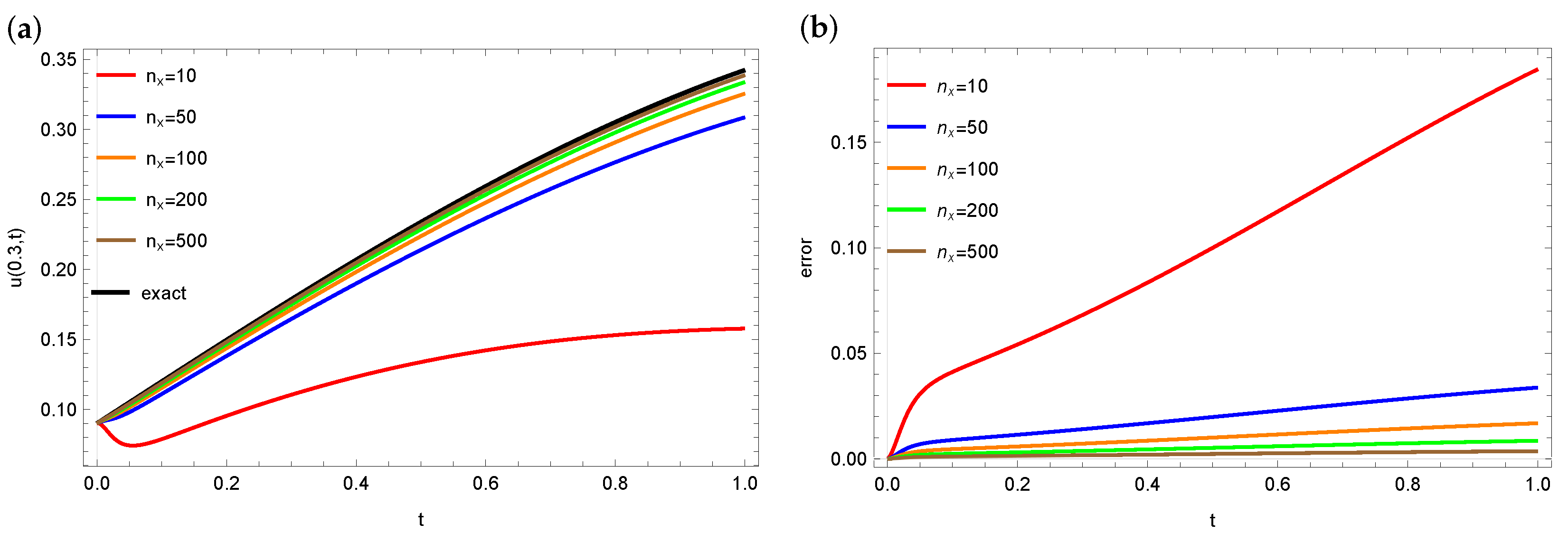
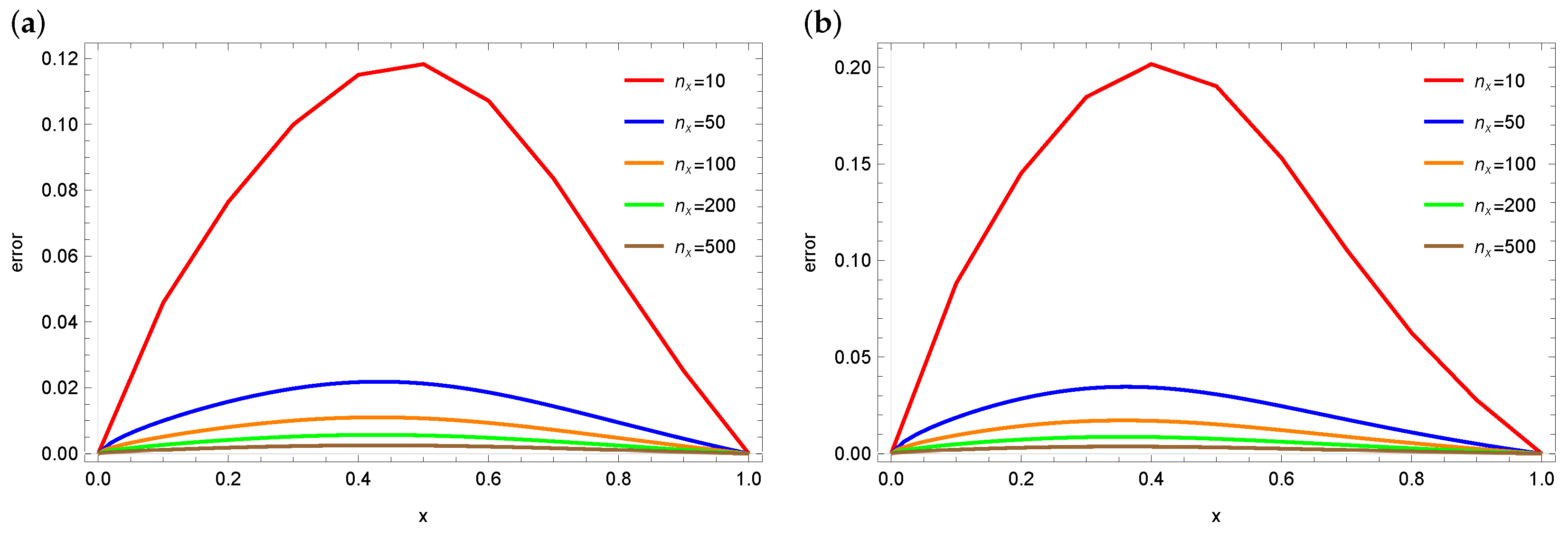
4. Numerical Calculations
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bhangale, N.; Kachhia, K.B.; Gómez-Aguilar, J.F. Fractional viscoelastic models with Caputo generalized fractional derivative. Math. Methods Appl. Sci. 2023, 46, 7835–7846. [Google Scholar] [CrossRef]
- Azeem, M.; Farman, M.; Akgül, A.; De la Sen, M. Fractional Order Operator for Symmetric Analysis of Cancer Model on Stem Cells with Chemotherapy. Symmetry 2023, 15, 533. [Google Scholar] [CrossRef]
- Nisar, K.S.; Farman, M.; Abdel-Aty, M.; Cao, J. A review on epidemic models in sight of fractional calculus. Alex. Eng. J. 2023, 75, 81–113. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Agarwal, R.P.; Pindza, E.; Bernstein, S.; Osman, M.S. Complex Turing patterns in chaotic dynamics of autocatalytic reactions with the Caputo fractional derivative. Neural Comput. Appl. 2023, 35, 11309–11335. [Google Scholar] [CrossRef]
- Kamdem, T.C.; Richard, K.G.; Béda, T. New description of the mechanical creep response of rocks by fractional derivative theory. Appl. Math. Model. 2023, 116, 624–635. [Google Scholar] [CrossRef]
- Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Comparison of mathematical models with fractional derivative for the heat conduction inverse problem based on the measurements of temperature in porous aluminum. Int. J. Heat Mass Transf. 2019, 143, 118440. [Google Scholar] [CrossRef]
- D’Elia, M.; Du, Q.; Glusa, C.; Gunzburger, M.; Tian, X.; Zhou, Z. Numerical methods for nonlocal and fractional models. Acta Numer. 2020, 29, 1–124. [Google Scholar] [CrossRef]
- Odibat, Z.; Baleanu, D. Numerical simulation of initial value problems with generalized Caputo-type fractional derivatives. Appl. Numer. Math. 2020, 156, 94–105. [Google Scholar] [CrossRef]
- Hajiseyedazizi, S.N.; Samei, M.E.; Alzabut, J.; Chu, Y. On multi-step methods for singular fractional q-integro-differential equations. Open Math. 2021, 19, 1378–1405. [Google Scholar] [CrossRef]
- Błasik, M. The Implicit Numerical Method for the Radial Anomalous Subdiffusion Equation. Symmetry 2023, 15, 1642. [Google Scholar] [CrossRef]
- Hou, J.; Meng, X.; Wang, J.; Han, Y.; Yu, Y. Local Error Estimate of an L1-Finite Difference Scheme for the Multiterm Two-Dimensional Time-Fractional Reaction–Diffusion Equation with Robin Boundary Conditions. Fractal Fract. 2023, 7, 453. [Google Scholar] [CrossRef]
- Sun, H.; Chang, A.; Zhang, Y.; Chen, W. A Review on Variable-Order Fractional Differential Equations: Mathematical Foundations, Physical Models, Numerical Methods and Applications. Fract. Calc. Appl. Anal. 2019, 22, 27–59. [Google Scholar] [CrossRef]
- Khan, M.; Rasheed, A.; Anwar, M.S.; Hussain Shah, S.T. Application of fractional derivatives in a Darcy medium natural convection flow of MHD nanofluid. Ain Shams Eng. J. 2023, 14, 102093. [Google Scholar] [CrossRef]
- Terpak, J. Fractional heat conduction models and their applications. In Volume 7 Applications in Engineering, Life and Social Sciences, Part A; Baleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 225–246. [Google Scholar] [CrossRef]
- Ji, C.-c.; Dai, W.; Sun, Z.-z. Numerical Schemes for Solving the Time-Fractional Dual-Phase-Lagging Heat Conduction Model in a Double-Layered Nanoscale Thin Film. J. Sci. Comput. 2019, 81, 1767–1800. [Google Scholar] [CrossRef]
- Gholizadeh, M.; Alipour, M.; Behroozifar, M. Numerical Solution of Two and Three-Dimensional Fractional Heat Conduction Equations via Bernstein Polynomials. Comput. Math. Math. Phys. 2022, 62, 1865–1884. [Google Scholar] [CrossRef]
- Kukla, S.; Siedlecka, U.; Ciesielski, M. Fractional Order Dual-Phase-Lag Model of Heat Conduction in a Composite Spherical Medium. Materials 2022, 15, 7251. [Google Scholar] [CrossRef]
- Brociek, R.; Hetmaniok, E.; Słota, D. Reconstruction of aerothermal heating for the thermal protection system of a reusable launch vehicle. Appl. Therm. Eng. 2023, 219, 119405. [Google Scholar] [CrossRef]
- Brociek, R.; Hetmaniok, E.; Napoli, C.; Capizzi, G.; Słota, D. Estimation of aerothermal heating for a thermal protection system with temperature dependent material properties. Int. J. Therm. Sci. 2023, 188, 108229. [Google Scholar] [CrossRef]
- Brociek, R.; Hetmaniok, E.; Napoli, C.; Capizzi, G.; Słota, D. Identification of aerothermal heating for thermal protection systems taking into account the thermal resistance between layers. Int. J. Heat Mass Transf. 2024, 218, 124772. [Google Scholar] [CrossRef]
- Zingales, M.; Alaimo, G. A physical description of fractional-order Fourier diffusion. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, Catania, Italy, 23–25 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Povstenko, Y. Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder. Fract. Calc. Appl. Anal. 2011, 14, 418–435. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional Thermoelasticity; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Hristov, J. Approximate solutions to fractional subdiffusion equations. Eur. Phys. J. Spec. Top. 2011, 193, 229–243. [Google Scholar] [CrossRef]
- Ceretani, A.; Tarzia, D. Determination of two unknown thermal coefficients through an inverse one-phase fractional Stefan problem. Fract. Calc. Appl. Anal. 2017, 20, 399–421. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Özişik, M. Heat Conduction; Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Jaluria, Y.; Torrance, K. Computational Heat Transfer; Taylor & Francis: New York, NY, USA, 2003. [Google Scholar] [CrossRef]
- Mochnacki, B.; Suchy, J. Numerical Methods in Computations of Foundry Processes; PFTA: Cracow, Poland, 1995. [Google Scholar]
- Meerschaert, M.; Tadjeran, C. Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 2006, 172, 65–77. [Google Scholar] [CrossRef]
- Owolabi, K.M. Efficient numerical simulation of non-integer-order space-fractional reaction-diffusion equation via the Riemann-Liouville operator. Eur. Phys. J. Plus 2018, 133, 98. [Google Scholar] [CrossRef]
- Cai, M.; Li, C. Numerical Approaches to Fractional Integrals and Derivatives: A Review. Mathematics 2020, 8, 43. [Google Scholar] [CrossRef]






| Max | Mean | |
|---|---|---|
| 10 | ||
| 50 | ||
| 100 | ||
| 200 | ||
| 500 |
| Max | Mean | |
|---|---|---|
| 10 | ||
| 50 | ||
| 100 | ||
| 200 | ||
| 500 |
| Max | Mean | |
|---|---|---|
| 10 | ||
| 50 | ||
| 100 | ||
| 200 | ||
| 500 |
| Max | Mean | |
|---|---|---|
| 10 | ||
| 50 | ||
| 100 | ||
| 200 | ||
| 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brociek, R.; Hetmaniok, E.; Słota, D. Numerical Solution for the Heat Conduction Model with a Fractional Derivative and Temperature-Dependent Parameters. Symmetry 2024, 16, 667. https://doi.org/10.3390/sym16060667
Brociek R, Hetmaniok E, Słota D. Numerical Solution for the Heat Conduction Model with a Fractional Derivative and Temperature-Dependent Parameters. Symmetry. 2024; 16(6):667. https://doi.org/10.3390/sym16060667
Chicago/Turabian StyleBrociek, Rafał, Edyta Hetmaniok, and Damian Słota. 2024. "Numerical Solution for the Heat Conduction Model with a Fractional Derivative and Temperature-Dependent Parameters" Symmetry 16, no. 6: 667. https://doi.org/10.3390/sym16060667






