New Parametric 2D Curves for Modeling Prostate Shape in Magnetic Resonance Images
Abstract
1. Introduction
- Circular bending along the y axiswhere , . The effect of this transformation is shown in Figure 2c.
- Rotation and translationwhere , .
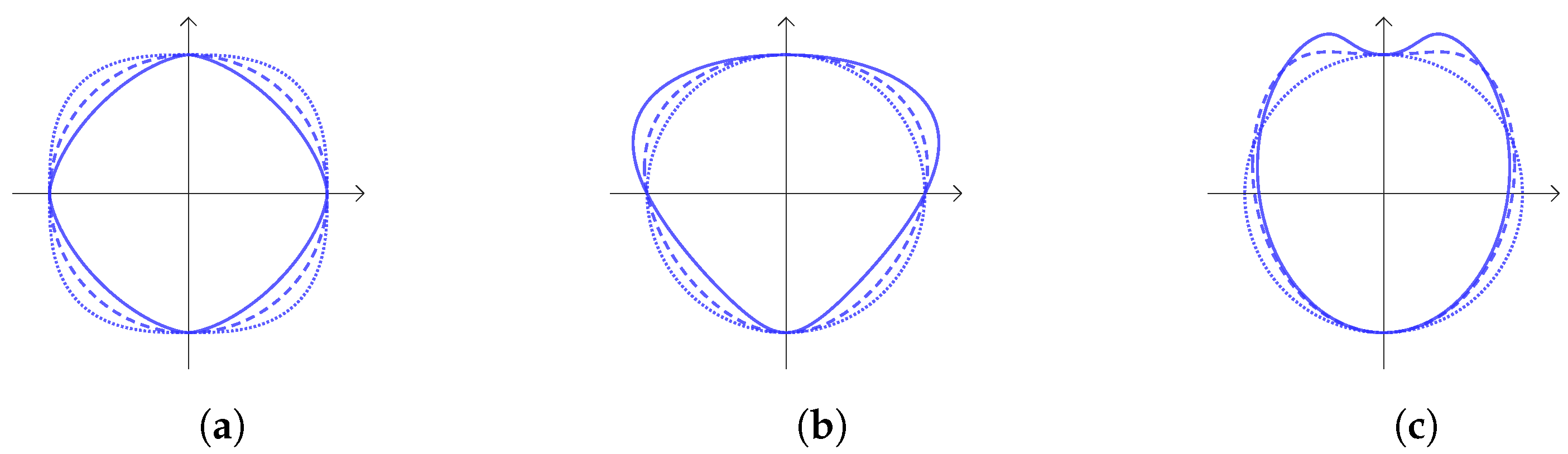
2. Our Models
2.1. Role of the Parameters
- CS curve:
- CC curve:
2.1.1. CS Curve
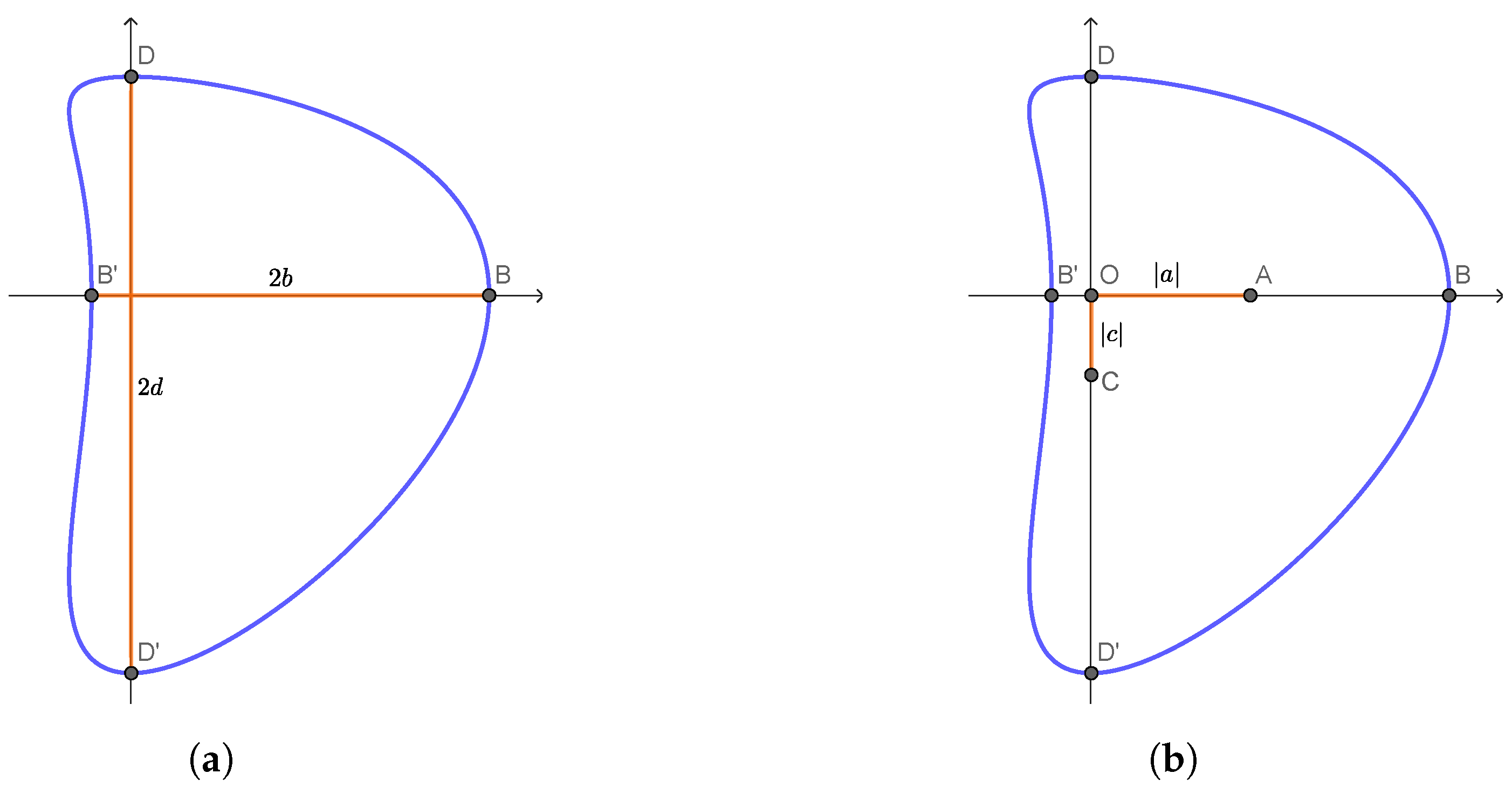

- The curve has a concavity around B if and only if ;
- The curve has a ‘flat side’ around B if and only if ;
- The curve has a ‘flat side’ around if and only if ;
- The curve has a concavity around if and only if ;
- The curve has a concavity around D if and only if ;
- The curve has a ‘flat side’ around D if and only if ;
- The curve has a ‘flat side’ around if and only if ;
- The curve has a concavity around if and only if .
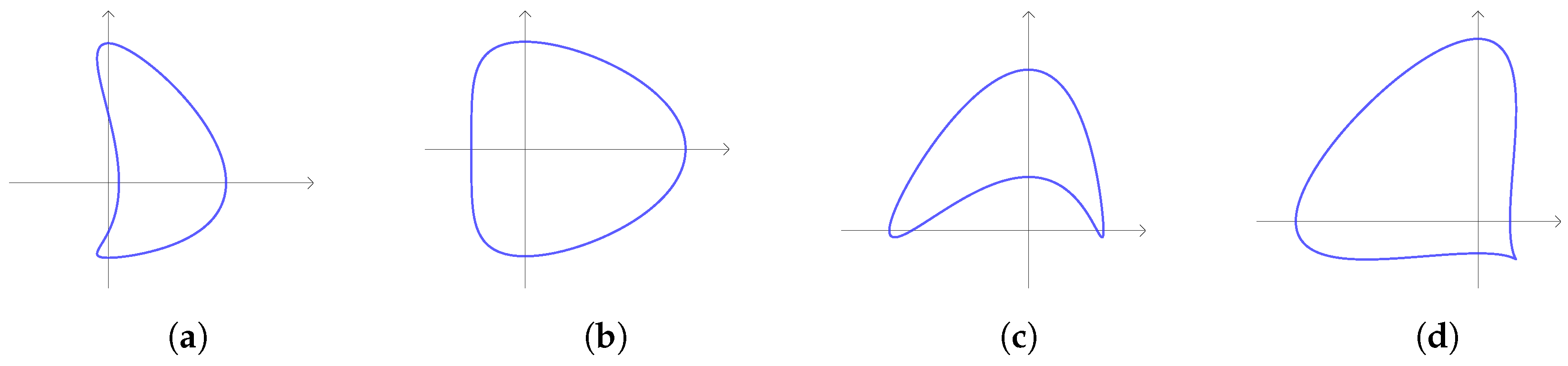
2.1.2. CC Curve
- The curve has a concavity around B if and only if ;
- The curve has a ‘flat side’ around B if and only if ;
- The curve has a ‘flat side’ around if and only if ;
- The curve has a concavity around if and only if .

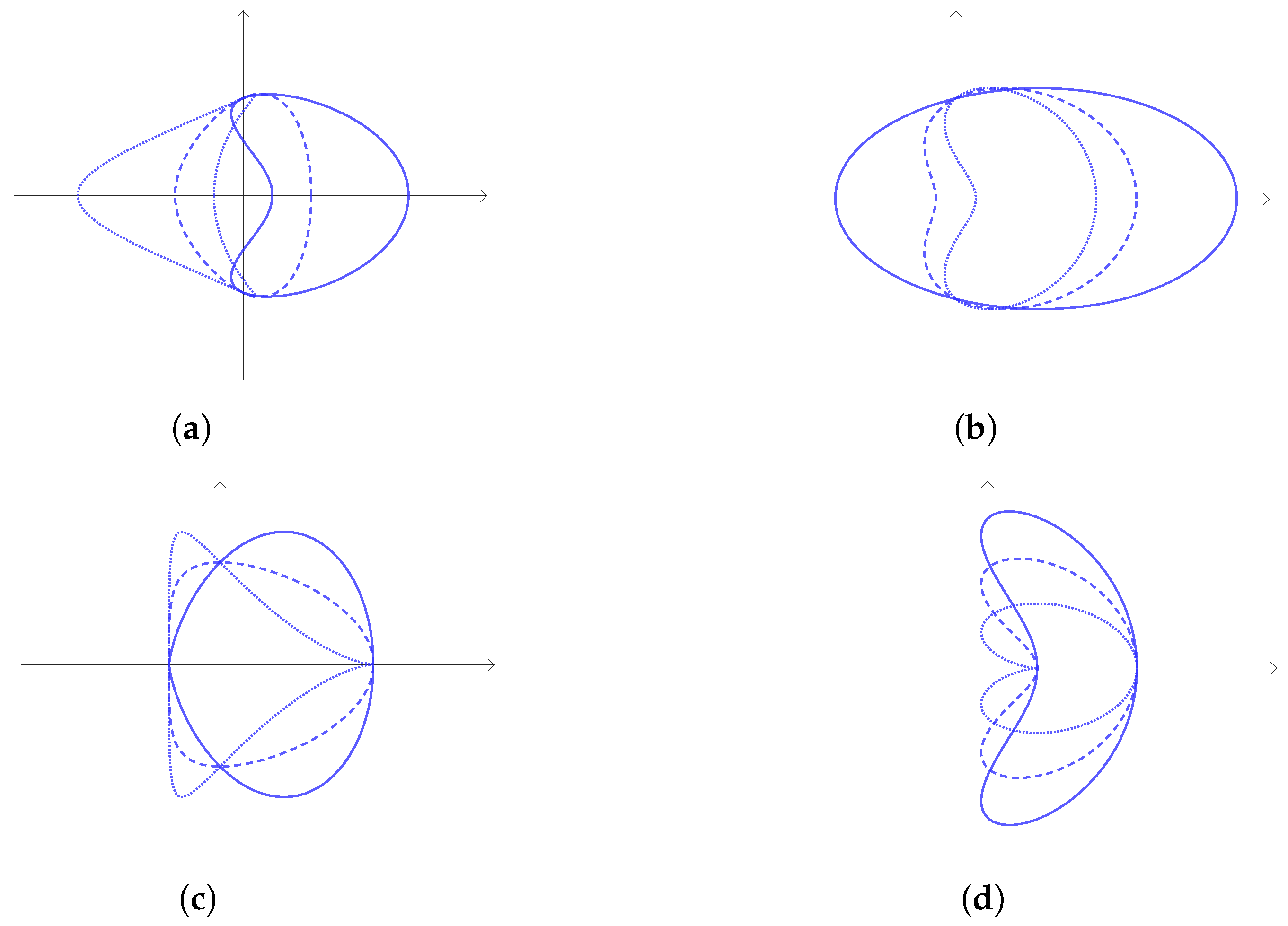
2.2. Symmetries and Invariants
2.2.1. CS Curve
- The transformation gives the symmetric curve with respect to the y axis. Thus, if , the curve is symmetric with respect to the y axis.
- The transformation gives the symmetric curve with respect to the x axis. Thus, if , the curve is symmetric with respect to the x axis.
- Each one of the transformations and leaves the curve invariant. This reason, together with the degenerate cases or , justifies our choice to consider b and d as positive numbers made in (6).
- The transformation gives the symmetric curve with respect to the origin (or, equivalently, the curve rotated by a straight angle with its center as the origin).
- The transformation gives the symmetric curve with respect to the line . Thus, if and , the curve is symmetric with respect to the line .
2.2.2. CC Curve
- The curve is always symmetric with respect to the x axis.
- Each one of the transformations , and gives the symmetric curve with respect to the y axis (or, equivalently, the curve rotated by a straight angle with its center at the origin, as in the previous remark).
- Each one of the transformations , and leaves the curve invariant. For this reason, we assume that b and d are non-negative numbers in (6).
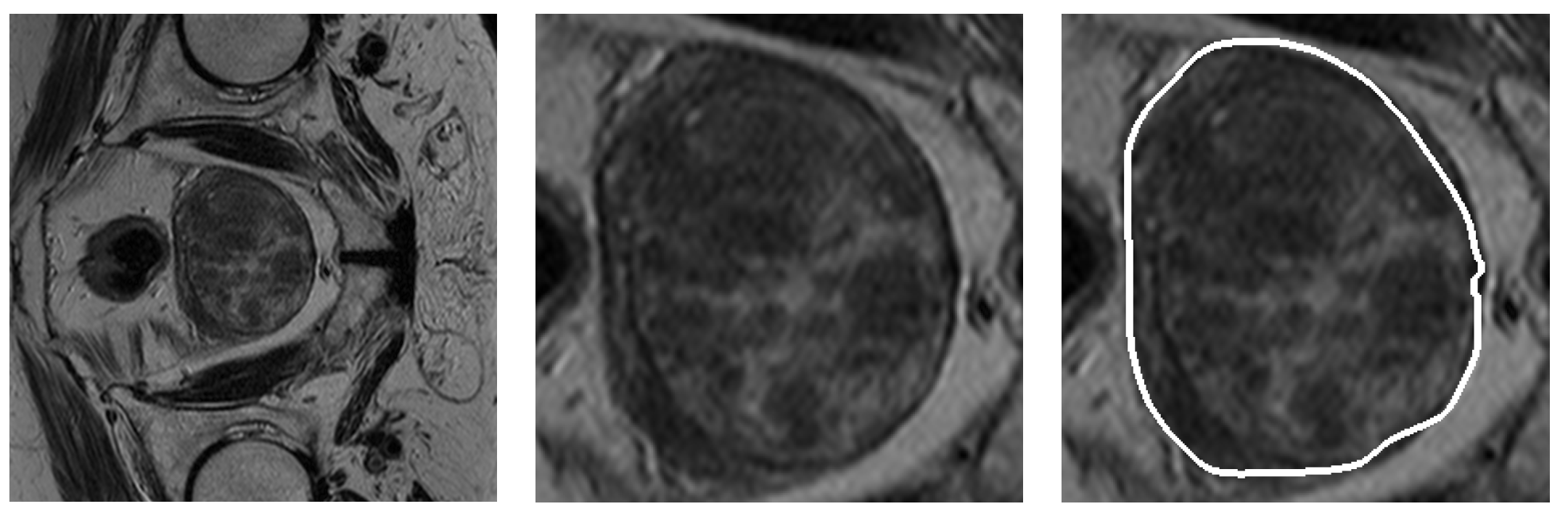
3. Validation of the Models
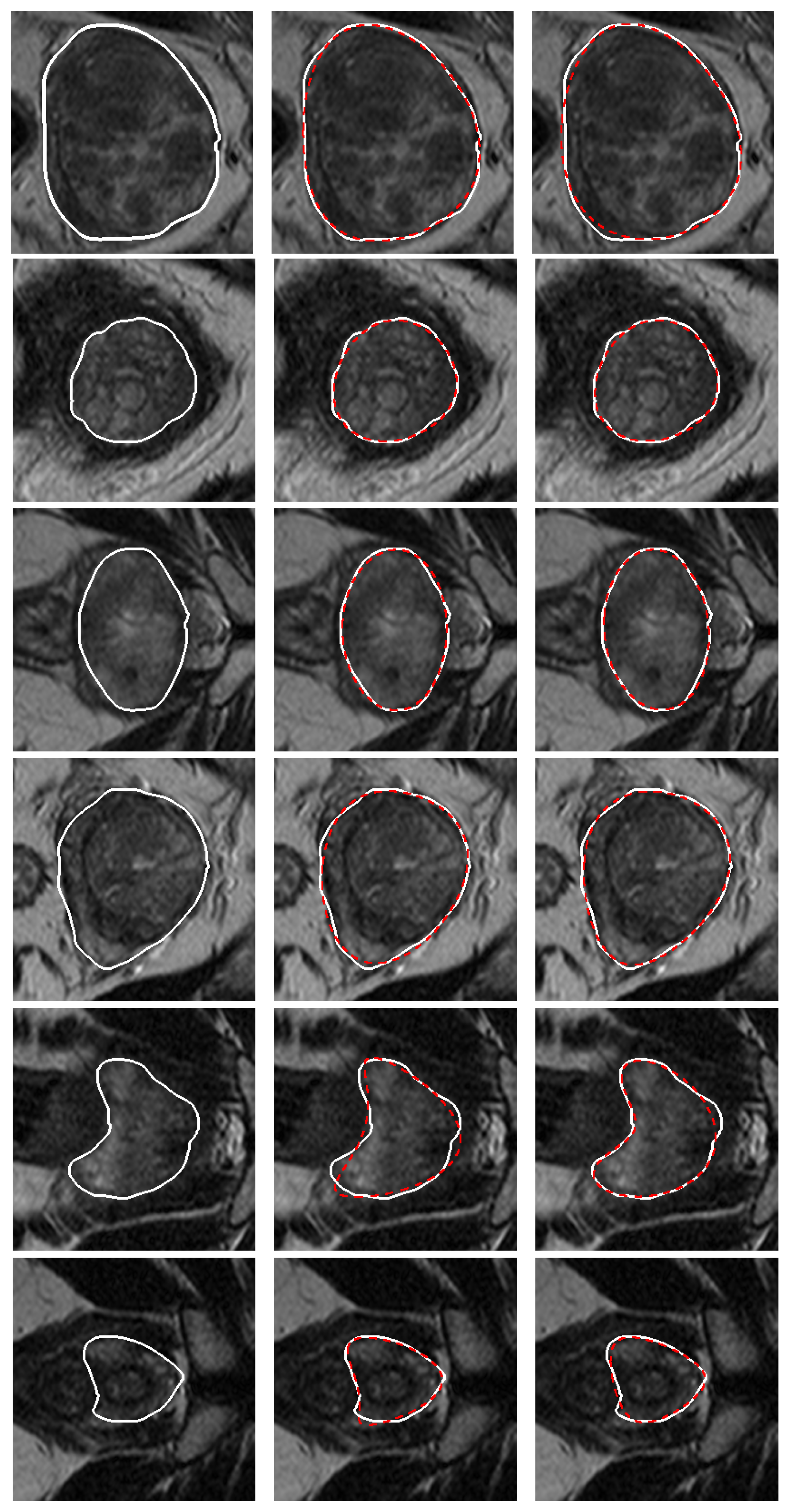
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Further Analysis of CS and CC Curves
Appendix A.1. Special Cases
Appendix A.1.1. CS Curve
- For and , the curve is the circle centered in the origin with radius r.
- For , the curve is the ellipse centered in the origin with semiaxes b and d.
Appendix A.1.2. CC Curve
- For and , the curve is the circle centered in the origin with radius r.
- For , the curve is the ellipse centered in the origin with semiaxes b and d.
- For , the curve is a Lissajous curve.
- For and , the curve is the lemniscate of Gerono.
- For , the curve is a cardioid.
- For and , the curve is a limaçon.
- For , the curve is a limaçon trisectrix.
- For and , the curve is a translation of a piriform quartic.
- For , the curve is a translation of a deltoid.
- For and , the curve is a translation of a hypotrochoid.
- For and , the curve is a translation of a regular trifolium.
Appendix A.2. Elliptic Fourier Descriptors
Appendix A.2.1. CS Curve
Appendix A.2.2. CC Curve
Appendix A.3. Simple Curves

Appendix A.3.1. CS Curve
- If holds, Equation (A5) means . Interchanging, eventually, with , we can suppose that , and then, taking into account that , we have . We write . So we have that and . Imposing that , we find thatFor symmetry reasons (see Section 2.2), we can confine ourselves to the case and ; therefore, by (A4), which is in contradiction to (A6).To summarize, in the case , the system (A2) has no solutions, i.e., the curve is simple.
Appendix A.3.2. CC Curve
- (i)
- ;
- (ii)
- and ;
- (iii)
- , and ;
- (iv)
- , and ;
- (v)
- , , and .
- , ;
- , and ;
- .
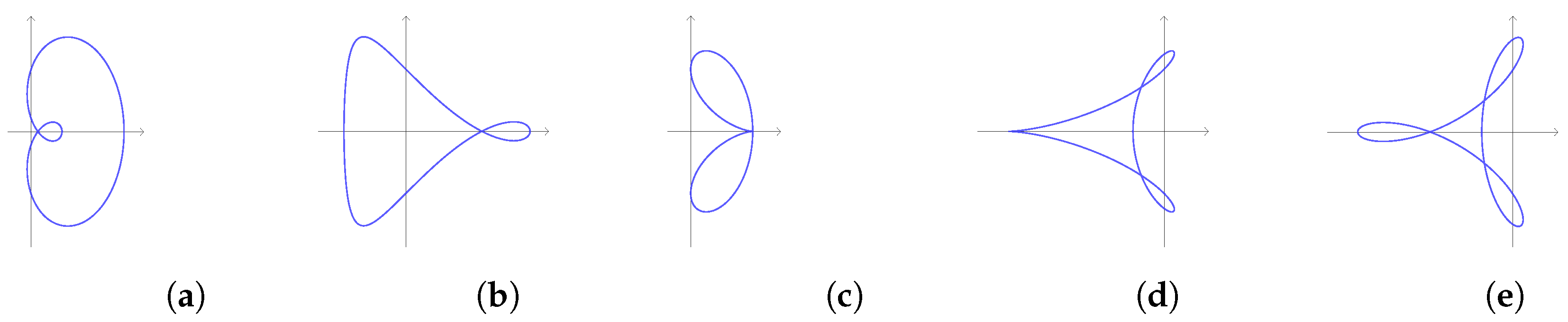
Appendix A.4. Area of the Enclosed Surface
- for CS curves (so it does not depend on the parameters and it is the same as the area of the surface inside an ellipse with semiaxes b and d);
- for CC curves.
References
- Mitterberger, M.; Horninger, W.; Aigner, F.; Pinggera, G.M.; Steppan, I.; Rehder, P.; Frauscher, F. Ultrasound of the prostate. Cancer Imaging 2010, 10, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Mobley, D.; Feibus, A.; Baum, N. Benign prostatic hyperplasia and urinary symptoms: Evaluation and treatment. Postgrad. Med. 2015, 127, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Jue, J.S.; Barboza, M.P.; Prakash, N.S.; Venkatramani, V.; Sinha, V.R.; Pavan, N.; Nahar, B.; Kanabur, P.; Ahdoot, M.; Dong, Y.; et al. Re-examining prostate-specific antigen (PSA) density: Defining the optimal PSA range and patients for using PSA density to predict prostate cancer using extended template biopsy. Urology 2017, 105, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Al-Khalil, S.; Boothe, D.; Durdin, T.; Sunkara, S.; Watkins, P.; Yang, S.; Haynes, A.; de Reise, W. Interactions between benign prostatic hyperplasia (BPH) and prostate cancer in large prostates: A retrospective data review. Int. Urol. Nephrol. 2016, 48, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.E.; Troncoso, P.; Johnston, D.; Tang, K.; Babaian, R.J. Prostate cancer detection: Relationship to prostate size. Urology 1999, 53, 764–768. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, Y.; Qin, Z.; Gao, X.; Xing, Q.; Li, R.; Wang, W.; Song, N.; Zhang, W. Correlation between prostatitis, benign prostatic hyperplasia and prostate cancer: A systematic review and meta-analysis. J. Cancer 2020, 11, 177–189. [Google Scholar] [CrossRef] [PubMed]
- Ghose, S.; Oliver, A.; Lladó, R.M.X.; Vilanova, J.C.; Freixenet, J.; Mitra, J.; Sidibé, D.; Meriaudeau, F. A survey of prostate segmentation methodologies in ultrasound, magnetic resonance and computed tomography images. Comput. Methods Programs Biomed. 2012, 108, 262–287. [Google Scholar] [CrossRef] [PubMed]
- Giubilei, G.; Ponchietti, R.; Biscioni, S.; Fanfani, A.; Ciatto, S.; Di Loro, F.; Gavazzi, A.; Mondaini, N. Accuracy of prostate volume measurements using transrectal multiplanar three-dimensional sonography. Int. J. Urol. 2005, 12, 936–938. [Google Scholar] [CrossRef] [PubMed]
- Terris, M.K.; Stamey, T.A. Determination of prostate volume by transrectal ultrasound. J. Urol. 1991, 145, 984–987. [Google Scholar] [CrossRef]
- Salvaggio, G.; Comelli, A.; Portoghese, M.; Cutaia, G.; Cannella, R.; Vernuccio, F.; Stefano, A.; Dispensa, N.; La Tona, G.; Salvaggio, L.; et al. Deep Learning Network for Segmentation of the Prostate Gland With Median Lobe Enlargement in T2-weighted MR Images: Comparison With Manual Segmentation Method. Curr. Probl. Diagn. Radiol. 2022, 51, 328–333. [Google Scholar] [CrossRef]
- Turkbey, B.; Fotin, S.V.; Huang, R.J.; Yin, Y.; Daar, D.; Aras, O.; Bernardo, M.; Garvey, B.E.; Weaver, J.; Haldankar, H.; et al. Fully automated prostate segmentation on MRI: Comparison with manual segmentation methods and specimen volumes. AJR Am. J. Roentgenol. 2013, 201, 720–729. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Pathak, S.D.; Haynor, D.R.; Cho, P.S.; Kim, Y. Parametric Shape Modeling Using deformable Superellipses for Prostate Segmentation. IEEE Trans. Med. Imaging 2004, 23, 340–349. [Google Scholar] [CrossRef] [PubMed]
- Kachouie, N.N.; Fieguth, P.; Rahnamayan, S. An Elliptical Level Set Method for Automatic TRUS Prostate Image Segmentation; IEEE Computer Society Press: Vancouver, BV, Canada, 2006; pp. 91–196. [Google Scholar]
- Klein, S.; Van Der Heide, U.A.; Lips, I.M.; Van Vulpen, M.; Staring, M.; Pluim, J.P. Automatic segmentation of the prostate in 3D MR images by atlas matching using localized mutual information. Med. Phys. 2008, 35, 1407–1417. [Google Scholar] [CrossRef] [PubMed]
- Knoll, C.; Alcañiz, M.; Monserrat, C.; Grau, V.; Juan, M.C. Outlining of the prostate using snakes with shape restrictions based on the wavelet transform (doctoral thesis: Dissertation). Pattern Recognit. 1999, 32, 1767–1781. [Google Scholar] [CrossRef]
- Ladak, H.M.; Mao, F.; Wang, Y.; Downey, D.B.; Steinman, D.A.; Fenster, A. Prostate boundary segmentation from 2D ultrasound images. Med. Phys. 2000, 27, 1777–1788. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Haider, M.A.; Yetik, I.S. Unsupervised 3D prostate segmentation based on diffusion-weighted imaging MRI using active contour models with a shape prior. J. Electr. Comput. Eng. 2011, 2011, 410912. [Google Scholar] [CrossRef]
- Liu, X.; Langer, D.; Haider, M.; Van der Kwast, T.; Evans, A.; Wernick, M.; Yetik, I. Unsupervised segmentation of the prostate using MR images based on level set with a shape prior. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, (EMBC’09), Minneapolis, MN, USA, 3–6 September 2009. [Google Scholar]
- Makni, N.; Iancu, A.; Colot, O.; Puech, P.; Mordon, S.; Betrouni, N. Zonal segmentation of prostate using multispectral magnetic resonance images. Med. Phys. 2011, 38, 6093–6105. [Google Scholar] [CrossRef] [PubMed]
- Saroul, L.; Bernard, O.; Vray, D.; Friboulet, D. Prostate Segmentation in Echographic Images: A Variational Approach Using Deformable Super-Ellipse and Rayleigh Distribution; IEEE Computer Society Press: Paris, France, 2008; pp. 29–132. [Google Scholar]
- Tian, Z.; Liu, L.; Zhang, Z.; Fei, B. Superpixel-based segmentation for 3D prostate MR images. IEEE Trans. Med. Imaging 2016, 35, 791–801. [Google Scholar] [CrossRef]
- Tsai, A.; Yezzi, A.; Wells, W.; Tempany, C.; Tucker, D.; Fan, A.; Grimson, W.E.; Willsky, A. A shape-based approach to the segmentation of medical imagery using level sets. IEEE Trans. Med. Imaging 2003, 22, 137–154. [Google Scholar] [CrossRef]
- Tutar, I.B.; Pathak, S.D.; Gong, L.; Cho, P.S.; Wallner, K.; Kim, Y. Semiautomatic 3D prostate segmentation from TRUS images using spherical harmonics. IEEE Trans. Med. Imaging 2006, 25, 1645–1654. [Google Scholar] [CrossRef]
- Tutar, I.B.; Pathak, S.D.; Kim, Y. 3D prostate shape modeling from sparsely acquired 2D images using deformable models. In Visualization, Image-Guided Procedures, and Display; Proc. 5367, Medical Imaging 2004; SPIE: San Diego, CA, USA, 2004. [Google Scholar]
- Yan, P.; Xu, S.; Turkbey, B.; Kruecker, J. Discrete Deformable Model Guided by Partial Active Shape Model for TRUS Image Segmentation. IEEE Trans. Biomed. Eng. 2010, 57, 1158–1166. [Google Scholar] [PubMed]
- Zhan, Y.; Shen, D. Deformable segmentation of 3-D ultrasound prostate images using statistical texture matching method. IEEE Trans. Med. Imaging 2006, 25, 256–272. [Google Scholar] [CrossRef]
- Badiei, S.; Salcudean, S.E.; Varah, J.; Morris, W.J. Prostate segmentation in 2D ultrasound images using image warping and ellipse fitting. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2006, Copenhagen, Denmark, 1–6 October 2006; Volume 9, pp. 7–24. [Google Scholar]
- Comelli, A.; Dahiya, N.; Stefano, A.; Vernuccio, F.; Portoghese, M.; Cutaia, G.; Bruno, A.; Salvaggio, G.; Yezzi, A. Deep Learning-Based Methods for Prostate Segmentation in Magnetic Resonance Imaging. Appl. Sci. 2021, 11, 782. [Google Scholar] [CrossRef]
- Kamilaris, A.; Prenafeta-Boldú, F. Deep learning in agriculture: A survey. Comput. Electron. Agric. 2018, 147, 70–90. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Alipanahi, B.; Delong, A.; Weirauch, M.T.; Frey, B.J. Predicting the sequence specificities of DNA- and RNA-binding proteins by deep learning. Nat. Biotechnol. 2015, 33, 831–838. [Google Scholar] [CrossRef]
- Hirling, D.; Horvath, P. Cell segmentation and representation with shape priors. Comput. Struct. Biotechnol. J. 2023, 21, 742–750. [Google Scholar] [CrossRef] [PubMed]
- Levine, S.; Pastor, P.; Krizhevsky, A.; Ibarz, J.; Quillen, D. Learning hand-eye coordination for robotic grasping with deep learning and large-scale data collection. Int. J. Robot. Res. 2018, 37, 421–436. [Google Scholar] [CrossRef]
- Cong, P.; Li, J.; Liu, J.; Xiao, Y.; Zhang, X. SEG-SLAM: Dynamic Indoor RGB-D Visual SLAM Integrating Geometric and YOLOv5-Based Semantic Information. Sensors 2024, 24, 2102. [Google Scholar] [CrossRef]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the IEEE International Conference on Computer Vision, 2015 International Conference on Computer Vision, ICCV 2015, Santiago, Chile, 7–13 December 2015; Volume 7410669, pp. 2722–2730. [Google Scholar]
- Fang, N.; Qiu, L.; Zhang, S.; Wang, Z.; Hu, K.; Wang, K. A Cross-Scale Hierarchical Transformer with Correspondence-Augmented Attention for Inferring Bird’s-Eye-View Semantic Segmentation. IEEE Trans. Intell. Transp. Syst. 2024, 1–12. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef]
- Gillies, R.J.; Kinahan, P.E.; Hricak, H. Radiomics: Images are more than pictures, they are data. Radiology 2016, 278, 563–577. [Google Scholar] [CrossRef]
- Corso, R.; Stefano, A.; Salvaggio, G.; Comelli, A. Shearlet Transform Applied to a Prostate Cancer Radiomics Analysis on MR Images. Mathematics 2024, 12, 1296. [Google Scholar] [CrossRef]
- Fooladi, M.; Soleymani, Y.; Rahmim, A.; Farzanefar, S.; Aghahosseini, F.; Seyyedi, N. Impact of different reconstruction algorithms and setting parameters on radiomics features of PSMA PET images: A preliminary study. Eur. J. Radiol. 2024, 172, 111349. [Google Scholar] [CrossRef] [PubMed]
- Gumus, K.Z.; Contreras, S.S.; Al-Toubat, M.; Harmon, I.; Hernandez, M.; Ozdemir, S.; Kumar, S.; Yuruk, N.; Mete, M.; Balaji, K.C.; et al. MRI-based radiomic features for identifying recurrent prostate cancer after proton radiation therapy. J. Appl. Clin. Med. Phys. 2024, 25, e14293. [Google Scholar] [CrossRef]
- Ali, M.; Benfante, V.; Cutaia, G.; Salvaggio, L.; Rubino, S.; Portoghese, M.; Ferraro, M.; Corso, R.; Piraino, G.; Ingrassia, T.; et al. Prostate Cancer Detection: Performance of Radiomics Analysis in Multiparametric MRI. In Image Analysis and Processing—ICIAP 2023 Workshops; Lecture Notes in Computer Science; Foresti, G.L., Fusiello, A., Hancock, E., Eds.; Springer: Cham, Swizterland, 2024; Volume 14366, pp. 83–92. [Google Scholar]
- McNeal, J.E. The zonal anatomy of the prostate. Prostate 1981, 2, 35–49. [Google Scholar] [CrossRef]
- Hughes, J.; van Dam, A.; McGuire, M.; Sklar, D.; Foley, J.; Feiner, S.; Akeley, K. Computer Graphics: Principles and Practice, 3rd ed.; Addison-Wesley Professional: Boston, MA, USA, 2013. [Google Scholar]
- Shi, P.; Yu, K.; Niklas, K.J.; Schrader, J.; Song, Y.; Zhu, R.; Li, Y.; Wei, H.; Ratkowsky, D.A. A General Model for Describing the Ovate Leaf Shape. Symmetry 2021, 13, 1524. [Google Scholar] [CrossRef]
- Arce, A.M.; Caroni, G.G.; Vázquez Noguera, J.L.; Pinto-Roa, D.P.; Legal-Ayala, H.; Grillo, S.A. A New Objective Function for the Recovery of Gielis Curves. Symmetry 2020, 12, 1016. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, G. A class of Bézier-like curves. Comput. Aided Geom. Des. 2003, 20, 29–39. [Google Scholar] [CrossRef]
- Jeong, Y.; Radke, R. Reslicing axially sampled 3D shapes using elliptic Fourier descriptors. Med. Image Anal. 2007, 11, 197–206. [Google Scholar] [CrossRef]
- Dura, E.; Bell, J.; Lane, D. Superellipse Fitting for the Recovery and Classification of Mine-Like Shapes in Sidescan Sonar Images. IEEE J. Ocean. Eng. 2008, 33, 434–444. [Google Scholar] [CrossRef]
- Huang, W.; Li, Y.; Niklas, K.J.; Gielis, J.; Ding, Y.; Cao, L.; Shi, P. A Superellipse with Deformation and Its Application in Describing the Cross-Sectional Shapes of a Square Bamboo. Symmetry 2020, 12, 2073. [Google Scholar] [CrossRef]
- Kurmi, Y.; Chaurasia, V.; Goel, A.; Joshi, D.; Kapoor, N. Tuberculosis bacteria analysis in acid fast stained images of sputum smear. Signal Image Video Process. 2021, 15, 175–183. [Google Scholar] [CrossRef]
- Méndez, I.; Casar, B. A novel approach for the definition of small-field sizes using the concept of superellipse. Radiat. Phys. Chem. 2021, 189, 109775. [Google Scholar] [CrossRef]
- Mizani, S.; Gurin, P.; Aliabadi, R.; Salehi, H.; Varga, S. Demixing and tetratic ordering in some binary mixtures of hard superellipses. J. Chem. Phys. 2020, 153, 034501. [Google Scholar] [CrossRef] [PubMed]
- Nodargi, N.A.; Bisegna, P. A new computational framework for the minimum thrust analysis of axisymmetric masonry domes. Eng. Struct. 2021, 234, 111962. [Google Scholar] [CrossRef]
- Rai, R.K.; Balmer, M.; Rieser, M.; Vaze, V.S.; Schönfelder, S.; Axhausen, K.W. Capturing Human Activity Spaces: New Geometries. Transp. Res. Rec. 2007, 2021, 70–80. [Google Scholar] [CrossRef]
- Rudek, M.; Canciglieri, J.O.; Greboge, T. A PSO Application in Skull Prosthesis Modelling by Superellipse. Electron. Lett. Comput. Vis. Image Anal. 2013, 12, 1–12. [Google Scholar] [CrossRef][Green Version]
- Yajima, T.; Nagahama, H. Finsler geometry of seismic ray path in anisotropic media. Proc. R. Soc. Math. Phys. Eng. Sci. 2009, 465, 1763–1777. [Google Scholar] [CrossRef]
- Saviot, L. Free Vibrations of Anisotropic Nano-Objects with Rounded or Sharp Corners. Nanomaterials 2021, 11, 1838. [Google Scholar] [CrossRef]
- Barr, A.H. Global and local deformations of solid primitives. Comput. Graphic. 1984, 18, 21–30. [Google Scholar] [CrossRef]
- Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Machine Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Sorensen, T. A method of establishing groups of equal amplitude in plant sociology based on similarity of species and its application to analyses of the vegetation on Danish commons. K. Dan. Vidensk. Selsk. 1948, 5, 1–34. [Google Scholar]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, C. Geometric and Solid Modeling: An Introduction; Morgan Kaufmann Publishers Inc.: Cambridge, MA, USA, 1989. [Google Scholar]
- Yalcin, H.; Unel, M.; Wolovich, W. Implicitization of parametric curves by matrix annihilation. Int. J. Comput. Vis. 2003, 54, 105–111. [Google Scholar] [CrossRef]
- Lawrence, J.D. A Catalog of Special Plane Curves; Courier Corporation: Dover, NY, USA, 1972. [Google Scholar]
- Granlund, G.H. Fourier preprocessing for hand print character recognition. IEEE Trans. Comp. 1972, 21, 195–201. [Google Scholar] [CrossRef]
- Kuhl, F.P.; Giardina, C.R. Elliptic Fourier descriptors of a closed contour. Comput. Graph. Image Process. 1982, 18, 236–258. [Google Scholar] [CrossRef]


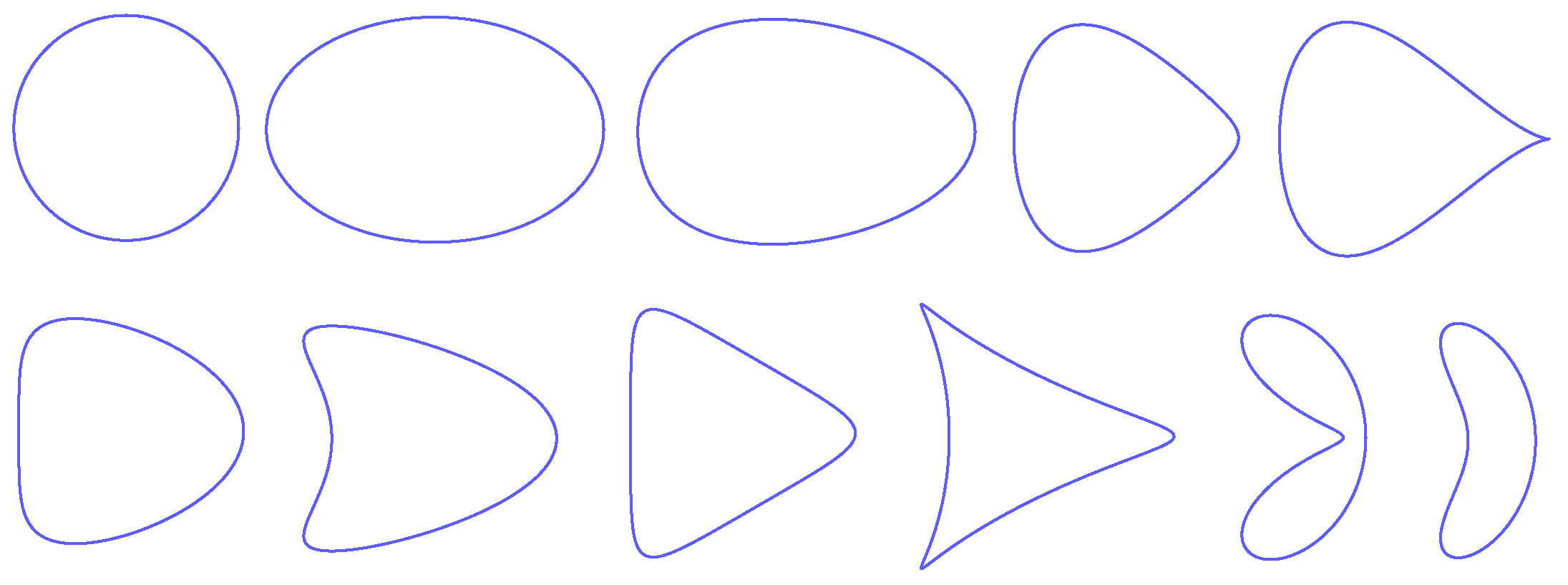

| Model | |||
|---|---|---|---|
| Best CS-CC | mm | mm | |
| CS | mm | mm | |
| CC | mm | mm | |
| Deformed superellipse | mm | mm |
| Model | Time Required by the Fitting Process |
|---|---|
| CS or CC (a single model) | s |
| Best between CS and CC models | s |
| Deformed superellipse | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Corso, R.; Comelli, A.; Salvaggio, G.; Tegolo, D. New Parametric 2D Curves for Modeling Prostate Shape in Magnetic Resonance Images. Symmetry 2024, 16, 755. https://doi.org/10.3390/sym16060755
Corso R, Comelli A, Salvaggio G, Tegolo D. New Parametric 2D Curves for Modeling Prostate Shape in Magnetic Resonance Images. Symmetry. 2024; 16(6):755. https://doi.org/10.3390/sym16060755
Chicago/Turabian StyleCorso, Rosario, Albert Comelli, Giuseppe Salvaggio, and Domenico Tegolo. 2024. "New Parametric 2D Curves for Modeling Prostate Shape in Magnetic Resonance Images" Symmetry 16, no. 6: 755. https://doi.org/10.3390/sym16060755
APA StyleCorso, R., Comelli, A., Salvaggio, G., & Tegolo, D. (2024). New Parametric 2D Curves for Modeling Prostate Shape in Magnetic Resonance Images. Symmetry, 16(6), 755. https://doi.org/10.3390/sym16060755








