Optimal Harvesting Strategies for Timber and Non-Timber Forest Products with Nonlinear Harvesting Terms
Abstract
1. Introduction
2. Model Building
3. Qualitative Analysis
3.1. Existence of Equilibrium Point
- (1)
- The equation always has a trivial equilibrium point .
- (2)
- Otherwise, there is
3.2. Stability of Equilibrium Point
4. Optimal Harvesting Strategy
5. Numerical Simulation
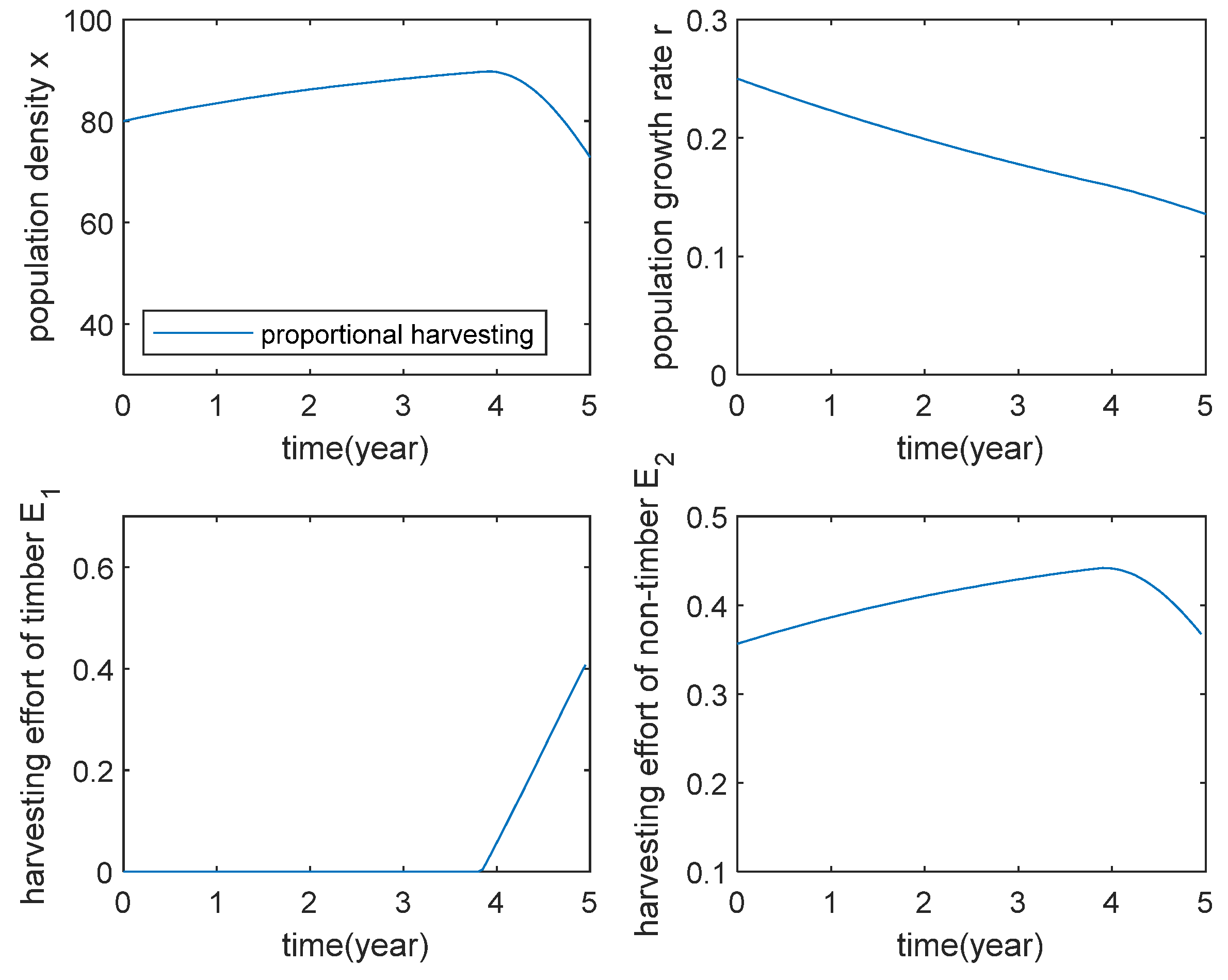
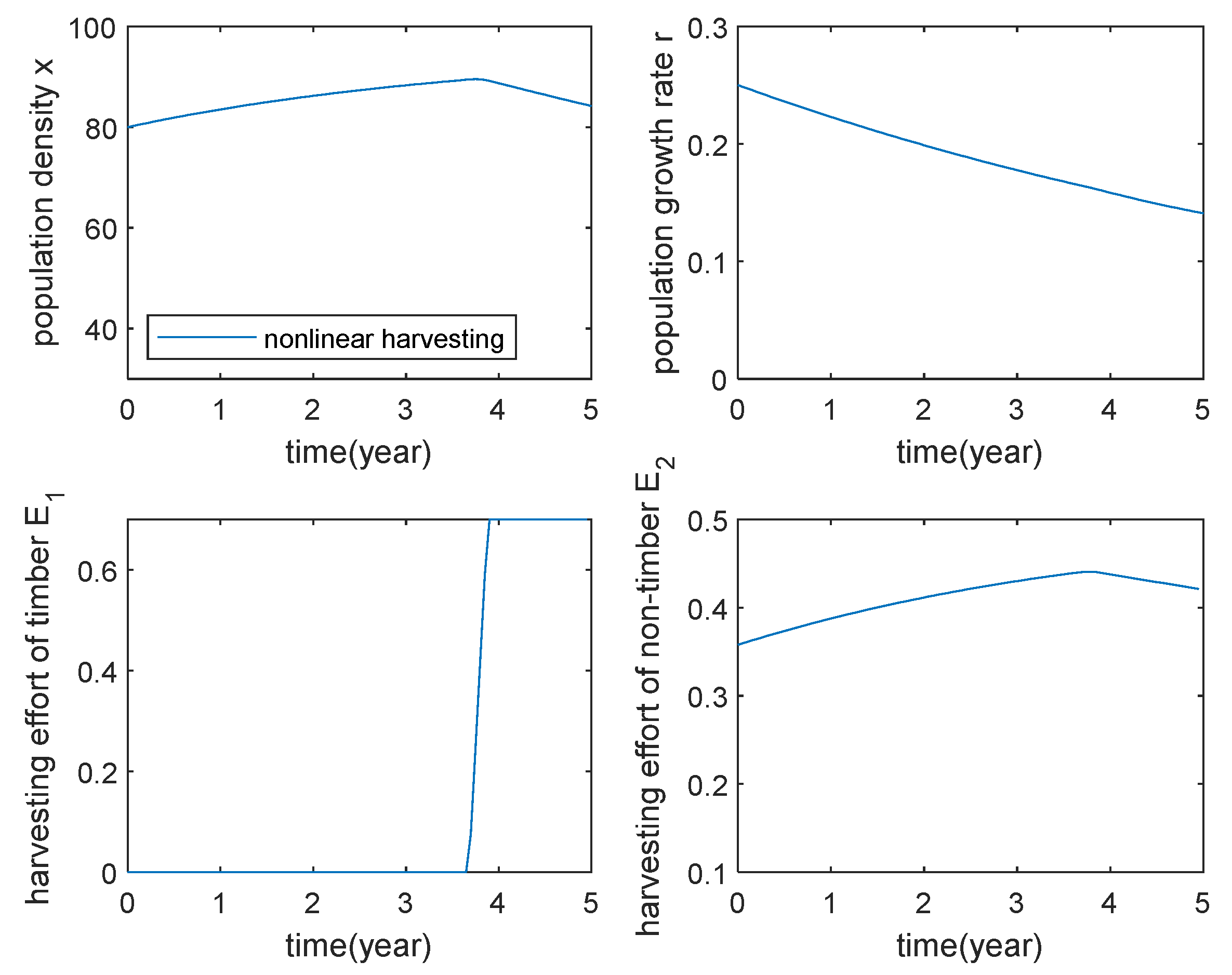
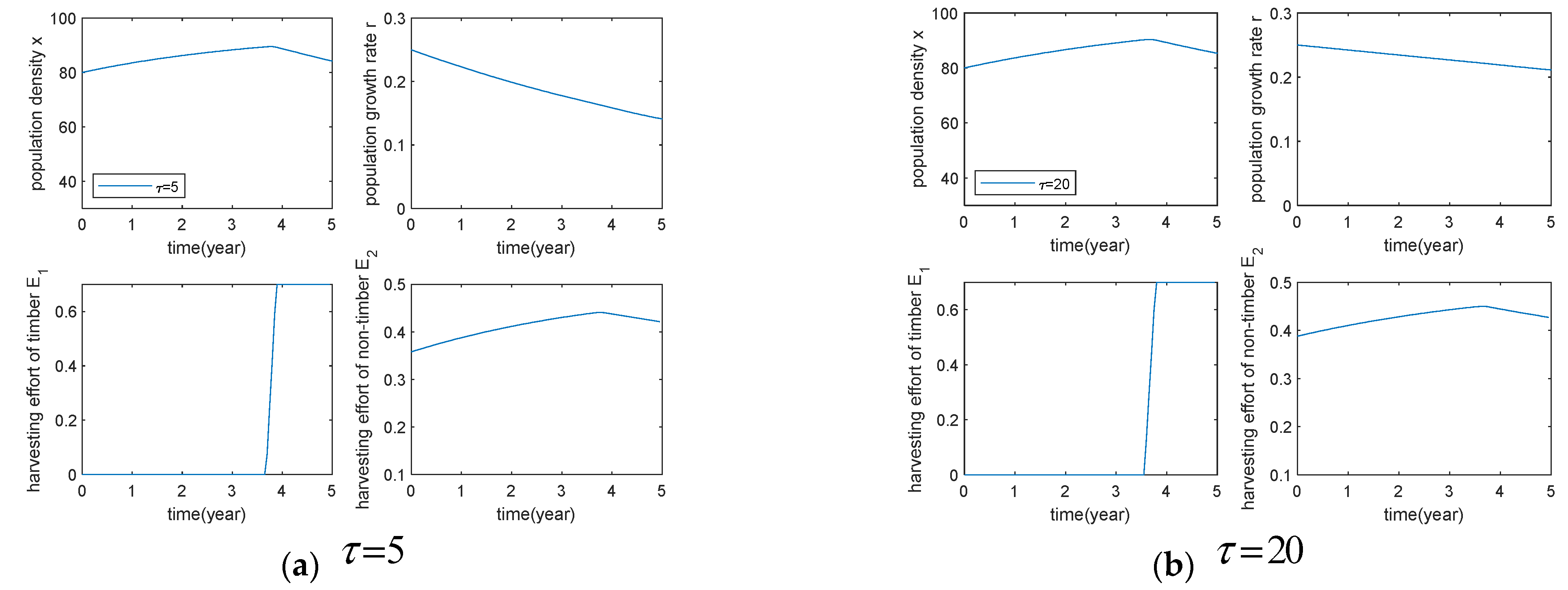
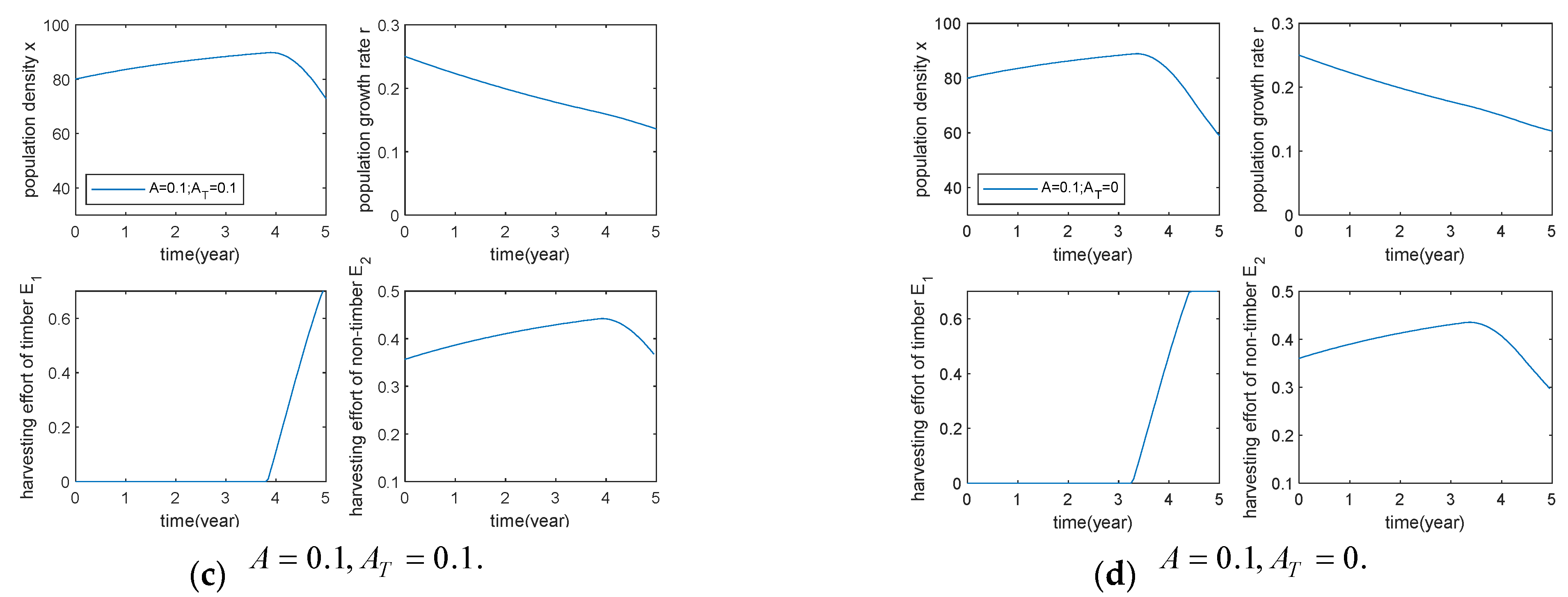
5.1. The Effect of Proportional Harvesting and Nonlinear Harvesting on the Optimal Harvesting Strategy
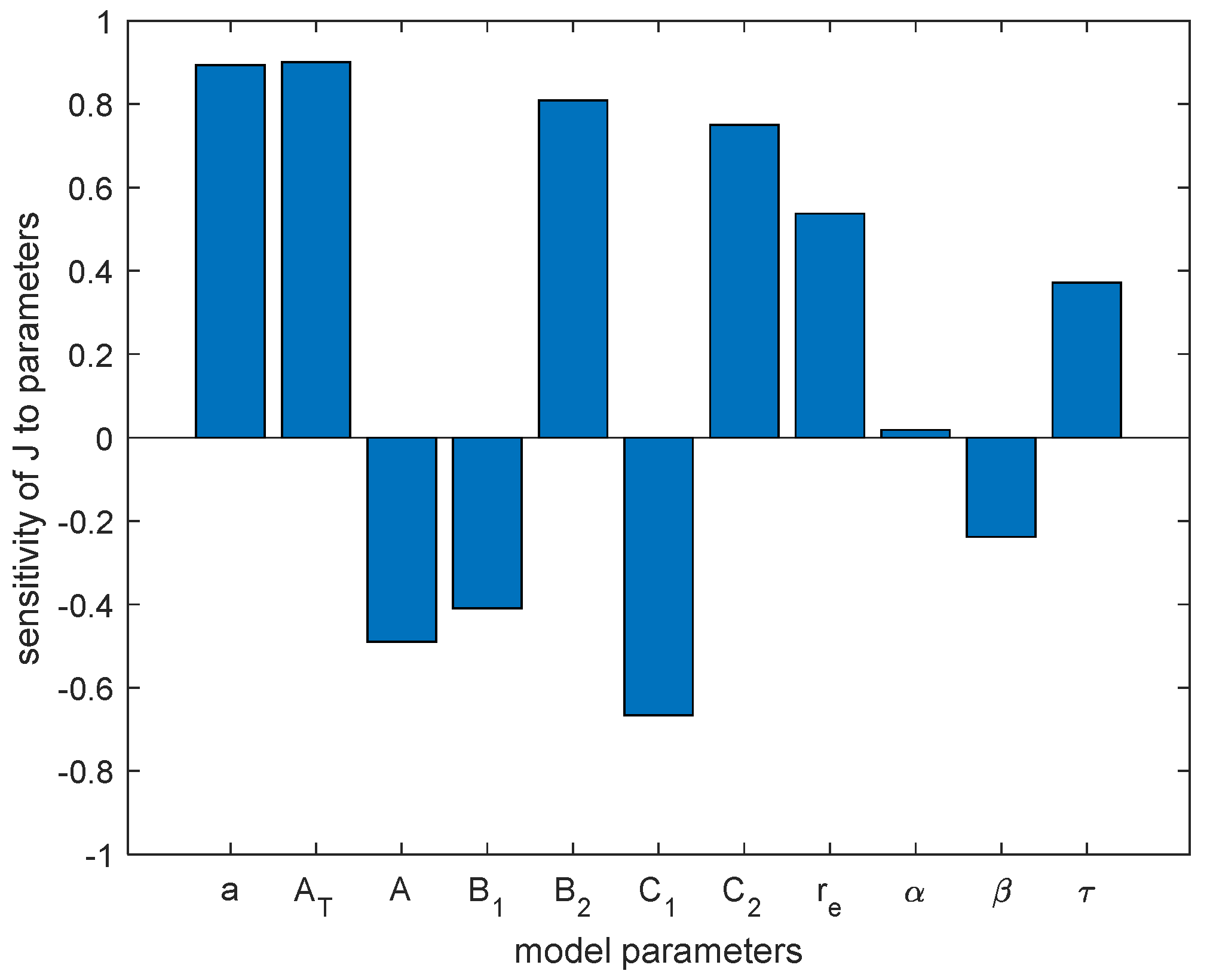
5.2. Sensitivity Analysis of Parameters
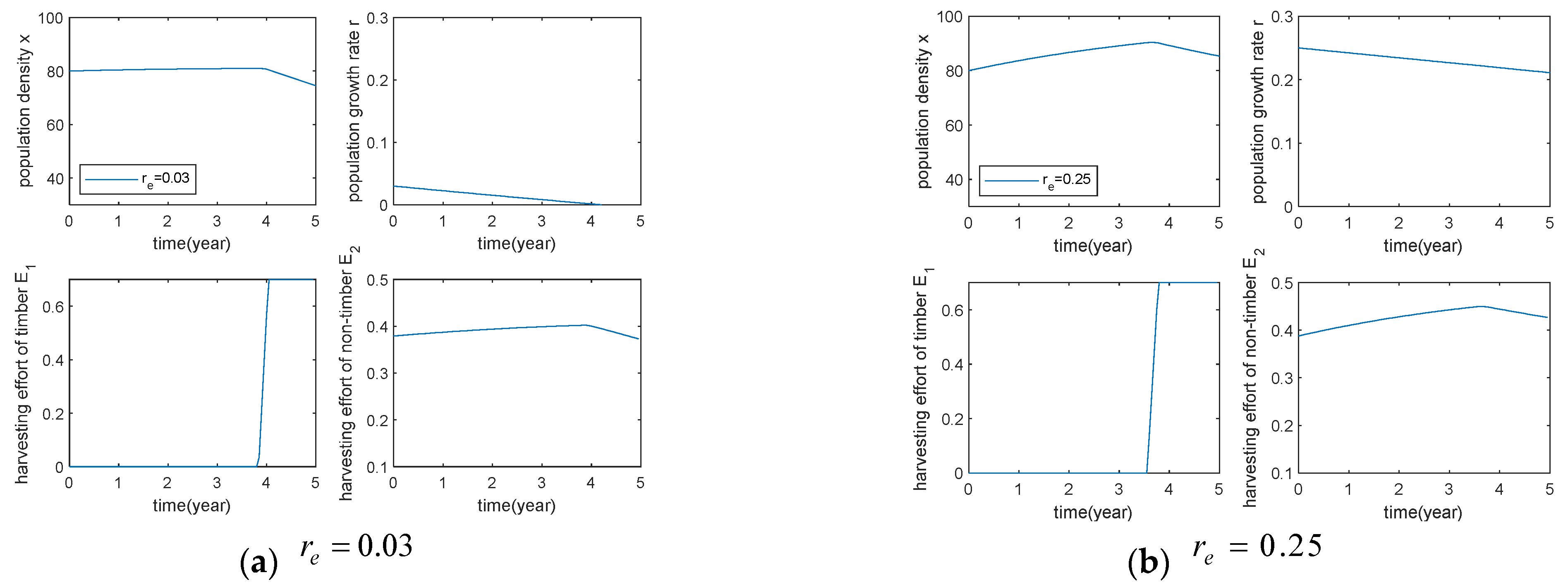
5.3. Effect of Different Parameters on the Optimal Harvesting Strategy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.X. Dynamics Analysis and Harvesting Strategy of Predation System; Jilin University: Changchun, China, 2019. [Google Scholar]
- Chen, X.F. Harvesting of a Prey-predator fisher based on leslie-gaower model. J. Math. Study 2010, 3, 256–263. [Google Scholar]
- Cheng, H.D.; Yin, Z.Y.; Liu, H.X. Analysis of the dynamic of stage-structured pest control model. Math. Appl. 2012, 25, 816–823. [Google Scholar]
- Sudhakar, Y.; Vivek, K. A prey-predator model and control of a nematodes pest using control in banana: Mathematical modeling and qualitative analysis. Int. J. Biomath. 2022, 15, 2150089. [Google Scholar]
- Argyros, I.K.; Shakhno, S.; Regmi, S.; Yarmola, H.; Argyros, M.I. Symmetric-Type Multi-Step Difference Methods for Solving Nonlinear Equations. Symmetry. 2024, 16, 330. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Pei, Y. Dynamics in two nonsmooth predator-prey models with threshold Harvesting. Nonlinear Dyn. 2013, 74, 107–132. [Google Scholar] [CrossRef]
- Mesterton-Gibbons, M. On the optimal policy for combining harvesting of predator and prey. Nat. Resour. Model. 1988, 3, 63–90. [Google Scholar] [CrossRef]
- Ding, W.L.; Jiang, S.S.; Liu, C.H.; Kang, H.L.; Deng, X.W.; Ding, S.L.; Xiao, Y.S.; Wen, X.D. Determination of the optimum rotation period of Chenshan red-heart Chinese fir plantation. For. Sci. South. China 2023, 51, 34–40. [Google Scholar]
- Ni, J.F. The application of linear programming in forestry production. Anhui For. 2004, 4, 25. [Google Scholar]
- Liu, X.Y. On the application of linear planning in forestry projects. Hebei For. Sci. Technol. 2016, 5, 84–85. [Google Scholar]
- Lu, A.J. Research on forest pest control in forest protection. New Farmers 2024, 8, 84–86. [Google Scholar]
- Zhao, G. Sustainable development strategy of forest resources based on forest resource management. New Farmers 2024, 7, 64–66. [Google Scholar]
- Yang, J.; Luan, X.F. Ecological impacts of non−timber forest product use. Chin. J. Appl. Ecol. 2011, 22, 800–809. [Google Scholar]
- Zhang, X.Y.; Xu, D.Y.; Wu, Y.H. Research on Value chain Model Construction and Brand value-added of Forest products. Chin. Bus. Theory. 2020, 2, 59–60+63. [Google Scholar] [CrossRef]
- Schmidt, I.B.; Mandle, L.; Ticktin, T.; Gaoue, O.G. What do matrix population model sreveal about the sustainability of non−timber forest product harvest? J. Appl. Ecol. 2011, 48, 815–826. [Google Scholar] [CrossRef]
- Gaoue, O.G.; Ngonghala, C.N.; Jiang, J.; Lelu, M. Towards a mechanistic understanding of the synergistic effects of harvesting timber and non−timber forest products. Methods Ecol. Evol. 2016, 7, 398–406. [Google Scholar] [CrossRef]
- Yu, X.; Chen, F.; Lai, L. Dynamic behaviors of may type cooperative system with Michaelis-menten type harvesting. Ann. Appl. Math. 2019, 35, 374–391. [Google Scholar]
- Heggerud, C.M.; Lan, K.Q. Local stability analysis of ratio-dependent predator–prey models with predator harvesting rates. Appl. Math. Comput. 2015, 270, 349–357. [Google Scholar] [CrossRef]
- Zhang, D.; Sun, G.; Xu, M.; Chen, J.; Zhou, W. Spatial Dynamic Predator-Prey System with Time Delay and Nonlinear Harvesting Effect. J. Jilin Univ. 2018, 56, 515–522. [Google Scholar]
- Agnew, T.T. Optimal exploitation of a fishery employ inganon−linear harvesting function. Ecol. Model. 1979, 6, 47–57. [Google Scholar] [CrossRef]
- Preisler, H.; Ager, A.; Hayes, J.L. Probabilistic risk models for multipl disturbances: An example of forest insects and wildfires. Gen. Tech. Rep. Pac. Northwest Res. Stn. 2010, 802, 371–379. [Google Scholar]
- Gaoue, O.G.; Jiang, J.; Ding, W.; Agusto, F.B.; Lenhart, S. Optimal harvesting strategies for timber and non−timber forest products in tropical ecosystems. Theor. Ecol. 2016, 9, 287–297. [Google Scholar] [CrossRef]
- Armsworth, P.R.; Block, B.A.; Eagle, J.; Roughgarden, J.E. The role of discounting and dynamics in determining the economic efficiency of time-area closures for managing fishery bycatch. Theor. Ecol. 2011, 4, 513–526. [Google Scholar] [CrossRef]
- Ticktin, T.; Nantel, P.; Ramirez, F.; Johns, T. Effects of variation on harvest limits for nontimber forest species in Mexico. Conserv. Biol. 2002, 16, 691–705. [Google Scholar] [CrossRef]
- Gaoue, O.G.; Ticktin, T. Fulani knowledge of the ecological impacts of Khaya senegalensis (Meliaceae) foliage harvest in Benin and its implications for sustainable harvest. Econ. Bot. 2009, 63, 256–270. [Google Scholar] [CrossRef]
- Lande, R.; Engen, S.; Saether, B.E. Optimal harvesting, economic discounting and extinction risk in fluctuating populations. Nature 1994, 372, 88–90. [Google Scholar] [CrossRef]


| Values | Definition | References | |
|---|---|---|---|
| 80 | Initial population density at (each−1) | [22] | |
| 100 | Carrying capacity for the plant (each−1) | [22] | |
| 0.03, 0.25 | Maximum growth rate without harvest (years−1) | [23,24] | |
| 1, 5, 10, 20 | Average lifespan of the plant in years (years−1) | Estimated | |
| 0.4 | Growth decay rate for non-timber harvest | [25] | |
| 0.23 | Growth decay rate due to timber harvest | [26] | |
| 0, 0.1 | Weight for the value of conservation | [22] | |
| 0, 0.1 | Weight for the value of conservation at the end of harvest | [22] | |
| 0.05 | Discount rate | [22] | |
| 0.3 | Benefit from timber harvest (1 × 10−2 dollar) | [22] | |
| 0.15 | Benefit from non-timber harvest (1 × 10−2 dollar) | [22] | |
| 15 | Cost coefficient of timber harvesting (dollar−1) | [22] | |
| 15 | Cost coefficient of non-timber harvest (dollar−1) | [22] | |
| 0.01, 0.1 | processing time for timber harvesting (year−1) | Estimated | |
| 0.7 | Upper bound for timber harvest rate | [22] | |
| 1 | Upper bound for non-timber harvest rate | [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Hao, L.; Zhang, S. Optimal Harvesting Strategies for Timber and Non-Timber Forest Products with Nonlinear Harvesting Terms. Symmetry 2024, 16, 806. https://doi.org/10.3390/sym16070806
Zhang Y, Hao L, Zhang S. Optimal Harvesting Strategies for Timber and Non-Timber Forest Products with Nonlinear Harvesting Terms. Symmetry. 2024; 16(7):806. https://doi.org/10.3390/sym16070806
Chicago/Turabian StyleZhang, Yaning, Lina Hao, and Shan Zhang. 2024. "Optimal Harvesting Strategies for Timber and Non-Timber Forest Products with Nonlinear Harvesting Terms" Symmetry 16, no. 7: 806. https://doi.org/10.3390/sym16070806
APA StyleZhang, Y., Hao, L., & Zhang, S. (2024). Optimal Harvesting Strategies for Timber and Non-Timber Forest Products with Nonlinear Harvesting Terms. Symmetry, 16(7), 806. https://doi.org/10.3390/sym16070806






