Radial Oscillations of Strange Quark Stars Admixed with Dark Matter
Abstract
1. Introduction
2. Equation of State
2.1. Strange Quark Matter
2.2. Dark Matter
3. Equilibrium Structure and Radial Oscillation of DMASSs
3.1. TOV Equations for Two-Fluid Stars
3.2. Radial Oscillation Equations of DMASSs
4. Numerical Results
4.1. Equilibrium Structure of DMASSs
4.2. Radial Oscillations and Stability
5. Discussion and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ehlers, J. Editorial note to: F. Zwicky The redshift of extragalactic nebulae. Gen. Relativ. Gravit. 2008, 41, 203–206. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar]
- Billard, J.; Boulay, M.; Cebrián, S.; Covi, L.; Fiorillo, G.; Green, A.; Kopp, J.; Majorovits, B.; Palladino, K.; Petricca, F.; et al. Direct detection of dark matter—APPEC committee report. Rep. Prog. Phys. 2022, 85, 056201. [Google Scholar] [CrossRef] [PubMed]
- Baltz, E.A. Dark matter candidates. New J. Phys. 2004, C040802, L002. [Google Scholar]
- Taoso, M.; Bertone, G.; Masiero, A. Dark Matter Candidates: A Ten-Point Test. J. Cosmol. Astropart. Phys. 2008, 3, 22. [Google Scholar] [CrossRef]
- Turck-Chieze, S.; Lopes, I. Solar-stellar astrophysics and dark matter. Res. Astron. Astrophys. 2012, 2012, 1107–1138. [Google Scholar] [CrossRef]
- Li, A.; Huang, F.; Xu, R.X. Too massive neutron stars: The role of dark matter? Astropart. Phys. 2012, 37, 70–74. [Google Scholar] [CrossRef]
- Li, X.Y.; Wang, F.Y.; Cheng, K.S. Gravitational effects of condensate dark matter on compact stellar objects. J. Cosmol. Astropart. Phys. 2012, 2012, 31. [Google Scholar] [CrossRef]
- Panotopoulos, G. How compact stars challenge our view about dark matter. In Proceedings of the 22nd Workshop What Comes Beyond the Standard Models, Bled, Slovenia, 6–14 July 2019; Volume 2012, p. 31. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Leahy, D.; Ouyed, R. Supernova SN2006gy as a first ever Quark Nova? Mon. Not. Roy. Astron. Soc. 2008, 387, 1193. [Google Scholar] [CrossRef]
- Leahy, D.; Ouyed, R. Predictions for signatures of the quark-nova in superluminous supernovae. arXiv 2009, arXiv:0911.5424. [Google Scholar]
- Witten, E. Cosmic Separation of Phases. Phys. Rev. D 1984, 30, 272–285. [Google Scholar] [CrossRef]
- Farhi, E.; Jaffe, R.L. Strange Matter. Phys. Rev. D 1984, 30, 2379. [Google Scholar] [CrossRef]
- Ivanenko, D.D.; Kurdgelaidze, D.F. Hypothesis concerning quark stars. Astrophysics 1965, 1, 251–252. [Google Scholar] [CrossRef]
- Itoh, N. Hydrostatic Equilibrium of Hypothetical Quark Stars. Prog. Theor. Phys. 1970, 44, 291. [Google Scholar] [CrossRef]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star. NATAS 2022, 6, 1444. [Google Scholar]
- Henriques, A.B.; Liddle, A.R.; Moorhouse, R.G. Combined Boson—Fermion Stars: Configurations and Stability. Nucl. Phys. B 1990, 337, 737–761. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Tolos, L.; Schaffner, B.J.; Dengler, Y. Dark Compact Planets. Phys. Rev. D 2015, 92, 123002. [Google Scholar] [CrossRef]
- Del, P.A.; Deliyergiyev, M.; Le, D.M. Solution to the hyperon puzzle using dark matter. Phys. Dark Universe 2020, 30, 100622. [Google Scholar]
- Kain, B. Dark matter admixed neutron stars. Phys. Rev. D 2021, 103, 043009. [Google Scholar] [CrossRef]
- Das, H.; Kumar, A.; Kumar, B.; Biswal, S.; Patra, S. Impacts of dark matter on the curvature of the neutron star. J. Cosmol. Astropart. Phys. 2021, 2021, 007. [Google Scholar] [CrossRef]
- Lopes, I.; Casanellas, J.; Eugenio, D. The capture of dark matter particles through the evolution of low-mass stars. Phys. Rev. D 2011, 83, 063521. [Google Scholar] [CrossRef]
- Del, P.A.; Le, D.M.; Deliyergiyev, M. Neutron Stars and Dark Matter. Universe 2020, 6, 222. [Google Scholar] [CrossRef]
- Bell, N.F.; Busoni, G.; Motta, T.F.; Robles, S.; Thomas, A.W.; Virgato, M. Nucleon Structure and Strong Interactions in Dark Matter Capture in Neutron Stars. Phys. Rev. Lett. 2021, 127, 111803. [Google Scholar] [CrossRef]
- Maity, T.N.; Queiroz, F.S. Detecting bosonic dark matter with neutron stars. Phys. Rev. D 2021, 104, 083019. [Google Scholar] [CrossRef]
- Anzuini, F.; Bell, N.F.; Busoni, G.; Motta, T.F.; Robles, S.; Thomas, A.W.; Virgato, M. Improved treatment of dark matter capture in neutron stars III: Nucleon and exotic targets. J. Cosmol. Astropart. Phys. 2021, 2021, 056. [Google Scholar] [CrossRef]
- Bose, D.; Maity, T.N.; Ray, T.S. Neutrinos from captured dark matter annihilation in a galactic population of neutron stars. J. Cosmol. Astropart. Phys. 2022, 2022, 001. [Google Scholar] [CrossRef]
- Kouvaris, C. WIMP annihilation and cooling of neutron stars. Phys. Rev. D 2008, 77, 023006. [Google Scholar] [CrossRef]
- Bertone, G.; Fairbairn, M. Compact stars as dark matter probes. Phys. Rev. D 2008, 77, 043515. [Google Scholar] [CrossRef]
- Gonzalez, D.; Reisenegger, A. Internal heating of old neutron stars: Contrasting different mechanisms. Astron. Astrophys. 2010, 522, A16. [Google Scholar] [CrossRef]
- Bertoni, B.; Nelson, A.E.; Reddy, S. Dark Matter Thermalization in Neutron Stars. Phys. Rev. D 2013, 88, 123505. [Google Scholar] [CrossRef]
- Garani, R.; Gupta, A.; Raj, N. Observing the thermalization of dark matter in neutron stars. Phys. Rev. D 2021, 103, 043019. [Google Scholar] [CrossRef]
- Coffey, J.; McKeen, D.; Morrissey, D.E.; Raj, N. Neutron star observations of pseudoscalar-mediated dark matter. Phys. Rev. D 2022, 106, 115019. [Google Scholar] [CrossRef]
- Fujiwara, M.; Hamaguchi, K.; Nagata, N.; Zheng, J.M. Capture of electroweak multiplet dark matter in neutron stars. Phys. Rev. D 2022, 106, 055031. [Google Scholar] [CrossRef]
- Gleason, T.; Brown, B.; Kain, B. Dynamical evolution of dark matter admixed neutron stars. Phys. Rev. D 2022, 105, 023010. [Google Scholar] [CrossRef]
- Quddus, A.; Panotopoulos, G.; Kumar, B.; Ahmad, S.; Patra, S.K. GW170817 constraints on the properties of a neutron star in the presence of WIMP dark matter. J. Phys. G 2020, 47, 095202. [Google Scholar] [CrossRef]
- Leung, K.L.; Chu, M.C.; Lin, L.M. Tidal deformability of dark matter admixed neutron stars. Phys. Rev. D 2022, 105, 123010. [Google Scholar] [CrossRef]
- Karkevandi, D.R.; Shakeri, S.; Sagun, V.; Ivanytskyi, O. Bosonic dark matter in neutron stars and its effect on gravitational wave signal. Phys. Rev. D 2022, 105, 023001. [Google Scholar] [CrossRef]
- Dengler, Y.; Schaffner, B.J.; Tolos, L. Second Love number of dark compact planets and neutron stars with dark matter. Phys. Rev. D 2022, 105, 043013. [Google Scholar] [CrossRef]
- Collier, M.; Croon, D.; Leane, R.K. Tidal Love numbers of novel and admixed celestial objects. Phys. Rev. D 2022, 106, 123027. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q Relations in Neutron Stars and their Applications to Astrophysics, Gravitational Waves and Fundamental Physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rep. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Godzieba, D.A.; Gamba, R.; Radice, D.; Bernuzzi, S. Updated universal relations for tidal deformabilities of neutron stars from phenomenological equations of state. Phys. Rev. D 2021, 103, 063036. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Equilibrium Structure and Radial Oscillations of Dark Matter Admixed Neutron Stars. Phys. Rev. D 2012, 85, 103528. [Google Scholar] [CrossRef]
- Routaray, P.; Quddus, A.; Chakravarti, K.; Kumar, B. Probing the impact of WIMP dark matter on universal relations, GW170817 posterior, and radial oscillations. Mon. Not. R. Astron. Soc. 2023, 525, 5492–5499. [Google Scholar] [CrossRef]
- Routaray, P.; Das, H.C.; Sen, S.; Kumar, B.; Panotopoulos, G.; Zhao, T.Q. Radial oscillations of dark matter admixed neutron stars. Phys. Rev. D 2023, 107, 103039. [Google Scholar] [CrossRef]
- Hong, B.; Ren, Z.Z.; Wu, C.; Mu, X.L. Impacts of symmetry energy slope on the oscillation frequencies of neutron stars with short-range correlation and admixed dark matter. Class. Quantum Gravity 2023, 40, 125007. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.; Schaffner, B.J. Quark stars admixed with dark matter. Phys. Rev. D 2016, 93, 083009. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with condensed dark matter. Phys. Rev. D 2017, 96, 083013. [Google Scholar] [CrossRef]
- Lopes, I.; Panotopoulos, G. Dark matter admixed strange quark stars in the Starobinsky model. Phys. Rev. D 2018, 97, 024030. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Millisecond pulsars modeled as strange quark stars admixed with condensed dark matter. Int. J. Mod. Phys. D. 2018, 27, 1850093. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with fermionic dark matter. Phys. Rev. D 2018, 98, 083001. [Google Scholar] [CrossRef]
- Yang, S.H.; Pi, C.M.; Zheng, X.P. Strange stars with a mirror-dark-matter core confronting with the observations of compact stars. Phys. Rev. D 2021, 104, 083016. [Google Scholar] [CrossRef]
- Jiménez, J.C.; Fraga, E.S. Radial oscillations of quark stars admixed with dark matter. Universe 2022, 8, 34. [Google Scholar] [CrossRef]
- Sen, D.; Guha, A. Vector dark boson mediated feeble interaction between fermionic dark matter and strange quark matter in quark stars. Mon. Not. R. Astron. Soc. 2022, 517, 518–525. [Google Scholar] [CrossRef]
- Ferreira, O.; Fraga, E.S. Strange magnetars admixed with fermionic dark matter. J. Cosmol. Astropart. Phys. 2023, 4, 12. [Google Scholar] [CrossRef]
- Lopes, L.L.; Das, H.C. Strange stars within bosonic and fermionic admixed dark matter. J. Cosmol. Astropart. Phys. 2023, 5, 34. [Google Scholar] [CrossRef]
- Pi, C.M.; Yang, S.H. Strange stars confronting with the observations: Non-Newtonian gravity effects, or the existence of a dark-matter core. Astron. Nachr. 2023, 344, e220083. [Google Scholar] [CrossRef]
- Yang, S.H.; Pi, C.M.; Zheng, X.P.; Weber, F. Confronting Strange Stars with Compact-Star Observations and New Physics. Universe 2023, 9, 202. [Google Scholar] [CrossRef]
- Passamonti, A.; Bruni, M.; Gualtieri, L.; Nagar, A.; Sopuerta, C.F. Coupling of radial and axial nonradial oscillations of compact stars: Gravitational waves from first-order differential rotation. Phys. Rev. D 2006, 73, 084010. [Google Scholar] [CrossRef]
- Passamonti, A.; Stergioulas, N.; Nagar, A. Gravitational waves from nonlinear couplings of radial and polar nonradial modes in relativistic stars. Phys. Rev. D 2007, 75, 084038. [Google Scholar] [CrossRef]
- Chirenti, C.; Miller, M.C.; Strohmayer, T.; Camp, J. Searching for hypermassive neutron stars with short gamma-ray bursts. Astrophys. J. Lett. 2019, 884, L16. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Dynamical Instability of Gaseous Masses Approaching the Schwarzschild Limit in General Relativity. Astrophys. J. 1964, 140, 417–433. [Google Scholar] [CrossRef]
- Chanmugam, G. Radial oscillations of zero-temperature white dwarfs and neutron stars below nuclear densities. Astrophys. J. 1977, 217, 799–808. [Google Scholar] [CrossRef]
- Gondek, D.; Haensel, P.; Zdunik, J.L. Radial pulsations and stability of protoneutron stars. Astron. Astrophys. 1997, 325, 217–227. [Google Scholar]
- Kokkotas, K.D.; Ruoff, J. Radial oscillations of relativistic stars. Astron. Astrophys. 2001, 366, 565–572. [Google Scholar] [CrossRef]
- Kain, B. Radial oscillations and stability of multiple-fluid compact stars. Phys. Rev. D 2020, 102, 023001. [Google Scholar] [CrossRef]
- Comer, G.L.; Langlois, D.; Lin, L.M. Quasinormal modes of general relativistic superfluid neutron stars. Phys. Rev. D 1999, 60, 104025. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Relativistic fluid dynamics: Physics for many different scales. Living Rev. Relativ. 2007, 10, 1. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B.; Weisskopf, V.F. A New Extended Model of Hadrons. Phys. Rev. D 1974, 9, 3471–3495. [Google Scholar] [CrossRef]
- Chodos, A.; Jaffe, R.L.; Johnson, K.; Thorn, C.B. Baryon Structure in the Bag Theory. Phys. Rev. D 1974, 10, 2599. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.; Roberts, M.; Hessels, J. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef] [PubMed]
- Margalit, B.; Metzger, B.D. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817y. Astrophys. J. Lett. 2017, 850, L19. [Google Scholar] [CrossRef]
- Lugones, G.; Horvath, J.E. Color flavor locked strange matter. Phys. Rev. D 2002, 66, 074017. [Google Scholar] [CrossRef]
- Flores, C.V.; Lugones, G. Radial oscillations of color superconducting self-bound quark stars. Phys. Rev. D 2010, 82, 063006. [Google Scholar] [CrossRef]
- Flores, C.V.; Lugones, G. Constraining color flavor locked strange stars in the gravitational wave era. Phys. Rev. C 2017, 95, 025808. [Google Scholar] [CrossRef]
- Cipolletta, F.; Cherubini, C.; Filippi, S.; Rueda, J.A.; Ruffini, R. Fast Rotating Neutron Stars with Realistic Nuclear Matter Equation of State. Phys. Rev. D 2015, 92, 023007. [Google Scholar] [CrossRef]
- Diener, J.P.W. Relativistic mean-field theory applied to the study of neutron star properties. arXiv 2008, arXiv:0806.0747. [Google Scholar]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Zhang, K.; Huang, G.Z.; Tsao, J.S.; Lin, F.L. GW170817 and GW190425 as hybrid stars of dark and nuclear matter. Eur. Phys. J. C 2022, 82, 366. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef]
- Acernese, F.A.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quantum Gravity 2014, 332, 024001. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER view of PSR J0030+0451: Millisecond pulsar parameter estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Arbañil, J.D.; Malheiro, M. Equilibrium and stability of charged strange quark stars. Phys. Rev. D 2015, 92, 084009. [Google Scholar] [CrossRef]
- Pereira, J.P.; Flores, C.V.; Lugones, G. Phase transition effects on the dynamical stability of hybrid neutron stars. Astrophys. J. 2018, 860, 12. [Google Scholar] [CrossRef]
- Gonçalves, V.P.; Lazzari, L. Impact of slow conversions on hybrid stars with sequential QCD phase transitions. Eur. Phys. J. C 2022, 82, 288. [Google Scholar] [CrossRef]
- Rau, P.B.; Sedrakian, A. Two first-order phase transitions in hybrid compact stars: Higher-order multiplet stars, reaction modes, and intermediate conversion speeds. Phys. Rev. D 2023, 107, 103042. [Google Scholar] [CrossRef]
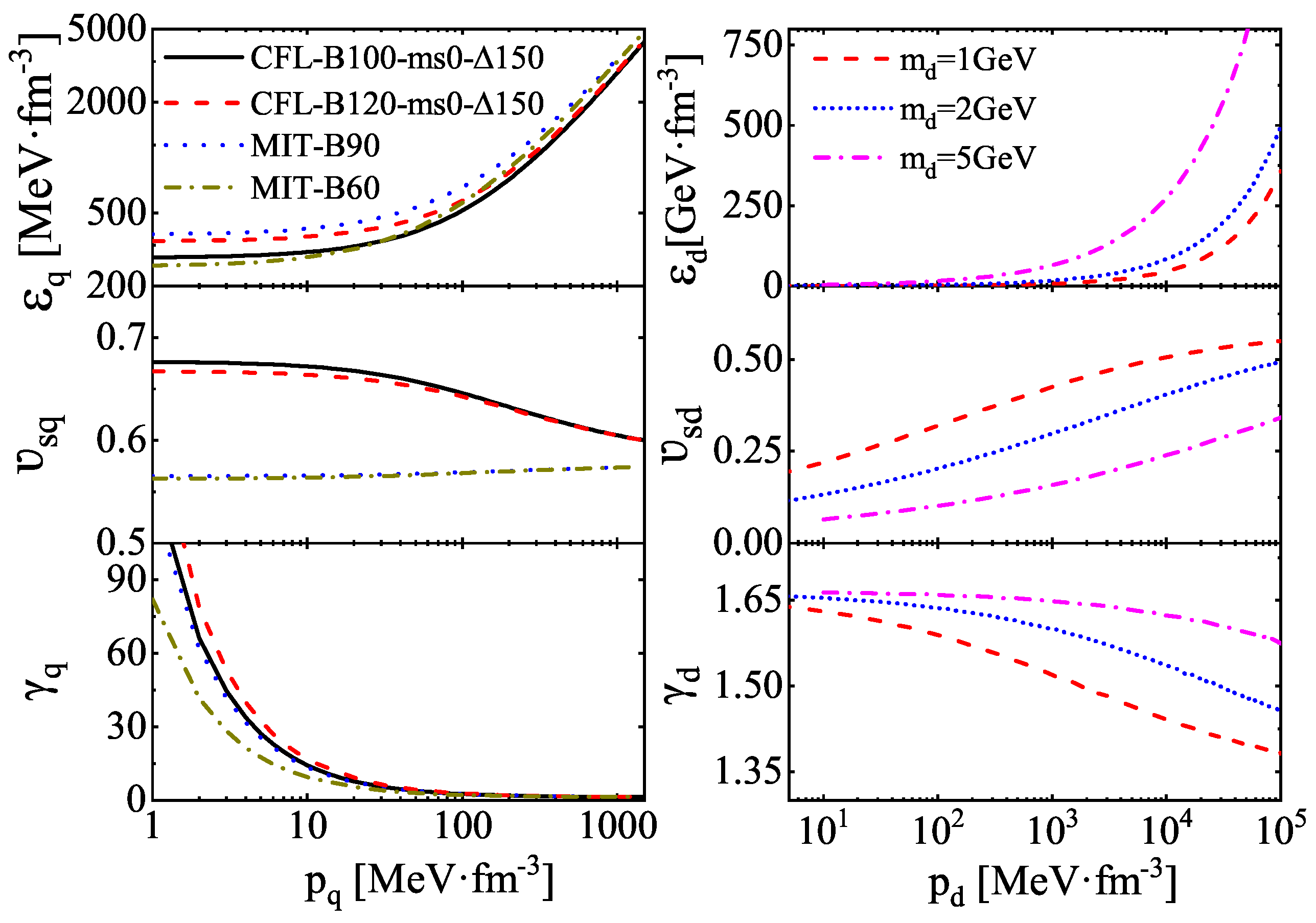
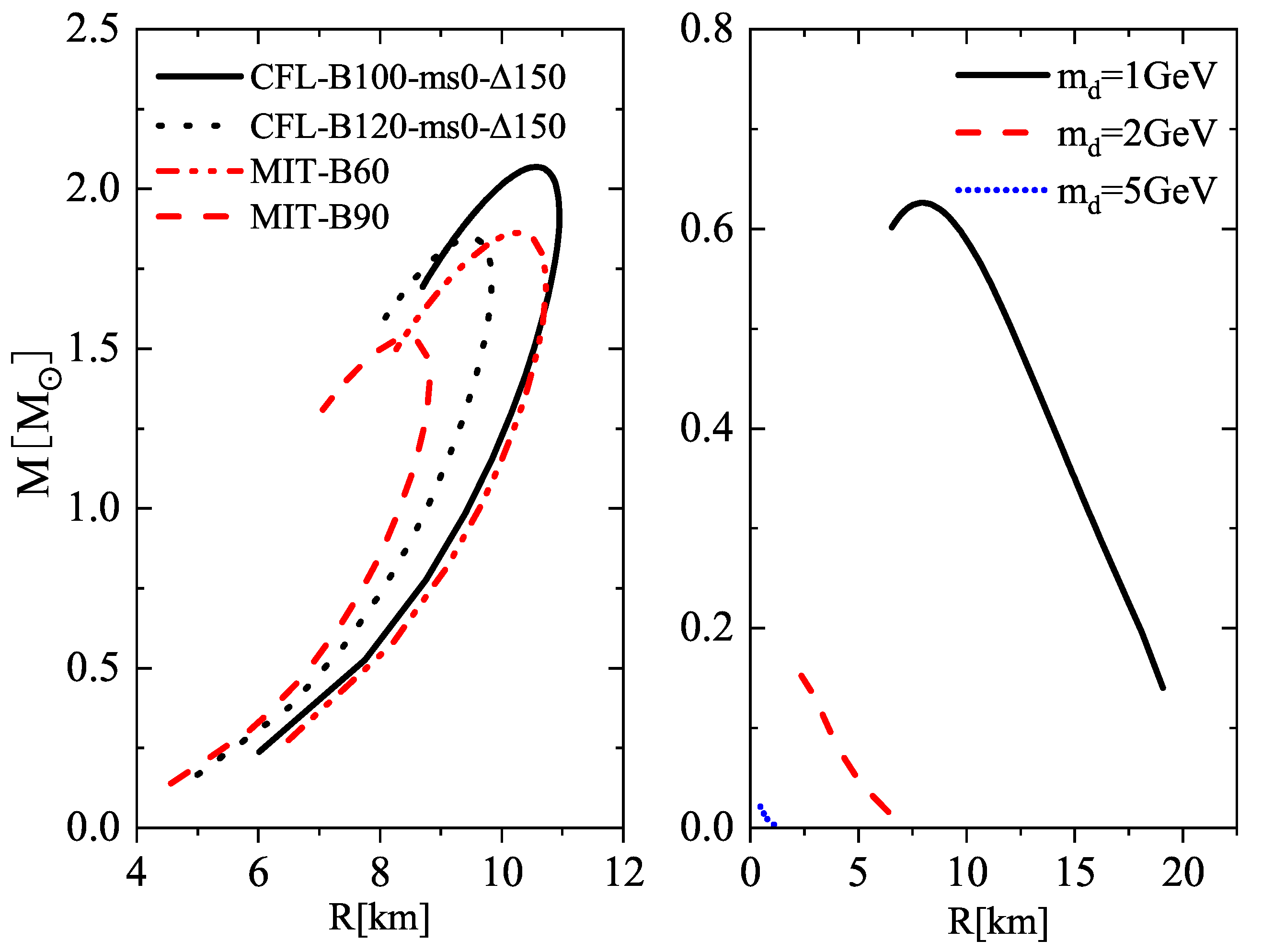
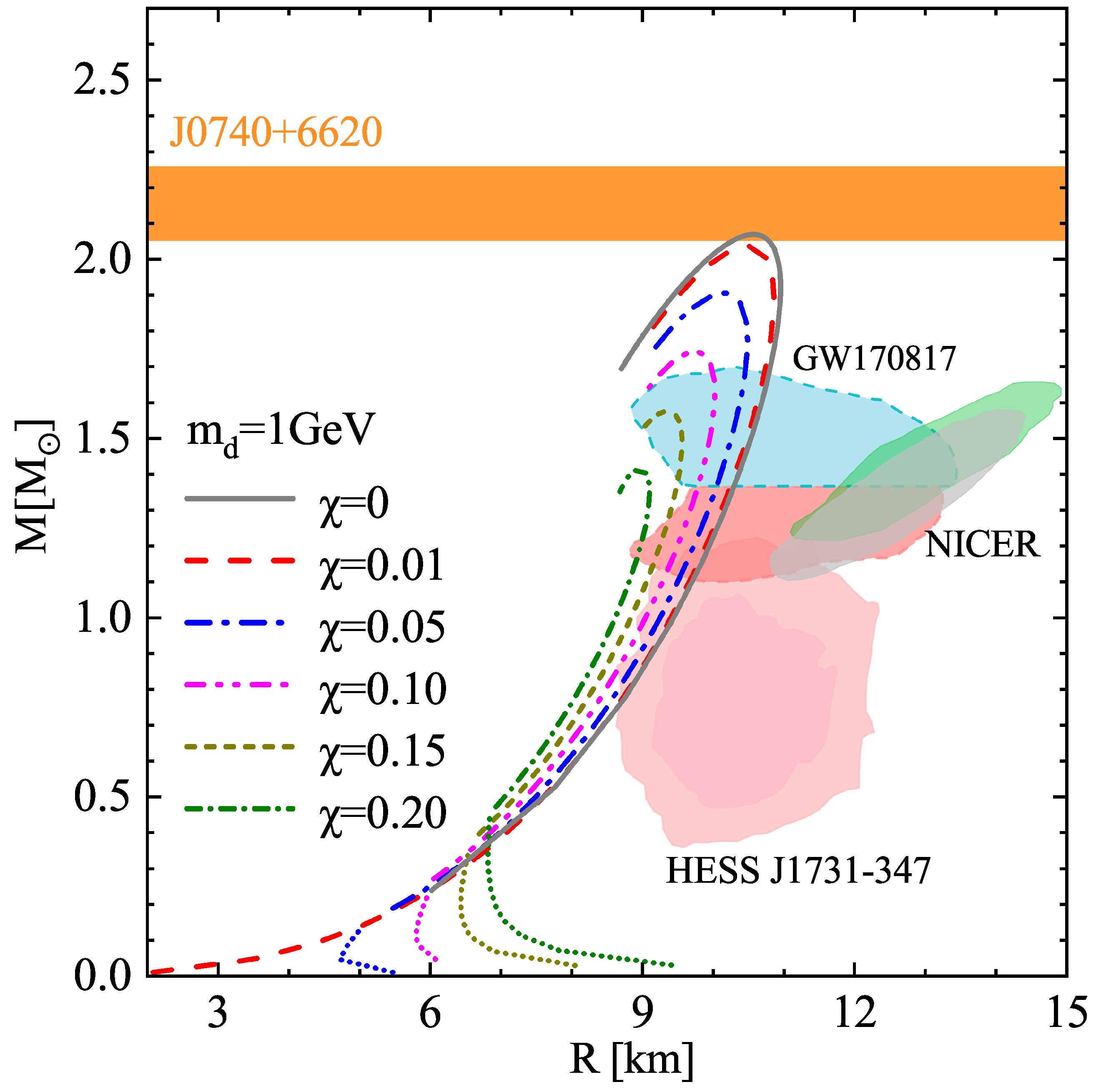

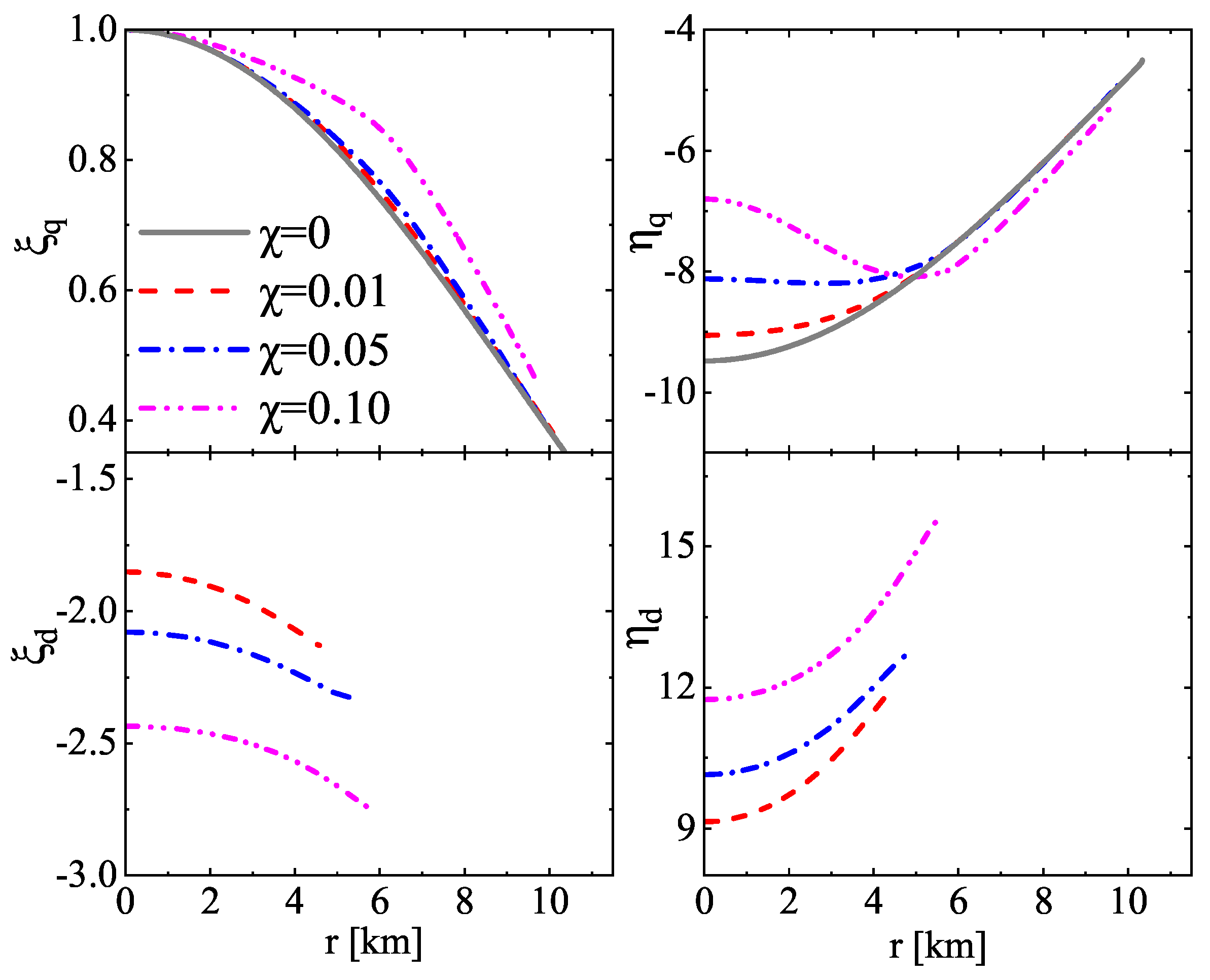
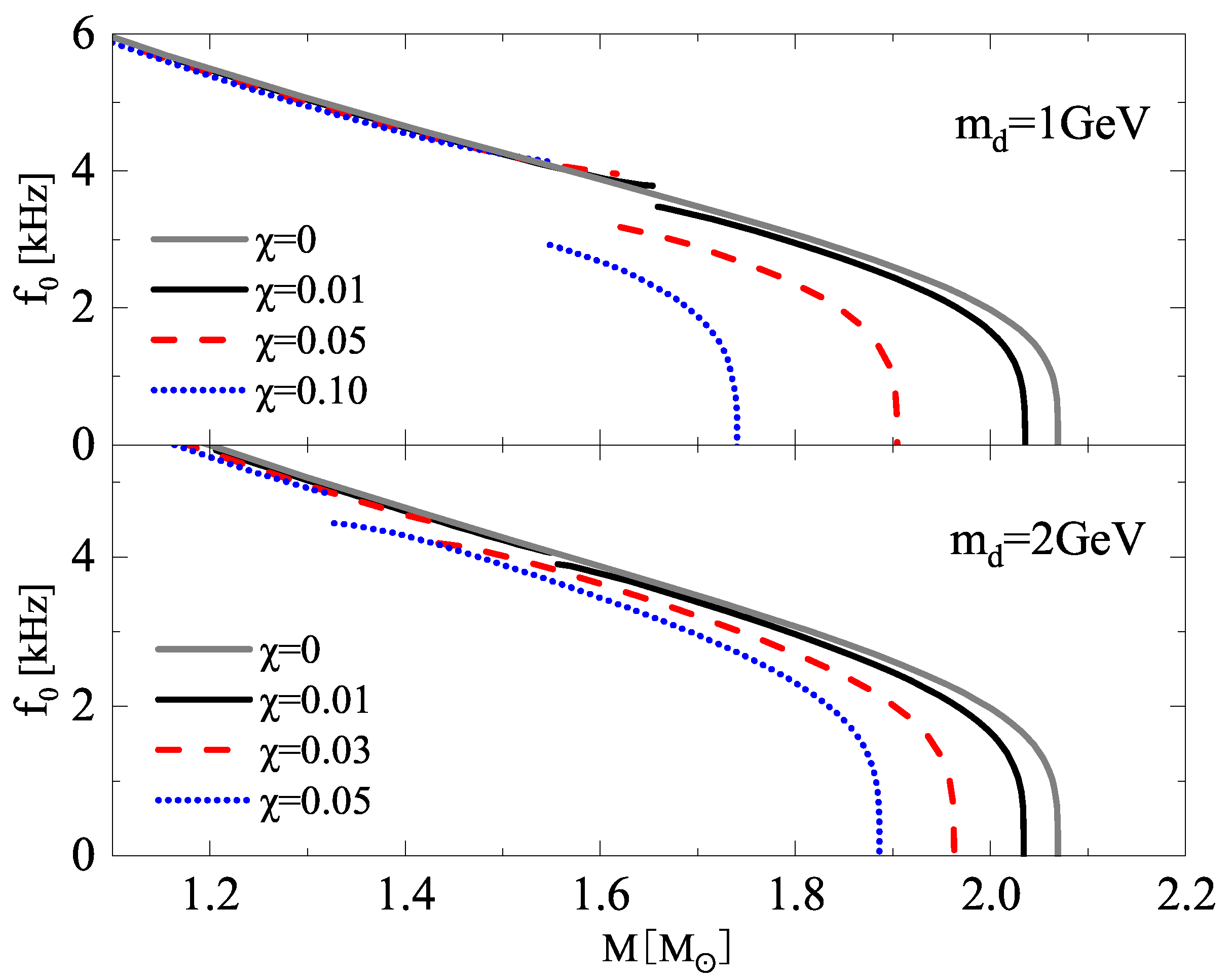
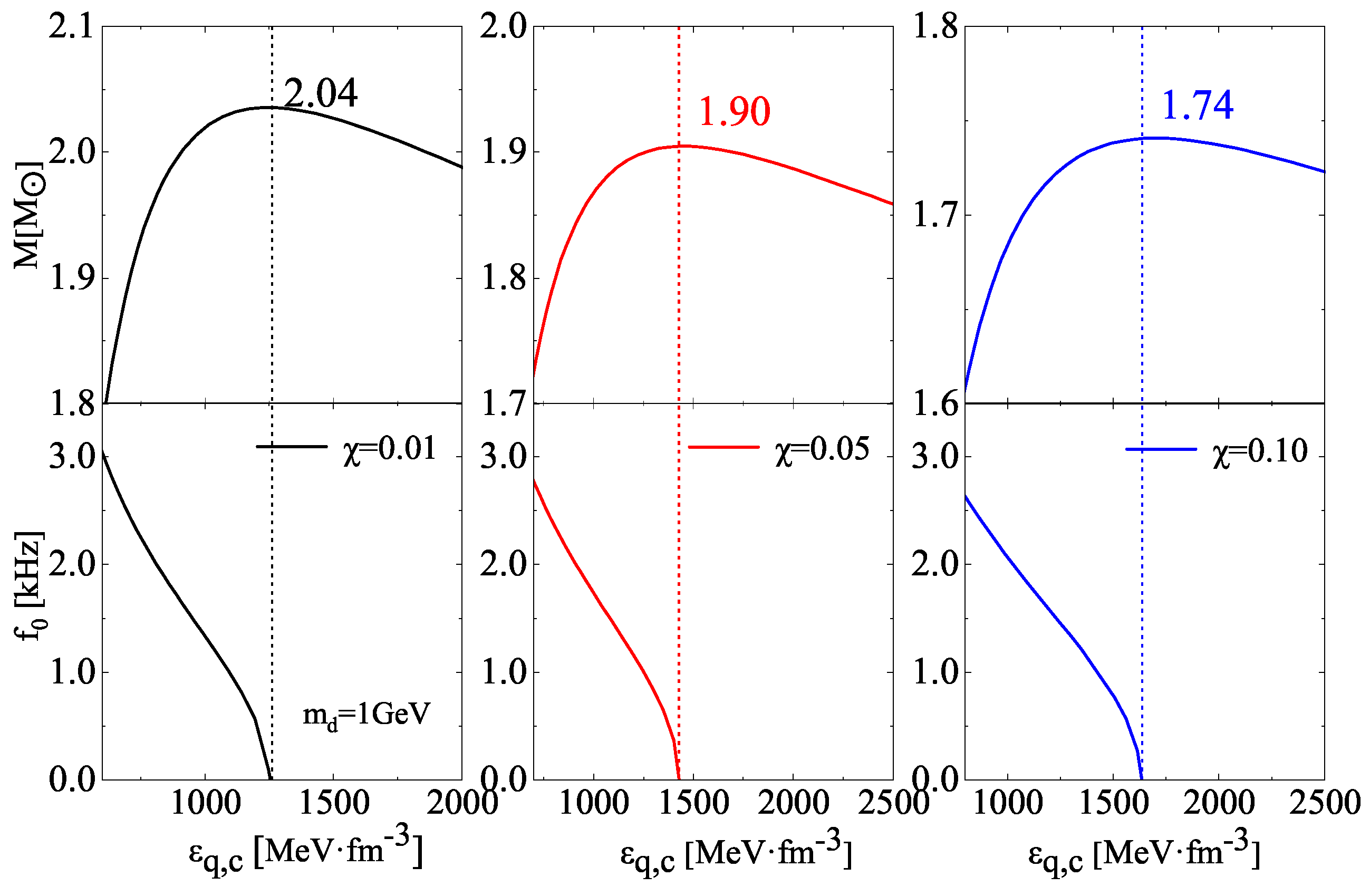
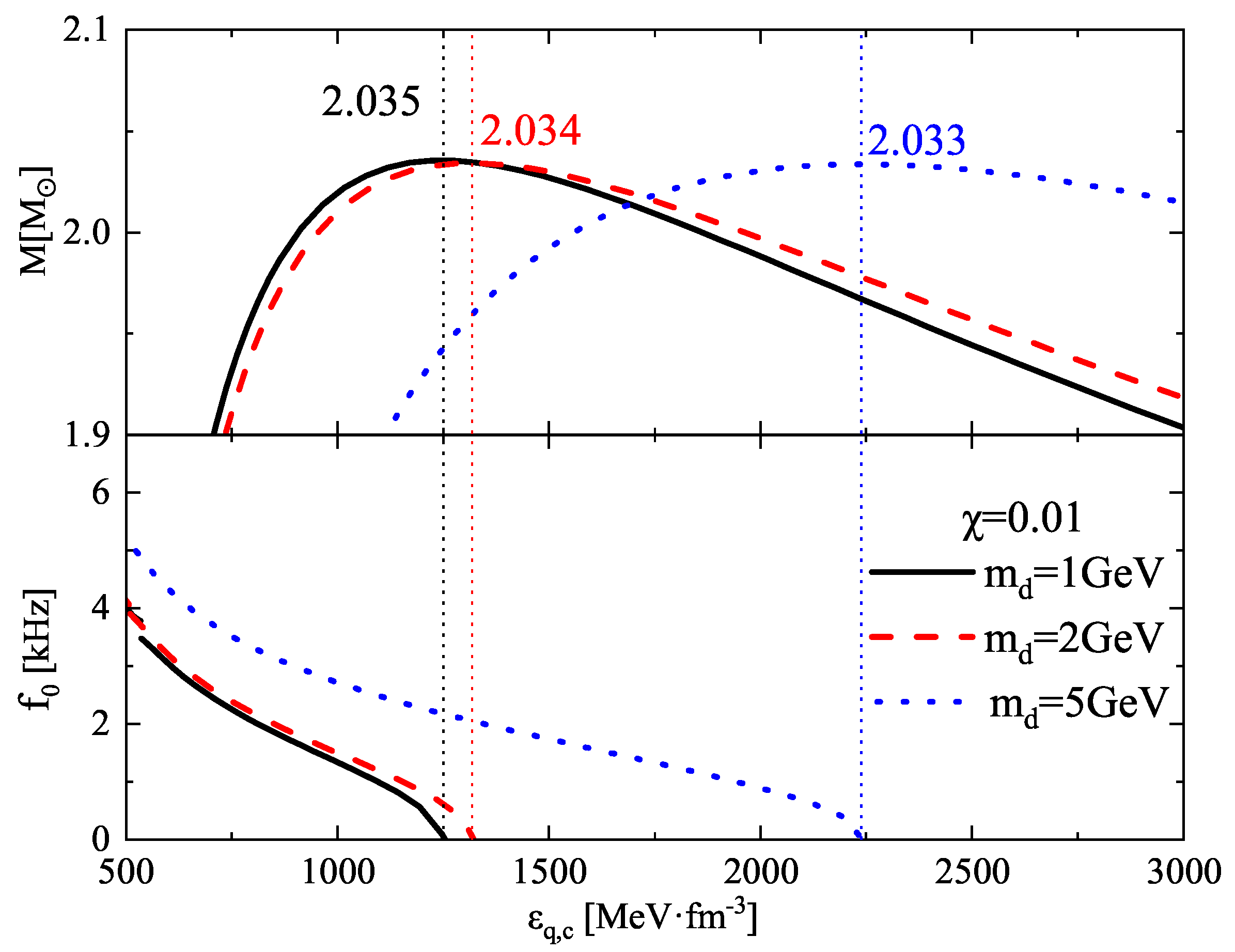


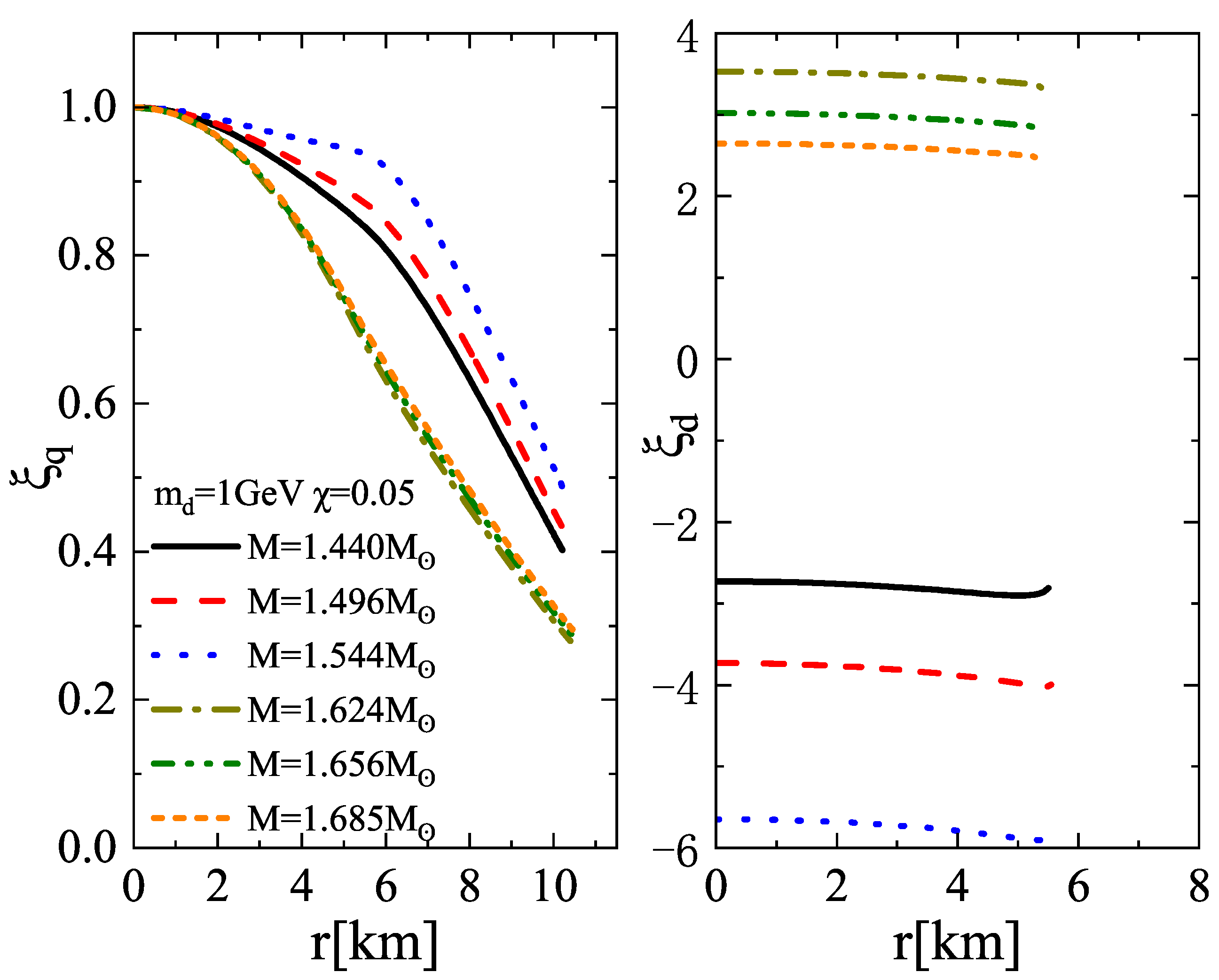
| R | R | |||||
|---|---|---|---|---|---|---|
| 1 | 0.01 | 2.035 | 385 | 10.49 | 71 | 10.25 |
| 0.05 | 1.904 | 461 | 10.16 | 91 | 10.07 | |
| 0.10 | 1.742 | 565 | 9.74 | 123 | 9.81 | |
| 2 | 0.01 | 2.034 | 425 | 10.46 | 80 | 10.35 |
| 0.03 | 1.963 | 542 | 10.31 | 101 | 10.22 | |
| 0.05 | 1.886 | 805 | 10.12 | 131 | 10.10 | |
| 5 | 0.010 | 2.033 | 755 | 10.48 | 121 | 10.31 |
| 0.015 | 1.665 | 665 | 10.66 | 203 | 10.27 | |
| 0.020 | 1.249 | 463 | 9.96 | |||
| 10 | 0.001 | 2.065 | 425 | 10.56 | 85 | 10.42 |
| 0.005 | 1.253 | 445 | 10.03 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhen, Y.; Sun, T.-T.; Wei, J.-B.; Zheng, Z.-Y.; Chen, H. Radial Oscillations of Strange Quark Stars Admixed with Dark Matter. Symmetry 2024, 16, 807. https://doi.org/10.3390/sym16070807
Zhen Y, Sun T-T, Wei J-B, Zheng Z-Y, Chen H. Radial Oscillations of Strange Quark Stars Admixed with Dark Matter. Symmetry. 2024; 16(7):807. https://doi.org/10.3390/sym16070807
Chicago/Turabian StyleZhen, Yu, Ting-Ting Sun, Jin-Biao Wei, Zi-Yue Zheng, and Huan Chen. 2024. "Radial Oscillations of Strange Quark Stars Admixed with Dark Matter" Symmetry 16, no. 7: 807. https://doi.org/10.3390/sym16070807
APA StyleZhen, Y., Sun, T.-T., Wei, J.-B., Zheng, Z.-Y., & Chen, H. (2024). Radial Oscillations of Strange Quark Stars Admixed with Dark Matter. Symmetry, 16(7), 807. https://doi.org/10.3390/sym16070807





