Minimization over Nonconvex Sets
Abstract
:1. Introduction
2. Materials and Methods
3. Results
- 1.
- .
- 2.
- If , then .
- 1.
- Fix an arbitrary . Suppose to the contrary that . Then, there exists satisfying at least one of the following two conditions:
- There exists with , for all and for all .
- There exists with , for all and for all .
We may assume, without any loss of generality, that the first condition holds. Notice thatandThis contradicts the fact that . - 2.
- Since , we have that . Notice that . It only remains to show that . Indeed, take any . Let . Then, for all and for all . Therefore,andAs a consequence, the arbitrariness of y shows that .
- 1.
- .
- 2.
- If , then .
- 3.
- If , then .
- 4.
- If and , then
- 1.
- Fix an arbitrary . Then, In this case, we can write . If we prove that , then we obtain that . Indeed, let us observe first that and , since and are positively homogeneous. As a consequence, is a feasible solution of (4). Suppose on the contrary that is not an optimal solution of (4); in other words, . Then, there exists such that and . Then, we obtain thatthus meaning that . Note that . Since by hypothesis, we reach the contradiction that .
- 2.
- Fix . If there exists , then we can find an sufficiently large so that . However, and , which implies the contradiction that . As a consequence, . Suppose next that there exists . We can find a sufficiently large so that . Then, and , which implies the contradiction that . As a consequence,
- 3.
- Fix an arbitrary . If , then there exists such that and , thus concluding that and reaching the contradiction that .
- 4.
- Fix an arbitrary . We will prove first that . So, suppose on the contrary that . We distinguish between two cases:
- . In this case, , so it only suffices to take any to reach the contradiction that , , and(note that , because , and ).
- . In this case, it only suffices to observe that and , butthus reaching a contradiction with the fact that .
As a consequence, . Next, suppose to the contrary that . Then, there exists satisfying at least one of the following two conditions:- and . In this case, and , which directly contradicts that .
- and . In this case, and , thus, since , it must occur that , hence , which means that , and this contradicts that .
- 1.
- .
- 2.
- If , then .
- 1.
- Suppose to the contrary that there exists . Then, for all , so we can takeObserve thatfor all . In particular,for all . Notice also that , so If we prove that , then we will reach a contradiction with the fact that . Indeed, fix an arbitrary . By relying on (7),As a consequence, , and we have obtained the desired contradiction. This contradiction forces that . Finally, the arbitrariness of implies that .
- 2.
- We prove first that . By hypothesis, , so it only remains to show that . Suppose to the contrary that there exists . There exists satisfying one of the following two conditions:
- for some , for all , and . Notice that . Since , we conclude that . Thus, , thus meaning that . By hypothesis, ; hence, , so for all . This contradicts the fact that .
- and for all . In this situation, . Since , we conclude that , which contradicts that .
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
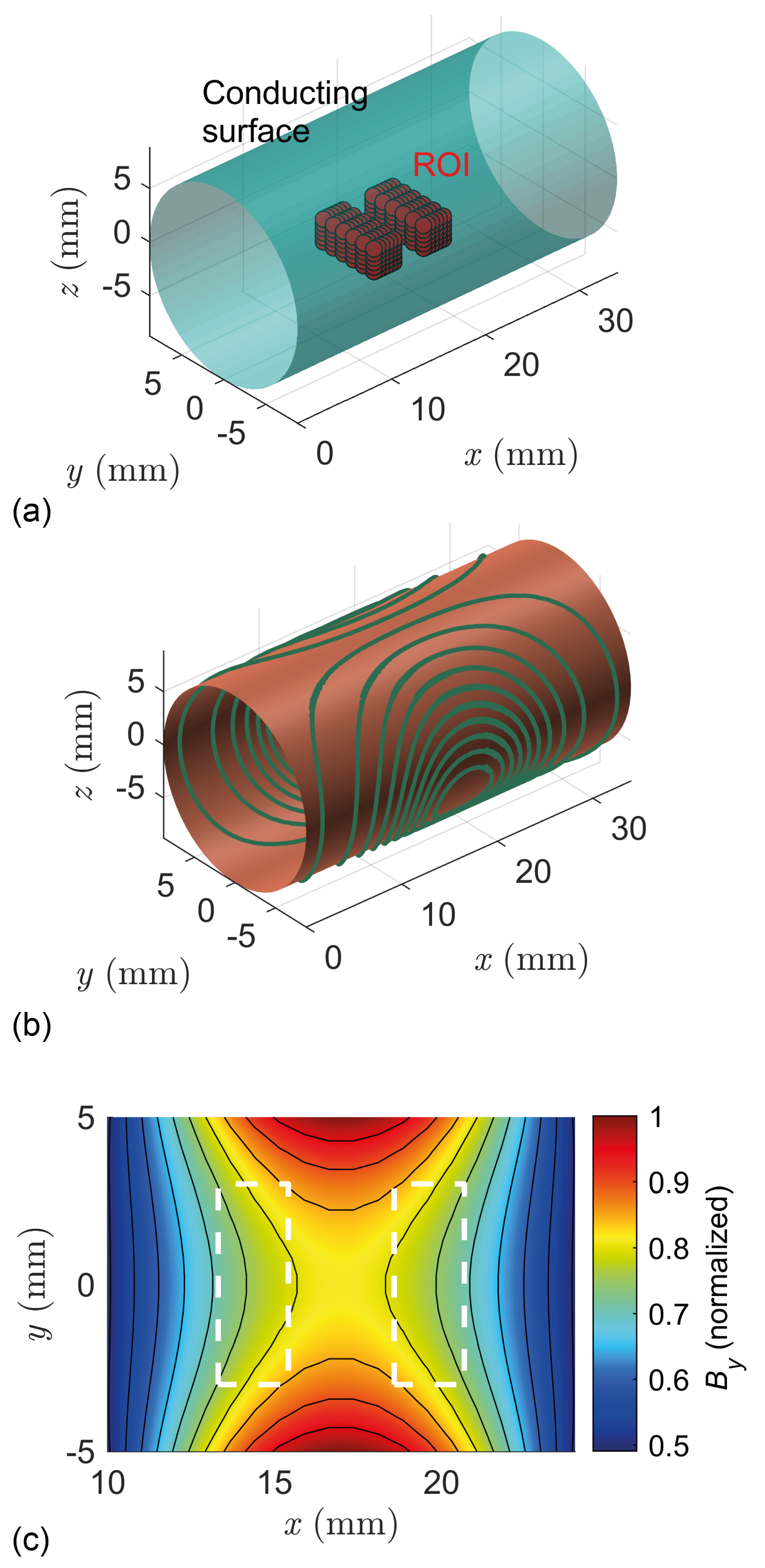
Appendix A. Application to Optimal Coil Design for Electronics Sensors
References
- Aizpuru, A.; García-Pacheco, F.J. Reflexivity, contraction functions and minimum-norm elements. Studia Sci. Math. Hungar. 2005, 42, 431–443. [Google Scholar] [CrossRef]
- Blatter, J. Reflexivity and the existence of best approximations. In Approximation Theory, II (Proceedings International Symposium, University of Texas at Austin, 1976); Academic Press: New York, NY, USA; London, UK, 1976; pp. 299–301. [Google Scholar]
- Campos-Jiménez, A.; Vílchez-Membrilla, J.A.; Cobos-Sánchez, C.; García-Pacheco, F.J. Analytical solutions to minimum-norm problems. Mathematics 2022, 10, 1454. [Google Scholar] [CrossRef]
- Moreno-Pulido, S.; Sánchez-Alzola, A.; García-Pacheco, F.J. Revisiting the minimum-norm problem. J. Inequal. Appl. 2022, 2022, 22. [Google Scholar] [CrossRef]
- Wassermann, E.; Epstein, C.; Ziemann, U.; Walsh, V.; Paus, T.; Lisanby, S. Oxford Handbook of Transcranial Stimulation (Oxford Handbooks), 1st ed.; Oxford University Press: New York, NY, USA, 2008; Available online: http://gen.lib.rus.ec/book/index.php?md5=BA11529A462FDC9C5A1EF1C28E164A7D (accessed on 18 June 2024).
- Huang, N.; Ma, C.-F. Modified conjugate gradient method for obtaining the minimum-norm solution of the generalized coupled Sylvester-conjugate matrix equations. Appl. Math. Model. 2016, 40, 1260–1275. [Google Scholar] [CrossRef]
- Pissanetzky, S. Minimum energy MRI gradient coils of general geometry. Meas. Sci. Technol. 1992, 3, 667. [Google Scholar] [CrossRef]
- Romei, V.; Murray, M.M.; Merabet, L.B.; Thut, G. Occipital transcranial magnetic stimulation has opposing effects on visual and auditory stimulus detection: Implications for multisensory interactions. J. Neurosci. 2007, 27, 11465–11472. [Google Scholar] [CrossRef] [PubMed]
- Márquez, A.P.; García-Pacheco, F.J.; Mengibar-Rodríguez, M.; Sxaxnchez-Alzola, A. Supporting vectors vs. principal components. AIMS Math. 2023, 8, 1937–1958. [Google Scholar] [CrossRef]
- Singer, I. On best approximation in normed linear spaces by elements of subspaces of finite codimension. Rev. Roum. Math. Pures Appl. 1972, 17, 1245–1256. [Google Scholar]
- Singer, I. The theory of best approximation and functional analysis. In Vol. No. 13 of Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1974. [Google Scholar]
- James, R.C. Characterizations of reflexivity. Studia Math. 1963, 23, 205–216. [Google Scholar] [CrossRef]
- James, R.C. A counterexample for a sup theorem in normed spaces. Israel J. Math. 1971, 9, 511–512. [Google Scholar] [CrossRef]
- Martín, M. On proximinality of subspaces and the lineability of the set of norm-attaining functionals of Banach spaces. J. Funct. Anal. 2020, 278, 108353. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.; Li, Y.; Lin, B.-L.; Narayana, D. Proximinality in Banach spaces. J. Math. Anal. Appl. 2008, 341, 309–317. [Google Scholar] [CrossRef]
- García-Pacheco, F.J.; Rambla-Barreno, F.; Seoane-Sepúlveda, J.B. Q-linear functions, functions with dense graph, and everywhere surjectivity. Math. Scand. 2008, 102, 156–160. [Google Scholar] [CrossRef]
- Read, C.J. Banach spaces with no proximinal subspaces of codimension 2. Israel J. Math. 2018, 223, 493–504. [Google Scholar] [CrossRef]
- Rmoutil, M. Norm-attaining functionals need not contain 2-dimensional subspaces. J. Funct. Anal. 2017, 272, 918–928. [Google Scholar] [CrossRef]
- Koponen, L.M.; Nieminen, J.O.; Ilmoniemi, R.J. Minimum-energy coils for transcranial magnetic stimulation: Application to focal stimulation. Brain Stimul. 2015, 8, 124–134. [Google Scholar] [CrossRef]
- Koponen, L.M.; Nieminen, J.O.; Mutanen, T.P.; Stenroos, M.; Ilmoniemi, R.J. Coil optimisation for transcranial magnetic stimulation in realistic head geometry. Brain Stimul. 2017, 10, 795–805. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Pulido, S.; Garcia-Pacheco, F.J.; Cobos-Sanchez, C.; Sanchez-Alzola, A. Exact solutions to the maxmin problem max‖Ax‖ subject to ‖Bx‖ ≤ 1. Mathematics 2020, 8, 85. [Google Scholar] [CrossRef]
- Garcia-Pacheco, F.J.; Cobos-Sanchez, C.; Moreno-Pulido, S.; Sanchez-Alzola, A. Exact solutions to max‖x‖=1‖Ti(x)‖2 with applications to Physics, Bioengineering and Statistics. Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105054. [Google Scholar] [CrossRef]
- Cobos-Sánchez, C.; Vilchez-Membrilla, J.A.; Campos-Jiménez, A.; García-Pacheco, F.J. Pareto optimality for multioptimization of continuous linear operators. Symmetry 2021, 13, 661. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilchez Membrilla, J.A.; Salas Moreno, V.; Moreno-Pulido, S.; Sánchez-Alzola, A.; Cobos Sánchez, C.; García-Pacheco, F.J. Minimization over Nonconvex Sets. Symmetry 2024, 16, 809. https://doi.org/10.3390/sym16070809
Vilchez Membrilla JA, Salas Moreno V, Moreno-Pulido S, Sánchez-Alzola A, Cobos Sánchez C, García-Pacheco FJ. Minimization over Nonconvex Sets. Symmetry. 2024; 16(7):809. https://doi.org/10.3390/sym16070809
Chicago/Turabian StyleVilchez Membrilla, José Antonio, Víctor Salas Moreno, Soledad Moreno-Pulido, Alberto Sánchez-Alzola, Clemente Cobos Sánchez, and Francisco Javier García-Pacheco. 2024. "Minimization over Nonconvex Sets" Symmetry 16, no. 7: 809. https://doi.org/10.3390/sym16070809
APA StyleVilchez Membrilla, J. A., Salas Moreno, V., Moreno-Pulido, S., Sánchez-Alzola, A., Cobos Sánchez, C., & García-Pacheco, F. J. (2024). Minimization over Nonconvex Sets. Symmetry, 16(7), 809. https://doi.org/10.3390/sym16070809







