On New Symmetric Fractional Discrete-Time Systems: Chaos, Complexity, and Control
Abstract
:1. Introduction
- A new symmetric fractional map with a sine function and complex nonlinear chaotic behavior is explored in two cases, commensurate order and incommensurate order, through numerical techniques.
- Preliminaries of discrete fractional calculus and a description of a new symmetric fractional-order map add to the analysis of the stability of equilibrium points.
- We give the approximate entropy (ApEn) and complexity for evaluating the complexity of chaos in the new symmetric fractional map in two cases.
- Stabilization of the symmetric fractional map is attained resting on the stability theorems of linear maps.
2. Model Description and Basic Tools
2.1. Basic Tools
2.2. Description of the Fractional Map
3. The Commensurate Fractional Map
3.1. Stability Analysis
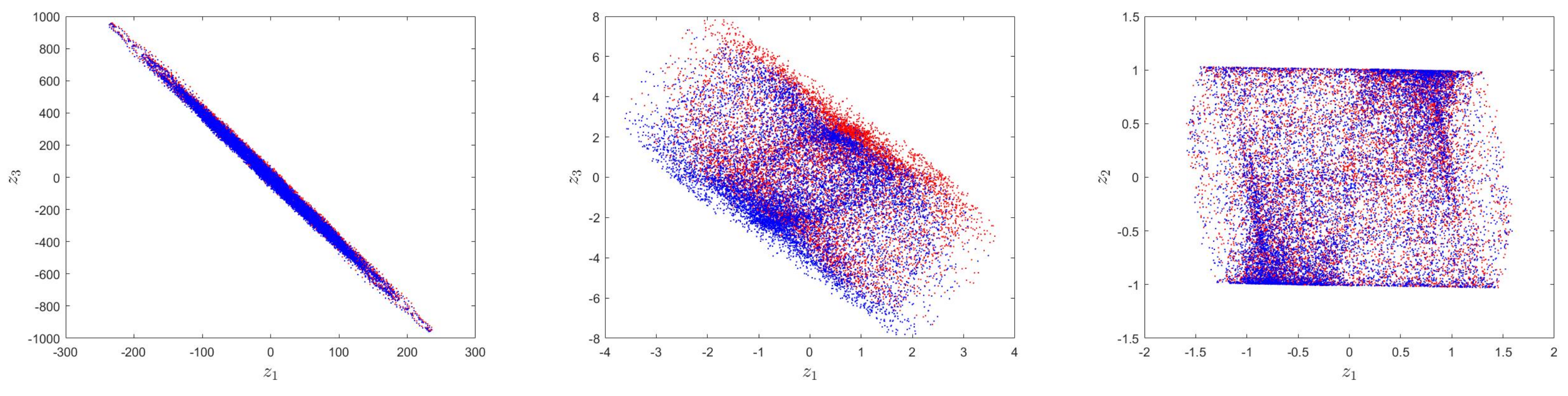
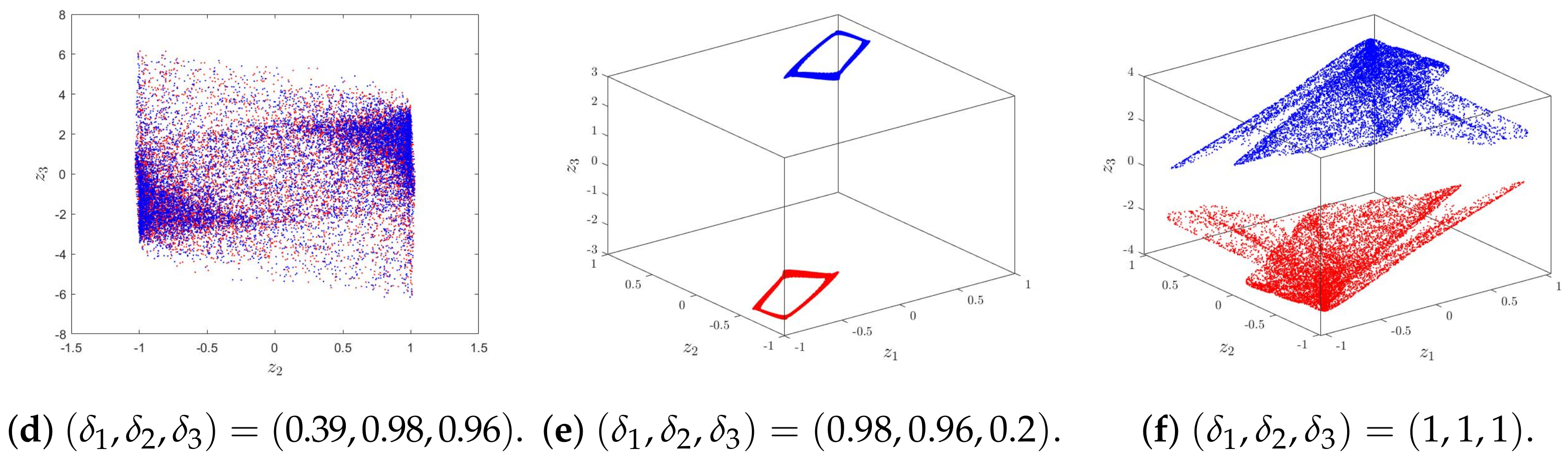
3.2. Dynamic Analysis
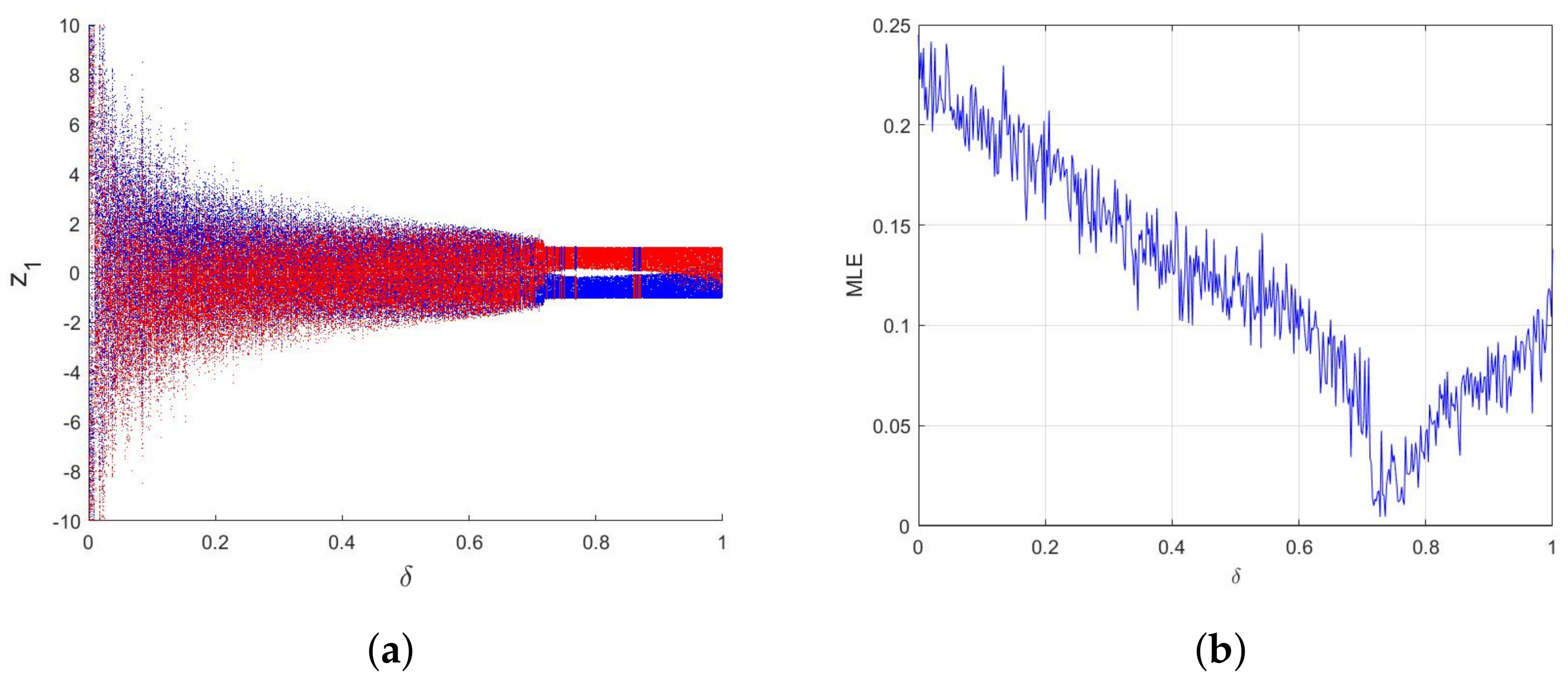
4. The Incommensurate Fractional System
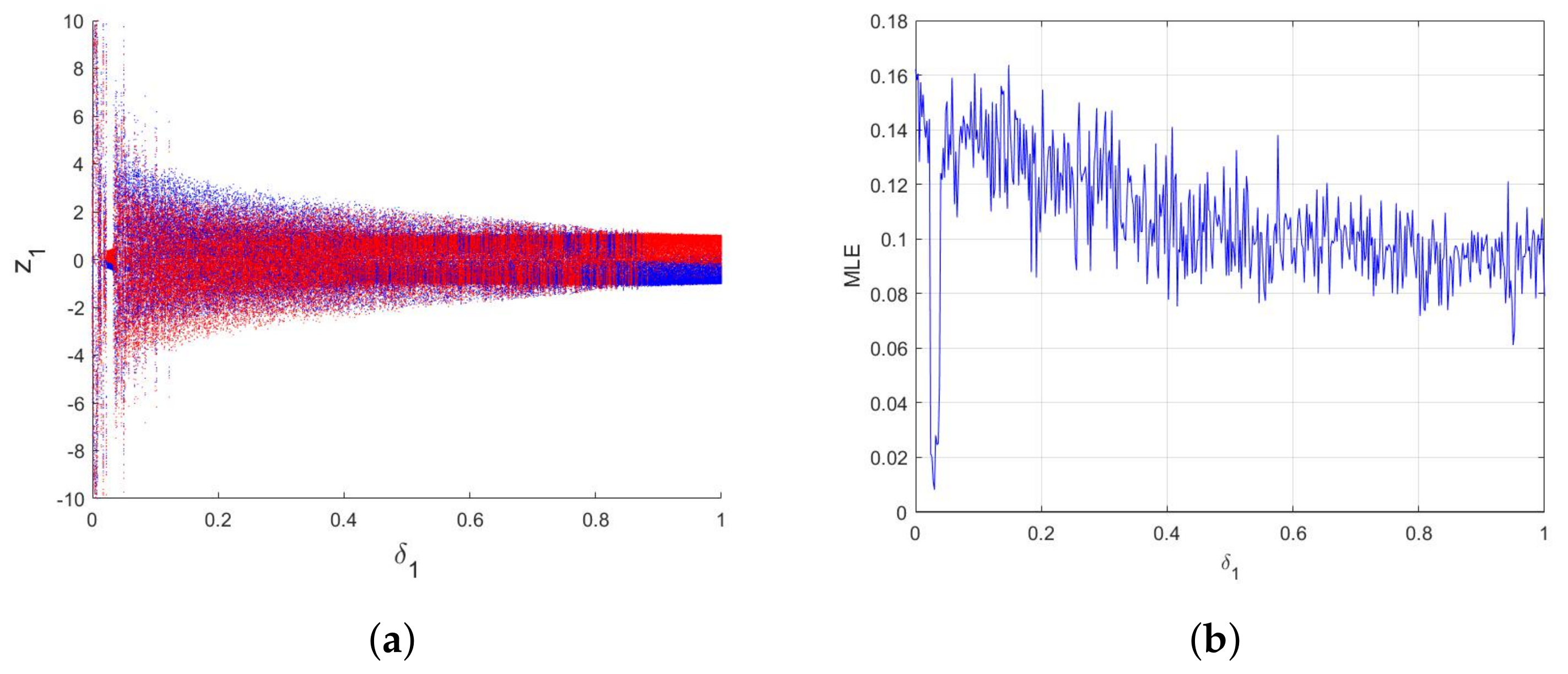
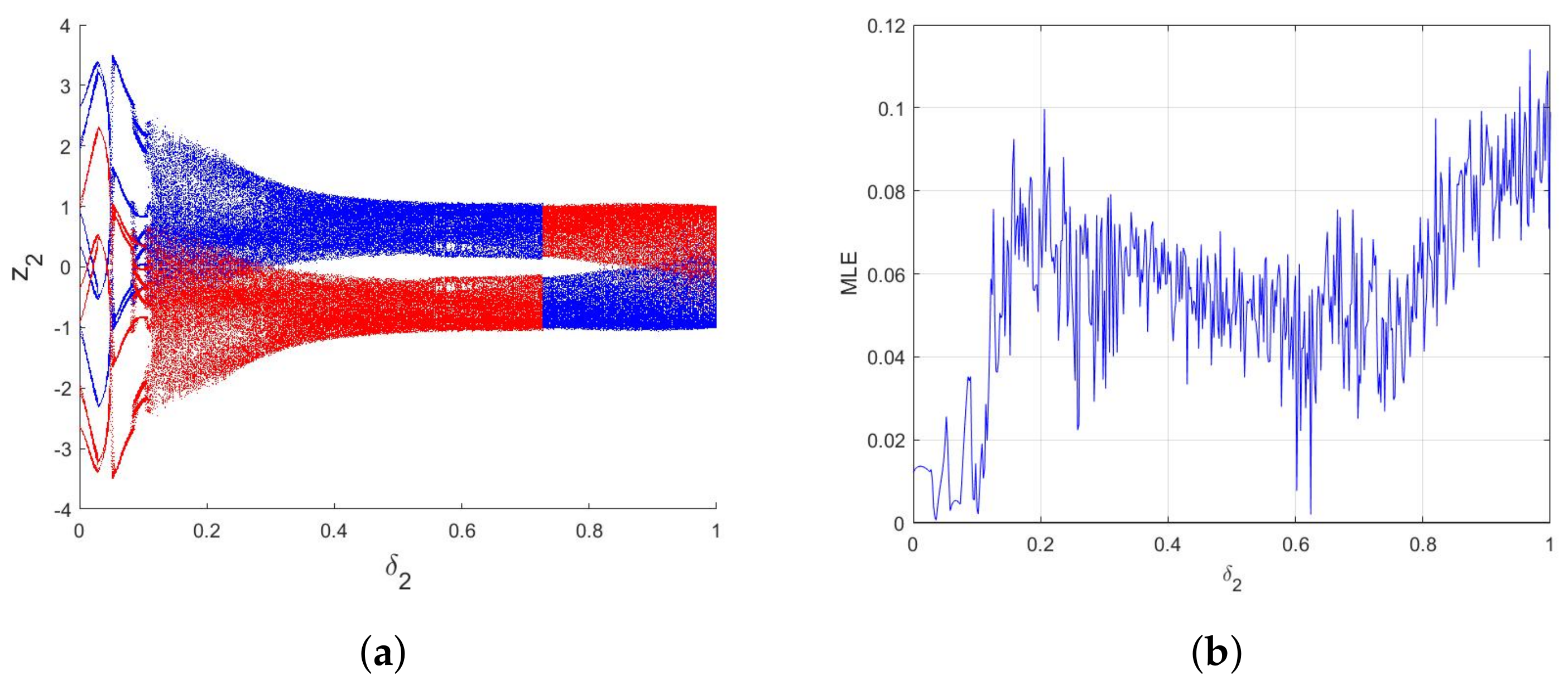
4.1. Equilibrium Stability
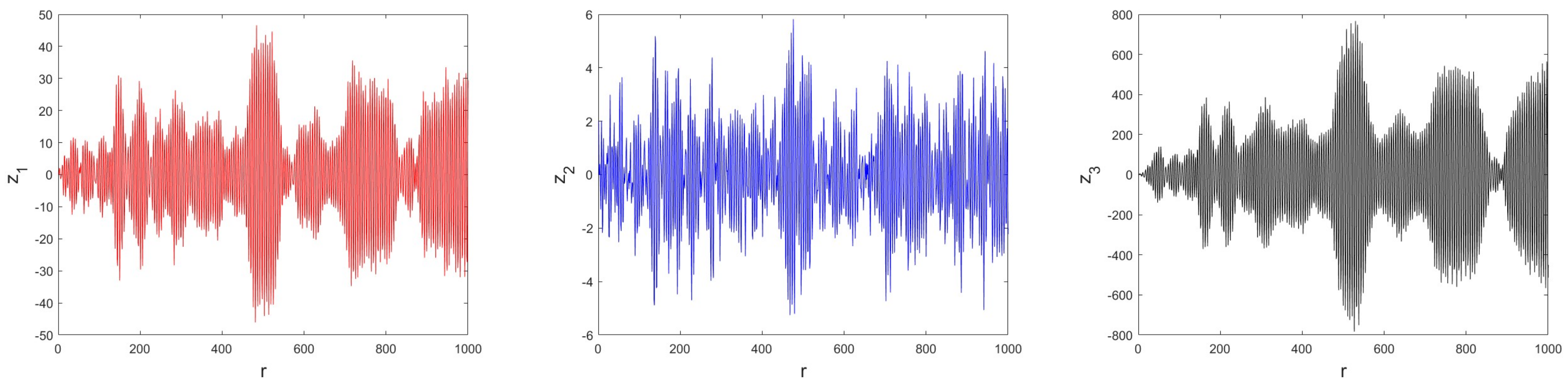
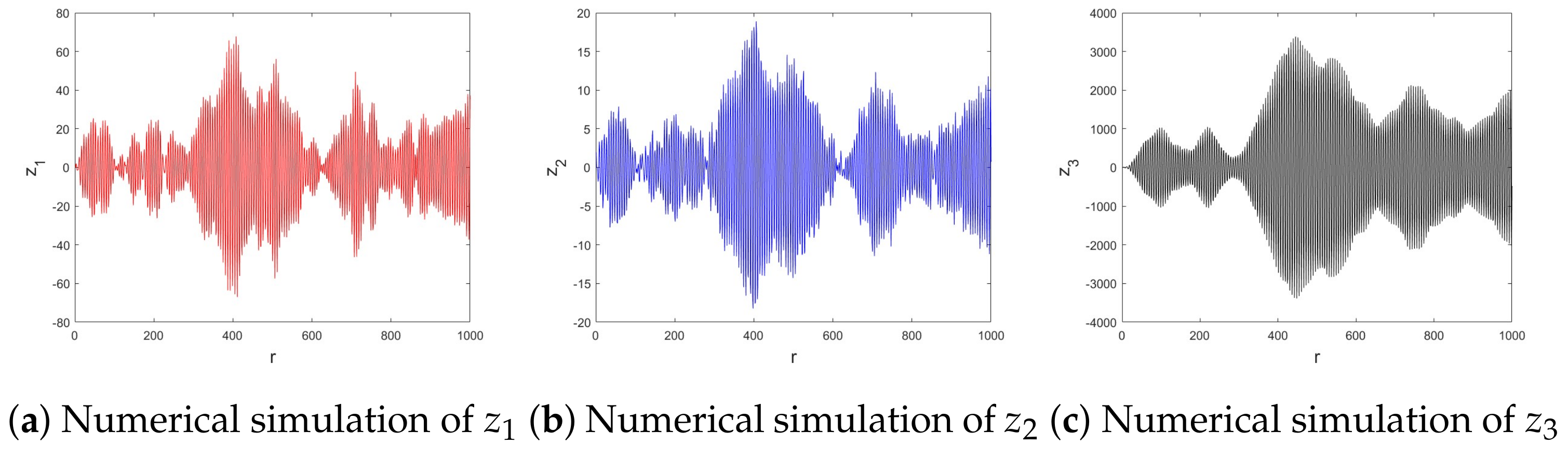
4.2. Numerical Chaos
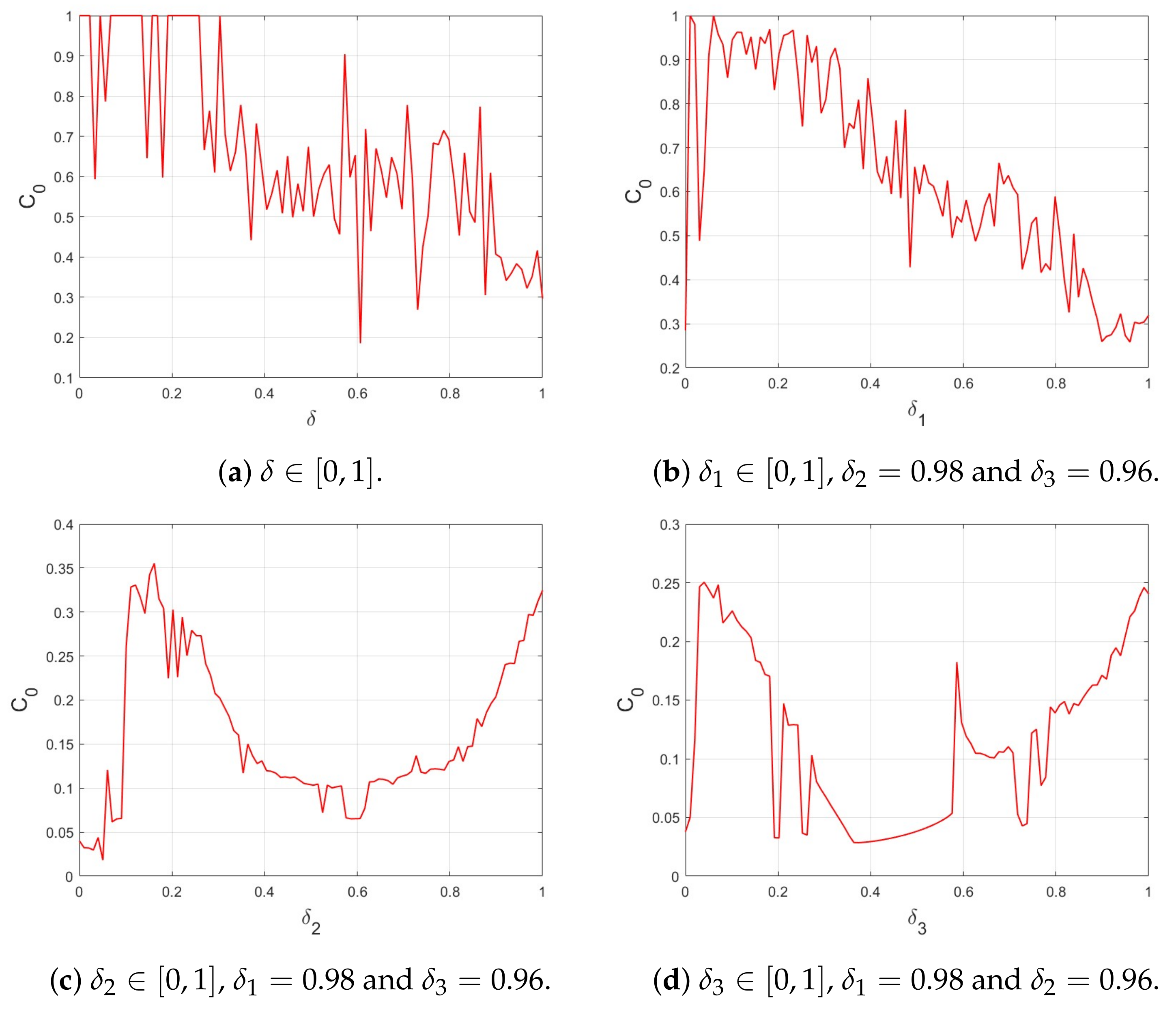
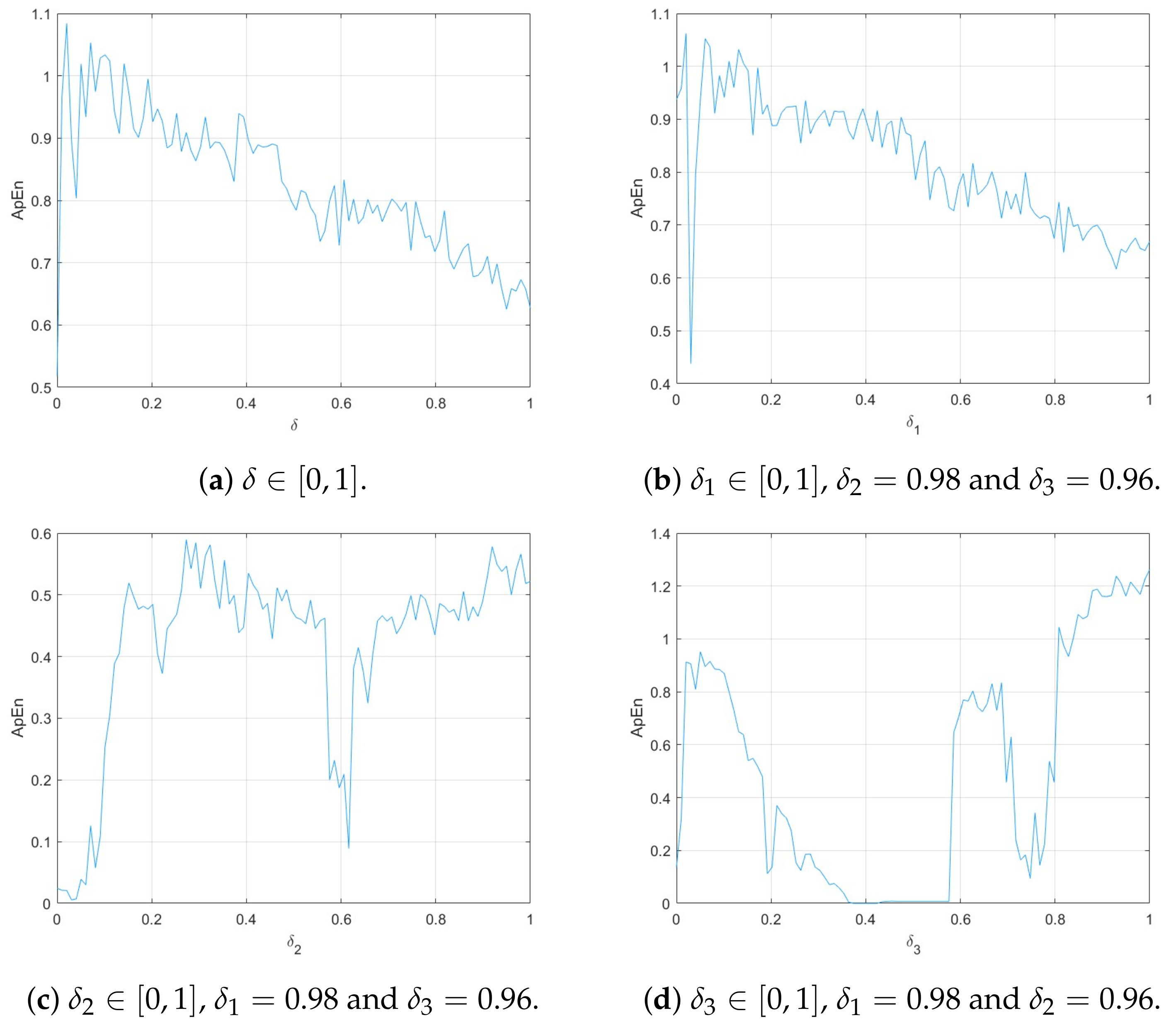
5. Chaotic Complexity
5.1. Complexity
- The Fourier transform of is determined by
- We characterized the mean square of as and set
- The following expression can be used to find the inverse Fourier transform:
- The complexity is determined by using the ensuing formula:
5.2. Approximate Entropy Test
6. Chaos Control
6.1. The Commensurate Case
6.2. The Incommensurate Case
7. Discussion, Conclusions, and Perspectives
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, L. Adaptive phase retrieval algorithm for local highlight area based on a piecewise sine function. Appl. Opt. 2024, 63, 927–939. [Google Scholar] [CrossRef] [PubMed]
- Hamadneh, T.; Ahmed, S.B.; Al-Tarawneh, H.; Alsayyed, O.; Gharib, G.M.; Al Soudi, M.S.; Ouannas, A. The New Four-Dimensional Fractional Chaotic Map with Constant and Variable-Order: Chaos, Control and Synchronization. Mathematics 2023, 11, 4332. [Google Scholar] [CrossRef]
- Peng, Y.; Lan, Z.; Li, W.; Li, Y.; Peng, J. Modeling different discrete memristive sine maps and its parameter identification. Eur. Phys. J. Spec. Top. 2022, 231, 3187–3196. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, J.; Zhang, F.; Ni, H.; Chen, J.; Huang, Z. Color image encryption using 2D sine-cosine coupling map. IEEE Access 2022, 10, 67669–67685. [Google Scholar] [CrossRef]
- Abu-Amara, F.; Abdel-Qader, I. Chaotic image encryption via convex sinusoidal map. WSEAS Trans. Signal Process. 2013, 9, 177–184. [Google Scholar]
- Hamadneh, T.; Abbes, A.; Al-Tarawneh, H.; Gharib, G.M.; Salameh, W.M.M.; Al Soudi, M.S.; Ouannas, A. On chaos and complexity analysis for a new sine-based memristor map with commensurate and incommensurate fractional orders. Mathematics 2023, 11, 4308. [Google Scholar] [CrossRef]
- Feng, W.; Zhao, X.; Zhang, J.; Qin, Z.; Zhang, J.; He, Y. Image encryption algorithm based on plane-level image filtering and discrete logarithmic transform. Mathematics 2022, 10, 2751. [Google Scholar] [CrossRef]
- Rajagopal, K.; Kanagaraj, S.; Volos, C.; Karthikeyan, A. Influence of parametric symmetry on the dynamics of 3D sinusoidal discrete systems. Symmetry 2023, 15, 780. [Google Scholar] [CrossRef]
- Elaskar, S. Symmetry in Nonlinear Dynamics and Chaos. Symmetry 2022, 15, 102. [Google Scholar] [CrossRef]
- Zhang, J. Control Analysis of Stochastic Lagging Discrete Ecosystems. Symmetry 2022, 14, 1039. [Google Scholar] [CrossRef]
- Andrianov, I.; Koblik, S.; Starushenko, G. Transition from discrete to continuous media: The impact of symmetry changes on asymptotic behavior of waves. Symmetry 2021, 13, 1008. [Google Scholar] [CrossRef]
- Ali, A.M.A.; Sriram, S.; Natiq, H.; Ahmadi, A.; Rajagopal, K.; Jafari, S. A novel multi-stable sinusoidal chaotic map with spectacular behaviors. Commun. Theor. Phys. 2022, 75, 115001. [Google Scholar] [CrossRef]
- Leutcho, G.D.; Wang, H.; Kengne, R.; Kengne, L.K.; Njitacke, Z.T.; Fozin, T.F. Symmetry-breaking, amplitude control and constant Lyapunov exponent based on single parameter snap flows. Eur. Phys. J. Spec. Top. 2022, 230, 1887–1903. [Google Scholar] [CrossRef]
- Erkan, U.; Toktas, A.; Lai, Q. Design of two dimensional hyperchaotic system through optimization benchmark function. Chaos Solitons Fractals 2023, 167, 113032. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Yang, F.; Mou, J.; Ma, C.; Cao, Y. Dynamic analysis of an improper fractional-order laser chaotic system and its image encryption application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]
- Vignesh, D.; Banerjee, S. Reversible chemical reactions model with fractional difference operator: Dynamical analysis and synchronization. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033126. [Google Scholar] [CrossRef] [PubMed]
- Pan, I.; Das, S.; Das, S. Multi-objective active control policy design for commensurate and incommensurate fractional order chaotic financial systems. Appl. Math. Model. 2015, 39, 500–514. [Google Scholar] [CrossRef]
- Wang, Y. Dynamic analysis and synchronization of conformable fractional-order chaotic systems. Eur. Phys. J. Plus 2018, 133, 481. [Google Scholar] [CrossRef]
- Gasri, A.; Ouannas, A.; Khennaoui, A.A.; Bendoukha, S.; Pham, V.T. On the dynamics and control of fractional chaotic maps with sine terms. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 589–601. [Google Scholar] [CrossRef]
- Hadjabi, F.; Ouannas, A.; Shawagfeh, N.; Khennaoui, A.A.; Grassi, G.A. On two-dimensional fractional chaotic maps with symmetries. Symmetry 2020, 12, 756. [Google Scholar] [CrossRef]
- Liu, X.; Tang, D.; Hong, L. A fractional-order sinusoidal discrete map. Entropy 2022, 24, 320. [Google Scholar] [CrossRef] [PubMed]
- Gasri, A.; Khennaoui, A.A.; Ouannas, A.; Grassi, G.; Iatropoulos, A.; Moysis, L.; Volos, C. A new fractional-order map with infinite number of equilibria and its encryption application. Complexity 2022, 1, 3592422. [Google Scholar] [CrossRef]
- Danca, M.F. Symmetry-breaking and bifurcation diagrams of fractional-order maps. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106760. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 62. [Google Scholar] [CrossRef]
- Čermák, J.; Győri, I.; Nechvátal, L. On explicit stability conditions for a linear fractional difference system. Electron. J. Qual. Theory Differ. Equ. [Electron. Only] 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G. Novel convenient conditions for the stability of nonlinear incommensurate fractional-order difference systems. Alex. Eng. J. 2022, 61, 1655–1663. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Wen, H. Exploiting newly designed fractional-order 3D Lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Kong, S.; Li, C.; Jiang, H.; Lai, Q.; Jiang, X. Symmetric image encryption algorithm based on a new product trigonometric chaotic map. Symmetry 2022, 14, 373. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Shen, E.-h.; Cai, Z.-j.; Gu, F.-j. Mathematical foundation of a new complexity measure. Appl. Math. Mech. 2005, 26, 1188–1196. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammad, M.A.; Diabi, L.; Dababneh, A.; Zraiqat, A.; Momani, S.; Ouannas, A.; Hioual, A. On New Symmetric Fractional Discrete-Time Systems: Chaos, Complexity, and Control. Symmetry 2024, 16, 840. https://doi.org/10.3390/sym16070840
Hammad MA, Diabi L, Dababneh A, Zraiqat A, Momani S, Ouannas A, Hioual A. On New Symmetric Fractional Discrete-Time Systems: Chaos, Complexity, and Control. Symmetry. 2024; 16(7):840. https://doi.org/10.3390/sym16070840
Chicago/Turabian StyleHammad, Ma’mon Abu, Louiza Diabi, Amer Dababneh, Amjed Zraiqat, Shaher Momani, Adel Ouannas, and Amel Hioual. 2024. "On New Symmetric Fractional Discrete-Time Systems: Chaos, Complexity, and Control" Symmetry 16, no. 7: 840. https://doi.org/10.3390/sym16070840