Study on the Effect of Burial Depth on Selection of Optimal Intensity Measures for Advanced Fragility Analysis of Horseshoe-Shaped Tunnels in Soft Soil
Abstract
:1. Introduction
2. Theory and Formula of Seismic Fragility Analysis
2.1. Basic Theory
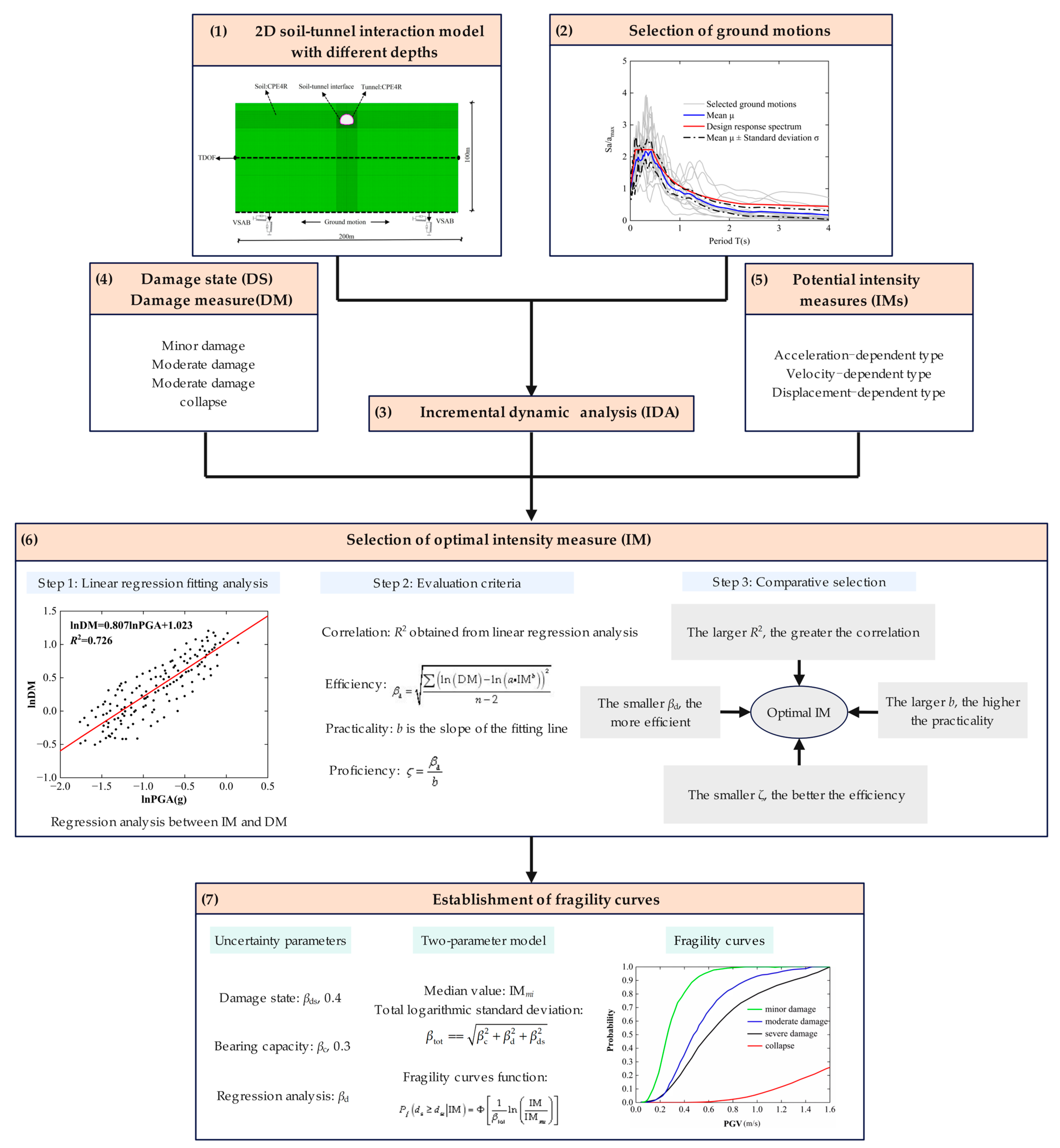
2.2. Main Process of Seismic Fragility Analysis
- (1)
- The 2D finite element model of the soil–tunnel interaction system is built.
- (2)
- The appropriate ground motions are selected according to the design response spectrum.
- (3)
- The 2D soil–tunnel numerical models are used to conduct IDA by adjusting PGA, and the evolution of damage with IM is obtained.
- (4)
- The definition of the damage state (DS) is to quantitatively characterize its DM after being subjected to earthquakes by comparing the actual bending moment M inside the tunnel structure with the design bending moment safety threshold MRD.
- (5)
- The commonly used potential IMs are selected.
- (6)
- The optimal seismic IMs are selected based on the results obtained from IDA and four evaluation criteria.
- (7)
- Based on DM and the selected optimal IM, the fragility curves are established by using a two-parameter lognormal distribution model.
2.3. Damage States and Damage Measures
3. Numerical Modeling
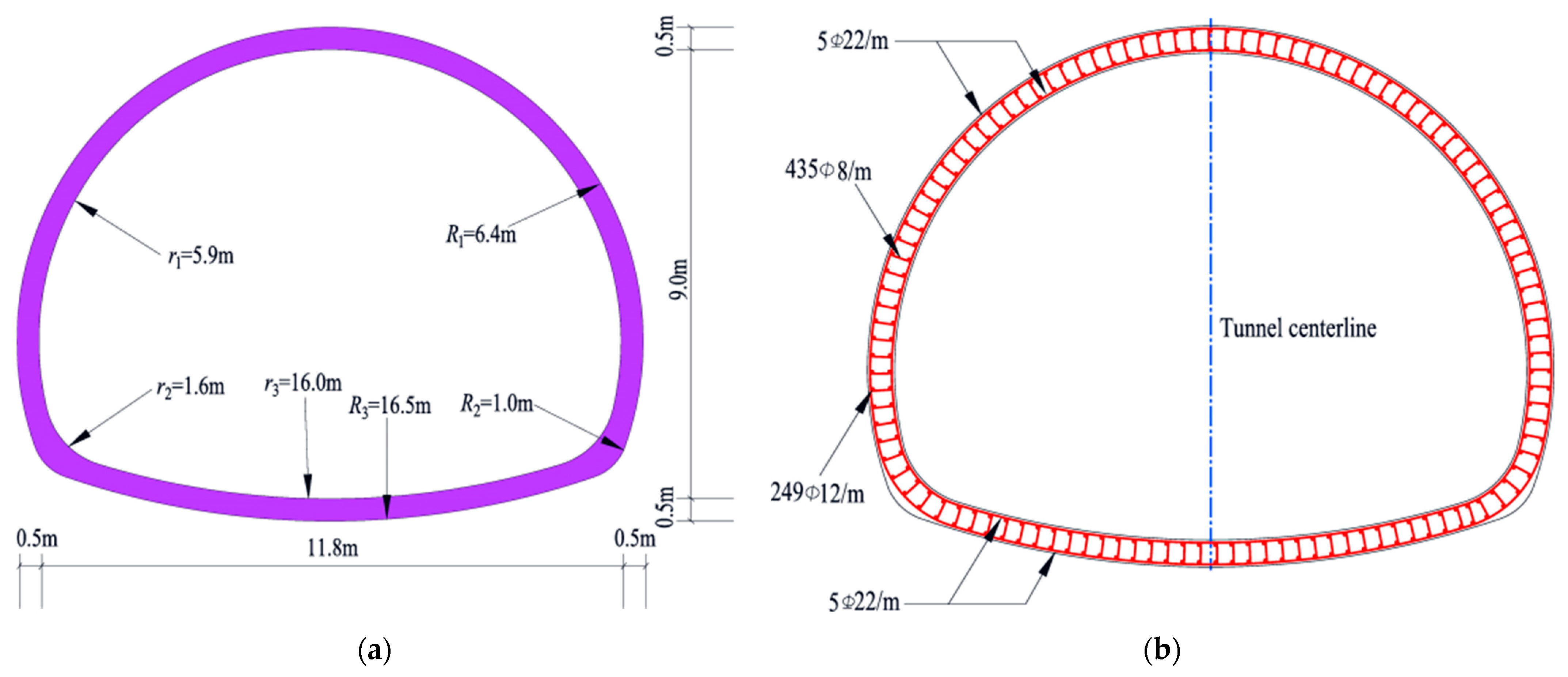
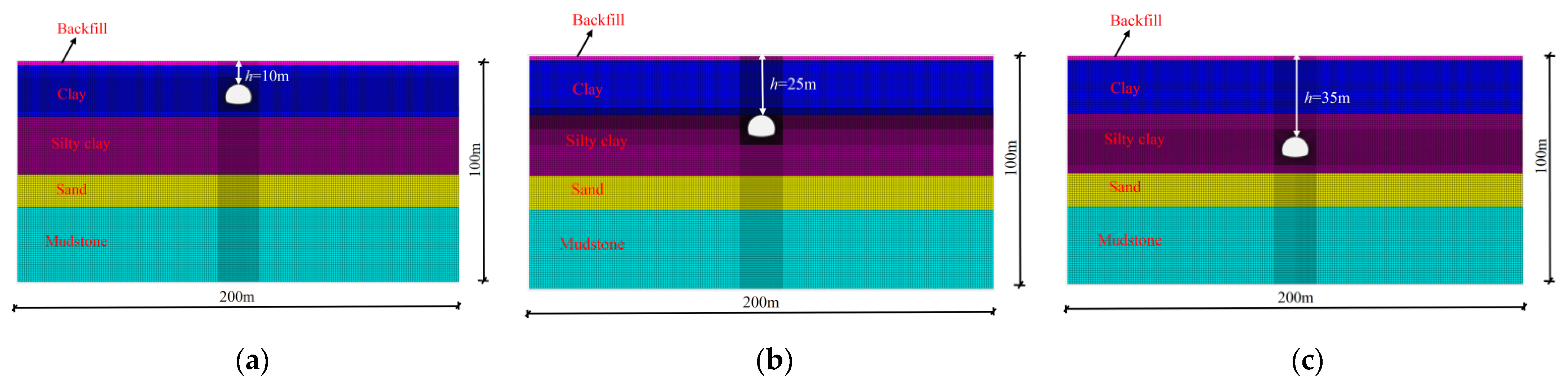
3.1. Description of Horseshoe-Shaped Tunnel
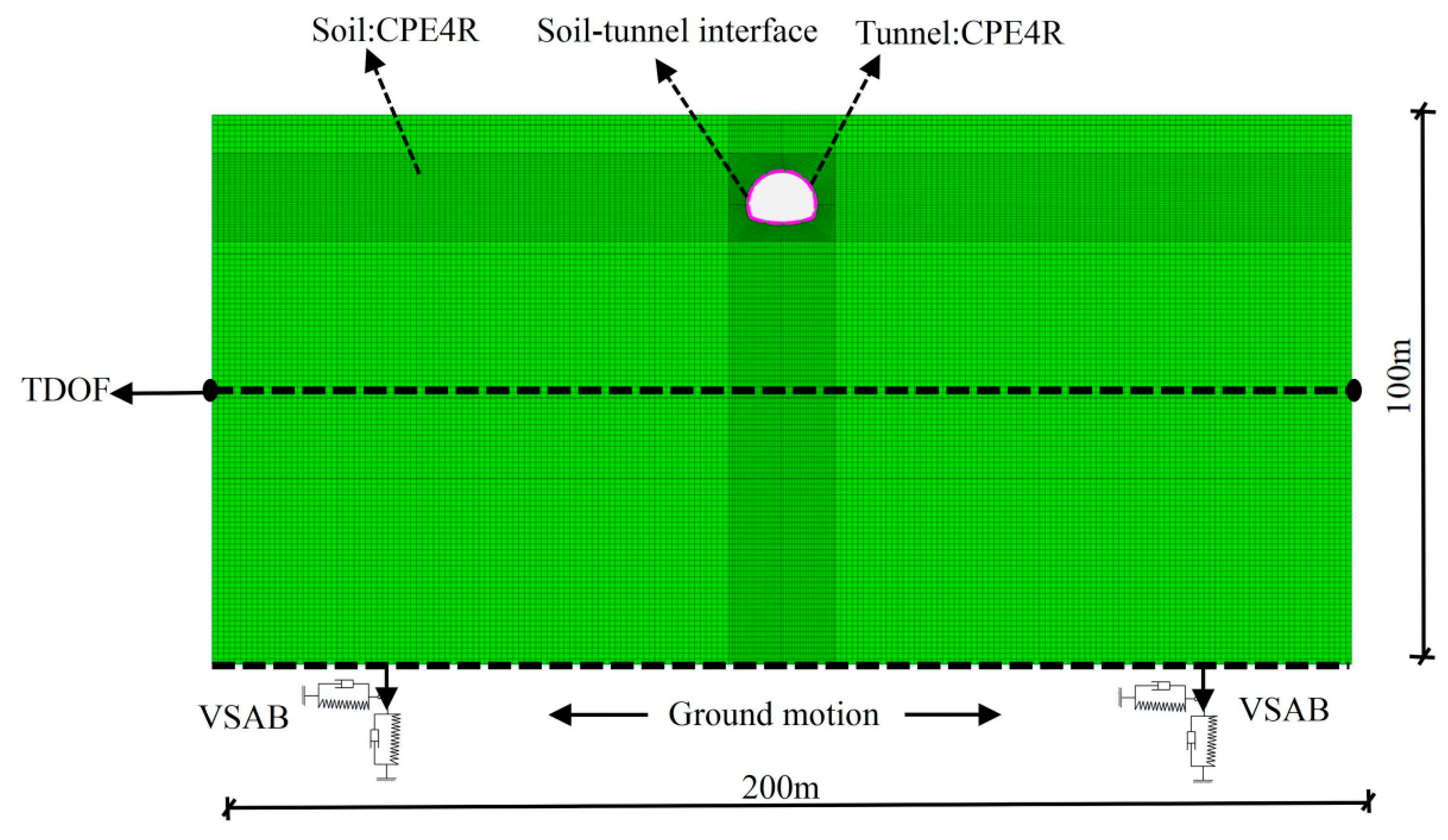
3.2. Numerical Simulation of Geometric Model
3.3. Boundary and Contact Conditions
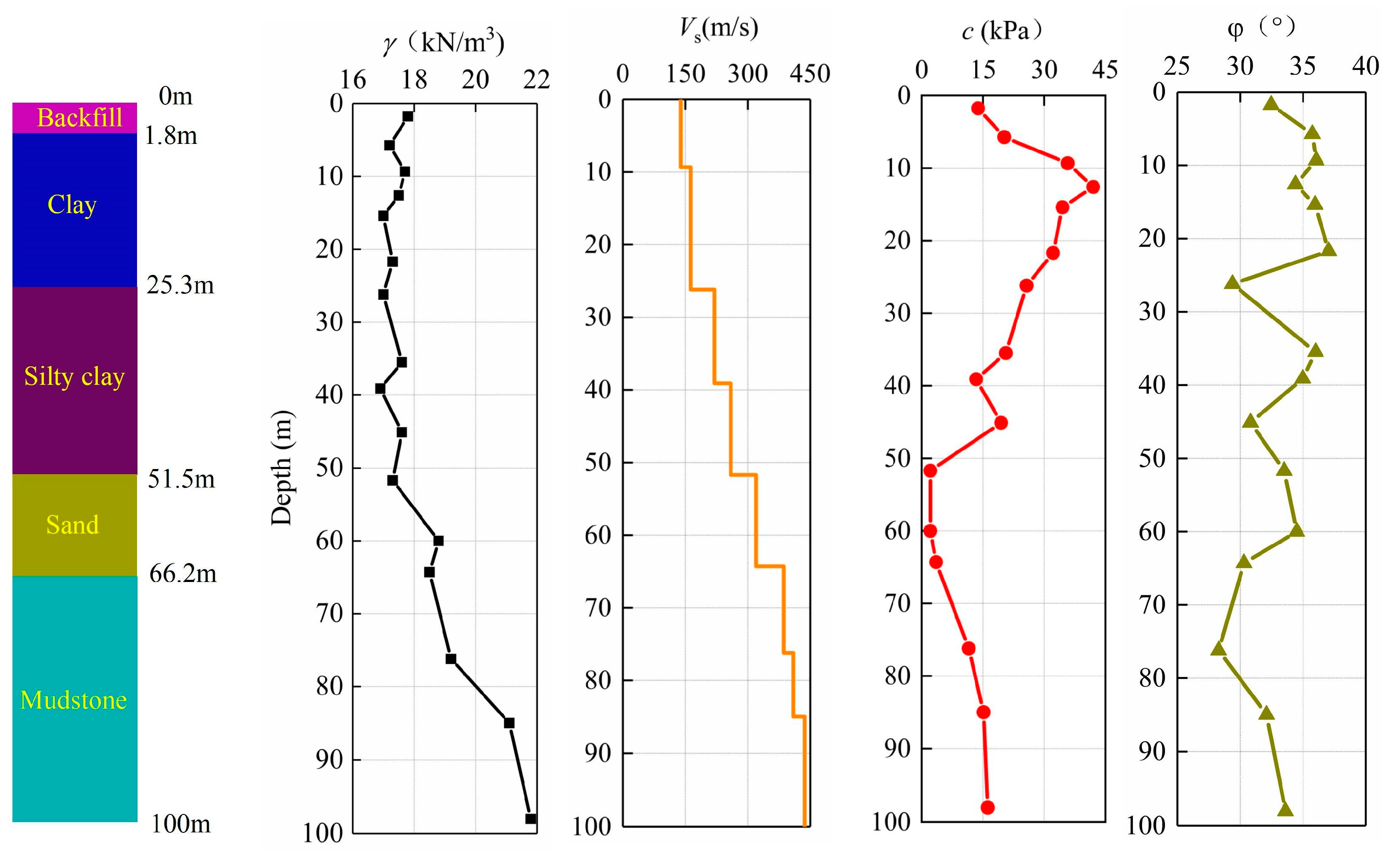
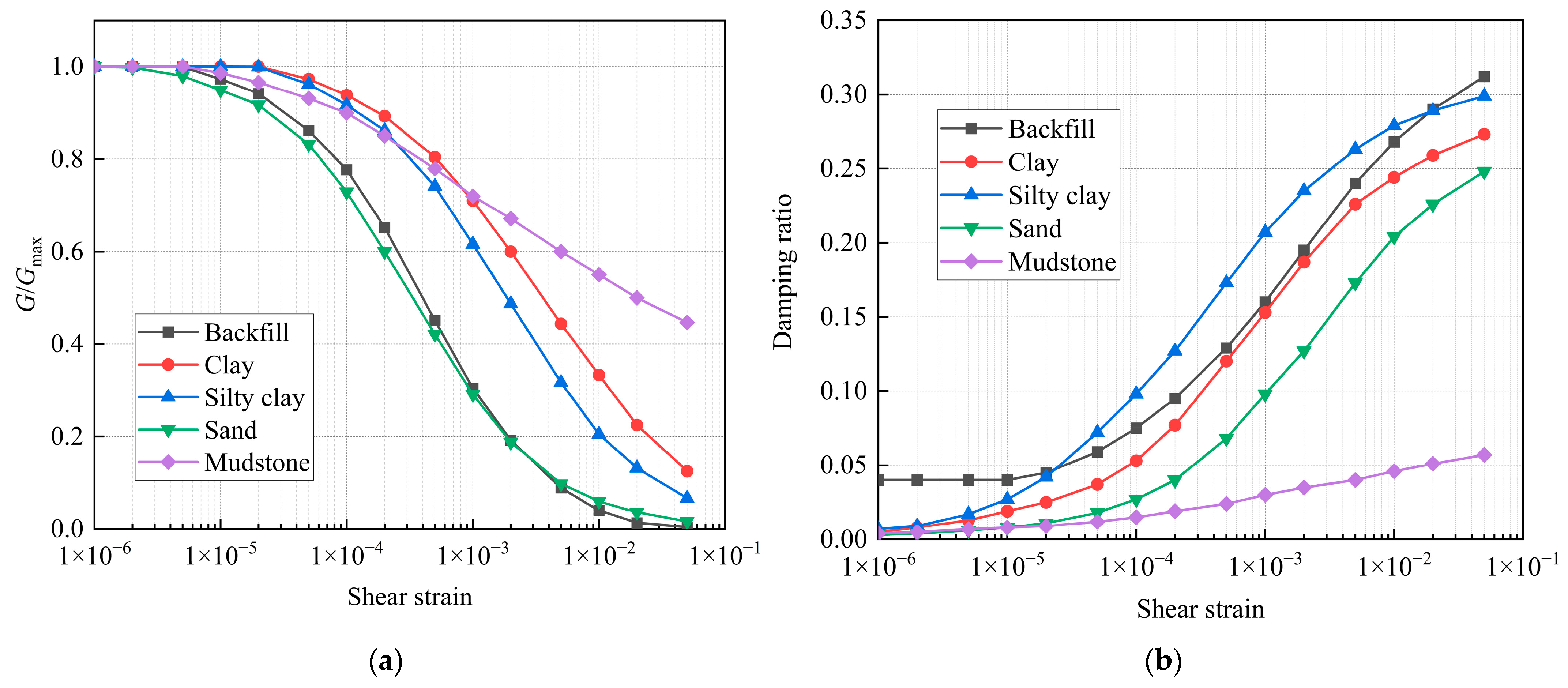
3.4. Material Properties
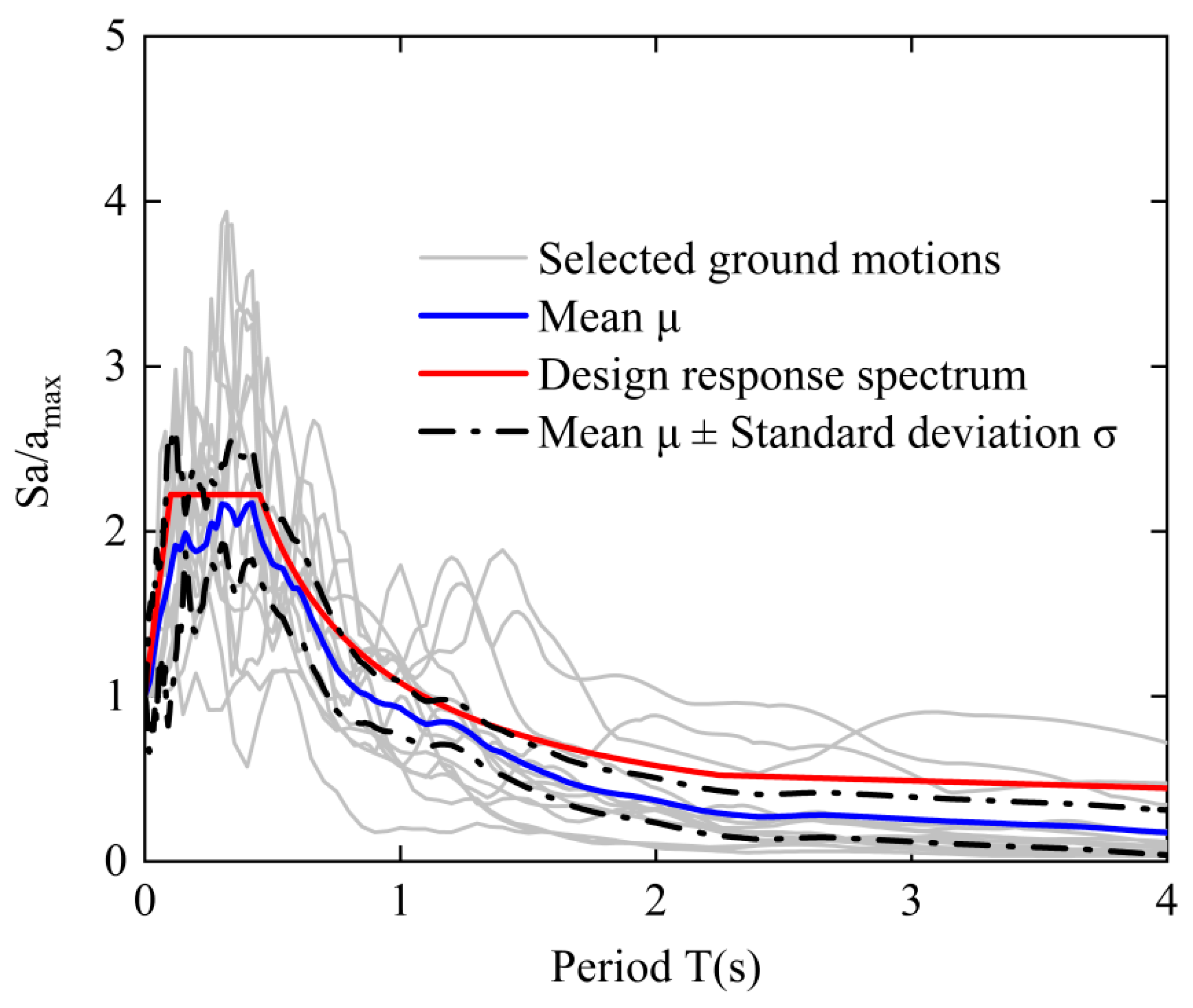
3.5. Selection of Ground Motions
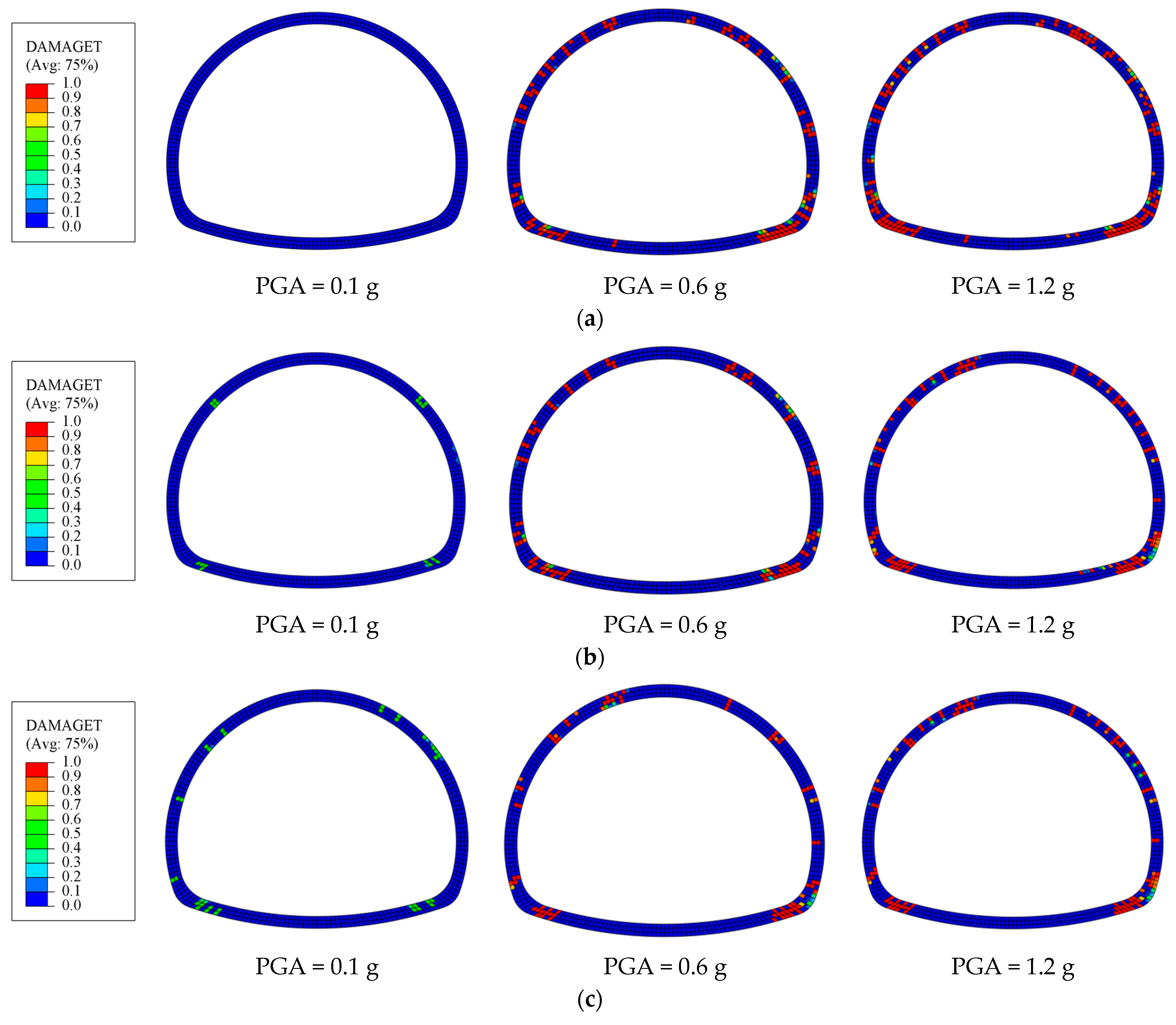
3.6. Structural Damage Evolution Analysis
4. Selection of Optimal Intensity Measures
4.1. Potential Intensity Measures
4.2. Correlation Analysis
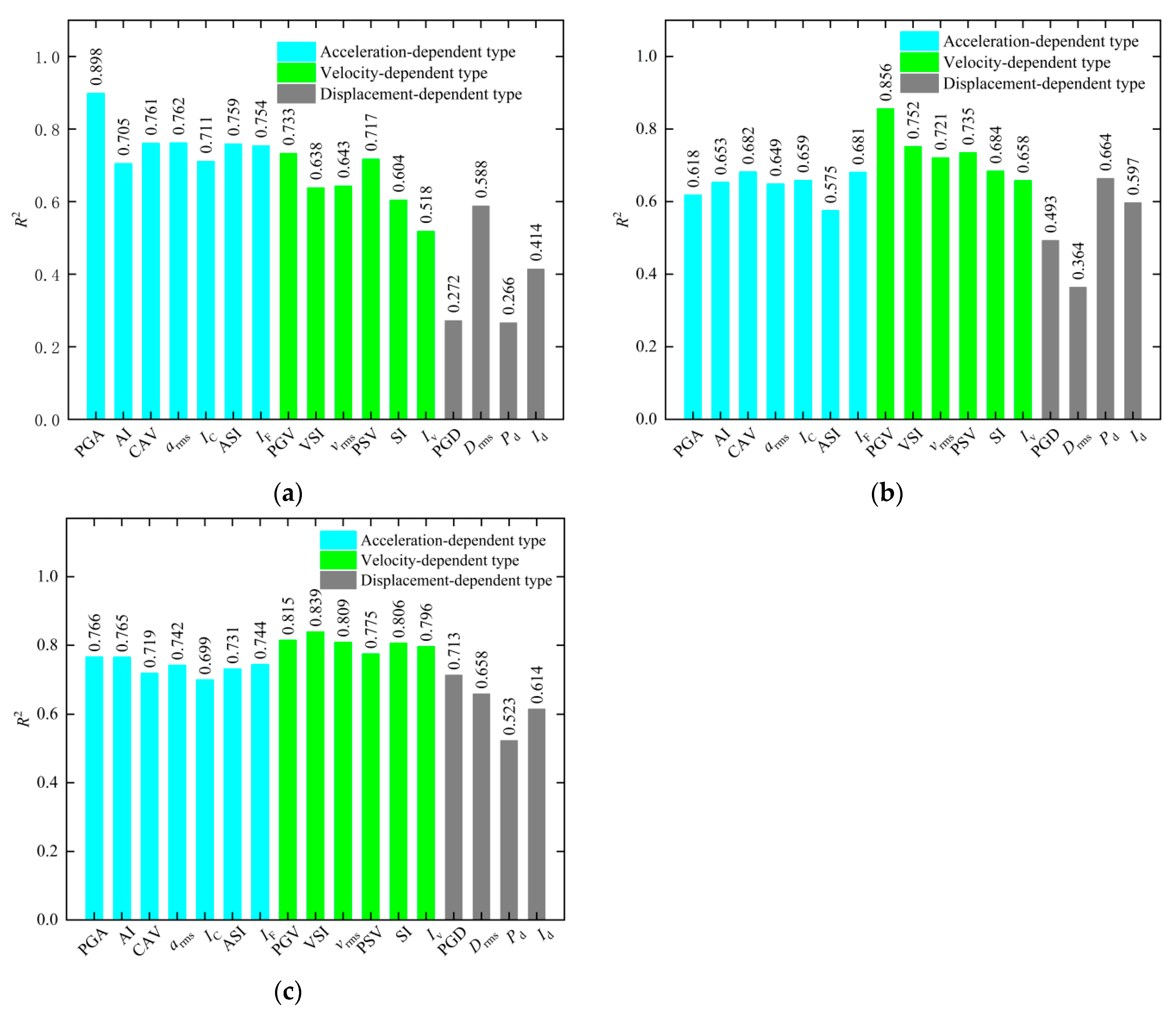
4.3. Efficiency Analysis
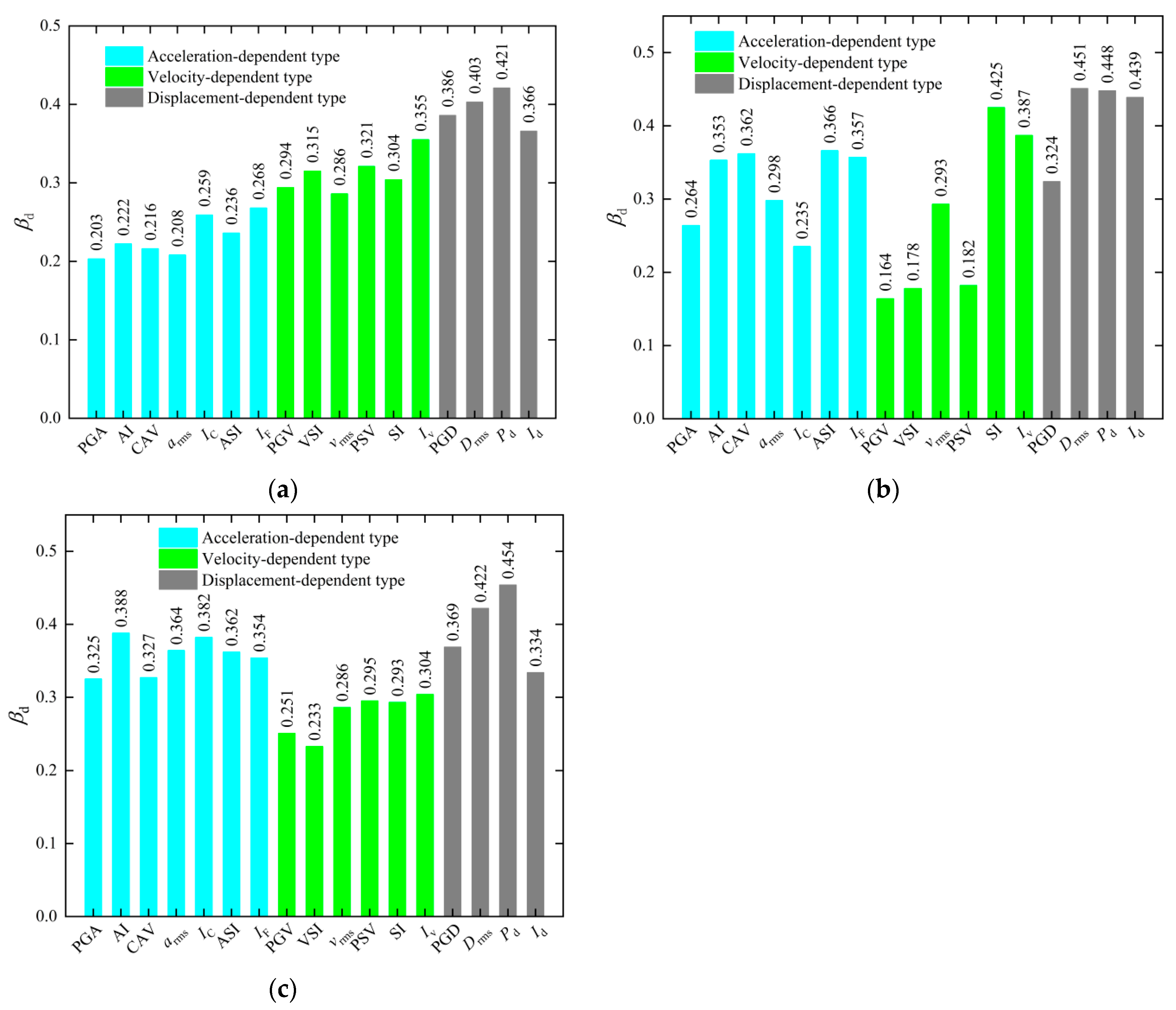
4.4. Practicality Analysis
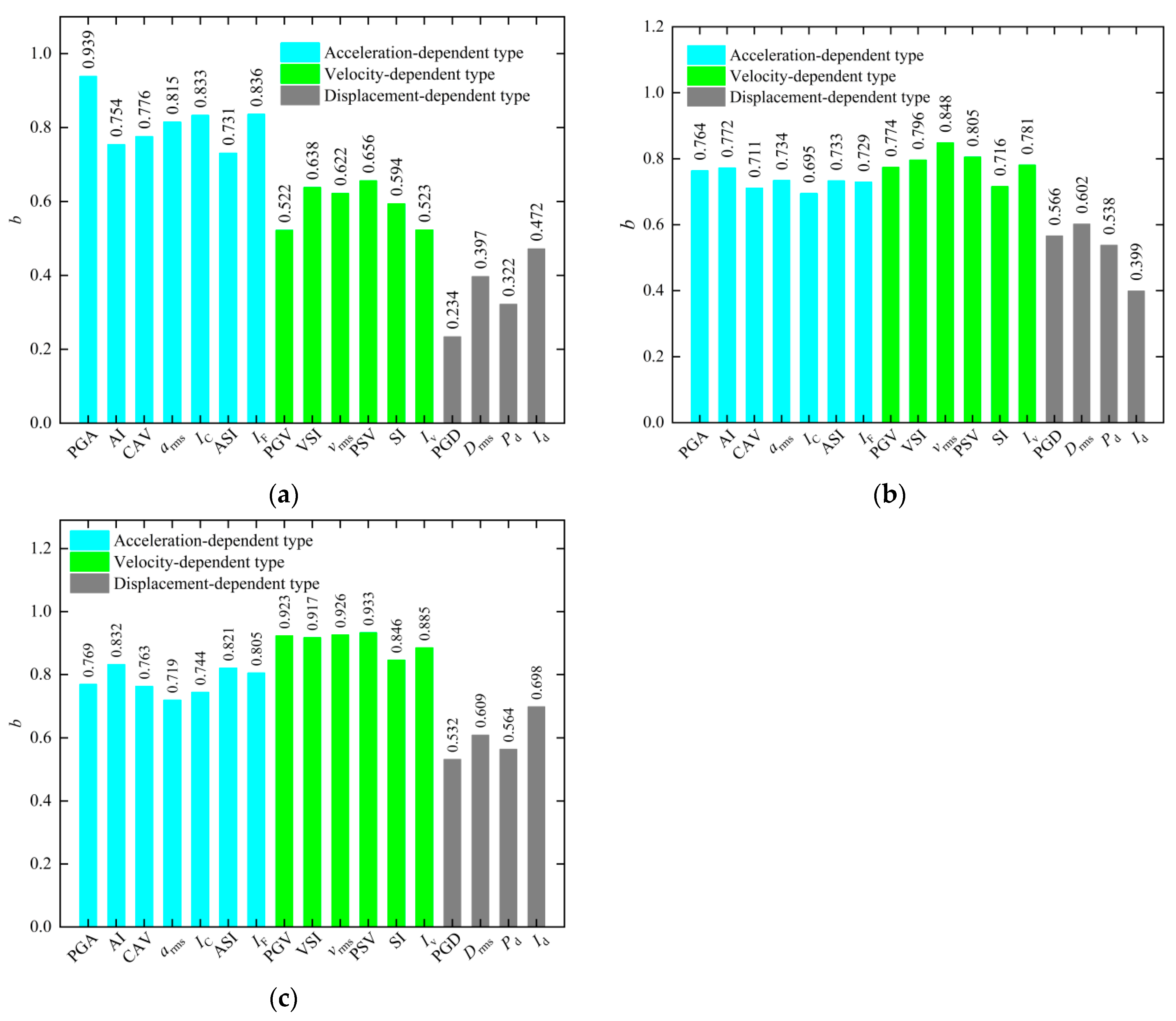
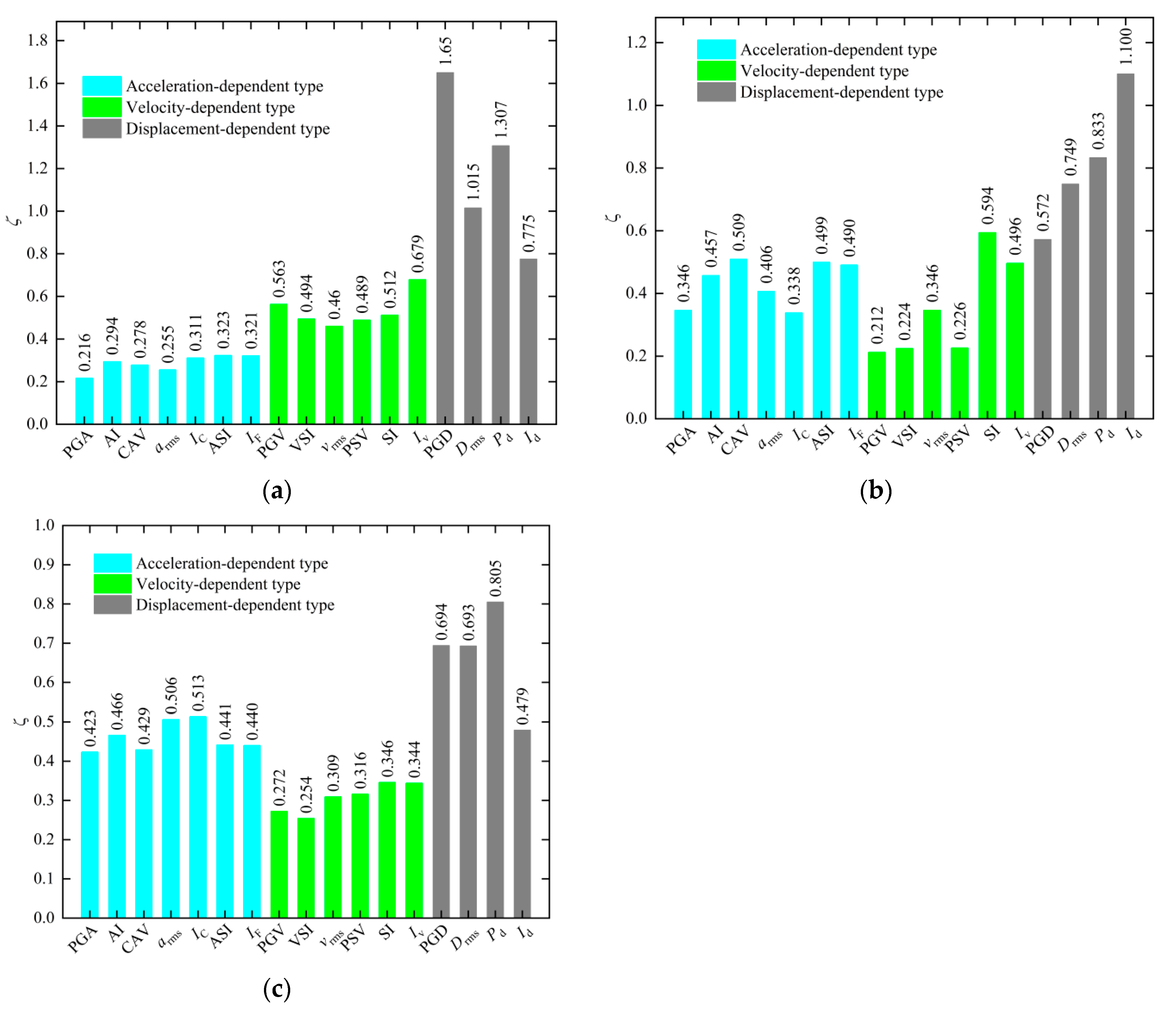
4.5. Proficiency Analysis
4.6. Determining the Optimal IM
5. Establishment of Fragility Curves
6. Conclusions
- (1)
- The seismic damage of horseshoe-shaped tunnels is mainly tensile damage, while the compression damage is not obvious. The extent of compression damage sustained by the tunnel intensifies as the burial depth increases, primarily being influenced by the depth of the overlying soil. As the burial depth increases, the tensile damage of the tunnel initially exhibits an upward trend, subsequently followed by a decrease during the earthquake process.
- (2)
- In the case of shallow tunnels, the optimal IM is PGA, with arms and CAV occupying subsequent positions. For the medium-deep tunnel, PGV is the optimal IM. Following closely are VSI and PSV. And under the conditions of the deep tunnel, the optimal IM is VSI, followed by PGV and vrms.
- (3)
- The acceleration-dependent-type IMs are particularly adept at forecasting the seismic response of the shallow tunnel, while for the medium-deep tunnel and deep tunnel, velocity-dependent-type IMs have more advantages in predicting the seismic response.
- (4)
- At a constant seismic intensity, the likelihood of extensive damage is the lowest, followed by moderate damage, and the likelihood of minor damage is the highest. The fragility curves derived from our study provide valuable insights for evaluating the seismic risk associated with horseshoe-shaped tunnels constructed in soft soil.
- (5)
- The findings can be used in future studies as a basis for fragility analysis of tunnels affected by burial depth conditions. Future research can consider additional geological factors, especially the presence of clay layers at the underside of the tunnels, toward more comprehensive probabilistic seismic fragility analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, H.; Wang, S.; Shen, W.; Zhang, W. The influence of pipe-jacking tunneling on deformation of existing tunnels in soft soils and the effectiveness of protection measures. Transp. Geotech. 2023, 42, 101061. [Google Scholar] [CrossRef]
- Jin, H.; Yuan, D.; Jin, D.; Wu, J.; Wang, X.; Han, B.; Mao, J. Ground deformation induced by shield tunneling posture in soft soil. Tunn. Undergr. Space Technol. 2023, 139, 105227. [Google Scholar] [CrossRef]
- Mohsenian, V.; Hajirasouliha, I.; Mariani, S.; Nikkhoo, A. Seismic reliability assessment of RC tunnel-form structures with geometric irregularities using a combined system approach. Soil Dyn. Earthq. Eng. 2020, 139, 106356. [Google Scholar] [CrossRef]
- Feng, S.; Lei, H.A. Settlement prediction model considering tidal loading and traffic loading of soft soil subgrade. Comput. Geotech. 2022, 144, 104639. [Google Scholar] [CrossRef]
- Lei, H.; Li, B.; Lu, H.; Ren, Q. Dynamic deformation behavior and cyclic degradation of ultrasoft soil under cyclic loading. J. Mater. Civ. Eng. 2016, 28, 04016135. [Google Scholar] [CrossRef]
- Sun, Q.; Dias, D.; e Sousa, L.R. Soft soil layer-tunnel interaction under seismic loading. Tunn. Undergr. Space Technol. 2020, 98, 103329. [Google Scholar] [CrossRef]
- Hao, Y.H.; Azzam, R. The plastic zones and displacements around underground openings in rock masses containing a fault. Tunn. Undergr. Space Technol. 2005, 20, 49–61. [Google Scholar] [CrossRef]
- Azadiab, M. The seismic behavior of urban tunnels in soft saturated soils. Procedia Eng. 2011, 14, 3069–3075. [Google Scholar] [CrossRef]
- Iida, H.; Hiroto, T.; Yoshida, N.; Iwafuji, M. Damage to Daikai subway station. Soils Found. 1996, 36, 283–300. [Google Scholar] [CrossRef]
- Lu, C.C.; Hwang, J.H. Damage analysis of the new Sanyi railway tunnel in the 1999 Chi-Chi earthquake: Necessity of second lining reinforcement. Tunn. Undergr. Space Technol. 2018, 73, 48–59. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, B.; Yang, X.; Tao, S. Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 2014, 180, 85–98. [Google Scholar] [CrossRef]
- Tothong, P.; Luco, N. Probabilistic seismic demand analysis using advanced ground motion intensity measures. Earthq. Eng. Struct. Dyn. 2007, 36, 1837–1860. [Google Scholar] [CrossRef]
- Giovenale, P.; Cornell, C.A.; Esteva, L. Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses. Earthq. Eng. Struct. Dyn. 2004, 33, 951–979. [Google Scholar] [CrossRef]
- Jiang, J.W.; Xu, C.S.; Du, X.L.; Chen, G.X.; Xu, Z.G. Optimal Index of Earthquake Intensity Measures for Seismic Design of Underground Frame Structure of Shallow-Buried Subway Station. Chin. J. Geotech. Eng. 2023, 45, 318–326. (In Chinese) [Google Scholar]
- De Biasio, M.; Grange, S.; Dufour, F.; Allain, F.; Petre-Lazar, I. Intensity measures for probabilistic assessment of non-structural components acceleration demand. Earthq. Eng. Struct. Dyn. 2015, 44, 2261–2280. [Google Scholar] [CrossRef]
- Finn, W.D.L. State-of-the-art of geotechnical earthquake engineering practice. Soil Dyn. Earthq. Eng. 2000, 20, 1–15. [Google Scholar] [CrossRef]
- Hao, M.; Xie, L.; Li, W. Study on physical measure of seismic intensity based on damage to masonry structures. Earthq. Eng. Eng. Vib. 2007, 27, 27. [Google Scholar]
- Shome, N.; Cornell, C.A.; Bazzurro, P.; Carballo, J.E. Earthquakes, records, and nonlinear responses. Earthq. Spectra 1998, 14, 469–500. [Google Scholar] [CrossRef]
- Dong, Z.F.; Cao, X.W.; Zeng, F.K.; Zhu, H.Y.; Liu, G.Z. Research on Reasonable Ground Motion Intensity Measure in Lateral Seismic of Tunnel. J. Basic Sci. Eng. 2022, 30, 776–789. (In Chinese) [Google Scholar]
- Lin, L.; Naumoski, N.; Saatcioglu, M.; Foo, S. Improved intensity measures for probabilistic seismic demand analysis. Part 1: Development of improved intensity measures. Can. J. Civ. Eng. 2011, 38, 79–88. [Google Scholar] [CrossRef]
- Zhang, C.M.; Zhong, Z.L.; Zhen, L.B.; Shen, Y.Y.; Zhao, M. Seismic intensity measures for the damage evaluation of circular tunnels. Eng. Mech. 2021, 38, 100–108. (In Chinese) [Google Scholar]
- Luco, N.; Cornell, C.A. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq. Spectra 2007, 23, 357–392. [Google Scholar] [CrossRef]
- Mackie, K.; Stojadinović, B. Probabilistic seismic demand model for California highway bridges. J. Bridge Eng. 2001, 6, 468–481. [Google Scholar] [CrossRef]
- Khosravikia, F.; Clayton, P. Updated evaluation metrics for optimal intensity measure selection in probabilistic seismic demand models. Eng. Struct. 2020, 202, 109899. [Google Scholar] [CrossRef]
- Heshmati, M.; Jahangiri, V. Appropriate intensity measures for probabilistic seismic demand estimation of steel diagrid systems. Eng. Struct. 2021, 249, 113260. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Park, D.; Shamsher, S.; Nguyen, V.Q.; Lee, T.H. Seismic vulnerability assessment of rectangular cut-and-cover subway tunnels. Tunn. Undergr. Space Technol. 2019, 86, 247–261. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, J. Correlation between ground motion parameters and lining damage indices for mountain tunnels. Nat. Hazards 2013, 65, 1683–1702. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, G.; Xue, B.; Kou, L.; Hu, L.; Liu, W. The analysis of the optimal scalar and vector intensity measurements for seismic performance assessment of deep-buried hydraulic arched tunnels. Undergr. Space 2023, 9, 218–233. [Google Scholar] [CrossRef]
- Sun, B.; Deng, M.; Zhang, S.; Wang, C.; Li, Y.; Song, R. Application of the endurance time methodology on seismic analysis and performance assessment of hydraulic arched tunnels. Tunn. Undergr. Space Technol. 2021, 115, 104022. [Google Scholar] [CrossRef]
- Huang, Z.K.; Argyroudis, S.; Pitilakis, K.; Zhang, D.M.; Tsinidis, G. Fragility assessment of tunnels in soft soils using artificial neural networks. Undergr. Space 2022, 7, 242–253. [Google Scholar] [CrossRef]
- Huang, Z.K.; Pitilakis, K.; Argyroudis, S.; Tsinidis, G.; Zhang, D.M. Selection of optimal intensity measures for fragility assessment of circular tunnels in soft soil deposits. Soil Dyn. Earthq. Eng. 2021, 145, 106724. [Google Scholar] [CrossRef]
- Zhong, Z.; Shen, Y.; Zhao, M.; Li, L.Y.; Du, X. Seismic performance evaluation of two-story and three-span subway station in different engineering sites. J. Earthq. Eng. 2022, 26, 7505–7535. [Google Scholar] [CrossRef]
- Zhuang, H.; Yang, J.; Chen, S.; Dong, Z.; Chen, G. Statistical numerical method for determining seismic performance and fragility of shallow-buried underground structure. Tunn. Undergr. Space Technol. 2021, 116, 104090. [Google Scholar] [CrossRef]
- Xu, Z.; Zhuang, H.; Xia, Z.; Yang, J.; Bu, X. Study on the effect of burial depth on seismic response and seismic intensity measure of underground structures. Soil Dyn. Earthq. Eng. 2023, 166, 107782. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S.P.G. Effect of depth on seismic response of circular tunnels. Can. Geoech. J. 2011, 48, 117–127. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Z.; Chen, H.; Ren, Y. Seismic fragility analysis of tunnels with different buried depths in a soft soil. Sustainability 2020, 12, 892. [Google Scholar] [CrossRef]
- Chian, S.C.; Madabhushi, S.P.G. Effect of buried depth and diameter on uplift of underground structures in liquefied soils. Soil Dyn. Earthq. Eng. 2012, 41, 181–190. [Google Scholar] [CrossRef]
- Cilingir, U.; Madabhushi, S.G. Effect of depth on the seismic response of square tunnels. Soils Found. 2011, 51, 449–457. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Pitilakis, K.D. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Tsinidis, G.; de Silva, F.; Anastasopoulos, I.; Bilotta, E.; Bobet, A.; Hashash, Y.M.; Fuentes, R. Seismic behaviour of tunnels: From experiments to analysis. Tunn. Undergr. Space Technol. 2020, 99, 103334. [Google Scholar] [CrossRef]
- Jiang, J.; Tao, R.; El Naggar, M.H.; Liu, H.; Du, X. Seismic performance and vulnerability analysis for bifurcated tunnels in soft soil. Comput. Geotech. 2024, 167, 106065. [Google Scholar] [CrossRef]
- Miao, Y.; Zhong, Y.; Ruan, B.; Cheng, K.; Wang, G. Seismic response of a subway station in soft soil considering the structure-soil-structure interaction. Tunn. Undergr. Space Technol. 2020, 106, 103629. [Google Scholar] [CrossRef]
- Pham, V.V.; Do, N.A.; Dias, D. Sub-rectangular tunnel behavior under seismic loading. Appl. Sci. 2021, 11, 9909. [Google Scholar] [CrossRef]
- Huang, Z.K.; Pitilakis, K.; Tsinidis, G.; Argyroudis, S.; Zhang, D.M. Seismic vulnerability of circular tunnels in soft soil deposits: The case of Shanghai metropolitan system. Tunn. Undergr. Space Technol. 2020, 98, 103341. [Google Scholar] [CrossRef]
- Zhong, Z.; Feng, L.; Shen, J.; Du, X. Seismic fragility analysis of subway station structure subjected to sequence-type ground motions. Tunn. Undergr. Space Technol. 2024, 144, 105570. [Google Scholar] [CrossRef]
- Xu, M.; Cui, C.; Zhao, J.; Xu, C.; Zhang, P.; Su, J. Fuzzy seismic fragility analysis of underground structures considering multiple failure criteria. Tunn. Undergr. Space Technol. 2024, 145, 105614. [Google Scholar] [CrossRef]
- Huang, Z.; Cheng, Y.; Zhang, D.; Yan, D.; Shen, Y. Seismic fragility and resilience assessment of shallowly buried large-section underground civil defense structure in soft soils: Framework and application. Tunn. Undergr. Space Technol. 2024, 146, 105640. [Google Scholar] [CrossRef]
- Stefanidou, S.P.; Kappos, A.J. Methodology for the development of bridge-specific fragility curves. Earthq. Eng. Struct. Dyn. 2017, 46, 73–93. [Google Scholar] [CrossRef]
- Du, X.L.; Zhao, M. Stability and identification for rational approximation of frequency response function of unbounded soil. Earthq. Eng. Struct. Dyn. 2010, 39, 165–186. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil. Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Tsinidis, G.; Pitilakis, K.; Madabhushi, G.; Heron, C. Dynamic response of flexible square tunnels: Centrifuge testing and validation of existing design methodologies. Geotechnique 2015, 65, 401–417. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Xu, C.S.; Du, X.L.; Li, Z. Earthquake input for finite element analysis of soil-structure interaction on rigid bedrock. Tunn. Undergr. Space Technol. 2018, 79, 250–262. [Google Scholar] [CrossRef]
- Li, Z.Y.; Hu, Z.Q.; Lin, G.; Li, J.B. A scaled boundary finite element method procedure for arch dam-water-foundation rock interaction in complex layered half-space. Comput. Geotech. 2022, 141, 104524. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development. Code for Seismic Design of Buildings; China Architecture and Building Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Zi, H.; Ding, Z.; Ji, X.; Liu, Z.; Shi, C. Effect of voids on the seismic vulnerability of mountain tunnels. Soil Dyn. Earthq. Eng. 2021, 148, 106833. [Google Scholar] [CrossRef]






| Damage States | Explanation | Range of DM | Median DM |
|---|---|---|---|
| No damage | The tunnel structure and its ancillary facilities are in good condition, without any visible or known physical damage, dysfunction, or performance degradation. | M/MRD ≤ 1.0 | - |
| Minor damage | Slight cracks appear in the tunnel lining or walls but do not hinder traffic. | 1.0 < M/MRD ≤ 1.5 | 1.25 |
| Moderate damage | The tunnel lining or walls appears wider or longer cracks, but the overall function of the tunnel equipment is normal and can operate normally after repair. | 1.5 < M/MRD ≤ 2.5 | 2.00 |
| Extensive damage | The concrete cover of the tunnel spalls off, the rebar is visible, and the concrete lining or walls are deformed. | 2.5 < M/MRD ≤ 3.5 | 3.00 |
| Collapse | The lining or wall of the tunnel breaks, bends, or twists, losing the original shape and support capacity, and the structural function of the tunnel is completely lost. | M/MRD > 3.5 | - |
| Material | Elastic Modulus Ec (GPa) | Poisson’s Ratio vc | Density ρc (kg/m3) | Dilation Angle ψ (°) | Tensile Yield Stress ft (MPa) | Ultimate Compressive Stress fc (MPa) |
|---|---|---|---|---|---|---|
| C50 | 30.0 | 0.2 | 2450 | 30.25 | 2.01 | 22.83 |
| CompressiveStress(MPa) | 15.97 | 22.83 | 16.08 | 13.02 | 10.80 | 9.17 | 7.94 | 6.24 | 2.98 |
| Plastic Strain (%) | 0 | 0.070 | 0.243 | 0.328 | 0.411 | 0.491 | 0.570 | 0.725 | 1.479 |
| dc | 0 | 0.276 | 0.572 | 0.656 | 0.714 | 0.756 | 0.788 | 0.832 | 0.918 |
| Tensile Stress (MPa) | 2.01 | 1.74 | 1.52 | 1.02 | 0.36 | 0.23 | 0.09 | 0.06 | 0.01 |
| Plastic Strain (%) | 0 | 0.009 | 0.012 | 0.023 | 0.096 | 0.175 | 0.651 | 1.279 | 9.532 |
| dt | 0 | 0.371 | 0.455 | 0.647 | 0.888 | 0.934 | 0.978 | 0.988 | 0.998 |
| NO. | Event | Station | Year | Magnitude (MW) | Epicentral Distance (km) | PGA (g) |
|---|---|---|---|---|---|---|
| Eq.1 | Chuetsu-oki, Japan | Tokamachi Chitosecho | 2007 | 6.80 | 47.73 | 0.22 |
| Eq.2 | Imperial Valley-06 | Cerro Prieto | 1979 | 6.53 | 24.82 | 0.17 |
| Eq.3 | Iwate, Japan | Yuzawa Town | 2008 | 6.90 | 29.33 | 0.20 |
| Eq.4 | Parkfield-02, CA | Parkfield–Cholame 5W | 2004 | 6.00 | 13.76 | 0.23 |
| Eq.5 | Chi-Chi, Taiwan | TCU045 | 1999 | 7.62 | 28.95 | 0.36 |
| Eq.6 | Darfield, New Zealand | TPLC | 2010 | 7.00 | 34.80 | 0.24 |
| Eq.7 | Mammoth Lakes-01 | Long Valley Dam | 1980 | 6.06 | 12.65 | 0.27 |
| Eq.8 | Spitak, Armenia | Gukasian | 1988 | 6.77 | 36.19 | 0.15 |
| Eq.9 | Hector Mine | Amboy | 1999 | 7.13 | 47.97 | 0.18 |
| Eq.10 | Kocaeli, Turkey | Yarimca | 1999 | 7.51 | 5.06 | 0.35 |
| Eq.11 | Northridge-01 | Moorpark–Fire Sta | 1994 | 6.69 | 31.45 | 0.24 |
| Eq.12 | Big Bear-01 | Desert Hot Springs | 1992 | 6.46 | 40.46 | 0.23 |
| Eq.13 | San Fernando | Old Ridge Route | 1971 | 6.61 | 25.36 | 0.29 |
| Eq.14 | Coalinga-05 | Pleasant Valley P.P.–FF | 1983 | 5.77 | 16.17 | 0.32 |
| Eq.15 | Niigata, Japan | NIG023 | 2004 | 6.63 | 36.47 | 0.39 |
| NO. | Name | Type | Definition |
|---|---|---|---|
| 1 | Peak ground acceleration | Acceleration-dependent type | |
| 2 | Arias intensity | ||
| 3 | Cumulative absolute velocity | ||
| 4 | Acceleration root mean square | ||
| 5 | Characteristic intensity | ||
| 6 | Acceleration spectrum intensity | ||
| 7 | Faifar intensity | ||
| 8 | Peak ground velocity | Velocity-dependent type | |
| 9 | Velocity spectrum intensity | ||
| 10 | Velocity root mean square | ||
| 11 | Peak spectrum velocity | ||
| 12 | Housner velocity intensity | ||
| 13 | Compound velocity | ||
| 14 | Peak ground displacement | Displacement-dependent type | |
| 15 | Displacement root mean square | ||
| 16 | Housner displacement intensity | ||
| 17 | Compound displacement |
| Tunnel Type | IM (Unit) | Minor Damage | Moderate Damage | Extensive Damage |
|---|---|---|---|---|
| Shallow tunnel | PGA (g) | 0.516 | 1.184 | 1.433 |
| Medium-deep tunnel | PGV (m/s) | 0.601 | 1.217 | 1.925 |
| Deep tunnel | VSI (m) | 0.948 | 1.785 | 2.616 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, T.; Zhang, T.; Zhou, S.; Zhang, J.; Zhang, Y.; Li, W. Study on the Effect of Burial Depth on Selection of Optimal Intensity Measures for Advanced Fragility Analysis of Horseshoe-Shaped Tunnels in Soft Soil. Symmetry 2024, 16, 859. https://doi.org/10.3390/sym16070859
Du T, Zhang T, Zhou S, Zhang J, Zhang Y, Li W. Study on the Effect of Burial Depth on Selection of Optimal Intensity Measures for Advanced Fragility Analysis of Horseshoe-Shaped Tunnels in Soft Soil. Symmetry. 2024; 16(7):859. https://doi.org/10.3390/sym16070859
Chicago/Turabian StyleDu, Tao, Tongwei Zhang, Shudong Zhou, Jinghan Zhang, Yi Zhang, and Weijia Li. 2024. "Study on the Effect of Burial Depth on Selection of Optimal Intensity Measures for Advanced Fragility Analysis of Horseshoe-Shaped Tunnels in Soft Soil" Symmetry 16, no. 7: 859. https://doi.org/10.3390/sym16070859





