Analyzing the Approximate Error and Applicable Condition of the Fractional Reduced Differential Transform Method
Abstract
:1. Introduction
2. Definitions and Some Properties of Fractional Calculus
3. Fractional Reduced Differential Transform Method
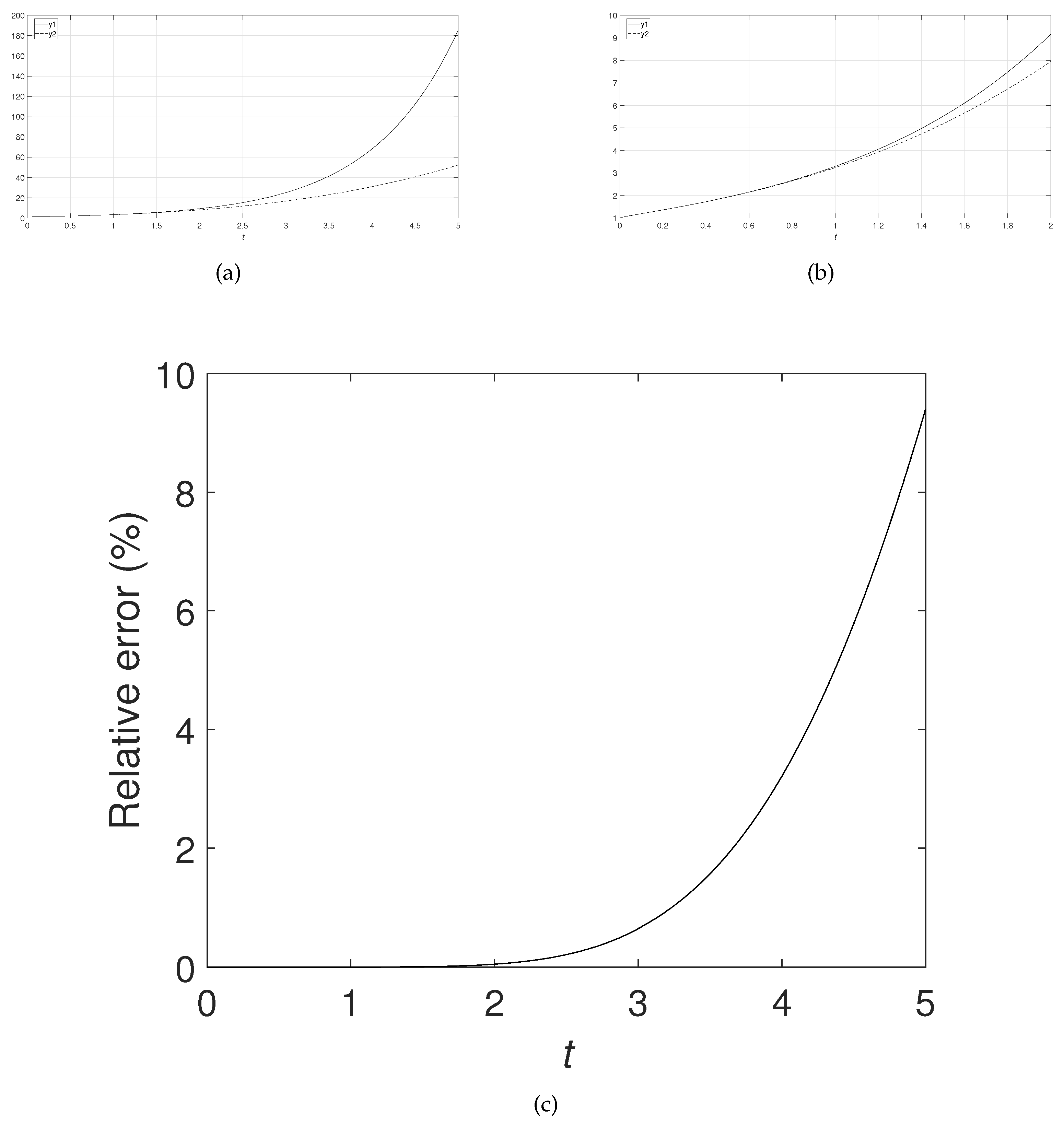
4. Analyzing the Approximate Error and Applicable Condition
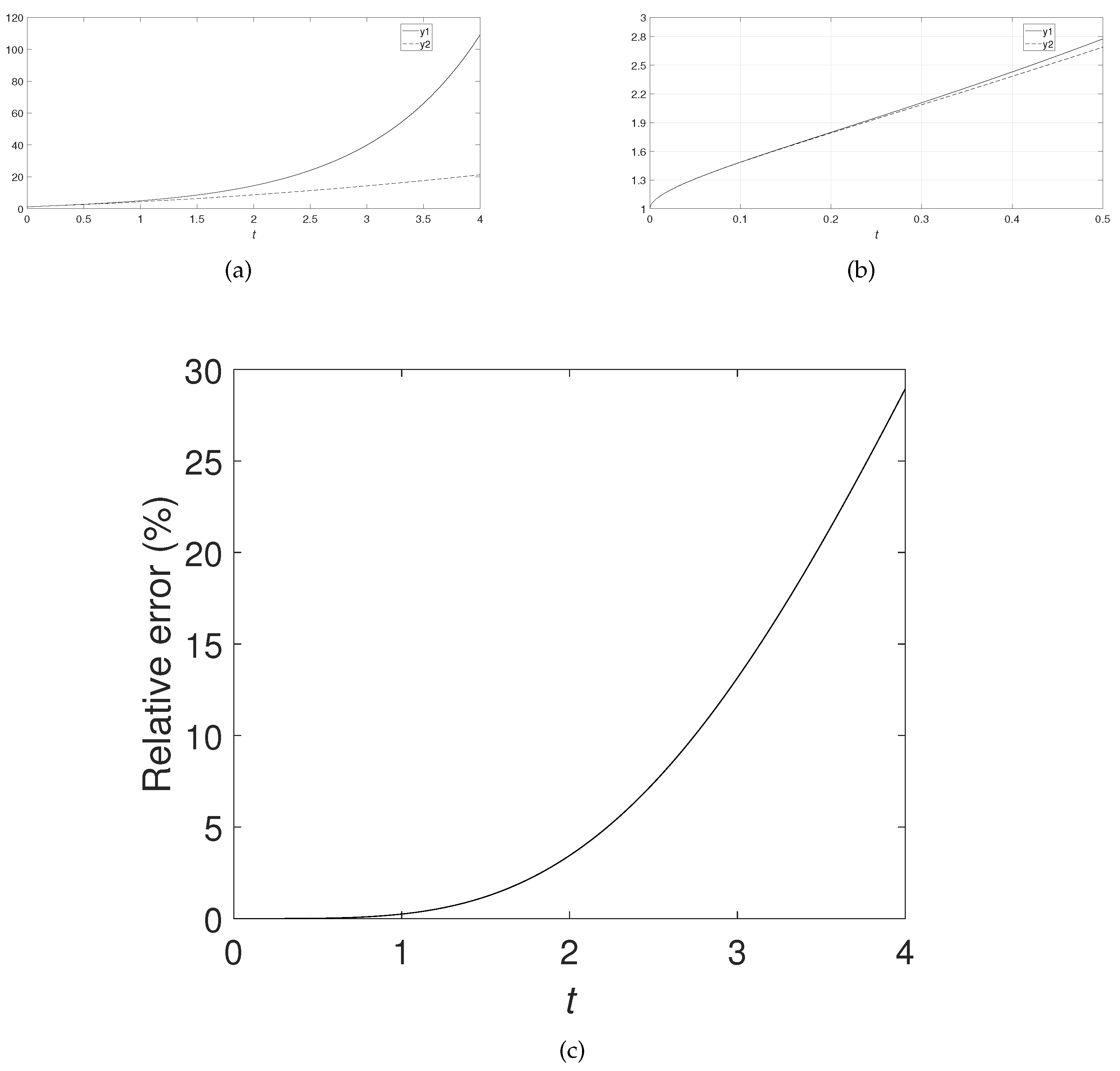
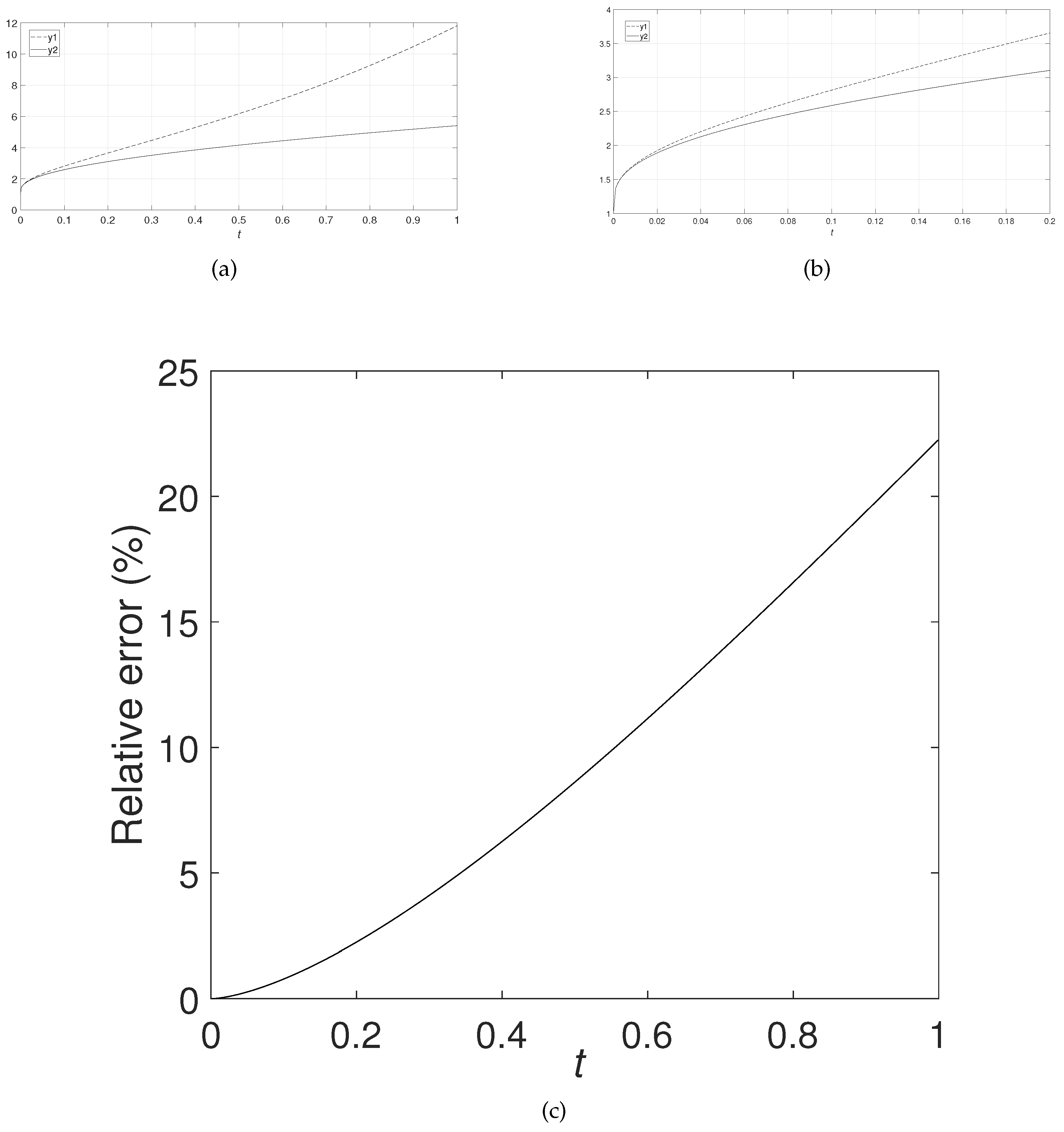
5. Examples

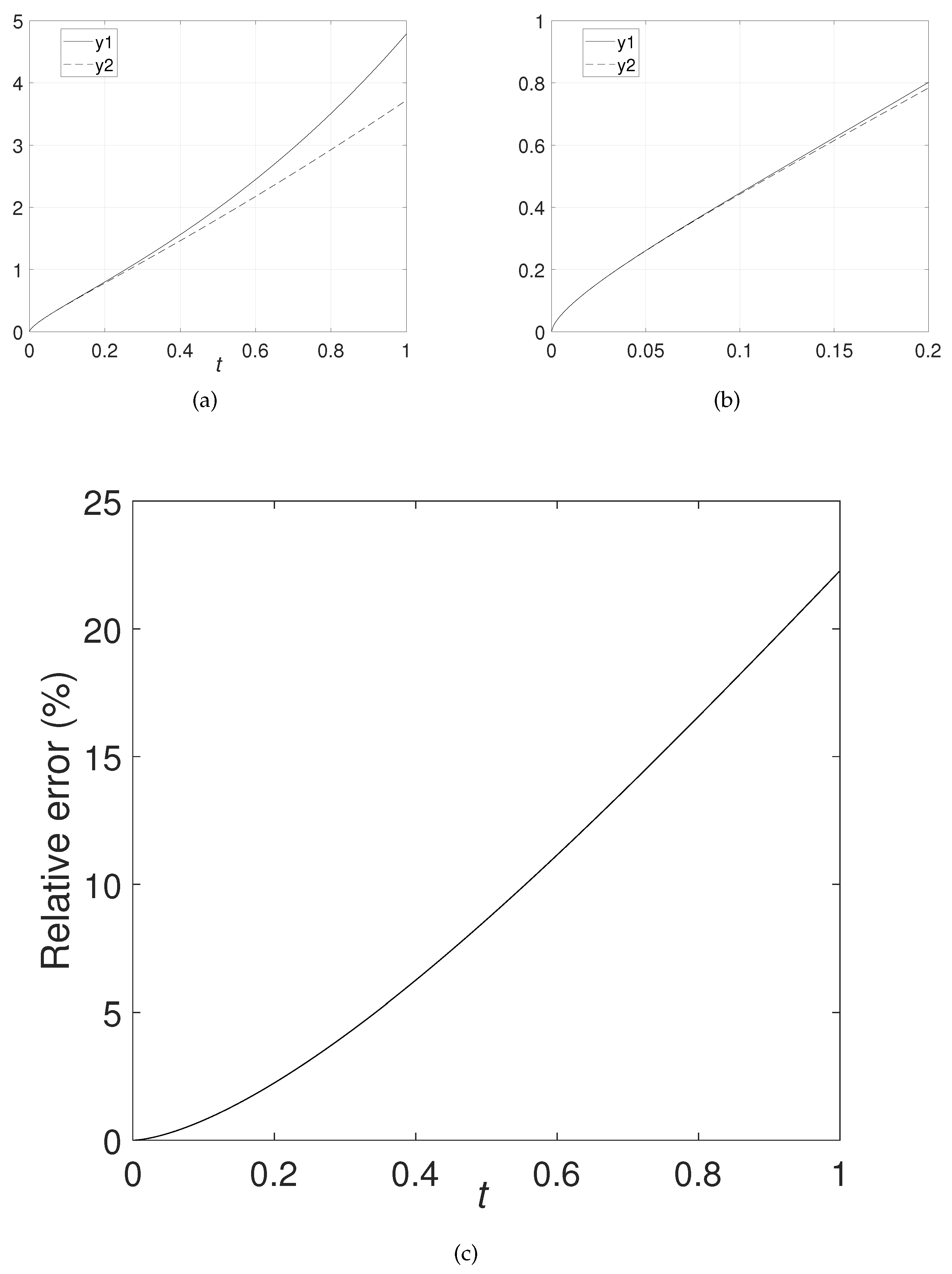
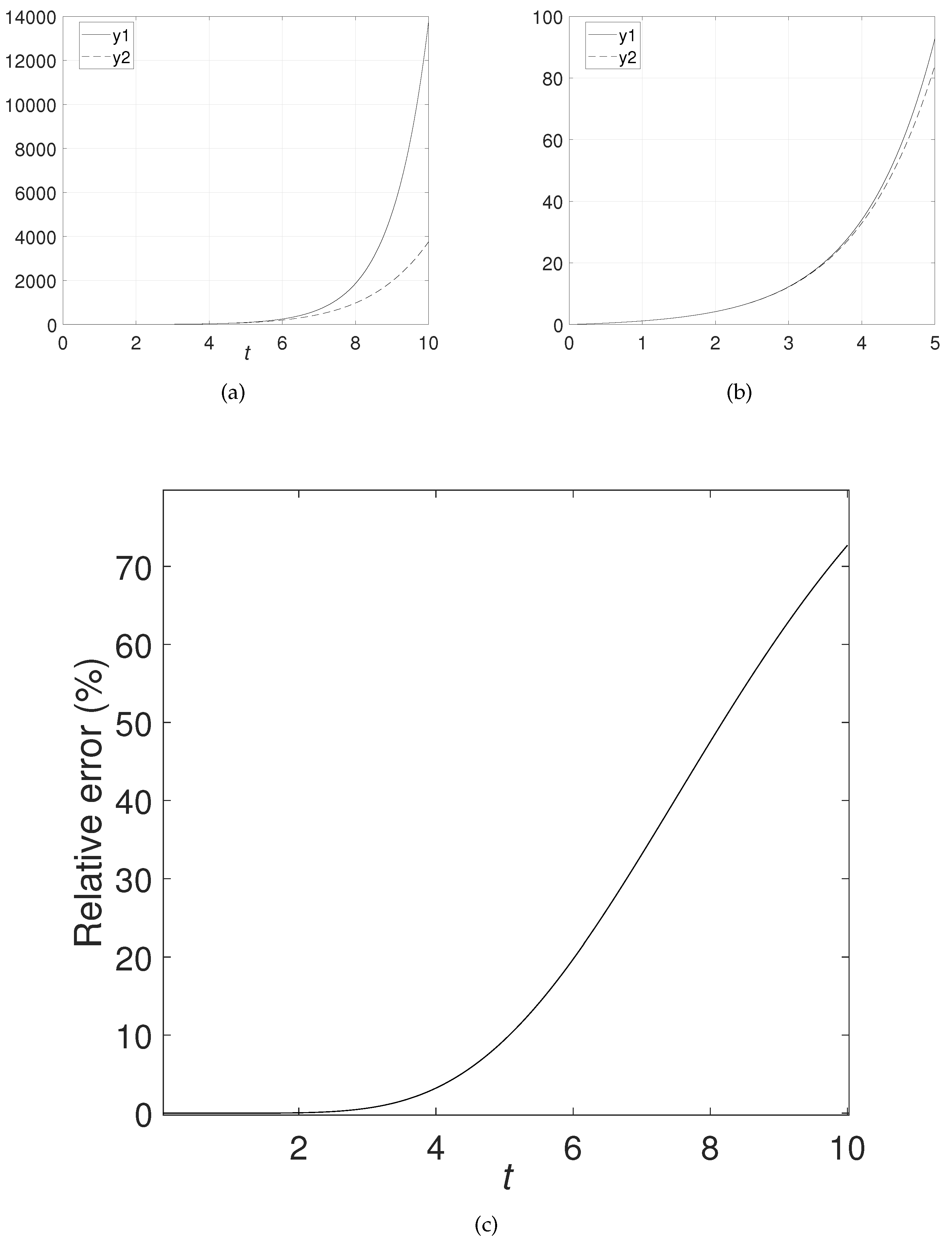
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, L. Comments on “Finite-Time Control of Uncertain Fractional-Order Positive Impulsive Switched Systems with Mode-Dependent Average Dwell Time”. Circuits Syst. Signal Process. 2020, 39, 6394–6397. [Google Scholar] [CrossRef]
- Zhao, L. A note on “Cluster synchronization of fractional-order directed networks via intermittent pinning control”. Phys. A-Stat. Mech. Its Appl. 2021, 561, 125150. [Google Scholar] [CrossRef]
- Shan, W.; Wang, Y.; Tang, W. Fractional Order Internal Model PID Control for Pulp Batch Cooking Process. J. Chem. Eng. Jpn. 2023, 56, 2201288. [Google Scholar] [CrossRef]
- Bishehniasar, M.; Salahshour, S.; Ahmadian, A.; Ismail, F.; Baleanu, D. An Accurate Approximate-Analytical Technique for Solving Time-Fractional Partial Differential Equations. Complexity 2017, 2017, 8718209. [Google Scholar] [CrossRef]
- Abdollahi, R.; Khastan, A.; Nieto, J.J.; Rodriguez-Lopez, R. On the linear fuzzy model associated with Caputo-Fabrizio operator. Bound. Value Probl. 2018, 1–18. [Google Scholar] [CrossRef]
- Alam Khan, N.; Abdul Razzaq, O.; Riaz, F.; Ahmadian, A.; Senu, N. Dynamics of fractional order nonlinear system: A realistic perception with neutrosophic fuzzy number and Allee effect. J. Adv. Res. 2021, 32, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian, A.; Salahshour, S.; Ali-Akbari, M.; Ismail, F.; Baleanu, D. A novel approach to approximate fractional derivative with uncertain conditions. Chaos Solitons Fractals 2017, 104, 68–76. [Google Scholar] [CrossRef]
- Singh, S.; Ray, S.S. Higher-order approximate solutions of fractional stochastic point kinetics equations in nuclear reactor dynamics. Nucl. Sci. Tech. 2019, 30, 49. [Google Scholar] [CrossRef]
- Bohaienko, V.; Bulavatsky, V. Simplified Mathematical Model for the Description of Anomalous Migration of Soluble Substances in Vertical Filtration Flow. Fractal Fract. 2020, 4, 20. [Google Scholar] [CrossRef]
- Salama, F.M.; Hamid, N.N.A.; Ali, N.H.M.; Ali, U. An efficient modified hybrid explicit group iterative method for the time-fractional diffusion equation in two space dimensions. AIMS Math. 2022, 7, 2370–2392. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Yousef, F.; Momani, S.; Baleanu, D. On (2+1)-dimensional physical models endowed with decoupled spatial and temporal memory indices⋆. Eur. Phys. J. Plus 2019, 134, 360. [Google Scholar] [CrossRef]
- Mukhtar, S.; Abuasad, S.; Hashim, I.; Abdul Karim, S.A. Effective Method for Solving Different Types of Nonlinear Fractional Burgers’ Equations. Mathematics 2020, 8, 729. [Google Scholar] [CrossRef]
- Liu, J.G.; Yang, X.J.; Feng, Y.Y.; Cui, P. On the (N+1)-dimensional local fractional reduced differential transform method and its applications. Math. Methods Appl. Sci. 2020, 43, 8856–8866. [Google Scholar] [CrossRef]
- Ali, G.; Ahmad, I.; Shah, K.; Abdeljawad, T. Iterative Analysis of Nonlinear BBM Equations under Nonsingular Fractional Order Derivative. Adv. Math. Phys. 2020, 2020, 3131856. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, Y. Comments on “a novel approach to approximate fractional derivative with uncertain conditions”. Chaos Solitons Fractals 2022, 154, 111651. [Google Scholar] [CrossRef]
- Arshad, M.; Lu, D.; Wang, J. (N + 1)-dimensional fractional reduced differential transform method for fractional order partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 509–519. [Google Scholar] [CrossRef]
- Yu, J.; Jing, J.; Sun, Y.; Wu, S. (n + 1)-Dimensional reduced differential transform method for solving partial differential equations’. Appl. Math. Comput. 2016, 273, 697–705. [Google Scholar] [CrossRef]
- Abuasad, S.; Alshammari, S.; Al-rabtah, A.; Hashim, I. Solving a Higher-Dimensional Time-Fractional Diffusion Equation via the Fractional Reduced Differential Transform Method. Fractal Fract. 2021, 5, 168. [Google Scholar] [CrossRef]
- Owyed, S.; Abdou, M.A.; Abdel-Aty, A.H.; Alharbi, W.; Nekhili, R. Numerical and approximate solutions for coupled time fractional nonlinear evolutions equations via reduced differential transform method. Chaos Solitons Fractals 2020, 131, 109474. [Google Scholar] [CrossRef]
- Maisuria, M.A.; Tandel, P.V.; Patel, T. Solution of Two-Dimensional Solute Transport Model for Heterogeneous Porous Medium Using Fractional Reduced Differential Transform Method. Axioms 2023, 12, 1039. [Google Scholar] [CrossRef]
- Mahdy, A.M.S.; Gepreel, K.A.; Lotfy, K.; El-Bary, A. Reduced differential transform and Sumudu transform methods for solving fractional financial models of awareness. Appl. Math.-A J. Chin. Univ. Ser. B 2023, 38, 338–356. [Google Scholar] [CrossRef]
- Al-rabtah, A.; Abuasad, S. Effective Modified Fractional Reduced Differential Transform Method for Solving Multi-Term Time-Fractional Wave-Diffusion Equations. Symmetry 2023, 15, 1721. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J. Analyzing the Approximate Error and Applicable Condition of the Fractional Reduced Differential Transform Method. Symmetry 2024, 16, 912. https://doi.org/10.3390/sym16070912
Hu J. Analyzing the Approximate Error and Applicable Condition of the Fractional Reduced Differential Transform Method. Symmetry. 2024; 16(7):912. https://doi.org/10.3390/sym16070912
Chicago/Turabian StyleHu, Jianbing. 2024. "Analyzing the Approximate Error and Applicable Condition of the Fractional Reduced Differential Transform Method" Symmetry 16, no. 7: 912. https://doi.org/10.3390/sym16070912



