Dynamic Analysis and Optimization of the Coupling System of Vibrating Flip-Flow Screen and Material Group
Abstract
:1. Introduction
2. Constitutive Model of Screen Panel
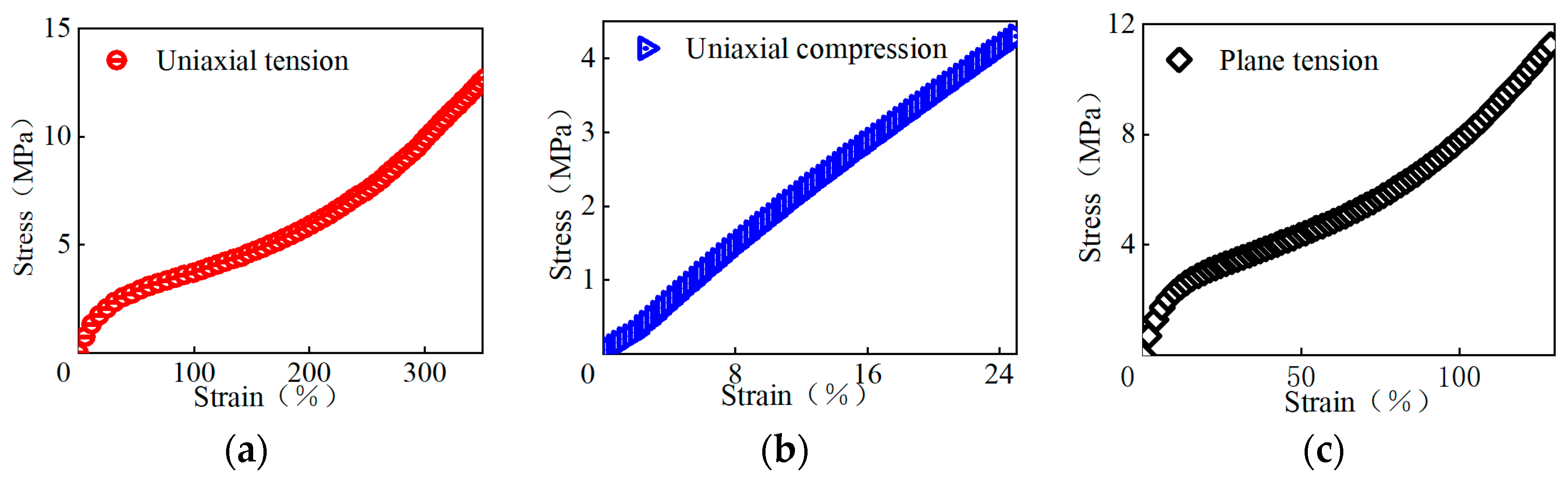
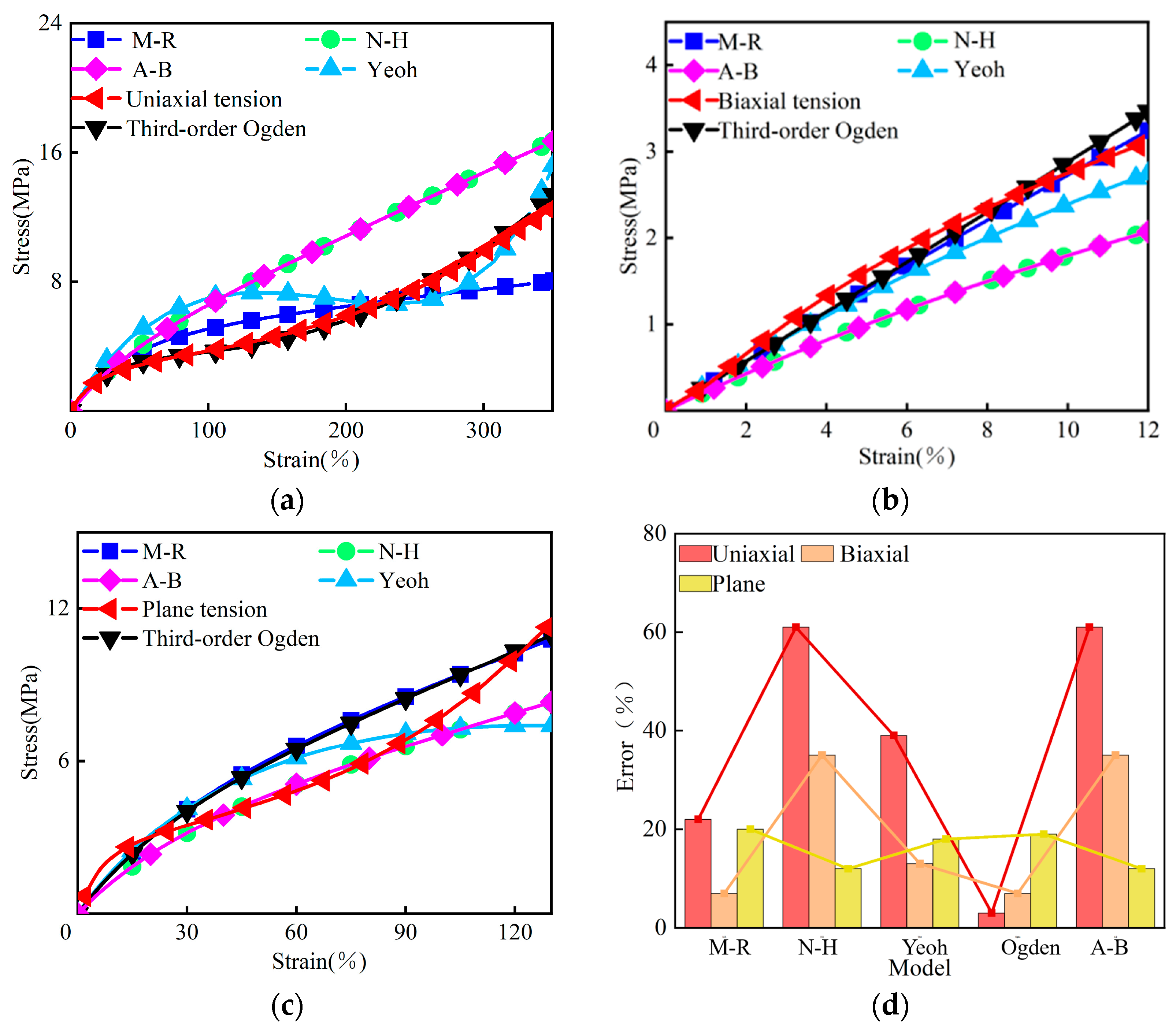
2.1. Hyperelastic Constitutive Model
2.2. Viscoelastic Constitutive Model
3. Dynamic Analysis of the Coupling System of VFFS and Material Group
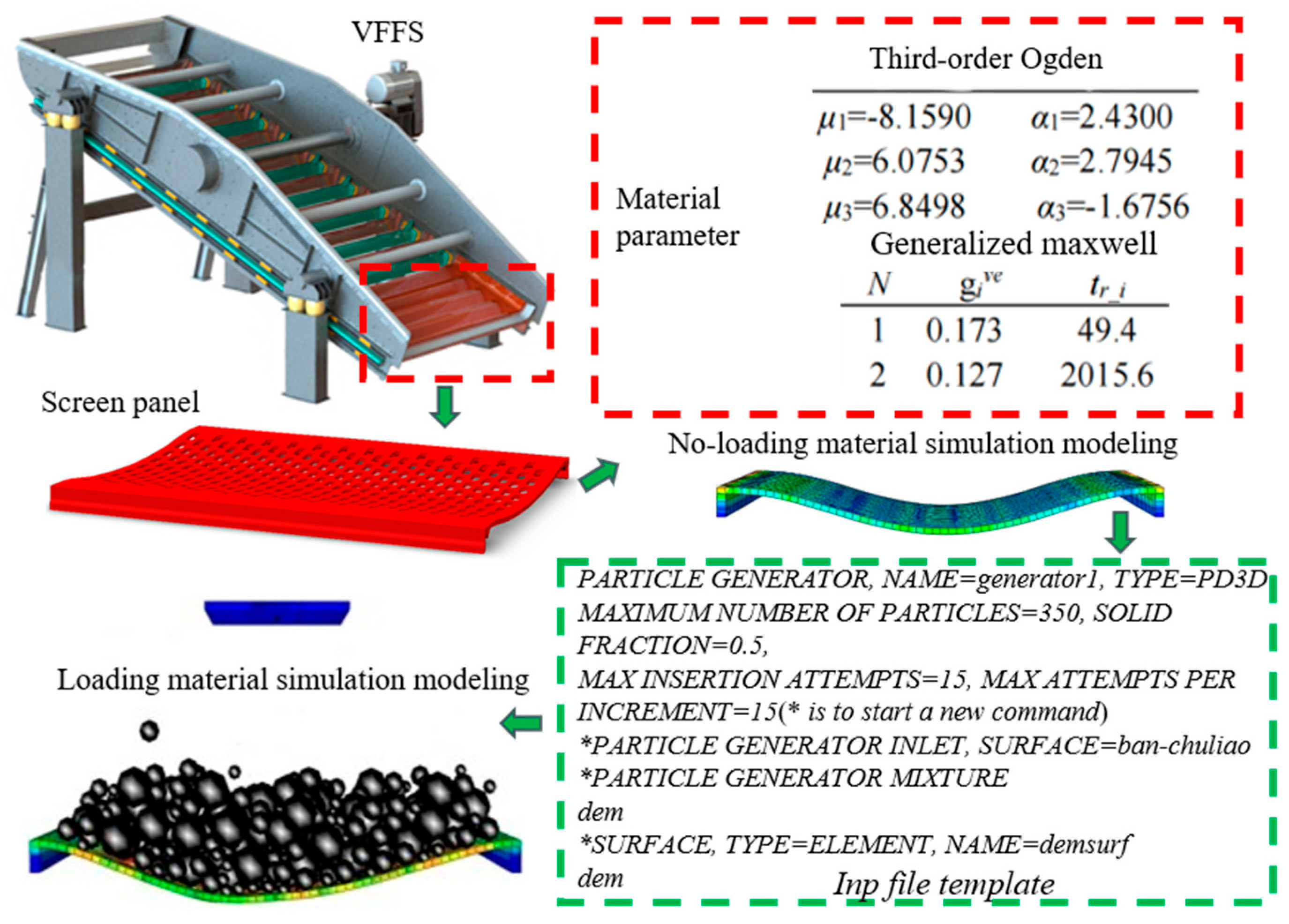
3.1. Simulation Modeling of the Coupling System of the Screen Panel and Material Group
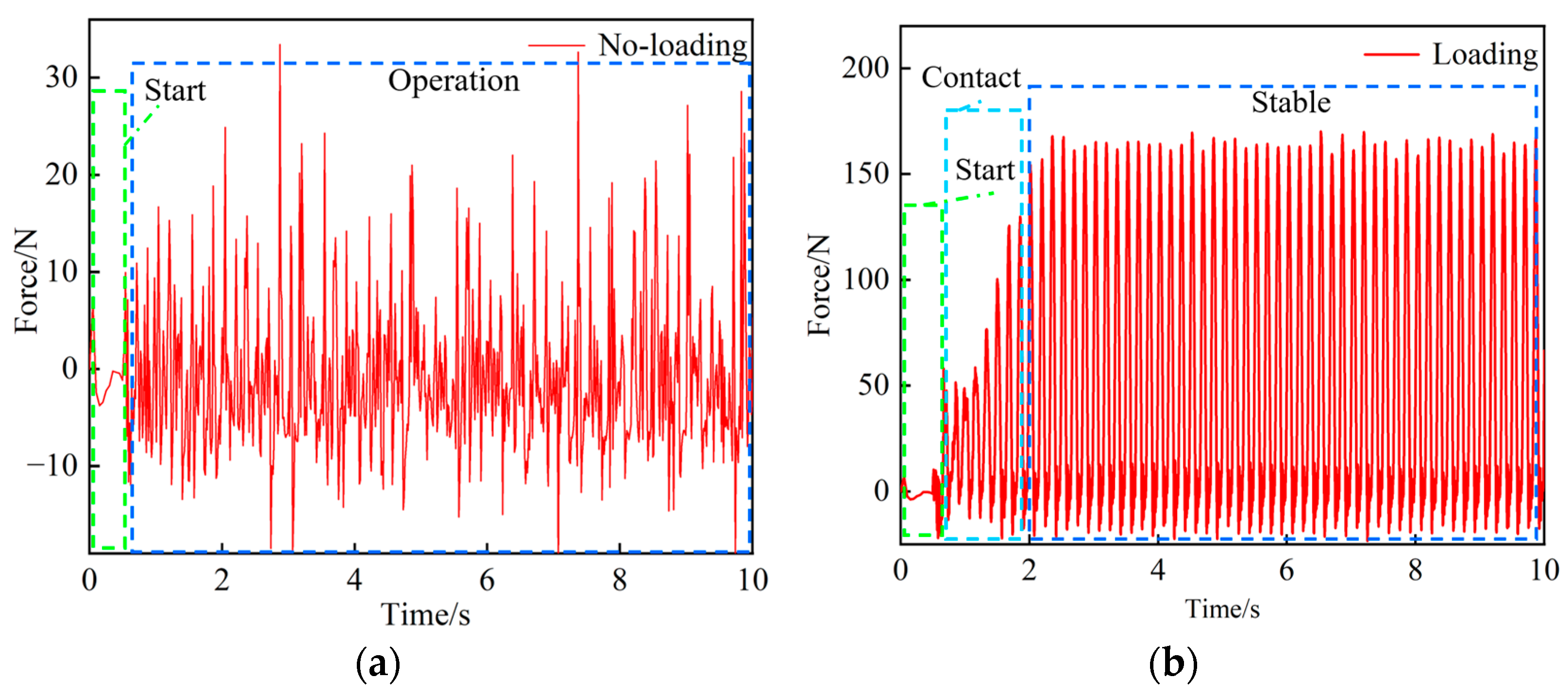
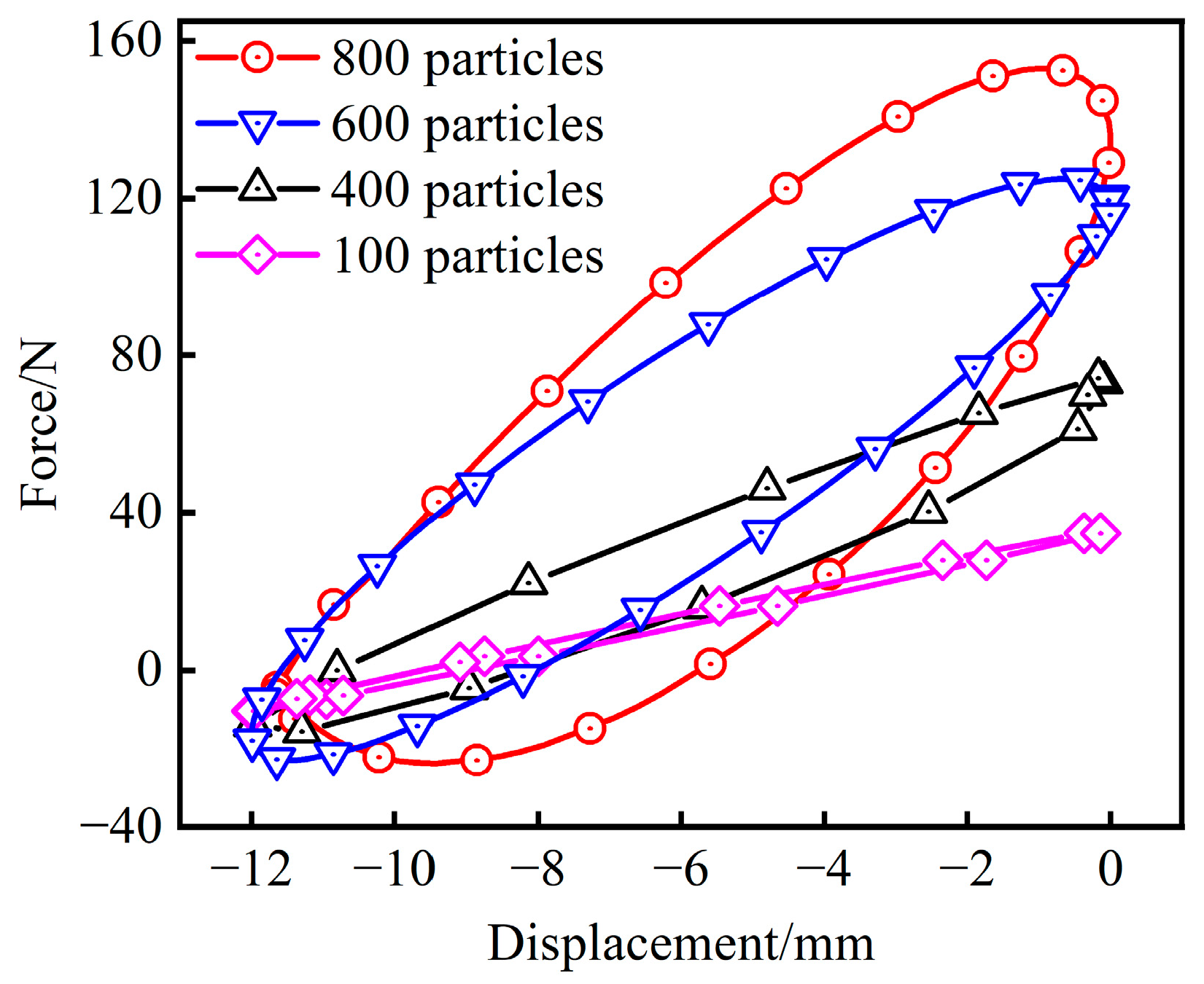
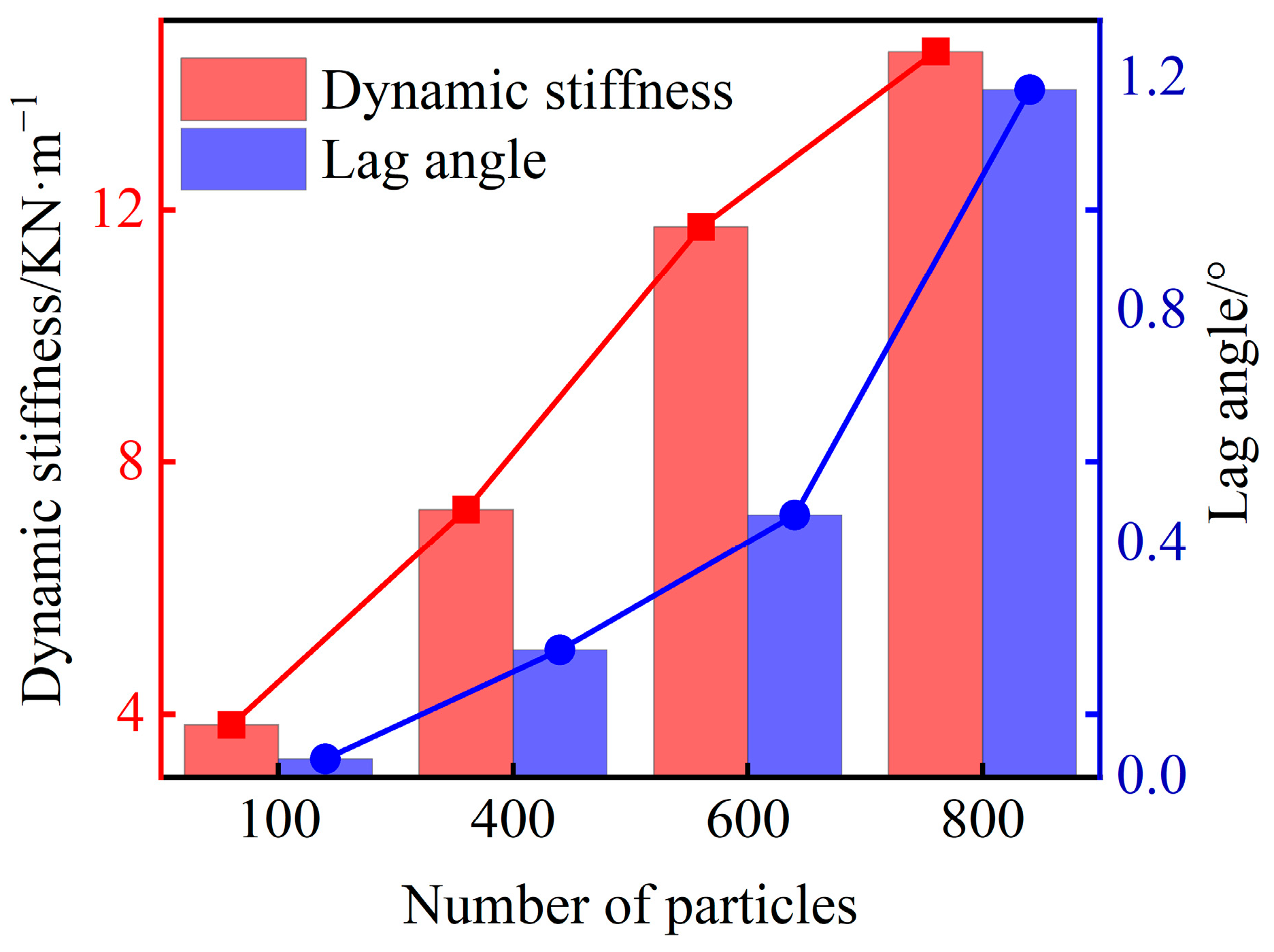
3.2. Dynamics of Screen Panel under Different Conditions
3.3. Dynamic Analysis of Screen Panel with Loading Materials
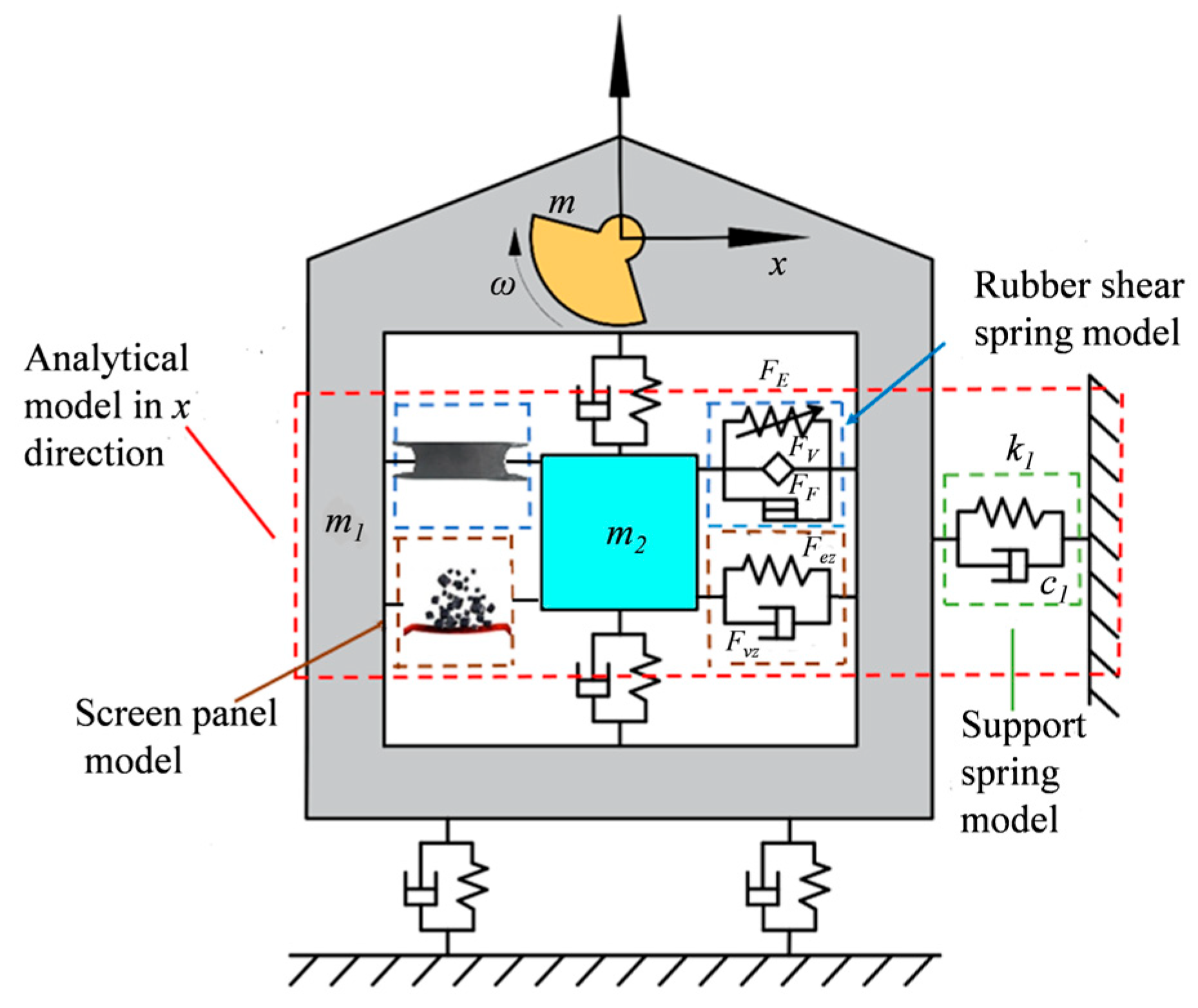
3.4. Dynamic Model of the Screen Panel and Material Group Coupling System
3.5. Dynamic Model of VFFSs under Loading Material Conditions
- for x2 = xs
- for x2 > xs
- for x2 < xs
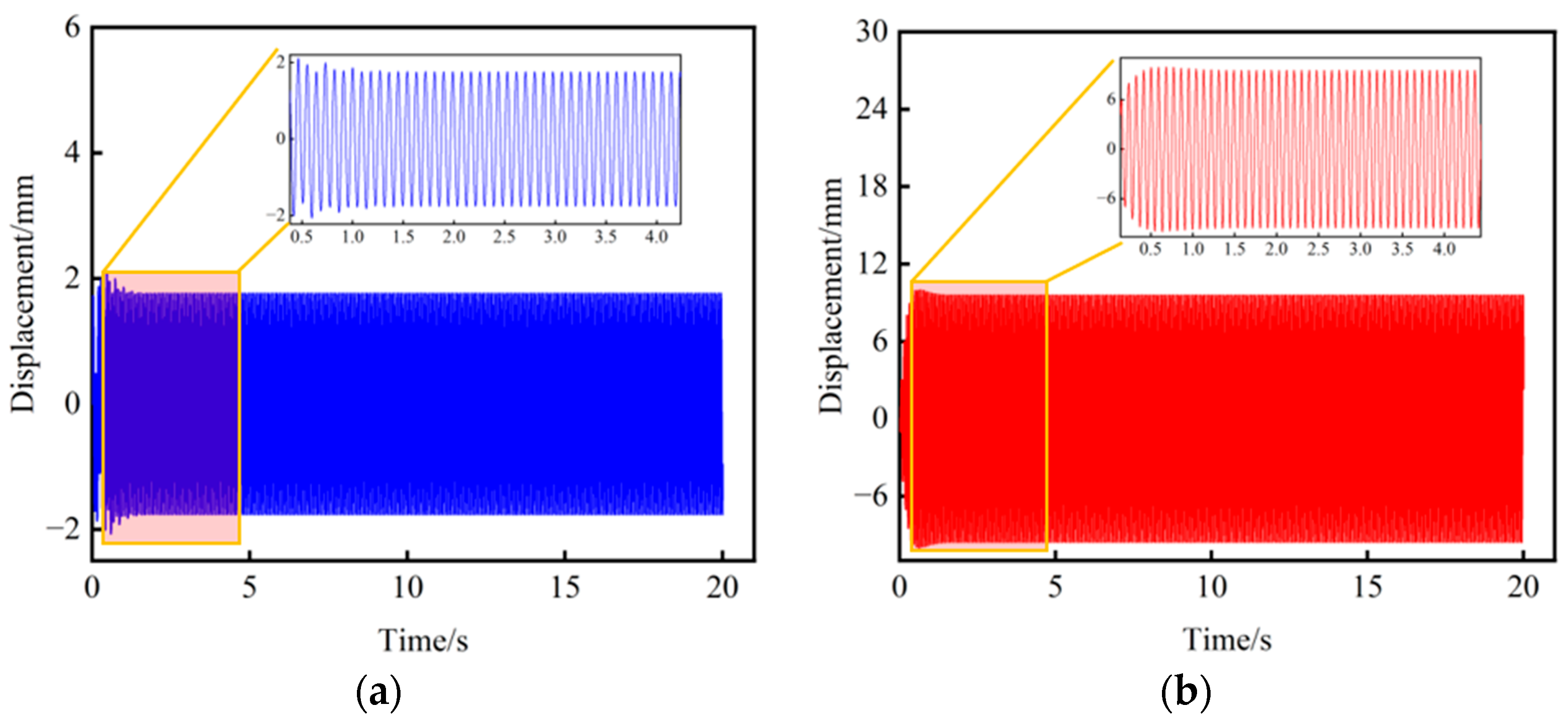
3.6. Analysis of Dynamic Response of VFFSs under Loading Material Condition
3.7. The Influence of Model Parameters on the Dynamic Response of VFFS under Loading Material Conditions
4. Dynamic Optimization of the VFFSs Coupling System
4.1. The Influence of External Conditions on the Dynamic Response of x2
4.2. Multi-Objective Optimization Design of Dynamic Response of VFFSs
4.3. Multi-Objective Optimization Results and Analysis of Dynamic Response of VFFSs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Duan, C.; Yuan, J.; Pan, M.; Huang, T.; Jiang, H.; Zhao, Y.; Qiao, J.; Wang, W.; Yu, S.; Lu, J. Variable elliptical vibrating screen: Particles kinematics and industrial application. Int. J. Min. Sci. Technol. 2021, 31, 1013–1022. [Google Scholar] [CrossRef]
- Fan, J.; He, Z.; Zhang, Y.; Wang, M. A Novel Kinematics Model of Flip-Flow Screen Panel: Inclined Catenary Model. Mathematics 2023, 11, 2028. [Google Scholar] [CrossRef]
- Wang, W.; Duan, C.; Jiang, H.; Yu, S.; Zhou, Z.; Qiao, J.; Zhao, Y.; Pan, M. Mechanism of overcoming plugging and optimization of parameters for rigid-flexible coupled elastic screening of moist fine coal. Powder Technol. 2020, 376, 113–125. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, W.; Zhou, Z.; Jun, H.; Wen, P.; Zhao, Y.; Duan, C.; Zhao, L.; Luo, Z.; Liu, C. Simultaneous multiple parameter optimization of variable-amplitude equal-thickness elastic screening of moist coal. Powder Powder Technol. 2019, 346, 217–227. [Google Scholar] [CrossRef]
- Yu, S.; Li, S.; Guo, P.; Zhang, Y.; Li, W.; Wang, H.; Shi, W.; Jiang, H.; Duan, C. Research on highly efficient quality improvement process and product blending scheme for fine coal. Powder Technol. 2023, 430, 119011. [Google Scholar] [CrossRef]
- Wang, W.; Lu, J.; Wang, C.; Yuan, J.; Hou, X.; Pan, M.; Jiang, H.; Qiao, J.; Duan, C.; Dombon, E. Study on screening probability model and particle-size effect of flip-flow screen. Adv. Powder Technol. 2022, 33, 103668. [Google Scholar] [CrossRef]
- Xiong, X.; Niu, L.; Gu, C.; Wang, Y. Vibration characteristics of an inclined flip-flow screen panel in banana flip-flow screens. J. Sound Vib. 2017, 411, 108–128. [Google Scholar] [CrossRef]
- Gong, S.; Oberst, S.; Wang, X. An experimentally validated rubber shear spring model for vibrating flip-flow screens. Mech. Syst. Signal Process. 2020, 139, 106619. [Google Scholar] [CrossRef]
- Lin, D.; Ji, J.; Yu, C.; Wang, X.; Xu, N. A non-linear model of screen panel for dynamics analysis of a flip-flow vibrating screen. Powder Technol. 2023, 418, 118312. [Google Scholar] [CrossRef]
- Hou, X.; Wang, W.; Pan, J.; Mao, P.; Zhang, S.; Duan, C. Optimization of flip-flow screen plate based on DEM-FEM coupling model and screening performance of fine minerals. Miner. Eng. 2024, 211, 108694. [Google Scholar] [CrossRef]
- Wang, W.; Hou, X.; Mao, P.; Pan, M.; Yu, S.; Jiang, H.; Qiao, J.; Duan, C. Kinematic characteristics of key structures and time evolution law of material distribution characteristics during flip-flow screening. Miner. Eng. 2023, 201, 108241. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, B.; Niu, L.; Xiong, X.; Dong, Z. Dynamic characteristics of two-way coupling between flip-flow screen and particles based on DEM. J. China Coal Soc. 2019, 44, 1930–1940. [Google Scholar]
- Wu, B.; Zhang, X.; Niu, L.; Xiong, X.; Dong, Z.; Tang, J. Research on sieving performance of flip-flow screen using two-way particles-screen panels coupling strategy. IEEE Access 2019, 7, 124461–124473. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Q.; Yang, L. The MFBD-DEM coupling simulation approach for the investigation of granules screening efficiency in 4-DOF Flip-Flow Screen. Granul. Matter 2024, 26, 5. [Google Scholar] [CrossRef]
- Xu, N.; Yu, C.; Gong, S.; Zhao, G.; Lin, D.; Wang, X. Numerical study and multi-objective optimization of flexible screening process of flip-flow screen: A DEM-FEM approach. Adv. Powder Technol. 2022, 33, 103650. [Google Scholar] [CrossRef]
- Zhao, G.; Pu, K.; Xu, N.; Gong, S.; Wang, X. Simulation of particles motion on a double vibrating flip-flow screen surface based on FEM and DEM coupling. Powder Technol. 2023, 421, 118422. [Google Scholar] [CrossRef]
- Hamza, M.; Alwan, H. Hyperelastic constitutive modeling of rubber and rubber- like materials under finite strain. ETJ 2010, 28, 2560–2575. [Google Scholar]
- Dal, H.; Acikgoz, K.; Badienia, Y. On the performance of isotropic hyperelastic constitutive models for rubber-like materials: A state of the art review. Appl. Mech. Rev. 2021, 73, 020802. [Google Scholar] [CrossRef]
- Yang, L.M.; Shim, V.P.W.; Lim, C.T. A visco-hyperelastic approach to modelling the constitutive behaviour of rubber. Int. J. Impact Eng. 2000, 24, 545–560. [Google Scholar] [CrossRef]
- Cao, L.; Sadeghi, F.; Stacke, L.-E. An explicit finite-element model to investigate the effects of elastomeric bushing on bearing dynamics. J. Tribol.-Trans. ASME 2016, 138, 031104. [Google Scholar] [CrossRef]
- Seibert, D.J.; Schoeche, N. Direct comparison of some recent rubber elasticity models. Rubber Chem. Technol. 2000, 73, 366–384. [Google Scholar] [CrossRef]
- Hu, X.; Liu, X.; Li, M.; Luo, W. Selection strategies of hyperelastic constitutive models for carbon black filled rubber. Eng. Mech. 2014, 31, 34–42. [Google Scholar]
- Lin, C.; Chen, Y.; Lin, C.; Chang, K. Constitutive equations for analyzing stress relaxation and creep of viscoelastic materials based on standard linear solid model derived with finite loading rate. Polymers 2022, 14, 2124. [Google Scholar] [CrossRef]
- Gil-Negrete, N.; Vinolas, J.; Kari, L. A simplified methodology to predict the dynamic stiffness of carbon-black filled rubber isolators using a finite element code. J. Sound Vib. 2006, 296, 757–776. [Google Scholar] [CrossRef]
- Gong, S.; Wu, T.; Gao, Y.; Ming, P.; Zhang, J.; Zhang, Y.; Wang, X. Study on dynamic characteristics of the coupling system of flip-flow screen panel and material group based on FEM-DEM. J. China Coal Soc. 2023, 48, 381–391. [Google Scholar]
- Shi, H.; Wu, P. A nonlinear rubber spring model containing fractional derivatives for use in railroad vehicle dynamic analysis. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2016, 230, 1745–1759. [Google Scholar] [CrossRef]
- Zhu, S.; Cai, C.; Spanos, P.D. A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab track systems. J. Sound Vib. 2015, 335, 304–320. [Google Scholar] [CrossRef]
- Sjöberg, M.M.; Kari, L. Non-linear behavior of a rubber isolator system using fractional derivatives. Vehicle Syst. Dyn. 2002, 37, 217–236. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, J.; Zhang, Y.; Feng, X. A novel air spring dynamic model with pneumatic thermodynamics, effective friction and viscoelastic damping. J. Sound Vib. 2017, 408, 87–104. [Google Scholar] [CrossRef]
- Wang, P.; Bai, Y.; Lin, C.; Han, X. A hybrid criterion-based sample infilling strategy for surrogate-assisted multi-objective optimization. Struct. Multidiscip. Optim. 2024, 67, 44. [Google Scholar] [CrossRef]
- Lu, J.; Lei, Z. Multi-objective optimization design of post-soil system for enhanced w-beam guardrail containment performance. Int. J. Crashworthiness 2023, 28, 116–126. [Google Scholar]
- Carvalho, É.C.R.; Carvalho, J.P.G.; Bernardino, H.S.; Lemonge, A.C.C.; Hallak, P.H.; Vargas, D.E.C. Solving multi-objective truss structural optimization problems considering natural frequencies of vibration and automatic member grouping. Evol. Intell. 2024, 17, 653–678. [Google Scholar] [CrossRef]
- Tong, S.; Guo, M.; Tian, Y.; Le, J.; Zhang, D.; Zhang, H. Multi-objective optimization design of scramjet nozzle based on grey wolf optimization algorithm and kernel extreme learning machine surrogate model. Phys. Fluids 2024, 36, 025104. [Google Scholar] [CrossRef]
- Cheng, F.; Liu, H. Surrogate model-based multi-objective optimization algorithm for train-ballast turnout system: Balancing safety and vibration damping in parameter design. Eng. Struct. 2024, 304, 117685. [Google Scholar] [CrossRef]




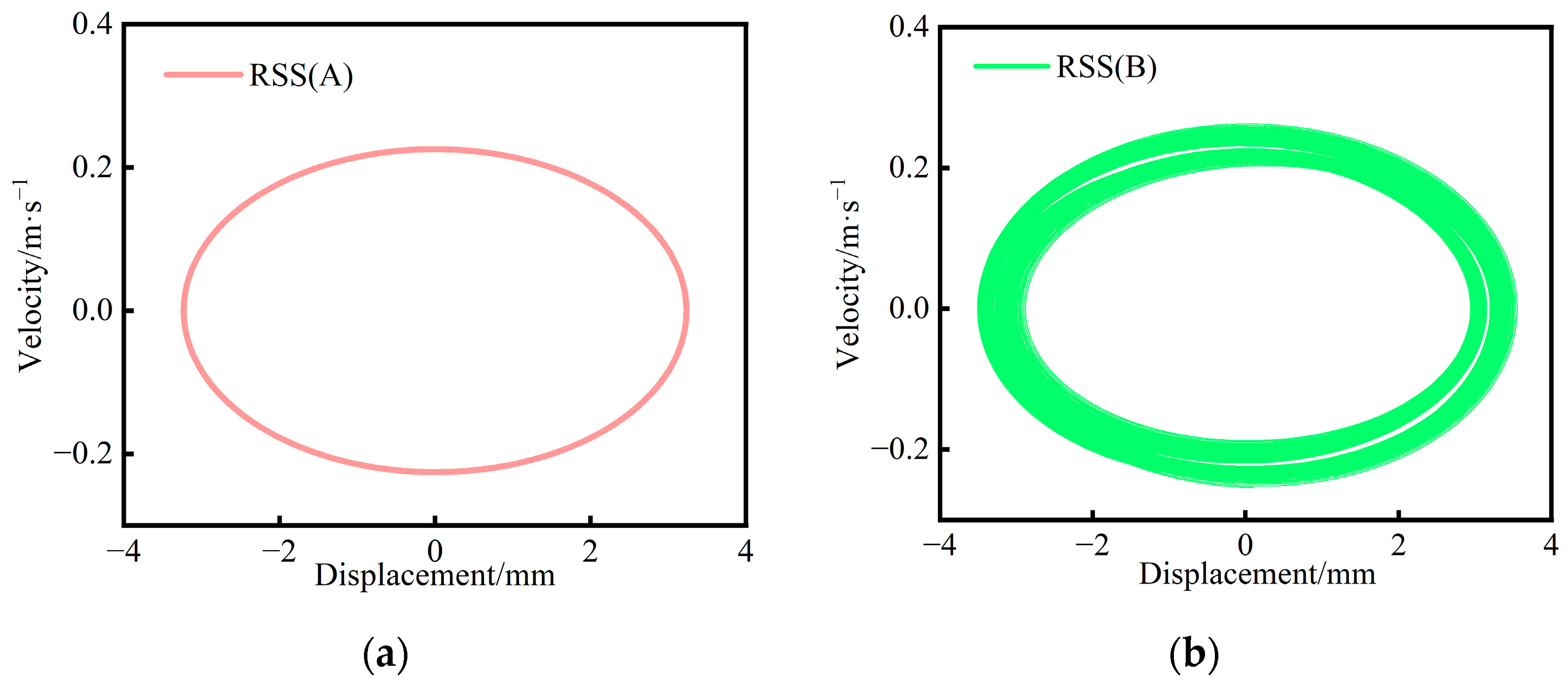
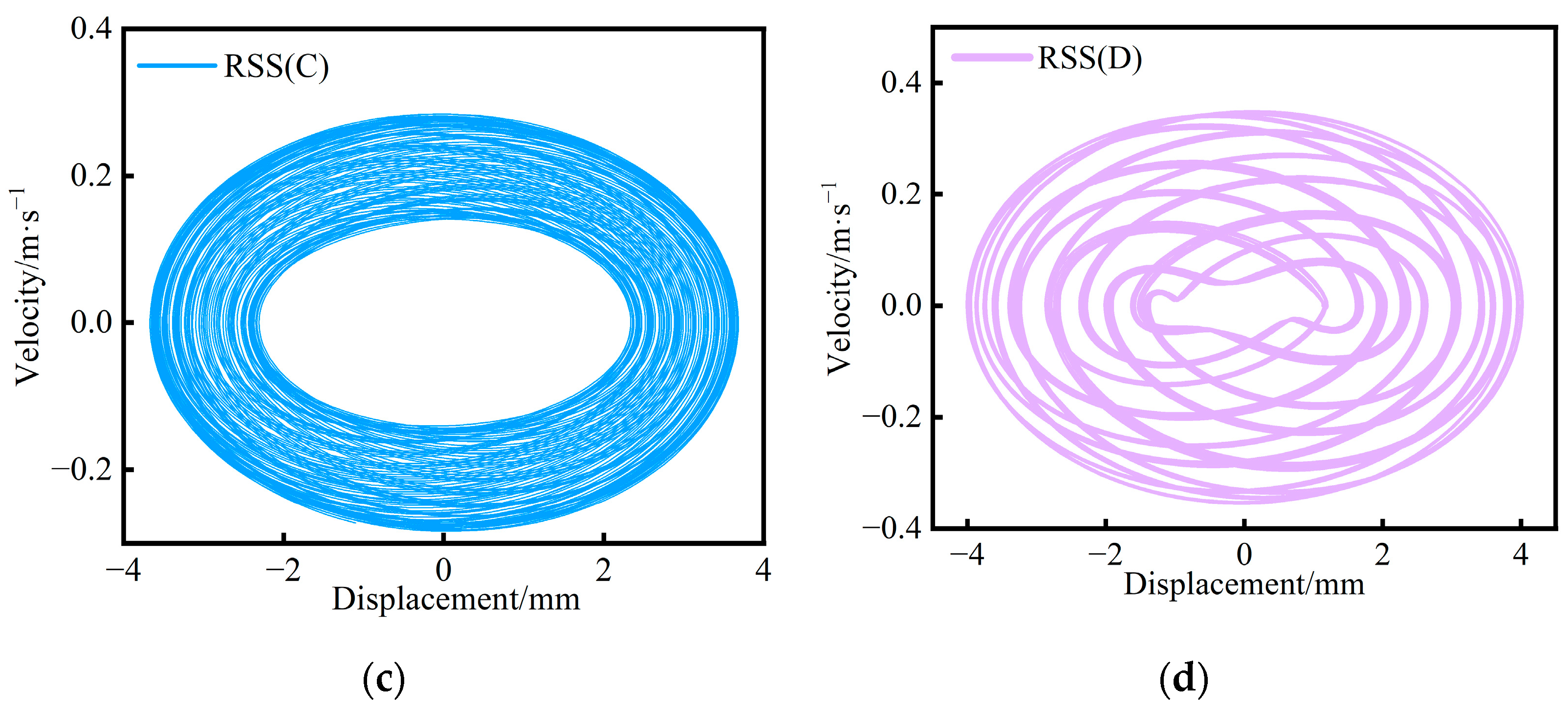
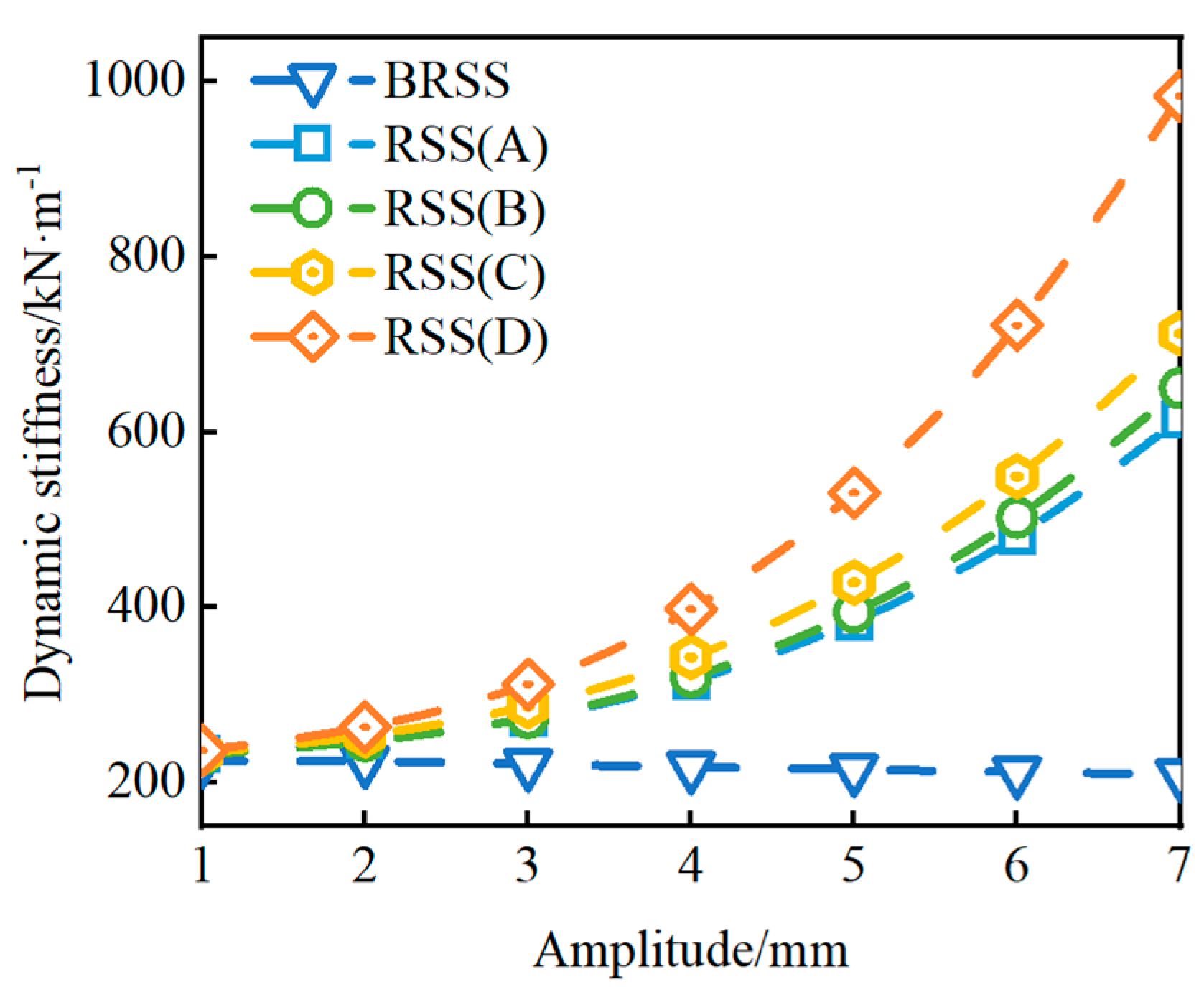
| i | αi | μi |
|---|---|---|
| 1 | 2.4300 | −8.1590 |
| 2 | 2.7945 | 6.0753 |
| 3 | −1.6756 | 6.8498 |
| N | give | tr−i |
|---|---|---|
| 1 | 0.173 | 49.4 |
| 2 | 0.127 | 2015.6 |
| Symbol | Parameter Value | Unit |
|---|---|---|
| ke | −0.0031 x03 + 0.192 x02 − 4.504 x0 + 207.77 | N/mm |
| Ffmax | 0.0077 x03 − 0.519 x02 + 16.322 x0 − 10.547 | N |
| a2 | −0.0047 x02 + 0.583 x0 − 0.561 | mm |
| α | 0.16 | - |
| b | 9.9 | N·sɑ/mm |
| m1 | 4130 | kg |
| m2 | 1309 | kg |
| k1 | 3,606,700 | N/m |
| c1 | 36614 | N·s/m |
| m | 242.24 | kg |
| Optimising factors: | Optimisation variables: | Variable range: |
| Objective function | Equation | Function description |
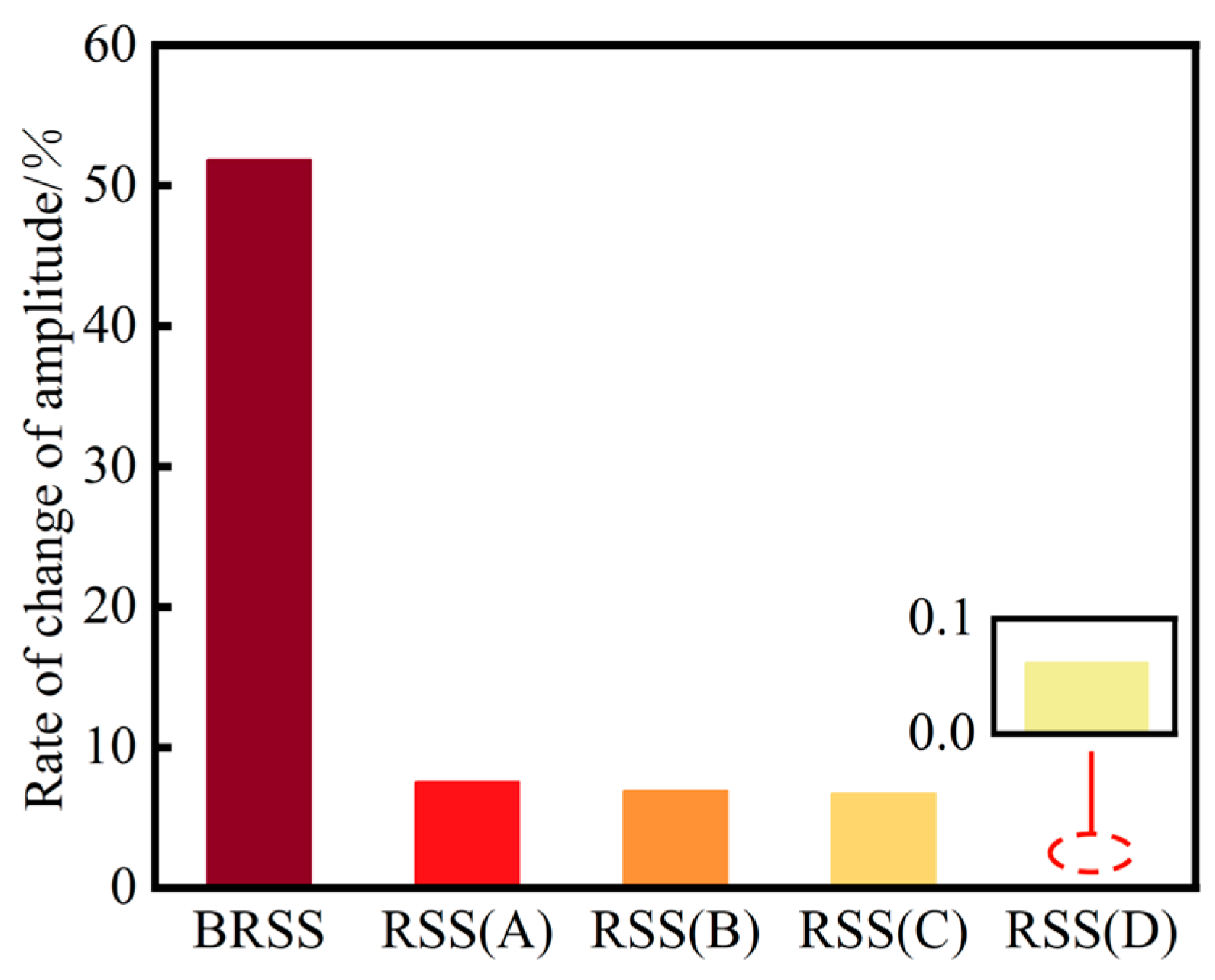
| Relative amplitude change rate of main float screen frame | and are the average value of all the amplitudes of x2 in the steady state with and , respectively. Here, is the amplitude of x2 during the ith period in the steady state without external conditions changed, and represents the amplitude of the jth period in the steady state of x2 with external conditions changed. | |
| Complexity of system’s motion state | : One-dimensional vector of resonance frequency |
| Population Size | Select Function | Crossover Fraction | Mutation Function | Crossover Function | Pareto Front Fraction |
|---|---|---|---|---|---|
| 150 | Tournament | 0.8 | Adaptive feasible | intermediate | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, S.; Wang, C.; Guo, J.; Qiao, Z.; Zhao, G.; Fan, J.; Xu, N.; Wang, X. Dynamic Analysis and Optimization of the Coupling System of Vibrating Flip-Flow Screen and Material Group. Symmetry 2024, 16, 913. https://doi.org/10.3390/sym16070913
Gong S, Wang C, Guo J, Qiao Z, Zhao G, Fan J, Xu N, Wang X. Dynamic Analysis and Optimization of the Coupling System of Vibrating Flip-Flow Screen and Material Group. Symmetry. 2024; 16(7):913. https://doi.org/10.3390/sym16070913
Chicago/Turabian StyleGong, Sanpeng, Chenhao Wang, Jialiang Guo, Ziqi Qiao, Guofeng Zhao, Junkai Fan, Ningning Xu, and Xinwen Wang. 2024. "Dynamic Analysis and Optimization of the Coupling System of Vibrating Flip-Flow Screen and Material Group" Symmetry 16, no. 7: 913. https://doi.org/10.3390/sym16070913






