Post-Earthquake Emergency Logistics Location-Routing Optimization Considering Vehicle Three-Dimensional Loading Constraints
Abstract
:1. Introduction
- (1)
- A multi-objective location-routing problem with a three-dimensional loading constraints optimization model is formulated. This model is unique in that it optimizes distribution centers, vehicle scheduling, and loading plans while considering three-dimensional loading constraints, facility disruptions, capacity limitations and expansions, and time window constraints while balancing social costs (logistical and deprivation costs) and risk to the logistics network. By integrating these two goals, the model not only enhances resource allocation efficiency but also strengthens the reliability of the ELN.
- (2)
- A multi-objective mixed genetic algorithm (MOGA) based on adaptive large neighborhood search (ALNS) is proposed. This MOGA-ALNS employs ALNS for neighborhood search, with five removal and insertion operators designed to enhance the diversity and flexibility of the search process, effectively preventing convergence to local optima. Simultaneously, it leverages the global search capability of genetic algorithms to ensure the diversity and comprehensiveness of the solutions.
2. Literature Review
2.1. Emergency Logistics Network
2.2. Integrating Research on Delivery Route Optimization and Three-Dimensional Packing Constraints (VRPTDLCs)
2.3. Compartmentalization Strategies for Vehicles
3. Model Formulation
3.1. Problem Description
3.2. Symbols
3.3. Emergency Logistics Network Risk Measurement Formula
3.4. Mathematical Model
4. Solution Method
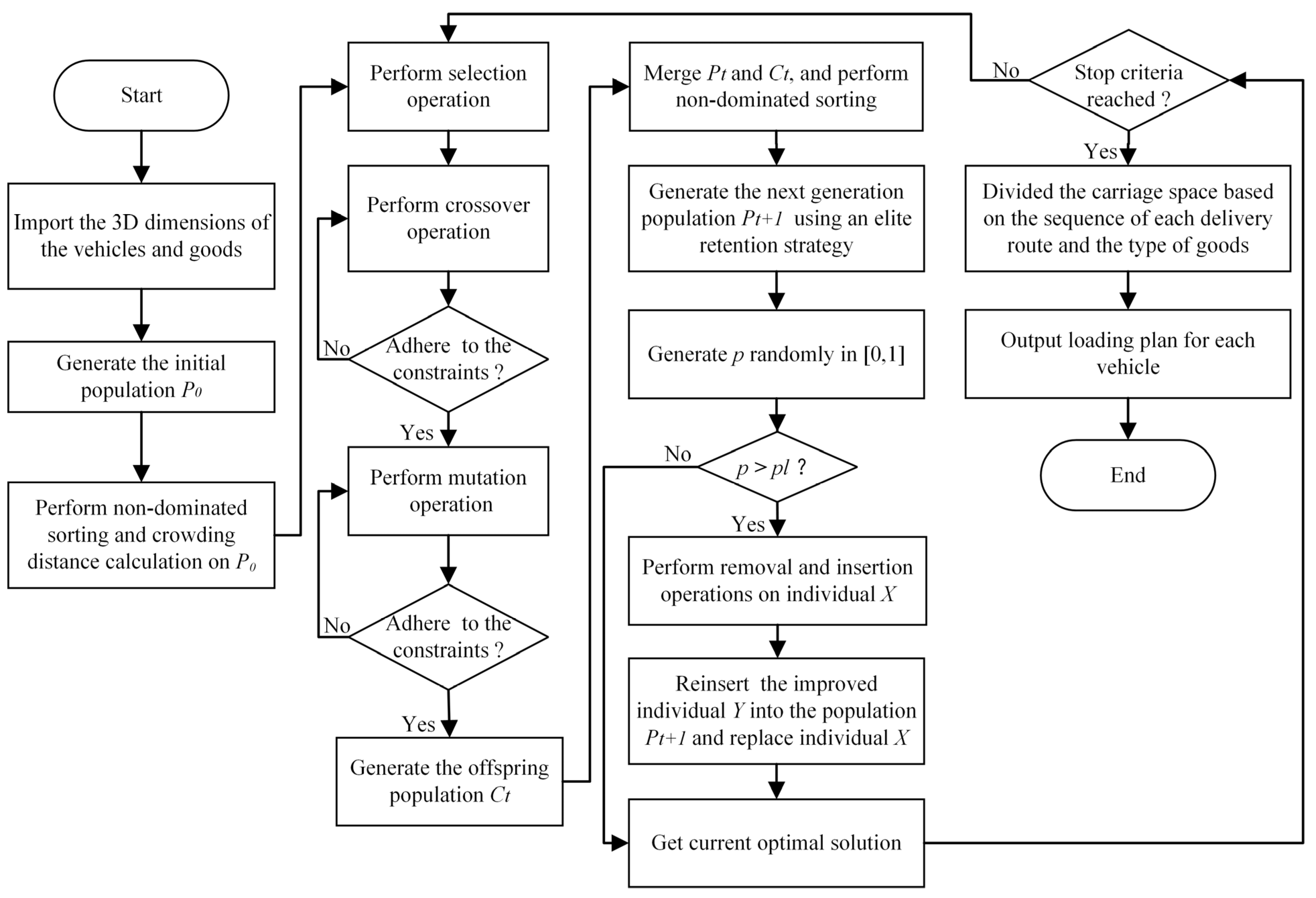
4.1. Main Framework of the Algorithm
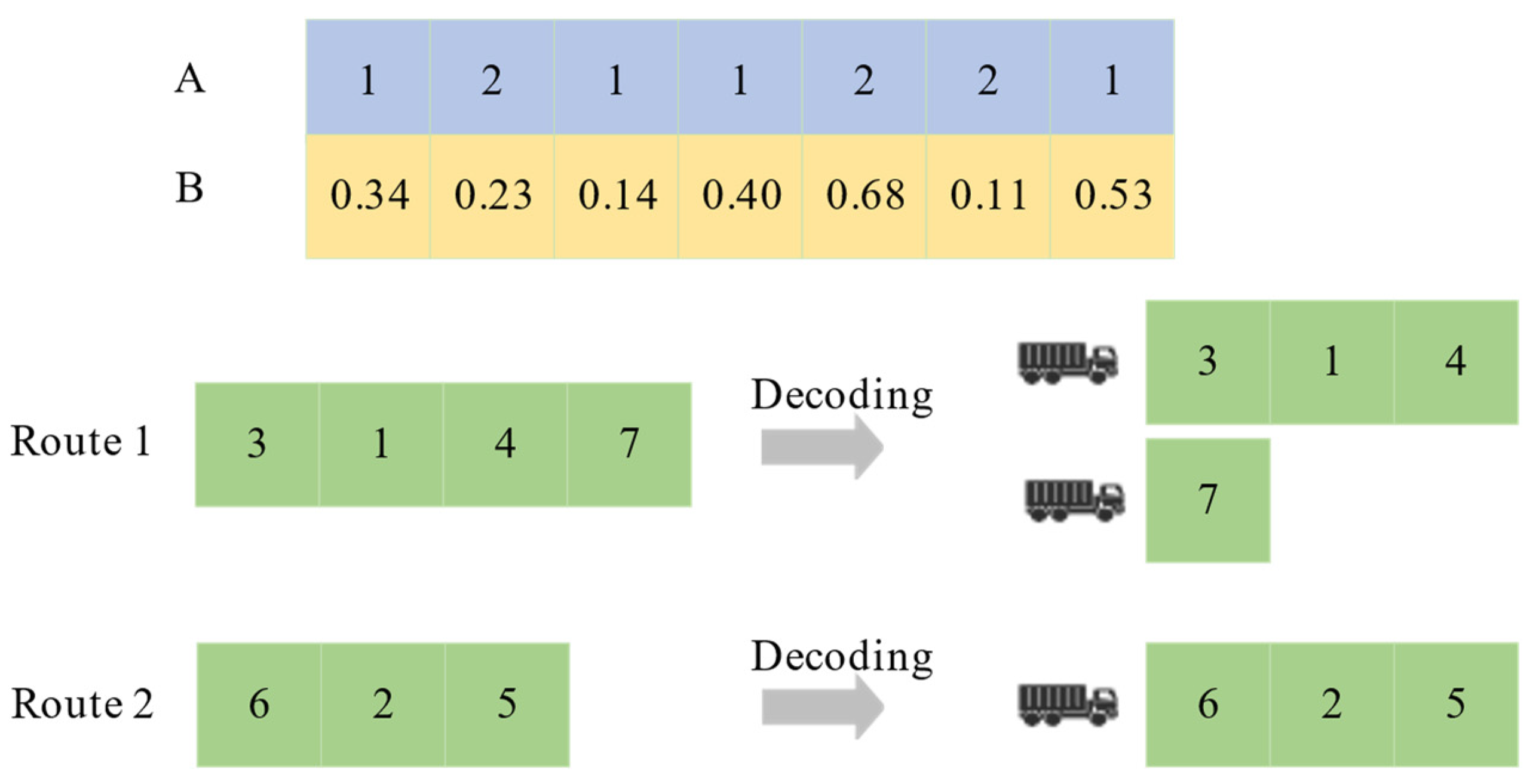
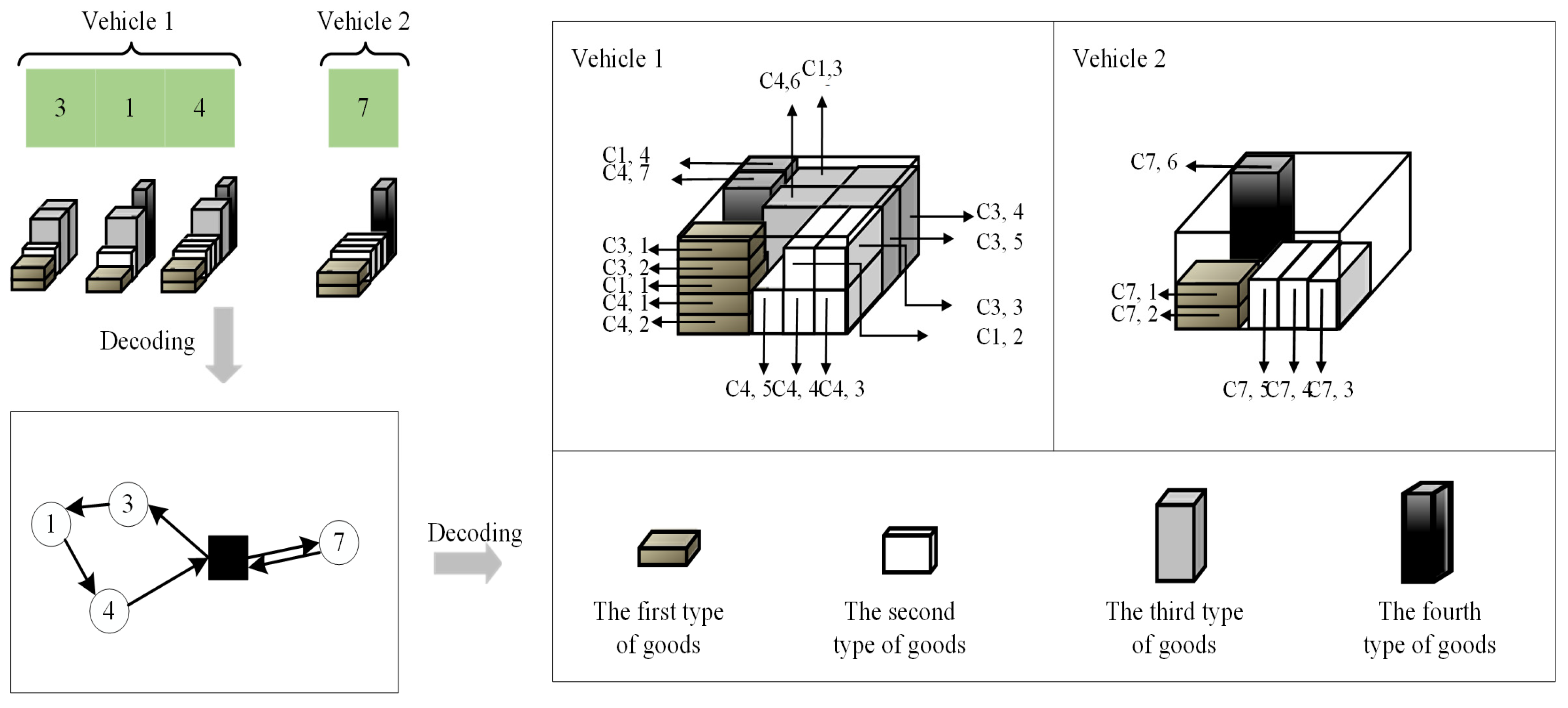
4.2. Representation of Solutions
4.3. Population Initialization
- (1)
- When considering the distance between demand points and distribution centers, the probability function [60] for assigning all demand points to distribution centers is given by Equation (37), where represents the Euclidean distance between the distribution center and demand point , signifies the average distance from demand point to all distribution centers, with representing the total count of demand points. The probability of assigning demand point to distribution center is calculated as follows:
- (2)
- After assigning demand points and distribution centers, we must determine the relationship between vehicles and demand points. In this paper, we use the greedy insertion operator for this initialization, as follows:Step 1: Arrange all demand points in ascending order of their earliest allowable arrival time within the time window.Step 2: Iterate through each vehicle to check if the supplies for each demand point can be inserted into that vehicle. This includes checking if there is enough capacity to carry the items in the task. If the quantity of any item in the task, when added to the quantity of supplies already in the vehicle, exceeds the limit, then that vehicle cannot be used for that demand point.Step 3: For each vehicle, calculate the score (objective function value) of inserting a certain node into it, and record the index of the insertion point, evaluating the effectiveness of different insertion strategies.Step 4: Among all available vehicles, select the one that results in the lowest insertion score. A lower score indicates that inserting this task contributes least to the growth of the objective function, which means it is a better insertion point.
4.4. Selection, Crossover, and Mutation
4.5. Neighborhood Search
- Shaw Removal Operator. Calculate the similarity based on the distance between nodes and the required service time, and remove the top tasks with the highest similarity.
- Random Removal Operator. Randomly remove task nodes from the vehicle’s delivery route.
- Worst Removal Operator. Remove the task nodes that result in the largest increase in total cost.
- Greedy Insertion Operator. Sort the task nodes to be inserted in ascending order of their left time windows and insert them to minimize the delivery time as much as possible.
- Regret Insertion Operator. For each unallocated task node, the algorithm calculates the score after inserting it at a certain position, sorts the scores, and selects the top scores as candidate insertion positions. It computes the sum of the absolute differences between the highest score and the scores of other candidate insertion positions as the regret value for that candidate insertion position. This operator iterates through the list of unallocated tasks, finding the insertion position with the highest regret value for each task.
| Algorithm 1. Procedure of the Neighborhood Search | |
| 1: | input: a feasible solution |
| 2: | ; ; ; |
| 3: | repeat |
| 4: | select removal and insertion operations and |
| 5: | using and ; |
| 6: | ; |
| 7: | if (any of five conditions is satisfied) then |
| 8: | |
| 9: | end if |
| 10: | if < then |
| 11: | |
| 12: | end if |
| 13: | update and ; |
| 14: | until stop criterion is met |
| 15: | return |
5. Numerical Experiments
- (1)
- SPEA-II adopts the solution representation method similar to the MOGA-ALNS, as detailed in Section 4.2. It begins with the generation of a random population using the method described in the same section. The selection and population update mechanisms adhere to the foundational structure of the SPEA-II, as outlined in the literature [62]. For genetic operations, SPEA-II incorporates the same crossover and mutation techniques as found in the MOGA-ALNS, ensuring consistency in the approach to evolving solutions.
- (2)
- Aligning with the MOGA-ALNS for solution representation, the MOEA/D leverages the Tchebycheff approach to create a series of subproblems targeting different parts of the objective space [63]. The processes for constructing neighborhoods, selecting individuals, and updating individual solutions are all based on the core principles of the MOEA/D [63]. Furthermore, the algorithm applies identical crossover and mutation strategies as the MOGA-ALNS, facilitating a uniform method of introducing genetic diversity and exploring the solution space.
5.1. Test Case
5.2. Performance Metrics
- (1)
- The C-metric, a tool for evaluating the comparative performance of two different algorithms through their solution sets and , quantifies the extent to which one set dominates another. Specifically, represents the proportion of solutions in set that are dominated by at least one solution in set . The formula for calculating this metric is as follows:
- (2)
- The IGD-metric calculates the minimum Euclidean distance between the approximate solution set and the Pareto-optimal front. A smaller IGD value indicates that the solution set generated by the algorithm is closer to the true front. Let and represent the optimal solution set and the approximate solution set, respectively. Formula (41) for IGD measurement is as follows:where is the Euclidean distance between a solution in and the closest solution to it in . Therefore, in the calculation of IGD, it is first necessary to have a known true front or an ideal front that represents the best solutions to the problem. Since the Pareto-optimal front of the studied problem is unknown, this study combines all non-dominated solutions obtained by various methods and considers them as an approximate Pareto-optimal front. Furthermore, this study normalizes all objective values, mapping them into the range [0, 1] before calculating the IGD.
- (3)
- The hypervolume-metric measures the coverage range size of the approximate set in the objective space. A higher hypervolume value indicates a broader coverage range of the approximate set in the objective space, which typically implies the higher quality of the obtained non-dominated solution set. Let be the reference point in the objective space dominated by all optimal solutions. Then, the hypervolume value of the solution set represents the volume of a region where all solutions are dominated by the solution set and dominate . When calculating the hypervolume-metric, a reference point needs to be selected. In this paper, (1, 1) is used as the reference point, and all objective values in the approximate solution set are normalized, mapping them into the range [0, 1].
5.3. Parameter Configuration
5.4. Effectiveness of Neighborhood Search
- (1)
- In the Friedman test, we organize the MOGA-ALNS and MOGA-ALNS-w/o-NS by descending average values of the hypervolume-metric and ascending average values for the IGD-metric, assigning them ranks of 1 and 2, respectively. We then calculate the average ranks across all instances as depicted in Table 5. For the hypervolume-metric, the average ranks are 1.05 for the MOGA-ALNS and 1.95 for MOGA-ALNS-w/o-NS. Similarly, for the IGD-metric, the average ranks stand at 1.1000 for the MOGA-ALNS and 1.9000 for MOGA-ALNS-w/o-NS. This differentiation in average ranks allows us to deduce a statistically significant disparity in performance between the MOGA-ALNS and MOGA-ALNS-w/o-NS according to the Friedman test.
- (2)
- To delve deeper into the distinctions between the MOGA-ALNS and MOGA-ALNS-w/o-NS, we employ the Nemenyi post-hoc test at a significance level of 0.05 to ascertain the critical discrepancy in their average rank values. The gap in average ranks for the hypervolume-metric is 0.9000, surpassing the critical threshold of 0.4382. Similarly, for the IGD metric, the difference in average ranks is 0.8000, also exceeding the critical value. These findings underscore the MOGA-ALNS’s notable superiority over MOGA-ALNS-w/o-NS across both evaluated metrics.
5.5. Experimental Results
5.5.1. Analysis of the C-Metric
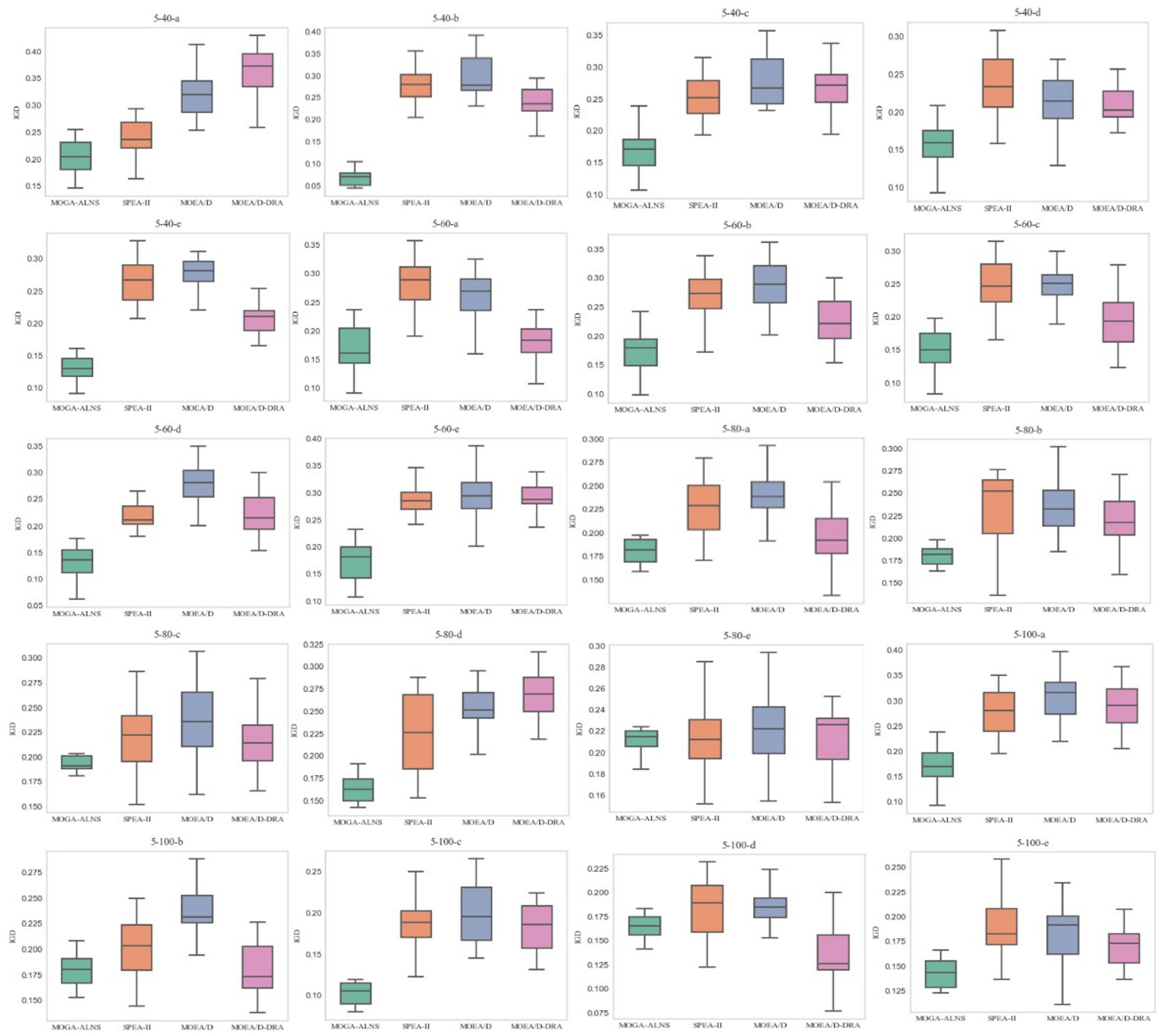
5.5.2. Analysis of the IGD-Metric
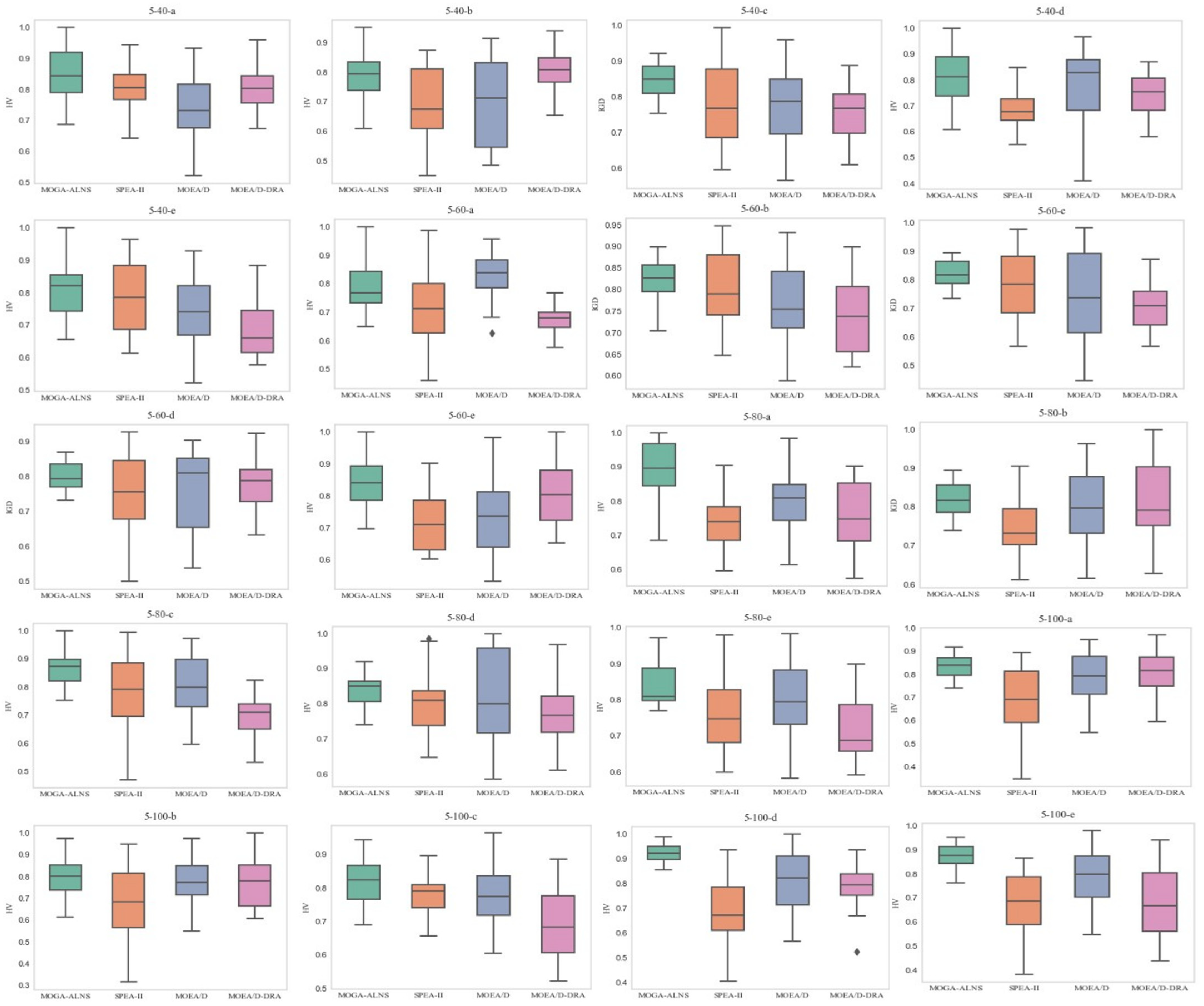
5.5.3. Analysis of Hypervolume-Metric
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Notation | Description |
|---|---|
| Indices | |
| Set of candidate distribution centers; indicates the number of candidate distribution centers. | |
| Set of demand points; represents the number of demand points. | |
| Set of distribution centers and demand points; . | |
| Set of segments in the distribution network; , and represent nodes in the network. | |
| Set of distribution vehicles; represents the total count of vehicles. | |
| Set of scenarios; where represents the number of scenarios, each of which has a set of distribution centers experiencing a simultaneous disruption. | |
| Set of demand points for vehicle services; . | |
| Set of goods types needed across all demand points; where denotes the type of goods. | |
| Set of spaces in the distribution vehicle compartment of vehicle , and is the overall count of spaces. | |
| Set of goods placed in the same space of the same vehicle with good and overlapping with the under-plane projection of goods in scenario . | |
| Set of goods placed in the same space of the same vehicle with good and the bottom surface of good is at the same height in scenario . | |
| Parameters | |
| Distance between the depot or demand point i and demand point j, . | |
| The base capacity of the distribution center . | |
| The maximum capacity of the distribution center can be expanded, . | |
| The cost of constructing the distribution center . | |
| The unit expansion cost of the distribution center . | |
| Fixed operating cost of the vehicle. | |
| The cost per unit distance traveled by the vehicle. | |
| The speed of vehicles. | |
| The maximum loading volume of the vehicle. | |
| The maximum load capacity of the vehicle. | |
| The actual count of layers of goods loaded in the space of vehicle . | |
| The actual count of rows of goods loaded in the space of vehicle . | |
| The actual count of columns of goods loaded in the space of vehicle . | |
| The count of goods placed within the space of vehicle in scenario . | |
| The number of goods loaded at demand point within region by delivery vehicle in scenario . | |
| The individual quality of the goods loaded in region by delivery vehicle . | |
| The overall quality of goods placed in the space of vehicle . | |
| The overall size of goods placed in the space of vehicle . | |
| The overall number of goods placed in the space of vehicle . | |
| The dimensions of the carriage, including its length, width, and height.. | |
| The length, width, and height of the space of vehicle . | |
| The length, width, and height of the goods loaded in the space of vehicle . | |
| The coordinate at the upper-right corner of the front side of the carriage of the point in the space of vehicle . | |
| The coordinate at the lower-left corner of the back side of the carriage of the point in the space of vehicle . | |
| The probability of scenario occurring, . | |
| The probability of secondary disasters such as aftershocks occurring at the distribution center . | |
| The probability of huge losses caused by disasters such as aftershocks affecting the distribution center in scenario . | |
| The cost of losses incurred by distribution center due to disaster risks such as aftershocks in scenario . | |
| The probability of transportation risk associated with the route section in scenario . | |
| The probability of significant loss of goods due to transportation risk occurring along route segment in scenario . | |
| The cost of loss due to transportation risk when goods are transported from to in scenario . | |
| The cargo load of vehicle when transporting from to in scenario | |
| The time for vehicle to reach point in scenario . | |
| The time vehicle requires to serve demand point in scenario . | |
| The penalty coefficient for vehicles arriving at demand point ahead of schedule, . | |
| The penalty coefficient for vehicles arriving at demand point behind schedule, . | |
| The earliest acceptable service time for demand point . | |
| The latest acceptable service time for demand point . | |
| The value is 1 if distribution center fails in scenario ; otherwise, it is 0, . | |
| The value is 1 if vehicle is loaded with class goods within region ; otherwise, it is 0, . | |
| Decision variable | |
| The value is 1 if a distribution center is established at location in scenario ; otherwise, it is 0, . | |
| The value is 1 if vehicle travels from node to node in scenario ; otherwise, it is 0, . | |
| The value is 1 if demand point is serviced by distribution center in scenario ; otherwise, it is 0, | |
| The value is 1 if vehicle carries the goods of demand point within region ; otherwise, it is 0, k.. | |
| The value is 1 if vehicle departs from distribution center to provide delivery services in scenario ; otherwise, it is 0, . | |
| The capacity expansion amount of distribution center in scenario . |
References
- Rahmani, D. Designing a robust and dynamic network for the emergency blood supply chain with the risk of disruptions. Ann. Oper. Res. 2018, 283, 613–641. [Google Scholar] [CrossRef]
- Shen, L.; Tao, F.; Shi, Y.; Qin, R. Optimization of Location-Routing Problem in Emergency Logistics Considering Carbon Emissions. Int. J. Environ. Res. Public Health 2019, 16, 2982. [Google Scholar] [CrossRef] [PubMed]
- Su, Z.; Zhang, G.; Liu, Y.; Yue, F.; Jiang, J. Multiple emergency resource allocation for concurrent incidents in natural disasters. Int. J. Disaster Risk Reduct. 2016, 17, 199–212. [Google Scholar] [CrossRef]
- Bagloee, S.A.; Sarvi, M.; Wolshon, B.; Dixit, V. Identifying critical disruption scenarios and a global robustness index tailored to real life road networks. Transp. Res. Part E Logist. Transp. Rev. 2017, 98, 60–81. [Google Scholar] [CrossRef]
- Jalali, S.; Seifbarghy, M.; Niaki, S.T.A. A risk-averse location-protection problem under intentional facility disruptions: A modified hybrid decomposition algorithm. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 196–219. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, N.; Zhang, J. Integrated temporary facility location and casualty allocation planning for post-disaster humanitarian medical service. Transp. Res. Part E Logist. Transp. Rev. 2019, 128, 1–16. [Google Scholar] [CrossRef]
- Huang, C.-H.; Chang, K.-H.; Liu, C.-H.; Chang, T.-Y.; Lin, Y.-K. Network reliability analysis on casualty rescue for natural disaster evaluation. Ann. Oper. Res. 2023, Feb 10, 1–21. [Google Scholar] [CrossRef]
- Qi, M.; Yang, Y.; Cheng, C. Location and inventory pre-positioning problem under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2023, 177, 103236. [Google Scholar] [CrossRef]
- Wang, Z.; Leng, L.; Ding, J.; Zhao, Y. Study on location-allocation problem and algorithm for emergency supplies considering timeliness and fairness. Comput. Ind. Eng. 2023, 177, 109078. [Google Scholar] [CrossRef]
- Meng, L.; Wang, X.; He, J.; Han, C.; Hu, S. A two-stage chance constrained stochastic programming model for emergency supply distribution considering dynamic uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2023, 179, 103296. [Google Scholar] [CrossRef]
- Zhang, J.; Long, D.Z.; Li, Y. A reliable emergency logistics network for COVID-19 considering the uncertain time-varying demands. Transp. Res. E Logist. Transp. Rev. 2023, 172, 103087. [Google Scholar] [CrossRef] [PubMed]
- Martins, S.; Ostermeier, M.; Amorim, P.; Hübner, A.; Almada-Lobo, B. Product-oriented time window assignment for a multi-compartment vehicle routing problem. Eur. J. Oper. Res. 2019, 276, 893–909. [Google Scholar] [CrossRef]
- Frank, M.; Ostermeier, M.; Holzapfel, A.; Hübner, A.; Kuhn, H. Optimizing routing and delivery patterns with multi-compartment vehicles. Eur. J. Oper. Res. 2021, 293, 495–510. [Google Scholar] [CrossRef]
- Bortfeldt, A.; Yi, J. The Split Delivery Vehicle Routing Problem with three-dimensional loading constraints. Eur. J. Oper. Res. 2020, 282, 545–558. [Google Scholar] [CrossRef]
- Castellucci, P.B.; Costa, A.M.; Toledo, F. Network scheduling problem with cross-docking and loading constraints. Comput. Oper. Res. 2021, 132, 105271. [Google Scholar] [CrossRef]
- Holguín-Veras, J.; Pérez, N.; Jaller, M.; Van Wassenhove, L.N.; Aros-Vera, F. On the appropriate objective function for post-disaster humanitarian logistics models. J. Oper. Manag. 2013, 31, 262–280. [Google Scholar] [CrossRef]
- Afify, B.; Soeanu, A.; Awasthi, A. Separation linearization approach for the capacitated facility location problem under disruption. Expert Syst. Appl. 2021, 169, 114187. [Google Scholar] [CrossRef]
- Wang, W.; Wu, S.; Wang, S.; Zhen, L.; Qu, X. Emergency facility location problems in logistics: Status and perspectives. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102465. [Google Scholar] [CrossRef]
- Yang, Y.; Yin, Y.; Wang, D.; Ignatius, J.; Cheng, T.C.E.; Dhamotharan, L. Distributionally robust multi-period location-allocation with multiple resources and capacity levels in humanitarian logistics. Eur. J. Oper. Res. 2023, 305, 1042–1062. [Google Scholar] [CrossRef]
- Men, J.; Jiang, P.; Zheng, S.; Kong, Y.; Zhao, Y.; Sheng, G.; Su, N.; Zheng, S. A Multi-Objective Emergency Rescue Facilities Location Model for Catastrophic Interlocking Chemical Accidents in Chemical Parks. IEEE Trans. Intell. Transp. Syst. 2020, 21, 4749–4761. [Google Scholar] [CrossRef]
- Maliki, F.; Souier, M.; Dahane, M.; Ben Abdelaziz, F. A multi-objective optimization model for a multi-period mobile facility location problem with environmental and disruption considerations. Ann. Oper. Res. 2022, Sep 8, 1–26. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Z.; Tian, Y.; Zhang, X.; Xiao, J. A Dual-Population Based Evolutionary Algorithm for Multi-Objective Location Problem Under Uncertainty of Facilities. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7692–7707. [Google Scholar] [CrossRef]
- Zhang, Y.; Diabat, A.; Zhang, Z.-H. Reliable closed-loop supply chain design problem under facility-type-dependent probabilistic disruptions. Transp. Res. Part B Methodol. 2021, 146, 180–209. [Google Scholar] [CrossRef]
- Zahedi, A.; Kargari, M.; Husseinzadeh Kashan, A. Multi-objective decision-making model for distribution planning of goods and routing of vehicles in emergency multi-objective decision-making model for distribution planning of goods and routing of vehicles in emergency. Int. J. Disaster Risk Reduct. 2020, 48, 101587. [Google Scholar] [CrossRef]
- Zhong, S.; Cheng, R.; Jiang, Y.; Wang, Z.; Larsen, A.; Nielsen, O.A. Risk-averse optimization of disaster relief facility location and vehicle routing under stochastic demand. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102015. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, N.; Ma, S.; Xia, J. Humanitarian relief network assessment using collaborative truck-and-drone system. Transp. Res. Part E Logist. Transp. Rev. 2021, 152, 102417. [Google Scholar] [CrossRef]
- Molina, J.; López-Sánchez, A.D.; Hernández-Díaz, A.G.; Martínez-Salazar, I. A Multi-start Algorithm with Intelligent Neighborhood Selection for solving multi-objective humanitarian vehicle routing problems. J. Heuristics 2017, 24, 111–133. [Google Scholar] [CrossRef]
- Khanchehzarrin, S.; Ghaebi Panah, M.; Mahdavi-Amiri, N.; Shiripour, S. A bi-level multi-objective location-routing optimization model for disaster relief operations considering public donations. Socio-Econ. Plan. Sci. 2022, 80, 101165. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Fan, J.; Wang, Z.; Zhen, L. Emergency logistics network optimization with time window assignment. Expert Syst. Appl. 2023, 214, 119145. [Google Scholar] [CrossRef]
- Reil, S.; Bortfeldt, A.; Mönch, L. Heuristics for vehicle routing problems with backhauls, time windows, and 3D loading constraints. Eur. J. Oper. Res. 2018, 266, 877–894. [Google Scholar] [CrossRef]
- Göçmen, E.; Erol, R. Transportation problems for intermodal networks: Mathematical models, exact and heuristic algorithms, and machine learning. Expert Syst. Appl. 2019, 135, 374–387. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Z.; Lim, A. An evolutionary local search for the capacitated vehicle routing problem minimizing fuel consumption under three-dimensional loading constraints. In Proceedings of the 2014 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; pp. 203–208. [Google Scholar] [CrossRef]
- Männel, D.; Bortfeldt, A. Solving the pickup and delivery problem with three-dimensional loading constraints and reloading ban. Eur. J. Oper. Res. 2018, 264, 119–137. [Google Scholar] [CrossRef]
- Rajaei, M.; Moslehi, G.; Reisi-Nafchi, M. The split heterogeneous vehicle routing problem with three-dimensional loading constraints on a large scale. Eur. J. Oper. Res. 2022, 299, 706–721. [Google Scholar] [CrossRef]
- Elbek, M.; Wøhlk, S. A variable neighborhood search for the multi-period collection of recyclable materials. Eur. J. Oper. Res. 2016, 249, 540–550. [Google Scholar] [CrossRef]
- Hübner, A.; Ostermeier, M. A Multi-Compartment Vehicle Routing Problem with Loading and Unloading Costs. Transp. Sci. 2019, 53, 282–300. [Google Scholar] [CrossRef]
- Yahyaoui, H.; Kaabachi, I.; Krichen, S.; Dekdouk, A. Two metaheuristic approaches for solving the multi-compartment vehicle routing problem. Oper. Res. 2018, 20, 2085–2108. [Google Scholar] [CrossRef]
- Zbib, H.; Laporte, G. The commodity-split multi-compartment capacitated arc routing problem. Comput. Oper. Res. 2020, 122, 104994. [Google Scholar] [CrossRef]
- Yang, J.; Tao, F.; Zhong, Y. Dynamic routing for waste collection and transportation with multi-compartment electric vehicle using smart waste bins. Waste Manag. Res. 2022, 40, 1199–1211. [Google Scholar] [CrossRef]
- Mohammadi, S.; Avakh Darestani, S.; Vahdani, B.; Alinezhad, A. A robust neutrosophic fuzzy-based approach to integrate reliable facility location and routing decisions for disaster relief under fairness and aftershocks concerns. Comput. Ind. Eng. 2020, 148, 106734. [Google Scholar] [CrossRef]
- Wei, X.; Qiu, H.; Wang, D.; Duan, J.; Wang, Y.; Cheng, T.C.E. An integrated location-routing problem with post-disaster relief distribution. Comput. Ind. Eng. 2020, 147, 106632. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Yu, G. A scenario-based hybrid robust and stochastic approach for joint planning of relief logistics and casualty distribution considering secondary disasters. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102029. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Xue, Y. A bi-objective robust optimization model for disaster response planning under uncertainties. Comput. Ind. Eng. 2021, 155, 107213. [Google Scholar] [CrossRef]
- Gao, X.; Jin, X.; Zheng, P.; Cui, C. Multi-modal transportation planning for multi-commodity rebalancing under uncertainty in humanitarian logistics. Adv. Eng. Inform. 2021, 47, 101223. [Google Scholar] [CrossRef]
- Abazari, S.R.; Aghsami, A.; Rabbani, M. Prepositioning and distributing relief items in humanitarian logistics with uncertain parameters. Socio-Econ. Plan. Sci. 2021, 74, 100933. [Google Scholar] [CrossRef]
- Cheng, J.; Feng, X.; Bai, X. Modeling equitable and effective distribution problem in humanitarian relief logistics by robust goal programming. Comput. Ind. Eng. 2021, 155, 107183. [Google Scholar] [CrossRef]
- Alem, D.; Bonilla-Londono, H.F.; Barbosa-Povoa, A.P.; Relvas, S.; Ferreira, D.; Moreno, A. Building disaster preparedness and response capacity in humanitarian supply chains using the Social Vulnerability Index. Eur. J. Oper. Res. 2021, 292, 250–275. [Google Scholar] [CrossRef]
- Peng, Z.X.; Wang, C.; Xu, W.Q.; Zhang, J.S. Research on Location-Routing Problem of Maritime Emergency Materials Distribution Based on Bi-Level Programming. Mathematics 2022, 10, 1243. [Google Scholar] [CrossRef]
- Ghasemi, P.; Goodarzian, F.; Abraham, A. A new humanitarian relief logistic network for multi-objective optimization under stochastic programming. Appl. Intell. 2022, 52, 13729–13762. [Google Scholar] [CrossRef]
- Vosooghi, Z.; Mirzapour Al-e-hashem, S.M.J.; Lahijanian, B. Scenario-based redesigning of a relief supply-chain network by considering humanitarian constraints, triage, and volunteers’ help. Socio-Econ. Plan. Sci. 2022, 84, 101399. [Google Scholar] [CrossRef]
- Bayraktar, O.B.; Günneç, D.; Salman, F.S.; Yücel, E. Relief Aid Provision to En Route Refugees: Multi-Period Mobile Facility Location with Mobile Demand. Eur. J. Oper. Res. 2022, 301, 708–725. [Google Scholar] [CrossRef]
- Wang, D.; Peng, J.; Yang, H.; Cheng, T.C.E.; Yang, Y. Distributionally robust location-allocation with demand and facility disruption uncertainties in emergency logistics. Comput. Ind. Eng. 2023, 184, 109617. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Zarrinpoor, N. Designing an integrated humanitarian logistics network for the preparedness and response phases under uncertainty. Socio-Econ. Plan. Sci. 2023, 86, 101496. [Google Scholar] [CrossRef]
- Li, J.; Chu, F.; Che, A.; Yin, Y. A Three-Stage Relief Network Design Approach for Predictable Disasters Considering Time-Dependent Uncertainty. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5418–5434. [Google Scholar] [CrossRef]
- Yang, R.; Li, Y.; Zhang, B.; Yang, R. Location–allocation problem in the emergency logistics system considering lateral transshipment strategy. Comput. Ind. Eng. 2024, 187, 109771. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, B. Multiperiod optimal emergency material allocation considering road network damage and risk under uncertain conditions. Oper. Res. 2021, 22, 2173–2208. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Guan, X.; Li, Q.; Fan, J.; Wang, H. A combined intelligent and game theoretical methodology for collaborative multicenter pickup and delivery problems with time window assignment. Appl. Soft Comput. 2021, 113, 107875. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, S.; Zhou, X.; Mahmoudi, M.; Zhen, L. Green logistics location-routing problem with eco-packages. Transp. Res. Part E Logist. Transp. Rev. 2020, 143, 102118. [Google Scholar] [CrossRef]
- Méndez-Fernández, I.; Lorenzo-Freire, S.; González-Rueda, Á.M. An Adaptive Large Neighbourhood Search algorithm for a real-world Home Care Scheduling Problem with time windows and dynamic breaks. Comput. Oper. Res. 2023, 159, 106351. [Google Scholar] [CrossRef]
- Kuo, Y.; Wang, C.-C. A variable neighborhood search for the multi-depot vehicle routing problem with loading cost. Expert Syst. Appl. 2012, 39, 6949–6954. [Google Scholar] [CrossRef]
- Lin, S.-W.; Ying, K.-C. Minimizing makespan and total flowtime in permutation flowshops by a bi-objective multi-start simulated-annealing algorithm. Comput. Oper. Res. 2013, 40, 1625–1647. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm. TIK Rep. 2001, 103, 35. [Google Scholar]
- Zhang, Q.F.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, W.; Li, H. The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 203–208. [Google Scholar] [CrossRef]
- Ghorai, C.; Shakhari, S.; Banerjee, I. A SPEA-Based Multimetric Routing Protocol for Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2021, 22, 6737–6747. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Liu, J.; Zhang, Y.T.; Gan, X.H. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems. Transp. Res. Part E-Logist. Transp. Rev. 2017, 99, 77–95. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, J.; Zhang, C.; Zhao, Y.; Wang, W.; Li, G. Decomposition-based hyperheuristic approaches for the bi-objective cold chain considering environmental effects. Comput. Oper. Res. 2020, 123, 105043. [Google Scholar] [CrossRef]
- Rabbani, M.; Nikoubin, A.; Farrokhi-Asl, H. Using modified metaheuristic algorithms to solve a hazardous waste collection problem considering workload balancing and service time windows. Soft Comput. 2020, 25, 1885–1912. [Google Scholar] [CrossRef]
- Li, H.; Li, G.; Jiang, Q.; Wang, J.; Wang, Z. MOEA/D with customized replacement neighborhood and dynamic resource allocation for solving 3L-SDHVRP. Swarm Evol. Comput. 2024, 85, 101463. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, H.; Tian, G.; Li, Z.; Hu, H. Two-agent stochastic flow shop deteriorating scheduling via a hybrid multi-objective evolutionary algorithm. J. Intell. Manuf. 2018, 30, 2257–2272. [Google Scholar] [CrossRef]
- Li, J.-Q.; Chen, X.-L.; Duan, P.-Y.; Mou, J.-H. KMOEA: A Knowledge-Based Multiobjective Algorithm for Distributed Hybrid Flow Shop in a Prefabricated System. IEEE Trans. Ind. Inform. 2022, 18, 5318–5329. [Google Scholar] [CrossRef]
- Ding, J.; Yang, C.; Xiao, Q.; Chai, T.; Jin, Y. Dynamic Evolutionary Multiobjective Optimization for Raw Ore Allocation in Mineral Processing. IEEE Trans. Emerg. Top. Comput. Intell. 2018, 3, 36–48. [Google Scholar] [CrossRef]
- Hou, Y.; Fu, Y.; Gao, K.; Zhang, H.; Sadollah, A. Modelling and optimization of integrated distributed flow shop scheduling and distribution problems with time windows. Expert Syst. Appl. 2022, 187, 115827. [Google Scholar] [CrossRef]
- Pereira, D.G.; Afonso, A.; Medeiros, F.M. Overview of Friedman’s test and post-hoc analysis. Commun. Stat.-Simul. Comput. 2015, 44, 2636–2653. [Google Scholar] [CrossRef]
- Chang, P.C.; Chen, S.H.; Zhang, Q.; Lin, J.L. MOEA/D for flowshop scheduling problems. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1433–1438. [Google Scholar] [CrossRef]





| Reference | Location | Allocation | Objective | Vulnerable Section | Key Constraints | Solution | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Facility | Link | Fac. Cap | Fac. Exp | TWs | 3D Loading | |||||
| Mohammadi et al. (2020) [40] | Total cost Makespan Transport cost bounds variation | Exa | ||||||||
| Wei et al. (2020) [41] | Total cost Demand satisfaction | Met | ||||||||
| Li et al. (2020) [42] | Total cost | Exa | ||||||||
| Sun et al. (2021) [43] | Total cost Injury severity score | Exa | ||||||||
| Gao et al. (2021) [44] | Fairness Makespan | Exa | ||||||||
| Abazari et al. (2021) [45] | Total cost Makespan | Met | ||||||||
| Cheng et al. (2021) [46] | Fairness | Exa | ||||||||
| Alem et al. (2021) [47] | Effectiveness | Exa | ||||||||
| Peng et al. (2022) [48] | Total cost Demand satisfaction | Met | ||||||||
| Ghasemi et al. (2022) [49] | Total costs Maximum number of unsatisfied demands | Met | ||||||||
| Vosooghi et al. (2022) [50] | Total cost Response time | Met | ||||||||
| Bayraktar et al. (2022) [51] | Total cost | Met | ||||||||
| Wang et al. (2023) [52] | Total cost Makespan | Exa | ||||||||
| Meng et al. (2023) [10] | Total cost Makespan | Exa | ||||||||
| Yang et al. (2023) [19] | Total cost Fairness | Exa | ||||||||
| Wang et al. (2023) [9] | Time cost Quantity of short supplies | Heu | ||||||||
| Sheikholeslami et al. (2023) [53] | Total cost Coverage of the network | Met | ||||||||
| Li et al. (2023) [54] | Total cost in the worst case | Heu | ||||||||
| Zhang et al. (2023) [11] | Total cost | Meta | ||||||||
| Yang et al. (2024) [55] | Total cost | Exa | ||||||||
| This study | Total cost Risk of network | Met | ||||||||
|
|
|
|
|
| No | ARV | |||
|---|---|---|---|---|
| 1 | 50 | 0.3 | 30 | 0.7555 |
| 2 | 50 | 0.5 | 60 | 0.7659 |
| 3 | 50 | 0.7 | 90 | 0.8319 |
| 4 | 50 | 0.9 | 120 | 0.8440 |
| 5 | 75 | 0.3 | 60 | 0.8035 |
| 6 | 75 | 0.5 | 30 | 0.8853 |
| 7 | 75 | 0.7 | 120 | 0.8059 |
| 8 | 75 | 0.9 | 90 | 0.9506 |
| 9 | 100 | 0.3 | 90 | 0.9447 |
| 10 | 100 | 0.5 | 120 | 0.8874 |
| 11 | 100 | 0.7 | 30 | 0.8825 |
| 12 | 100 | 0.9 | 60 | 0.8303 |
| 13 | 125 | 0.3 | 120 | 0.8796 |
| 14 | 125 | 0.5 | 90 | 0.9341 |
| 15 | 125 | 0.7 | 60 | 0.8624 |
| 16 | 125 | 0.9 | 30 | 0.9682 |
| Level | |||
|---|---|---|---|
| 1 | 0.7993 | 0.8458 | 0.8729 |
| 2 | 0.8613 | 0.8682 | 0.8155 |
| 3 | 0.8862 | 0.8456 | 0.9153 |
| 4 | 0.9111 | 0.8983 | 0.8542 |
| Delta | 0.1117 | 0.0526 | 0.0998 |
| Rank | 1 | 3 | 2 |
| Instance | Hypervolume-Metric | IGD-Metric | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MOGA-ALNS | MOGA-ALNS-w/o-NS | MOGA-ALNS | MOGA-ALNS-w/o-NS | |||||||||
| Mean | Var | Rank | Mean | Var | Rank | Mean | Var | Rank | Mean | Var | Rank | |
| 5-40-a | 0.8442 | 0.0083 | 1 | 0.7442 | 0.0161 | 2 | 0.2064 | 0.0015 | 1 | 0.2679 | 0.0016 | 2 |
| 5-40-b | 0.7867 | 0.0101 | 1 | 0.7589 | 0.0108 | 2 | 0.0726 | 0.0005 | 1 | 0.2746 | 0.0009 | 2 |
| 5-40-c | 0.8359 | 0.0104 | 1 | 0.7537 | 0.0105 | 2 | 0.1721 | 0.0011 | 1 | 0.2642 | 0.0014 | 2 |
| 5-40-d | 0.8119 | 0.0131 | 1 | 0.7894 | 0.0086 | 2 | 0.1621 | 0.0017 | 1 | 0.2222 | 0.0018 | 2 |
| 5-40-e | 0.8217 | 0.0097 | 1 | 0.7670 | 0.0093 | 2 | 0.1329 | 0.0005 | 1 | 0.2541 | 0.0013 | 2 |
| 5-60-a | 0.7867 | 0.0106 | 2 | 0.7936 | 0.0103 | 1 | 0.1708 | 0.0018 | 1 | 0.2468 | 0.0022 | 2 |
| 5-60-b | 0.7986 | 0.0182 | 1 | 0.7274 | 0.0203 | 2 | 0.1739 | 0.0013 | 1 | 0.2630 | 0.0016 | 2 |
| 5-60-c | 0.8148 | 0.0190 | 1 | 0.7952 | 0.0152 | 2 | 0.1500 | 0.0009 | 1 | 0.2173 | 0.0014 | 2 |
| 5-60-d | 0.7829 | 0.0180 | 1 | 0.7577 | 0.0153 | 2 | 0.1308 | 0.0008 | 1 | 0.2500 | 0.0014 | 2 |
| 5-60-e | 0.8466 | 0.0060 | 1 | 0.7323 | 0.0146 | 2 | 0.1713 | 0.0013 | 1 | 0.2790 | 0.0023 | 2 |
| 5-80-a | 0.8939 | 0.0089 | 1 | 0.7733 | 0.0140 | 2 | 0.1714 | 0.0022 | 1 | 0.2062 | 0.0012 | 2 |
| 5-80-b | 0.8251 | 0.0148 | 1 | 0.7641 | 0.0195 | 2 | 0.1803 | 0.0016 | 1 | 0.2119 | 0.0011 | 2 |
| 5-80-c | 0.8641 | 0.0043 | 1 | 0.7670 | 0.0184 | 2 | 0.1966 | 0.0009 | 1 | 0.2035 | 0.0013 | 2 |
| 5-80-d | 0.8354 | 0.0030 | 1 | 0.7626 | 0.0076 | 2 | 0.1580 | 0.0017 | 1 | 0.2647 | 0.0015 | 2 |
| 5-80-e | 0.8456 | 0.0043 | 1 | 0.7557 | 0.0125 | 2 | 0.2485 | 0.0027 | 2 | 0.2094 | 0.0013 | 1 |
| 5-100-a | 0.8317 | 0.0024 | 1 | 0.7618 | 0.0104 | 2 | 0.1700 | 0.0016 | 1 | 0.3164 | 0.0010 | 2 |
| 5-100-b | 0.7985 | 0.0098 | 1 | 0.7070 | 0.0054 | 2 | 0.1795 | 0.0007 | 1 | 0.2278 | 0.0010 | 2 |
| 5-100-c | 0.8173 | 0.0056 | 1 | 0.8095 | 0.0154 | 2 | 0.0988 | 0.0007 | 1 | 0.1916 | 0.0010 | 2 |
| 5-100-d | 0.9211 | 0.0015 | 1 | 0.7455 | 0.0178 | 2 | 0.1797 | 0.0007 | 2 | 0.1587 | 0.0013 | 1 |
| 5-100-e | 0.8750 | 0.0024 | 1 | 0.7647 | 0.0105 | 2 | 0.1401 | 0.0007 | 1 | 0.1633 | 0.0006 | 2 |
| Average | 0.8319 | 0.0090 | 1.0500 | 0.7605 | 0.0131 | 1.9500 | 0.1632 | 0.0012 | 1.1000 | 0.2346 | 0.0013 | 1.9000 |
| Instance | C (GA, EAD) | C (EAD, GA) | t-Test | C (GA, SPEA) | C (SPEA, GA) | t-Test | C (GA, DRA) | C (DRA, GA) | t-Test |
|---|---|---|---|---|---|---|---|---|---|
| 5-40-a | 0.7589 | 0.0807 | 0.7267 | 0.0863 | 0.5183 | 0.0923 | |||
| 5-40-b | 0.8063 | 0.0208 | 0.8110 | 0.0513 | 0.7292 | 0.0618 | |||
| 5-40-c | 0.8481 | 0.0310 | 0.6696 | 0.0575 | 0.6801 | 0.0836 | |||
| 5-40-d | 0.7870 | 0.0518 | 0.8489 | 0.0499 | 0.6589 | 0.0731 | |||
| 5-40-e | 0.8945 | 0.0146 | 0.8588 | 0.0208 | 0.7427 | 0.0427 | |||
| 5-60-a | 0.7667 | 0.0458 | 0.7828 | 0.0739 | 0.2857 | 0.1631 | |||
| 5-60-b | 0.7624 | 0.0000 | 0.7983 | 0.0405 | 0.6721 | 0.1010 | |||
| 5-60-c | 0.8135 | 0.0467 | 0.8265 | 0.0351 | 0.6653 | 0.0494 | |||
| 5-60-d | 0.8787 | 0.0000 | 0.8546 | 0.0310 | 0.6967 | 0.1147 | |||
| 5-60-e | 0.8237 | 0.0208 | 0.8574 | 0.0296 | 0.5813 | 0.1120 | |||
| 5-80-a | 0.6475 | 0.0143 | 0.6276 | 0.0482 | 0.4677 | 0.0488 | |||
| 5-80-b | 0.6470 | 0.0250 | 0.8523 | 0.0350 | 0.4133 | 0.0417 | |||
| 5-80-c | 0.8275 | 0.0333 | 0.7361 | 0.0393 | 0.6665 | 0.0714 | |||
| 5-80-d | 0.8558 | 0.0458 | 0.6980 | 0.1244 | 0.7835 | 0.0796 | |||
| 5-80-e | 0.7614 | 0.0125 | 0.8023 | 0.0000 | 0.6322 | 0.0333 | |||
| 5-100-a | 0.9483 | 0.0083 | 0.9217 | 0.0167 | 0.7924 | 0.0917 | |||
| 5-100-b | 0.7964 | 0.0283 | 0.7343 | 0.0767 | 0.5742 | 0.1233 | |||
| 5-100-c | 0.5983 | 0.0444 | 0.7663 | 0.1409 | 0.6745 | 0.1937 | |||
| 5-100-d | 0.8598 | 0.0100 | 0.7638 | 0.0267 | 0.4888 | 0.1600 | |||
| Average | 0.7902 | 0.0284 | 0.7848 | 0.0495 | 0.5218 | 0.0429 |
| Instance | MOGA-ALNS | SPEA-II | MOEA/D | MOEA/D-DRA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Var | Mean | Var | t-Test | Mean | Var | t-Test | Mean | Var | t-Test | |
| 5-40-a | 0.2065 | 0.0030 | 0.2411 | 0.0011 | 0.3199 | 0.0019 | 0.3630 | 0.0022 | |||
| 5-40-b | 0.0697 | 0.0003 | 0.2794 | 0.0016 | 0.2995 | 0.0024 | 0.2411 | 0.0011 | |||
| 5-40-c | 0.1722 | 0.0012 | 0.2538 | 0.0014 | 0.2764 | 0.0015 | 0.2674 | 0.0011 | |||
| 5-40-d | 0.1572 | 0.0008 | 0.2361 | 0.0020 | 0.2110 | 0.0016 | 0.2097 | 0.0006 | |||
| 5-40-e | 0.1315 | 0.0004 | 0.2647 | 0.0014 | 0.2763 | 0.0007 | 0.2065 | 0.0005 | |||
| 5-60-a | 0.1708 | 0.0018 | 0.2783 | 0.0017 | 0.2598 | 0.0020 | 0.1805 | 0.0009 | |||
| 5-60-b | 0.1740 | 0.0013 | 0.2698 | 0.0016 | 0.2881 | 0.0019 | 0.2234 | 0.0022 | |||
| 5-60-c | 0.1501 | 0.0009 | 0.2499 | 0.0014 | 0.2499 | 0.0009 | 0.1951 | 0.0015 | |||
| 5-60-d | 0.1309 | 0.0009 | 0.2195 | 0.0006 | 0.2787 | 0.0013 | 0.2235 | 0.0018 | |||
| 5-60-e | 0.1714 | 0.0013 | 0.2898 | 0.0009 | 0.2954 | 0.0017 | 0.2907 | 0.0009 | |||
| 5-80-a | 0.1799 | 0.0002 | 0.2267 | 0.0011 | 0.2392 | 0.0007 | 0.1949 | 0.0011 | |||
| 5-80-b | 0.1808 | 0.0001 | 0.2345 | 0.0015 | 0.2353 | 0.0011 | 0.2204 | 0.0009 | |||
| 5-80-c | 0.1938 | 0.0001 | 0.2180 | 0.0017 | 0.2328 | 0.0016 | 0.2175 | 0.0010 | |||
| 5-80-d | 0.1642 | 0.0002 | 0.2260 | 0.0021 | 0.2528 | 0.0007 | 0.2670 | 0.0008 | |||
| 5-80-e | 0.2110 | 0.0002 | 0.2102 | 0.0012 | 0.2255 | 0.0013 | 0.2129 | 0.0008 | |||
| 5-100-a | 0.1658 | 0.0019 | 0.2771 | 0.0019 | 0.3093 | 0.0026 | 0.2875 | 0.0021 | |||
| 5-100-b | 0.1806 | 0.0003 | 0.2027 | 0.0008 | 0.2371 | 0.0007 | 0.1808 | 0.0007 | |||
| 5-100-c | 0.1023 | 0.0002 | 0.1886 | 0.0012 | 0.2019 | 0.0014 | 0.1830 | 0.0008 | |||
| 5-100-d | 0.1649 | 0.0002 | 0.1840 | 0.0010 | 0.1856 | 0.0003 | 0.1356 | 0.0008 | |||
| 5-100-e | 0.1434 | 0.0002 | 0.1929 | 0.0011 | 0.1814 | 0.0010 | 0.1717 | 0.0005 | |||
| Average | 0.1610 | 0.0008 | 0.2372 | 0.0014 | 0.2528 | 0.0014 | 0.2236 | 0.0011 | |||
| Instance | MOGA-ALNS | SPEA-II | MOEA/D | MOEA/D-DRA | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Var | Rank | Mean | Var | Rank | t-Test | Mean | Var | Rank | t-Test | Mean | Var | Rank | t-Test | |
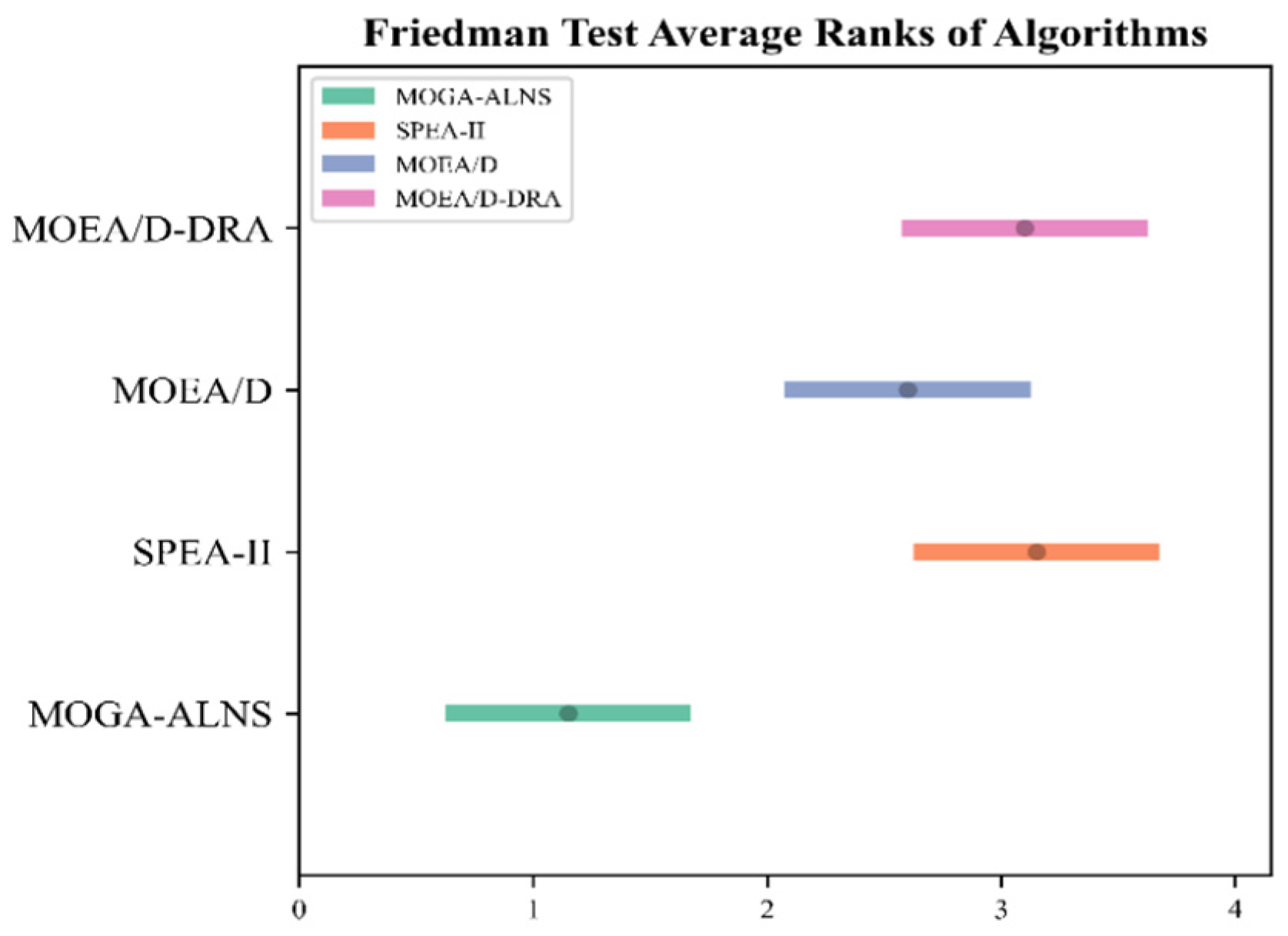
| 5-40-a | 0.8442 | 0.0083 | 1 | 0.8029 | 0.0079 | 3 | 0.7315 | 0.0153 | 4 | 0.8139 | 0.0087 | 2 | |||
| 5-40-b | 0.7867 | 0.0101 | 2 | 0.6933 | 0.0140 | 4 | 0.6990 | 0.0211 | 3 | 0.8072 | 0.0061 | 1 | |||
| 5-40-c | 0.8438 | 0.0022 | 1 | 0.7788 | 0.0145 | 2 | 0.7765 | 0.0131 | 3 | 0.7543 | 0.0064 | 4 | |||
| 5-40-d | 0.8119 | 0.0131 | 1 | 0.6793 | 0.0120 | 4 | 0.7678 | 0.0248 | 2 | 0.7413 | 0.0057 | 3 | |||
| 5-40-e | 0.8217 | 0.0097 | 1 | 0.7861 | 0.0135 | 2 | 0.7499 | 0.0129 | 3 | 0.6809 | 0.0079 | 4 | |||
| 5-60-a | 0.7867 | 0.0106 | 2 | 0.7191 | 0.0195 | 3 | 0.8342 | 0.0084 | 1 | 0.6746 | 0.0028 | 4 | |||
| 5-60-b | 0.8196 | 0.0027 | 1 | 0.8064 | 0.0086 | 2 | 0.7689 | 0.0089 | 3 | 0.7410 | 0.0083 | 4 | |||
| 5-60-c | 0.8232 | 0.0024 | 1 | 0.7793 | 0.0153 | 2 | 0.7480 | 0.0259 | 3 | 0.7100 | 0.0063 | 4 | |||
| 5-60-d | 0.8006 | 0.0021 | 1 | 0.7486 | 0.0157 | 4 | 0.7565 | 0.0145 | 3 | 0.7781 | 0.0083 | 2 | |||
| 5-60-e | 0.8466 | 0.0060 | 1 | 0.7180 | 0.0094 | 4 | 0.7361 | 0.0147 | 3 | 0.8044 | 0.0088 | 2 | |||
| 5-80-a | 0.8939 | 0.0089 | 1 | 0.7364 | 0.0074 | 4 | 0.7963 | 0.0087 | 2 | 0.7631 | 0.0106 | 3 | |||
| 5-80-b | 0.8198 | 0.0023 | 1 | 0.7488 | 0.0064 | 4 | 0.8016 | 0.0110 | 3 | 0.8182 | 0.0116 | 2 | |||
| 5-80-c | 0.8641 | 0.0043 | 1 | 0.7834 | 0.0199 | 3 | 0.8006 | 0.0127 | 2 | 0.6968 | 0.0075 | 4 | |||
| 5-80-d | 0.8354 | 0.0030 | 1 | 0.7983 | 0.0084 | 3 | 0.8183 | 0.0189 | 2 | 0.7729 | 0.0092 | 4 | |||
| 5-80-e | 0.8456 | 0.0043 | 1 | 0.7583 | 0.0112 | 3 | 0.7937 | 0.0145 | 2 | 0.7237 | 0.0083 | 4 | |||
| 5-100-a | 0.8317 | 0.0024 | 1 | 0.6763 | 0.0324 | 4 | 0.7940 | 0.0120 | 3 | 0.8087 | 0.0119 | 2 | |||
| 5-100-b | 0.7985 | 0.0098 | 1 | 0.6820 | 0.0434 | 4 | 0.7718 | 0.0163 | 3 | 0.7810 | 0.0143 | 2 | |||
| 5-100-c | 0.8173 | 0.0056 | 1 | 0.7787 | 0.0042 | 2 | 0.7697 | 0.0102 | 3 | 0.6957 | 0.0127 | 4 | |||
| 5-100-d | 0.9211 | 0.0015 | 1 | 0.6818 | 0.0192 | 4 | 0.8211 | 0.0156 | 2 | 0.7957 | 0.0091 | 3 | |||
| 5-100-e | 0.8750 | 0.0024 | 1 | 0.6833 | 0.0231 | 3 | 0.7831 | 0.0171 | 2 | 0.6674 | 0.0222 | 4 | |||
| Average | 0.8343 | 0.0055 | 1.1000 | 0.7419 | 0.0153 | 3.2000 | 0.7759 | 0.0148 | 2.6000 | 0.7514 | 0.0093 | 3.1000 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, X.; Zhao, X. Post-Earthquake Emergency Logistics Location-Routing Optimization Considering Vehicle Three-Dimensional Loading Constraints. Symmetry 2024, 16, 1080. https://doi.org/10.3390/sym16081080
Pu X, Zhao X. Post-Earthquake Emergency Logistics Location-Routing Optimization Considering Vehicle Three-Dimensional Loading Constraints. Symmetry. 2024; 16(8):1080. https://doi.org/10.3390/sym16081080
Chicago/Turabian StylePu, Xujin, and Xu Zhao. 2024. "Post-Earthquake Emergency Logistics Location-Routing Optimization Considering Vehicle Three-Dimensional Loading Constraints" Symmetry 16, no. 8: 1080. https://doi.org/10.3390/sym16081080





