Tri-Phase Implementation of an Innovative Fuzzy Logic Approach for Decision-Making

Abstract

This paper proposes a novel approach to decision-making based on a three-phase application of a new fuzzy logic model that embraces the principles of symmetry by balancing competing objectives in data collection and analysis. Our study, which employs a three-stage stratified random sample strategy with a randomized response technique, addresses the critical challenges of cost management and volatility reduction. Using the alpha-cut method, our model creates an effective allocation strategy that finds a balance between cost constraints and variance reduction objectives. We use numerical examples from real-world scenarios to demonstrate our approach’s durability and practicality. Our revolutionary technique maintains data quality and cost-effectiveness while offering a game-changing answer to sensitive information acquisition concerns. By combining randomized response techniques and fuzzy logic, this study establishes a new standard for decision-making models that prioritizes both data-gathering precision and privacy preservation, encapsulating the essential principle of symmetry in balancing competing aims.

1. Introduction

Within the field of statistical inference, numerous approaches can be utilized to arrive at findings, depending on the circumstances and goals of the investigation. A common method is to include the inference procedure in a probabilistic framework by utilizing models designed for enumeration-based and analytical inference. This technique is widely recognized as a fundamental component of statisticians’ arsenal, supporting the development of trustworthy inferences from observable data. It is crucial to understand, however, that enumeration inference requires a different probability structure than analytical inference. This discrepancy highlights the necessity for flexibility in statistical modeling and results from the different conditions and assumptions inherent in these approaches. A turning point in statistical inquiry was reached with the extraordinary upsurge in sampling-related research that followed World War II. Few statistical problems attracted as much attention and scientific investigation at this time as sampling theory. The main driver of this increase may be traced to the wide range of real-world uses of sampling theory, which sparked a radical change in data-gathering techniques. This revolutionary influence is demonstrated by the large number of distinguished statisticians who have devoted large amounts of their research efforts to the analysis of sample surveys. In practical applications, these surveys are vital instruments for gathering information from segments of the general public. Survey settings are noteworthy for their capacity to utilize supplementary data. Redistributing some of the survey resources makes it possible to expedite access to additional data. A vast array of repositories, such as census data, previous surveys, or pilot studies, might be included in these auxiliary data sources. These flexible data streams can take many different shapes and offer insightful information about one or more relevant variables. Specific questions are frequently asked in surveys, and answers are gathered from a carefully chosen sample of the community being studied. One such innovative survey approach that has surfaced is the randomized response (RR) technique, which was first developed by [1]. Using this method, a basic random sample, usually consisting of ‘n’ individuals, is selected with replacement from the population. The main goal is to determine the percentage of the population that possesses a sensitive characteristic, represented by the letter “G”. Every member of the sample receives an identical randomization device designed to produce results based on a predetermined probability distribution. “I do not possess the trait G” and “I possess the trait G” are both considered genuine with a predefined probability “P”. The respondent then chooses “Yes” or “No”, depending on how well the results of the randomization device match their real situation. Interested parties can consult a number of seminal articles written by [2,3,4,5,6,7,8,9], among others, for a more in-depth examination of the nuances and complexity present in these methodologies. These publications provide thorough insights and direction in this area. These scholarly works provide deeper insights into statistical inference, sampling strategies, and the changing landscape of data-gathering methodologies, making them invaluable knowledge repositories for both researchers and practitioners.

2. Some Related Models

Ref. [10] used the randomization device carrying three types of cards bearing statements: (i) “I belong to sensitive group A₁”, (ii) “I belong to group A₂”, and (iii) “Blank cards”, with corresponding probabilities Q₁, Q₂, and Q₃, respectively, such that ${\displaystyle \sum _{i=1}^3{Q}_1}=1$. If the blank card is drawn by the respondent, he/she will report “no.” The rest of the procedure remains as usual. The probability of a “Yes” answer is given by

$${\theta }_1=Q_1{\pi }_1+Q_2{\pi }_2$$

where ${\pi }_1$ and ${\pi }_2$ are the true proportion of the rare sensitive attribute A1 and the rare unrelated attribute A2 in the population, respectively. From the above Equation, the estimator of ${\pi }_1$ is as

$${\widehat{\pi }}_1={\displaystyle \frac{{\widehat{\theta }}_1-P_2{\pi }_2}{P_1}}$$

where ${\widehat{\theta }}_1$ the observed proportion of “yes” answers in the sample. The variance of the estimator ${\widehat{\pi }}_1$ is given as

$$V({\widehat{\pi }}_1)={\displaystyle \frac{{\pi }_1(1-{\pi }_1)}{n}}+{\displaystyle \frac{{\pi }_1(1-P_1-2P_2{\pi }_1)}{n{P}_1}}+{\displaystyle \frac{P_2{\pi }_2(1-P_2{\pi }_1)}{n{P}_1^2}}$$

An approach to calculating the mean number of persons possessing a rare sensitive trait using stratified sampling was proposed by Ref. [9], Bayesian by Ref. [11], and others Refs. [12,13,14,15,16,17,18,19,20,21]. In light of the aforementioned research, we have attempted in this paper to extend the unrelated randomized response model of [10] to a three-stage procedure for unrelated randomized responses in stratified and stratified random double sampling using a Poisson distribution to estimate the rare sensitive attribute in cases where the rare unrelated question’s parameter is known. The recommended model has been shown to perform better through empirical investigations. Analyses of the data are provided, along with appropriate suggestions.

3. Problem Formulation

Over time, significant advancements in electrical system size and efficiency have been observed, mostly as a result of the use of optimization techniques. By continuously modifying and optimizing parameters in real-time, these approaches are crucial for improving the performance of both linear and nonlinear systems. Whether they represent maxima or minima, optimization strategies are flexible and able to find optimal values by fine-tuning system parameters. It is important to recognize, though, that it would be premature to declare any specific electrical system design to be the best option, given how quickly technology is developing. Technology constantly reshapes what is possible, pushing the envelope and breaking preconceived notions of what is possible. A problem of optimization occurs in the context of Tarray and Singh’s two-stage stratified random sampling model with fuzzy costs. In 2015, fuzzy, nonlinear programming was used to solve this problem. This model’s optimal allocation was the main problem to be solved. The method of Lagrange multipliers, a potent optimization tool, was employed to solve the problem. Furthermore, at a predefined alpha threshold, the fuzzy numbers—which represented the ideal allocation—were transformed into discrete integers using the alpha-cut approach. For practical applications, working with integer sample sizes is essential;hence, finding an integer-based solution is quite important. Utilizing LINGO software 21.0, the researchers were able to arrive at this answer without having to round off the continuous data. By framing the issue as a fuzzy integer nonlinear programming problem, this method produced a more accurate and useful solution for electrical system design. This methodology allows for the reliable collection of data on sensitive attributes within the population while also protecting the privacy of the respondents. The challenge of optimal allocation in stratified random sampling with fuzzy costs is successfully addressed through the innovative use of fuzzy nonlinear programming and sophisticated optimization techniques, offering important insights for the design and enhancement of electrical systems.

Initially, Ω is a finite population of size N, which is composed of L strata of size N_h (h = 1, 2, 3…, L). A sample of size n_h is drawn by simple random sampling with replacement (SRSWR) from the hth stratum. It is assumed that the stratum ${\pi }_{sh2}$ is known. The n_h respondents from the hth stratum are provided with the following three-stage randomization device:

Statements	Selection probability
Statement 1: Are you a member of a rare sensitive Group A1? Statement 2: Go to randomization device R2h	${\alpha }_h$ $1-{\alpha }_h$

Second-stage randomization device R₂h consists of two statements

Statements	Selection probability
Statement 1: Are you a member of a rare sensitive Group A1? Statement 2: Go to randomization device R3h	Ph (1 − Ph)

The randomization device R_3h utilized three statements. Let X_h and Y_h denotethe number of cards that the respondent drew from the first and second decks, respectively, to obtain the cards that represent their personal status. ${\phi }_{hi}$ might be stated as, if ${\phi }_{hi}$ is the ith respondent in the hth stratum:

$${\phi }_h={\alpha }_h{\pi }_{sh1}+(1-{\alpha }_{hi})[P_h{\pi }_{sh1}+(1-P_h)(Q_{1h}{\pi }_{sh1}+Q_{2h}{\pi }_{sh2})]$$

(1)

$${\widehat{\pi }}_{sh1}={\displaystyle \frac{{\widehat{\phi }}_h-Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)}{{\alpha }_h+(1-{\alpha }_h)P_h+(1-{\alpha }_h)(1-P_{h)})Q_{1h}}}$$

(2)

with

$$V({\pi }_{sh1})={\displaystyle \frac{{\pi }_{sh1}(1-{\pi }_{sh1})}{n_h}}+{\displaystyle \frac{Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)(1-Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)}{n_h{({\alpha }_h+(1-{\alpha }_h)P_h+(1-{\alpha }_h)(1-P_{h)})Q_{1h})}^2}}$$

(3)

and

$${\widehat{\pi }}_s={\displaystyle \sum _{h=1}^L{W}_h{\widehat{\pi }}_{sh1}}$$

(4)

Using (2)

$${\widehat{\pi }}_s={\displaystyle \sum _{h=1}^L{W}_h}\left[{\displaystyle \frac{{\widehat{\phi }}_{hi}-Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)}{{\alpha }_h+(1-{\alpha }_h)P_h+(1-{\alpha }_h)(1-P_{h)})Q_{1h}}}\right]$$

(5)

with a sampling variance

$$V({\widehat{\pi }}_s)={\displaystyle \sum _{h=1}^L{W_h}^{2}V({\widehat{\pi }}_{sh1})}$$

(6)

or

$$V({\widehat{\pi }}_s)={\displaystyle \sum _{h=1}^L{W_h}^2}\left[{\displaystyle \frac{{\pi }_{sh1}(1-{\pi }_{sh1})}{n_h}}+{\displaystyle \frac{Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)(1-Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)}{n_h{[({\alpha }_h+(1-{\alpha }_h)P_h+(1-{\alpha }_h)(1-P_{h)})Q_{1h})]}^2}}\right]$$

(7)

where

$${\beta }_h=\left[{\displaystyle \frac{Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)(1-Q_{2h}{\pi }_{sh2}(1-P_h)(1-{\alpha }_h)}{{[({\alpha }_h+(1-{\alpha }_h)P_h+(1-{\alpha }_h)(1-P_{h)})Q_{1h})]}^2}}\right]$$

with variance

$$V({\widehat{\pi }}_S)={\displaystyle \sum _{h=1}^L\frac{w_h^2}{n_h}{\beta }_h}$$

(8)

$$Cost Function = {\subset }_0+{\displaystyle \sum _{h=1}^k{\subset }_h{n}_h}$$

where ${\subset }_0$ is the available fixed budget for the survey, ${\subset }_0$ is the available fixed budget for the survey, and is the overhead expense. Nonlinear programming (NLPP) problem with fixed costs

$$\left.\begin{array}{l}Minimize V({\widehat{\pi }}_s)= {\displaystyle \sum _{h=1}^k \frac{{W_h}^2}{n_h}{\beta }_h} \\ subject to {\displaystyle \sum _{h=1}^k {\subset }_h{n}_h \le {\subset }_0} \\ 1 \le n_h \le N_h \\ and n_h \mathrm{int}egers, h = 1,2,\dots k\end{array}\right\}$$

The limitations $1 \le n_h$ and $n_h \le N_h$ are put in place, respectively.

4. Fuzzy Formulation

This new problem has led to the development of a field called privacy-preserving data mining (PPDM). Randomization is one of the potential techniques for privacy-preserving data mining. Before providing the actual data to data sleuths, this technique disguises it. Fuzzy numbers can be classified as triangular fuzzy numbers (TFN).

$$\left.\begin{array}{l}Minimize {\displaystyle \sum _{h=1}^k \frac{{w_h}^2}{n_h}{\beta }_h} \\ subject to {\displaystyle \sum _{h=1}^k\begin{array}{l} ({\subset }_h^1,{\subset }_h^2,{\subset }_h^3)n_h\\ \le ({\subset }_0^1,{\subset }_0^2,{\subset }_0^3)\end{array}} \\ 1 \le n_h \le N_h \\ and n_h \mathrm{int}egers, h = 1,2,\dots k\end{array}\right\}$$

and ${\tilde{\subset }}_h=({\subset }_h^1,{\subset }_h^2,{\subset }_h^3)$ is triangular fuzzy numbers with membership function

$${\mu }_{\tilde{\subset }{h}_i}(x)=\left\{\begin{array}{l}{\displaystyle \frac{x - {\subset }_h^1}{{\subset }_h^2-{\subset }_h^1}}, if {\subset }_h^1 \le x \le {\subset }_h^2,\\ {\displaystyle \frac{{\subset }_i^3-x}{{\subset }_h^3-{\subset }_h^2}}, if {\subset }_h^2 \le x \le {\subset }_h^3,\\ 0, otherwise\end{array}\right.$$

The following is a comparable description of the membership function for the available budget:

$${\mu }_{{\tilde{\subset }}_0}(x)=\left\{\begin{array}{l}{\displaystyle \frac{x - {\subset }_0^1}{{\subset }_h^2-{\subset }_0^1}}, if {\subset }_0^1 \le x \le {\subset }_0^2,\\ {\displaystyle \frac{{\subset }_0^3-x}{{\subset }_0^3-{\subset }_0^2}}, if {\subset }_0^2 \le x \le {\subset }_0^3,\\ 0, otherwise\end{array}\right.$$

Moreover, we discuss the trapezoidal fuzzy number (TrFN).

$$\left.\begin{array}{l}Minimize {\displaystyle \sum _{h=1}^k \frac{{W_h}^2}{n_h}{\beta }_h} \\ subject to {\displaystyle \sum _{h=1}^k\begin{array}{l} ({\subset }_h^1,{\subset }_h^2,{\subset }_h^3,{\subset }_h^4)n_h\\ \le ({\subset }_0^1,{\subset }_0^2,{\subset }_0^3{\subset }_0^4)\end{array}} \\ 1 \le n_h \le N_h \\ and n_h \mathrm{int}egers, h = 1,2,\dots k\end{array}\right\}$$

and ${\tilde{\subset }}_i =({\subset }_h^1,{\subset }_h^2,{\subset }_h^3,{\subset }_h^4)$ is trapezoidal fuzzy numbers with membership function.

$${\mu }_{{\tilde{\varsigma }}_i}(x)=\left\{\begin{array}{l}0, if x \le {\subset }_h^1,\\ {\displaystyle \frac{x -{\subset }_h^1}{{\subset }_h^2-{\subset }_h^1}}, if {\subset }_h^1 \le x \le {\subset }_h^2,\\ 1, if {\subset }_h^2 \le x \le {\subset }_h^3,\\ {\displaystyle \frac{{\subset }_h^4- x}{{\subset }_h^4-{\subset }_h^3}}, if {\subset }_h^3 \le x \le {\subset }_h^4,\\ 0, if {\subset }_h^4 \le x\end{array}\right.$$

with this

$${\mu }_{{\tilde{\subset }}_0}(x)=\left\{\begin{array}{l}0, if x \le {\subset }_0^1,\\ {\displaystyle \frac{x -{\subset }_0^1}{{\subset }_0^2-{\subset }_0^1}}, if {\subset }_0^1 \le x \le {\subset }_0^2,\\ 1, if {\subset }_0^2 \le x \le {\subset }_0^3,\\ {\displaystyle \frac{{\subset }_0^4- x}{{\subset }_0^4-{\subset }_0^3}}, if {\subset }_0^3 \le x \le {\subset }_0^4,\\ 0, if {\subset }_0^4 \le x\end{array}\right.$$

5. Lagrange Multipliers Formulation

Possibly, the Lagrangian function

$$\phi \left(n_h,\lambda \right) = {\displaystyle \sum _{i=1}^k \frac{{w_i}^2}{n_i}\left\{{\beta }_{hi}\right\}} +\lambda \left[{\displaystyle \sum _{i=1}^k\left({{\subset }_i}^{(1)},{{\subseteq }_i}^{(2)},{{\subset }_i}^{(3)}\right)n_i-\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)}\right)}\right]$$

with

$${\displaystyle \frac{\overline{V}\phi }{\overline{V}{n}_i}}=0\Rightarrow n_i=-{\displaystyle \frac{w_i^2}{n_h^2}}\left\{{\beta }_i\right\}+\lambda \left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)$$

or

$$n_i={\displaystyle \frac{1}{\sqrt{\lambda }}}{\displaystyle \frac{\sqrt{\left\{{\beta }_i\right\}}}{\sqrt{\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}}}$$

Also,

$${\displaystyle \frac{\overline{V}\phi }{\overline{V}\lambda }}=\left\{{\displaystyle \sum _{i=1}^k\begin{array}{l}\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)n_i\\ -\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)}\right)\end{array}}\right\}=0$$

which gives

$${\displaystyle \sum _{i=1}^k{w}_i\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}\sqrt{{\displaystyle \frac{\left\{A_i\right\}}{\lambda \left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}}}-\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)}\right)=0$$

or

$${\displaystyle \frac{1}{\sqrt{\lambda }}}={\displaystyle \frac{\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)}\right)}{{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{{\beta }_i\right\}\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}} }}$$

also,

$$n_i^{\ast }={\displaystyle \frac{\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)}\right)w_i\sqrt{\frac{\left\{{\beta }_i\right\}}{\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}}}{{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{{\beta }_i\right\}\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)}\right)}} }}$$

and

$$n_i^{\ast }={\displaystyle \frac{\left({{\subset }_0}^{(1)},{{\subset }_0}^{(2)},{{\subset }_0}^{(3)},{{\subset }_0}^{(4)}\right)w_i\sqrt{\frac{\left\{{\beta }_i\right\}}{\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)},{{\subset }_i}^{(4)}\right)}}}{{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{{\beta }_i\right\}\left({{\subset }_i}^{(1)},{{\subset }_i}^{(2)},{{\subset }_i}^{(3)},{{\subset }_i}^{(4)}\right)}} }}$$

Convert fuzzy allocations into a crisp allocation using the cut method.

6. Procedure for Conversation of Fuzzy Numbers

An alpha-cut for $\tilde{M}$, ${\tilde{M}}_{\alpha }$ computed as

$$\alpha ={\displaystyle \frac{x-p}{q-p }}\Rightarrow {{\tilde{M}}_{\alpha }}^L=x=(q-p)\alpha +p$$

and

$$\alpha ={\displaystyle \frac{r-x}{r-q }}\Rightarrow {{\tilde{M}}_{\alpha }}^U=x=r-(r-q)\alpha$$

where ${\tilde{M}}_{\alpha }=[{{\tilde{M}}_{\alpha }}^L, {{\tilde{M}}_{\alpha }}^U]$.

Given by is the analogous crisp allocation,

$$n_i^{\ast }={\displaystyle \frac{\left({{\subset }_0}^{(3)}- ({{\subset }_0}^{(3)}-{{\subset }_0}^{(2)})\right)w_i\sqrt{\frac{\left\{{\beta }_i\right\}}{\left({{\subset }_h}^{(1)}+({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)}}}{{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{A_i\right\}\left({{\subset }_h}^{(1)}+ ({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)}} }}$$

Equal Disbursement. This method divides the total sample size n equally among the strata, yielding the hth stratum, so the reduced equation will be

$$n_i^{\ast }={\displaystyle \frac{\left({{\subset }_0}^{(4)}- ({{\subset }_0}^{(4)}-{{\subset }_0}^{(3)})\right)w_i\sqrt{\frac{\left\{{\beta }_i\right\}}{\left({{\subset }_h}^{(1)}+({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)}}}{{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{{\beta }_i\right\}\left({{\subset }_h}^{(1)}+ ({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)}} }}$$

with

$$n_i={\displaystyle \frac{n}{k }}$$

n can be computed from,

$$\begin{array}{l}{\displaystyle \sum _{i=1}^k{w}_i\sqrt{\left\{A_i\right\}\left({{\subset }_h}^{(1)}+ ({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)}}{n}_i\\ =\left({{\subset }_0}^{(4)}- ({{\subset }_0}^{(4)}-{{\subset }_0}^{(3)})\right)\end{array}$$

And $n_i\propto w_i$

or

$$n_i=n{w}_i$$

and for $n_i$

$$n_i={\displaystyle \frac{N\left({{\subset }_0}^{(4)}- ({{\subset }_0}^{(4)}-{{\subset }_0}^{(3)})\right)}{{\displaystyle \sum _{i=1}^k\sqrt{\left({{\subset }_h}^{(1)}+ ({{\subset }_h}^{(2)}-{{\subset }_h}^{(1)})\right)N_h}}}}$$

having

$$n_i=n{\displaystyle \frac{N_i}{N}}$$

7. Numerical Illustration

Using a population size of 1000 and total survey budgets of 3500, 4000, and 4800 units, respectively, for TFNs and 3500, 4000, 4400, and 4600 units for TrFNS, the required FNLLP is calculated based on the values provided in Table 1 and Table 2 as follows:

$$\left.\begin{array}{l}Minimize V({\hat{\pi }}_S)= {\displaystyle \frac{0.0224937869}{n_1}} +{\displaystyle \frac{0.1236160385}{n_2}} \\ sujbect to (1,2,4)n_1\\ +(18,20,24)n_2\\ \le (3500,4000,4800)\\ 1 \le n_1 \le 300\\ 1 \le n_2 \le 700 \end{array}\right\}$$

(9)

Table 1. The stratified population with two strata.

St.	$({\subset }_h^1,{\subset }_h^2,{\subset }_h^3)$	$({\subset }_0^1,{\subset }_0^2,{\subset }_0^3)$
1	(1,2,4)	(1,2,4,7)
2	(18,20,24)	(18,20,24,26)

Table 2. Calculated values of ${\beta }_i$ and ${\beta }_i{w}_i^2$.

St.	Xi	${\beta }_i{w}_i^2$
1	0.0224937869	0.00045
2	0.1236160385	0.00833

The required optimal allocations for the issue may be obtained by entering the values from Table 1 and Table 2 in (9) at =0.5.

$$\begin{array}{l}{n}_1={\displaystyle \frac{(4800-800\alpha )0.3\sqrt{(0.4(1-0.4)+0.005)/(\alpha +1)}}{0.3\sqrt{(0.24+0.005)(\alpha +1)}+0.7\sqrt{(0.24+0.017)(2\alpha +180)}}} \\ n_2={\displaystyle \frac{(4800-800\alpha )0.7\sqrt{(0.24+0.17/(2\alpha +18)}}{0.3\sqrt{(0.24+0.005)(\alpha +1)}+0.7\sqrt{(0.24+0.17)(2\alpha +18)}}} ;\\ n_1=308.5986; n_2=211.858\end{array}$$

In a similar way, the problem of the optimal allocation will be determined by inserting values from Table 1, Table 2 and Table 3 at a value of 0.50.

$$\begin{array}{l}{n}_1={\displaystyle \frac{(4400-200\alpha )0.3\sqrt{(0.4(1-0.4)+0.005)/(\alpha +1)}}{0.3\sqrt{(0.24+0.005)(\alpha +1)}+0.7\sqrt{(0.24+0.017)(2\alpha +180)}}} \\ n_2={\displaystyle \frac{(4400-200\alpha )0.7\sqrt{(0.24+0.17/(2\alpha +18)}}{0.3\sqrt{(0.24+0.005)(\alpha +1)}+0.7\sqrt{(0.24+0.17)(2\alpha +18)}}} \\ n_1=301.585 ; n_2=207.043\end{array}$$

Table 3. Optimum allocation and variance values.

Case of	Variance
TFN	0.000665369
TrFN	0.000681371

Case—I:

$$\left.\begin{array}{l}Minimize V({\hat{\pi }}_S)= {\displaystyle \frac{0.0224937869}{n_1}} +{\displaystyle \frac{0.1236160385}{n_2}} \\ sujbect to (1)n_1+(18)n_2 \le (3500)\\ 1 \le n_1 \le 300\\ 1 \le n_2 \le 700 \end{array}\right\}$$

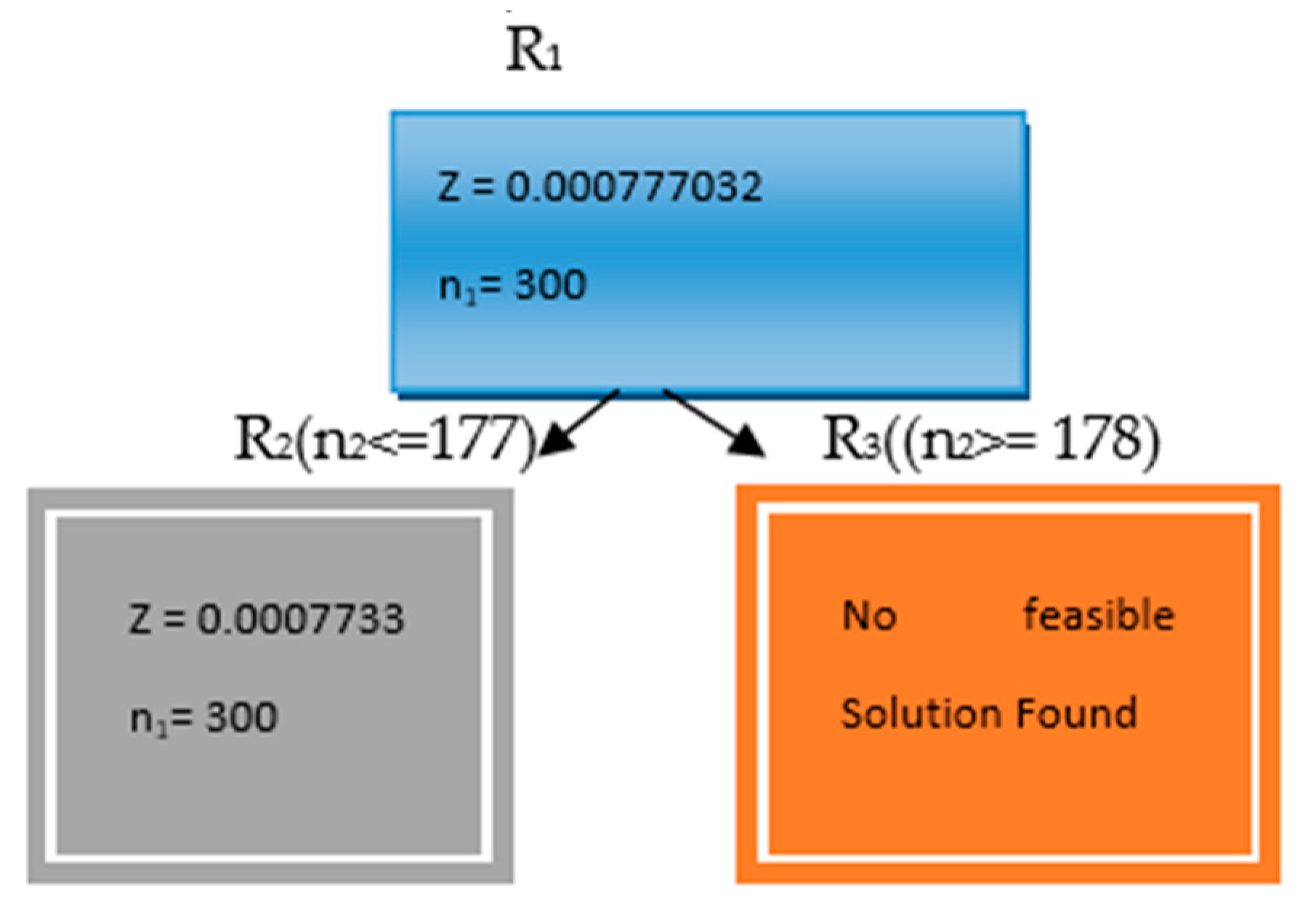
Using the above minimization problem, we obtain the optimal solution as $n_1=300$, $n_2=177.77$, and the optimal value is Minimize $V({\hat{\pi }}_S)$ = 0.000777032.

Since n₁ and n₂ are required to be integers, we branch problem R₁ into two sub-problems, R₂ and R₃, by introducing the constraints n₂ ≤ 177 and n₂ ≥ 178, respectively, indicated by the value n₁ = 300. The optimal solution is then determined as n₁ = 300 and n₂ = 177, minimizing V (${\stackrel{⌢}{\pi }}_S$) = 0.000777032. Notably, these optimal integer values are the same as those obtained by rounding n_i to the nearest integer. Assuming V (${\stackrel{⌢}{\pi }}_S$) = Z, the various nodes for the NLPP using case I are illustrated in Figure 1.

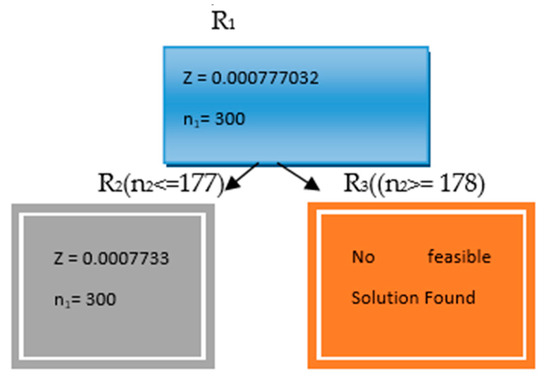
Figure 1. Various nodes of NLPP.

Case—II:

$$\left.\begin{array}{l}Minimize V({\hat{\pi }}_S)= {\displaystyle \frac{0.0224937869}{n_1}} +{\displaystyle \frac{0.1236160385}{n_2}} \\ sujbect to (2)n_1+(20)n_2 \le (4000)\\ 1 \le n_1 \le 300\\ 1 \le n_2 \le 700 \end{array}\right\}$$

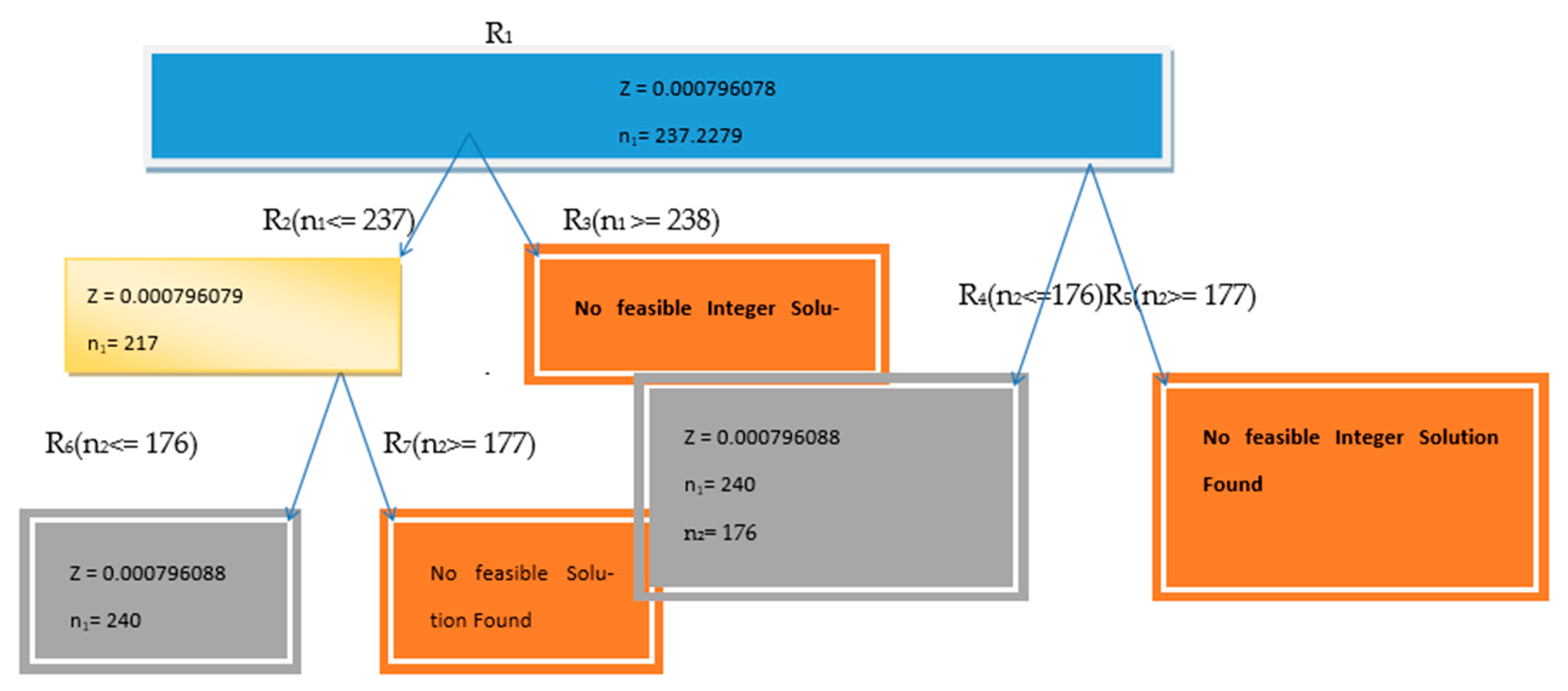
Using the above minimization problem, we obtain the optimal solution as $n_1=237.2279$, $n_2=176.2279$, and the optimal value is minimized $V({\hat{\pi }}_S)=0.00079607$.

Since n₁ and n₂ are required to be integers, problem R₁ is further branched into sub-problems R₂, R₃, R₄, and R₅ with additional constraints of n₁ ≤ 237, n₁ ≥ 238, n₂ ≤ 176, and n₂ ≥ 177, respectively. Problem R₄ is resolved optimally as the solutions for n₁ and n₂ are integers. Problem R₂ is further divided into sub-problems R₆ and R₇ with constraints n₂ ≤ 176 and n₂ ≥ 177, respectively. R₆ is resolved optimally, while R₇ has no feasible solution. The optimal solution is n₁ = 240 and n₂ = 176, minimizing V (${\stackrel{⌢}{\pi }}_S$) = 0.000796088. Assuming V (${\stackrel{⌢}{\pi }}_S$) = Z, the various nodes for the NLPP using case II are shown in Figure 2.

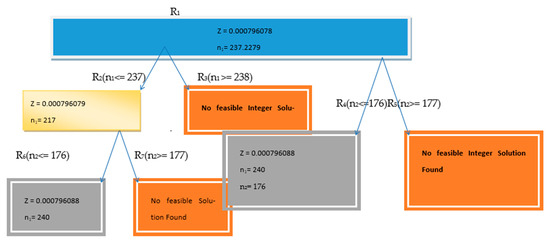
Figure 2. Various nodes of NLPP.

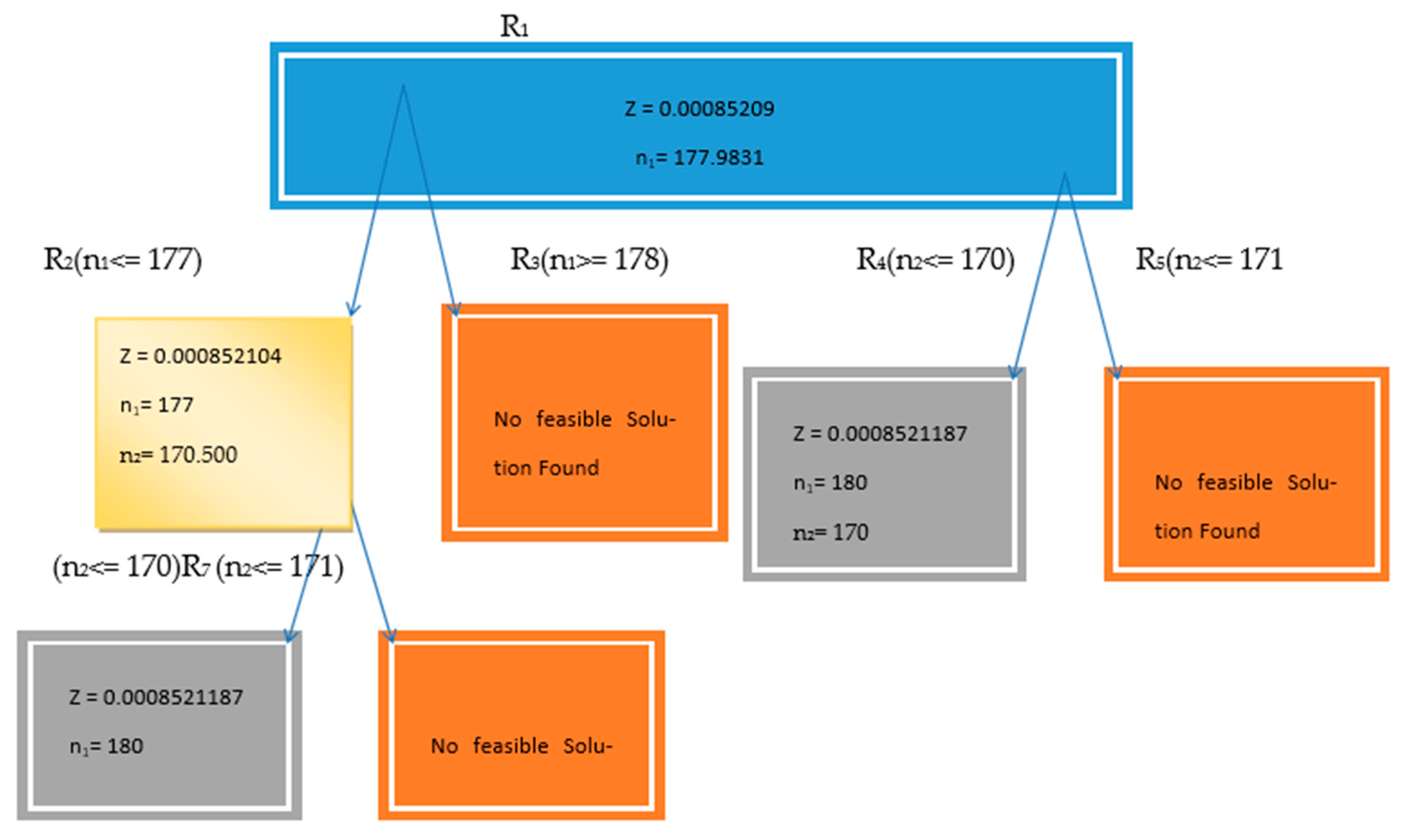
Case—III:

$$\left.\begin{array}{l}Minimize V({\hat{\pi }}_S) = {\displaystyle \frac{0.0224937869}{n_1}} +{\displaystyle \frac{0.1236160385}{n_2}} \\ sujbect to (4)n_1+(24)n_2 \le (4800)\\ 1 \le n_1 \le 300\\ 1 \le n_2 \le 700 \end{array}\right\}$$

Using the above minimization problem, we obtain the optimal solution as $n_1=177.9831$, $n_2=170.3361$, and the optimal value is minimized $V({\hat{\pi }}_S)$ = 0.00085209. Since n₁ and n₂ are required to be integers, problem R₁ is further branched into sub-problems R₂ and R₃, R₄, and R₅ with additional constraints of n₁ ≤ 177 and n₁ ≥ 178, respectively. Problems R₄ are resolved optimally with integer solutions for n₁ and n₂. Problem R₂ is further divided into sub-problems R₆ and R₇ with constraints of n₂ ≤ 170 and n₂ ≥ 171, respectively. R₆ is resolved optimally, while R₇ has no feasible solution. The optimal solution is n₁ = 180 and n₂ = 170, minimizing V (${\stackrel{⌢}{\pi }}_S$) = 0.0008521187. Assuming V(${\stackrel{⌢}{\pi }}_S$) = Z, the various nodes for the NLPP using case III are shown in Figure 3.

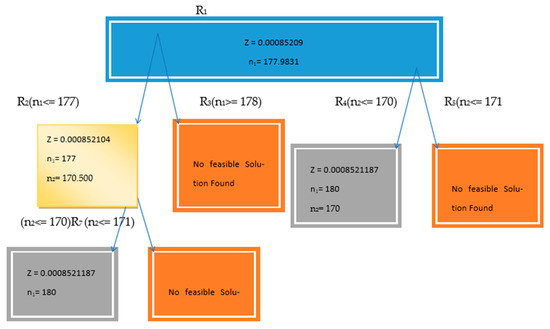
Figure 3. Various nodes of NLPP.

8. Discussion Section

Using a randomized response technique, we have developed a novel fuzzy logic approach to decision-making that can be implemented in three phases and is specifically designed to minimize variation while taking costs into consideration in stratified random sampling. Although our model is useful in practice and provides a thorough framework for enhancing data collection techniques, it is crucial to recognize its limitations and consider future research directions. Our method assumes fixed costs for each stratum, but additional research into adaptive models will be necessary because these costs could change as a result of logistical issues, inflation, and resource availability. Although our model allocates using the alpha-cut method, it might not accurately reflect the uncertainty in real-world data. Machine learning or other alternative fuzzy logic approaches could increase the flexibility and robustness of the model. Additionally, the main focus of our research has been the theoretical and numerical verification of the suggested model. To evaluate the practical applicability and efficacy of our technique in various circumstances, empirical validation via real-world case studies is necessary. Field research and partnerships with business partners may yield insightful information and aid in the model’s empirical, evidence-based refinement. We demonstrated the practical value of our concept by applying it to three different cases. Our approach’s effectiveness was validated in each case by the notable decrease in variance that was maintained at a reasonable cost. However, the results also pointed out several areas that needed work. These point to the need for more accurate cost estimation methods as well as more optimization of the allocation process inside the model.

9. Conclusions

A comprehensive investigation was conducted for this research project with the goal of creating and evaluating a three-stage randomized response model. The model attracted a great deal of scholarly attention for its novel features and tactical suggestions. It was painstakingly created to answer a particular difficulty. The main goal was to investigate and evaluate the efficacy of the methods used in this model. With fuzzy cost considerations, the project’s main goal was to solve the optimal allocation problem that arises in a three-stage stratified random sampling system. Fuzzy nonlinear programming techniques were the main emphasis of the resilient solution approach that was used to address this challenging challenge. The main problem was figuring out how to allocate resources inside this complex system, which was skillfully solved by applying the Lagrange multipliers approach, a powerful optimization technique. This comprehensive study’s results provided an important realization: the suggested approach routinely beats a recently created estimate. This important finding emphasizes the usefulness and effectiveness of the suggested approach, emphasizing its advantage over competing tactics. The outcomes provide insight into the model’s functionality and show how it might improve decision-making in situations where three-stage randomized response models are used. The present investigation not only confirms the effectiveness of the suggested methodologies but also underscores their significance in enhancing the precision and dependability of data gathering and examination in intricate sampling contexts.