Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach
Abstract
1. Introduction
Notations
2. Problem Formulation
3. Main Results
3.1. Stability Analysis
3.2. Controller Design
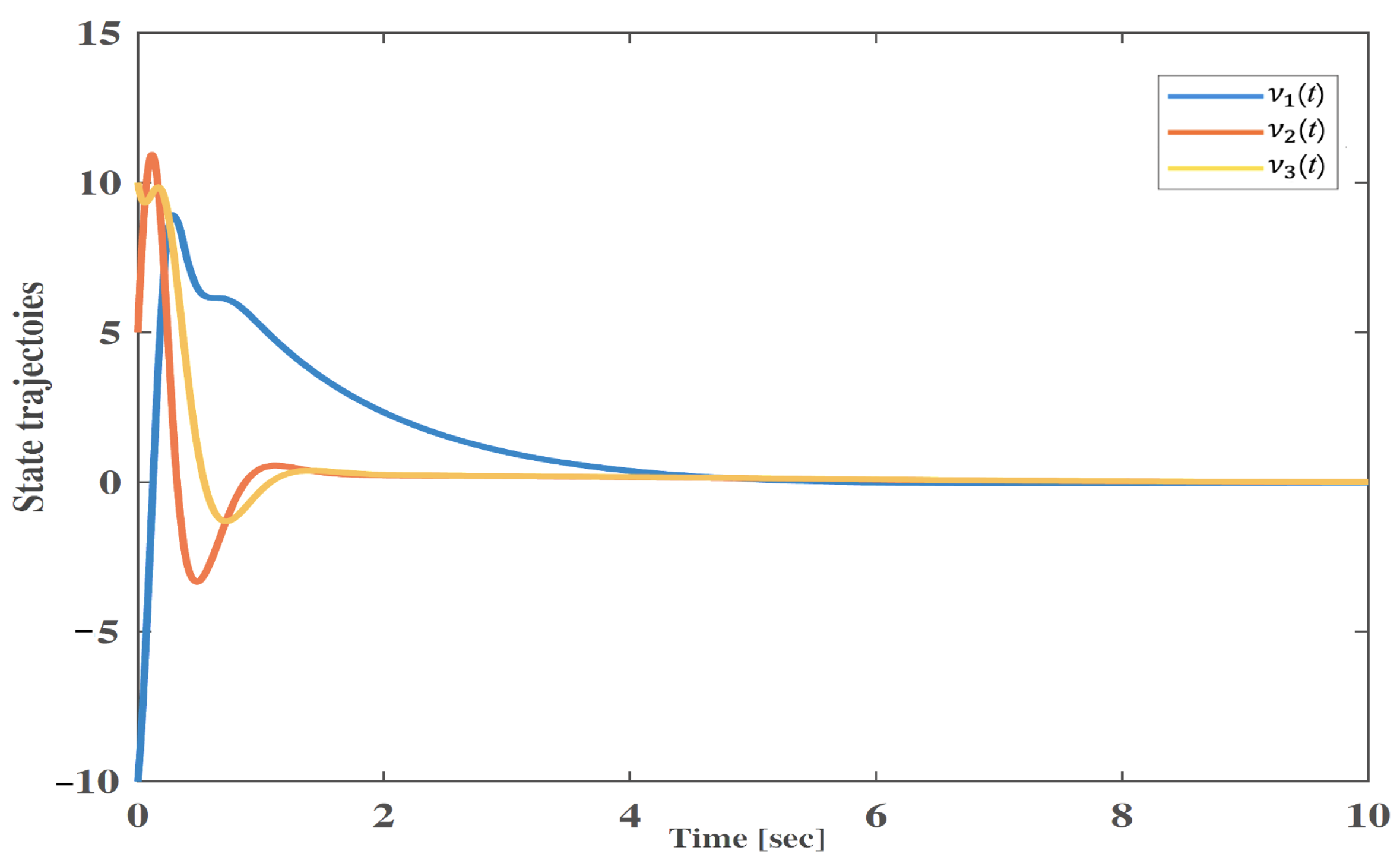
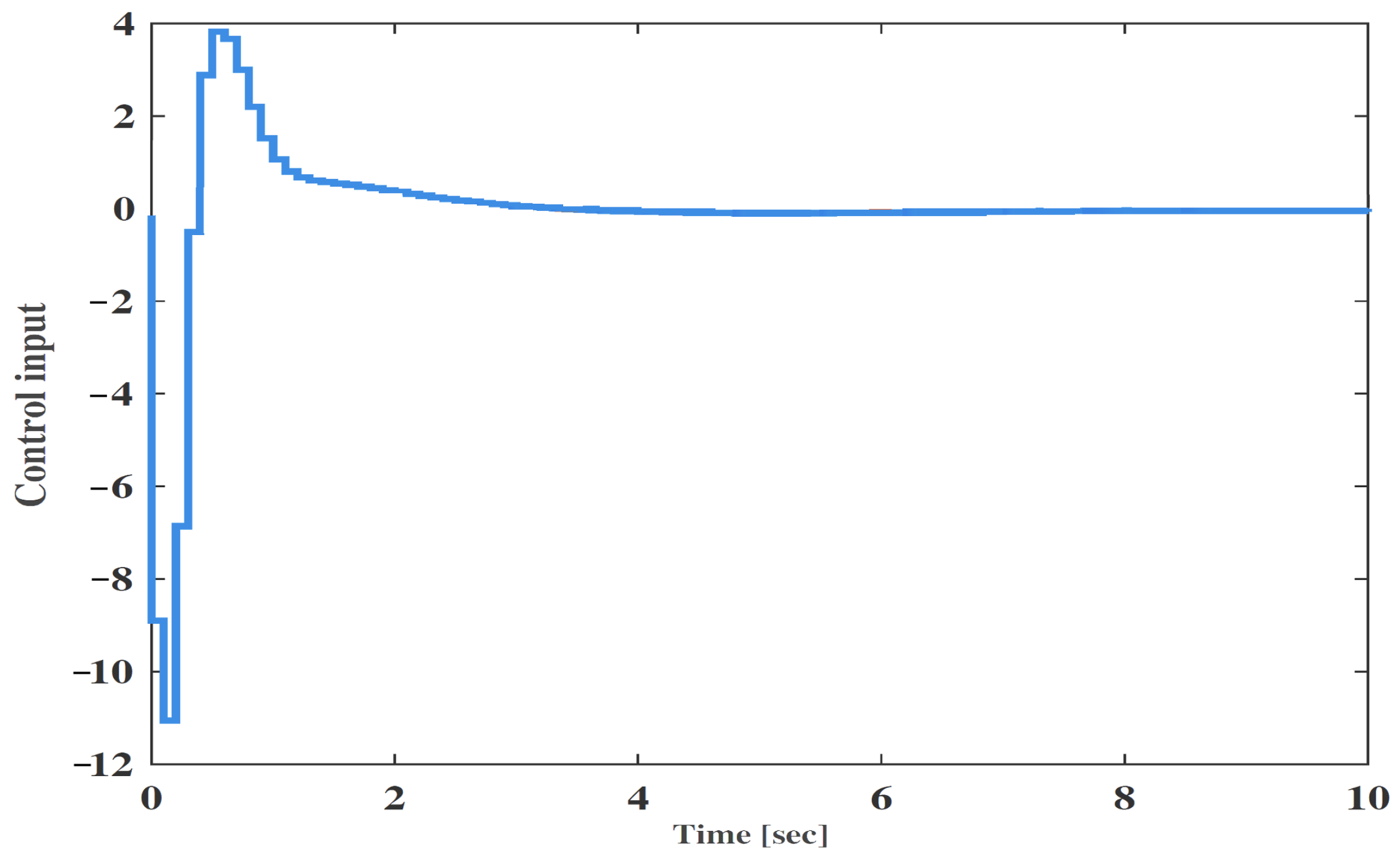
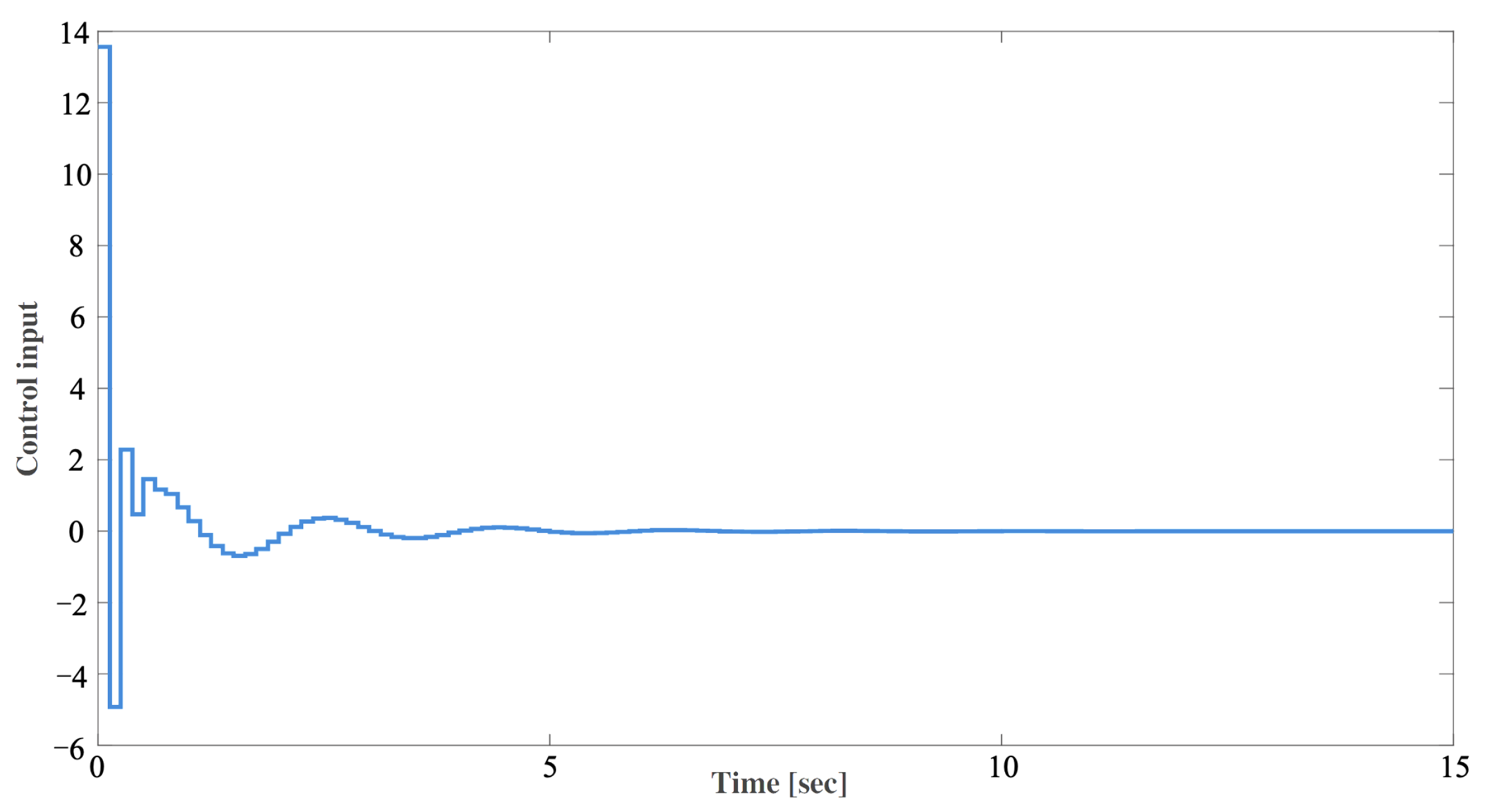
4. Numerical Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baillieul, J.; Antsaklis, P.J. Control and communication challenges in networked real-time systems. Proc. IEEE 2007, 95, 9–28. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, H.; Ding, S.X. Recent advances on fuzzy-model-based nonlinear networked control systems: A survey. IEEE Trans. Ind. Electr. 2015, 63, 1207–1217. [Google Scholar] [CrossRef]
- Sun, H.; Han, H.G.; Qiao, J.F. Observer-based control for networked Takagi-Sugeno fuzzy systems with stochastic packet losses. Inf. Sci. 2023, 644, 119275. [Google Scholar] [CrossRef]
- Xue, W.; Jin, Z.; Tian, Y. Finite-time fault-tolerant control of nonlinear spacecrafts with randomized actuator fault: Fuzzy model approach. Symmetry 2024, 16, 873. [Google Scholar] [CrossRef]
- Niu, Y.; Xu, X.; Liu, M. Fixed time synchronization of stochastic Takagi-Sugeno fuzzy recurrent neural net-works with distributed delay under feedback and adaptive controls. Axioms 2024, 13, 391. [Google Scholar] [CrossRef]
- Castorena, G.A.H.; Mendez, G.M.; Lopez-Juarez, I.; Garcia, M.A.A.; Artinez-Peon, D.C.; Mon-tes-Dorantes, P.N. Parameter prediction with novel enhanced wagner hagras interval type-3 Takagi-Sugeno-Kang fuzzy system with type-1 non-singleton inputs. Mathematics 2024, 12, 1976. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.J.; Lee, S.H.; Kwon, O.M. Enhancing stability criteria for linear systems with interval time-Varying delays via augmented Lyapunov-Krasovskii functional. Mathematics 2024, 12, 2241. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; She, K.; Zhong, S.M.; Shi, L. Stabilization of chaotic systems with T-S fuzzy model and nonuniform sampling: A switched fuzzy control approach. IEEE Trans. Fuzzy Syst. 2018, 27, 1263–1271. [Google Scholar] [CrossRef]
- Tseng, C.S.; Chen, B.S.; Uang, H.J. Fuzzy tracking control design for nonlinear dynamic systems via TS fuzzy model. IEEE Trans. Fuzzy Syst. 2001, 9, 381–392. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Chang, X.H. H∞ filtering for nonlinear discrete-time singular systems in encrypted state. Neur. Proc. Lett. 2023, 55, 2843–2866. [Google Scholar] [CrossRef]
- Rhee, B.J.; Won, S. A new fuzzy Lyapunov function approach for a Takagi-Sugeno fuzzy control system design. Fuzzy Sets Syst. 2006, 157, 1211–1228. [Google Scholar] [CrossRef]
- Wang, X.Y.; Chang, X.H. Nonlinear continuous-time system H∞ control based on dynamic quantization and event-triggered mechanism. Neur. Proc. Lett. 2023, 55, 12223–12238. [Google Scholar] [CrossRef]
- Zhao, N.; Zhao, X.; Zong, G.; Xu, N. Resilient event-triggered filtering for networked switched T-S fuzzy systems under denial-of-service attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 2140–2152. [Google Scholar] [CrossRef]
- Tan, Y.; Yuan, Y.; Xie, X.; Niu, B. Dynamic event-triggered security control for networked T-S fuzzy system with non-uniform sampling. Fuzzy Sets Syst. 2023, 452, 91–109. [Google Scholar] [CrossRef]
- Yang, T.; Zou, R.; Liu, F.; Liu, C.; Sidorov, D. Improved stabilization condition of delayed T-S fuzzy systems via an extended quadratic function negative-determination lemma. Chaos Solitons Fractals 2023, 175, 114055. [Google Scholar] [CrossRef]
- An, J.H.; Kim, H.S. Interval type-2 duzzy-model-based sampled-data control of an AUV depth system with input saturation. Actuators 2024, 13, 71. [Google Scholar] [CrossRef]
- Zheng, M.; Su, Y.; Yan, C. Further stability criteria for sampled-data-based dynamic positioning ships using Takagi-Sugeno fuzzy models. Symmetry 2024, 16, 108. [Google Scholar] [CrossRef]
- Dhanya, V.; Arunkumar, A.; Chaisena, K. Sampled-data based fault-tolerant control design for uncertain CE151 helicopter system with random delays: Takagi-Sugeno fuzzy approach. Fractal Fract. 2022, 6, 498. [Google Scholar] [CrossRef]
- Chen, T.; Francis, B.A. Optimal Sampled-Data Control Systems; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Arthanari, S.; Joo, Y.H. Memory sampled-data control for T-S fuzzy-based permanent magnet synchronous generator via an improved looped functional. IEEE Trans. Syst. Man Cybern Syst. 2023, 53, 4417–4428. [Google Scholar] [CrossRef]
- Xu, X.; Wang, L.; Du, Z.; Kao, Y. H∞ sampled-data control for uncertain fuzzy systems under Markovian jump and FBm. Appl. Math. Comput. 2023, 451, 128014. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Yang, H.; Zhao, G.; Zhong, S. An improved fuzzy sampled-data control to stabilization of T-S fuzzy systems with state delays. IEEE Trans. Cybern. 2020, 50, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Hua, C.; Wang, Y. Nonfragile sampled-data control of T-S fuzzy systems with time delay. IEEE Trans. Fuzzy Syst. 2021, 30, 3202–3210. [Google Scholar] [CrossRef]
- Ge, C.; Shi, Y.; Park, J.H.; Hua, C. Robust H∞ stabilization for T-S fuzzy systems with time-varying delays and memory sampled-data control. Appl. Math. Comput. 2019, 346, 500–512. [Google Scholar] [CrossRef]
- Liu, Y.; Park, J.H.; Guo, B.; Shu, Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans. Fuzzy Syst. 2018, 26, 1040–1045. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y.; Wang, W. Sampled-data stabilization of chaotic systems based on a T-S fuzzy model. Inf. Sci. 2019, 483, 262–272. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, D.; Park, J.H.; Lam, H.K.; Xie, X. Fuzzy sampled-data control for synchronization of T-S fuzzy reaction-diffusion neural networks with additive time-varying delays. IEEE Trans. Cybern. 2020, 251, 2384–2397. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Design of interval type-2 fuzzy-based sampled-data controller for nonlinear sys-tems using novel fuzzy Lyapunov functional and its application to PMSM. IEEE Trans. Syst. Man Cybern. 2021, 51, 542–551. [Google Scholar] [CrossRef]
- Zhu, X.L.; Chen, B.; Yue, D.; Wang, Y. An improved input delay approach to stabilization of fuzzy systems under variable sampling. IEEE Trans. Fuzzy Syst. 2012, 20, 330–341. [Google Scholar] [CrossRef]
- Wu, Z.G.; Shi, P.; Su, H.; Chu, J. Sampled-data fuzzy control of chaotic systems based on a T-S fuzzy model. IEEE Trans. Fuzzy Syst. 2013, 22, 153–163. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N. On fuzzy sampled-data control of chaotic systems via a time-dependent Lyapunov functional approach. IEEE Trans. Cybern. 2014, 45, 819–829. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Stability criteria for fuzzy-based sampled-data control systems via a fractional parameter-based refined looped Lyapunov functional. IEEE Trans. Fuzzy Syst. 2022, 30, 2538–2549. [Google Scholar] [CrossRef]
- Sheng, Z.; Xu, S. A sampled-data control method related to time for Takagi-Sugeno fuzzy systems via novel sampling-dependent functional approach. IEEE Trans. Fuzzy Syst. 2024, 31, 460–469. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Tkach, R.W. Capacity trends and limits of optical communication networks. Proc. IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
- Seuret, A. A novel stability analysis of linear systems under asynchronous samplings. Automatica 2012, 48, 177–182. [Google Scholar] [CrossRef]
- Oncoy, D.J.; Cardim, R.; Teixeira, M.C.; Faria, F.A.; Assuncao, E.; Lazarini, A.Z. New stabilization conditions for fuzzy-based sampled-data control systems using a fuzzy Lyapunov functional. IEEE Access 2023, 11, 15390–15403. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y. A new looped-functional for stability analysis of sampled-data systems. Automatica 2017, 82, 328–331. [Google Scholar] [CrossRef]
- Park, J.; Park, P. An extended looped-functional for stability analysis of sampled-data systems. Int. J. Robust Nonlinear Control 2020, 30, 7962–7969. [Google Scholar] [CrossRef]
- Guan, C.; Fei, Z.; Park, P. Modified looped functional for sampled-data control of T-S fuzzy Markovian jump systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2543–2552. [Google Scholar] [CrossRef]
- Park, J.; Park, P. A less conservative stability criterion for sampled-data system via a fractional-delayed state and its state-space model. Int. J. Robust Nonlinear Control 2021, 29, 2561–2572. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ning, B.; Zhang, B.L. Sampled-data control systems with non-uniform sampling: A survey of methods and trends. Annu. Rev. Control 2023, 55, 70–91. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E. Networked-based stabilization via discontinuous Lyapunov functionals. Int. J. Robust Nonlinear Control 2012, 22, 420–436. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H. Stability analysis of sampled-data systems via free-matrix-based time-dependent dis-continuous Lyapunov approach. IEEE Trans. Autom. Control 2017, 62, 3653–3657. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Wang, Z. Sampled-data synchronization for complex networks based on discontinuous LKF and mixed convex combination. J. Franklin Inst. 2015, 352, 4741–4757. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 30, 2860–2866. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel-Legendre ine-qualities. IEEE Trans. Autom. Control 2018, 63, 225–232. [Google Scholar] [CrossRef]
- Wang, L.; Lam, H. New stability criterion for continuous-time Takagi-Sugeno fuzzy systems with time-varying delay. IEEE Trans. Cybern. 2019, 49, 1551–1556. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Gao, W. Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry 2024, 16, 1119. https://doi.org/10.3390/sym16091119
Yang J, Gao W. Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry. 2024; 16(9):1119. https://doi.org/10.3390/sym16091119
Chicago/Turabian StyleYang, Jin, and Wenke Gao. 2024. "Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach" Symmetry 16, no. 9: 1119. https://doi.org/10.3390/sym16091119
APA StyleYang, J., & Gao, W. (2024). Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry, 16(9), 1119. https://doi.org/10.3390/sym16091119






