Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach
Abstract
:1. Introduction
Notations
2. Problem Formulation
3. Main Results
3.1. Stability Analysis
3.2. Controller Design
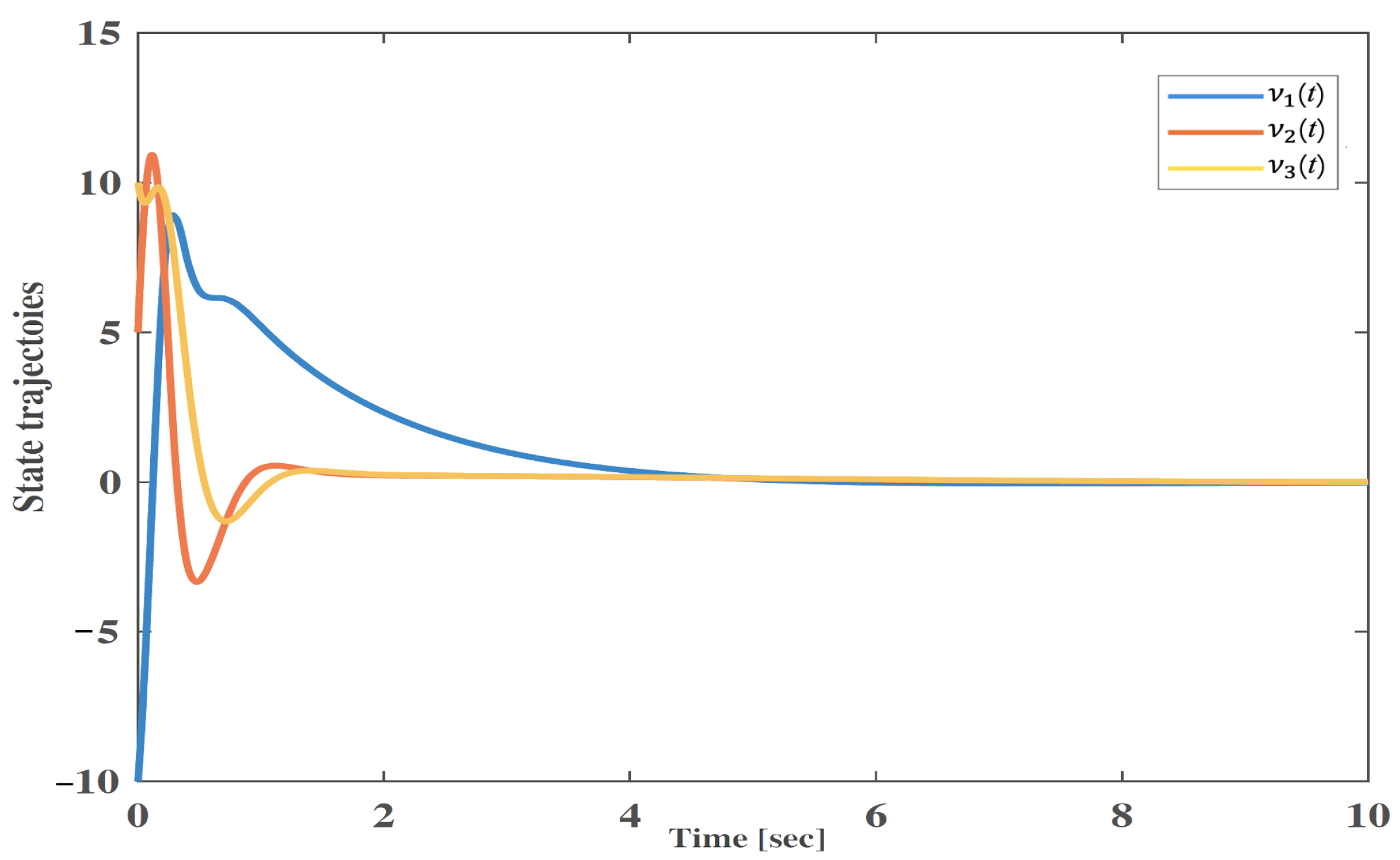
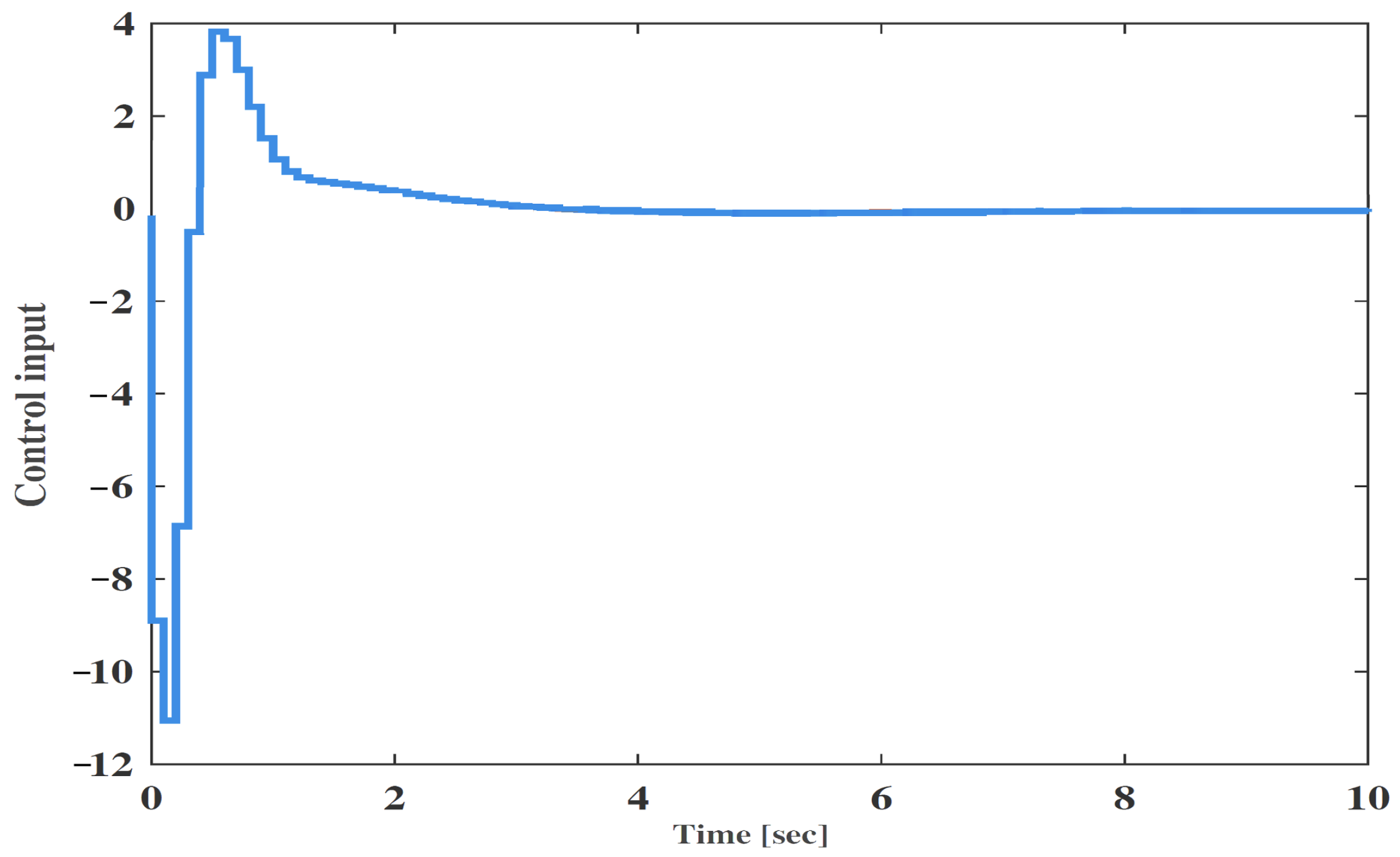
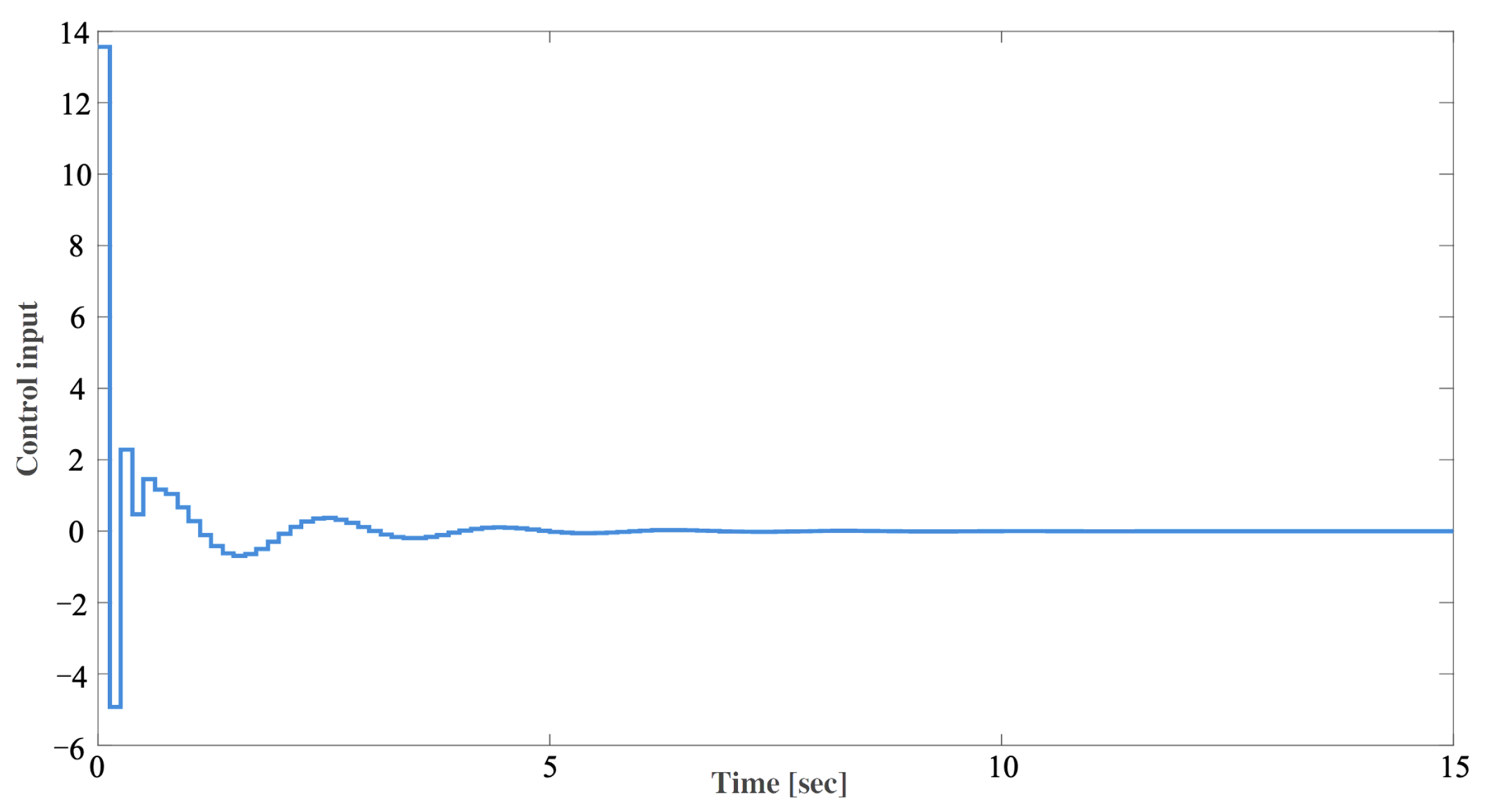
4. Numerical Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baillieul, J.; Antsaklis, P.J. Control and communication challenges in networked real-time systems. Proc. IEEE 2007, 95, 9–28. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, H.; Ding, S.X. Recent advances on fuzzy-model-based nonlinear networked control systems: A survey. IEEE Trans. Ind. Electr. 2015, 63, 1207–1217. [Google Scholar] [CrossRef]
- Sun, H.; Han, H.G.; Qiao, J.F. Observer-based control for networked Takagi-Sugeno fuzzy systems with stochastic packet losses. Inf. Sci. 2023, 644, 119275. [Google Scholar] [CrossRef]
- Xue, W.; Jin, Z.; Tian, Y. Finite-time fault-tolerant control of nonlinear spacecrafts with randomized actuator fault: Fuzzy model approach. Symmetry 2024, 16, 873. [Google Scholar] [CrossRef]
- Niu, Y.; Xu, X.; Liu, M. Fixed time synchronization of stochastic Takagi-Sugeno fuzzy recurrent neural net-works with distributed delay under feedback and adaptive controls. Axioms 2024, 13, 391. [Google Scholar] [CrossRef]
- Castorena, G.A.H.; Mendez, G.M.; Lopez-Juarez, I.; Garcia, M.A.A.; Artinez-Peon, D.C.; Mon-tes-Dorantes, P.N. Parameter prediction with novel enhanced wagner hagras interval type-3 Takagi-Sugeno-Kang fuzzy system with type-1 non-singleton inputs. Mathematics 2024, 12, 1976. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.J.; Lee, S.H.; Kwon, O.M. Enhancing stability criteria for linear systems with interval time-Varying delays via augmented Lyapunov-Krasovskii functional. Mathematics 2024, 12, 2241. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; She, K.; Zhong, S.M.; Shi, L. Stabilization of chaotic systems with T-S fuzzy model and nonuniform sampling: A switched fuzzy control approach. IEEE Trans. Fuzzy Syst. 2018, 27, 1263–1271. [Google Scholar] [CrossRef]
- Tseng, C.S.; Chen, B.S.; Uang, H.J. Fuzzy tracking control design for nonlinear dynamic systems via TS fuzzy model. IEEE Trans. Fuzzy Syst. 2001, 9, 381–392. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Chang, X.H. H∞ filtering for nonlinear discrete-time singular systems in encrypted state. Neur. Proc. Lett. 2023, 55, 2843–2866. [Google Scholar] [CrossRef]
- Rhee, B.J.; Won, S. A new fuzzy Lyapunov function approach for a Takagi-Sugeno fuzzy control system design. Fuzzy Sets Syst. 2006, 157, 1211–1228. [Google Scholar] [CrossRef]
- Wang, X.Y.; Chang, X.H. Nonlinear continuous-time system H∞ control based on dynamic quantization and event-triggered mechanism. Neur. Proc. Lett. 2023, 55, 12223–12238. [Google Scholar] [CrossRef]
- Zhao, N.; Zhao, X.; Zong, G.; Xu, N. Resilient event-triggered filtering for networked switched T-S fuzzy systems under denial-of-service attacks. IEEE Trans. Fuzzy Syst. 2024, 32, 2140–2152. [Google Scholar] [CrossRef]
- Tan, Y.; Yuan, Y.; Xie, X.; Niu, B. Dynamic event-triggered security control for networked T-S fuzzy system with non-uniform sampling. Fuzzy Sets Syst. 2023, 452, 91–109. [Google Scholar] [CrossRef]
- Yang, T.; Zou, R.; Liu, F.; Liu, C.; Sidorov, D. Improved stabilization condition of delayed T-S fuzzy systems via an extended quadratic function negative-determination lemma. Chaos Solitons Fractals 2023, 175, 114055. [Google Scholar] [CrossRef]
- An, J.H.; Kim, H.S. Interval type-2 duzzy-model-based sampled-data control of an AUV depth system with input saturation. Actuators 2024, 13, 71. [Google Scholar] [CrossRef]
- Zheng, M.; Su, Y.; Yan, C. Further stability criteria for sampled-data-based dynamic positioning ships using Takagi-Sugeno fuzzy models. Symmetry 2024, 16, 108. [Google Scholar] [CrossRef]
- Dhanya, V.; Arunkumar, A.; Chaisena, K. Sampled-data based fault-tolerant control design for uncertain CE151 helicopter system with random delays: Takagi-Sugeno fuzzy approach. Fractal Fract. 2022, 6, 498. [Google Scholar] [CrossRef]
- Chen, T.; Francis, B.A. Optimal Sampled-Data Control Systems; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Arthanari, S.; Joo, Y.H. Memory sampled-data control for T-S fuzzy-based permanent magnet synchronous generator via an improved looped functional. IEEE Trans. Syst. Man Cybern Syst. 2023, 53, 4417–4428. [Google Scholar] [CrossRef]
- Xu, X.; Wang, L.; Du, Z.; Kao, Y. H∞ sampled-data control for uncertain fuzzy systems under Markovian jump and FBm. Appl. Math. Comput. 2023, 451, 128014. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Yang, H.; Zhao, G.; Zhong, S. An improved fuzzy sampled-data control to stabilization of T-S fuzzy systems with state delays. IEEE Trans. Cybern. 2020, 50, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Hua, C.; Wang, Y. Nonfragile sampled-data control of T-S fuzzy systems with time delay. IEEE Trans. Fuzzy Syst. 2021, 30, 3202–3210. [Google Scholar] [CrossRef]
- Ge, C.; Shi, Y.; Park, J.H.; Hua, C. Robust H∞ stabilization for T-S fuzzy systems with time-varying delays and memory sampled-data control. Appl. Math. Comput. 2019, 346, 500–512. [Google Scholar] [CrossRef]
- Liu, Y.; Park, J.H.; Guo, B.; Shu, Y. Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans. Fuzzy Syst. 2018, 26, 1040–1045. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y.; Wang, W. Sampled-data stabilization of chaotic systems based on a T-S fuzzy model. Inf. Sci. 2019, 483, 262–272. [Google Scholar] [CrossRef]
- Zhang, R.; Zeng, D.; Park, J.H.; Lam, H.K.; Xie, X. Fuzzy sampled-data control for synchronization of T-S fuzzy reaction-diffusion neural networks with additive time-varying delays. IEEE Trans. Cybern. 2020, 251, 2384–2397. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Design of interval type-2 fuzzy-based sampled-data controller for nonlinear sys-tems using novel fuzzy Lyapunov functional and its application to PMSM. IEEE Trans. Syst. Man Cybern. 2021, 51, 542–551. [Google Scholar] [CrossRef]
- Zhu, X.L.; Chen, B.; Yue, D.; Wang, Y. An improved input delay approach to stabilization of fuzzy systems under variable sampling. IEEE Trans. Fuzzy Syst. 2012, 20, 330–341. [Google Scholar] [CrossRef]
- Wu, Z.G.; Shi, P.; Su, H.; Chu, J. Sampled-data fuzzy control of chaotic systems based on a T-S fuzzy model. IEEE Trans. Fuzzy Syst. 2013, 22, 153–163. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N. On fuzzy sampled-data control of chaotic systems via a time-dependent Lyapunov functional approach. IEEE Trans. Cybern. 2014, 45, 819–829. [Google Scholar] [CrossRef]
- Shanmugam, L.; Joo, Y.H. Stability criteria for fuzzy-based sampled-data control systems via a fractional parameter-based refined looped Lyapunov functional. IEEE Trans. Fuzzy Syst. 2022, 30, 2538–2549. [Google Scholar] [CrossRef]
- Sheng, Z.; Xu, S. A sampled-data control method related to time for Takagi-Sugeno fuzzy systems via novel sampling-dependent functional approach. IEEE Trans. Fuzzy Syst. 2024, 31, 460–469. [Google Scholar] [CrossRef]
- Essiambre, R.J.; Tkach, R.W. Capacity trends and limits of optical communication networks. Proc. IEEE 2012, 100, 1035–1055. [Google Scholar] [CrossRef]
- Seuret, A. A novel stability analysis of linear systems under asynchronous samplings. Automatica 2012, 48, 177–182. [Google Scholar] [CrossRef]
- Oncoy, D.J.; Cardim, R.; Teixeira, M.C.; Faria, F.A.; Assuncao, E.; Lazarini, A.Z. New stabilization conditions for fuzzy-based sampled-data control systems using a fuzzy Lyapunov functional. IEEE Access 2023, 11, 15390–15403. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y. A new looped-functional for stability analysis of sampled-data systems. Automatica 2017, 82, 328–331. [Google Scholar] [CrossRef]
- Park, J.; Park, P. An extended looped-functional for stability analysis of sampled-data systems. Int. J. Robust Nonlinear Control 2020, 30, 7962–7969. [Google Scholar] [CrossRef]
- Guan, C.; Fei, Z.; Park, P. Modified looped functional for sampled-data control of T-S fuzzy Markovian jump systems. IEEE Trans. Fuzzy Syst. 2021, 29, 2543–2552. [Google Scholar] [CrossRef]
- Park, J.; Park, P. A less conservative stability criterion for sampled-data system via a fractional-delayed state and its state-space model. Int. J. Robust Nonlinear Control 2021, 29, 2561–2572. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L.; Ge, X.; Ning, B.; Zhang, B.L. Sampled-data control systems with non-uniform sampling: A survey of methods and trends. Annu. Rev. Control 2023, 55, 70–91. [Google Scholar] [CrossRef]
- Liu, K.; Fridman, E. Networked-based stabilization via discontinuous Lyapunov functionals. Int. J. Robust Nonlinear Control 2012, 22, 420–436. [Google Scholar] [CrossRef]
- Lee, T.H.; Park, J.H. Stability analysis of sampled-data systems via free-matrix-based time-dependent dis-continuous Lyapunov approach. IEEE Trans. Autom. Control 2017, 62, 3653–3657. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, H.; Wang, Z. Sampled-data synchronization for complex networks based on discontinuous LKF and mixed convex combination. J. Franklin Inst. 2015, 352, 4741–4757. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 30, 2860–2866. [Google Scholar] [CrossRef]
- Zeng, H.B.; He, Y.; Wu, M.; She, J. Free-matrix-based integral inequality for stability analysis of systems with time-varying delay. IEEE Trans. Autom. Control 2015, 60, 2768–2772. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Stability of linear systems with time-varying delays using Bessel-Legendre ine-qualities. IEEE Trans. Autom. Control 2018, 63, 225–232. [Google Scholar] [CrossRef]
- Wang, L.; Lam, H. New stability criterion for continuous-time Takagi-Sugeno fuzzy systems with time-varying delay. IEEE Trans. Cybern. 2019, 49, 1551–1556. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Gao, W. Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry 2024, 16, 1119. https://doi.org/10.3390/sym16091119
Yang J, Gao W. Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry. 2024; 16(9):1119. https://doi.org/10.3390/sym16091119
Chicago/Turabian StyleYang, Jin, and Wenke Gao. 2024. "Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach" Symmetry 16, no. 9: 1119. https://doi.org/10.3390/sym16091119
APA StyleYang, J., & Gao, W. (2024). Sampled-Data Control for T-S Fuzzy Systems Using Refined Looped Lyapunov Functional Approach. Symmetry, 16(9), 1119. https://doi.org/10.3390/sym16091119






