Comparative Analysis of Influenza Modeling Using Novel Fractional Operators with Real Data
Abstract
1. Introduction
2. Preliminaries
3. The Development of the Model in the Classical Meaning
4. The Development of the Model in the Fractional Meaning
4.1. Caputo Meaning
4.2. Caputo–Fabrizio Meaning
4.3. Atangana–Baleanu–Caputo Meaning
5. Analysis of the Model
5.1. Disease-Free Equilibrium Point
5.2. Positivity and Boundedness
5.3. Reproduction Numbers
5.4. Stability Analysis
5.5. Global Stability of the Disease-Free Equilibrium
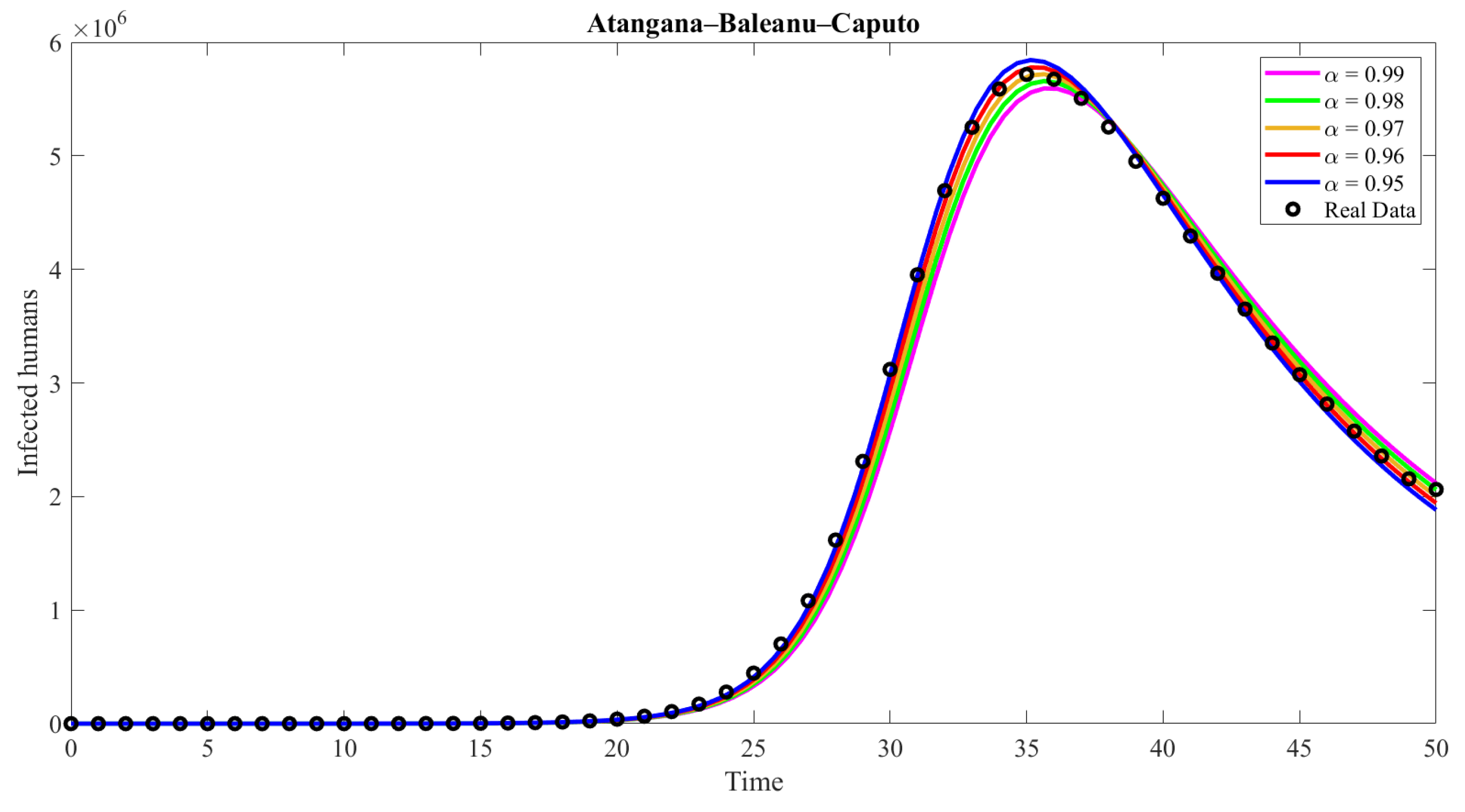
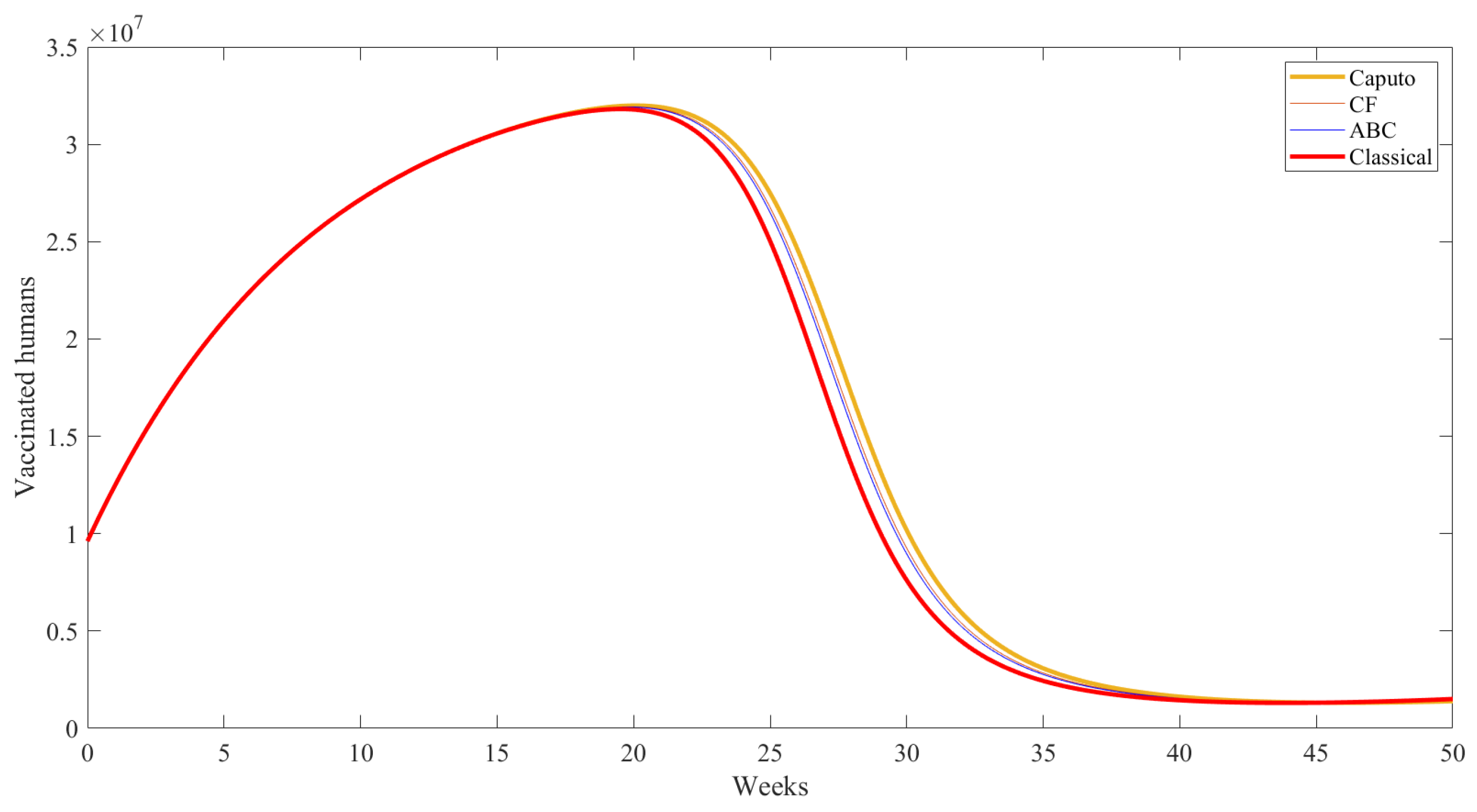
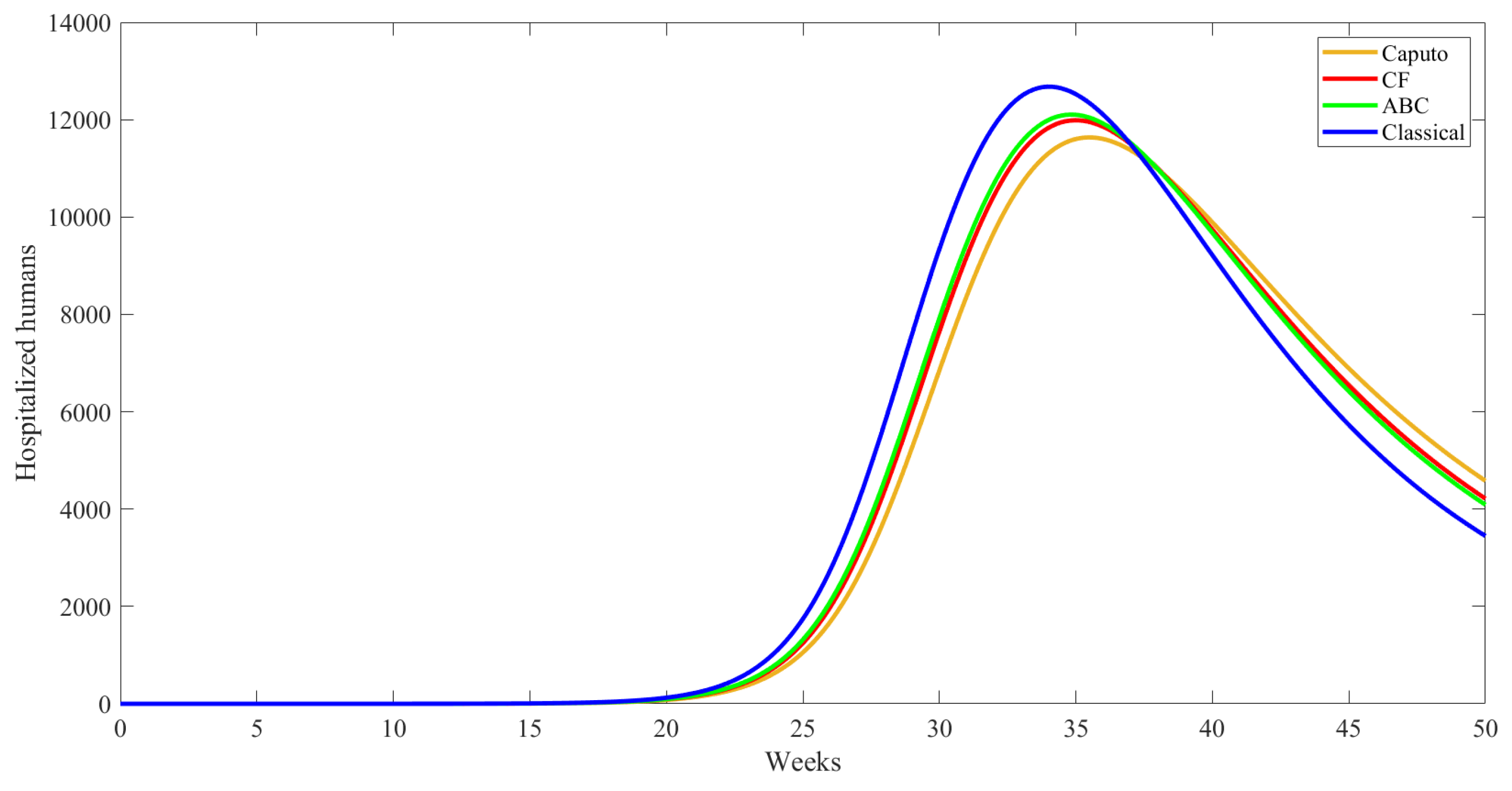
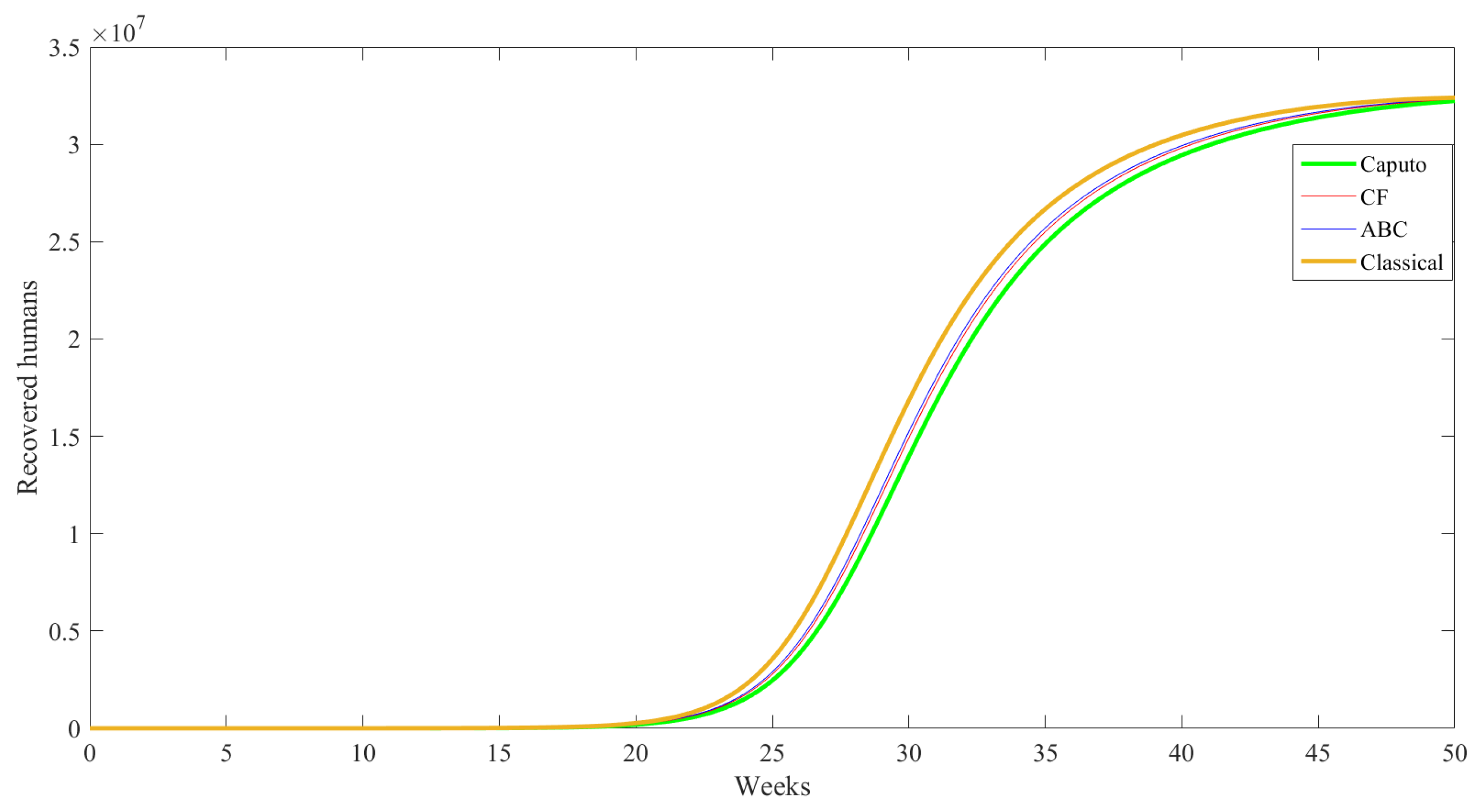
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hutchinson, E.C. Influenza virus. Trends Microbiol. 2018, 26, 809–810. [Google Scholar] [CrossRef] [PubMed]
- Al-Khuwaitir, T.S.; Al-Abdulkarim, A.S.; Abba, A.A.; Yousef, A.M.; El-Din, M.A.; Rahman, K.T.; Ali, M.A.; Mohamed, M.E.; Arnous, N.E. H1N1 influenza A. Preliminary evaluation in hospitalized patients in a secondary care facility in Saudi Arabia. Saudi Med. J. 2009, 30, 1532–1536. [Google Scholar]
- Clark, N.M.; Lynch, J.P. Influenza: Epidemiology, clinical features, therapy, and prevention. Semin. Respir. Crit. Care Med. 2011, 32, 373–392. [Google Scholar] [CrossRef]
- Javanian, M.; Barary, M.; Ghebrehewet, S.; Koppolu, V.; Vasigala, V.; Ebrahimpour, S. A brief review of influenza virus infection. J. Med. Virol. 2021, 93, 4638–4646. [Google Scholar] [CrossRef] [PubMed]
- Sinha, R.; Paredis, C.J.; Liang, V.C.; Khosla, P.K. Modeling and simulation methods for design of engineering systems. J. Comput. Inf. Sci. Eng. 2001, 1, 84–91. [Google Scholar] [CrossRef]
- Chinviriyasit, W. Numerical modeling of the transmission dynamics of influenza. In Proceedings of the First International Symposium on Optimization and Systems Biology, Beijing, China, 8–10 August 2007; pp. 52–59. [Google Scholar]
- Casagrandi, R.; Bolzoni, L.; Levin, S.A.; Andreasen, V. The SIRC model and influenza A. Math. Biosci. 2006, 200, 152–169. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Elbasha, E.H.; Podder, C.N.; Gumel, A.B. Analyzing the dynamics of an SIRS vaccination model with waning natural and vaccine-induced immunity. Nonlinear Anal. Real World Appl. 2011, 12, 2692–2705. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Liu, X. Avian–human influenza epidemic model. Math. Biosci. 2007, 207, 1–25. [Google Scholar] [CrossRef]
- Jung, E.; Iwami, S.; Takeuchi, Y.; Jo, T.C. Optimal control strategy for prevention of avian influenza pandemic. J. Theor. Biol. 2009, 260, 220–229. [Google Scholar] [CrossRef]
- Lucchetti, J.; Roy, M.; Martcheva, M. An avian influenza model and its fit to human avian influenza cases. Adv. Dis. Epidemiol. 2009, 1, 1–30. [Google Scholar]
- Iwami, S.; Takeuchi, Y.; Liu, X.; Nakaoka, S. A geographical spread of vaccine-resistance in avian influenza epidemics. J. Theor. Biol. 2009, 259, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Ruan, S.; Wang, W. Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equations 2003, 188, 135–163. [Google Scholar] [CrossRef]
- Khader, M.M.; Sweilam, N.H.; Mahdy, A.M.S.; Moniem, N.K. Numerical simulation for the fractional SIRC model and influenza A. Appl. Math. Inf. Sci. 2014, 8, 1029. [Google Scholar] [CrossRef]
- Alsubaie, N.E.; EL Guma, F.; Boulehmi, K.; Al-kuleab, N.; Abdoon, M.A. Improving Influenza Epidemiological Models under Caputo Fractional-Order Calculus. Symmetry 2024, 16, 929. [Google Scholar] [CrossRef]
- Al-Qureshi, M.; Rashid, S.; Jarad, F.; Alharthi, M.S. Dynamical behavior of a stochastic highly pathogenic avian influenza A (HPAI) epidemic model via piecewise fractional differential technique. AIMS Math. 2023, 8, 1737–1756. [Google Scholar] [CrossRef]
- Alharbi, S.A.; Abdoon, M.A.; Saadeh, R.; Alsemiry, R.D.; Allogmany, R.; Berir, M.; EL Guma, F. Modeling and analysis of visceral leishmaniasis dynamics using fractional-order operators: A comparative study. Math. Methods Appl. Sci. 2024, 47, 9918–9937. [Google Scholar] [CrossRef]
- Algahtani, O.J.J. Comparing the Atangana–Baleanu and Caputo–Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 2016, 89, 552–559. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef]
- Alkahtani, B.S.T. Chua’s circuit model with Atangana–Baleanu derivative with fractional order. Chaos Solitons Fractals 2016, 89, 547–551. [Google Scholar] [CrossRef]
- Yavuz, M.; Özdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Abdoon, M.A.; Saadeh, R.; Berir, M.; Guma, F.E. Analysis, modeling and simulation of a fractional-order influenza model. Alex. Eng. J. 2023, 74, 231–240. [Google Scholar] [CrossRef]
- Alzahrani, S.M.; Saadeh, R.; Abdoon, M.A.; Qazza, A.; Guma, F.E.; Berir, M. Numerical Simulation of an Influenza Epidemic: Prediction with Fractional SEIR and the ARIMA Model. Appl. Math. 2024, 18, 1–12. [Google Scholar]
- Saadeh, R.; Abdoon, M.A.; Qazza, A.; Berir, M. A numerical solution of generalized Caputo fractional initial value problems. Fractal Fract. 2023, 7, 332. [Google Scholar] [CrossRef]
- Elbadri, M.; Abdoon, M.A.; Berir, M.; Almutairi, D.K. A symmetry chaotic model with fractional derivative order via two different methods. Symmetry 2023, 15, 1151. [Google Scholar] [CrossRef]
- Alzahrani, A.B.; Abdoon, M.A.; Elbadri, M.; Berir, M.; Elgezouli, D.E. A comparative numerical study of the symmetry chaotic jerk system with a hyperbolic sine function via two different methods. Symmetry 2023, 15, 1991. [Google Scholar] [CrossRef]
- Khan, H.; Rajpar, A.H.; Alzabut, J.; Aslam, M.; Etemad, S.; Rezapour, S. On a Fractal–Fractional-Based Modeling for Influenza and Its Analytical Results. Qual. Theory Dyn. Syst. 2024, 23, 70. [Google Scholar] [CrossRef]
- Huang, J.; Cen, Z.; Xu, A.; He, T.; Liu, Q. A Fractional SIR Model for the Simulation of the Spread of Influenza A during the Post COVID-19 Period. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4786433 (accessed on 8 April 2024).
- Andreu-Vilarroig, C.; Villanueva, R.J.; González-Parra, G. Mathematical modeling for estimating influenza vaccine efficacy: A case study of the Valencian Community, Spain. Infect. Dis. Model. 2024, 9, 744–762. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, C.; Duan, W.; Yuan, J.; Wu, S.; Sun, Y.; Zhang, J.; Liu, J.; Wang, Q.; Liu, M. The role of absolute humidity in influenza transmission in Beijing, China: Risk assessment and attributable fraction identification. Int. J. Environ. Health Res. 2024, 34, 767–778. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. Dynamical Behavior and Numerical Simulation of an Influenza A Epidemic Model with Log-Normal Ornstein–Uhlenbeck Process. Qual. Theory Dyn. Syst. 2024, 23, 190. [Google Scholar] [CrossRef]
- Alshareef, A. Quantitative analysis of a fractional order of the SEIcIηVR epidemic model with vaccination strategy. AIMS Math. 2024, 9, 6878–6903. [Google Scholar] [CrossRef]
- Yavuz, M.; Arfan, M.; Sami, A. Theoretical and numerical investigation of a modified ABC fractional operator for the spread of polio under the effect of vaccination. AIMS Biophys. 2024, 11, 97–120. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. arXiv 2016, arXiv:1602.03408. [Google Scholar] [CrossRef]
- Malomed, B.A. Fractional wave models and their experimental applications. In Fractional Dispersive Models and Applications: Recent Developments and Future Perspectives; Springer: Berlin/Heidelberg, Germany, 2024; pp. 1–30. [Google Scholar]
- Macrotrends: Saudi Arabia Population 1950–2023. 2021–2022. Available online: https://www.macrotrends.net/countries/SAU/saudi-arabia/population (accessed on 3 August 2024).
- Cori, A.; Valleron, A.J.; Carrat, F.; Tomba, G.S.; Thomas, G.; Boëlle, P.Y. Estimating influenza latency and infectious period durations using viral excretion data. Epidemics 2012, 4, 132–138. [Google Scholar] [CrossRef]
- Takele, R. Stochastic modelling for predicting COVID-19 prevalence in East Africa Countries. Infect. Dis. Model. 2020, 5, 598–607. [Google Scholar] [CrossRef]
- Ahmad, J.; Ali, F.; Murtaza, S.; Khan, I. Caputo time fractional model based on generalized Fourier’s and Fick’s laws for Jeffrey nanofluid: Applications in automobiles. Math. Probl. Eng. 2021, 2021, 4611656. [Google Scholar] [CrossRef]
- Kumar, S.; Shaw, P.K.; Abdel-Aty, A.H.; Mahmoud, E.E. A numerical study on fractional differential equation with population growth model. Numer. Methods Partial. Differ. Equations 2024, 40, e22684. [Google Scholar] [CrossRef]
- Khan, F.M.; Khan, Z.U. Numerical analysis of fractional order drinking mathematical model. J. Math. Tech. Model. 2024, 1, 11–24. [Google Scholar]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Qureshi, S.; Atangana, A. Mathematical analysis of dengue fever outbreak by novel fractional operators with field data. Phys. A Stat. Mech. Its Appl. 2019, 526, 121127. [Google Scholar] [CrossRef]
- Statista. Saudi Arabia: Life Expectancy at Birth from 2011 to 2021. Available online: https://www.statista.com/statistics/262477/life-expectancy-at-birth-in-saudi-arabia/ (accessed on 27 May 2024).
- Mao, Y.; Yu, X. A hybrid forecasting approach for China’s national carbon emission allowance prices with balanced accuracy and interpretability. J. Environ. Manag. 2024, 351, 119873. [Google Scholar] [CrossRef]
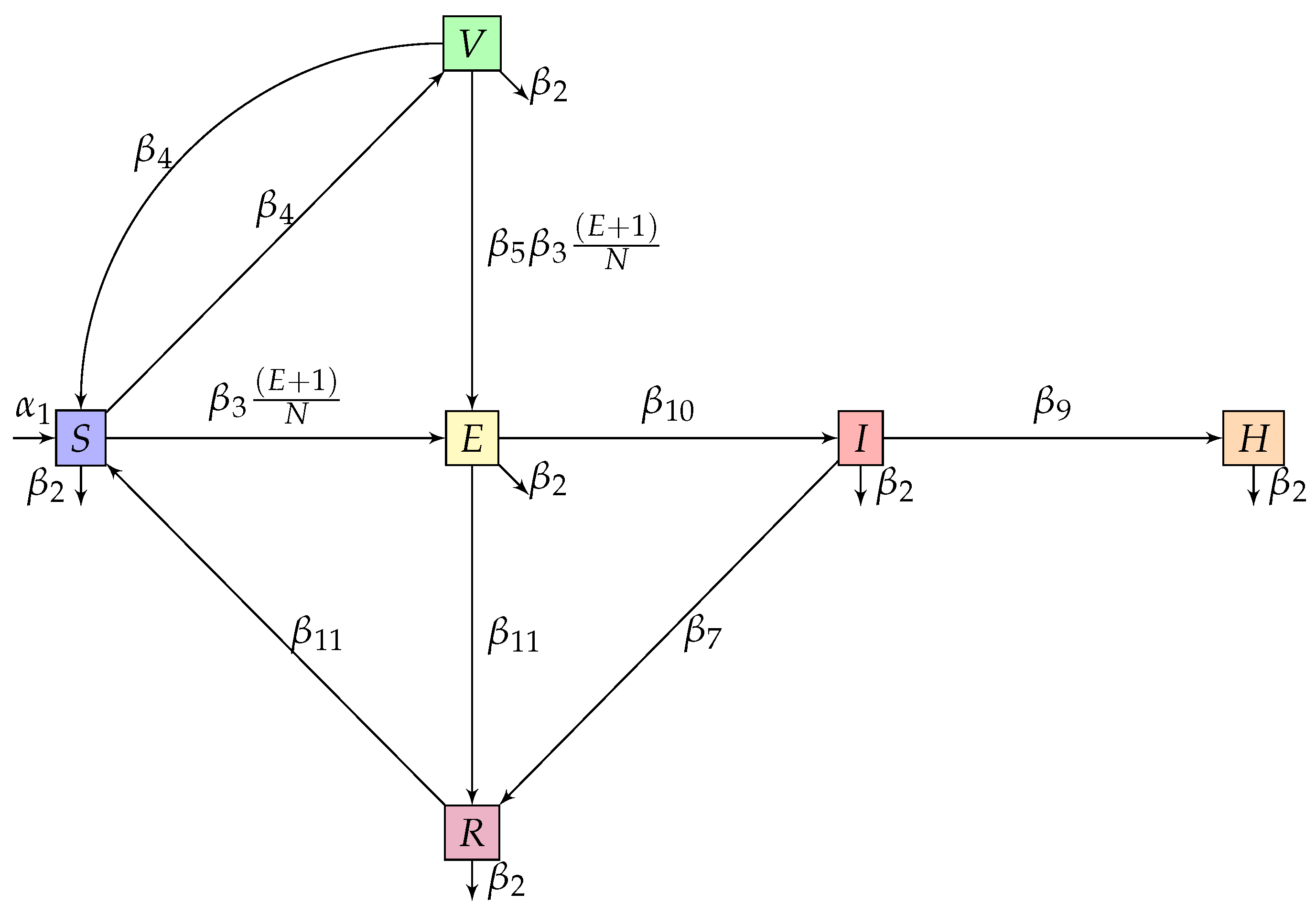
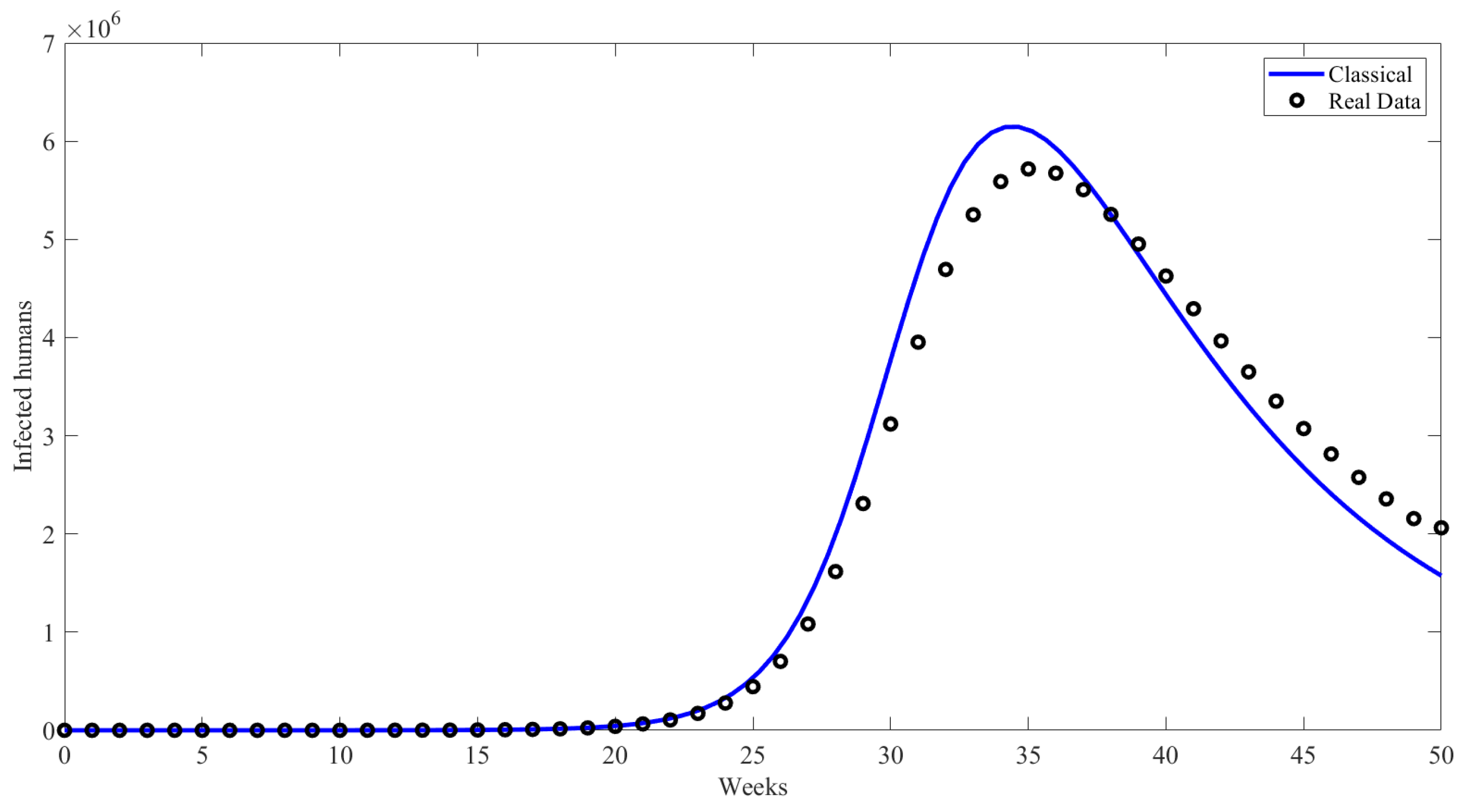
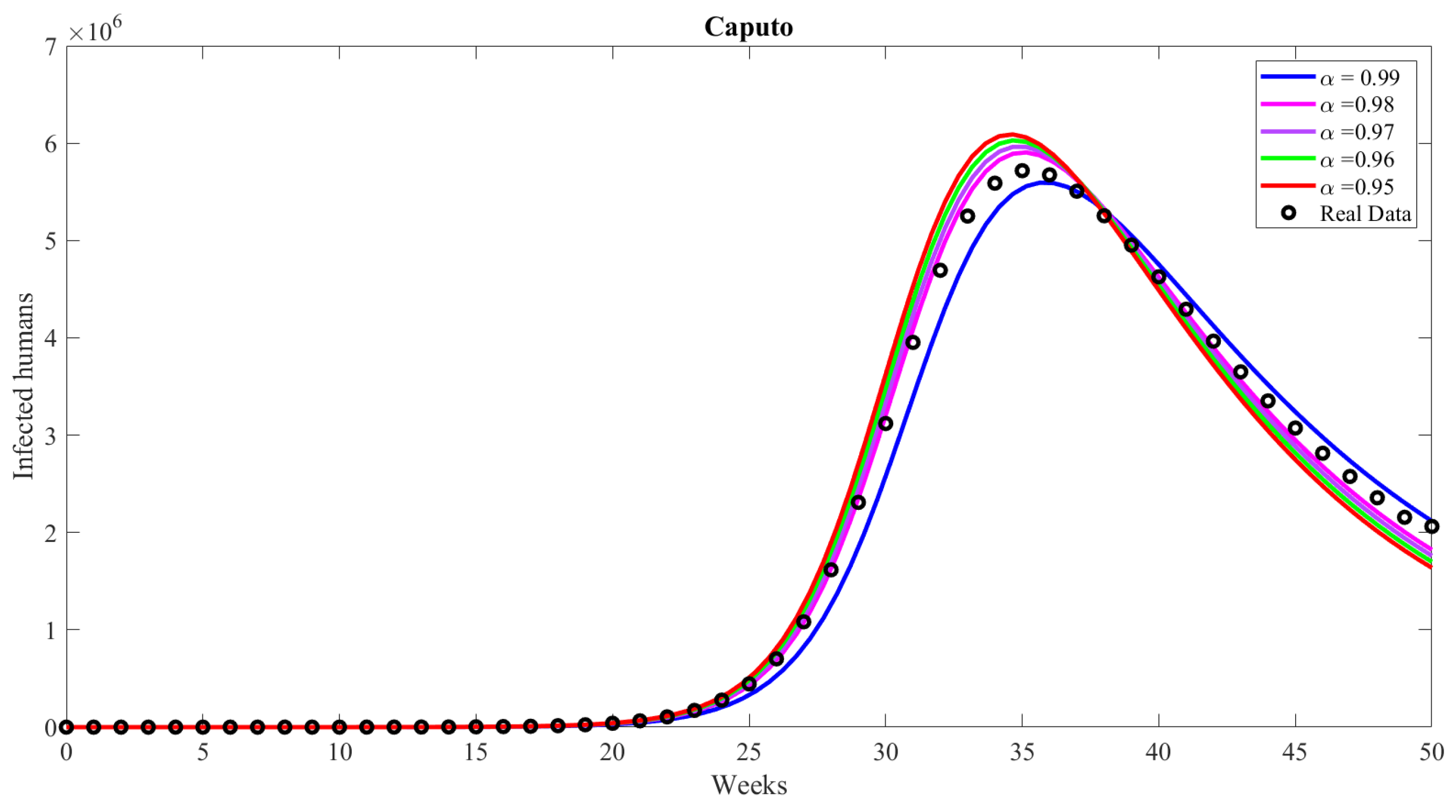
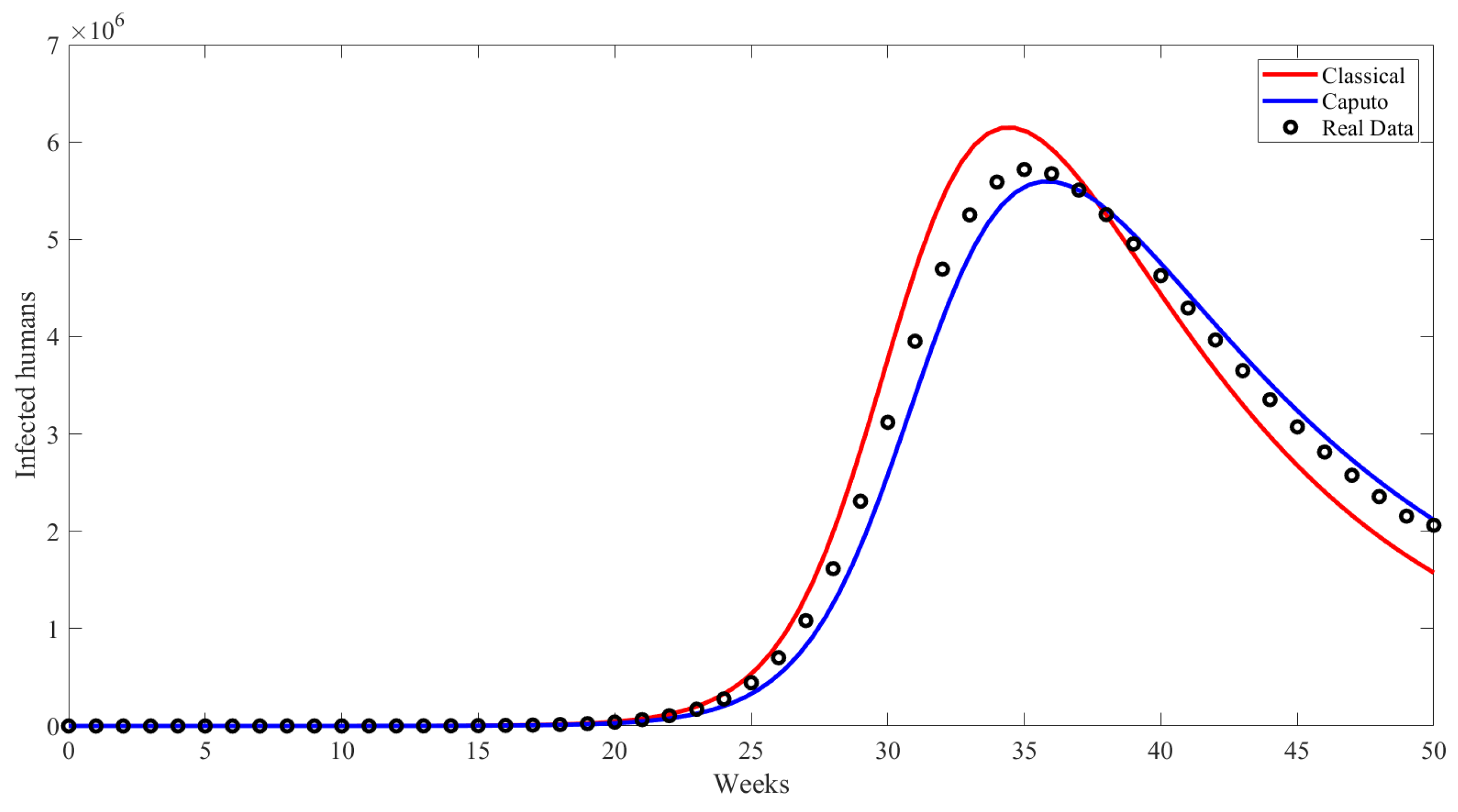






| Compartment | Description |
|---|---|
| S | Susceptible class |
| V | Vaccinated class |
| E | Exposed class |
| I | Infected class |
| H | Hospitalized class |
| R | Recovered class |
| Parameter | Description | Value | Source |
|---|---|---|---|
| Population recruitment rate | [39] | ||
| Natural death rate | 0.000254 weeks−1 | [39] | |
| Average effective contact rate | 0.858 | Fitted | |
| Vaccination rate | 0.114 | Fitted | |
| Vaccine inefficacy | 1 | Fitted | |
| Average hospitalization rate | 0.0015 | Fitted | |
| Recovery rate for infected class | 0.385 day−1 | [40] | |
| Recovery rate for exposed class | 0.34 | Fitted | |
| Recovery rate for hospitalized individuals | 0.68 | Fitted | |
| Average latent or incubation period | 0.625 day−1 | [41] | |
| Rate at which individuals lose immunity | 0.0067 day−1 | [39] |
| Fractional Order | MAE | RMSE |
|---|---|---|
| 0.99 | ||
| 0.98 | ||
| 0.97 | ||
| 0.96 | ||
| 0.95 |
| Fractional Order | MAE | RMSE |
|---|---|---|
| 0.99 | ||
| 0.98 | ||
| 0.97 | ||
| 0.96 | ||
| 0.95 |
| Fractional Order | MAE | RMSE |
|---|---|---|
| 0.99 | ||
| 0.98 | ||
| 0.97 | ||
| 0.96 | ||
| 0.95 | ||
| Classical |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdoon, M.A.; Alzahrani, A.B.M. Comparative Analysis of Influenza Modeling Using Novel Fractional Operators with Real Data. Symmetry 2024, 16, 1126. https://doi.org/10.3390/sym16091126
Abdoon MA, Alzahrani ABM. Comparative Analysis of Influenza Modeling Using Novel Fractional Operators with Real Data. Symmetry. 2024; 16(9):1126. https://doi.org/10.3390/sym16091126
Chicago/Turabian StyleAbdoon, Mohamed A., and Abdulrahman B. M. Alzahrani. 2024. "Comparative Analysis of Influenza Modeling Using Novel Fractional Operators with Real Data" Symmetry 16, no. 9: 1126. https://doi.org/10.3390/sym16091126
APA StyleAbdoon, M. A., & Alzahrani, A. B. M. (2024). Comparative Analysis of Influenza Modeling Using Novel Fractional Operators with Real Data. Symmetry, 16(9), 1126. https://doi.org/10.3390/sym16091126







