The Optimal Experimental Design for Exponentiated Frech’et Lifetime Products
Abstract
1. Introduction
2. Introduction to the Testing Procedure for the Lifetime Performance Index and Minimum Sample Size
3. Reliability Sampling Design
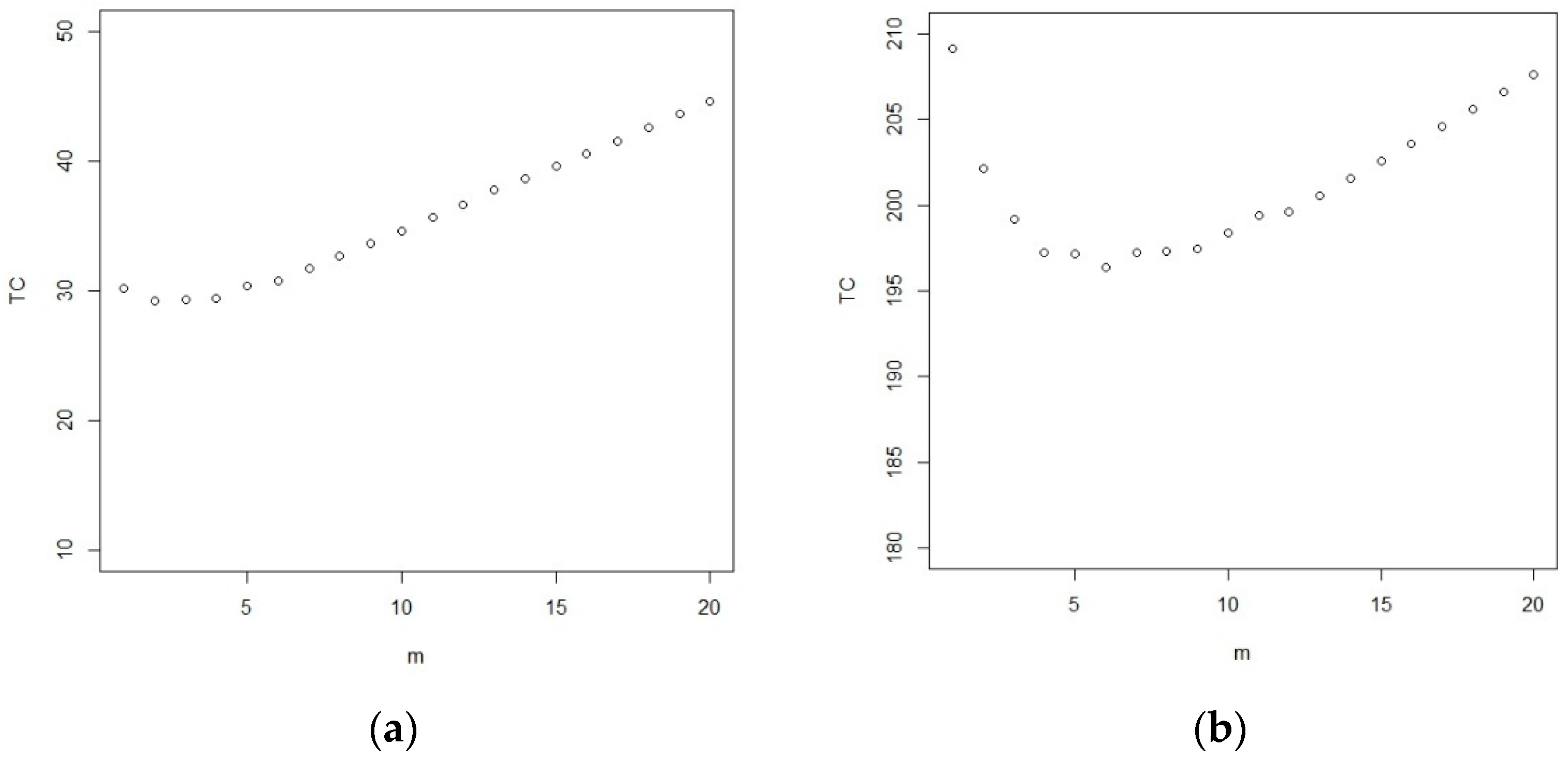
3.1. The Determination of the Optimal m and n When the Termination Time T Is Fixed
- Inspection cost CI: the cost of using the inspection equipment for each inspection;
- Sample cost Cs: the cost for one test unit in the sample;
- Operation cost Co: the cost per unit of time, encompassing expenses like personnel costs and the depreciation of test equipment;
- Installation cost Ca: the fixed cost for installing all test units.
- Step 1: Provide the predetermined values of c0, c1, , , , T, L, and the costs of CI = a Ca, Cs = b Ca, Co = c Ca.
- Step 2: Compute and
- Step 3: Set m = 1.
- Step 4: Calculate the sample size n using Equation (11), followed by determining the associated total cost TC(m,n) by the use of Equation (12).
- Step 5: If , then m = m + 1 and go to Step 4; otherwise, go to Step 6.
- Step 6: The optimal value of m denoted by m* is found to be the minimum value of m such that TC* = TC(m,n) is attained and the related sample size n* can be obtained by using Equation (11).
- Step 7: The critical value in the critical region can be calculated as .
3.2. The Determination of the Optimal m, t and n When the Termination Time T Is Varying
- Step 1: Provide the predetermined values of c0, c1, , , , L, and the costs of CI = a Ca, Cs = b Ca, Co = c Ca.
- Step 2: Compute and
- Step 3: Set m = 1.
- Step 4: The optimal value of t* is determined to minimize the total cost TC(m,t,n) given in Equation (13). Calculate the sample size n using Equation (11) and then compute the related total cost TC(m,t*,n) by using Equation (13).
- Step 5: If , then m = m + 1 and go to Step 4; otherwise, go to Step 6.
- Step 6: We determine the optimal choice of m denoted by m* as the minimum value of m such that TC** = TC(m,t*,n) is reached and then the corresponding sample size n* is determined by using Equation (11).
- Step 7: The critical value can be calculated as .
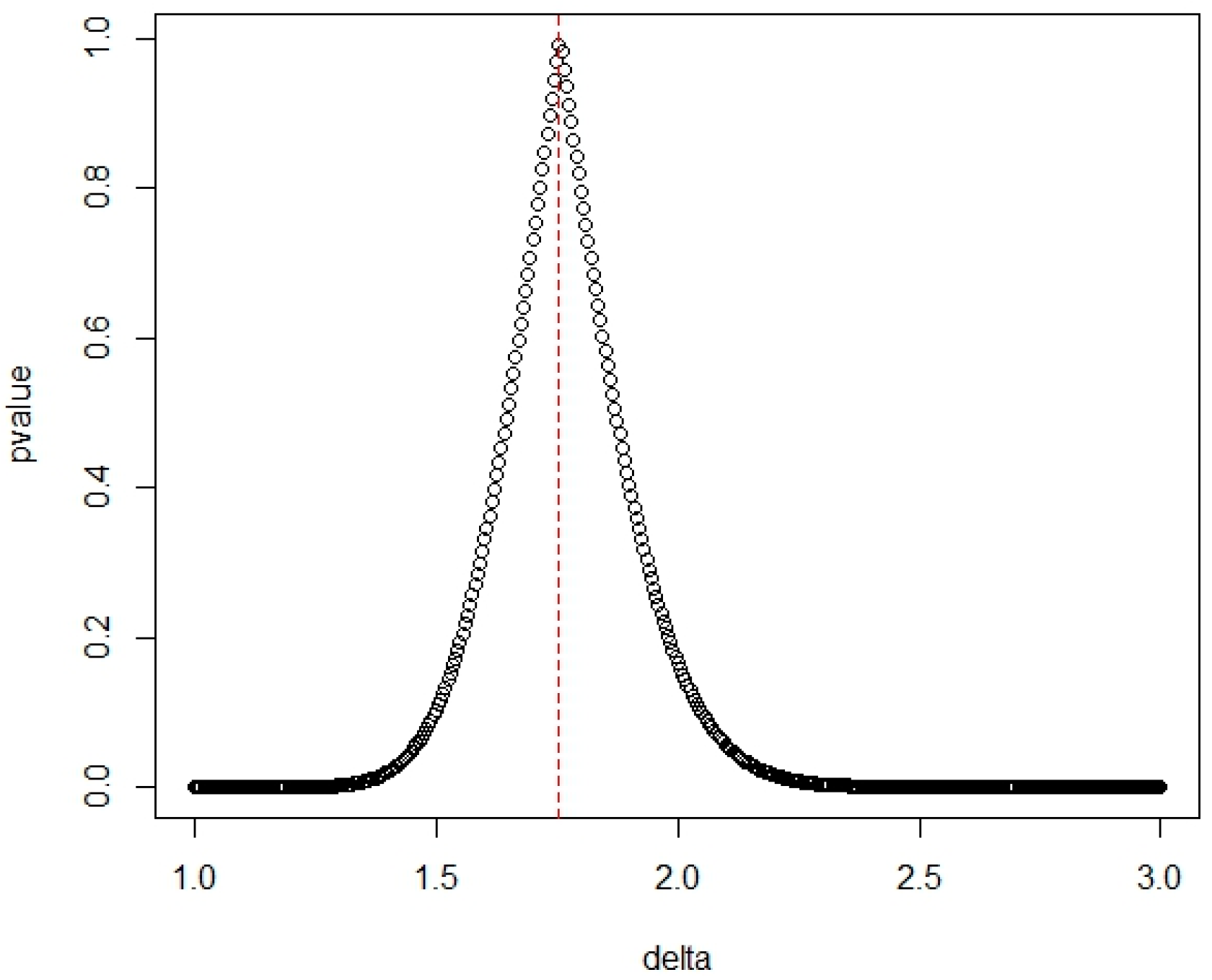
3.3. Example
- Step 1: Take a random sample 36 in size with m* = 2 from the data set. Collect the progressive type I interval censored sample (7, 24) at the pre-set times (0.4, 0.8) with censoring schemes of 0, 5).
- Step 2: Calculate the maximum likelihood estimator for as = 8.9934. We can find the maximum likelihood estimator for c as = 1 − 8.9934 (0.00255) = 0.9907.
- Step 3: For the level of = 0.01 test, the critical value is found to be = 0.8707.
- Step 4: Since 0.9907 > = 0.8707, we can infer that the null hypothesis should be rejected and conclude that the lifetime performance index attains the required target level c0, and we claim that the production process is capable.
- Step 1: Take a random sample 43 in size from the data set. Observe the progressive type I interval censored sample = (0, 2, 4) at the pre-set times = (0.15, 0.30, 0.45) with censoring schemes of = (5, 4, 28).
- Step 2: Calculate the maximum likelihood estimator for as = 13.3962. Then, we can find the maximum likelihood estimator for as = 1 − 13.3962 (0.00255) = 0.9658.
- Step 3: For the level of the = 0.01 test, the critical value is found to be 0.8541.
- Step 4: Since 0.9658 > 0.8541, we arrive at the same conclusion to substantiate the alternative hypothesis.
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| 0.025 | 0.05 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p | ||||||||||
| 0.01 | 0.20 | 0.050 | 20 | 1629 | 1650.8 | 0.7667 | 11 | 386 | 398.8 | 0.7847 |
| 0.075 | 18 | 1654 | 1673.8 | 0.7667 | 10 | 391 | 402.8 | 0.7847 | ||
| 0.100 | 17 | 1673 | 1691.8 | 0.7667 | 9 | 395 | 405.8 | 0.7847 | ||
| 0.15 | 0.050 | 15 | 1371 | 1387.8 | 0.7678 | 9 | 328 | 338.8 | 0.7867 | |
| 0.075 | 12 | 1398 | 1411.8 | 0.7678 | 8 | 333 | 342.8 | 0.7867 | ||
| 0.100 | 10 | 1419 | 1430.8 | 0.7678 | 8 | 336 | 345.8 | 0.7867 | ||
| 0.10 | 0.050 | 10 | 1202 | 1213.8 | 0.7688 | 8 | 288 | 297.8 | 0.7886 | |
| 0.075 | 9 | 1224 | 1234.8 | 0.7688 | 7 | 293 | 301.8 | 0.7886 | ||
| 0.100 | 8 | 1243 | 1252.8 | 0.7688 | 6 | 298 | 305.8 | 0.7886 | ||
| 0.05 | 0.20 | 0.050 | 18 | 1056 | 1075.8 | 0.7647 | 9 | 247 | 257.8 | 0.7808 |
| 0.075 | 16 | 1072 | 1089.8 | 0.7647 | 8 | 250 | 259.8 | 0.7808 | ||
| 0.100 | 15 | 1084 | 1100.8 | 0.7647 | 7 | 253 | 261.8 | 0.7808 | ||
| 0.15 | 0.050 | 13 | 861 | 875.8 | 0.7659 | 8 | 203 | 212.8 | 0.7831 | |
| 0.075 | 11 | 877 | 889.8 | 0.7659 | 7 | 206 | 214.8 | 0.7831 | ||
| 0.100 | 9 | 890 | 900.8 | 0.7659 | 6 | 209 | 216.8 | 0.7831 | ||
| 0.10 | 0.050 | 9 | 732 | 742.8 | 0.7671 | 6 | 175 | 182.8 | 0.7852 | |
| 0.075 | 8 | 745 | 754.8 | 0.7671 | 5 | 178 | 184.8 | 0.7853 | ||
| 0.100 | 7 | 756 | 764.8 | 0.7671 | 6 | 178 | 185.8 | 0.7853 | ||
| 0.10 | 0.20 | 0.050 | 16 | 802 | 819.8 | 0.7632 | 6 | 188 | 195.8 | 0.7778 |
| 0.075 | 14 | 814 | 829.8 | 0.7632 | 6 | 189 | 196.8 | 0.7778 | ||
| 0.100 | 13 | 823 | 837.8 | 0.7632 | 6 | 190 | 197.8 | 0.7778 | ||
| 0.15 | 0.050 | 12 | 637 | 650.8 | 0.7644 | 6 | 150 | 157.8 | 0.7803 | |
| 0.075 | 10 | 649 | 660.8 | 0.7644 | 5 | 153 | 159.8 | 0.7803 | ||
| 0.100 | 9 | 658 | 668.8 | 0.7644 | 5 | 154 | 160.8 | 0.7802 | ||
| 0.10 | 0.050 | 9 | 528 | 538.8 | 0.7657 | 5 | 126 | 132.8 | 0.7826 | |
| 0.075 | 7 | 539 | 547.8 | 0.7657 | 5 | 127 | 133.8 | 0.7826 | ||
| 0.100 | 7 | 546 | 554.8 | 0.7657 | 5 | 128 | 134.8 | 0.7826 |
| 0.125 | 0.15 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| p | ||||||||||
| 0.01 | 0.20 | 0.050 | 3 | 54 | 58.8 | 0.8468 | 2 | 36 | 39.8 | 0.8707 |
| 0.075 | 3 | 54 | 58.8 | 0.8469 | 2 | 36 | 39.8 | 0.8708 | ||
| 0.100 | 3 | 54 | 58.8 | 0.8470 | 2 | 36 | 39.8 | 0.8708 | ||
| 0.15 | 0.050 | 4 | 46 | 51.8 | 0.8509 | 3 | 31 | 35.8 | 0.8747 | |
| 0.075 | 3 | 48 | 52.8 | 0.8503 | 3 | 31 | 35.8 | 0.8748 | ||
| 0.100 | 3 | 48 | 52.8 | 0.8505 | 2 | 33 | 36.8 | 0.8739 | ||
| 0.10 | 0.050 | 3 | 43 | 47.8 | 0.8537 | 3 | 28 | 32.8 | 0.8785 | |
| 0.075 | 3 | 43 | 47.8 | 0.8539 | 2 | 30 | 33.8 | 0.8778 | ||
| 0.100 | 3 | 43 | 47.8 | 0.8541 | 2 | 30 | 33.8 | 0.8779 | ||
| 0.05 | 0.20 | 0.050 | 2 | 33 | 36.8 | 0.8392 | 2 | 21 | 24.8 | 0.8618 |
| 0.075 | 2 | 33 | 36.8 | 0.8392 | 2 | 21 | 24.8 | 0.8618 | ||
| 0.100 | 2 | 33 | 36.8 | 0.8392 | 2 | 21 | 24.8 | 0.8619 | ||
| 0.15 | 0.050 | 2 | 29 | 32.8 | 0.8434 | 1 | 20 | 22.8 | 0.8684 | |
| 0.075 | 2 | 29 | 32.8 | 0.8434 | 1 | 20 | 22.8 | 0.8684 | ||
| 0.100 | 2 | 29 | 32.8 | 0.8435 | 1 | 20 | 22.8 | 0.8684 | ||
| 0.10 | 0.050 | 2 | 26 | 29.8 | 0.8470 | 2 | 17 | 20.8 | 0.8700 | |
| 0.075 | 2 | 26 | 29.8 | 0.8471 | 2 | 17 | 20.8 | 0.8701 | ||
| 0.100 | 2 | 26 | 29.8 | 0.8472 | 2 | 17 | 20.8 | 0.8702 | ||
| 0.10 | 0.20 | 0.050 | 1 | 25 | 27.8 | 0.8328 | 1 | 16 | 18.8 | 0.8535 |
| 0.075 | 1 | 25 | 27.8 | 0.8328 | 1 | 16 | 18.8 | 0.8535 | ||
| 0.100 | 1 | 25 | 27.8 | 0.8328 | 1 | 16 | 18.8 | 0.8535 | ||
| 0.15 | 0.050 | 2 | 20 | 23.8 | 0.8376 | 1 | 14 | 16.8 | 0.8602 | |
| 0.075 | 2 | 20 | 23.8 | 0.8376 | 1 | 14 | 16.8 | 0.8602 | ||
| 0.100 | 2 | 20 | 23.8 | 0.8377 | 1 | 14 | 16.8 | 0.8602 | ||
| 0.10 | 0.050 | 2 | 18 | 21.8 | 0.8408 | 1 | 13 | 15.8 | 0.8640 | |
| 0.075 | 2 | 18 | 21.8 | 0.8409 | 1 | 13 | 15.8 | 0.8640 | ||
| 0.100 | 2 | 18 | 21.8 | 0.8410 | 1 | 13 | 15.8 | 0.8640 |
| 0.025 | 0.05 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | ||||||||||||
| 0.01 | 0.20 | 0.050 | 20 | 0.03 | 1628 | 1649.6 | 0.7667 | 11 | 0.04 | 385 | 397.4 | 0.7847 |
| 0.075 | 18 | 0.04 | 1653 | 1672.6 | 0.7667 | 9 | 0.04 | 391 | 401.3 | 0.7847 | ||
| 0.100 | 14 | 0.04 | 1676 | 1691.5 | 0.7667 | 8 | 0.04 | 395 | 404.3 | 0.7848 | ||
| 0.15 | 0.050 | 20 | 0.07 | 1358 | 1380.3 | 0.7679 | 10 | 0.07 | 327 | 338.7 | 0.7867 | |
| 0.075 | 17 | 0.08 | 1386 | 1405.3 | 0.7679 | 9 | 0.08 | 332 | 342.7 | 0.7867 | ||
| 0.100 | 13 | 0.09 | 1411 | 1426.1 | 0.7678 | 8 | 0.10 | 336 | 345.8 | 0.7867 | ||
| 0.10 | 0.050 | 19 | 0.11 | 1169 | 1191.0 | 0.7691 | 9 | 0.11 | 285 | 296.0 | 0.7887 | |
| 0.075 | 15 | 0.12 | 1198 | 1215.8 | 0.7691 | 8 | 0.13 | 290 | 300.1 | 0.7887 | ||
| 0.100 | 13 | 0.13 | 1220 | 1235.7 | 0.7690 | 7 | 0.14 | 295 | 304.0 | 0.7887 | ||
| 0.05 | 0.20 | 0.050 | 17 | 0.03 | 1057 | 1075.5 | 0.7647 | 7 | 0.04 | 249 | 257.3 | 0.7809 |
| 0.075 | 14 | 0.03 | 1074 | 1089.5 | 0.7647 | 7 | 0.03 | 251 | 259.2 | 0.7809 | ||
| 0.100 | 12 | 0.04 | 1087 | 1100.4 | 0.7647 | 6 | 0.05 | 253 | 260.3 | 0.7809 | ||
| 0.15 | 0.050 | 17 | 0.07 | 853 | 872.2 | 0.7659 | 8 | 0.09 | 203 | 212.7 | 0.7831 | |
| 0.075 | 13 | 0.08 | 872 | 887.0 | 0.7659 | 6 | 0.08 | 208 | 215.5 | 0.7831 | ||
| 0.100 | 13 | 0.09 | 883 | 898.2 | 0.7659 | 7 | 0.10 | 208 | 216.7 | 0.7831 | ||
| 0.10 | 0.050 | 15 | 0.11 | 714 | 731.6 | 0.7672 | 7 | 0.12 | 173 | 181.8 | 0.7853 | |
| 0.075 | 12 | 0.12 | 731 | 745.5 | 0.7672 | 6 | 0.14 | 176 | 183.8 | 0.7853 | ||
| 0.100 | 11 | 0.14 | 743 | 756.6 | 0.7672 | 6 | 0.13 | 178 | 185.8 | 0.7853 | ||
| 0.10 | 0.20 | 0.050 | 15 | 0.03 | 803 | 819.4 | 0.7632 | 6 | 0.05 | 187 | 194.3 | 0.7779 |
| 0.075 | 14 | 0.04 | 813 | 828.6 | 0.7632 | 6 | 0.05 | 188 | 195.3 | 0.7779 | ||
| 0.100 | 12 | 0.04 | 823 | 836.5 | 0.7632 | 6 | 0.06 | 189 | 196.3 | 0.7779 | ||
| 0.15 | 0.050 | 14 | 0.07 | 633 | 649.0 | 0.7644 | 7 | 0.09 | 149 | 157.6 | 0.7802 | |
| 0.075 | 12 | 0.08 | 645 | 659.0 | 0.7644 | 5 | 0.09 | 153 | 159.5 | 0.7803 | ||
| 0.100 | 11 | 0.09 | 654 | 667.0 | 0.7644 | 5 | 0.09 | 154 | 160.5 | 0.7802 | ||
| 0.10 | 0.050 | 13 | 0.11 | 517 | 532.4 | 0.7658 | 6 | 0.15 | 124 | 131.9 | 0.7826 | |
| 0.075 | 12 | 0.12 | 527 | 541.5 | 0.7658 | 5 | 0.13 | 127 | 133.7 | 0.7826 | ||
| 0.100 | 10 | 0.13 | 537 | 549.3 | 0.7658 | 5 | 0.14 | 128 | 134.7 | 0.7826 | ||
| 0.125 | 0.15 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | ||||||||||||
| 0.01 | 0.20 | 0.050 | 3 | 0.06 | 53 | 57.2 | 0.8477 | 2 | 0.03 | 36 | 39.1 | 0.8707 |
| 0.075 | 2 | 0.04 | 55 | 58.1 | 0.8477 | 2 | 0.03 | 36 | 39.1 | 0.8708 | ||
| 0.100 | 2 | 0.04 | 55 | 58.1 | 0.8478 | 2 | 0.03 | 36 | 39.1 | 0.8708 | ||
| 0.15 | 0.050 | 3 | 0.12 | 47 | 51.4 | 0.8512 | 2 | 0.11 | 32 | 35.2 | 0.8757 | |
| 0.075 | 3 | 0.07 | 48 | 52.2 | 0.8503 | 2 | 0.12 | 32 | 35.2 | 0.8758 | ||
| 0.100 | 3 | 0.08 | 48 | 52.2 | 0.8505 | 2 | 0.13 | 32 | 35.3 | 0.8759 | ||
| 0.10 | 0.050 | 3 | 0.12 | 43 | 47.4 | 0.8537 | 3 | 0.18 | 28 | 32.5 | 0.8785 | |
| 0.075 | 3 | 0.13 | 43 | 47.4 | 0.8539 | 2 | 0.13 | 30 | 33.3 | 0.8778 | ||
| 0.100 | 3 | 0.15 | 43 | 47.5 | 0.8541 | 2 | 0.13 | 30 | 33.3 | 0.8779 | ||
| 0.05 | 0.20 | 0.050 | 2 | 0.04 | 33 | 36.1 | 0.8392 | 1 | 0.06 | 22 | 24.1 | 0.8632 |
| 0.075 | 2 | 0.05 | 33 | 36.1 | 0.8392 | 1 | 0.06 | 22 | 24.1 | 0.8632 | ||
| 0.100 | 2 | 0.05 | 33 | 36.1 | 0.8392 | 1 | 0.06 | 22 | 24.1 | 0.8632 | ||
| 0.15 | 0.050 | 2 | 0.09 | 29 | 32.2 | 0.8434 | 1 | 0.12 | 20 | 22.1 | 0.8684 | |
| 0.075 | 2 | 0.09 | 29 | 32.2 | 0.8434 | 1 | 0.12 | 20 | 22.1 | 0.8684 | ||
| 0.100 | 2 | 0.10 | 29 | 32.2 | 0.8435 | 1 | 0.12 | 20 | 22.1 | 0.8684 | ||
| 0.10 | 0.050 | 2 | 0.12 | 26 | 29.2 | 0.8470 | 2 | 0.12 | 17 | 20.2 | 0.8700 | |
| 0.075 | 2 | 0.13 | 26 | 29.3 | 0.8471 | 2 | 0.12 | 17 | 20.2 | 0.8701 | ||
| 0.100 | 2 | 0.13 | 26 | 29.3 | 0.8472 | 2 | 0.13 | 17 | 20.3 | 0.8702 | ||
| 0.10 | 0.20 | 0.050 | 1 | 0.05 | 25 | 27.0 | 0.8328 | 1 | 0.03 | 16 | 18.0 | 0.8535 |
| 0.075 | 1 | 0.05 | 25 | 27.0 | 0.8328 | 1 | 0.03 | 16 | 18.0 | 0.8535 | ||
| 0.100 | 1 | 0.05 | 25 | 27.0 | 0.8328 | 1 | 0.03 | 16 | 18.0 | 0.8535 | ||
| 0.15 | 0.050 | 2 | 0.12 | 20 | 23.2 | 0.8376 | 1 | 0.10 | 14 | 16.1 | 0.8602 | |
| 0.075 | 2 | 0.13 | 20 | 23.3 | 0.8376 | 1 | 0.10 | 14 | 16.1 | 0.8602 | ||
| 0.100 | 2 | 0.14 | 20 | 23.3 | 0.8377 | 1 | 0.10 | 14 | 16.1 | 0.8602 | ||
| 0.10 | 0.050 | 2 | 0.12 | 18 | 21.2 | 0.8408 | 1 | 0.13 | 13 | 15.1 | 0.8640 | |
| 0.075 | 2 | 0.12 | 18 | 21.2 | 0.8409 | 1 | 0.13 | 13 | 15.1 | 0.8640 | ||
| 0.100 | 2 | 0.12 | 18 | 21.2 | 0.8410 | 1 | 0.13 | 13 | 15.1 | 0.8640 | ||
References
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley and Sons Inc.: New York, NY, USA, 1985. [Google Scholar]
- Tong, L.I.; Chen, K.S.; Chen, H.T. Statistical testing for assessing the performance of lifetime index of electronic components with exponential distribution. Int. J. Qual. Reliab. Manag. 2002, 19, 812–824. [Google Scholar] [CrossRef]
- Cohen, A.C.; Sackrowitz, H. Progressively Censored Data with Unbalanced Groups. Technometrics 1997, 39, 425–432. [Google Scholar]
- Balakrishnan, N.; Zhang, D. Progressively Censored Data Analysis with Applications. J. Stat. Plan. Inference 2003, 113, 37–52. [Google Scholar]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods and Applications; Birkhäuser: Boston, MA, USA, 2000. [Google Scholar]
- Gupta, A.K.; Sinha, A. Inference for Progressive Censoring in Exponential Distributions with Applications to Lifetime Data. Commun. Stat.—Theory Methods 2022, 51, 4151–4168. [Google Scholar]
- Chen, M.; Zhang, X. Bayesian Methods for Progressive Censoring in Reliability Testing. J. Stat. Comput. Simul. 2023, 93, 1234–1251. [Google Scholar]
- Wang, Y.; Liu, J. Advanced Methods for Progressive Censoring in Survival Analysis. Stat. Med. 2023, 42, 1802–1820. [Google Scholar]
- Wu, S.F.; Lin, Y.P. Computational testing algorithmic procedure of assessment for lifetime performance index of products with one-parameter exponential distribution under progressive type I interval censoring. Math. Comput. Simul. 2016, 120, 79–90. [Google Scholar] [CrossRef]
- Wu, S.F.; Chen, Z.C.; Chang, W.J.; Chang, C.W.; Lin, C. A hypothesis testing procedure for the evaluation on the lifetime performance index of products with Burr XII distribution under progressive type I interval censoring. Commun. Stat.—Simul. Comput. 2018, 47, 2670–2683. [Google Scholar] [CrossRef]
- Wu, S.F.; Chang, W.T. The evaluation on the process capability index CL for exponentiated Frech’et lifetime product under progressive type I interval censoring. Symmetry 2021, 13, 1032. [Google Scholar] [CrossRef]
- Huang, S.R.; Wu, S.J. Reliability sampling plans under progressive type-I interval censoring using cost functions. IEEE Trans. Reliab. 2008, 57, 445–451. [Google Scholar] [CrossRef]
- Wingo, D.R. Maximum likelihood methods for fitting the Burr type XII distribution to life test data. Biom. J. 1983, 25, 77–84. [Google Scholar] [CrossRef]
- Gail, M.H.; Gastwirth, J.L. A scale-free goodness of fit test for the exponential distribution based on the Gini Statistic. J. R. Stat. Soc. B 1978, 40, 350–357. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.-F. The Optimal Experimental Design for Exponentiated Frech’et Lifetime Products. Symmetry 2024, 16, 1132. https://doi.org/10.3390/sym16091132
Wu S-F. The Optimal Experimental Design for Exponentiated Frech’et Lifetime Products. Symmetry. 2024; 16(9):1132. https://doi.org/10.3390/sym16091132
Chicago/Turabian StyleWu, Shu-Fei. 2024. "The Optimal Experimental Design for Exponentiated Frech’et Lifetime Products" Symmetry 16, no. 9: 1132. https://doi.org/10.3390/sym16091132
APA StyleWu, S.-F. (2024). The Optimal Experimental Design for Exponentiated Frech’et Lifetime Products. Symmetry, 16(9), 1132. https://doi.org/10.3390/sym16091132





