Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals
Abstract
:1. Introduction
2. Theoretical and Numerical Calculations
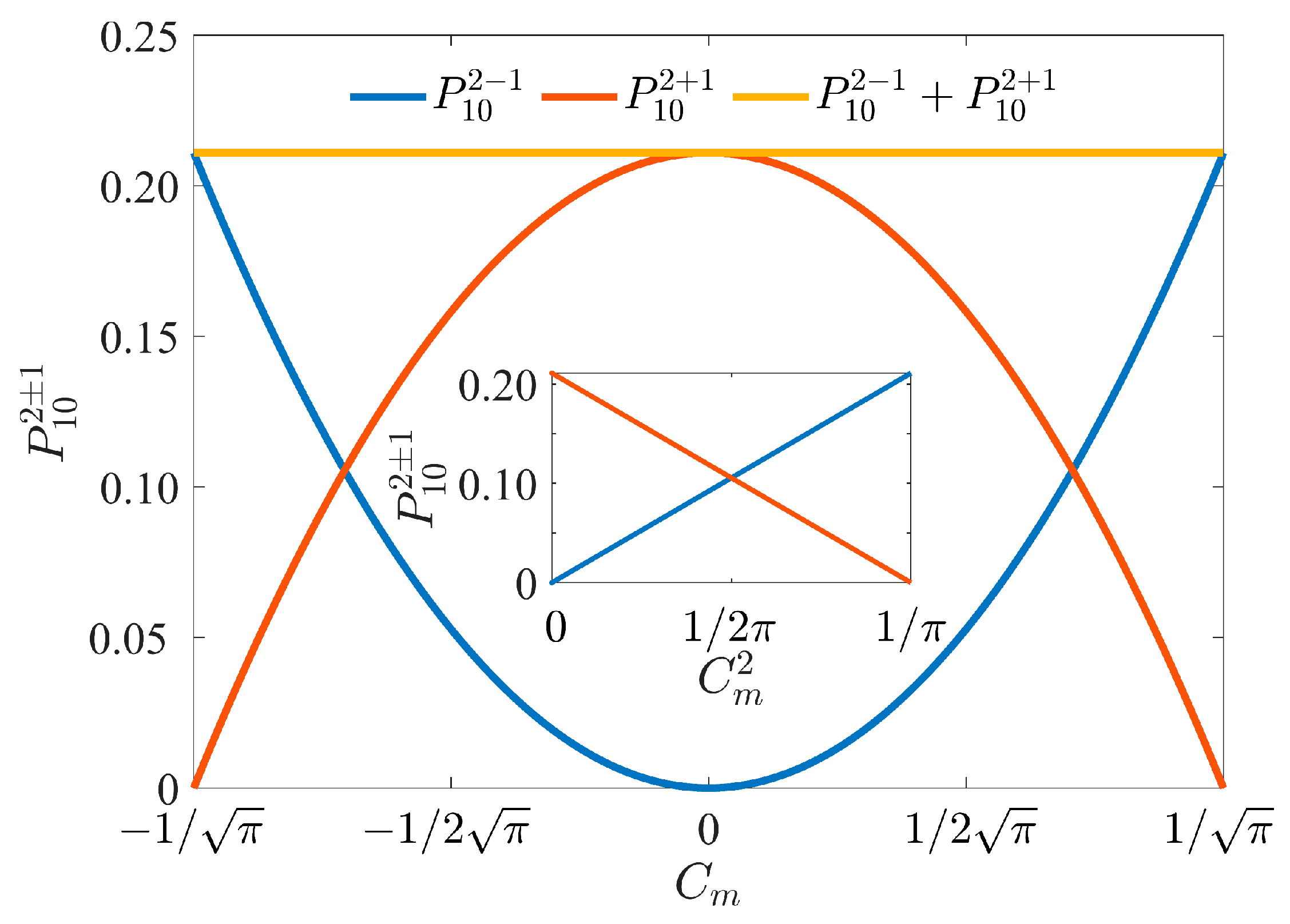
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Orthogonality of Azimuthal Wavefunctions
Appendix B. Proof of Cartesian Representation of Azimuthal Wavefunctions
References
- Pal, A.; Zhang, S.; Chavan, T.; Agashiwala, K.; Yeh, C.-H.; Cao, W.; Banerjee, K. Quantum-Engineered Devices Based on 2D Materials for Next-Generation Information Processing and Storage. Adv. Mater. 2023, 35, 2109894. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Kang, J.-H. Light-induced edge-excitation of two-dimensional surface polaritons in atomically thin crystals. Results Phys. 2024, 57, 107400. [Google Scholar] [CrossRef]
- Xue, L.; Ren, Y.; He, J.-R.; Zhao, Y.; Xu, S.-L.; Hu, Y.; Hua, C.-B. The mechanical and thermal parameters of two-dimensional hexagonal materials evaluated using elastic properties: Monolayer MoS2 as an example. Results Phys. 2024, 57, 107418. [Google Scholar] [CrossRef]
- Pramjorn, N.; Amthong, A. Donor binding energies in a curved two-dimensional electron system. Appl. Surf. Sci. 2020, 508, 145195. [Google Scholar] [CrossRef]
- Chouef, S.; Mommadi, O.; Boussetta, R.; Hbibi, M.; El Moussaouy, A.; Şahin, M.; Falyouni, F.; Duque, C.A. Effects of surface curvature and electric field on electronic and optical properties of an off-center hydrogenic donor impurity in 2D nanostructures. Eur. Phys. J. Plus 2024, 139, 381. [Google Scholar] [CrossRef]
- García Flórez, F.; Siebbeles, L.D.A.; Stoof, H.T.C. Effects of material thickness and surrounding dielectric medium on Coulomb interactions and two-dimensional excitons. Phys. Rev. B 2020, 102, 125303. [Google Scholar] [CrossRef]
- Mora-Ramos, M.E.; Duque, C.A. The formation of indirect excitons in atomic layer doped systems. Superlattices Microstruct. 2015, 87, 32–37. [Google Scholar] [CrossRef]
- Abadillo-Uriel, J.C.; Koiller, B.; Calderón, M.J. Two-dimensional semiconductors pave the way towards dopant-based quantum computing. Beilstein J. Nanotechnol. 2018, 9, 2668–2673. [Google Scholar] [CrossRef]
- Becher, C.; Gao, W.; Kar, S.; Marciniak, C.D.; Monz, T.; Bartholomew, J.G.; Goldner, P.; Loh, H.; Marcellina, E.; Goh, K.E.J.; et al. 2023 roadmap for materials for quantum technologies. Mater. Quantum Technol. 2023, 3, 012501. [Google Scholar] [CrossRef]
- Hollenberg, L.C.L.; Greentree, A.D.; Fowler, A.G.; Wellard, C.J. Two-dimensional architectures for donor-based quantum computing. Phys. Rev. B 2006, 74, 045311. [Google Scholar] [CrossRef]
- Moraru, D.; Udhiarto, A.; Anwar, M.; Nowak, R.; Jablonski, R.; Hamid, E.; Tarido, J.C.; Mizuno, T.; Tabe, M. Atom devices based on single dopants in silicon nanostructures. Nanoscale Res. Lett. 2011, 6, 479. [Google Scholar] [CrossRef] [PubMed]
- Yadav, P.; Arora, H.; Samanta, A. Nitrogen in silicon for room temperature single-electron tunneling devices. Appl. Phys. Lett. 2023, 122, 083502. [Google Scholar] [CrossRef]
- Wang, X.; Wyrick, J.; Kashid, R.V.; Namboodiri, P.; Schmucker, S.W.; Murphy, A.; Stewart, M.D., Jr.; Silver, R.M. Atomic-scale control of tunneling in donor-based devices. Commun. Phys. 2020, 3, 82. [Google Scholar] [CrossRef]
- Mueller, T.; Malic, E. Exciton physics and device application of two-dimensional transition metal dichalcogenide semiconductors. npj 2D Mater. Appl. 2.1 2018, 2, 29. [Google Scholar] [CrossRef]
- Sharma, A.; Hasan, M.M.; Lu, Y. Exciton dynamics in 2D organic semiconductors. Mater. Futures 2022, 1, 042001. [Google Scholar] [CrossRef]
- Xiao, J.; Zhao, M.; Wang, Y.; Zhang, X. Excitons in atomically thin 2D semiconductors and their applications. Nanophotonics 2017, 6, 1309–1328. [Google Scholar] [CrossRef]
- Parfitt, D.G.W.; Portnoi, M.E. The two-dimensional hydrogen atom revisited. J. Math. Phys. 2002, 43, 4681–4691. [Google Scholar] [CrossRef]
- Stephanovich, V.A. On the discreet spectrum of fractional quantum hydrogen atom in two dimensions. Phys. Scr. 2019, 94, 125108. [Google Scholar] [CrossRef]
- Kirchbach, M.; Vallejo, J.A. Wave functions of the Hydrogen atom in the momentum representation. J. Phys. A Math. Theor. 2023, 56, 125302. [Google Scholar] [CrossRef]
- Zaslow, B.; Zandler, M.E. Two-dimensional analog to the hydrogen atom. Am. J. Phys. 1967, 35, 1118–1119. [Google Scholar] [CrossRef]
- Yang, X.L.; Guo, S.H.; Chan, F.T.; Wong, K.W.; Ching, W.Y. Analytic solution of a two-dimensional hydrogen atom. I. Nonrelativ. Theory. Phys. Rev. A 1991, 43, 1186. [Google Scholar]
- Stevanović, L.; Sen, K.D. Simultaneous degeneracy of the confined 2D hydrogen atom energy levels. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 205002. [Google Scholar] [CrossRef]
- Aquino, N.; Campoy, G.; Flores-Riveros, A. Accurate energy eigenvalues and eigenfunctions for the two-dimensional confined hydrogen atom. Int. J. Quantum Chem. 2005, 103, 267–277. [Google Scholar] [CrossRef]
- Chaos-Cador, L.; Ley-Koo, E. Two-dimensional hydrogen atom confined in circles, angles, and circular sectors. Int. J. Quantum Chem. 2005, 103, 369–387. [Google Scholar] [CrossRef]
- Szmytkowski, R. Two-dimensional hydrogen-like atom in a weak magnetic field. Eur. Phys. J. Plus 2018, 133, 311. [Google Scholar] [CrossRef]
- Le, D.-N.; Hoang, N.-T.D.; Le, V.-H. Exact analytical solutions of a two-dimensional hydrogen atom in a constant magnetic field. J. Math. Phys. 2017, 58, 042102. [Google Scholar] [CrossRef]
- Szmytkowski, R. Second-order stark effect and polarizability of a relativistic two-dimensional hydrogenlike atom in the ground state. Phys. Rev. A 2018, 98, 042507. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Mera, H.; Nikolić, B.K. Stark effect in low-dimensional hydrogen. Phys. Rev. A 2016, 93, 013409. [Google Scholar] [CrossRef]
- Robnik, M.; Romanovski, V.G. Two-dimensional hydrogen atom in a strong magnetic field. J. Phys. A Math. Gen. 2003, 36, 7923. [Google Scholar] [CrossRef]
- Soylu, A.; Bayrak, O.; Boztosun, I. The energy eigenvalues of the two dimensional hydrogen atom in a magnetic field. Int. J. Mod. Phys. E 2006, 15, 1263–1271. [Google Scholar] [CrossRef]
- Meleshenko, P.A.; Nguyen, H.T.T.; Klinskikh, A.F. Spectroscopic peculiarities in a 2D Coulomb potential under Aharonov-Bohm effect. Eur. Phys. J. D 2013, 67, 209. [Google Scholar] [CrossRef]
- Koval, E.A.; Koval, O.A. Excited states of two-dimensional hydrogen atom in tilted magnetic field: Quantum chaos. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 93, 160–166. [Google Scholar] [CrossRef]
- Koval, E.A.; Koval, O.A. Anisotropic features of two-dimensional hydrogen atom in magnetic field. J. Exp. Theor. Phys. 2017, 125, 35–42. [Google Scholar] [CrossRef]
- Xie, W. A study of a hydrogen atom in a two-dimensional quantum well. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 3321–3324. [Google Scholar] [CrossRef]
- Grimaldi, C. Energy levels of a two-dimensional hydrogen atom with spin-orbit Rashba interaction. Phys. Rev. B 2008, 77, 113308. [Google Scholar] [CrossRef]
- Poszwa, A. Two-dimensional hydrogen-like atom in magnetic field in the presence of Rashba spin–orbit coupling. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 124, 114247. [Google Scholar] [CrossRef]
- Szafran, B.; Adamowski, J.; Bednarek, S. Electron–electron correlation in quantum dots. Phys. E Low-Dimens. Syst. Nanostruct. 1999, 5, 185–195. [Google Scholar] [CrossRef]
- Kormányos, A.; Zólyomi, V.; Drummond, N.D.; Burkard, G. Spin-orbit coupling, quantum dots, and qubits in monolayer transition metal dichalcogenides. Phys. Rev. X 2014, 4, 011034. [Google Scholar] [CrossRef]
- Prabhakar, S.; Melnik, R.; Bonilla, L.L. Coupled multiphysics, barrier localization, and critical radius effects in embedded nanowire superlattices. J. Appl. Phys. 2013, 113, 244306. [Google Scholar] [CrossRef]
- Joonhuay, J.; Sathongpaen, P.; Amthong, A. Structural design of triangular core–shell nanowires for sensing polarized mid-infrared light. Mater. Des. 2023, 230, 111983. [Google Scholar] [CrossRef]
- Amore, P.; Fernández, F.M. Bound states for the quantum dipole moment in two dimensions. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 235004. [Google Scholar] [CrossRef]
- Dasbiswas, K.; Goswami, D.; Yoo, C.-D.; Dorsey, A.T. Bound states of edge dislocations: The quantum dipole problem in two dimensions. Phys. Rev. B 2010, 81, 064516. [Google Scholar] [CrossRef]
- Thongnak, V.; Joonhuay, J.; Amthong, A. Polarization-selective absorption in an off-centered core-shell square quantum wire. Opt. Lett. 2021, 46, 3259–3262. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Schroeter, D.F. Introduction to Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Ashkenazi, G. The meaning of d-orbital labels. J. Chem. Educ. 2005, 82, 323. [Google Scholar] [CrossRef]
- Gil, V.M.S. Orbitals in Chemistry: A Modern Guide for Students; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Le, N.H.; Lanskii, G.V.; Aeppli, G.; Murdin, B.N. Giant non-linear susceptibility of hydrogenic donors in silicon and germanium. Light Sci. Appl. 2019, 8, 64. [Google Scholar] [CrossRef]
- Acosta-Humánez, M.F.; Acosta-Humánez, P.B.; Tuirán, E. Generalized Lennard-Jones Potentials, SUSYQM and Differential Galois Theory. SIGMA. Symmetry Integr. Geom. Methods Appl. 2018, 14, 099. [Google Scholar] [CrossRef]
- Badalov, V.H.; Ahmadov, H.I.; Ahmadov, A.I. Analytical solutions of the Schrödinger equation with the Woods–Saxon potential for arbitrary l state. Int. J. Mod. Phys. E 2009, 18, 631–641. [Google Scholar] [CrossRef]
| Error (%) | |||
|---|---|---|---|
| 1 | −4.00000 | −3.97619 | 0.59525 |
| 2 | −0.44444 | −0.44442 | 0.00450 |
| −0.44444 | −0.44442 | 0.00450 | |
| −0.44444 | −0.44149 | 0.66376 | |
| 3 | −0.16000 | −0.15998 | 0.01250 |
| −0.16000 | −0.15993 | 0.04375 | |
| −0.16000 | −0.15987 | 0.08125 | |
| −0.16000 | −0.15987 | 0.08125 | |
| −0.16000 | −0.15872 | 0.80000 | |
| 4 | −0.08160 | −0.08164 | 0.04901 |
| −0.08160 | −0.08164 | 0.04901 | |
| −0.08160 | −0.08164 | 0.03676 | |
| −0.08160 | −0.08164 | 0.03676 | |
| −0.08160 | −0.08164 | 0.03676 | |
| −0.08160 | −0.08163 | 0.03676 | |
| −0.08160 | −0.08163 | 0.94363 |
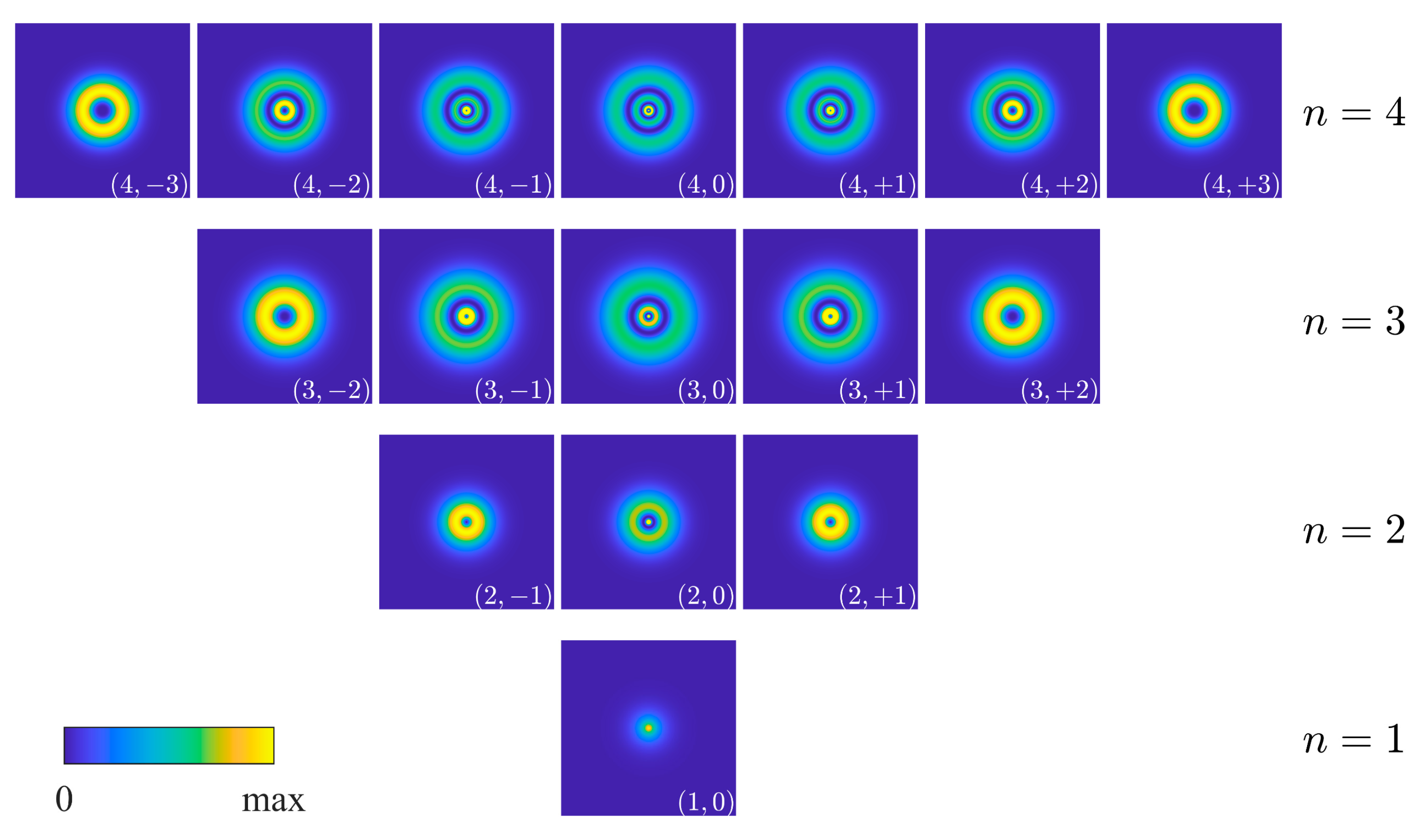
| Energy Level | Numerical Eigenfunctions | Analytic Eigenfunctions | ||||
|---|---|---|---|---|---|---|
| 1 |  | (1,0) |  | 0.0000 | 0.9997 | |
| 2 |  | (2,0) |  | 0.0000 | 0.9998 | |
 | (2,+1) |  | −0.5407 | 0.1611 | 0.9999 | |
 | (2,−1) |  | −0.1611 | 0.5407 | 0.9999 | |
| 3 |  | (3,0) |  | 0.0000 | 0.9989 | |
 | (3,+1) |  | 0.5422 | 0.1560 | 0.9995 | |
 | (3,−1) |  | −0.1560 | −0.5422 | 0.9995 | |
 | (3,+2) |  | −0.5642 | 0.0000 | 0.9998 | |
 | (3,−2) |  | 0.0000 | −0.5642 | 0.9999 | |
| 4 |  | (4,0) |  | 0.0000 | 0.9981 | |
 | (4,+1) |  | 0.4501 | −0.3402 | 0.9904 | |
 | (4,−1) |  | −0.3402 | 0.4501 | 0.9904 | |
 | (4,+2) |  | −0.5642 | 0.0000 | 1.0000 | |
 | (4,−2) |  | 0.0000 | 0.5642 | 1.0000 | |
 | (4,+3) |  | −0.5605 | 0.0644 | 0.9904 | |
 | (4,−3) |  | −0.0644 | 0.5605 | 0.9904 | |
Due to the Conventional Eigenfunctions | Due to Our Proposed Eigenfunctions | |
|---|---|---|
| 0.2109 | 0.2109 | |
| 0.0381 | 0.0381 | |
| 0.0132 | 0.0132 |
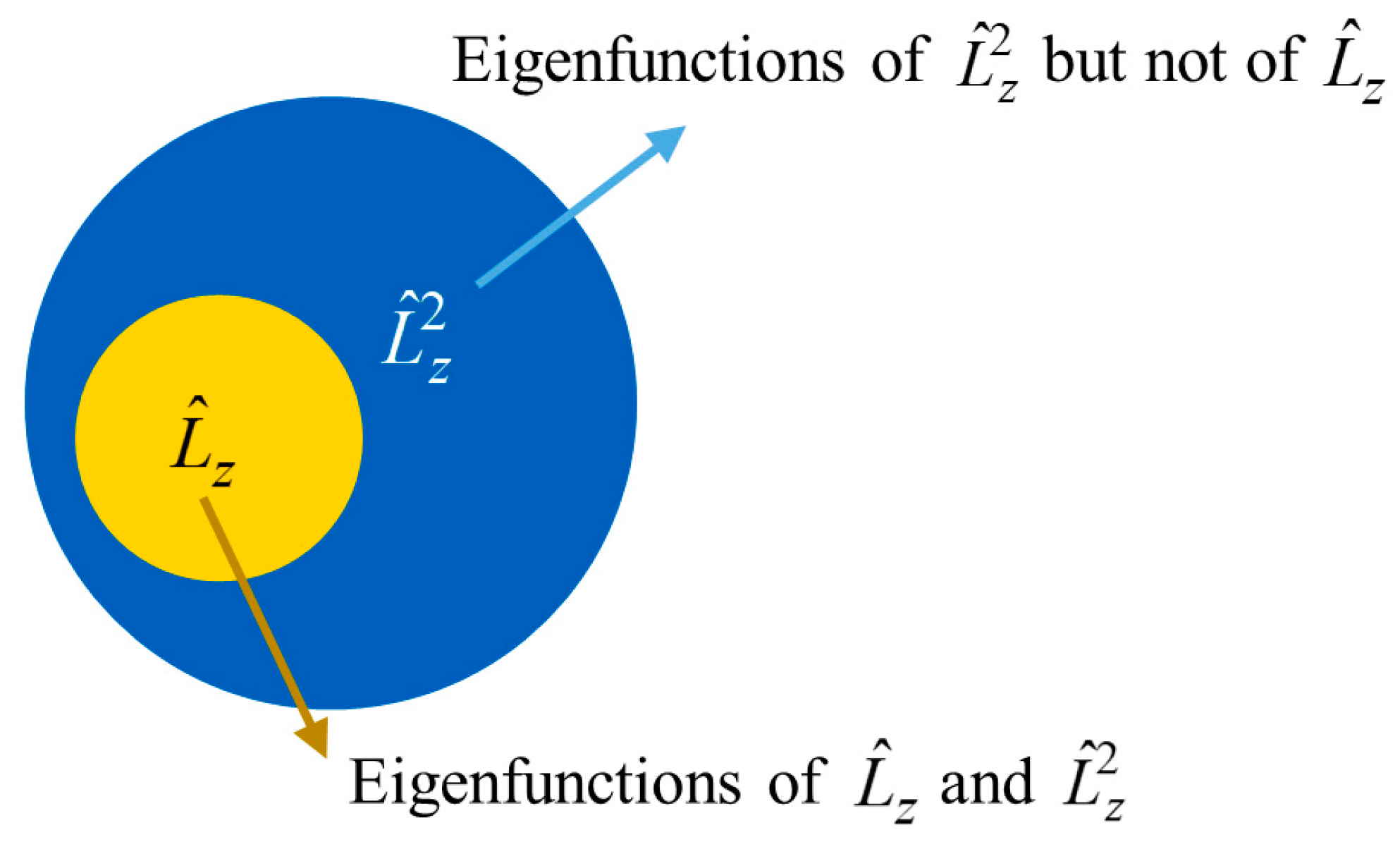
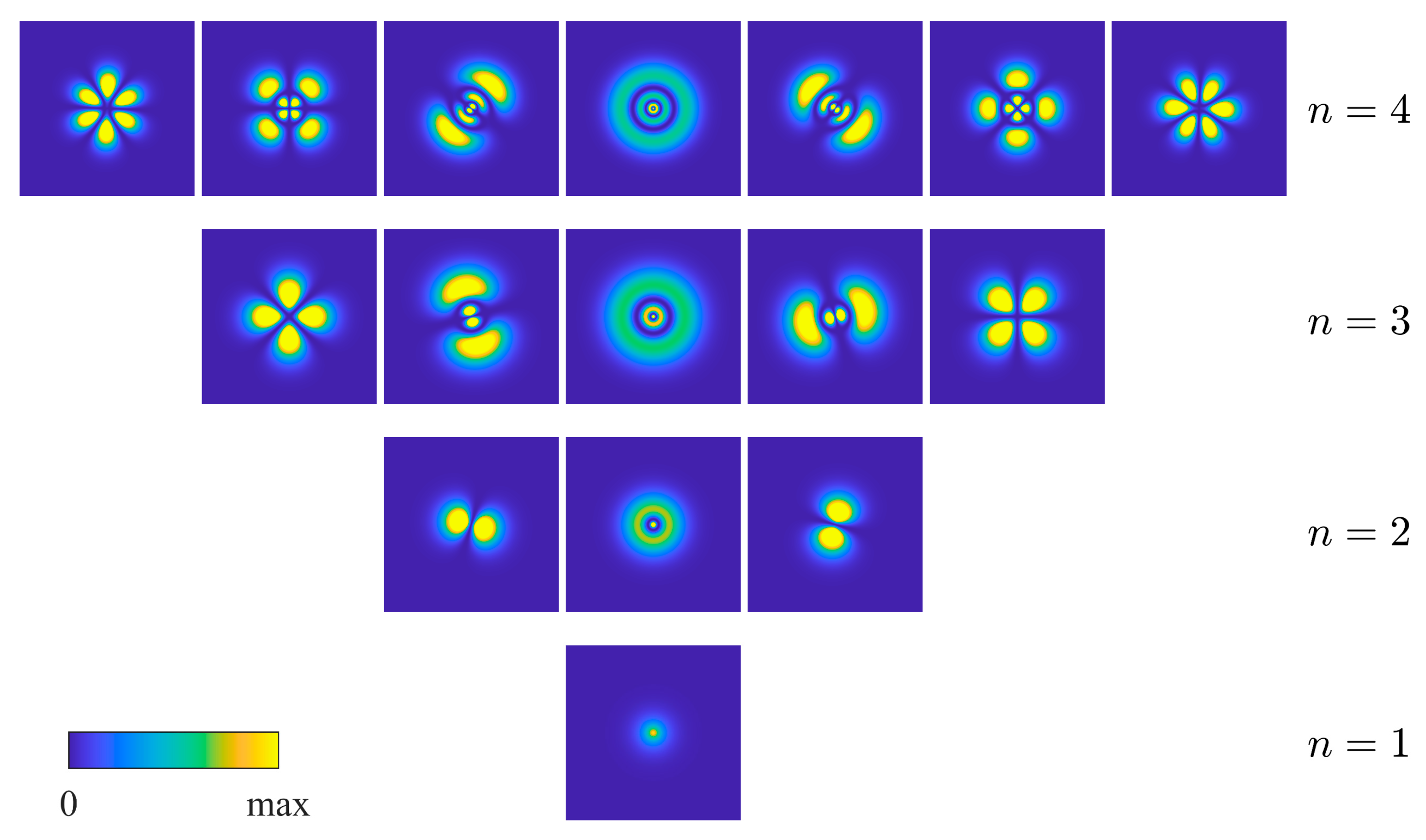
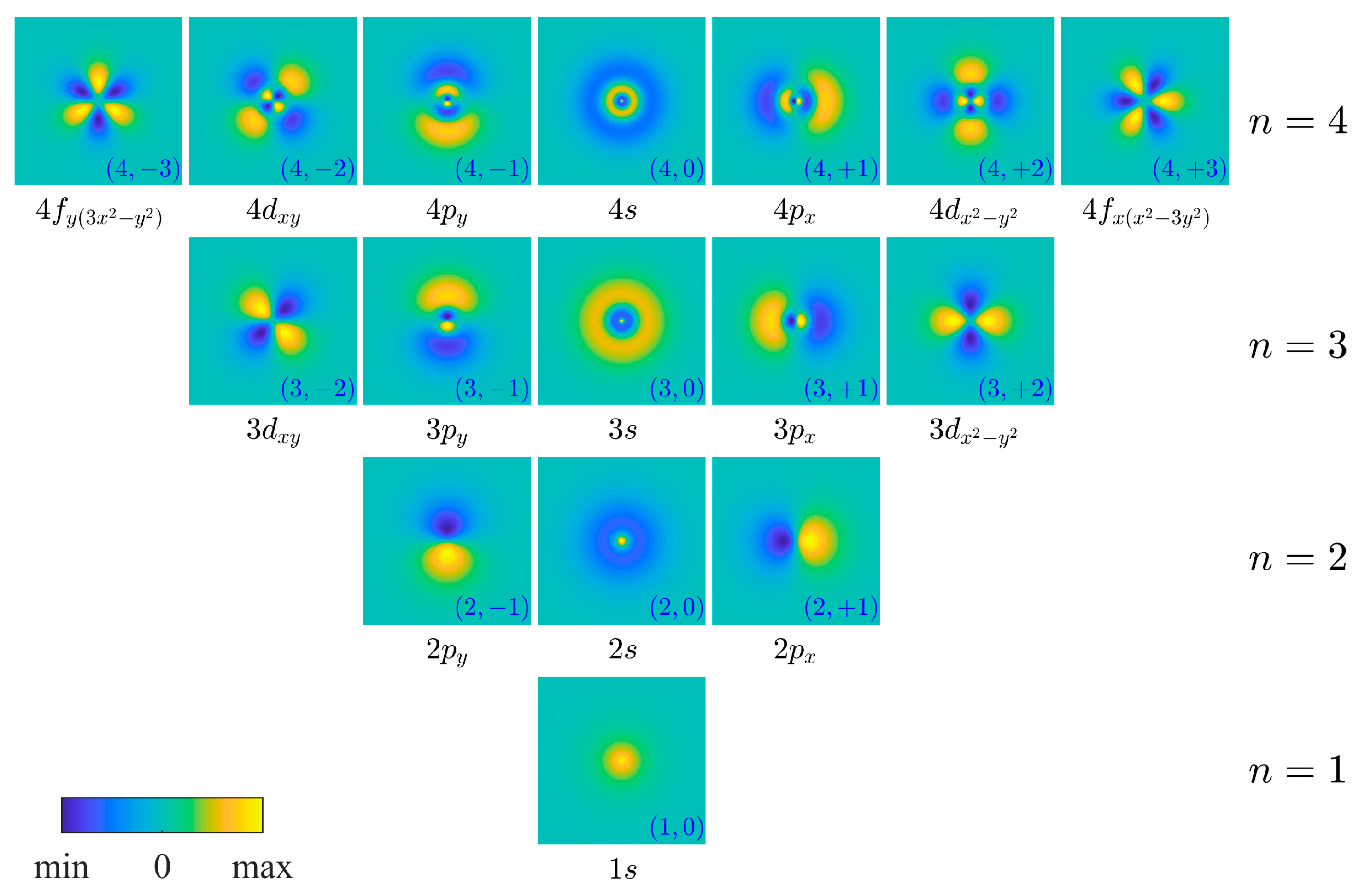
| Angular Momentum | Azimuthal Wavefunctions | Cartesian Representation on a Circle | Orbitals with Labeling Orientation |
|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sathongpaen, P.; Jindanate, S.; Amthong, A. Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals. Symmetry 2024, 16, 1163. https://doi.org/10.3390/sym16091163
Sathongpaen P, Jindanate S, Amthong A. Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals. Symmetry. 2024; 16(9):1163. https://doi.org/10.3390/sym16091163
Chicago/Turabian StyleSathongpaen, Phatlada, Suphawich Jindanate, and Attapon Amthong. 2024. "Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals" Symmetry 16, no. 9: 1163. https://doi.org/10.3390/sym16091163
APA StyleSathongpaen, P., Jindanate, S., & Amthong, A. (2024). Revisiting the Two-Dimensional Hydrogen Atom: Azimuthal Wavefunctions for Illustrating s, p, d, and f Orbitals. Symmetry, 16(9), 1163. https://doi.org/10.3390/sym16091163








