Magnetohydrodynamic Waves in Asymmetric Waveguides and Their Applications in Solar Physics—A Review
Abstract
1. Introduction
2. Methods: A Brief Account of MHD Wave Theory in Cartesian and Cylindrical Models
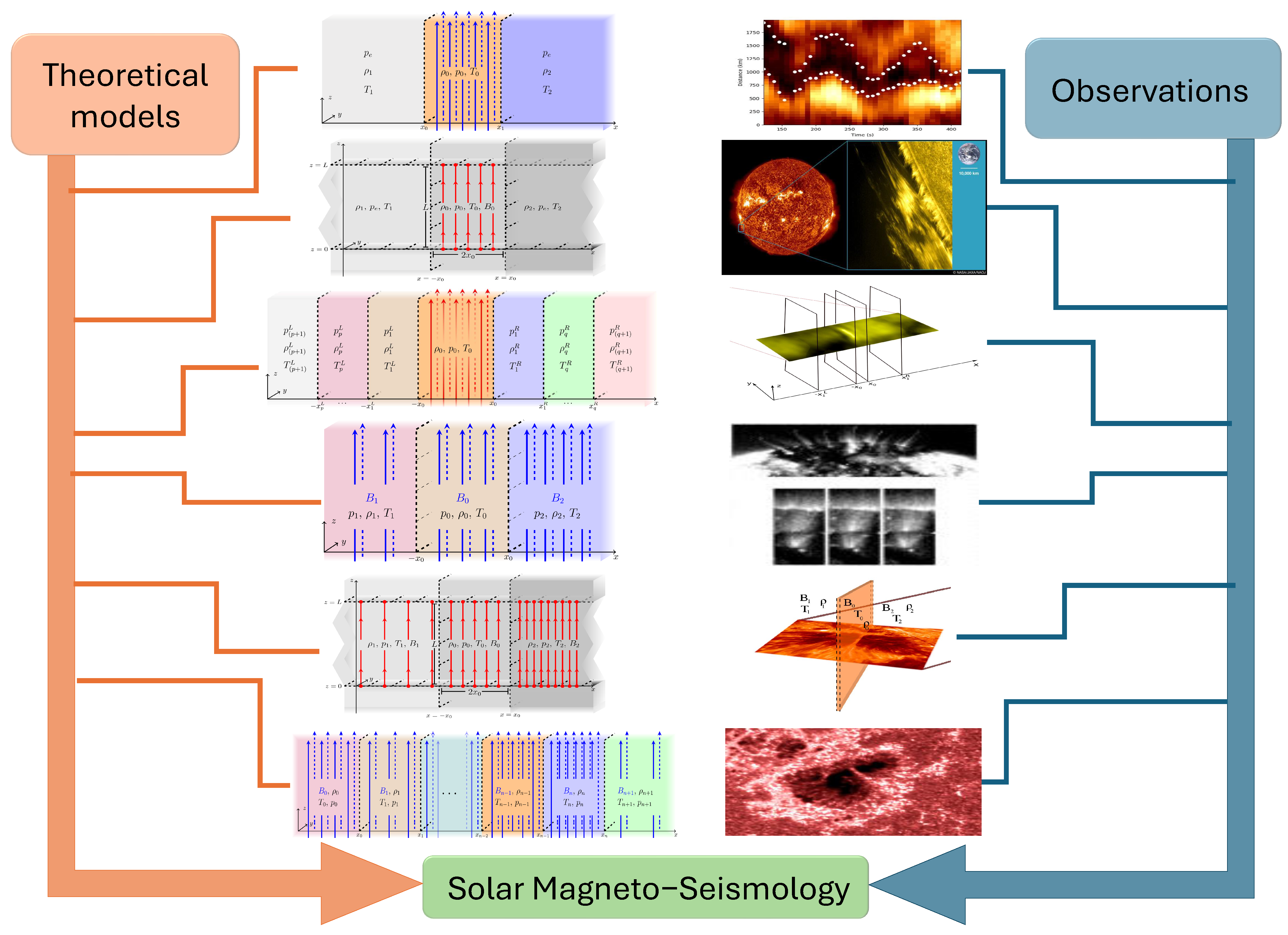
2.1. Solar Magneto-Seismology
2.2. On Flux Tube and Slab Models of the Solar Atmosphere
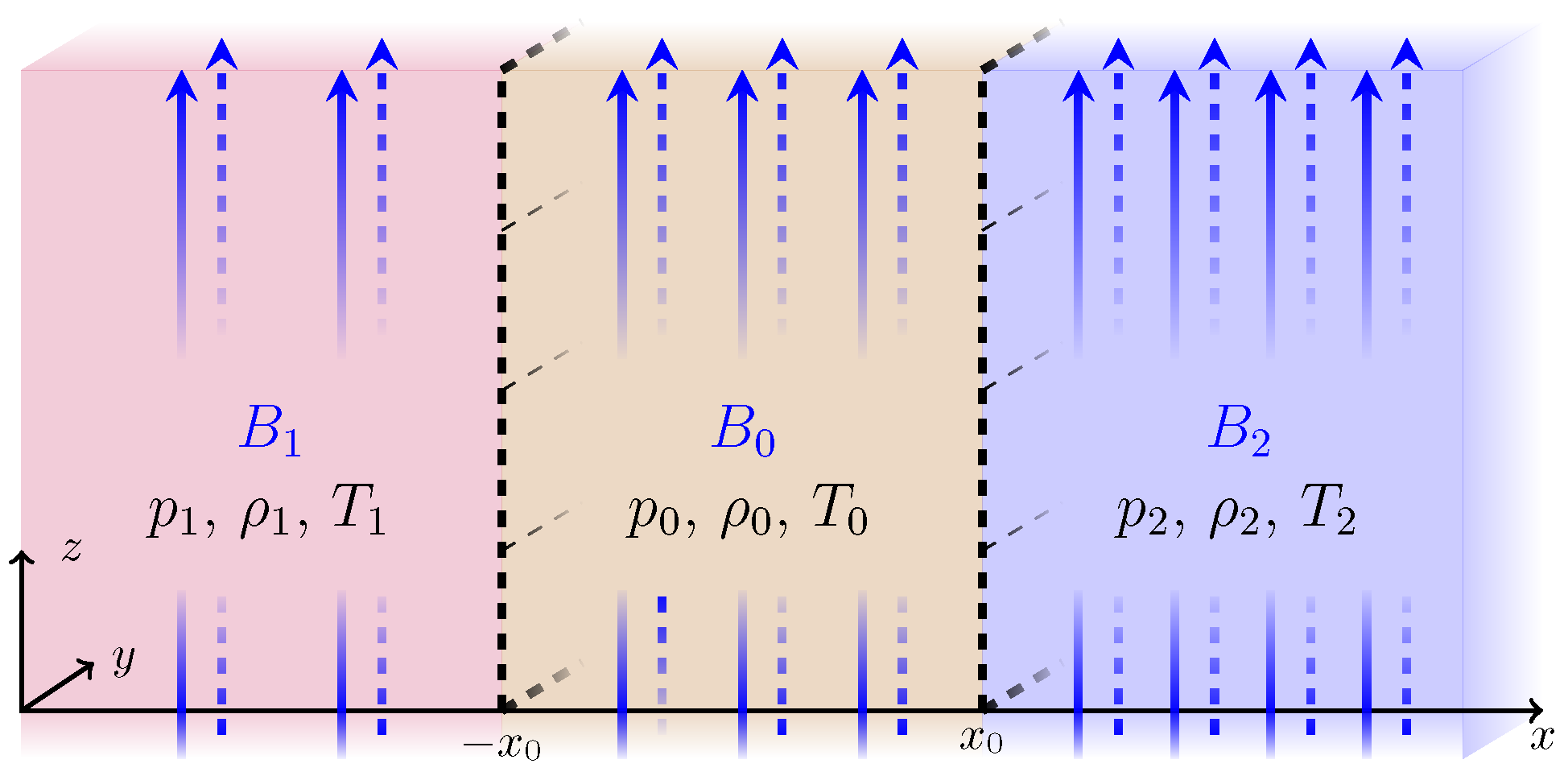
2.2.1. Cartesian Models
2.2.2. Cylindrical Models
3. Results: MHD Waves in the Presence of Asymmetric Flows
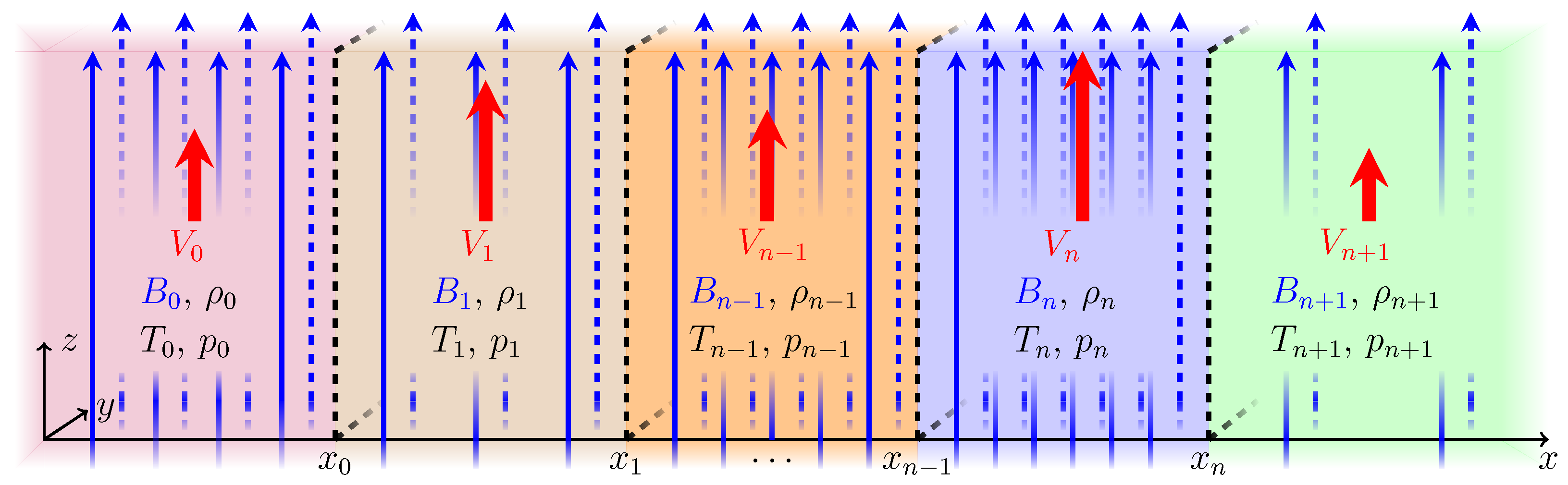
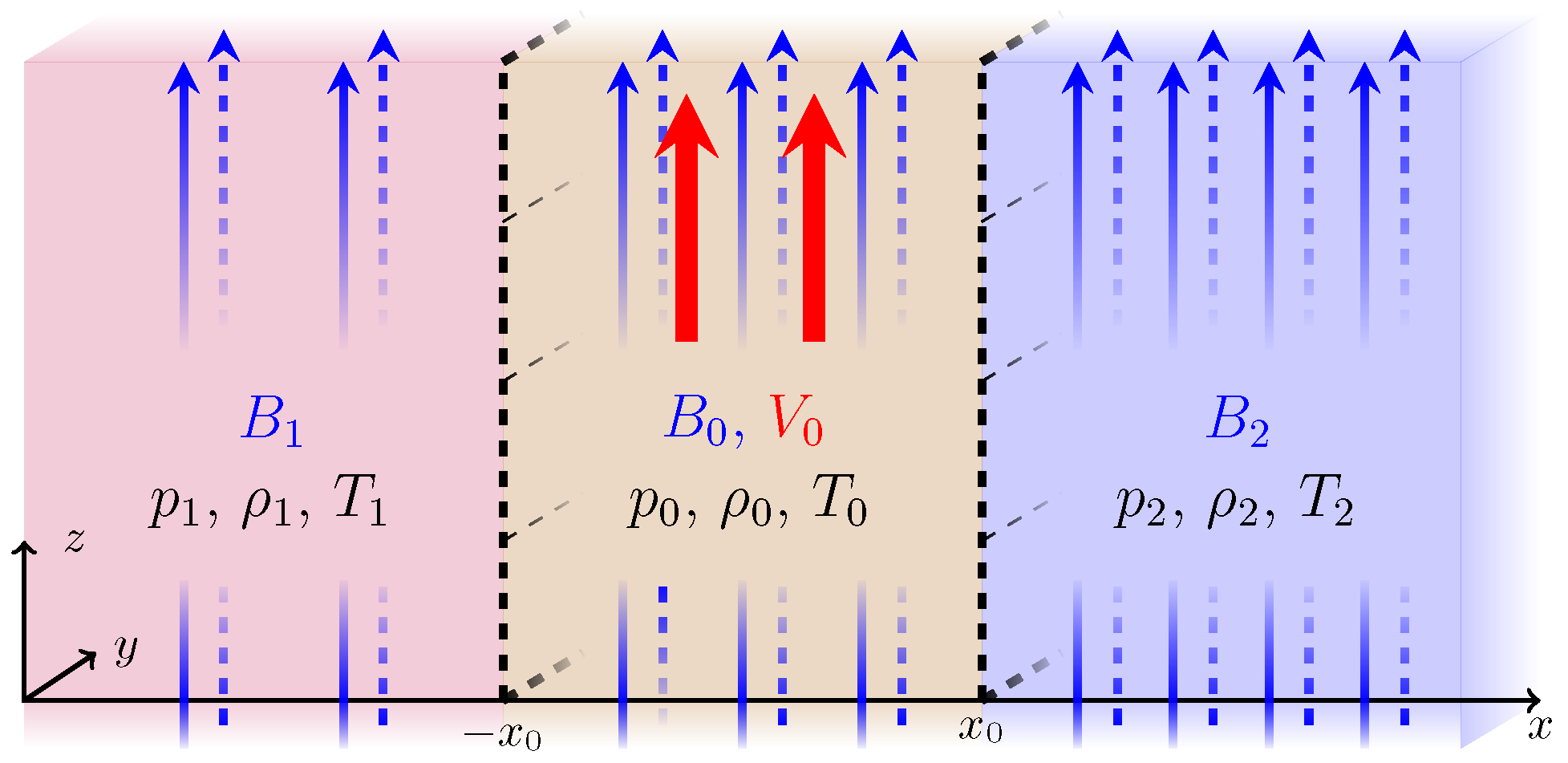
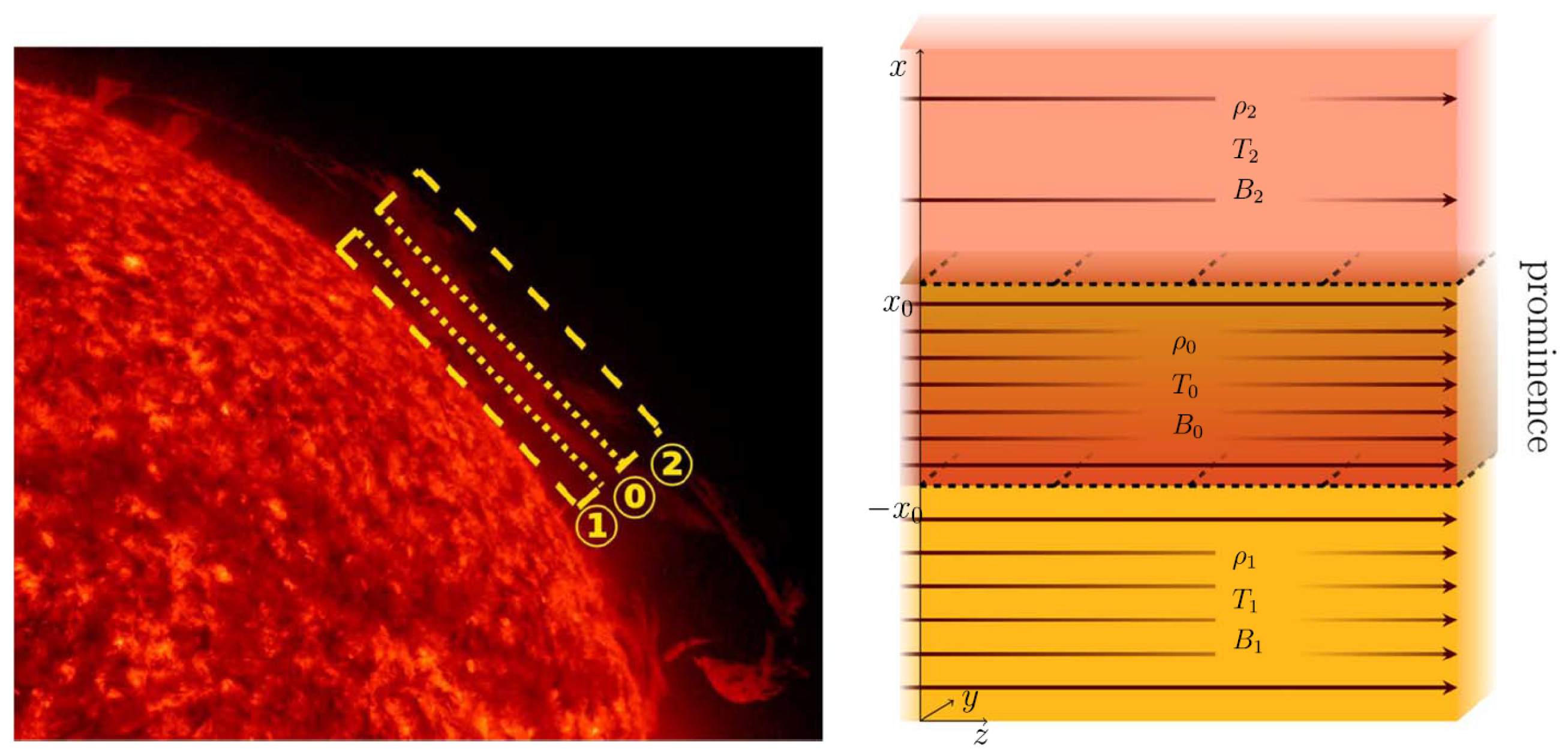
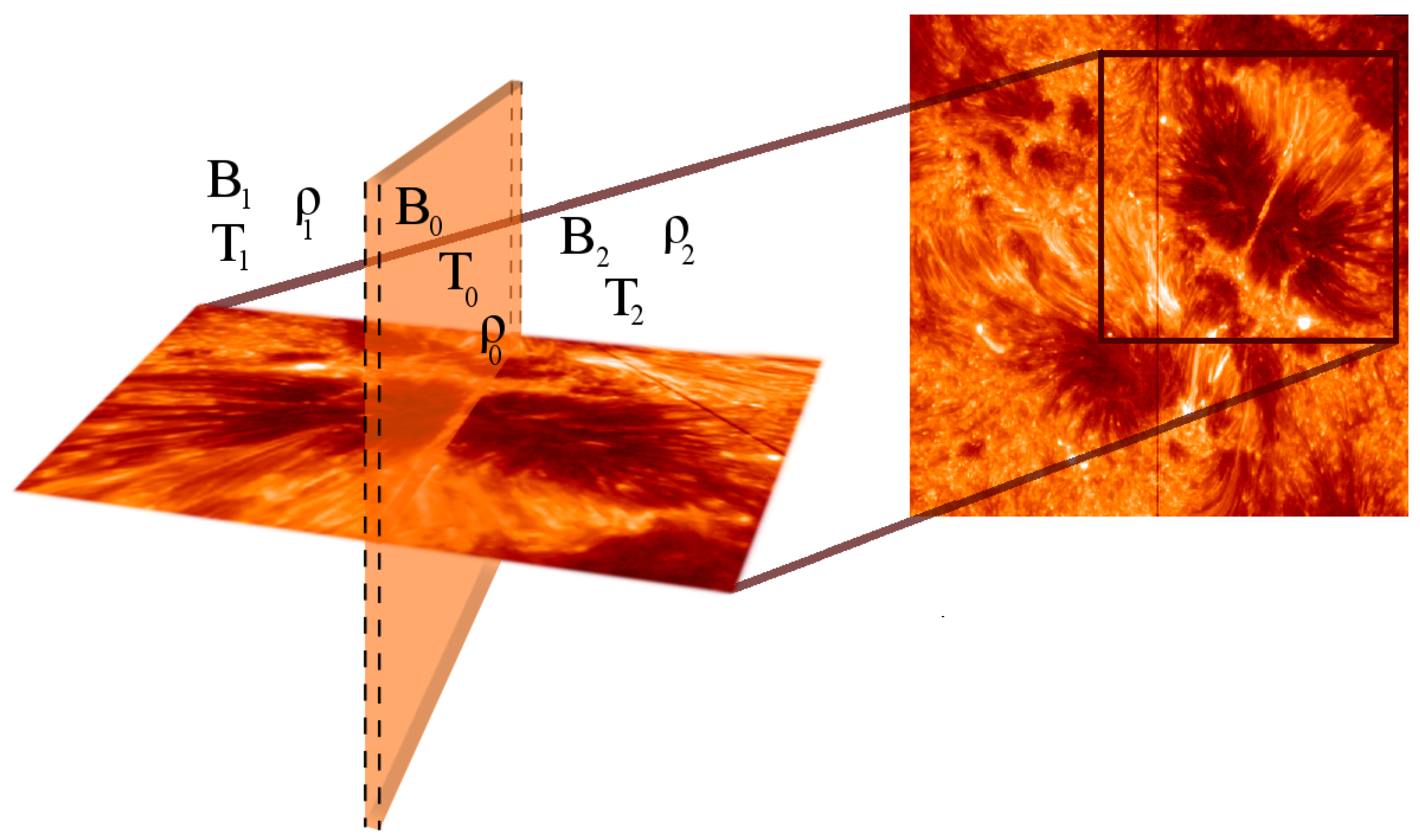
3.1. Generalised Slab Model
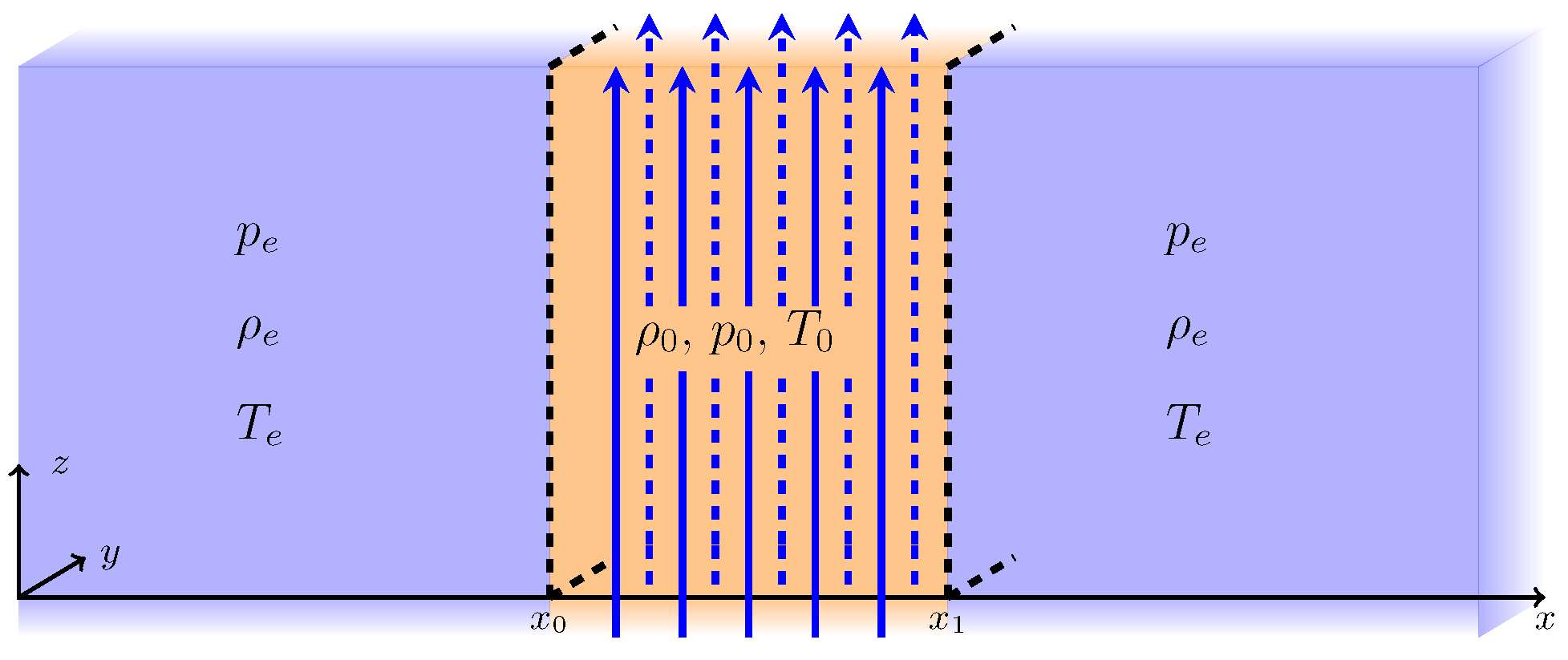
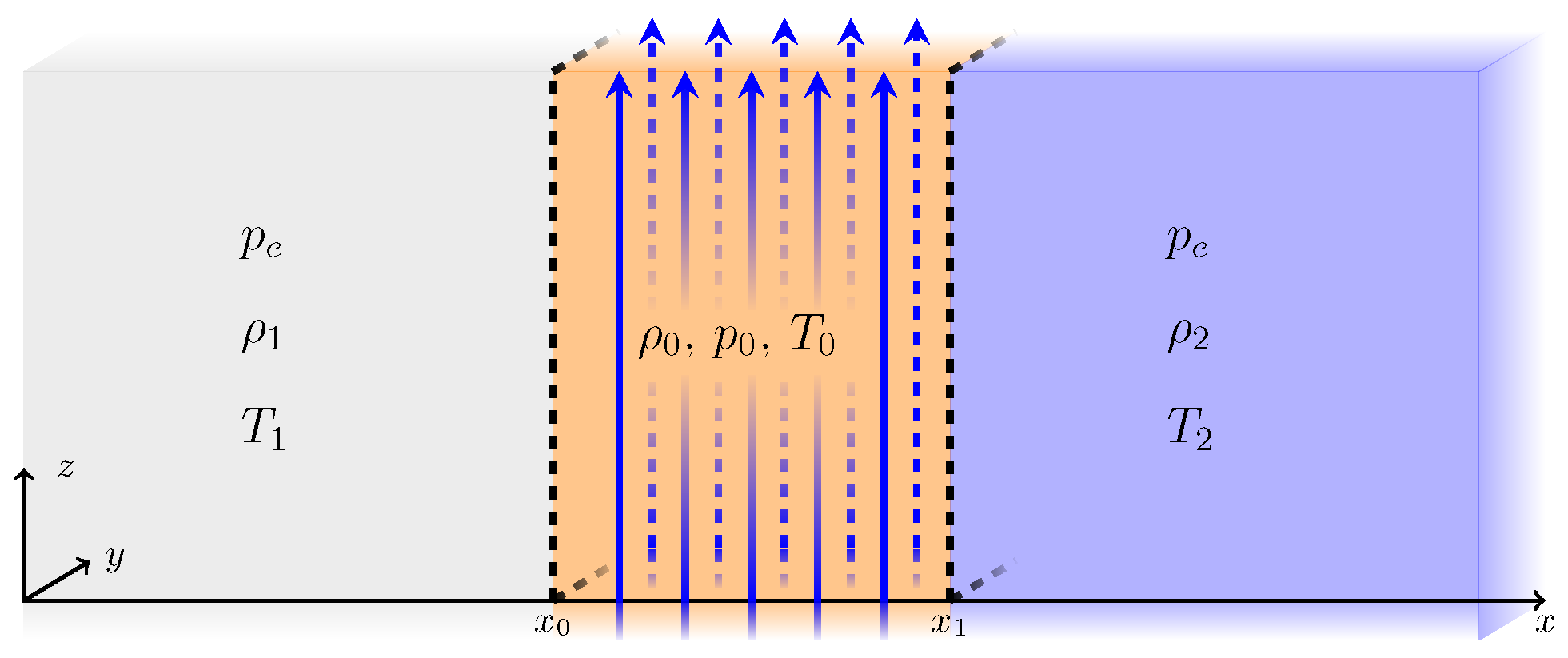
3.2. Sources and Effects of Waveguide Asymmetry
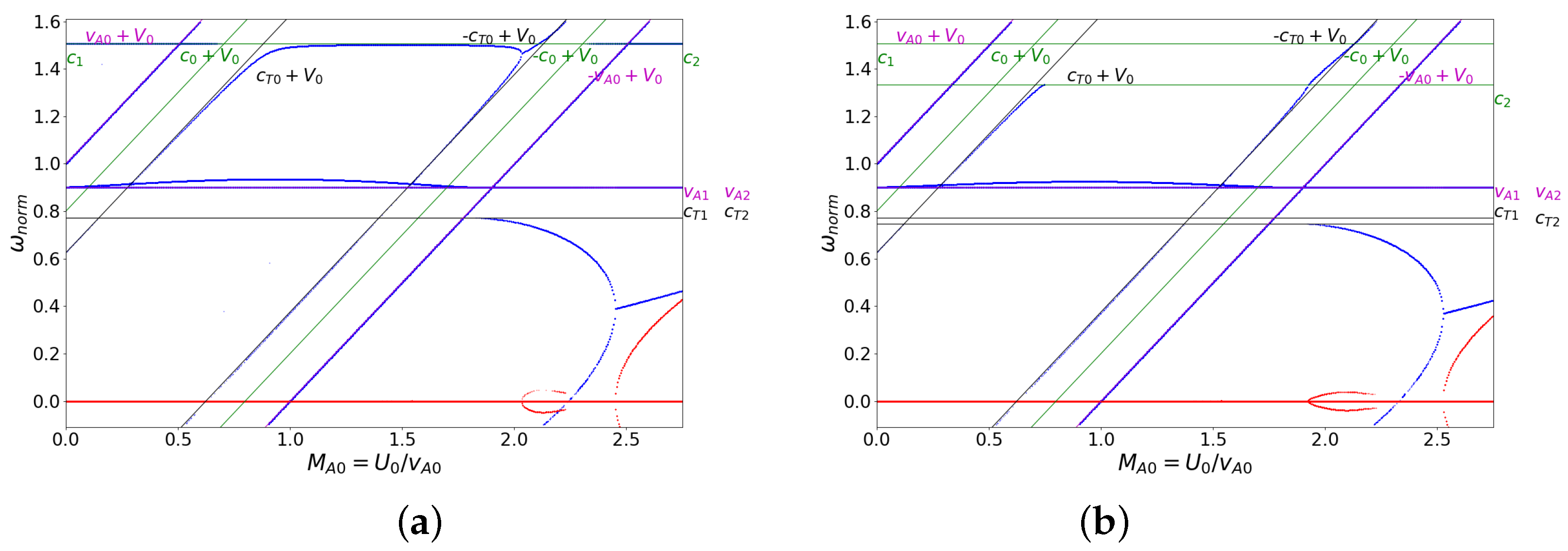
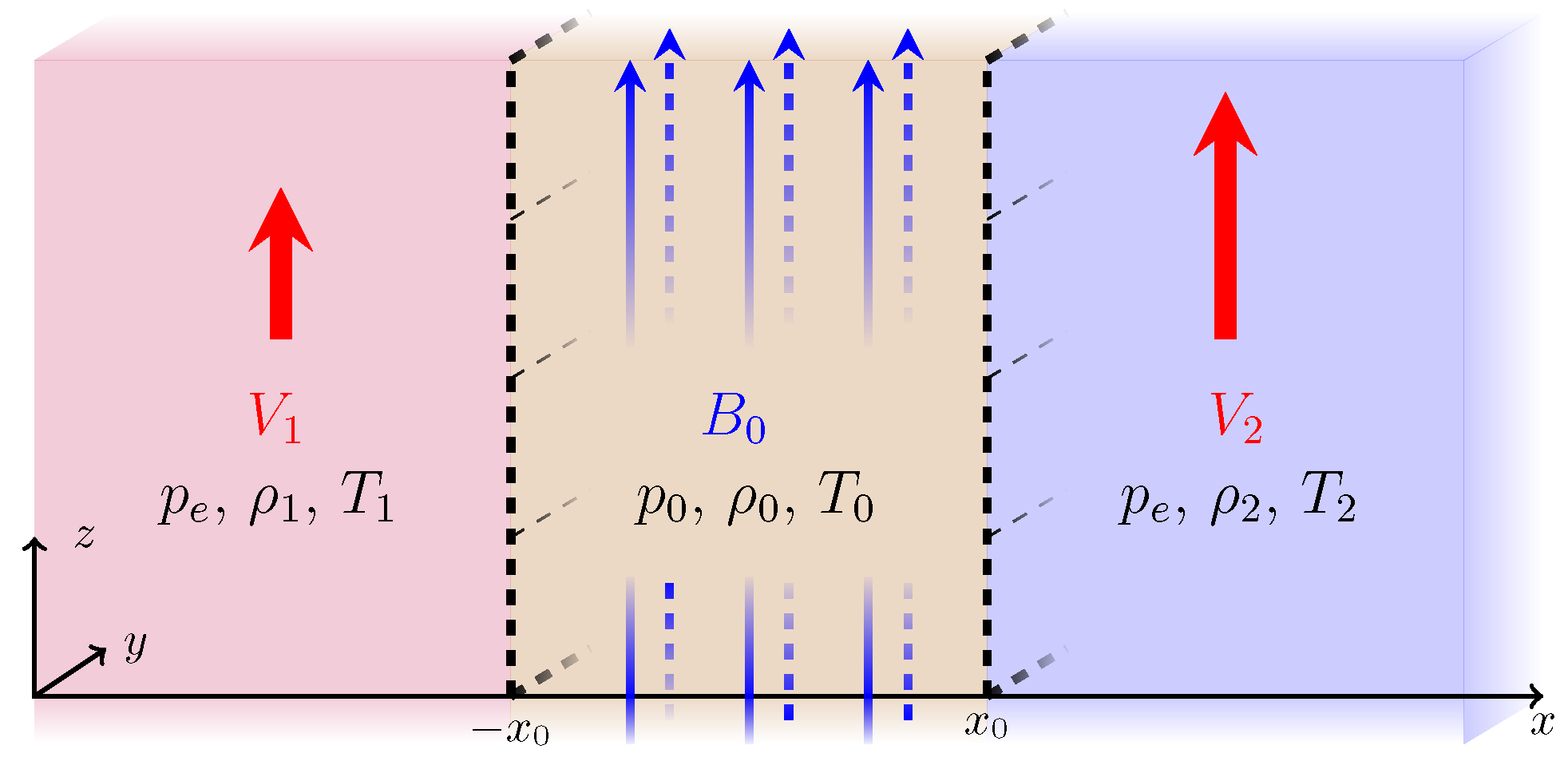
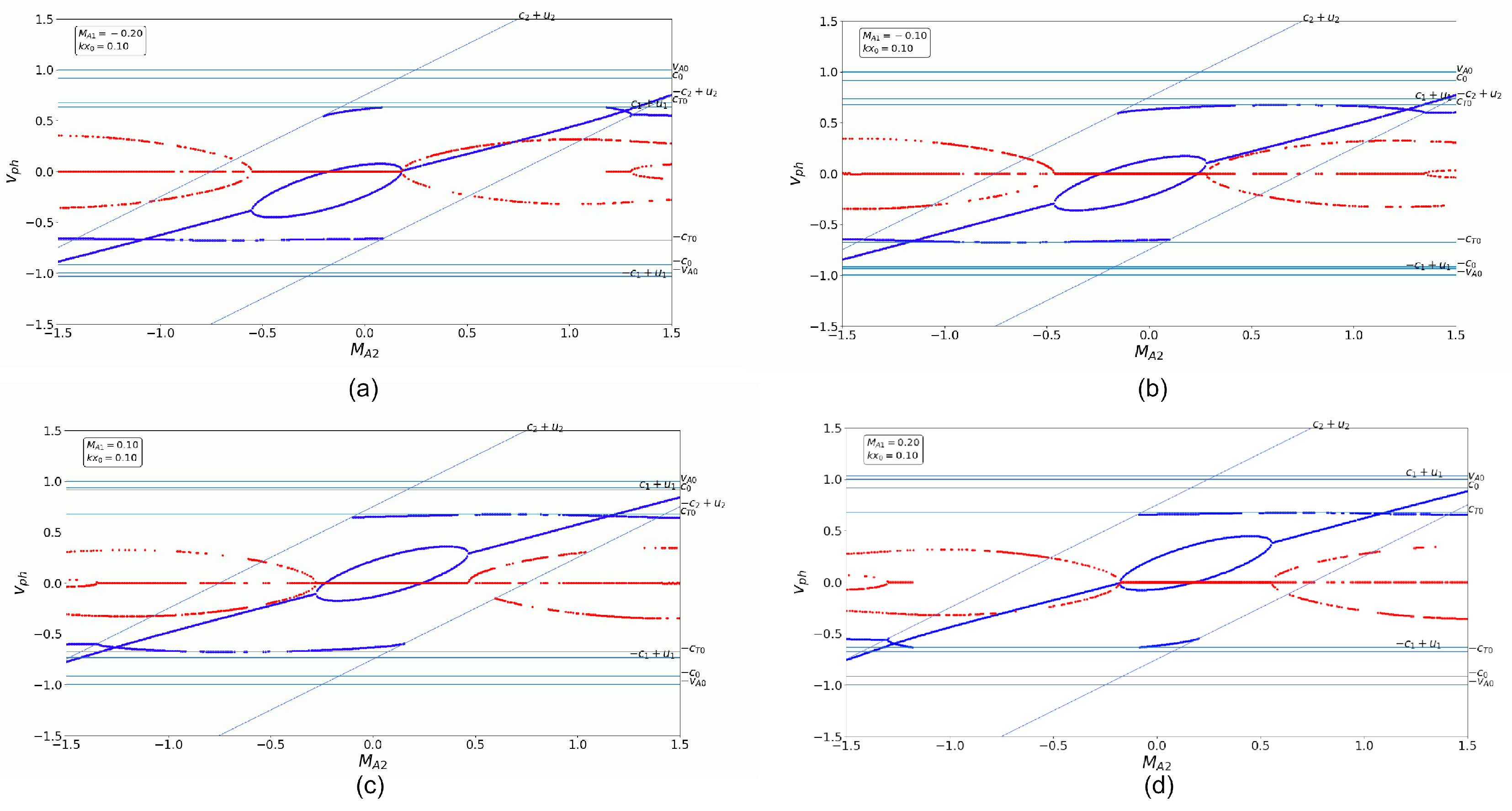
3.3. Flow Asymmetry
4. Discussion: Solar Applications
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Rast, M.P.; Bello González, N.; Bellot Rubio, L.; Cao, W.; Cauzzi, G.; Deluca, E.; de Pontieu, B.; Fletcher, L.; Gibson, S.E.; Judge, P.G.; et al. Critical Science Plan for the Daniel K. Inouye Solar Telescope (DKIST). Sol. Phys. 2021, 296, 70. [Google Scholar] [CrossRef]
- Quintero Noda, C.; Schlichenmaier, R.; Bellot Rubio, L.R.; Löfdahl, M.G.; Khomenko, E.; Jurčák, J.; Leenaarts, J.; Kuckein, C.; González Manrique, S.J.; Gunár, S.; et al. The European Solar Telescope. Astron. Astrophys. 2022, 666, A21. [Google Scholar] [CrossRef]
- Erdélyi, R. Magnetic coupling of waves and oscillations in the lower solar atmosphere: Can the tail wag the dog? Philos. Trans. R. Soc. Lond. Ser. A 2006, 364, 351–381. [Google Scholar] [CrossRef] [PubMed]
- Erdélyi, R. Magnetic seismology of the lower solar atmosphere. In Proceedings of the SOHO 18/GONG 2006/HELAS I, Beyond the Spherical Sun, Sheffield, UK, 7–11 August 2006; ESA Special Publication: Noordwijk, The Netherlands, 2006; Volume 624, p. 15.1. [Google Scholar]
- Banerjee, D.; Erdélyi, R.; Oliver, R.; O’Shea, E. Present and Future Observing Trends in Atmospheric Magnetoseismology. Sol. Phys. 2007, 246, 3–29. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Pilipenko, V.; Heilig, B.; Jelínek, P.; Karlický, M.; Klimushkin, D.Y.; Kolotkov, D.Y.; Lee, D.H.; Nisticò, G.; Van Doorsselaere, T.; et al. Magnetohydrodynamic Oscillations in the Solar Corona and Earth’s Magnetosphere: Towards Consolidated Understanding. Space Sci. Rev. 2016, 200, 75–203. [Google Scholar] [CrossRef]
- Jess, D.B.; Jafarzadeh, S.; Keys, P.H.; Stangalini, M.; Verth, G.; Grant, S.D.T. Waves in the lower solar atmosphere: The dawn of next-generation solar telescopes. Living Rev. Sol. Phys. 2023, 20, 1. [Google Scholar] [CrossRef]
- Leighton, R.B.; Noyes, R.W.; Simon, G.W. Velocity Fields in the Solar Atmosphere. I. Preliminary Report. Astrophys. J. 1962, 135, 474. [Google Scholar] [CrossRef]
- Ulrich, R.K. The Five-Minute Oscillations on the Solar Surface. Astrophys. J. 1970, 162, 993. [Google Scholar] [CrossRef]
- Leibacher, J.W.; Stein, R.F. A New Description of the Solar Five-Minute Oscillation. Astrophys. J. Lett. 1971, 7, 191–192. [Google Scholar]
- Roberts, B.; Edwin, P.M.; Benz, A.O. On coronal oscillations. Astrophys. J. 1984, 279, 857–865. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Ofman, L. Determination of the coronal magnetic field by coronal loop oscillations. Astron. Astrophys. 2001, 372, L53–L56. [Google Scholar] [CrossRef]
- Wang, T.; Innes, D.E.; Qiu, J. Determination of the Coronal Magnetic Field from Hot-Loop Oscillations Observed by SUMER and SXT. Astrophys. J. 2007, 656, 598–609. [Google Scholar] [CrossRef]
- Erdélyi, R.; Taroyan, Y. Hinode EUV spectroscopic observations of coronal oscillations. Astron. Astrophys. 2008, 489, L49–L52. [Google Scholar] [CrossRef]
- Andries, J.; Arregui, I.; Goossens, M. Determination of the Coronal Density Stratification from the Observation of Harmonic Coronal Loop Oscillations. Astrophys. J. Lett. 2005, 624, L57–L60. [Google Scholar] [CrossRef]
- Van Doorsselaere, T.; Wardle, N.; Del Zanna, G.; Jansari, K.; Verwichte, E.; Nakariakov, V.M. The First Measurement of the Adiabatic Index in the Solar Corona Using Time-dependent Spectroscopy of Hinode/EIS Observations. Astrophys. J. Lett. 2011, 727, L32. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Verwichte, E. Coronal Waves and Oscillations. Living Rev. Sol. Phys. 2005, 2, 3. [Google Scholar] [CrossRef]
- De Moortel, I.; Nakariakov, V.M. Magnetohydrodynamic waves and coronal seismology: An overview of recent results. Philos. Trans. R. Soc. Lond. Ser. A 2012, 370, 3193–3216. [Google Scholar] [CrossRef]
- Andries, J.; van Doorsselaere, T.; Roberts, B.; Verth, G.; Verwichte, E.; Erdélyi, R. Coronal Seismology by Means of Kink Oscillation Overtones. Space Sci. Rev. 2009, 149, 3–29. [Google Scholar] [CrossRef]
- Ruderman, M.S.; Erdélyi, R. Transverse Oscillations of Coronal Loops. Space Sci. Rev. 2009, 149, 199–228. [Google Scholar] [CrossRef]
- Guo, Y.; Erdélyi, R.; Srivastava, A.K.; Hao, Q.; Cheng, X.; Chen, P.F.; Ding, M.D.; Dwivedi, B.N. Magnetohydrodynamic Seismology of a Coronal Loop System by the First Two Modes of Standing Kink Waves. Astrophys. J. 2015, 799, 151. [Google Scholar] [CrossRef]
- Chen, G.Y.; Guo, Y.; Ding, M.D.; Erdélyi, R. Measuring local physical parameters in coronal loops with spatial seismology. Astron. Astrophys. 2023, 678, A205. [Google Scholar] [CrossRef]
- Beckers, J.M. Solar Spicules. Annu. Rev. Astron. Astrophys. 1972, 10, 73. [Google Scholar] [CrossRef]
- Sterling, A.C. Solar Spicules: A Review of Recent Models and Targets for Future Observations—(Invited Review). Sol. Phys. 2000, 196, 79–111. [Google Scholar] [CrossRef]
- De Pontieu, B.; Erdélyi, R.; James, S.P. Solar chromospheric spicules from the leakage of photospheric oscillations and flows. Nature 2004, 430, 536–539. [Google Scholar] [CrossRef] [PubMed]
- Pereira, T.M.D.; De Pontieu, B.; Carlsson, M. Quantifying Spicules. Astrophys. J. 2012, 759, 18. [Google Scholar] [CrossRef]
- Martínez-Sykora, J.; De Pontieu, B.; Hansteen, V.H.; Rouppe van der Voort, L.; Carlsson, M.; Pereira, T.M.D. On the generation of solar spicules and Alfvénic waves. Science 2017, 356, 1269–1272. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Erdélyi, R. Oscillations and Waves in Solar Spicules. Space Sci. Rev. 2009, 149, 355–388. [Google Scholar] [CrossRef]
- Komm, R.; De Moortel, I.; Fan, Y.; Ilonidis, S.; Steiner, O. Sub-photosphere to Solar Atmosphere Connection. Space Sci. Rev. 2015, 196, 167–199. [Google Scholar] [CrossRef]
- Berger, T.E.; Slater, G.; Hurlburt, N.; Shine, R.; Tarbell, T.; Title, A.; Lites, B.W.; Okamoto, T.J.; Ichimoto, K.; Katsukawa, Y.; et al. Quiescent Prominence Dynamics Observed with the Hinode Solar Optical Telescope. I. Turbulent Upflow Plumes. Astrophys. J. 2010, 716, 1288–1307. [Google Scholar] [CrossRef]
- Ryutova, M.; Berger, T.; Frank, Z.; Tarbell, T.; Title, A. Observation of Plasma Instabilities in Quiescent Prominences. Sol. Phys. 2010, 267, 75–94. [Google Scholar] [CrossRef]
- Skirvin, S.J.; Fedun, V.; Verth, G.I. The effect of symmetric and spatially varying equilibria and flow on MHD wave modes: Slab geometry. Mon. Not. Roy. Astron. Soc. 2021, 504, 4077–4092. [Google Scholar] [CrossRef]
- Yu, H.; Li, B.; Chen, S.; Guo, M. Resonant Damping of Kink Modes in Solar Coronal Slabs. Sol. Phys. 2021, 296, 95. [Google Scholar] [CrossRef]
- Chen, S.X.; Li, B.; Guo, M.; Shi, M.; Yu, H. Oblique Quasi-kink Modes in Solar Coronal Slabs Embedded in an Asymmetric Magnetic Environment: Resonant Damping, Phase and Group Diagrams. Astrophys. J. 2022, 940, 157. [Google Scholar] [CrossRef]
- Shi, M.; Li, B.; Yuan, S. Horizontally Polarized Kink Oscillations Supported by Solar Coronal Loops in an Asymmetric Environment. arXiv 2024. [Google Scholar] [CrossRef]
- Tirry, W.J.; Cadez, V.M.; Erdelyi, R.; Goossens, M. Resonant flow instability of MHD surface waves. Astron. Astrophys. 1998, 332, 786–794. [Google Scholar]
- Walker, A.D.M. Reflection and transmission at the boundary between two counterstreaming MHD plasmas—Active boundaries or negative-energy waves? J. Plasma Phys. 2000, 63, 203–219. [Google Scholar] [CrossRef]
- Taroyan, Y.; Erdélyi, R. Resonant and Kelvin–Helmholtz instabilities on the magnetopause. Phys. Plasmas 2002, 9, 3121–3129. [Google Scholar] [CrossRef]
- Erkaev, N.V.; Semenov, V.S.; Biernat, H.K. Magnetic Double-Gradient Instability and Flapping Waves in a Current Sheet. Phys. Rev. Lett. 2007, 99, 235003. [Google Scholar] [CrossRef]
- Korovinskiy, D.B.; Divin, A.; Erkaev, N.V.; Ivanova, V.V.; Ivanov, I.B.; Semenov, V.S.; Lapenta, G.; Markidis, S.; Biernat, H.K.; Zellinger, M. MHD modeling of the double-gradient (kink) magnetic instability. J. Geophys. Res. (Space Phys.) 2013, 118, 1146–1158. [Google Scholar] [CrossRef]
- Zelenyi, L.; Artemyev, A.; Petrukovich, A. Properties of Magnetic Field Fluctuations in the Earth’s Magnetotail and Implications for the General Problem of Structure Formation in Hot Plasmas. Space Sci. Rev. 2015, 188, 287–310. [Google Scholar] [CrossRef]
- Zaqarashvili, T.V.; Lomineishvili, S.; Leitner, P.; Hanslmeier, A.; Gömöry, P.; Roth, M. Kink instability of triangular jets in the solar atmosphere. Astron. Astrophys. 2021, 649, A179. [Google Scholar] [CrossRef]
- Aschwanden, M.J.; Fletcher, L.; Schrijver, C.J.; Alexander, D. Coronal Loop Oscillations Observed with the Transition Region and Coronal Explorer. Astrophys. J. 1999, 520, 880–894. [Google Scholar] [CrossRef]
- Nakariakov, V.M.; Ofman, L.; Deluca, E.E.; Roberts, B.; Davila, J.M. TRACE observation of damped coronal loop oscillations: Implications for coronal heating. Science 1999, 285, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Van Doorsselaere, T.; Nakariakov, V.M.; Young, P.R.; Verwichte, E. Coronal magnetic field measurement using loop oscillations observed by Hinode/EIS. Astron. Astrophys. 2008, 487, L17–L20. [Google Scholar] [CrossRef]
- Allcock, M.; Shukhobodskaia, D.; Zsámberger, N.K.; Erdélyi, R. Magnetohydrodynamic waves in multi-layered asymmetric waveguides: Solar magneto-seismology theory and application. Front. Astron. Space Sci. 2019, 6, 48. [Google Scholar] [CrossRef]
- Roberts, B. Wave Propagation in a Magnetically Structured Atmosphere—Part One—Surface Waves at a Magnetic Interface. Sol. Phys. 1981, 69, 27–38. [Google Scholar] [CrossRef]
- Roberts, B. Wave Propagation in a Magnetically Structured Atmosphere—Part Two—Waves in a Magnetic Slab. Sol. Phys. 1981, 69, 39–56. [Google Scholar] [CrossRef]
- Edwin, P.M.; Roberts, B. Wave Propagation in a Magnetically Structured Atmosphere—Part Three—The Slab in a Magnetic Environment. Sol. Phys. 1982, 76, 239–259. [Google Scholar] [CrossRef]
- Ruderman, M.S. Soliton propagation on multiple-interface magnetic structures. J. Geophys. Res. 1992, 97, 16. [Google Scholar] [CrossRef]
- Díaz, A.J.; Oliver, R.; Ballester, J.L. Fast magnetohydrodynamic oscillations in a multifibril Cartesian prominence model. Astron. Astrophys. 2005, 440, 1167–1175. [Google Scholar] [CrossRef]
- Díaz, A.J.; Roberts, B. Fast Magnetohydrodynamic Oscillations in a Fibril Prominence Model. Sol. Phys. 2006, 236, 111–126. [Google Scholar] [CrossRef]
- Luna, M.; Terradas, J.; Oliver, R.; Ballester, J.L. Fast magnetohydrodynamic waves in a two-slab coronal structure: Collective behaviour. Astron. Astrophys. 2006, 457, 1071–1079. [Google Scholar] [CrossRef]
- De Pontieu, B.; McIntosh, S.; Hansteen, V.H.; Carlsson, M.; Schrijver, C.J.; Tarbell, T.D.; Title, A.M.; Shine, R.A.; Suematsu, Y.; Tsuneta, S.; et al. A Tale of Two Spicules: The Impact of Spicules on the Magnetic Chromosphere. Pub. Astron. Soc. Jpn. 2007, 59, S655. [Google Scholar] [CrossRef]
- Pike, C.D.; Mason, H.E. Rotating Transition Region Features Observed with the SOHO Coronal Diagnostic Spectrometer. Sol. Phys. 1998, 182, 333–348. [Google Scholar] [CrossRef]
- Shibata, K.; Ishido, Y.; Acton, L.W.; Strong, K.T.; Hirayama, T.; Uchida, Y.; McAllister, A.H.; Matsumoto, R.; Tsuneta, S.; Shimizu, T.; et al. Observations of X-Ray Jets with the YOHKOH Soft X-Ray Telescope. Pub. Astron. Soc. Jpn. 1992, 44, L173–L179. [Google Scholar] [CrossRef][Green Version]
- Nakariakov, V.M.; Roberts, B. Magnetosonic Waves in Structured Atmospheres with Steady Flows, I. Sol. Phys. 1995, 159, 213–228. [Google Scholar] [CrossRef]
- Parker, E.N. The Nature of the Sunspot Phenomenon. II: Internal Overstable Modes. Sol. Phys. 1974, 37, 127–144. [Google Scholar] [CrossRef]
- Defouw, R.J. Wave propagation along a magnetic tube. Astrophys. J. 1976, 209, 266–269. [Google Scholar] [CrossRef]
- Ryutov, D.A.; Ryutova, M.P. Sound oscillations in a plasma with “magnetic filaments”. Sov. J. Exp. Theor. Phys. 1976, 43, 491. [Google Scholar]
- Roberts, B.; Webb, A.R. Vertical motions in an intense magnetic flux tube. Sol. Phys. 1978, 56, 5–35. [Google Scholar] [CrossRef]
- Wentzel, D.G. On the role of hydrodynamic waves in the corona and the base of the solar wind. Sol. Phys. 1977, 52, 163–177. [Google Scholar] [CrossRef]
- Wentzel, D.G. Hydromagnetic surface waves. Astrophys. J. 1979, 227, 319–322. [Google Scholar] [CrossRef]
- Zaitsev, V.V.; Stepanov, A.V.; Sterlin, A.M. The Microwave Pulsations in Solar Flares—Magnetohydrodynamic and Plasma Models. Sov. Astron. Lett. 1985, 11, 192–194. [Google Scholar]
- Spruit, H.C.; Roberts, B. Magnetic flux tubes on the Sun. Nature 1983, 304, 401–406. [Google Scholar] [CrossRef]
- Edwin, P.M.; Roberts, B. Wave Propagation in a Magnetic Cylinder. Sol. Phys. 1983, 88, 179–191. [Google Scholar] [CrossRef]
- Gu, Y.N.; Qiu, N.X. Kink instabilities of a plasma column with elliptical cross-section. Acta Phys. Sin. 1980, 29, 1367–1377. [Google Scholar]
- Ruderman, M.S. The resonant damping of oscillations of coronal loops with elliptic cross-sections. Astron. Astrophys. 2003, 409, 287–297. [Google Scholar] [CrossRef]
- Erdélyi, R.; Morton, R.J. Magnetohydrodynamic waves in a compressible magnetic flux tube with elliptical cross-section. Astron. Astrophys. 2009, 494, 295–309. [Google Scholar] [CrossRef]
- Morton, R.J.; Ruderman, M.S. Kink and fluting modes of stratified coronal magnetic loops with elliptical cross-sections. Astron. Astrophys. 2011, 527, A53. [Google Scholar] [CrossRef]
- Aldhafeeri, A.A.; Verth, G.; Brevis, W.; Jess, D.B.; McMurdo, M.; Fedun, V. Magnetohydrodynamic Wave Modes of Solar Magnetic Flux Tubes with an Elliptical Cross Section. Astrophys. J. 2021, 912, 50. [Google Scholar] [CrossRef]
- Mikhalyaev, B.B.; Solov’ev, A.A. MHD Waves in Coronal Loops with a Shell. Astron. Lett. 2004, 30, 268–275. [Google Scholar] [CrossRef]
- Mikhalyaev, B.B.; Solov’ev, A.A. The Oscillations of Coronal Loops Including the Shell. Sol. Phys. 2005, 227, 249–263. [Google Scholar] [CrossRef]
- Carter, B.K.; Erdélyi, R. Sausage and kink oscillations in incompressible annular magnetic cylinders. Astron. Astrophys. 2007, 475, 323–331. [Google Scholar] [CrossRef]
- Carter, B.K.; Erdélyi, R. Kink oscillations in magnetic tubes with twisted annulus. Astron. Astrophys. 2008, 481, 239–246. [Google Scholar] [CrossRef]
- Lopin, I. Kink oscillations in a coronal loop arcade with finite plasma-β: Effect of oblique propagation. Mon. Not. Roy. Astron. Soc. 2022, 514, 4329–4342. [Google Scholar] [CrossRef]
- Dover, F.M.; Sharma, R.; Korsós, M.B.; Erdélyi, R. Signatures of Cross-sectional Width Modulation in Solar Spicules due to Field-aligned Flows. Astrophys. J. 2020, 905, 72. [Google Scholar] [CrossRef]
- Mackenzie Dover, F.; Sharma, R.; Erdélyi, R. Magnetohydrodynamic Simulations of Spicular Jet Propagation Applied to Lower Solar Atmosphere Model. II. Case Studies with Tilted Jets. Astrophys. J. 2022, 929, 88. [Google Scholar] [CrossRef]
- Skirvin, S.J.; Gao, Y.; Van Doorsselaere, T. Alfvénic Motions Arising from Asymmetric Acoustic Wave Drivers in Solar Magnetic Structures. Astrophys. J. 2023, 949, 38. [Google Scholar] [CrossRef]
- Mather, J.F.; Erdélyi, R. Magneto-Acoustic Waves in a Gravitationally Stratified Magnetized Plasma: Eigen-Solutions and their Applications to the Solar Atmosphere. Astrophys. J. 2016, 822, 116. [Google Scholar] [CrossRef]
- Lopin, I.; Nagorny, I. Kink Waves in Non-isothermal Stratified Solar Waveguides: Effect of the External Magnetic Field. Astron. J. 2017, 154, 141. [Google Scholar] [CrossRef]
- Oxley, W.; Zsámberger, N.K.; Erdélyi, R. Standing MHD Waves in a Magnetic Slab Embedded in an Asymmetric Plasma Environment: Slow Surface Waves. Astrophys. J. 2020, 890, 109. [Google Scholar] [CrossRef]
- Oxley, W.; Zsámberger, N.K.; Erdélyi, R. Standing MHD Waves in a Magnetic Slab Embedded in an Asymmetric Magnetic Plasma Environment: Surface Waves. Astrophys. J. 2020, 898, 19. [Google Scholar] [CrossRef]
- Allcock, M.; Erdélyi, R. Magnetohydrodynamic Waves in an Asymmetric Magnetic Slab. Sol. Phys. 2017, 292, 35. [Google Scholar] [CrossRef] [PubMed]
- Shukhobodskaia, D.; Erdélyi, R. Propagation of Surface Magnetohydrodynamic Waves in Asymmetric Multilayered Plasma. Astrophys. J. 2018, 868, 128. [Google Scholar] [CrossRef]
- Lopin, I.; Nagorny, I. Oscillations of a coronal plasma slab excited by an external source. Mon. Not. Roy. Astron. Soc. 2020, 496, 3035–3042. [Google Scholar] [CrossRef]
- Li, B.; Antolin, P.; Guo, M.Z.; Kuznetsov, A.A.; Pascoe, D.J.; Van Doorsselaere, T.; Vasheghani Farahani, S. Magnetohydrodynamic Fast Sausage Waves in the Solar Corona. Space Sci. Rev. 2020, 216, 136. [Google Scholar] [CrossRef]
- Allcock, M.; Erdélyi, R. Solar Magnetoseismology with Magnetoacoustic Surface Waves in Asymmetric Magnetic Slab Waveguides. Astrophys. J. 2018, 855, 90. [Google Scholar] [CrossRef]
- Zsámberger, N.K.; Allcock, M.; Erdélyi, R. Magneto-acoustic Waves in a Magnetic Slab Embedded in an Asymmetric Magnetic Environment: The Effects of Asymmetry. Astrophys. J. 2018, 853, 136. [Google Scholar] [CrossRef]
- Zsámberger, N.K.; Erdélyi, R. Solar Magneto-seismology of a Magnetic Slab in an Asymmetric Magnetic Environment. Astrophys. J. 2022, 934, 155. [Google Scholar] [CrossRef]
- Allcock, M.M. Asymmetric Magnetohydrodynamic Waves of the Solar Atmosphere. Ph.D. Dissertation, University of Sheffield, Sheffield, UK, 2020. [Google Scholar]
- Zsámberger, N.K.; Tong, Y.; Asztalos, B.; Erdélyi, R. MHD Wave Propagation and the Kelvin–Helmholtz Instability in an Asymmetric Magnetic Slab System. Astrophys. J. 2022, 935, 41. [Google Scholar] [CrossRef]
- Zsámberger, N.K.; Erdélyi, R. Magnetoacoustic Waves in a Magnetic Slab Embedded in an Asymmetric Magnetic Environment. II. Thin and Wide Slabs, Hot and Cold Plasmas. Astrophys. J. 2020, 894, 123. [Google Scholar] [CrossRef]
- Taroyan, Y.; Ruderman, M.S. MHD Waves and Instabilities in Space Plasma Flows. Space Sci. Rev. 2011, 158, 505–523. [Google Scholar] [CrossRef]
- Ryutova, M. Physics of Magnetic Flux Tubes; Astrophysics and Space Science Library, Springer: Berlin/Heidelberg, Germany, 2015; Volume 417. [Google Scholar] [CrossRef]
- Barbulescu, M.; Erdélyi, R. Magnetoacoustic Waves and the Kelvin–Helmholtz Instability in a Steady Asymmetric Slab. I: The Effects of Varying Density Ratios. Sol. Phys. 2018, 293, 86. [Google Scholar] [CrossRef] [PubMed]
- Foullon, C.; Verwichte, E.; Nykyri, K.; Aschwanden, M.J.; Hannah, I.G. Kelvin–Helmholtz Instability of the CME Reconnection Outflow Layer in the Low Corona. Astrophys. J. 2013, 767, 170. [Google Scholar] [CrossRef]
- Zsámberger, N.K.; Sánchez Montoya, C.M.; Erdélyi, R. Magnetohydrodynamic Waves in an Asymmetric Magnetic Slab with Different External Flows. Astrophys. J. 2022, 937, 23. [Google Scholar] [CrossRef]
- Morton, R.J.; Verth, G.; Jess, D.B.; Kuridze, D.; Ruderman, M.S.; Mathioudakis, M.; Erdélyi, R. Observations of ubiquitous compressive waves in the Sun’s chromosphere. Nat. Commun. 2012, 3, 1315. [Google Scholar] [CrossRef]
- Mooroogen, K.; Morton, R.J.; Henriques, V. Dynamics of internetwork chromospheric fibrils: Basic properties and magnetohydrodynamic kink waves. Astron. Astrophys. 2017, 607, A46. [Google Scholar] [CrossRef]
- Priest, E. Magnetohydrodynamics of the Sun; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Zsámberger, N.K.; Erdélyi, R. Magnetoacoustic Waves in a Magnetic Slab Embedded in an Asymmetric Magnetic Environment. III. Applications to the Solar Atmosphere. Astrophys. J. 2021, 906, 122. [Google Scholar] [CrossRef]
- Arregui, I.; Oliver, R.; Ballester, J.L. Prominence Oscillations. Living Rev. Sol. Phys. 2012, 9, 2. [Google Scholar] [CrossRef]
- Abramenko, V.; Yurchyshyn, V.; Goode, P.; Kilcik, A. Statistical Distribution of Size and Lifetime of Bright Points Observed with the New Solar Telescope. Astrophys. J. Lett. 2010, 725, L101–L105. [Google Scholar] [CrossRef]
- Bovelet, B.; Wiehr, E. Dynamics of the solar active region finestructure. Astron. Astrophys. 2003, 412, 249–255. [Google Scholar] [CrossRef]
- DeForest, C.E.; Gurman, J.B. Observation of Quasi-periodic Compressive Waves in Solar Polar Plumes. Astrophys. J. Lett. 1998, 501, L217–L220. [Google Scholar] [CrossRef]
- Poletto, G. Solar Coronal Plumes. Living Rev. Sol. Phys. 2015, 12, 7. [Google Scholar] [CrossRef]
- Vazquez, M. A Morphological Study of the Light-Bridges in Sunspots. Sol. Phys. 1973, 31, 377–387. [Google Scholar] [CrossRef]
- Sobotka, M.; Švanda, M.; Jurčák, J.; Heinzel, P.; Del Moro, D.; Berrilli, F. Dynamics of the solar atmosphere above a pore with a light bridge. Astron. Astrophys. 2013, 560, A84. [Google Scholar] [CrossRef]
- Lagg, A.; Solanki, S.K.; van Noort, M.; Danilovic, S. Vigorous convection in a sunspot granular light bridge. Astron. Astrophys. 2014, 568, A60. [Google Scholar] [CrossRef]
- Foullon, C.; Verwichte, E.; Nakariakov, V.M.; Nykyri, K.; Farrugia, C.J. Magnetic Kelvin–Helmholtz Instability at the Sun. Astrophys. J. Lett. 2011, 729, L8. [Google Scholar] [CrossRef]
- Tsiropoula, G. Physical parameters and flows along chromospheric penumbral fibrils. Astron. Astrophys. 2000, 357, 735–742. [Google Scholar]
- Borrero, J.M.; Ichimoto, K. Magnetic Structure of Sunspots. Living Rev. Sol. Phys. 2011, 8, 4. [Google Scholar] [CrossRef]
- Turkakin, H.; Rankin, R.; Mann, I.R. Primary and secondary compressible Kelvin–Helmholtz surface wave instabilities on the Earth’s magnetopause. J. Geophys. Res. Space Phys. 2013, 118, 4161–4175. [Google Scholar] [CrossRef]
- Nenovski, P. MHD surface waves—A source of global magnetospheric modes (resonances)? Adv. Space Res. 2021, 67, 731–738. [Google Scholar] [CrossRef]
- Erdélyi, R.; Fedun, V. Are There Alfvén Waves in the Solar Atmosphere? Science 2007, 318, 1572. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Nelson, C.J.; Snow, B.; Wang, Y.; Erdélyi, R. Evidence of ubiquitous Alfvén pulses transporting energy from the photosphere to the upper chromosphere. Nat. Commun. 2019, 10, 3504. [Google Scholar] [CrossRef] [PubMed]
- Van Doorsselaere, T.; Srivastava, A.K.; Antolin, P.; Magyar, N.; Vasheghani Farahani, S.; Tian, H.; Kolotkov, D.; Ofman, L.; Guo, M.; Arregui, I.; et al. Coronal Heating by MHD Waves. Space Sci. Rev. 2020, 216, 140. [Google Scholar] [CrossRef]
- Taroyan, Y.; Erdélyi, R. Heating Diagnostics with MHD Waves. Space Sci. Rev. 2009, 149, 229–254. [Google Scholar] [CrossRef]
- Cargill, P.; de Moortel, I. Solar physics: Waves galore. Nature 2011, 475, 463–464. [Google Scholar] [CrossRef]
- Jess, D.B.; Morton, R.J.; Verth, G.; Fedun, V.; Grant, S.D.T.; Giagkiozis, I. Multiwavelength Studies of MHD Waves in the Solar Chromosphere. An Overview of Recent Results. Space Sci. Rev. 2015, 190, 103–161. [Google Scholar] [CrossRef]
- Stangalini, M. Wave energy in the solar atmosphere. Nat. Astron. 2023, 7, 761–762. [Google Scholar] [CrossRef]
- Berghmans, D.; Clette, F. Active region EUV transient brightenings—First Results by EIT of SOHO JOP80. Sol. Phys. 1999, 186, 207–229. [Google Scholar] [CrossRef]
- Ofman, L.; Nakariakov, V.M.; DeForest, C.E. Slow Magnetosonic Waves in Coronal Plumes. Astrophys. J. 1999, 514, 441–447. [Google Scholar] [CrossRef]
- Ofman, L.; Nakariakov, V.M.; Sehgal, N. Dissipation of Slow Magnetosonic Waves in Coronal Plumes. Astrophys. J. 2000, 533, 1071–1083. [Google Scholar] [CrossRef]
- Joarder, P.S.; Roberts, B. The modes of oscillation of a prominence. I—The slab with longitudinal magnetic field. Astron. Astrophys. 1992, 256, 264–272. [Google Scholar]
- Joarder, P.S.; Roberts, B. The modes of oscillation of a prominence. II—The slab with transverse magnetic field. Astron. Astrophys. 1992, 261, 625–632. [Google Scholar]
- Joarder, P.S.; Roberts, B. The modes of oscillation of a prominence. III. The slab in a skewed magnetic field. Astron. Astrophys. 1993, 277, 225. [Google Scholar]
- Arregui, I.; Ballester, J.L. Damping Mechanisms for Oscillations in Solar Prominences. Space Sci. Rev. 2011, 158, 169–204. [Google Scholar] [CrossRef]
- Oliver, R. Prominence Seismology Using Small Amplitude Oscillations. Space Sci. Rev. 2009, 149, 175–197. [Google Scholar] [CrossRef]
- Yuan, D.; Nakariakov, V.M.; Huang, Z.; Li, B.; Su, J.; Yan, Y.; Tan, B. Oscillations in a Sunspot with Light Bridges. Astrophys. J. 2014, 792, 41. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Jiang, F.; Xiang, Y. Oscillating Light Wall Above a Sunspot Light Bridge. Astrophys. J. Lett. 2015, 804, L27. [Google Scholar] [CrossRef]
- Hou, Y.J.; Li, T.; Yang, S.H.; Zhang, J. Light walls around sunspots observed by the Interface Region Imaging Spectrograph. Astron. Astrophys. 2016, 589, L7. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Erdélyi, R. Enhancement of a Sunspot Light Wall with External Disturbances. Astrophys. J. Lett. 2016, 833, L18. [Google Scholar] [CrossRef]
- Yuan, D.; Walsh, R.W. Abnormal oscillation modes in a waning light bridge. Astron. Astrophys. 2016, 594, A101. [Google Scholar] [CrossRef]
- Bharti, L. Fine structure above a light bridge in the transition region and corona. Mon. Not. Roy. Astron. Soc. 2015, 452, L16–L20. [Google Scholar] [CrossRef]
- Rouppe van der Voort, L.H.M.; Hansteen, V.H.; Carlsson, M.; Fossum, A.; Marthinussen, E.; van Noort, M.J.; Berger, T.E. Solar magnetic elements at 0.1 arcsec resolution. II. Dynamical evolution. Astron. Astrophys. 2005, 435, 327–337. [Google Scholar] [CrossRef]
- Crockett, P.J.; Mathioudakis, M.; Jess, D.B.; Shelyag, S.; Keenan, F.P.; Christian, D.J. The Area Distribution of Solar Magnetic Bright Points. Astrophys. J. Lett. 2010, 722, L188–L193. [Google Scholar] [CrossRef]
- Keys, P.H.; Mathioudakis, M.; Jess, D.B.; Shelyag, S.; Christian, D.J.; Keenan, F.P. Tracking magnetic bright point motions through the solar atmosphere. Mon. Not. Roy. Astron. Soc. 2013, 428, 3220–3226. [Google Scholar] [CrossRef]
- Berger, T.E.; Schrijver, C.J.; Shine, R.A.; Tarbell, T.D.; Title, A.M.; Scharmer, G. New Observations of Subarcsecond Photospheric Bright Points. Astrophys. J. 1995, 454, 531. [Google Scholar] [CrossRef]
- Briand, C.; Solanki, S.K. Velocity fields below the magnetic canopy of solar flux tubes: Evidence for high-speed downflows? Astron. Astrophys. 1998, 330, 1160–1168. [Google Scholar]
- Socas-Navarro, H.; Martínez Pillet, V.; Lites, B.W. Magnetic Properties of the Solar Internetwork. Astrophys. J. 2004, 611, 1139–1148. [Google Scholar] [CrossRef]
- Danilovic, S.; Schüssler, M.; Solanki, S.K. Magnetic field intensification: Comparison of 3D MHD simulations with Hinode/SP results. Astron. Astrophys. 2010, 509, A76. [Google Scholar] [CrossRef]
- Michalke, A. On the inviscid instability of the hyperbolictangent velocity profile. J. Fluid Mech. 1964, 19, 543–556. [Google Scholar] [CrossRef]
- Blumen, W. Shear layer instability of an inviscid compressible fluid. J. Fluid Mech. 1970, 40, 769–781. [Google Scholar] [CrossRef]
- Ray, T.P. The Effects of a Simple Shear Layer on the Growth of Kelvin–Helmholtz Instabilities. Mon. Not. Roy. Astron. Soc. 1982, 198, 617. [Google Scholar] [CrossRef]
- Wu, D.; Wang, D. The Kelvin–Helmholtz instability of a cylindrical flow with a shear layer. Mon. Not. Roy. Astron. Soc. 1991, 250, 760–768. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erdélyi, R.; Zsámberger, N.K. Magnetohydrodynamic Waves in Asymmetric Waveguides and Their Applications in Solar Physics—A Review. Symmetry 2024, 16, 1228. https://doi.org/10.3390/sym16091228
Erdélyi R, Zsámberger NK. Magnetohydrodynamic Waves in Asymmetric Waveguides and Their Applications in Solar Physics—A Review. Symmetry. 2024; 16(9):1228. https://doi.org/10.3390/sym16091228
Chicago/Turabian StyleErdélyi, Robertus, and Noémi Kinga Zsámberger. 2024. "Magnetohydrodynamic Waves in Asymmetric Waveguides and Their Applications in Solar Physics—A Review" Symmetry 16, no. 9: 1228. https://doi.org/10.3390/sym16091228
APA StyleErdélyi, R., & Zsámberger, N. K. (2024). Magnetohydrodynamic Waves in Asymmetric Waveguides and Their Applications in Solar Physics—A Review. Symmetry, 16(9), 1228. https://doi.org/10.3390/sym16091228






