Bridging 3D Confinement and 2D Correlations in Counterion Layers at Charged Interfaces: An Extended Percus Relation from First Principles
Abstract
1. Introduction
2. System Setup: Charged Plate with Counterions Only
- The coupling constant is proportional to the term .
- It also depends on the ratio for , which represents the ratio of the attractive force on a counterion from the external electric field to the repulsive Coulomb force between counterions separated by the WS radius a.
- When the Bjerrum length becomes large due to low temperature T and low dielectric permittivity .
- For multivalent counterions with a large valence q.
- For high surface charge density on the charged plate.
- When the attractive force from the external electric field pulling the counterions toward the plate is sufficiently larger than the repulsive force from an adjacent counterion.
3. Analytical Results: Density Distribution at Strong 3D Coupling
3.1. Hybrid Method of the DFT and Statistical Field Theory [21,45,46]
3.2. Gaussian Approximation as an Extension of the Percus Test-Particle Method
3.3. Dimensional Reduction in the Limit of Strong 3D Coupling
4. Numerical Results: Oscillatory Wavelength in Liquid Systems of Localized Counterions
4.1. Computational Setup
- When the Bjerrum length becomes large due to low temperature T and low dielectric permittivity .
- For multivalent counterions with a large valence q.
4.2. Data Trends and Physical Interpretation
4.3. Assessment of Sum Rules
5. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Full Name | First Appearance |
| 2D | two-dimensional | Section 1 |
| 3D | three-dimensional | Section 1 |
| OCP | one-component plasma | Section 1 |
| DFT | density functional theory | Section 1 |
| HNC | hypernetted-chain | Section 1 |
| WS | Wigner–Seitz | Section 2 |
| RHS | right-hand side | Section 2 |
| DCF | direct correlation function | Section 3.1 |
| TCF | total correlation function | Section 3.1 |
| RY | Ramakrishnan–Yussouff | Section 3.2 |
| OZ | Ornstein–Zernike | Section 3.3 |
Appendix A. Derivation of Equations (35) and (36) in the Gaussian Approximation
References
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577–1632. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nguyen, T.T.; Shklovskii, B.I. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Boroudjerdi, H.; Kim, Y.; Naji, A.; Netz, R.; Schlagberger, X.; Serr, A. Statics and dynamics of strongly charged soft matter. Phys. Rep. 2005, 416, 129–199. [Google Scholar] [CrossRef]
- Naji, A.; Jungblut, S.; Moreira, A.G.; Netz, R.R. Electrostatic interactions in strongly coupled soft matter. Phys. A Stat. Mech. Its Appl. 2005, 352, 131–170. [Google Scholar] [CrossRef]
- Naji, A.; Kanduč, M.; Forsman, J.; Podgornik, R. Perspective: Coulomb fluids—Weak coupling, strong coupling, in between and beyond. J. Chem. Phys. 2013, 139, 150901. [Google Scholar] [CrossRef] [PubMed]
- Wu, J. Understanding the Electric Double-Layer Structure, Capacitance, and Charging Dynamics. Chem. Rev. 2022, 122, 10821–10859. [Google Scholar] [CrossRef]
- Baus, M. Statistical mechanics of simple coulomb systems. Phys. Rep. 1980, 59, 1–94. [Google Scholar] [CrossRef]
- Ichimaru, S. Strongly coupled plasmas: High-density classical plasmas and degenerate electron liquids. Rev. Mod. Phys. 1982, 54, 1017–1059. [Google Scholar] [CrossRef]
- Martin, P.A. Sum rules in charged fluids. Rev. Mod. Phys. 1988, 60, 1075–1127. [Google Scholar] [CrossRef]
- Netz, R. Electrostatistics of counter-ions at and between planar charged walls: From Poisson-Boltzmann to the strong-coupling theory. Eur. Phys. J. E 2001, 5, 557–574. [Google Scholar] [CrossRef]
- Frusawa, H. Coarse-Grained Counterions in the Strong Coupling Limit. J. Phys. Soc. Jpn. 2004, 73, 507–510. [Google Scholar] [CrossRef]
- Chen, Y.G.; Weeks, J.D. Local molecular field theory for effective attractions between like charged objects in systems with strong Coulomb interactions. Proc. Natl. Acad. Sci. USA 2006, 103, 7560–7565. [Google Scholar] [CrossRef] [PubMed]
- Santangelo, C.D. Computing counterion densities at intermediate coupling. Phys. Rev. E 2006, 73, 041512. [Google Scholar] [CrossRef] [PubMed]
- Hatlo, M.M.; Lue, L. Electrostatic interactions of charged bodies from the weak- to the strong-coupling regime. Europhys. Lett. 2010, 89, 25002. [Google Scholar] [CrossRef]
- Šamaj, L.; Trizac, E. Wigner-crystal formulation of strong-coupling theory for counterions near planar charged interfaces. Phys. Rev. E 2011, 84, 041401. [Google Scholar] [CrossRef]
- Šamaj, L.; Trulsson, M.; Trizac, E. Strong-coupling theory of counterions between symmetrically charged walls: From crystal to fluid phases. Soft Matter 2018, 14, 4040–4052. [Google Scholar] [CrossRef]
- Palaia, I.; Trulsson, M.; Šamaj, L.; Trizac, E. A correlation-hole approach to the electric double layer with counter-ions only. Mol. Phys. 2018, 116, 3134–3146. [Google Scholar] [CrossRef]
- Frusawa, H. Transverse Density Fluctuations around the Ground State Distribution of Counterions near One Charged Plate: Stochastic Density Functional View. Entropy 2019, 22, 34. [Google Scholar] [CrossRef]
- Frusawa, H. Ground-state correlation energy of counterions at a charged planar wall: Gibbs-Bogoliubov lower-bound approach. Phys. Lett. A 2020, 384, 126512. [Google Scholar] [CrossRef]
- de Souza, J.P.; Bazant, M.Z. Continuum Theory of Electrostatic Correlations at Charged Surfaces. J. Phys. Chem. C 2020, 124, 11414–11421. [Google Scholar] [CrossRef]
- Frusawa, H. On the equivalence of self-consistent equations for nonuniform liquids: A unified description of the various modifications. J. Stat. Mech. Theory Exp. 2021, 2021, 013213. [Google Scholar] [CrossRef]
- Jancovici, B. Exact Results for the Two-Dimensional One-Component Plasma. Phys. Rev. Lett. 1981, 46, 386–388. [Google Scholar] [CrossRef]
- Hansen, J.P.; Levesque, D. The two-dimensional one-component plasma in the hypernetted chain approximation. J. Phys. C Solid State Phys. 1981, 14, L603–L608. [Google Scholar] [CrossRef]
- de Leeuw, S.; Perram, J. Statistical mechanics of two-dimensional Coulomb systems. Phys. A Stat. Mech. Its Appl. 1982, 113, 546–558. [Google Scholar] [CrossRef]
- Caillol, J.M.; Levesque, D.; Weis, J.J.; Hansen, J.P. A Monte Carlo study of the classical two-dimensional one-component plasma. J. Stat. Phys. 1982, 28, 325–349. [Google Scholar] [CrossRef]
- Piasecki, J.; Levesque, D. From monotonic to oscillatory decay of correlations: Analytical approximation for the two-dimensional, one-component plasma. J. Stat. Phys. 1987, 47, 489–503. [Google Scholar] [CrossRef]
- Šamaj, L.; Percus, J.K.; Kolesík, M. Two-dimensional one-component plasma at coupling Γ = 4: Numerical study of pair correlations. Phys. Rev. E 1994, 49, 5623–5627. [Google Scholar] [CrossRef] [PubMed]
- Muto, S.; Aoki, H. Crystallization of a classical two-dimensional electron system: Positional and orientational orders. Phys. Rev. B 1999, 59, 14911–14914. [Google Scholar] [CrossRef]
- Levesque, D.; Weis, J.J.; Lebowitz, J.L. Charge Fluctuations in the Two-Dimensional One-Component Plasma. J. Stat. Phys. 2000, 100, 209–222. [Google Scholar] [CrossRef]
- Šamaj, L. Is the Two-Dimensional One-Component Plasma Exactly Solvable? J. Stat. Phys. 2004, 117, 131–158. [Google Scholar] [CrossRef]
- Antlanger, M.; Mazars, M.; Šamaj, L.; Kahl, G.; Trizac, E. Taking one charge off a two-dimensional Wigner crystal. Mol. Phys. 2014, 112, 1336–1349. [Google Scholar] [CrossRef]
- Cardoso, G.; Stéphan, J.M.; Abanov, A.G. The boundary density profile of a Coulomb droplet. Freezing at the edge. J. Phys. A Math. Theor. 2020, 54, 015002. [Google Scholar] [CrossRef]
- Cardoso, G.; Stéphan, J.M.; Abanov, A.G. The density profile of a Coulomb plasma on a cylinder: Boundary oscillations. J. Phys. A Math. Theor. 2025, 58, 245002. [Google Scholar] [CrossRef]
- Kirchner, K.; Kirchner, T.; Ivaništšev, V.; Fedorov, M. Electrical double layer in ionic liquids: Structural transitions from multilayer to monolayer structure at the interface. Electrochim. Acta 2013, 110, 762–771. [Google Scholar] [CrossRef]
- de Souza, J.P.; Goodwin, Z.A.; McEldrew, M.; Kornyshev, A.A.; Bazant, M.Z. Interfacial Layering in the Electric Double Layer of Ionic Liquids. Phys. Rev. Lett. 2020, 125, 116001. [Google Scholar] [CrossRef]
- Jeanmairet, G.; Rotenberg, B.; Salanne, M. Microscopic Simulations of Electrochemical Double-Layer Capacitors. Chem. Rev. 2022, 122, 10860–10898. [Google Scholar] [CrossRef]
- Angiolari, F.; Coretti, A.; Salanne, M.; Bonella, S. Electrically driven first-order phase transition of a 2D ionic crystal at the electrode/electrolyte interface. arXiv 2025, arXiv:2507.19087. [Google Scholar] [CrossRef]
- Laanait, N.; Mihaylov, M.; Hou, B.; Yu, H.; Vanýsek, P.; Meron, M.; Lin, B.; Benjamin, I.; Schlossman, M.L. Tuning ion correlations at an electrified soft interface. Proc. Natl. Acad. Sci. USA 2012, 109, 20326–20331. [Google Scholar] [CrossRef]
- Miller, M.; Chu, M.; Lin, B.; Meron, M.; Dutta, P. Observation of Ordered Structures in Counterion Layers near Wet Charged Surfaces: A Potential Mechanism for Charge Inversion. Langmuir 2015, 32, 73–77. [Google Scholar] [CrossRef]
- Miller, M.; Chu, M.; Lin, B.; Bu, W.; Dutta, P. Atomic Number Dependent “Structural Transitions” in Ordered Lanthanide Monolayers: Role of the Hydration Shell. Langmuir 2017, 33, 1412–1418. [Google Scholar] [CrossRef] [PubMed]
- Sloutskin, E.; Tamam, L.; Sapir, Z.; Ocko, B.M.; Bain, C.D.; Kuzmenko, I.; Gog, T.; Deutsch, M. Counterions under a Surface-Adsorbed Cationic Surfactant Monolayer: Structure and Thermodynamics. Langmuir 2022, 38, 12356–12366. [Google Scholar] [CrossRef]
- Wang, J.; Li, H.; Tavakol, M.; Serva, A.; Nener, B.; Parish, G.; Salanne, M.; Warr, G.G.; Voïtchovsky, K.; Atkin, R. Ions Adsorbed at Amorphous Solid/Solution Interfaces Form Wigner Crystal-like Structures. ACS Nano 2023, 18, 1181–1194. [Google Scholar] [CrossRef] [PubMed]
- Han, T.; Xu, W.; Han, J.; Adibnia, V.; He, H.; Zhang, C.; Luo, J. Counterion Distribution in the Stern Layer on Charged Surfaces. Nano Lett. 2024, 24, 10443–10450. [Google Scholar] [CrossRef]
- Chau, H.H.; Li, H.; Atkin, R. Anion Size Controls Cation Wigner Crystal-Like Structures at Silica Interfaces. J. Phys. Chem. Lett. 2025, 16, 5695–5699. [Google Scholar] [CrossRef]
- Frusawa, H. Stochastic dynamics and thermodynamics around a metastable state based on the linear Dean–Kawasaki equation. J. Phys. A Math. Theor. 2019, 52, 065003. [Google Scholar] [CrossRef]
- Frusawa, H. Non-hyperuniform metastable states around a disordered hyperuniform state of densely packed spheres: Stochastic density functional theory at strong coupling. Soft Matter 2021, 17, 8810–8831. [Google Scholar] [CrossRef]
- Percus, J.K. Approximation Methods in Classical Statistical Mechanics. Phys. Rev. Lett. 1962, 8, 462–463. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids: With Applications to Soft Matter; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar] [CrossRef]
- Schneider, R. Convex Bodies: The Brunn–Minkowski Theory; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Cañete, A.; González Merino, B. On the isodiametric and isominwidth inequalities for planar bisections. Rev. Matemática Iberoam. 2020, 37, 1247–1275. [Google Scholar] [CrossRef]
- Ramakrishnan, T.V.; Yussouff, M. First-principles order-parameter theory of freezing. Phys. Rev. B 1979, 19, 2775–2794. [Google Scholar] [CrossRef]
- Evans, R. The nature of the liquid-vapour interface and other topics in the statistical mechanics of nonuniform, classical fluids. Adv. Phys. 1979, 28, 143–200. [Google Scholar] [CrossRef]
- Wu, J.; Li, Z. Density-Functional Theory for Complex Fluids. Annu. Rev. Phys. Chem. 2007, 58, 85–112. [Google Scholar] [CrossRef]
- Lado, F. Effective potentials in the integral quantum Hall effect. Phys. Rev. B 2003, 67, 245322. [Google Scholar] [CrossRef]
- Aupic, J.; Urbic, T. Thermodynamics and structure of a two-dimensional electrolyte by integral equation theory. J. Chem. Phys. 2014, 140, 184509. [Google Scholar] [CrossRef]
- Lomba, E.; Weis, J.J.; Lado, F. Structure and thermodynamics of a two-dimensional Coulomb fluid in the strong association regime. J. Chem. Phys. 2007, 127, 074501. [Google Scholar] [CrossRef]
- Ng, K.C. Hypernetted chain solutions for the classical one-component plasma up to Γ = 7000. J. Chem. Phys. 1974, 61, 2680–2689. [Google Scholar] [CrossRef]
- Anderson, D.G. Iterative Procedures for Nonlinear Integral Equations. J. ACM 1965, 12, 547–560. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P.; Olivares, J. Analytic approximation to Bessel function J0(x). Comput. Appl. Math. 2020, 39, 222. [Google Scholar] [CrossRef]
- Walters, M.C.; Subramanian, P.; Archer, A.J.; Evans, R. Structural crossover in a model fluid exhibiting two length scales: Repercussions for quasicrystal formation. Phys. Rev. E 2018, 98, 012606. [Google Scholar] [CrossRef] [PubMed]
- Torquato, S. Hyperuniform states of matter. Phys. Rep. 2018, 745, 1–95. [Google Scholar] [CrossRef]
- Velev, O.D.; Bhatt, K.H. On-chip micromanipulation and assembly of colloidal particles by electric fields. Soft Matter 2006, 2, 738. [Google Scholar] [CrossRef]
- Besra, L.; Liu, M. A review on fundamentals and applications of electrophoretic deposition (EPD). Prog. Mater. Sci. 2007, 52, 1–61. [Google Scholar] [CrossRef]
- Chai, Z.; Childress, A.; Busnaina, A.A. Directed Assembly of Nanomaterials for Making Nanoscale Devices and Structures: Mechanisms and Applications. ACS Nano 2022, 16, 17641–17686. [Google Scholar] [CrossRef] [PubMed]


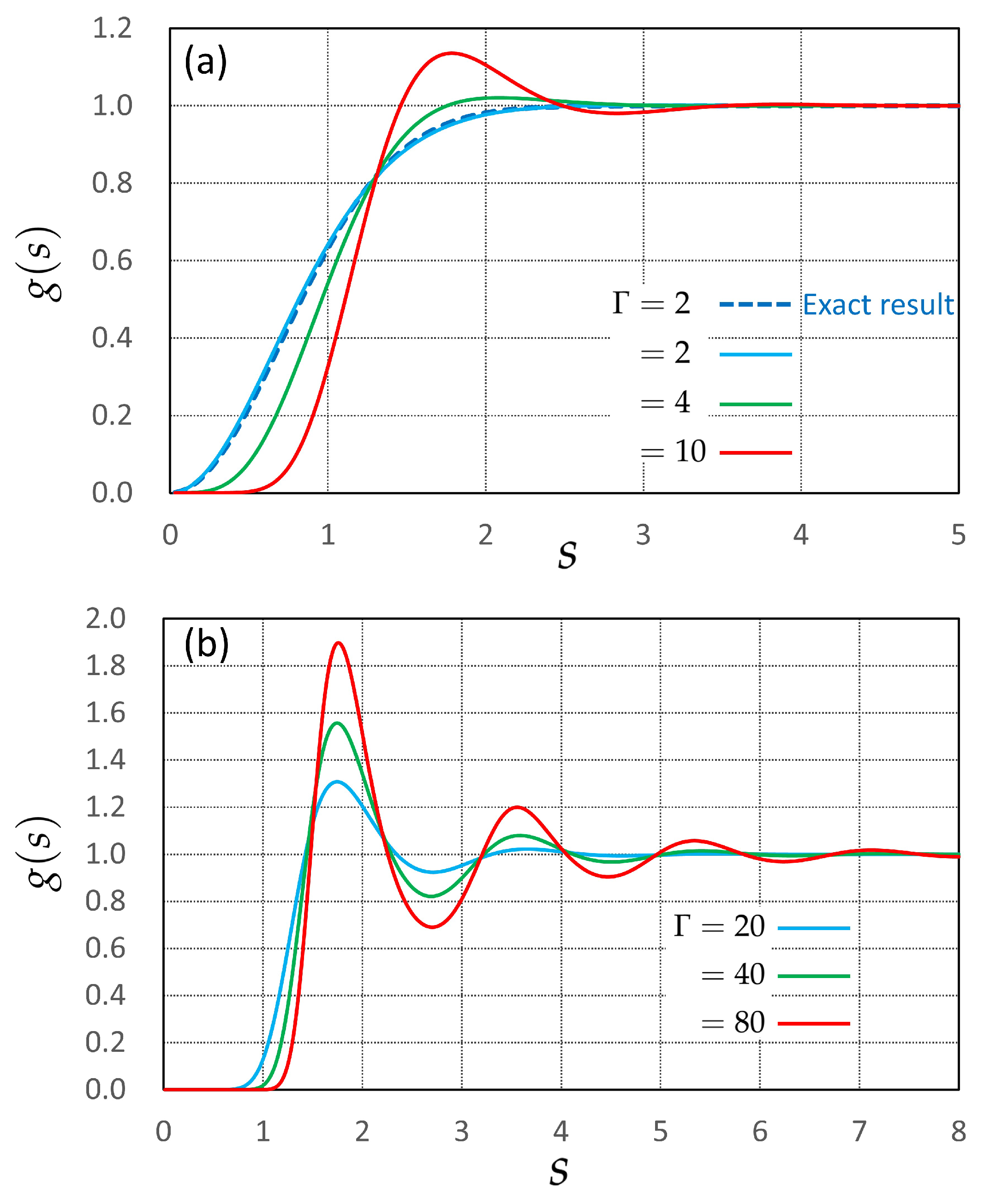
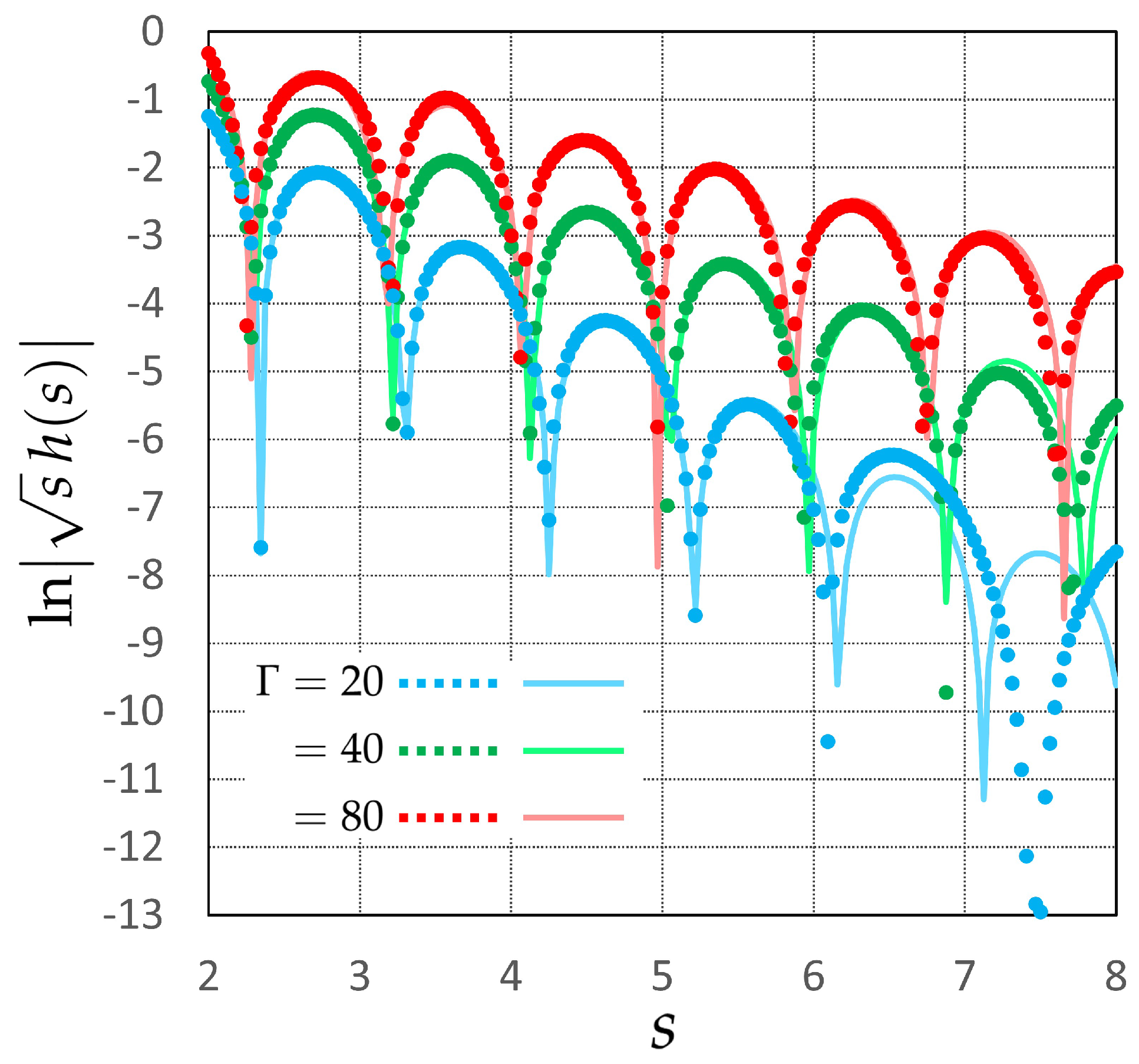
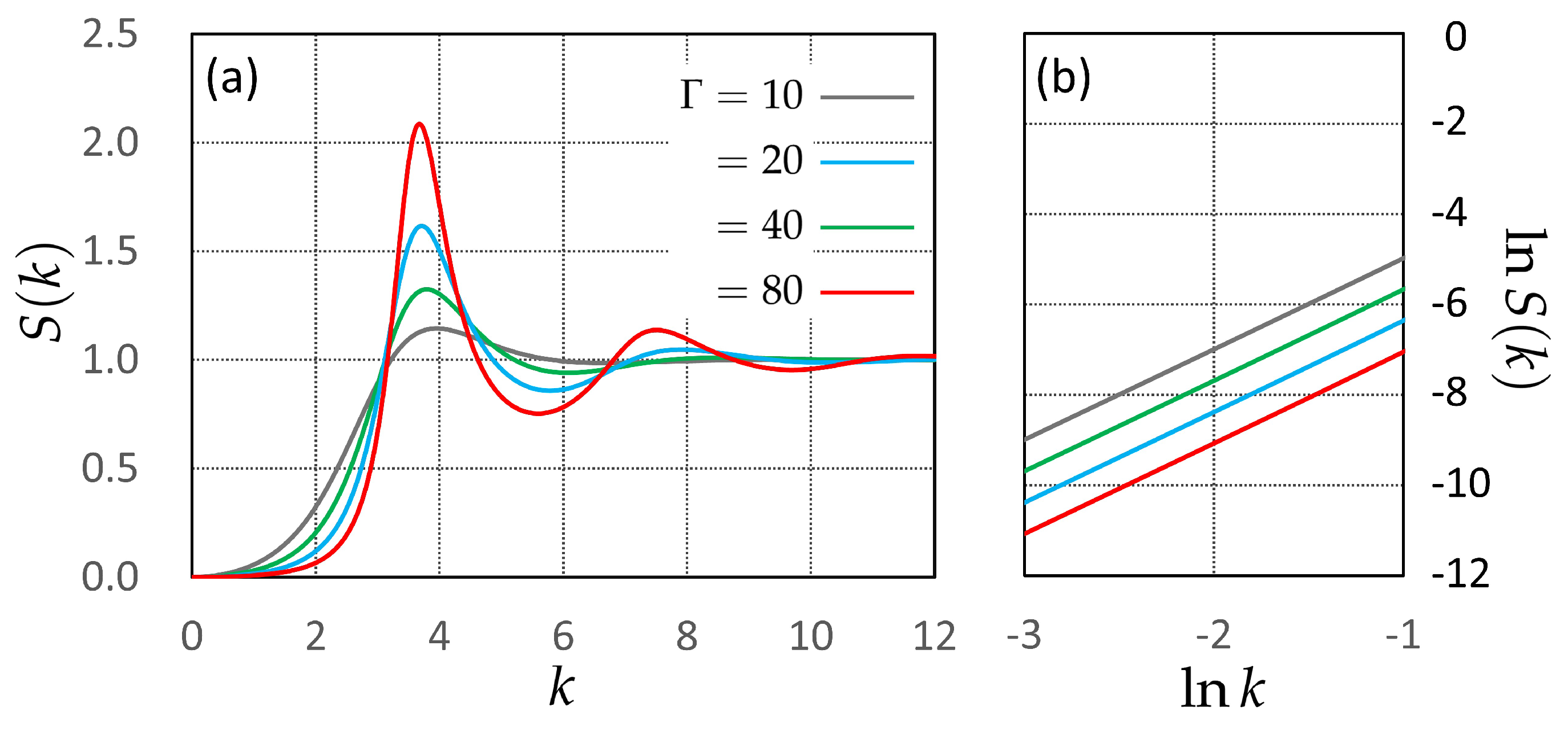
| Wavelength | Decay Length | |
|---|---|---|
| 20 | 1.910 | 0.852 |
| 40 | 1.834 | 1.256 |
| 80 | 1.793 | 1.912 |
| Slope | Intercept | Relative Error [%] | ||
|---|---|---|---|---|
| 10 | 2.01 | 2.97 | 19.59 | 1.05 |
| 20 | 2.01 | 3.66 | 38.94 | 1.35 |
| 40 | 2.01 | 4.35 | 77.58 | 1.55 |
| 80 | 2.01 | 5.04 | 154.05 | 1.91 |
| Step | Physical Quantity | Equations | Interpretation |
|---|---|---|---|
| 1 | (grand potential) | (29) and (30) | Hybrid theory combining DFT and statistical field theory |
| 2 | (grand potential) | (35) and (36) | Resulting form in the Gaussian approximation |
| 3 | (equilibrium 3D density) | (46) | Extended relation of the Percus test-particle method in 3D systems |
| 4 | (equilibrium 2D density) | (56) | Conventional Percus relation in 2D systems |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frusawa, H. Bridging 3D Confinement and 2D Correlations in Counterion Layers at Charged Interfaces: An Extended Percus Relation from First Principles. Symmetry 2025, 17, 1783. https://doi.org/10.3390/sym17111783
Frusawa H. Bridging 3D Confinement and 2D Correlations in Counterion Layers at Charged Interfaces: An Extended Percus Relation from First Principles. Symmetry. 2025; 17(11):1783. https://doi.org/10.3390/sym17111783
Chicago/Turabian StyleFrusawa, Hiroshi. 2025. "Bridging 3D Confinement and 2D Correlations in Counterion Layers at Charged Interfaces: An Extended Percus Relation from First Principles" Symmetry 17, no. 11: 1783. https://doi.org/10.3390/sym17111783
APA StyleFrusawa, H. (2025). Bridging 3D Confinement and 2D Correlations in Counterion Layers at Charged Interfaces: An Extended Percus Relation from First Principles. Symmetry, 17(11), 1783. https://doi.org/10.3390/sym17111783






