A Gauss Hypergeometric-Type Model for Heavy-Tailed Survival Times in Biomedical Research
Abstract
1. Introduction
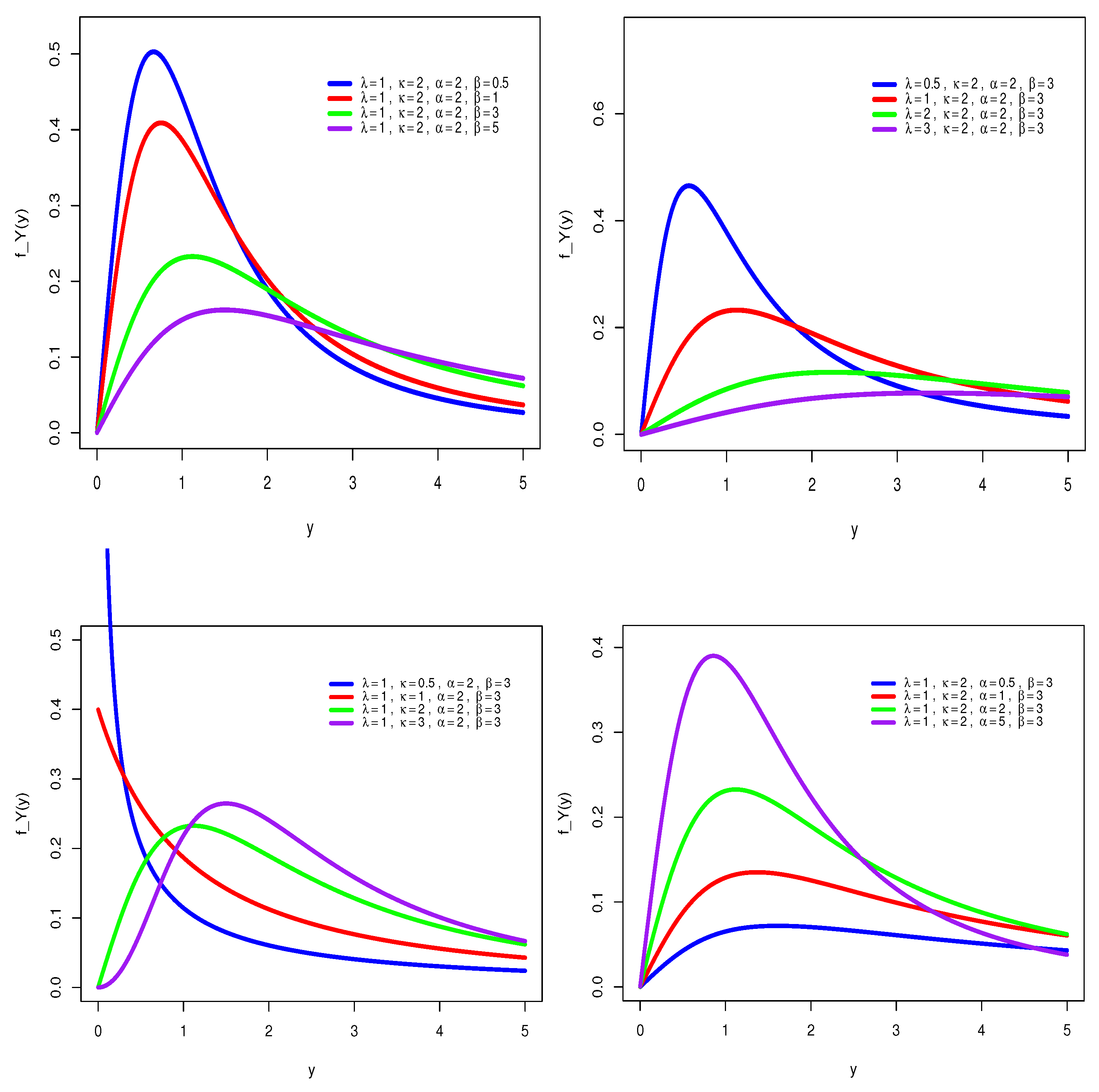
2. Slash–Log–Logistic Distribution
2.1. Structure of the SlaLL Model
2.2. Characterizations
- (i)
- for every ;
- (ii)
- and ;
- (iii)
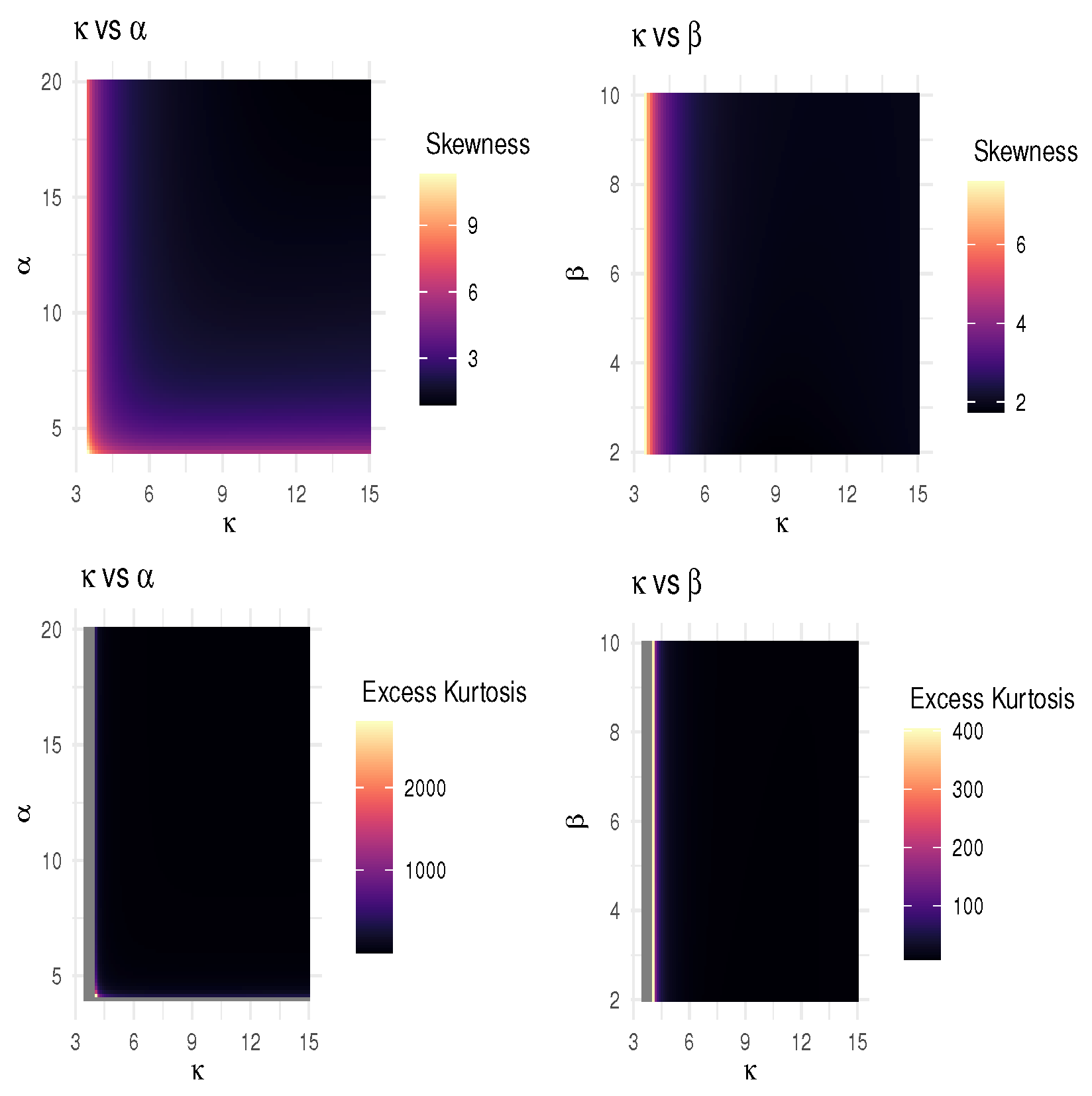
2.3. Moments of SlaLL Random Variable
3. Estimation and Simulation
3.1. Maximum Likelihood Estimation
- Generate .
- Generate .
- Compute .
3.2. Bayesian Estimation
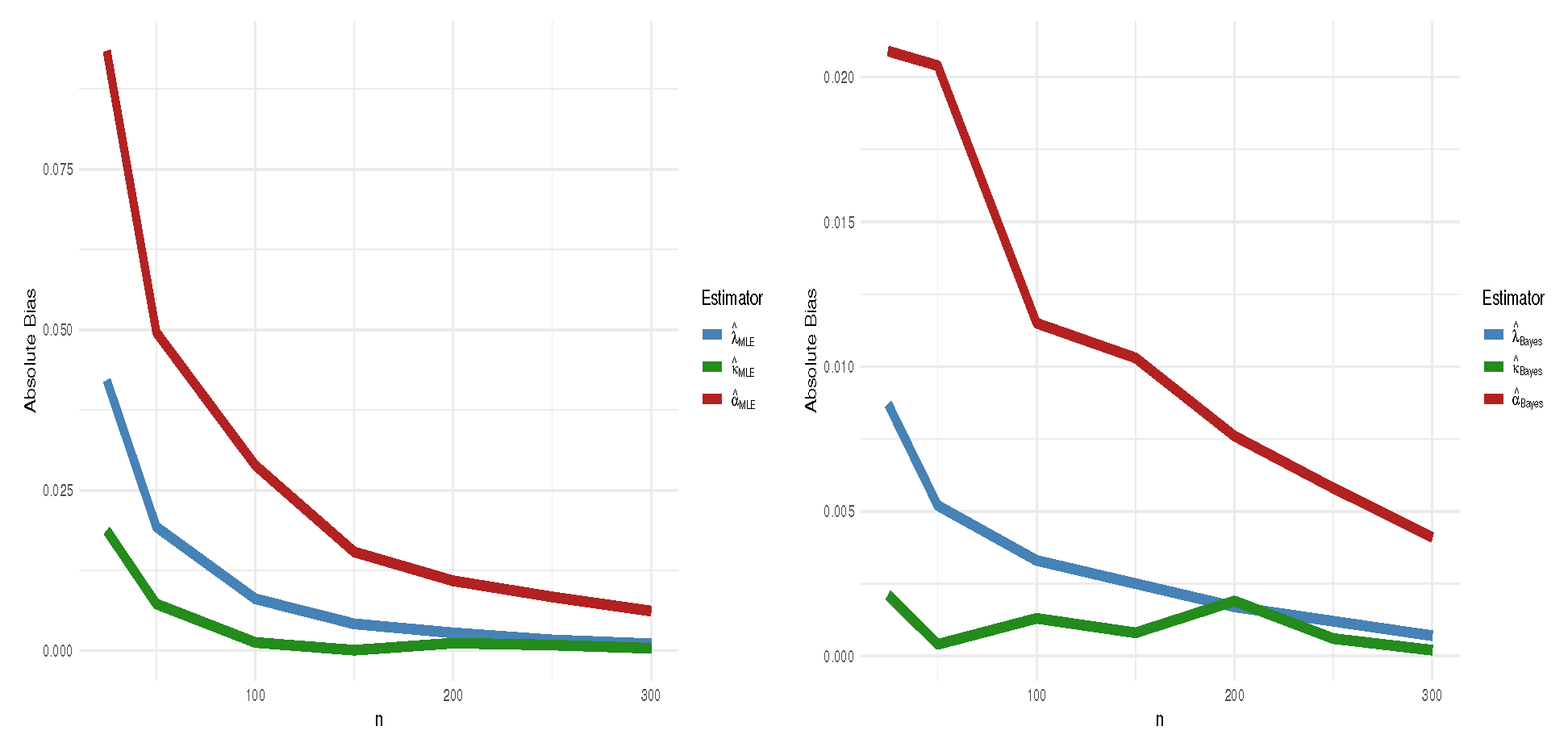
3.3. Simulation Study
- Set 1: .
- Set 2: .
- The empirical bias and mean squared error (MSE) of ;
- The lower and upper bounds (LB, UB) of the nominal 95% CI and CrI.
4. Modeling Heavy-Tailed Survival Times
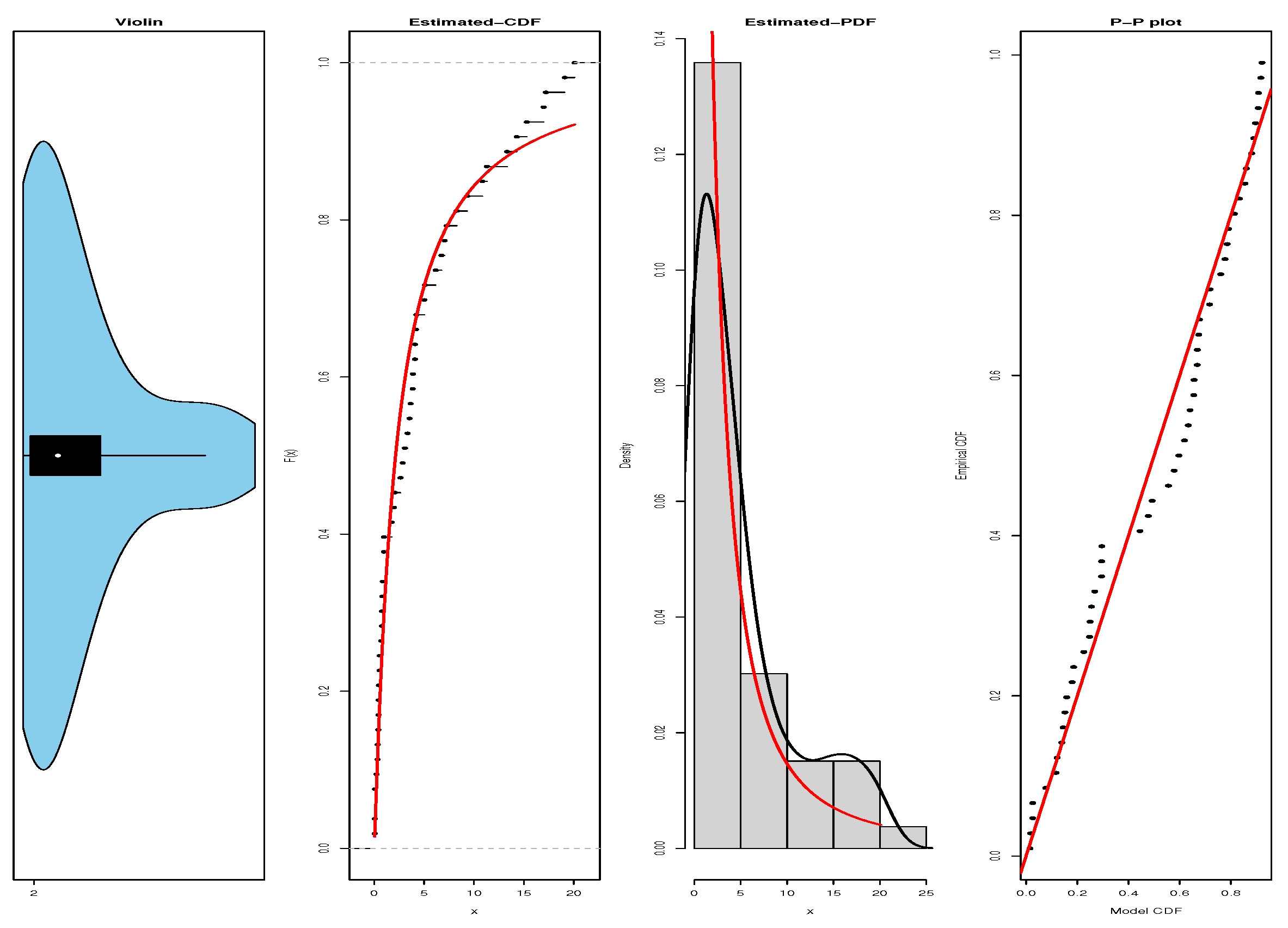
4.1. Dataset 1: AML Survival Times
4.2. Dataset 2: COVID-19 Patient Survival Times
4.3. Model Fit Metrics for Dataset 3
4.4. Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Listing A1. R routines for the SlaLL distribution. |
 |
References
- Fisk, P.R. The Graduation of Income Distributions. Econometrica 1961, 29, 171–185. [Google Scholar] [CrossRef]
- Bennett, S. Log–logistic regression models for survival data. J. R. Stat. Soc. Ser. C 1983, 32, 165–171. [Google Scholar] [CrossRef]
- Kariuki, V.; Wanjoya, A.; Ngesa, O.; Aljohani, H.M. Properties, estimation and applications of the extended log–logistic distribution. Sci. Rep. 2024, 14, 20967. [Google Scholar] [CrossRef] [PubMed]
- Afify, A.Z.; Abdelall, Y.Y.; AlQadi, H.; Mahran, H.A. The modified log–logistic distribution: Properties and inference with real-life data applications. Contemp. Math. 2025, 6, 862–890. [Google Scholar] [CrossRef]
- Ishaq, A.I.; Panitanarak, U.; Abiodun, A.A.; Daud, H.; Suleiman, A.A. A new Maxwell–log–logistic distribution and its applications for mortality rate data. J. Niger. Soc. Phys. Sci. 2025, 7, 1976–1989. [Google Scholar]
- Mahto, A.K.; Tripathi, Y.M.; Dey, S.; Alsaedi, B.S.; Alhelali, M.H.; Alghamdi, F.M.; Alrumayh, A.; Alshawarbeh, E. Bayesian estimation and prediction under progressive-stress accelerated life tests for a log–logistic model. Alex. Eng. J. 2024, 101, 330–342. [Google Scholar] [CrossRef]
- Lee, S.; Moriasi, D.N.; Mehr, A.D.; Mirchi, A. Sensitivity of the Standardised Precipitation–Evapotranspiration Index to distribution choice and PET method. J. Hydrol. Reg. Stud. 2024, 53, 101761. [Google Scholar] [CrossRef]
- Gui, W. Statistical properties and applications of the Lindley slash distribution. J. Appl. Stat. Sci. 2012, 20, 283–298. [Google Scholar]
- Rojas, M.A.; Bolfarine, H.; Gómez, H.W. An extension of the slash-elliptical distribution. SORT 2014, 38, 215–230. [Google Scholar]
- Therneau, T.M. Survival analysis. In The aml Dataset in R’s survival Package Records Weeks to Relapse or Censoring for AML Patients; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Liu, X.; Ahmad, Z.; Gemeay, A.M.; Abdulrahman, T.A.; Hafez, E.H.; Khalil, N. Modeling the survival times of COVID-19 patients with a new statistical model: A case study from China. PLoS ONE 2021, 16, e0254999. [Google Scholar] [CrossRef] [PubMed]
- Miller, R.G. Survival Analysis, 2nd ed.; Wiley Classics Library; John Wiley & Sons: Hoboken, NJ, USA, 1997; ISBN 0-471-25218-2. [Google Scholar]
- Rojas, M.A.; Iriarte, Y.A. A Lindley-Type Distribution for Modeling High-Kurtosis Data. Mathematics 2022, 10, 2240. [Google Scholar] [CrossRef]
- Gillariose, J.; Joseph, J.; Chesneau, C. Extended Slash Modified Lindley Distribution to Model Economic Variables Showing Asymmetry. Comput. Econ. 2024, 66, 3497–3516. [Google Scholar] [CrossRef]
- Elbatal, I.; Joseph, J.; Gillariose, J.; Jamal, F.; Ben Ghorbal, A. Confluent hypergeometric inverse exponential distribution with application to climate and economic data. J. Radiat. Res. Appl. Sci. 2025, 18, 101516. [Google Scholar] [CrossRef]
- Kamal, M.; Alsolmi, M.M.; Nayabuddin; Al Mutairi, A.; Hussam, E.; SidAhmed Mustafa, M.; Nassr, S.G. A new distributional approach: Estimation, Monte Carlo simulation and applications to the biomedical data sets. Netw. Heterog. Media 2023, 18, 1575–1599. [Google Scholar] [CrossRef]
- Ewuru, D.A.; Etikan, I. The Survival Analysis of Veterans’ Administration Lung Cancer Dataset. medRxiv 2022. [Google Scholar] [CrossRef]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data; Wiley: New York, NY, USA, 1980. [Google Scholar]
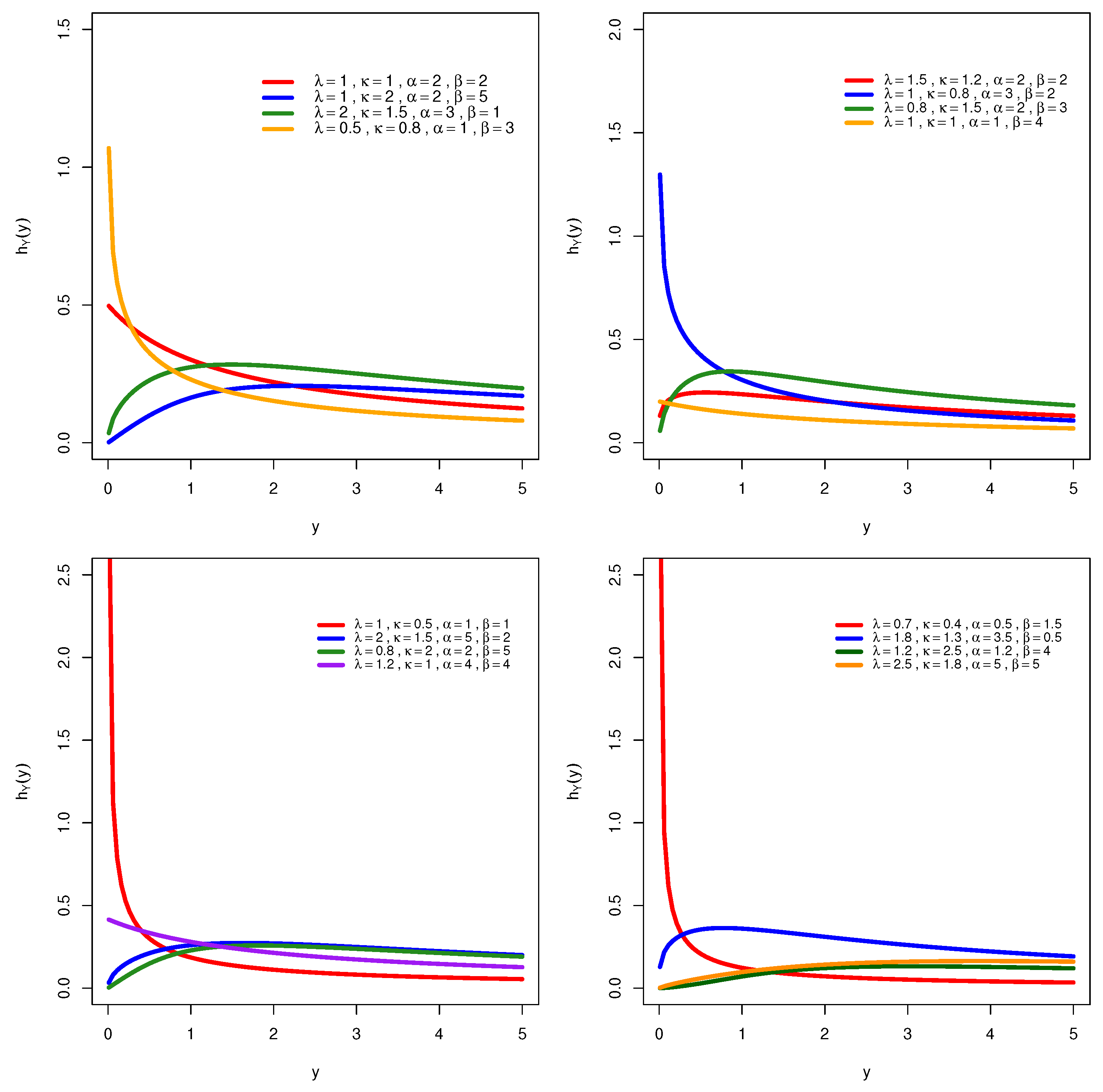

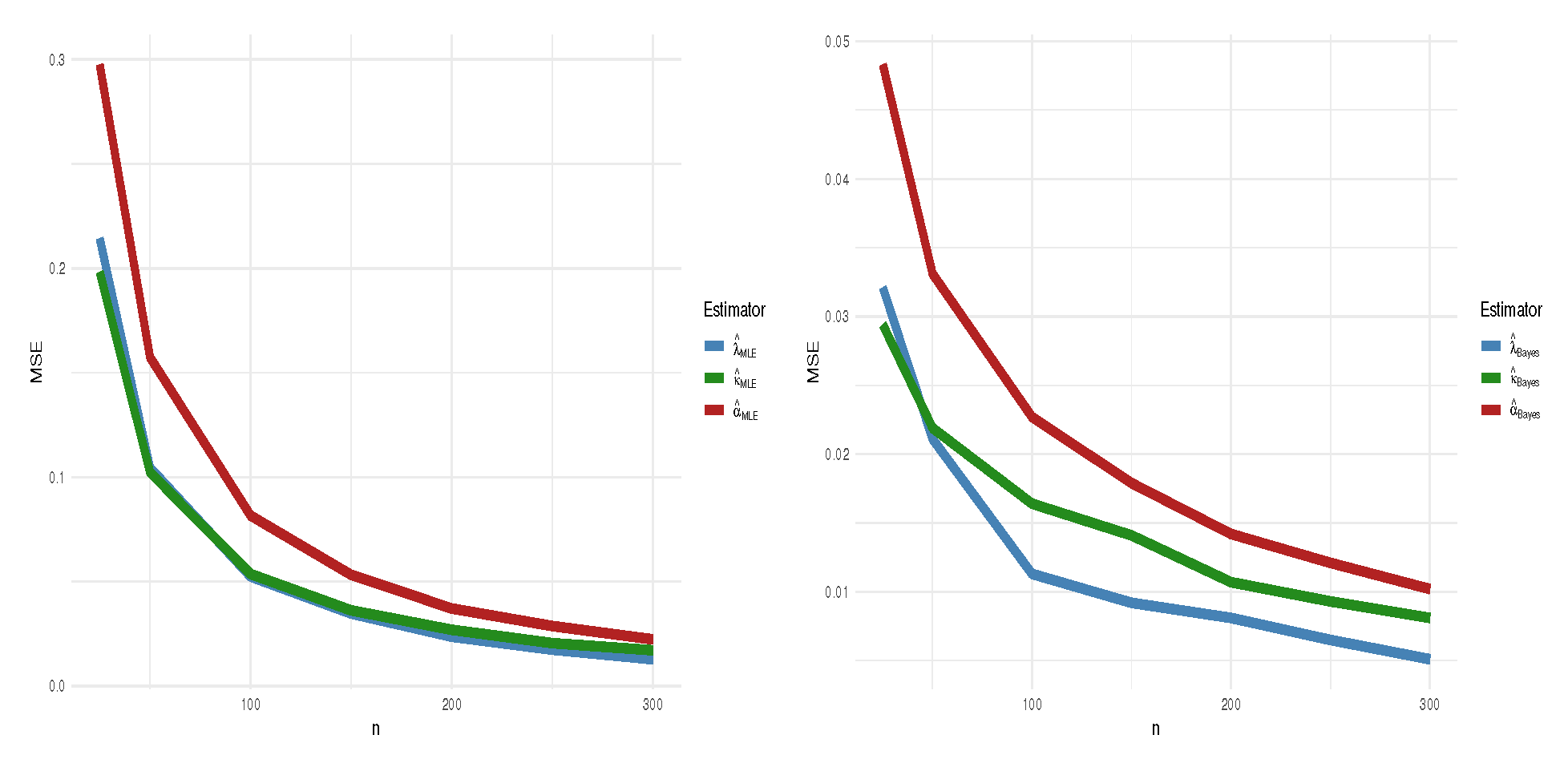
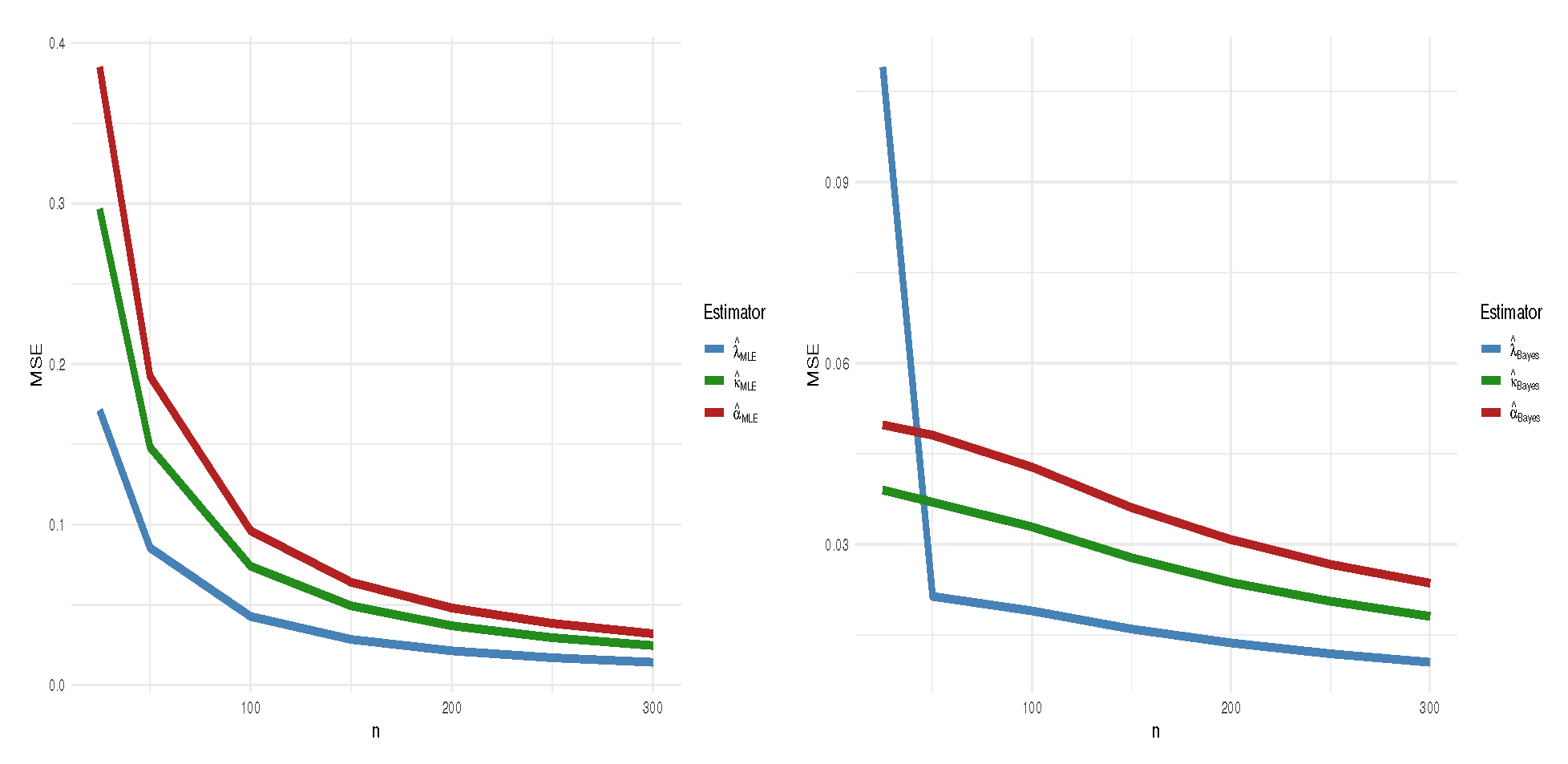


| n | MLE | MSE | CILB | CIUB | BE | MSE | CrILB | CrIUB | |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 3.0421 | 0.2143 | 3.0114 | 3.0728 | 3.0087 | 0.0321 | 3.0002 | 3.0172 | |
| 25 | 1.4813 | 0.1982 | 1.4567 | 1.5059 | 1.5021 | 0.0294 | 1.4903 | 1.5139 | |
| 25 | 2.0934 | 0.2975 | 2.0621 | 2.1247 | 2.0209 | 0.0483 | 2.0002 | 2.0232 | |
| 50 | 3.0193 | 0.1045 | 3.0027 | 3.0360 | 3.0052 | 0.0211 | 2.9967 | 3.0137 | |
| 50 | 1.4927 | 0.1023 | 1.4736 | 1.5118 | 1.4996 | 0.0219 | 1.4883 | 1.5109 | |
| 50 | 2.0496 | 0.1574 | 2.0269 | 2.0723 | 2.0204 | 0.0331 | 2.0093 | 2.0315 | |
| 100 | 3.0081 | 0.0524 | 2.9972 | 3.0190 | 3.0033 | 0.0113 | 2.9968 | 3.0098 | |
| 100 | 1.4987 | 0.0536 | 1.4889 | 1.5085 | 1.5013 | 0.0164 | 1.4928 | 1.5098 | |
| 100 | 2.0289 | 0.0816 | 2.0135 | 2.0443 | 2.0115 | 0.0227 | 2.0013 | 2.0217 | |
| 150 | 3.0042 | 0.0347 | 2.9961 | 3.0123 | 3.0025 | 0.0092 | 2.9956 | 3.0094 | |
| 150 | 1.5001 | 0.0362 | 1.4925 | 1.5077 | 1.5008 | 0.0141 | 1.4935 | 1.5081 | |
| 150 | 2.0154 | 0.0532 | 2.0038 | 2.0270 | 2.0103 | 0.0179 | 2.0016 | 2.0190 | |
| 200 | 3.0028 | 0.0236 | 2.9955 | 3.0101 | 3.0017 | 0.0081 | 2.9952 | 3.0082 | |
| 200 | 1.5012 | 0.0269 | 1.4946 | 1.5078 | 1.5019 | 0.0107 | 1.4955 | 1.5083 | |
| 200 | 2.0109 | 0.0371 | 2.0012 | 2.0206 | 2.0076 | 0.0142 | 1.9998 | 2.0154 | |
| 250 | 3.0017 | 0.0174 | 2.9954 | 3.0080 | 3.0012 | 0.0065 | 2.9954 | 3.0070 | |
| 250 | 1.5009 | 0.0205 | 1.4947 | 1.5071 | 1.5006 | 0.0093 | 1.4943 | 1.5069 | |
| 250 | 2.0084 | 0.0287 | 2.0003 | 2.0165 | 2.0058 | 0.0121 | 1.9987 | 2.0129 | |
| 300 | 3.0011 | 0.0128 | 2.9955 | 3.0067 | 3.0007 | 0.0051 | 2.9953 | 3.0061 | |
| 300 | 1.5004 | 0.0171 | 1.4950 | 1.5058 | 1.5002 | 0.0081 | 1.4949 | 1.5055 | |
| 300 | 2.0062 | 0.0223 | 1.9993 | 2.0131 | 2.0041 | 0.0102 | 1.9978 | 2.0104 |
| n | MLE | MSE | CILB | CIUB | BE | MSE | CrILB | CrIUB | |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 2.0224 | 0.1712 | 1.9968 | 2.048 | 2.0075 | 0.1090 | 1.9989 | 2.016 | |
| 25 | 2.4894 | 0.2964 | 2.4557 | 2.5231 | 2.4965 | 0.0390 | 2.4852 | 2.5077 | |
| 25 | 3.0570 | 0.3848 | 3.0186 | 3.0954 | 3.0190 | 0.0498 | 3.0062 | 3.0318 | |
| 50 | 2.0112 | 0.0856 | 1.9931 | 2.0293 | 2.0056 | 0.0214 | 1.9965 | 2.0147 | |
| 50 | 2.4947 | 0.1482 | 2.4708 | 2.5186 | 2.4973 | 0.0370 | 2.4854 | 2.5093 | |
| 50 | 3.0285 | 0.1924 | 3.0013 | 3.0557 | 3.0143 | 0.0481 | 3.0007 | 3.0278 | |
| 100 | 2.0056 | 0.0428 | 1.9928 | 2.0184 | 2.0037 | 0.0190 | 1.9952 | 2.0123 | |
| 100 | 2.4973 | 0.0741 | 2.4805 | 2.5142 | 2.4982 | 0.0329 | 2.4870 | 2.5095 | |
| 100 | 3.0143 | 0.0962 | 2.9950 | 3.0335 | 3.0095 | 0.0428 | 2.9967 | 3.0223 | |
| 150 | 2.0037 | 0.0285 | 1.9933 | 2.0142 | 2.0028 | 0.0160 | 1.9949 | 2.0107 | |
| 150 | 2.4982 | 0.0494 | 2.4845 | 2.5120 | 2.4987 | 0.0278 | 2.4883 | 2.5090 | |
| 150 | 3.0095 | 0.0641 | 2.9938 | 3.0252 | 3.0071 | 0.0361 | 2.9954 | 3.0189 | |
| 200 | 2.0028 | 0.0214 | 1.9937 | 2.0119 | 2.0022 | 0.0137 | 1.9950 | 2.0095 | |
| 200 | 2.4987 | 0.0370 | 2.4867 | 2.5106 | 2.4989 | 0.0237 | 2.4894 | 2.5085 | |
| 200 | 3.0071 | 0.0481 | 2.9935 | 3.0207 | 3.0057 | 0.0308 | 2.9948 | 3.0166 | |
| 250 | 2.0022 | 0.0171 | 1.9941 | 2.0103 | 2.0019 | 0.0119 | 1.9951 | 2.0086 | |
| 250 | 2.4989 | 0.0296 | 2.4883 | 2.5096 | 2.4991 | 0.0206 | 2.4902 | 2.5080 | |
| 250 | 3.0057 | 0.0385 | 2.9935 | 3.0179 | 3.0048 | 0.0267 | 2.9946 | 3.0149 | |
| 300 | 2.0019 | 0.0143 | 1.9945 | 2.0093 | 2.0016 | 0.0105 | 1.9953 | 2.0079 | |
| 300 | 2.4991 | 0.0247 | 2.4894 | 2.5089 | 2.4992 | 0.0181 | 2.4909 | 2.5076 | |
| 300 | 3.0048 | 0.0321 | 2.9937 | 3.0158 | 3.0041 | 0.0236 | 2.9946 | 3.0136 |
| Distribution | Estimates | −Logl | AIC | BIC | K-S | p-Value | ||
|---|---|---|---|---|---|---|---|---|
| SlaLL | 151.9841 | 311.9683 | 317.5731 | 0.11469 | 0.8249 | 0.44319 | 0.08109 | |
| SL | 176.0303 | 358.0606 | 365.8761 | 0.84724 | <2.2 × 10−16 | 91.038 | 8.2901 | |
| SML | 212.7549 | 431.5097 | 439.3252 | 0.39514 | 0.000125 | 7.4294 | 1.4276 | |
| SI | 153.8979 | 313.7957 | 317.9993 | 0.14453 | 0.5579 | 0.61235 | 0.08441 | |
| Distribution | Estimates | −Logl | AIC | BIC | K-S | p-Value | ||
|---|---|---|---|---|---|---|---|---|
| SlaLL | 136.7253 | 281.4506 | 289.3318 | 0.1076 | 0.5718 | 0.7929 | 0.1263 | |
| SL | 137.9096 | 295.8192 | 291.7301 | 0.1561 | 0.1508 | 1.0068 | 0.1553 | |
| SML | 212.7549 | 431.5097 | 439.3252 | 0.1708 | 0.0907 | 3.9034 | 0.4814 | |
| SI | 153.8979 | 313.7957 | 317.9993 | 0.1708 | 0.0907 | 3.6643 | 0.5643 | |
| Distribution | Estimates | −Logl | AIC | BIC | K-S | p-Value | ||
|---|---|---|---|---|---|---|---|---|
| SlaLL | = 4.6677 | 793.8678 | 1595.736 | 1607.416 | 0.0791 | 0.3586 | 0.7319 | 0.1156 |
| = 1.4038 | ||||||||
| = 6.4576 | ||||||||
| = 75.4064 | ||||||||
| SL | = 37.8879 | 934.9096 | 1775.0992 | 1881.7301 | 0.7974 | <2.2 × 10−16 | 3.5788 | 6.9228 |
| = 31.1101 | ||||||||
| = 23.7142 | ||||||||
| SML | = 1.87432 | 912.7549 | 2318.0090 | 2436.3252 | 0.7974 | <2.2 × 10−16 | 6.8642 | 7.9642 |
| = 8.7069 | ||||||||
| = 43.9153 | ||||||||
| SI | = 0.1369 | 807.4439 | 1620.888 | 1629.648 | 0.1128 | 0.0612 | 2.7439 | 3.8753 |
| = 1.5058 | ||||||||
| = 266.9019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gillariose, J.; Abdelwahab, M.M.; Joseph, J.; Hasaballah, M.M. A Gauss Hypergeometric-Type Model for Heavy-Tailed Survival Times in Biomedical Research. Symmetry 2025, 17, 1795. https://doi.org/10.3390/sym17111795
Gillariose J, Abdelwahab MM, Joseph J, Hasaballah MM. A Gauss Hypergeometric-Type Model for Heavy-Tailed Survival Times in Biomedical Research. Symmetry. 2025; 17(11):1795. https://doi.org/10.3390/sym17111795
Chicago/Turabian StyleGillariose, Jiju, Mahmoud M. Abdelwahab, Joshin Joseph, and Mustafa M. Hasaballah. 2025. "A Gauss Hypergeometric-Type Model for Heavy-Tailed Survival Times in Biomedical Research" Symmetry 17, no. 11: 1795. https://doi.org/10.3390/sym17111795
APA StyleGillariose, J., Abdelwahab, M. M., Joseph, J., & Hasaballah, M. M. (2025). A Gauss Hypergeometric-Type Model for Heavy-Tailed Survival Times in Biomedical Research. Symmetry, 17(11), 1795. https://doi.org/10.3390/sym17111795









