Stability Control Method Utilizing Grid-Forming Converters for Active Symmetry in the Elastic Balance Region of the Distribution Grid
Abstract
1. Introduction
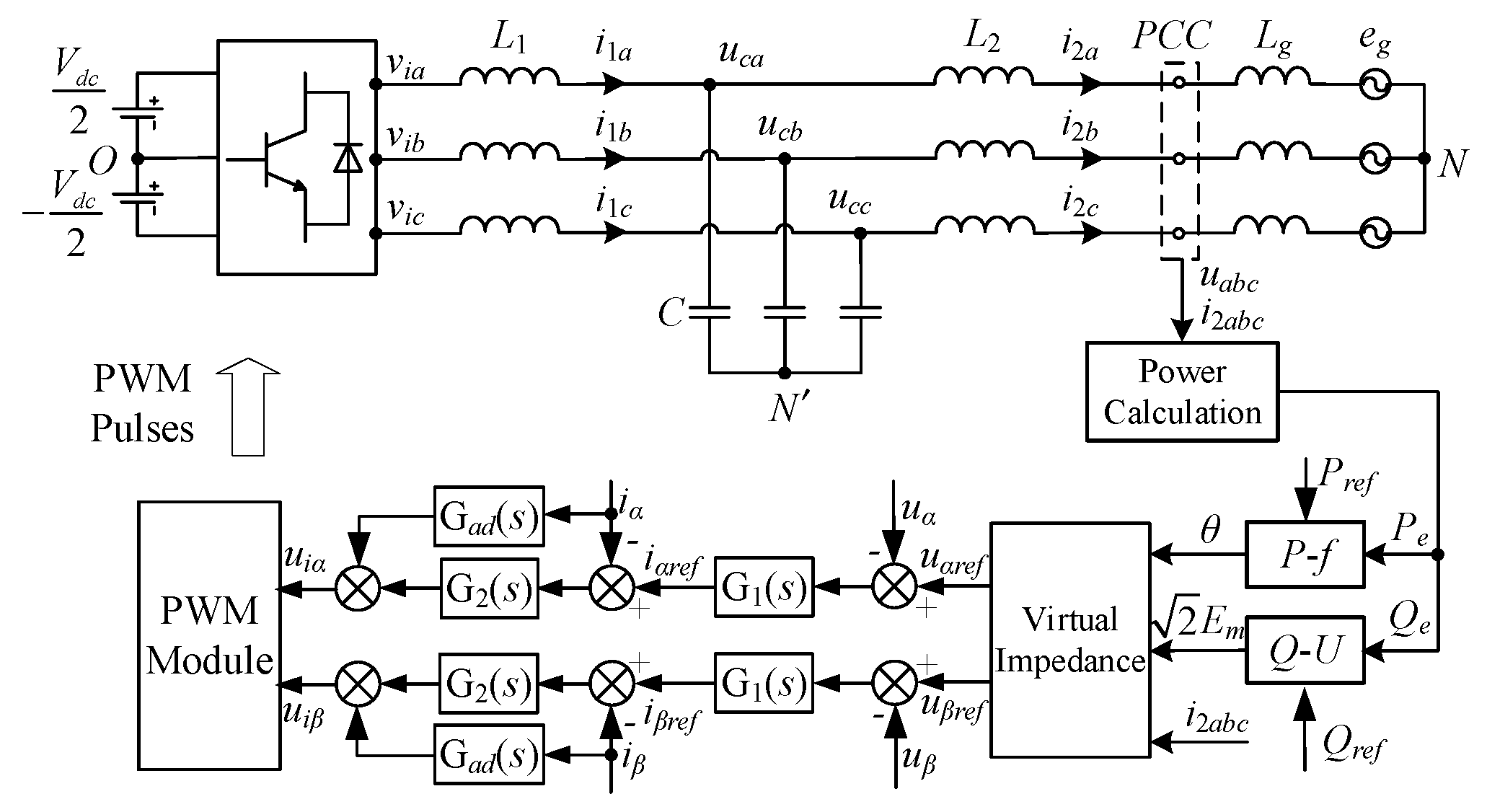
2. Topology and Control Strategies of VSG
2.1. P-f Control
2.2. Q-U Control
2.3. Virtual Impedance Control
2.4. VSG Voltage Loop Control
2.5. VSG Current Loop Control
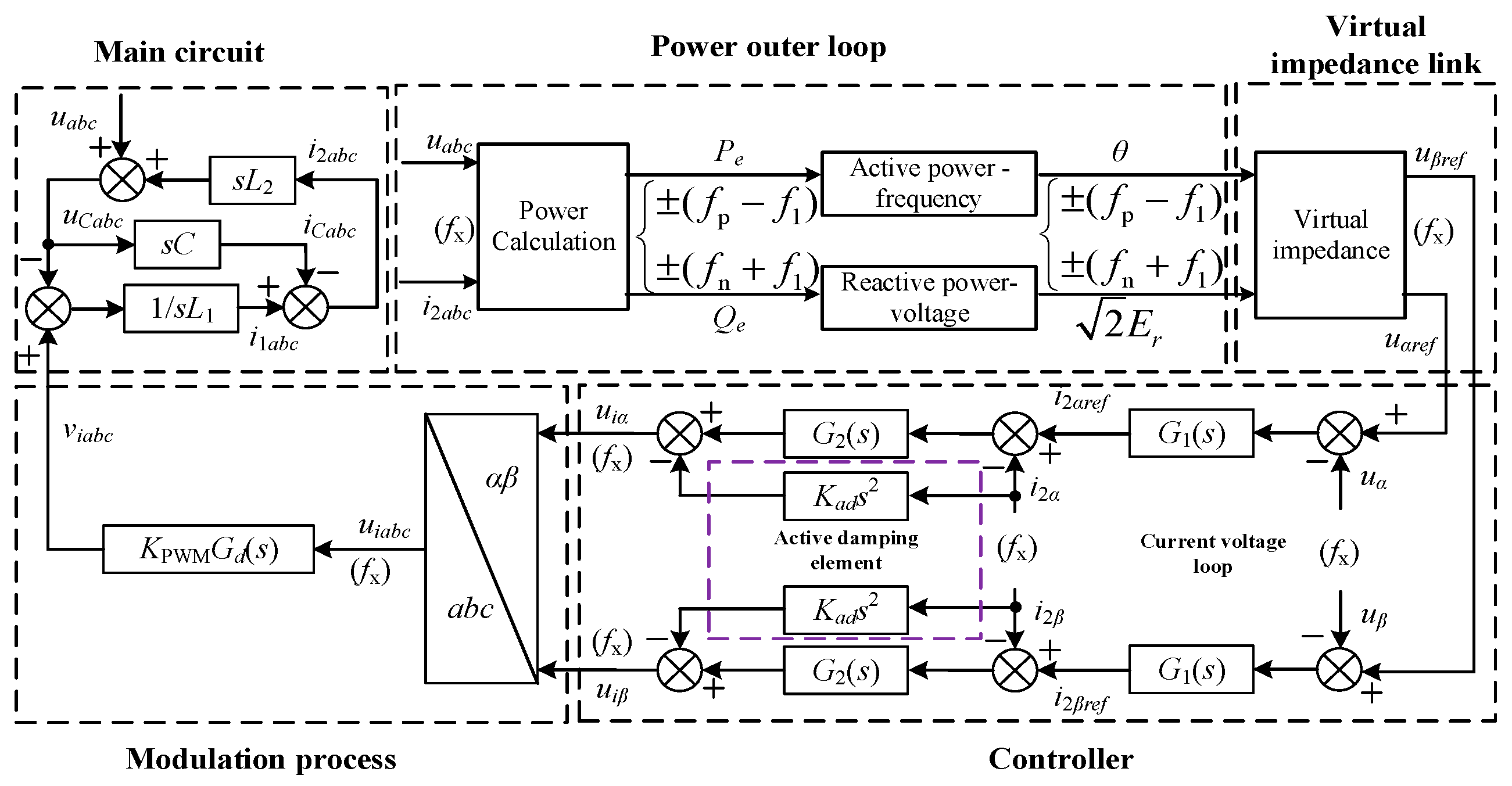
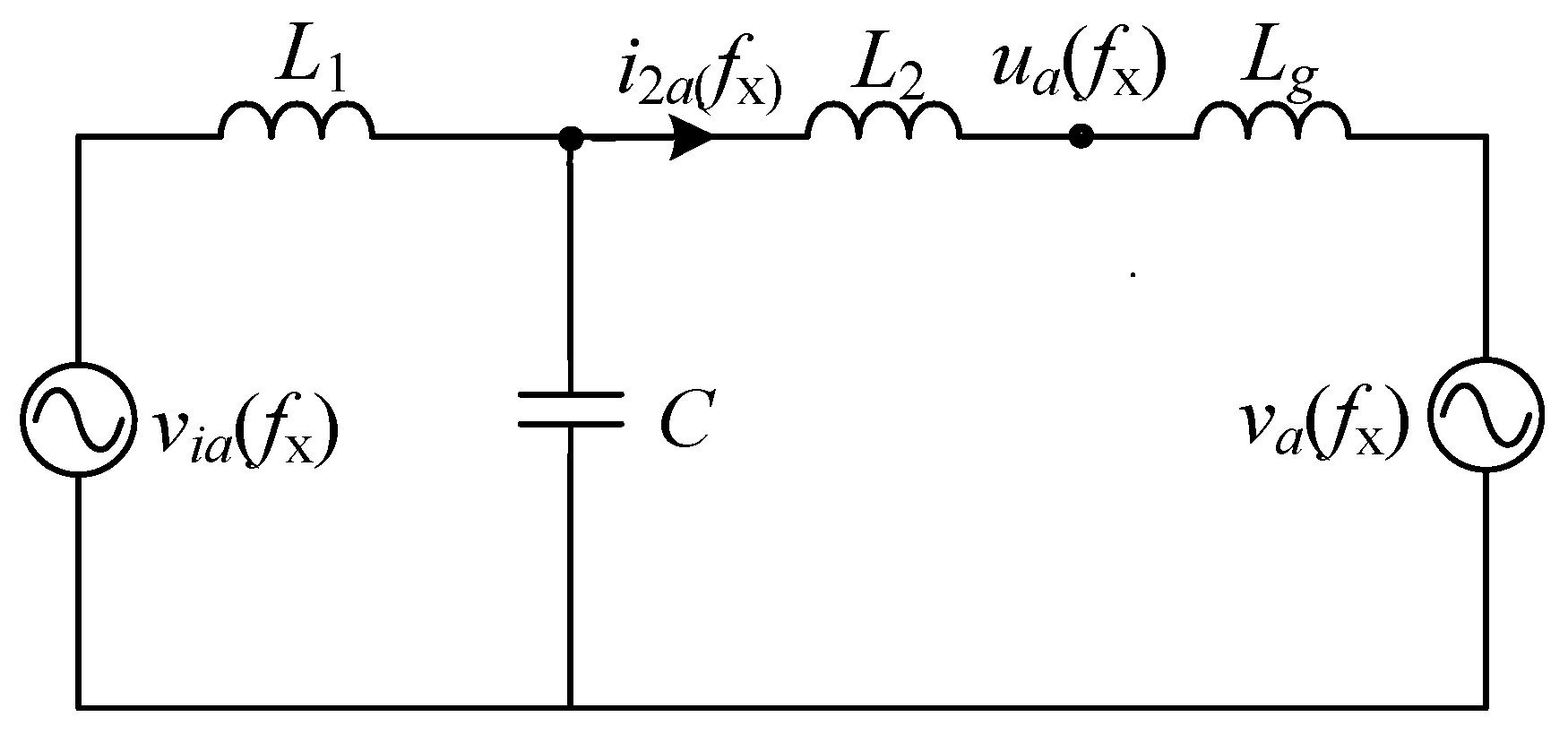
3. Impedance Modeling of Grid-Forming Inverters Based on VSG Under Weak Grid Conditions
3.1. Sequence Impedance Modeling
3.2. Modeling of the Main Circuit for the VSG Grid-Connected Systems
3.3. VSG Power Outer Loop Modeling
3.4. Virtual Impedance Modeling of the VSG
3.5. VSG Inner Loop Modeling
3.6. Modulation Link Modeling
4. Stability Analysis
5. Simulation Analysis
5.1. Verification of the Dynamic Performance of the VSG
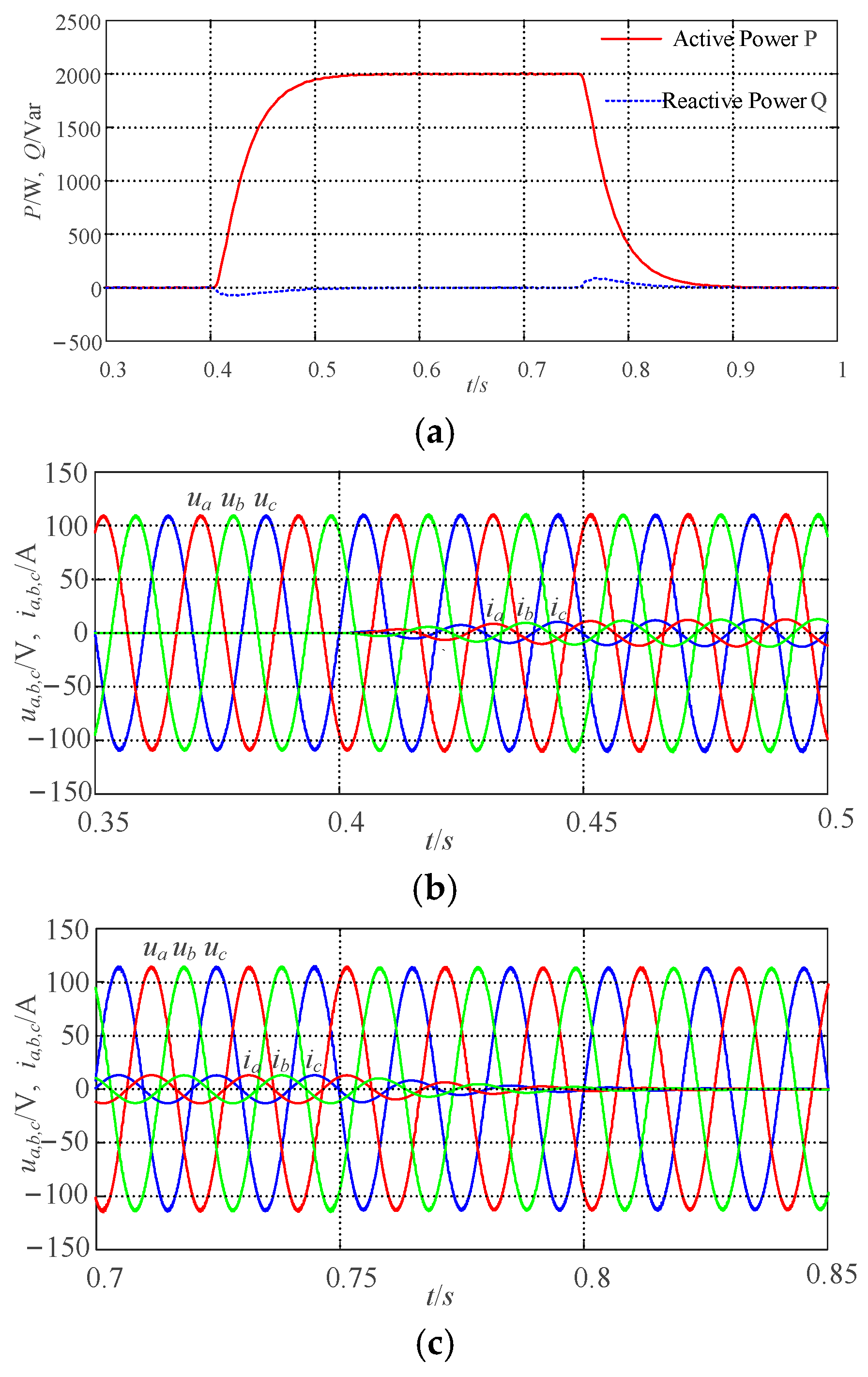
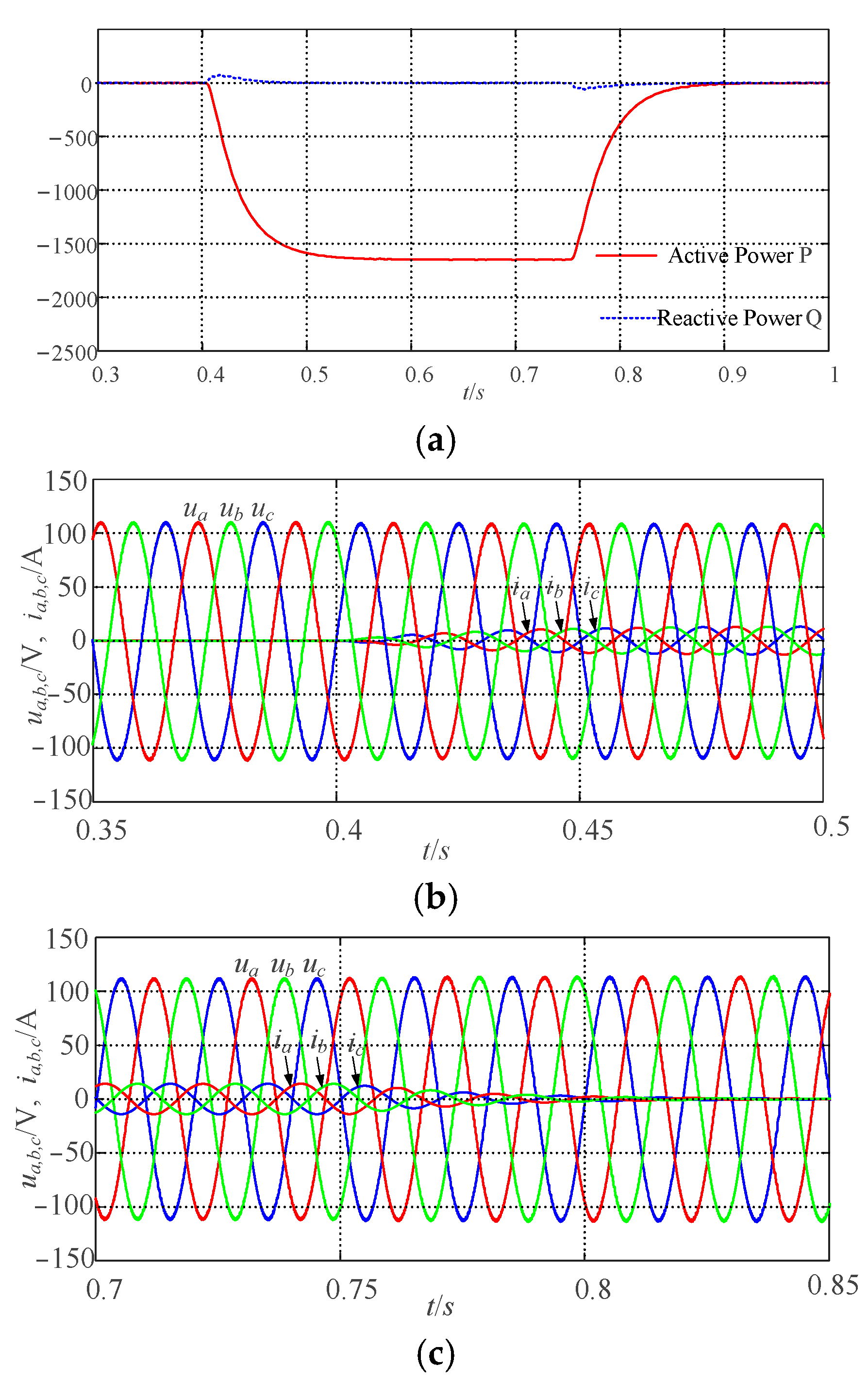
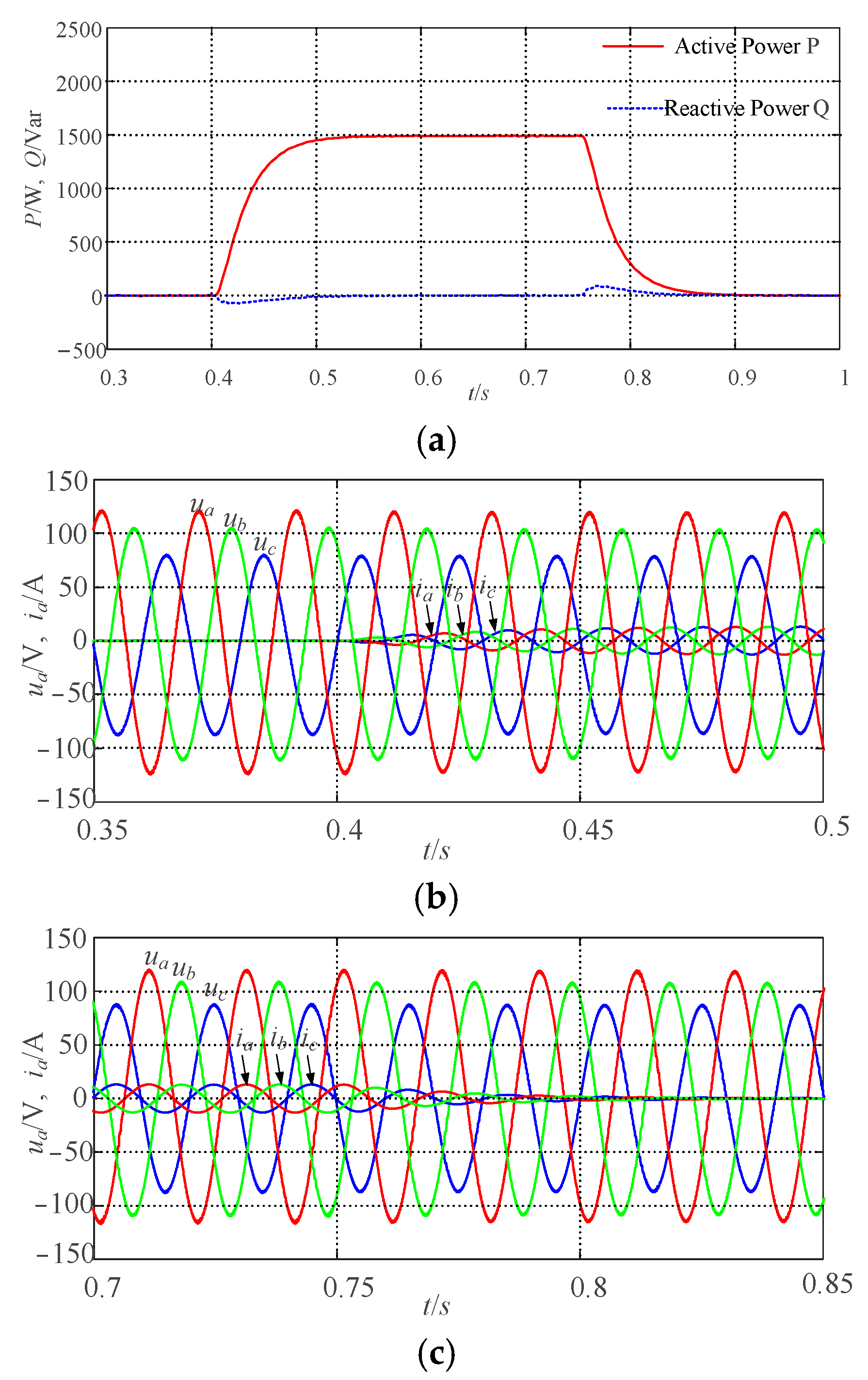
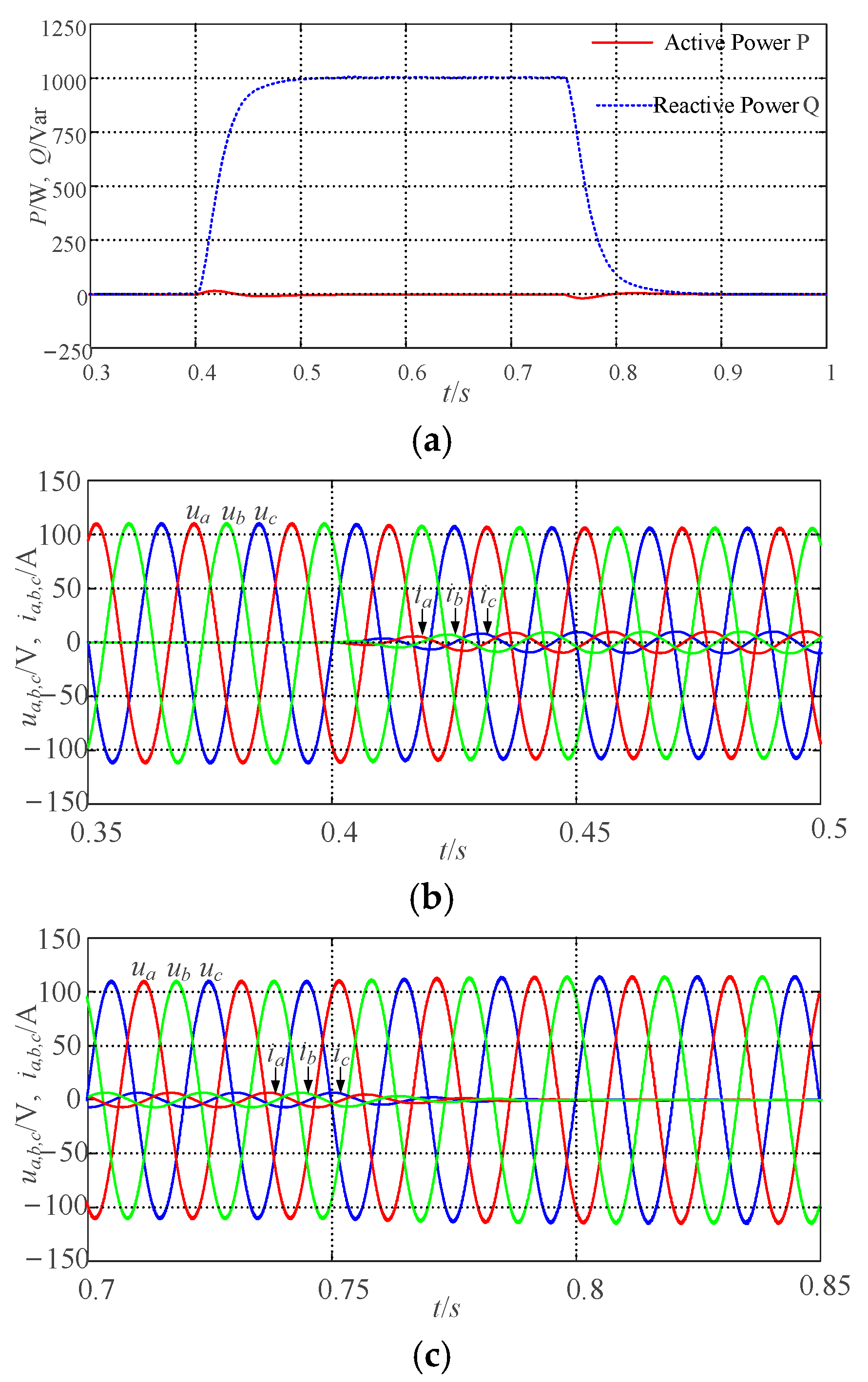
5.1.1. Participate in the Grid Frequency Modulation Capability Verification
5.1.2. Participate in the Grid Voltage Modulation Capability Verification
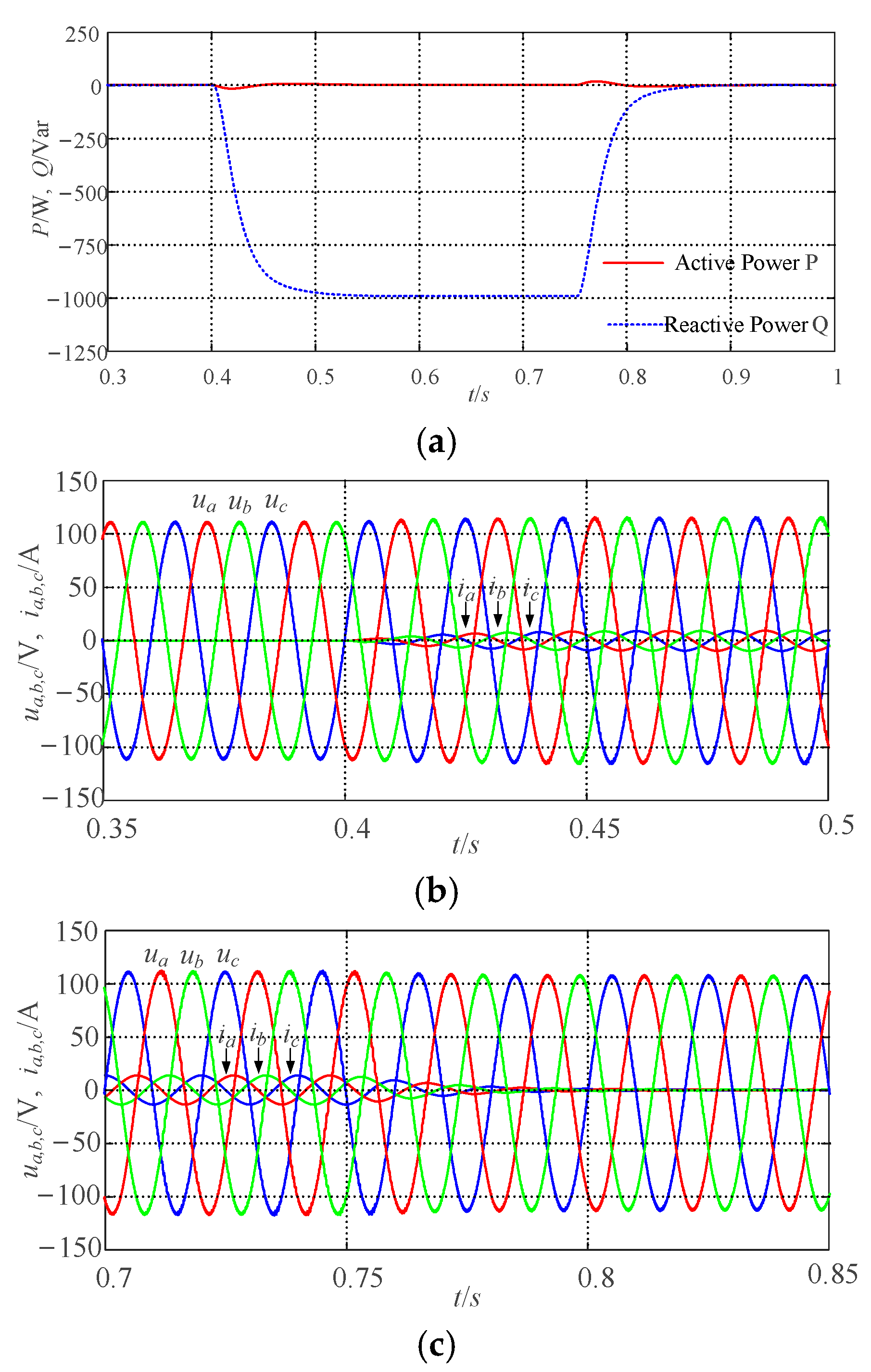
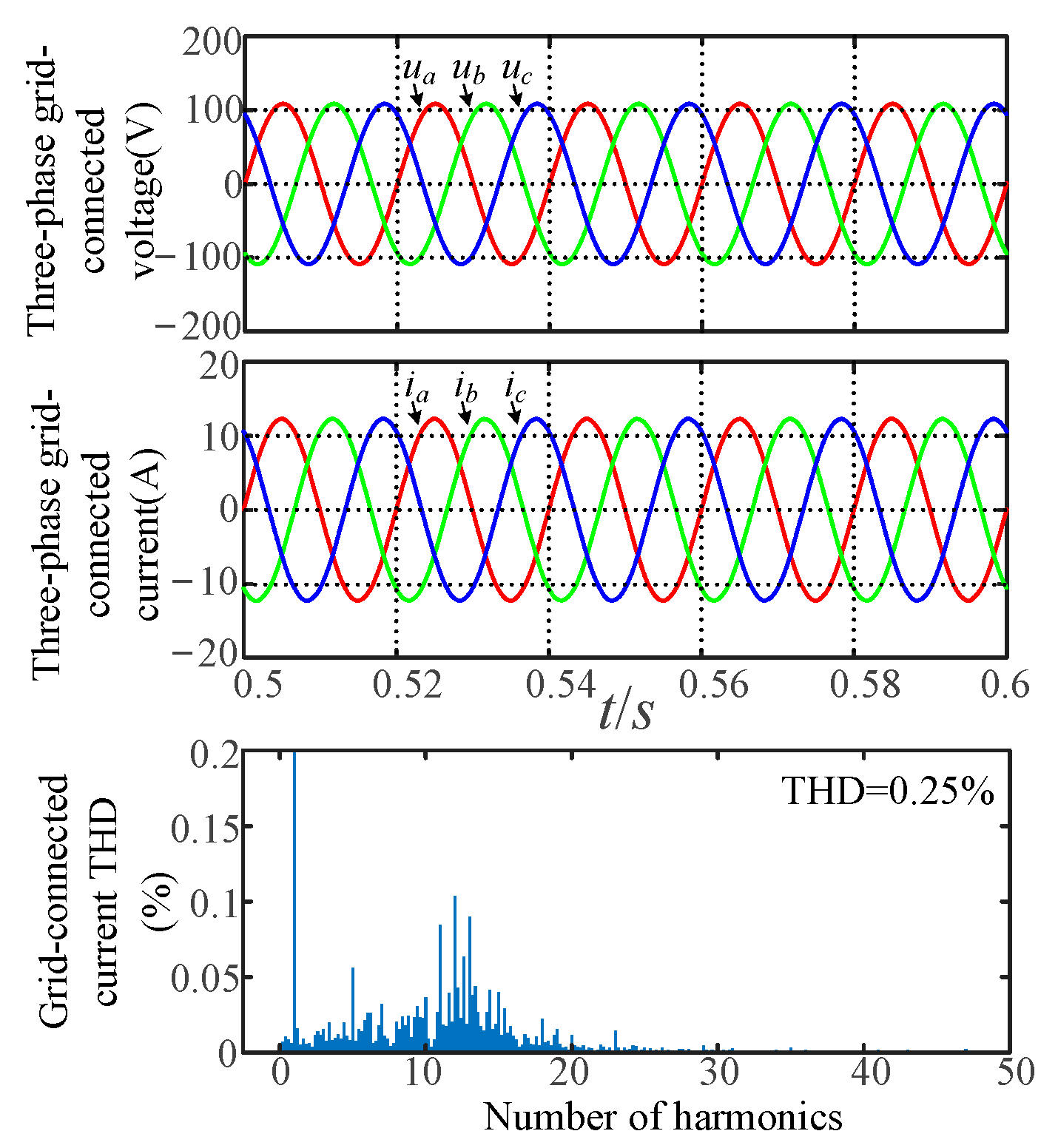
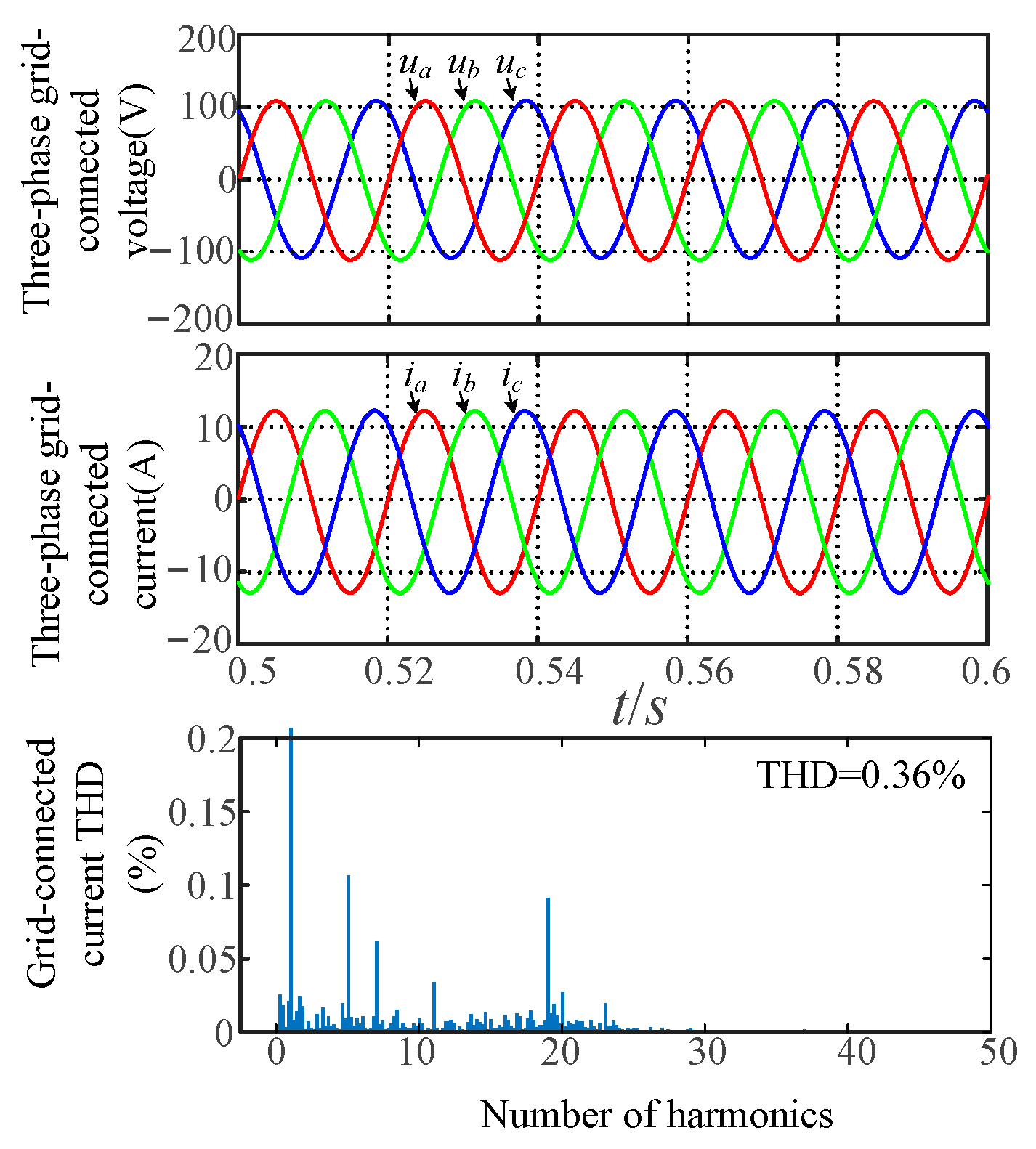
5.2. Verification of Steady-State Performance of the VSG
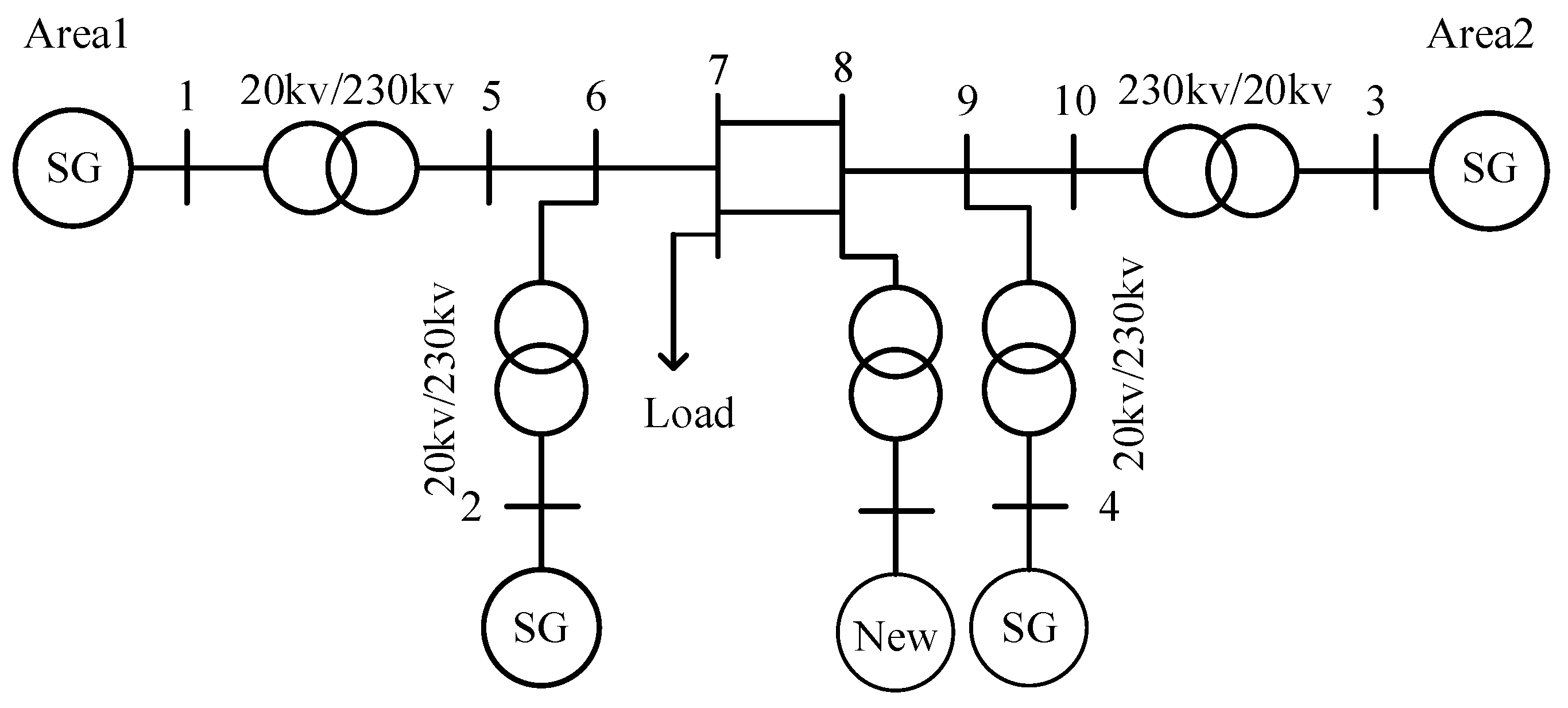
5.3. IEEE Equivalent Power System Model Validation
5.3.1. Verification of System Frequency Regulation Capability
5.3.2. Verification of System Voltage Regulation Capability
5.4. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Song, Y.; Wang, G.; Wang, W. A Comprehensive Review on the Development of Sustainable Energy Strategy and Implementation in China. IEEE Trans. Sustain. Energy 2010, 1, 57–65. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation Systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-Forming Inverters: A Critical Asset for the Power Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 925–935. [Google Scholar] [CrossRef]
- Elmelegi, A.; Mohamed, E.A.; Aly, M.; Ahmed, E.M.; Al-Attar, M.; Elbaksawi, O. Optimized Tilt Fractional Order Cooperative Controllers for Preserving Frequency Stability in Renewable Energy-Based Power Systems. IEEE Access 2020, 9, 8261–8277. [Google Scholar] [CrossRef]
- Wang, J.; Ma, K. Inertia and Grid Impedance Emulation of Power Grid for Stability Test of Grid-Forming Converter. IEEE Trans. Power Electron. 2023, 38, 2469–2480. [Google Scholar] [CrossRef]
- Du, W.; Chen, Z.; Kevin, P.; Schneider, K.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 8, 963–975. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Liu, T.; Liu, J.; Liu, Z.; Liu, Z. A Study of Virtual Resistor-Based Active Damping Alternatives for LCL Resonance in Grid-Connected Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 247–262. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, W.; Orabi, M.; Koutroulis, E.; Chung, H.S.-H.; Blaabjerg, F. A Passive Damping Design Method of Three-phase Asymmetric-LCL Power filter for Grid-Tied Voltage Source Inverter. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 94–98. [Google Scholar]
- Sharma, H.R.; Suryawanshi, H.M.; Chaturvedi, P.; Govind, D. Implementation of Passive Damping Technique in LCL Filter for Three-Phase Grid Connected Inverter. In Proceedings of the 2022 IEEE 2nd International Conference on Sustainable Energy and Future Electric Transportation (SeFeT), Hyderabad, India, 4–6 August 2022; pp. 1–6. [Google Scholar]
- Fonsêca, T.Q.; Ribeiro, R.L.A.; Rocha, T.d.O.A.; Costa, F.B.; Guerrero, J.M. Voltage Grid Supporting by Using Variable Structure Adaptive Virtual Impedance for LCL-Voltage Source Converter DG Converters. IEEE Trans. Ind. Electron. 2020, 67, 9326–9336. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef]
- Yao, W.; Yang, Y.; Zhang, X.; Blaabjerg, F.; Loh, P.C. Design and analysis of robust active damping for LCL filters using digital notch filters. IEEE Trans. Power Electron. 2016, 32, 2360–2375. [Google Scholar] [CrossRef]
- Peña-Alzola, R.; Liserre, M.; Blaabjerg, F.; Ordonez, M.; Kerekes, T. A Self-commissioning notch filter for active damping in three phase LCL-filter based grid-tied converter. IEEE Trans. Power Electron. 2014, 29, 6754–6761. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Yang, P.; Wang, C.; Xu, L.; Guerrero, J.M. Analysis and Design of Improved Weighted Average Current Control Strategy for LCL-Type Grid-Connected Inverters. IEEE Trans. Energy Convers. 2017, 32, 941–952. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y.; Yang, H.; Dai, H. Grid-Connected Current Double Loop Feedback Suppression Strategy of Parallel Inverter in the Weak Grid. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Xi’an, China, 10–13 November 2023; pp. 2023–2028. [Google Scholar]
- Xu, J.; Xie, S.; Tang, T. Active Damping-Based Control for Grid-Connected LCL-Filtered Inverter with Injected Grid Current Feedback Only. IEEE Trans. Ind. Electron. 2014, 61, 4746–4758. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Y.; Zhou, L.; Luo, A.; Zhou, X.; He, Z.; Yang, L.; Xie, Z.; Liu, J.; Zhang, M. Sequence Impedance Modeling and Stability Comparative Analysis of Voltage-Controlled VSGs and Current-Controlled VSGs. IEEE Trans. Ind. Electron. 2018, 66, 6460–6472. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, H.; Song, Q.; Sun, K. Control strategy for parallel-operated virtual synchronous generators. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC 2016–ECCE Asia), Hefei, China, 22–26 May 2016. [Google Scholar]
- Liu, J.; Miura, Y.; Bevran, H.; Ise, T. Enhanced virtual synchronous generator control for parallel inverters in microgrids. IEEE Trans. Smart Grid 2017, 8, 2268–2277. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, D.; Yin, S.; Lei, Y.; He, T. Improved Adaptive Inertia and Damping Coefficient Control Strategy of VSG Based on Optimal Damping Ratio. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 102–107. [Google Scholar]
- Ibrahim, N.F.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. Comparative Analysis of Three-Phase PV Grid Connected Inverter Current Control Schemes in Unbalanced Grid Conditions. IEEE Access 2023, 11, 42204–42221. [Google Scholar] [CrossRef]
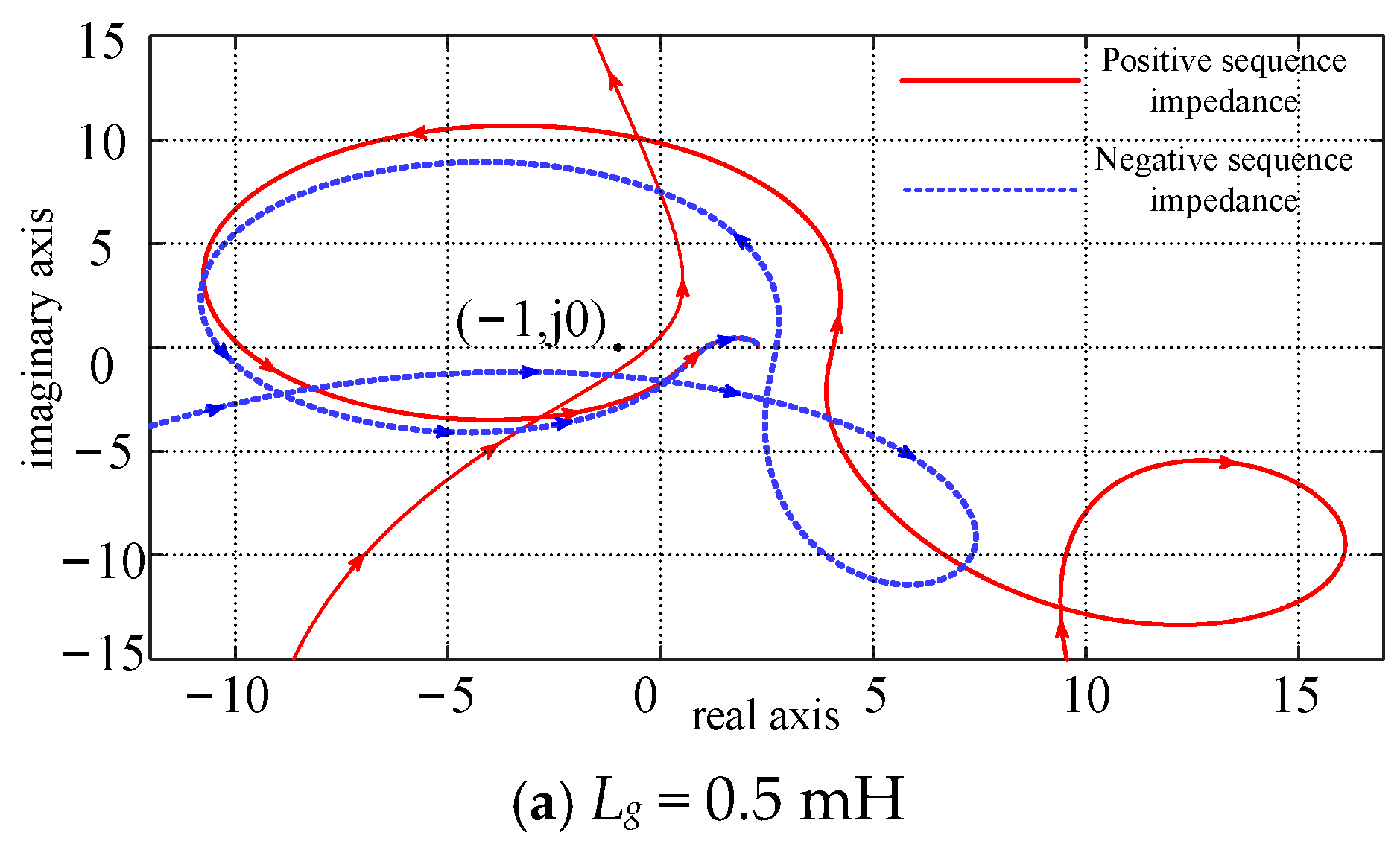






| Lg/mH | N + (Hvp(s)) | N − (Hvn(s)) | 2[(N+) − (N−)] | Stability |
|---|---|---|---|---|
| 0.5 | 1 | 1 | 2 | stable |
| 1.5 | 1 | 1 | 2 | stable |
| 3 | 1 | 1 | 2 | stable |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| L1 | 2 mH | L2 | 1 mH |
| C | 50 μF | Lg | 0~3 mH |
| Vdc | 300 V | Ug | 76.7 V |
| Pref | 2000 W | Qref | 0 Var |
| J | 0.5 | Dp | 5 |
| Kq | 5.8 | Dq | 368 |
| Rv | 0.1Ω | Lv | 3 mH |
| Kp1 | 0.01 | Kr1 | 2.1 |
| Kp2 | 0.06 | Kad | 6*10−9 |
| fs | 10 kHz | fsw | 10 kHz |
| Lg/mH | THD |
|---|---|
| 0 | 0.25% |
| 1.5 | 0.36% |
| 3 | 0.37% |
| Parameters | Numeric Value |
|---|---|
| Zone 1 generator capacity (MW) | 198 |
| Zone 2 generator capacity (MW) | 198 |
| Rated power output of the PV array (KW) | 500 |
| The number of photovoltaic power station units | 150 |
| Voltage side capacitor DC voltage (V) | 1500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Jia, B.; Song, Z.; Li, H.; Zhou, S.; Li, Z. Stability Control Method Utilizing Grid-Forming Converters for Active Symmetry in the Elastic Balance Region of the Distribution Grid. Symmetry 2025, 17, 263. https://doi.org/10.3390/sym17020263
Lv Z, Jia B, Song Z, Li H, Zhou S, Li Z. Stability Control Method Utilizing Grid-Forming Converters for Active Symmetry in the Elastic Balance Region of the Distribution Grid. Symmetry. 2025; 17(2):263. https://doi.org/10.3390/sym17020263
Chicago/Turabian StyleLv, Zhipeng, Bingjian Jia, Zhenhao Song, Hao Li, Shan Zhou, and Zhizhou Li. 2025. "Stability Control Method Utilizing Grid-Forming Converters for Active Symmetry in the Elastic Balance Region of the Distribution Grid" Symmetry 17, no. 2: 263. https://doi.org/10.3390/sym17020263
APA StyleLv, Z., Jia, B., Song, Z., Li, H., Zhou, S., & Li, Z. (2025). Stability Control Method Utilizing Grid-Forming Converters for Active Symmetry in the Elastic Balance Region of the Distribution Grid. Symmetry, 17(2), 263. https://doi.org/10.3390/sym17020263





