Effect of Laying Angle on the Stress Distribution and Stiffness Degradation of Symmetrically Cracked Laminates
Abstract
:1. Introduction
2. Mathematical Modeling and Theoretical Formulation
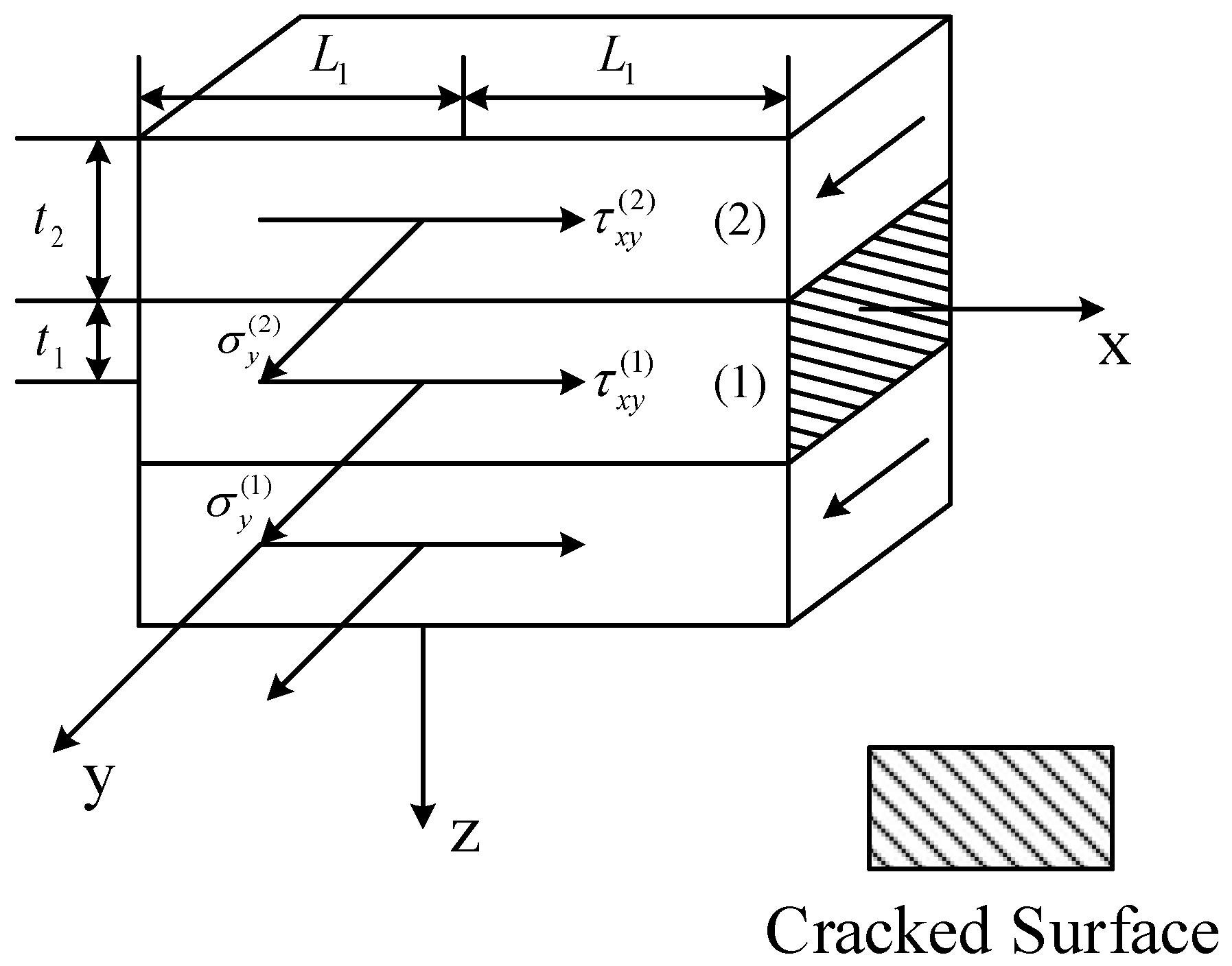
2.1. Analysis Unit Model
2.2. Boundary Conditions and Representations of the Stress Components
2.3. Governing and Supplementary Equations and Their Solutions
2.4. Effective Mechanical Properties
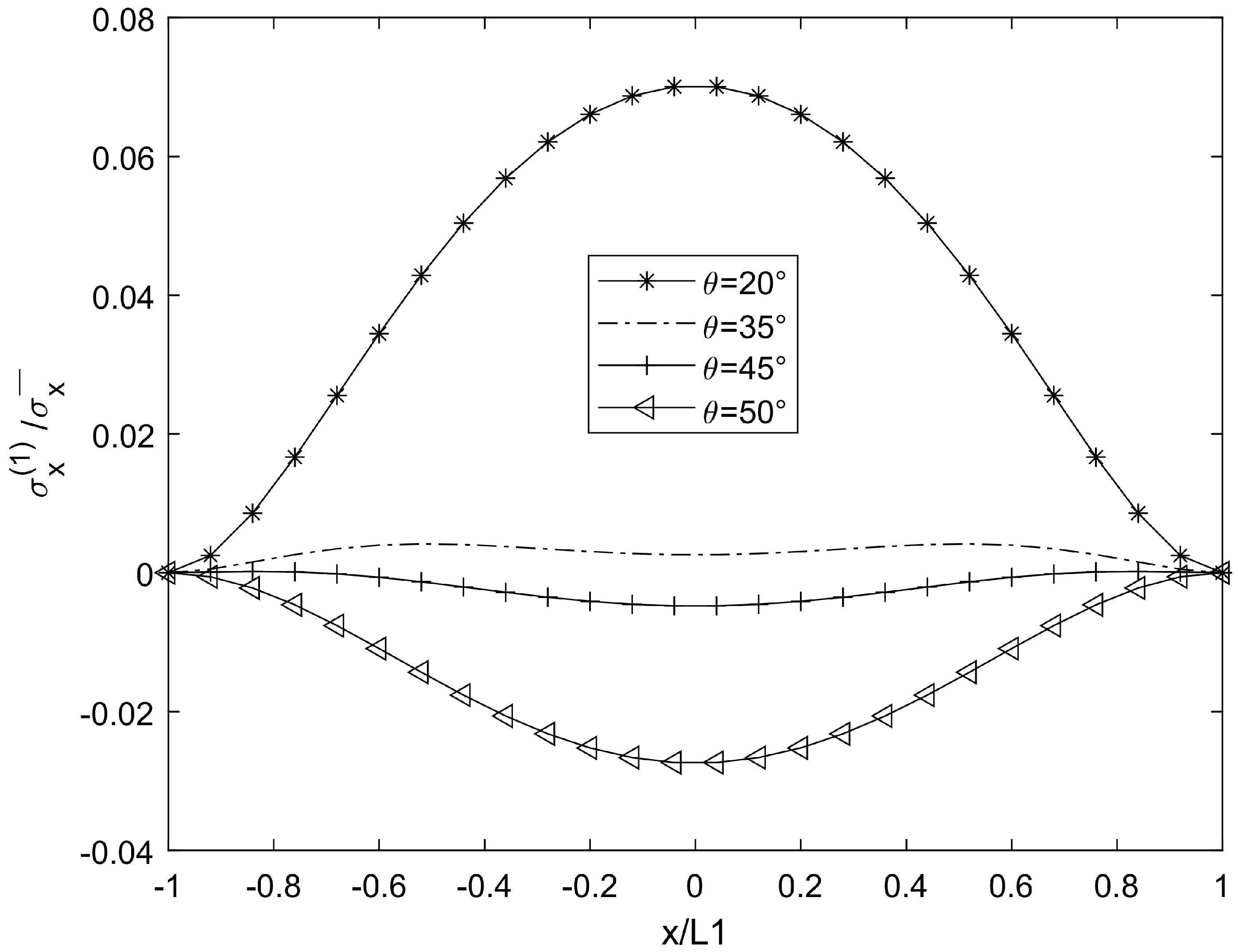
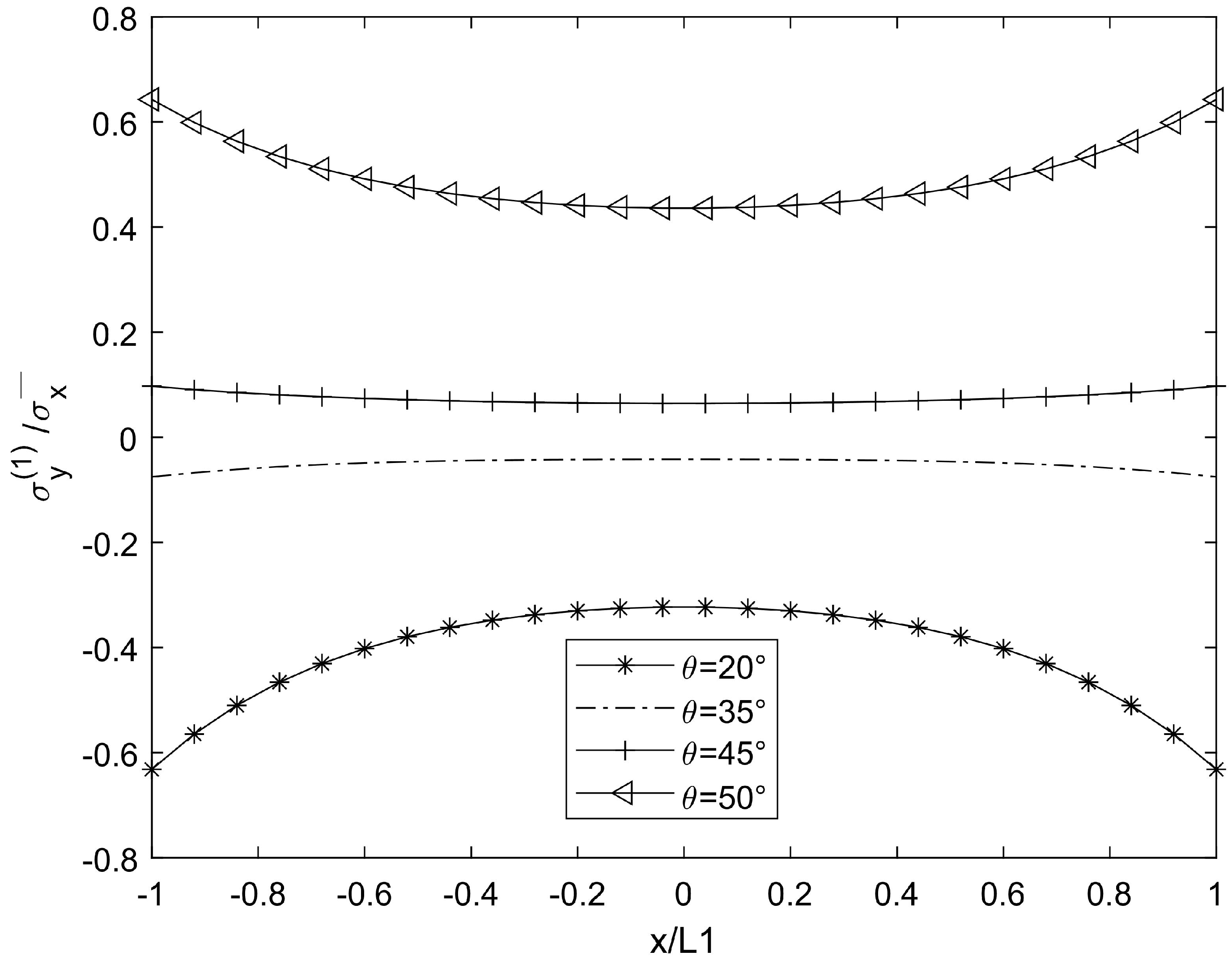
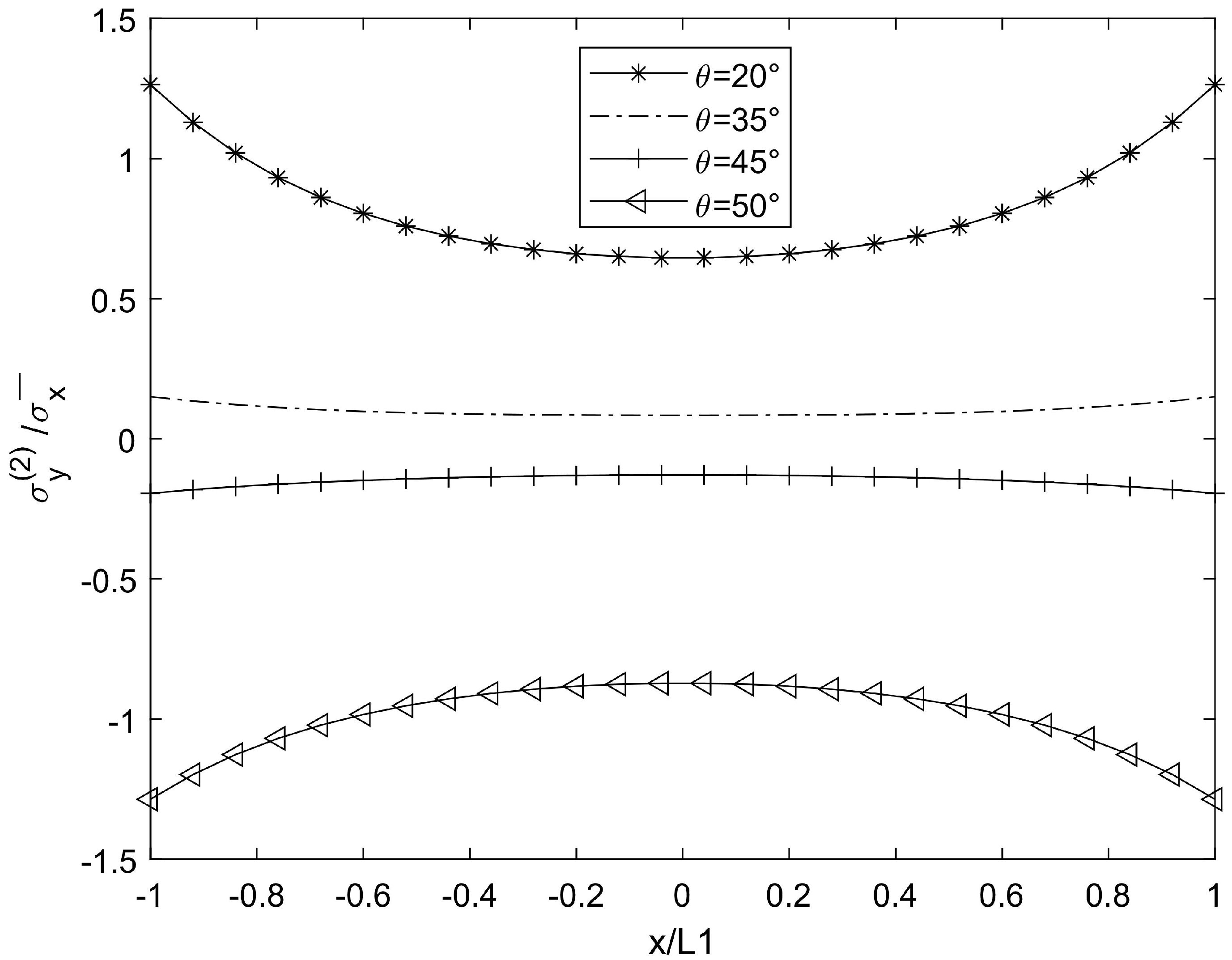
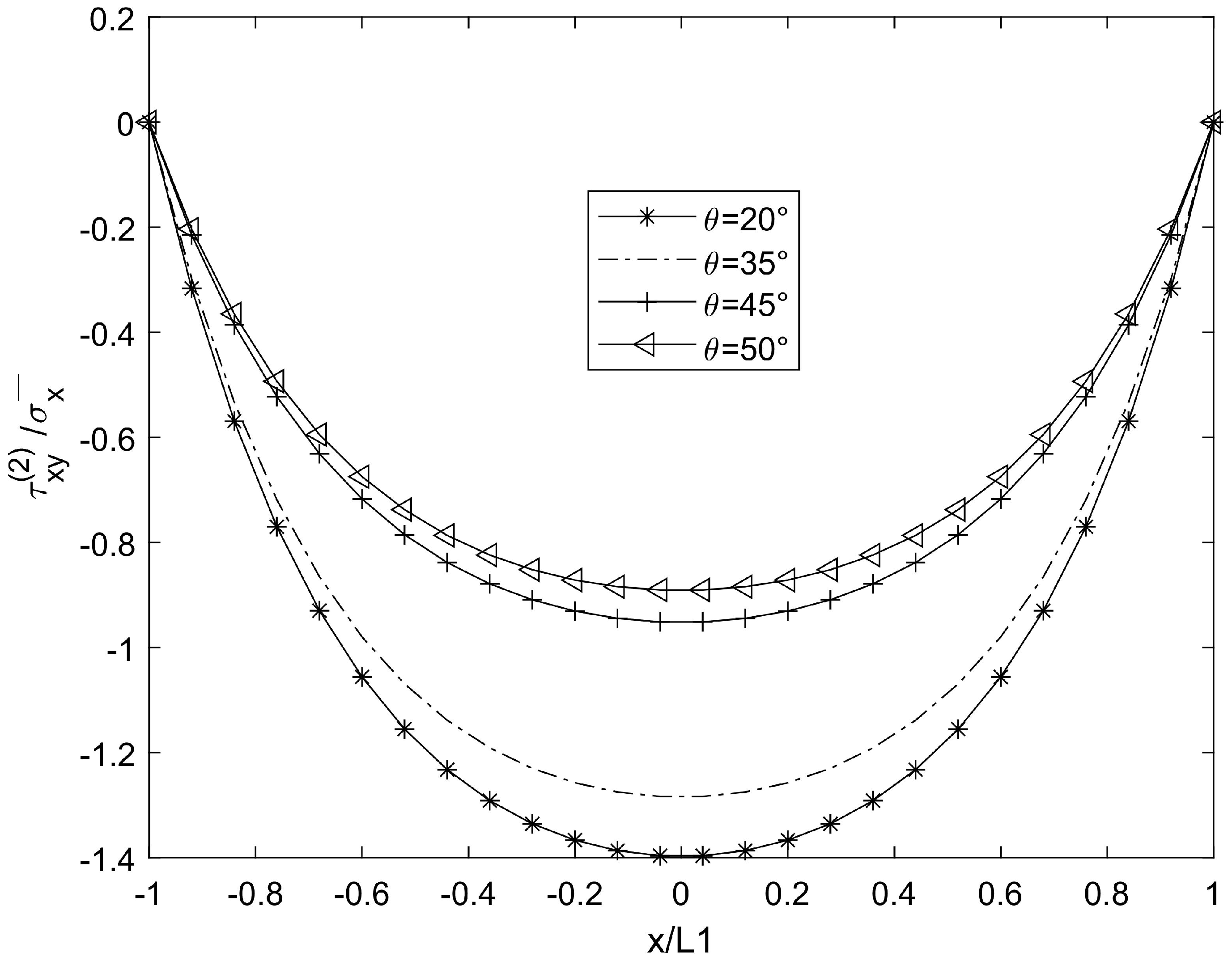
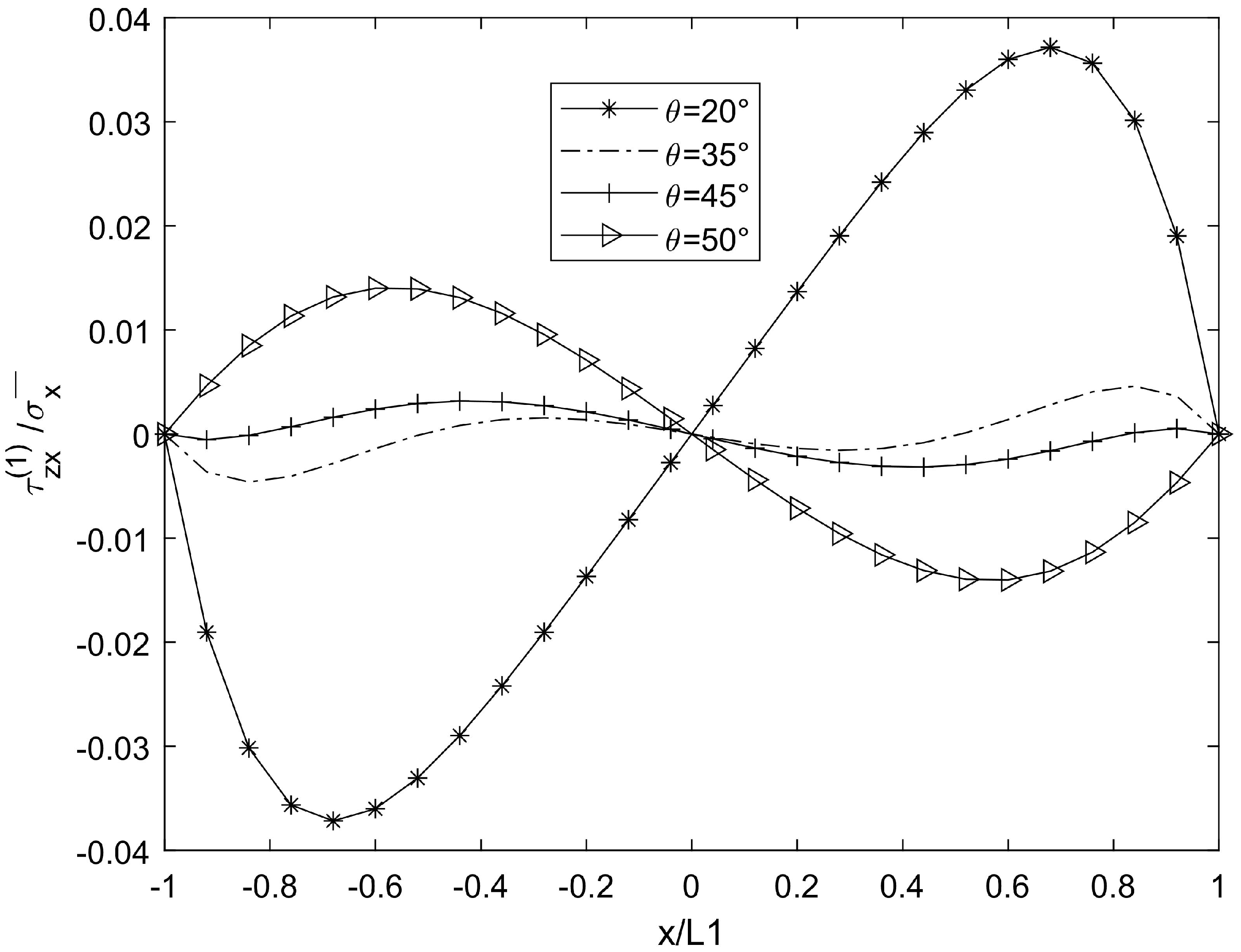
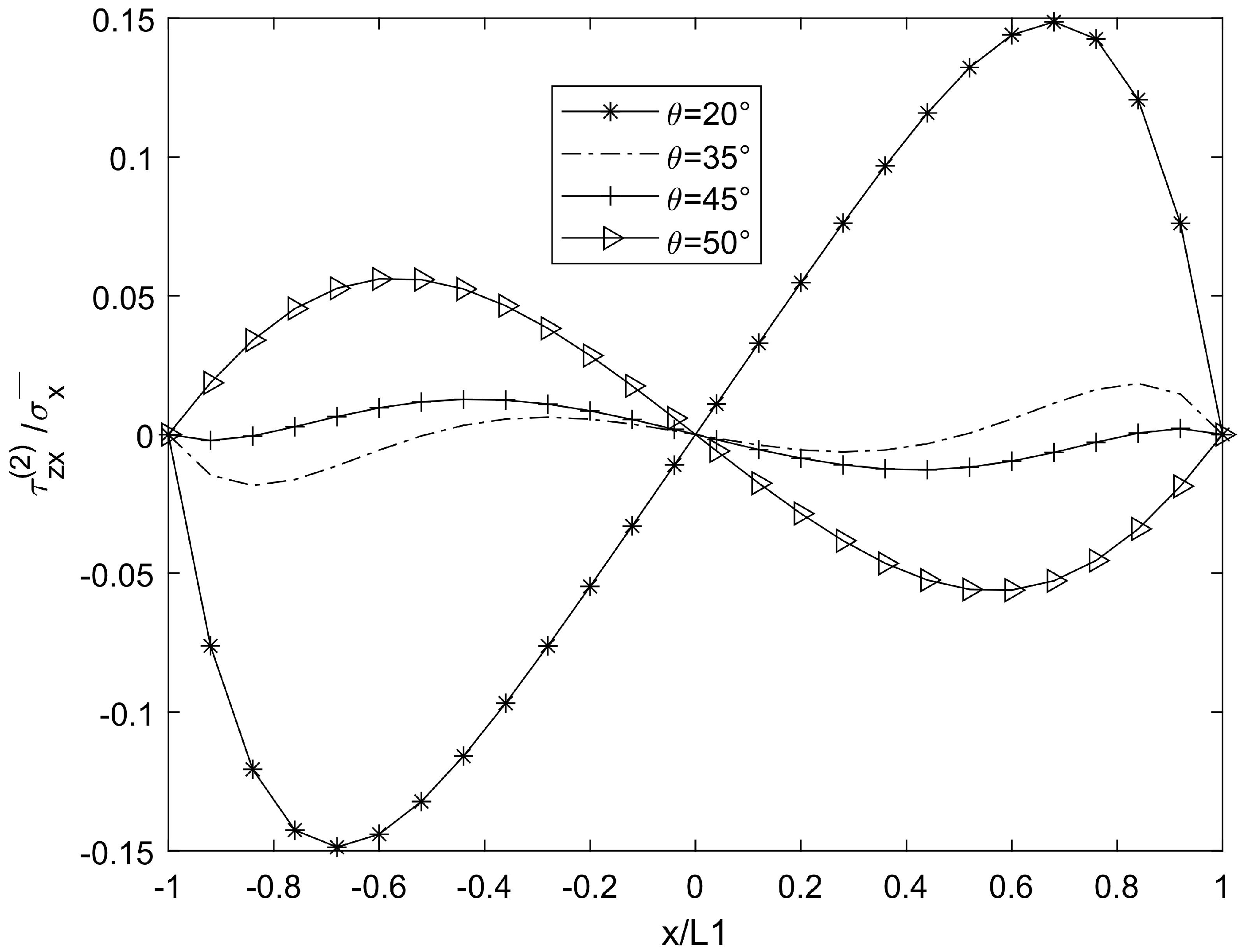
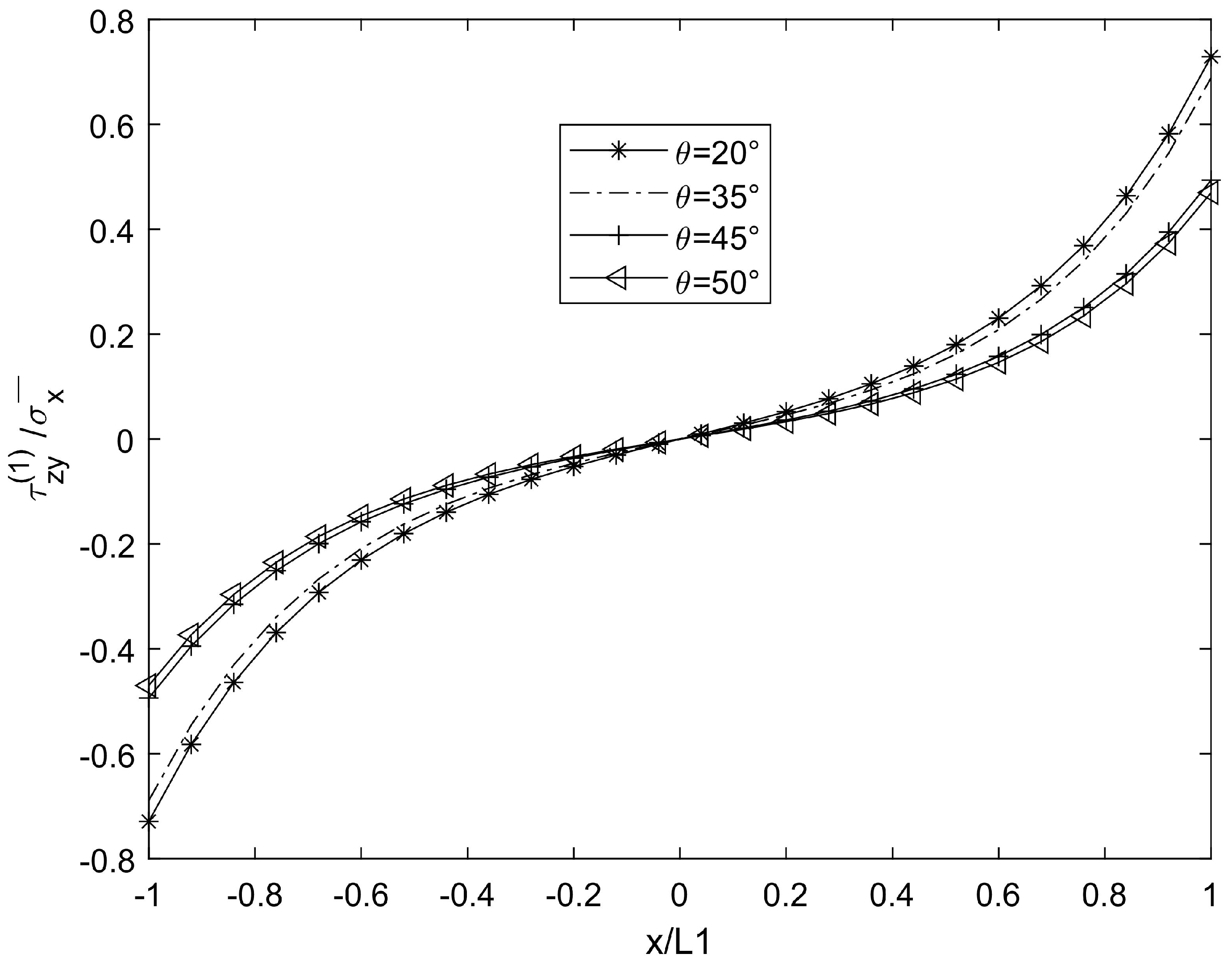
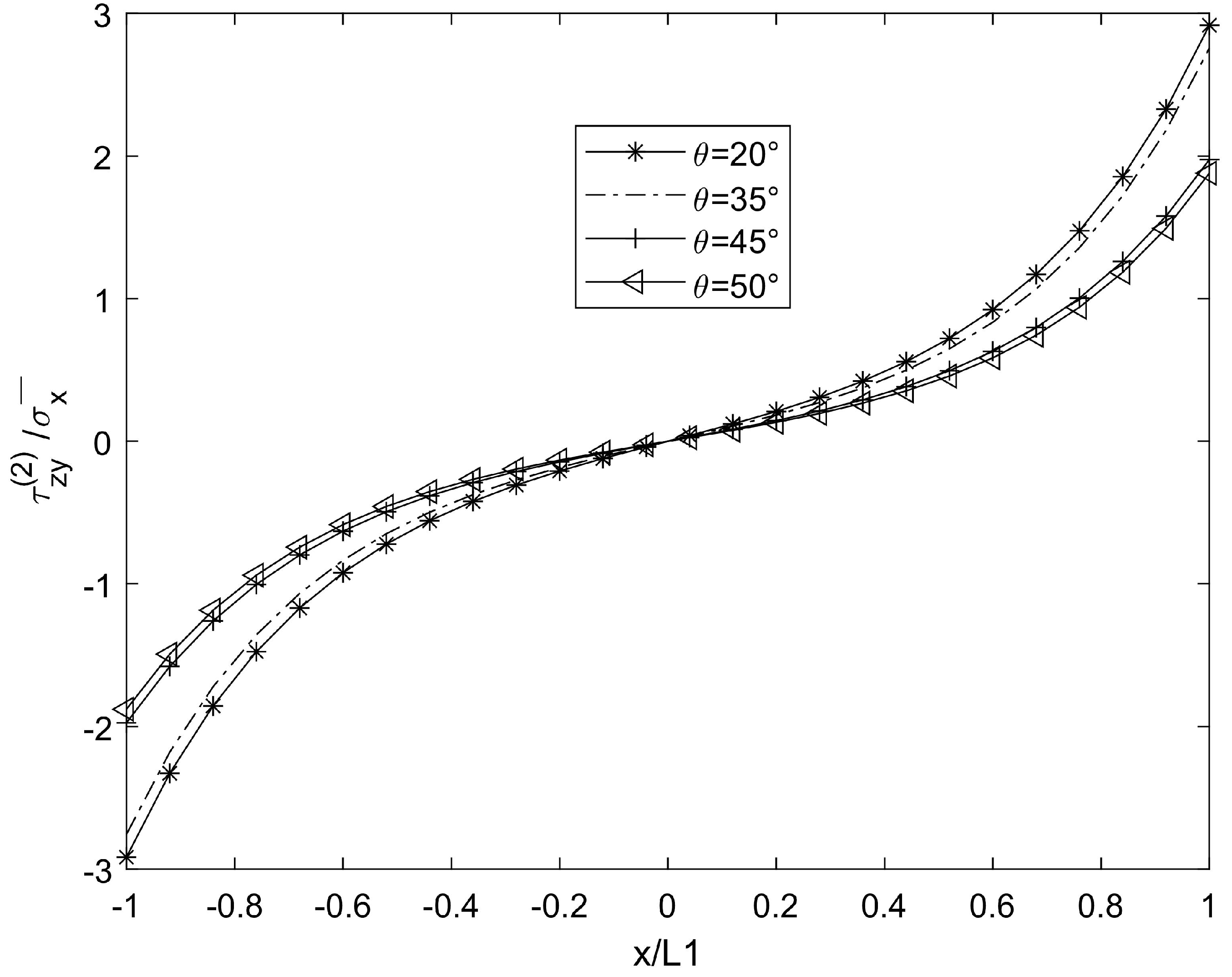
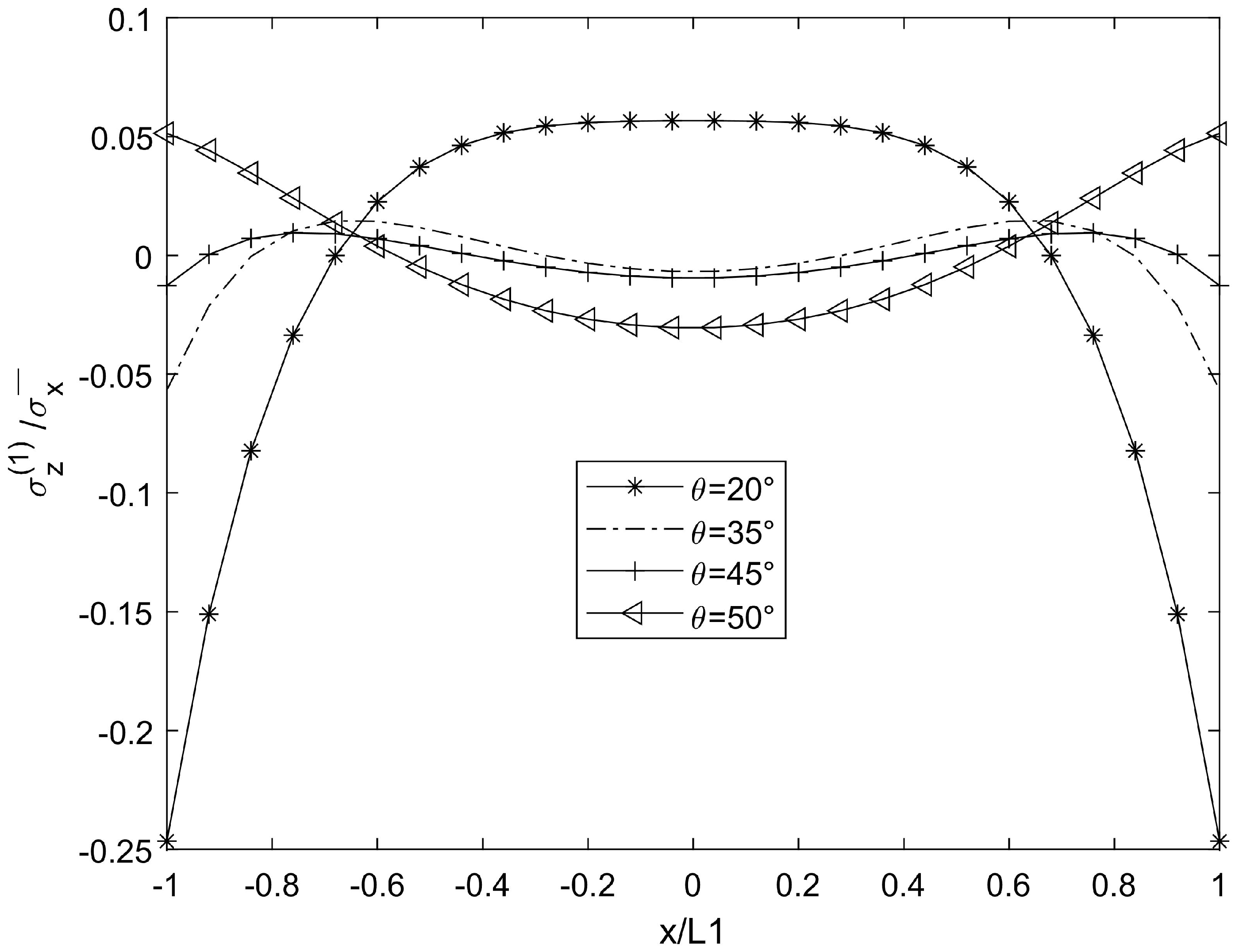
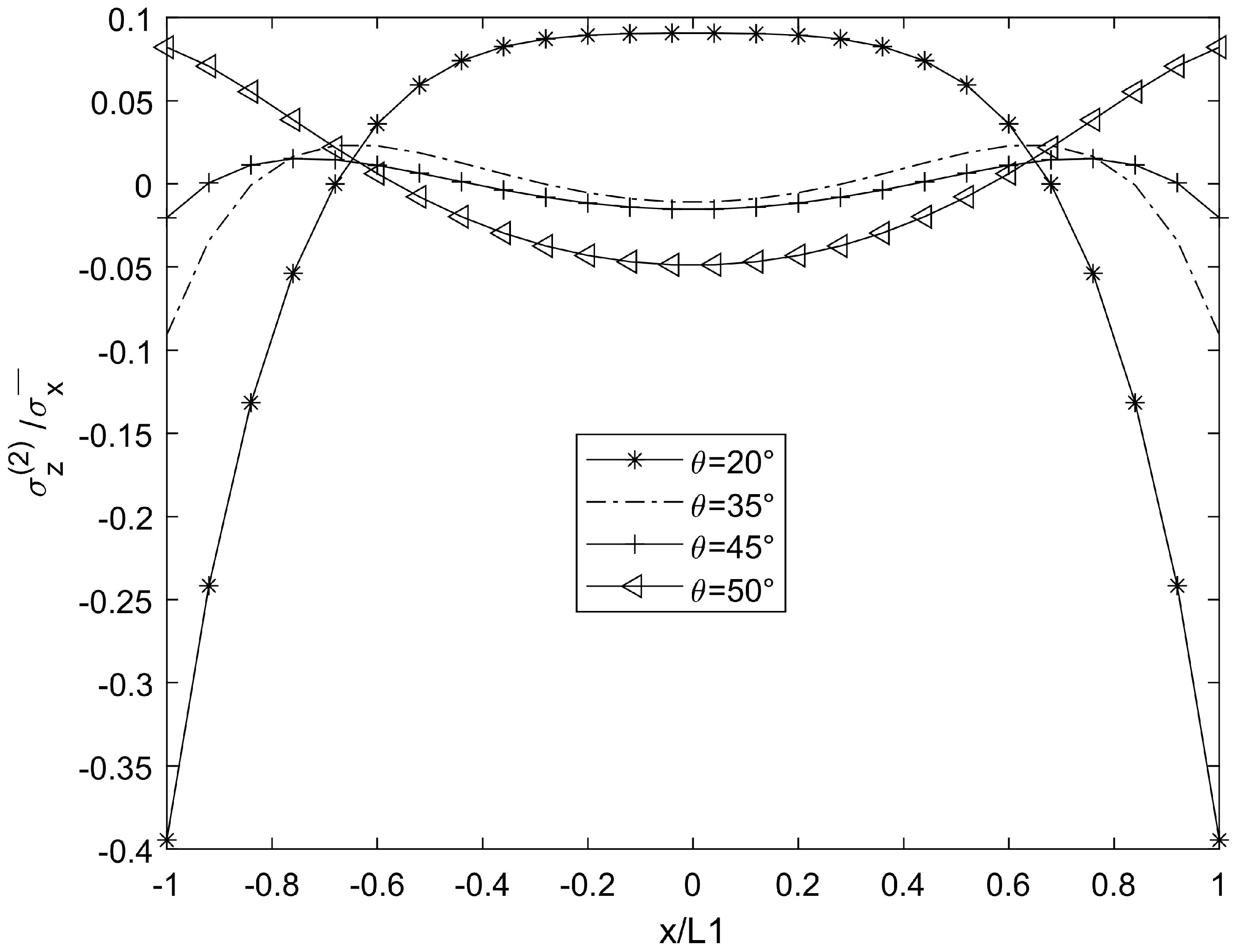
3. Numerical Results and Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shen, G.; Hu, G. Mechanics of Composite Materials; Tsinghua University Press: Beijing, China, 2013; Volume 9, pp. 30–44. [Google Scholar]
- De Luca, A.; Greco, A.; Rezazadeh, N.; Perfetto, D.; Aversano, A. Guided Waves Propagation in Additively Manufactured GF30-PA6 Panel. Macromol. Symp. 2024, 413, 2400042. [Google Scholar]
- Fikry, M.J.M.; Ogihara, S.; Vinogradov, V. The effect of matrix cracking on mechanical properties in FRP laminates. Mech. Adv. Mater. Mod. Process. 2018, 4, 3. [Google Scholar]
- Ramezani, H.; Kazemirad, S.; Shokrieh, M.; Mardanshahi, A. Effects of adding carbon nanofibers on the reduction of matrix cracking in laminated composites: Experimental and analytical approaches. Polym. Test. 2021, 94, 106988. [Google Scholar]
- Ghadami, M. An anisotropic nonlinear multiscale damage model for mechanical behavior of a composite laminate with matrix cracks. Meccanica 2023, 58, 1809–1822. [Google Scholar]
- Chaupal, P.; Rohit, S.; Rajendran, P. Matrix cracking and delamination detection in GFRP laminates using pre-trained CNN models. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 136. [Google Scholar]
- Fakoor, M.; Rafiee, R.; Sheikhansari, M. The influence of fiber-crack angle on the crack tip parameters in orthotropic materials. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 418–431. [Google Scholar]
- Farrokhabadi, A.; Bahrami, M.; Babaei, R. Predicting the matrix cracking formation in symmetric composite laminates subjected to bending loads. Compos. Struct. 2019, 223, 110945. [Google Scholar]
- Mohammadi, B.; Pakdel, H. Fatigue driven matrix crack propagation in laminated composites. Mater. Des. 2018, 146, 108–115. [Google Scholar]
- Pakdel, H.; Mohammadi, B. Experimental observation and energy based analytical investigation of matrix cracking distribution pattern in angle-ply laminates. Theor. Appl. Fract. Mech. 2017, 92, 146–154. [Google Scholar]
- Qi, W.; Huang, J.; Yao, W.; Shen, H. A damage model for matrix cracks in composite laminates under fatigue loading based on continuum damage mechanics. Int. J. Fatigue 2024, 184, 108315. [Google Scholar]
- Rezaei Jafari, S.; Farrokhabadi, A.; Montesano, J. The effect of staggered matrix crack induced delamination growth on the mechanical properties of cross-ply laminates. Compos. Struct. 2021, 272, 114196. [Google Scholar]
- Socci, C.A.; Kassapoglou, C. Prediction of matrix crack initiation and evolution and their effect on the stiffness of laminates with off-axis plies under in-plane loading. Compos. Sci. Technol. 2020, 200, 108427. [Google Scholar]
- Yuan, M.; Zhao, H.; Liu, S.; Ren, H.; Zhang, B.; Chen, J. Prediction of matrix-cracking-induced stiffness degradation of cross-ply laminates based on data-driven method. Compos. Sci. Technol. 2022, 230, 109716. [Google Scholar]
- Zhang, J.; Fan, J.; Soutis, C. Analysis of multiple matrix cracking in composite laminates. Part 1, In-plane stiffness properties. Composites 1992, 23, 291–298. [Google Scholar]
- Berthelot, J.M. Analysis of the transverse cracking of cross-ply laminates: A generalized approach. J. Compos. Mater. 1997, 31, 1780–1805. [Google Scholar]
- Kashtalyan, M.; Soutis, C. Analysis of composite laminates with intra-and interlaminate damage. Prog. Aerosp. Sci. 2005, 41, 152–173. [Google Scholar]
- Hajikazemi, M.; Sadr, M.; Hosseini-Toudeshky, H.; Mohammadi, B. Thermo-elastic constants of cracked symmetric laminates: A refined variational approach. Int. J. Mech. Sci. 2014, 89, 47–57. [Google Scholar]
- Carraro, P.A.; Maragoni, L.; Quaresimin, M. Stiffness degradation of symmetric laminates with off-axis cracks and delamination: An analytical model. Int. J. Solids Struct. 2021, 213, 50–62. [Google Scholar]
- Wang, F.; Wang, B.; Kong, F.; Ouyang, J.; Ma, T.; Chen, Y. Assessment of degraded stiffness matrices for composite laminates under low-velocity impact based on modified characteristic length model. Compos. Struct. 2021, 272, 114145. [Google Scholar] [CrossRef]
- Herrmann, L.; Mikkelsen, L.P.; Legarth, B.N.; Duddeck, F.; Niordson, C.F. An efficient stiffness degradation model for layered composites with arbitrarily oriented tunneling and delamination cracks. Compos. Sci. Technol. 2022, 230, 109729. [Google Scholar]
- Wu, T.; Wang, G.; Wang, J.; Wang, Y.; Xu, R. Variational principles of laminated plates considering interlayer slip. Compos. Struct. 2022, 281, 114937. [Google Scholar] [CrossRef]
- Vinogradov, V.; Hashin, Z. Variational analysis of cracked angle-ply laminates. Compos. Sci. Technol. 2010, 70, 638–646. [Google Scholar]
- Behera, A.; Thawre, M.M.; Ballal, A. Effect of matrix crack generation on Fatigue life of CFRP multidirectional laminates. Mater. Today Proc. 2018, 9 Pt 3, 20078–20084. [Google Scholar] [CrossRef]
- Li, S.; Hafeez, F. Variation-based cracked laminate analysis revisited and fundamentally extended. Int. J. Solids Struct. 2009, 46, 3505–3515. [Google Scholar] [CrossRef]
- Katerelos, D.G.; Mccartney, L.N.; Galiotis, C. Local strain re-distribution and stiffness degradation in cross-ply polymer composites under tension. Acta Mater. 2005, 53, 3335–3343. [Google Scholar] [CrossRef]
- Mohammad-Zaheri, F.; Mohammadi, B.; Taheri-Behrooz, F. Prediction of stress distribution and stiffness degradation in fiber metal laminates containing matrix cracking. Compos. Struct. 2023, 311, 116820. [Google Scholar]
- Hashin, Z. Analysis of orthogonally cracked laminates under tension. J. Appl. Mech. 1987, 54, 872–879. [Google Scholar]
- Huang, Z.; Yi, S.; Chen, H.; He, X. Parameter analysis of damaged region for laminates with matrix defects. J. Sandw. Struct. Mater. 2021, 23, 580–620. [Google Scholar]
- Huang, Z.Q.; Nie, G.H.; Chan, C.K. An exact solution for stresses in cracked composite laminates and evaluation of the characteristic damage state. Compos. Part B Eng. 2011, 42, 1008–1014. [Google Scholar]
- Carraro, P.A.; Quaresimin, M. A stiffness degradation model for cracked multidirectional laminates with cracks in multiple layers. Int. J. Solids Struct. 2015, 58, 34–51. [Google Scholar]



| /GPa | /GPa | /GPa | /GPa | /mm | |||
|---|---|---|---|---|---|---|---|
| Glass/epoxy1 | 42.0 | 13.0 | 3.60 | 4.50 | 0.25 | 0.38 | 0.330 |
| Glass/epoxy2 | 41.7 | 13.0 | 3.40 | 4.58 | 0.30 | 0.42 | 0.100 |
| L1/t1 | Present | Huang et al. [30] | Huang et al. [29] | Hashin [28] |
|---|---|---|---|---|
| Ex/Ex0 | Ex/Ex0 | Ex/Ex0 | Ex/Ex0 | |
| 50 | 0.987 | 0.978 | 0.980 | 0.980 |
| 20 | 0.958 | 0.948 | 0.952 | 0.951 |
| 10 | 0.914 | 0.902 | 0.908 | 0.907 |
| 5 | 0.837 | 0.821 | 0.832 | 0.830 |
| 3 | 0.754 | 0.735 | 0.748 | 0.745 |
| 2 | 0.669 | 0.653 | 0.665 | 0.661 |
| 1 | 0.556 | 0.551 | 0.553 | 0.548 |
| 0.5 | 0.532 | 0.529 | 0.529 | 0.524 |
| L1/t1 | Present | Huang et al. [30] | Huang et al. [29] | Hashin [28] |
|---|---|---|---|---|
| Ex/Ex0 | Ex/Ex0 | Ex/Ex0 | Ex/Ex0 | |
| 50 | 0.998 | 0.989 | 0.990 | 0.990 |
| 20 | 0.984 | 0.974 | 0.976 | 0.975 |
| 10 | 0.961 | 0.950 | 0.954 | 0.953 |
| 5 | 0.918 | 0.905 | 0.911 | 0.910 |
| 3 | 0.868 | 0.854 | 0.861 | 0.859 |
| 2 | 0.822 | 0.812 | 0.816 | 0.813 |
| 1 | 0.784 | 0.778 | 0.778 | 0.775 |
| 0.5 | 0.779 | 0.773 | 0.773 | 0.770 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Xiong, B.; Wang, X.; Chu, F. Effect of Laying Angle on the Stress Distribution and Stiffness Degradation of Symmetrically Cracked Laminates. Symmetry 2025, 17, 495. https://doi.org/10.3390/sym17040495
Huang Z, Xiong B, Wang X, Chu F. Effect of Laying Angle on the Stress Distribution and Stiffness Degradation of Symmetrically Cracked Laminates. Symmetry. 2025; 17(4):495. https://doi.org/10.3390/sym17040495
Chicago/Turabian StyleHuang, Zhicheng, Biao Xiong, Xingguo Wang, and Fulei Chu. 2025. "Effect of Laying Angle on the Stress Distribution and Stiffness Degradation of Symmetrically Cracked Laminates" Symmetry 17, no. 4: 495. https://doi.org/10.3390/sym17040495
APA StyleHuang, Z., Xiong, B., Wang, X., & Chu, F. (2025). Effect of Laying Angle on the Stress Distribution and Stiffness Degradation of Symmetrically Cracked Laminates. Symmetry, 17(4), 495. https://doi.org/10.3390/sym17040495





