Non-Perturbative Quantum Yang–Mills at Finite Temperature Beyond Lattice: A Dyson–Schwinger Approach
Abstract
1. Introduction
2. Gaussian Solution of Quantum Yang–Mills Theory
3. Partition Function in the IR Regime
4. Thermal Yang–Mills Theory
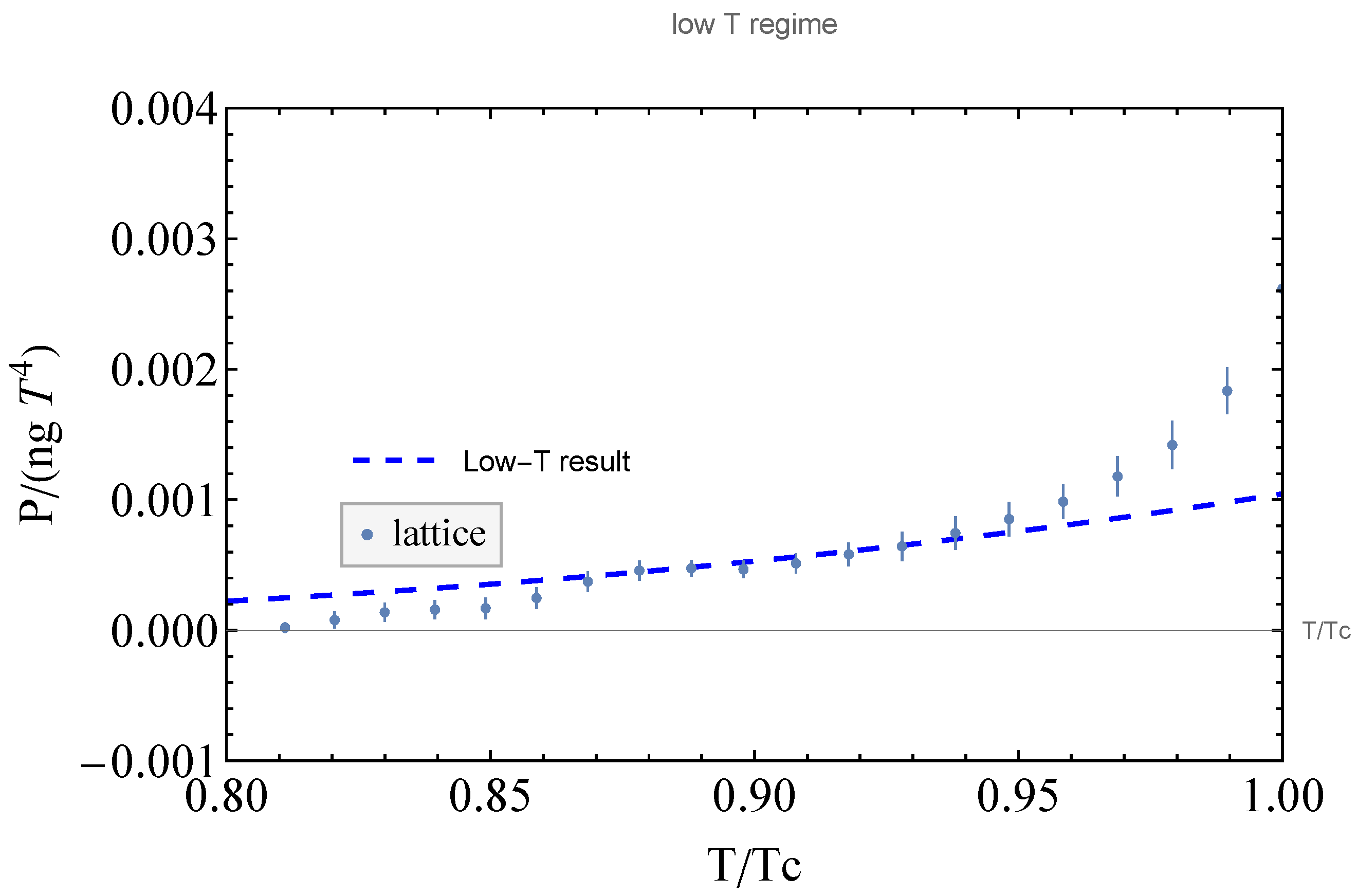
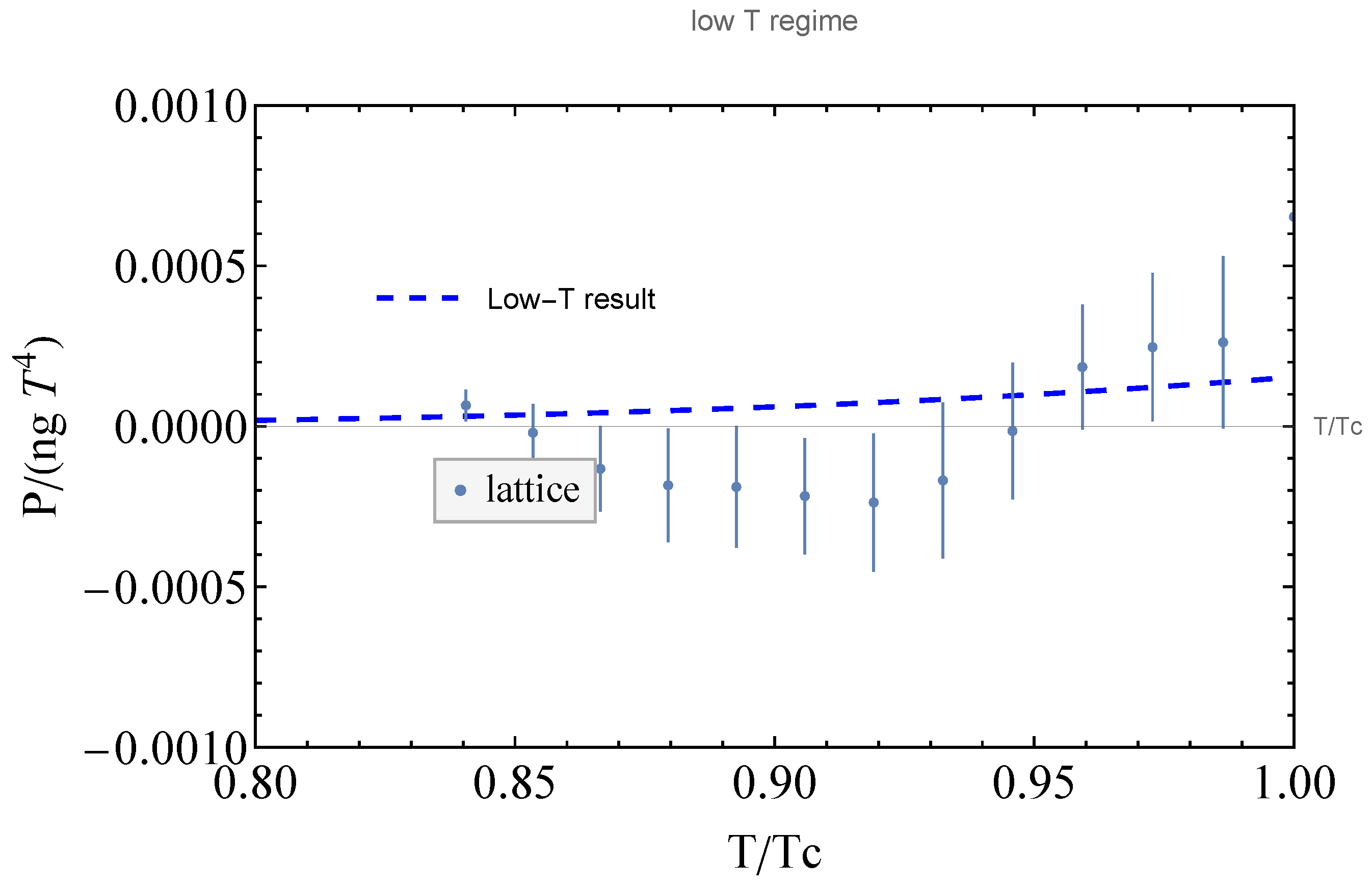
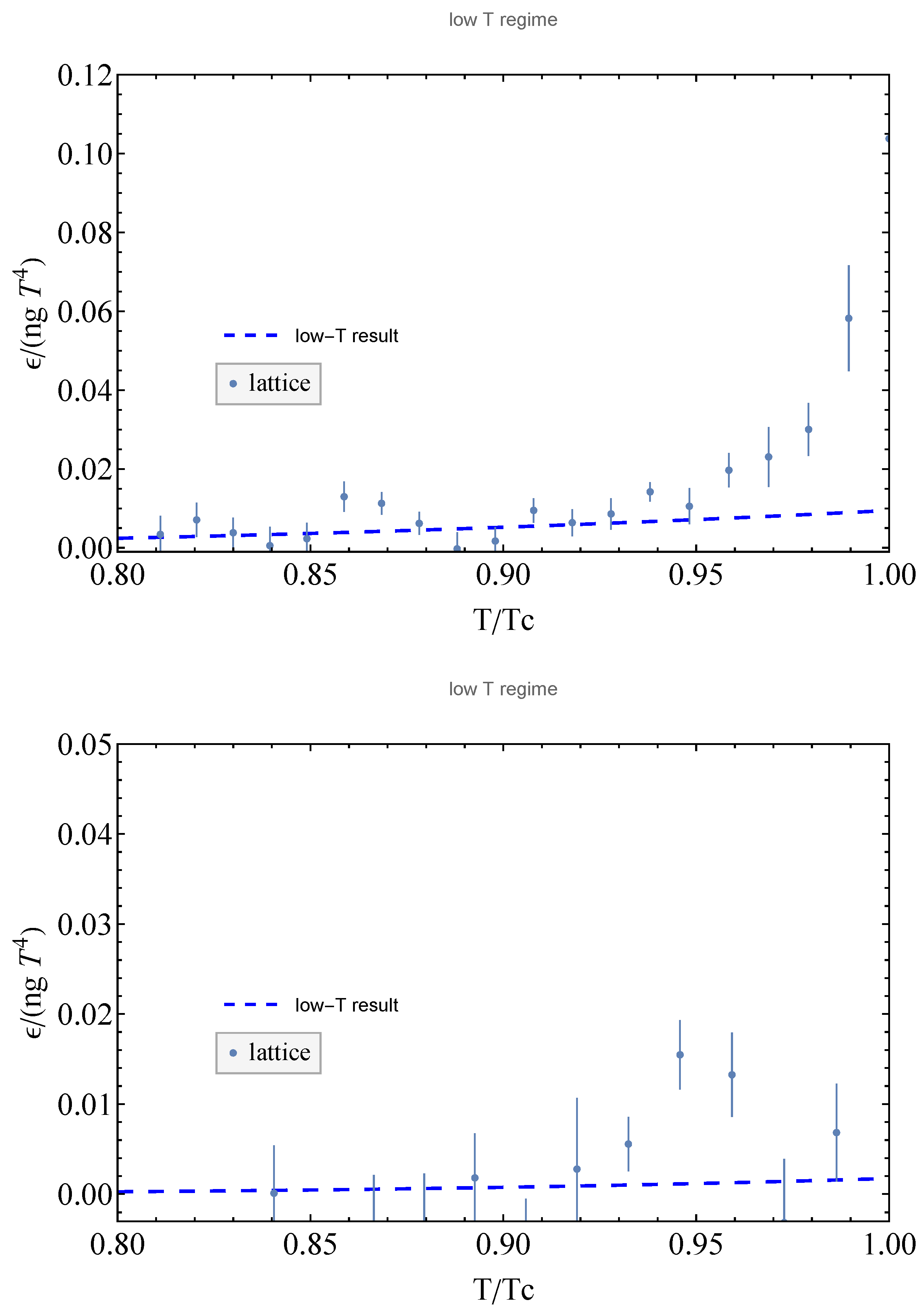
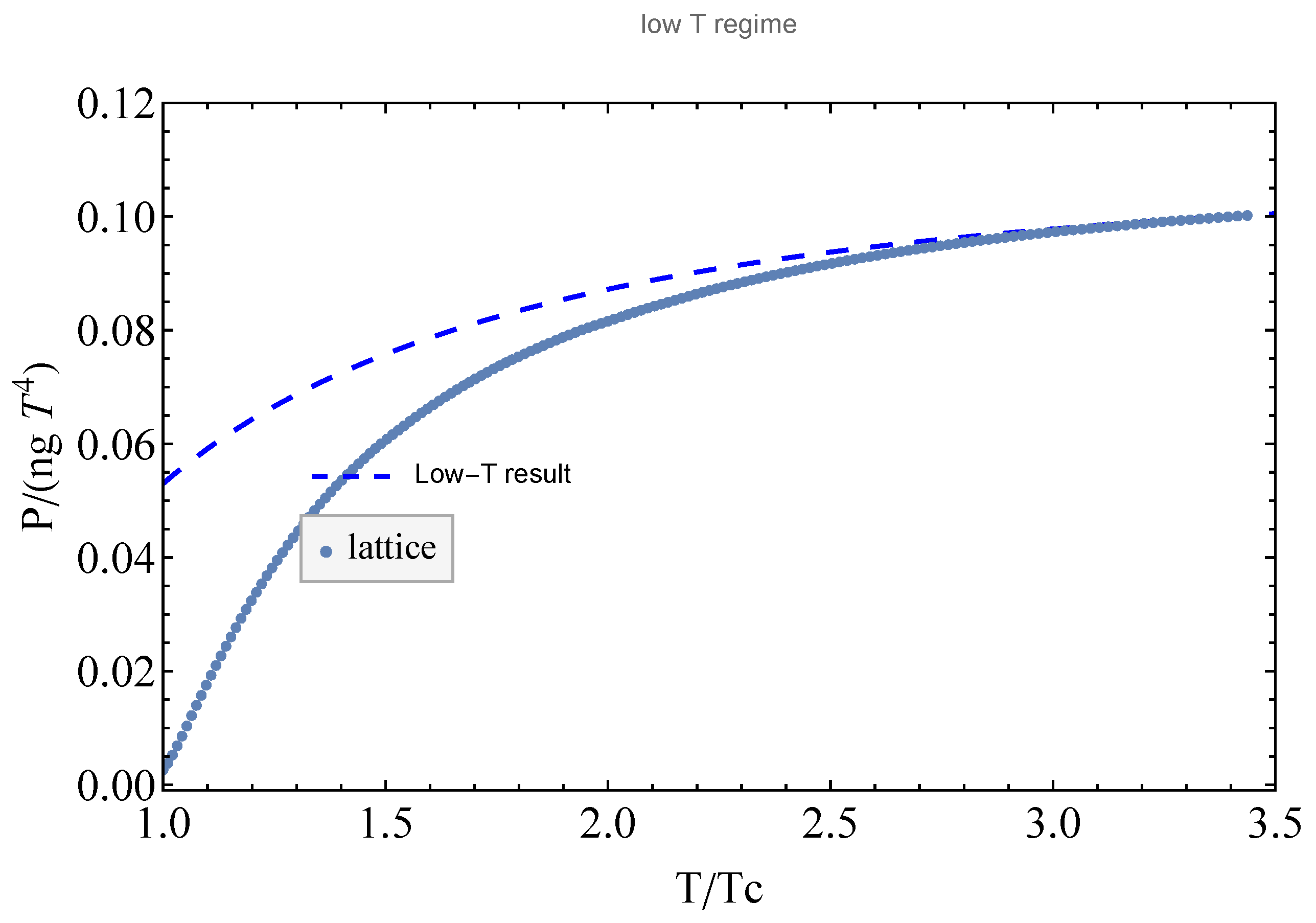
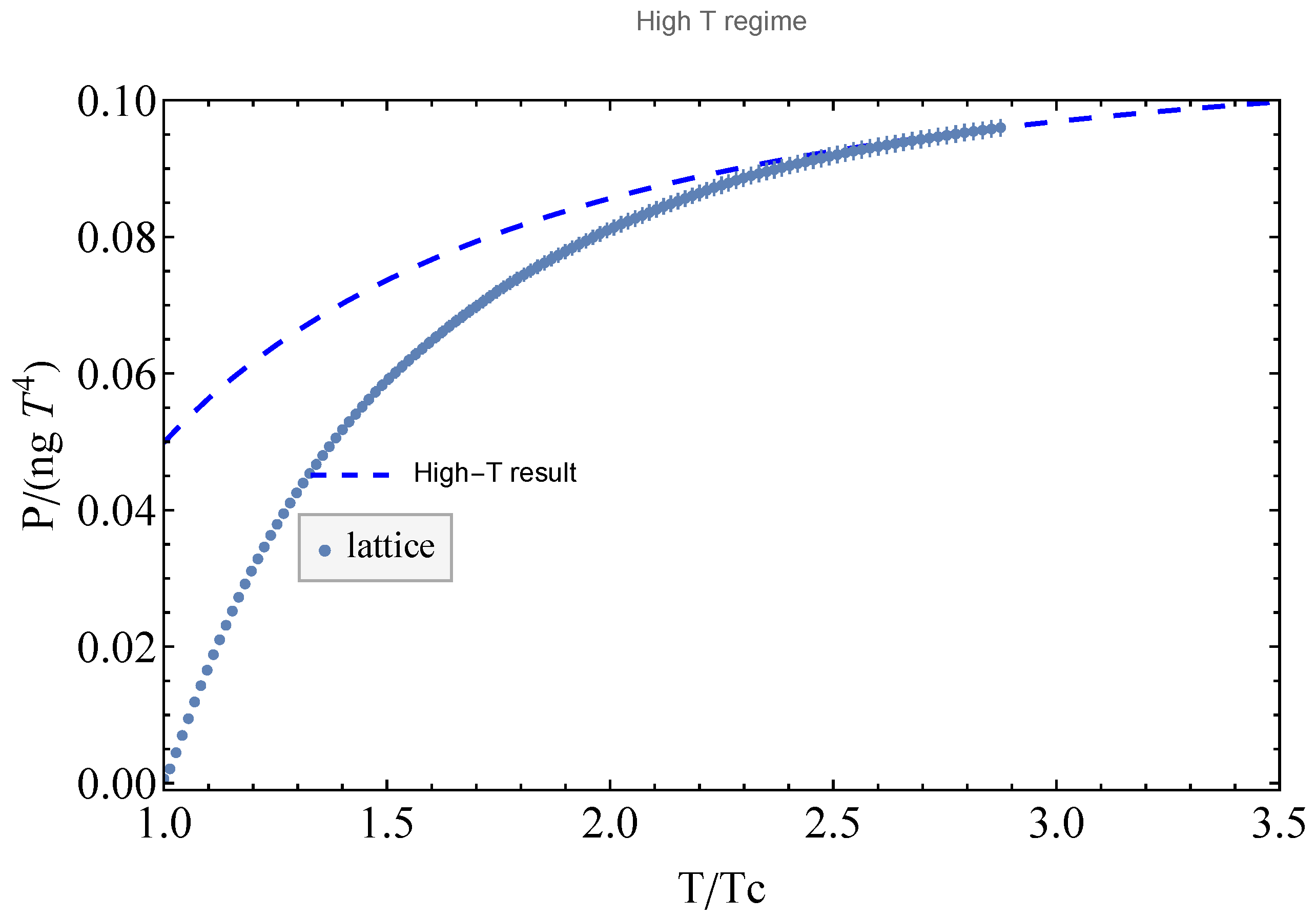
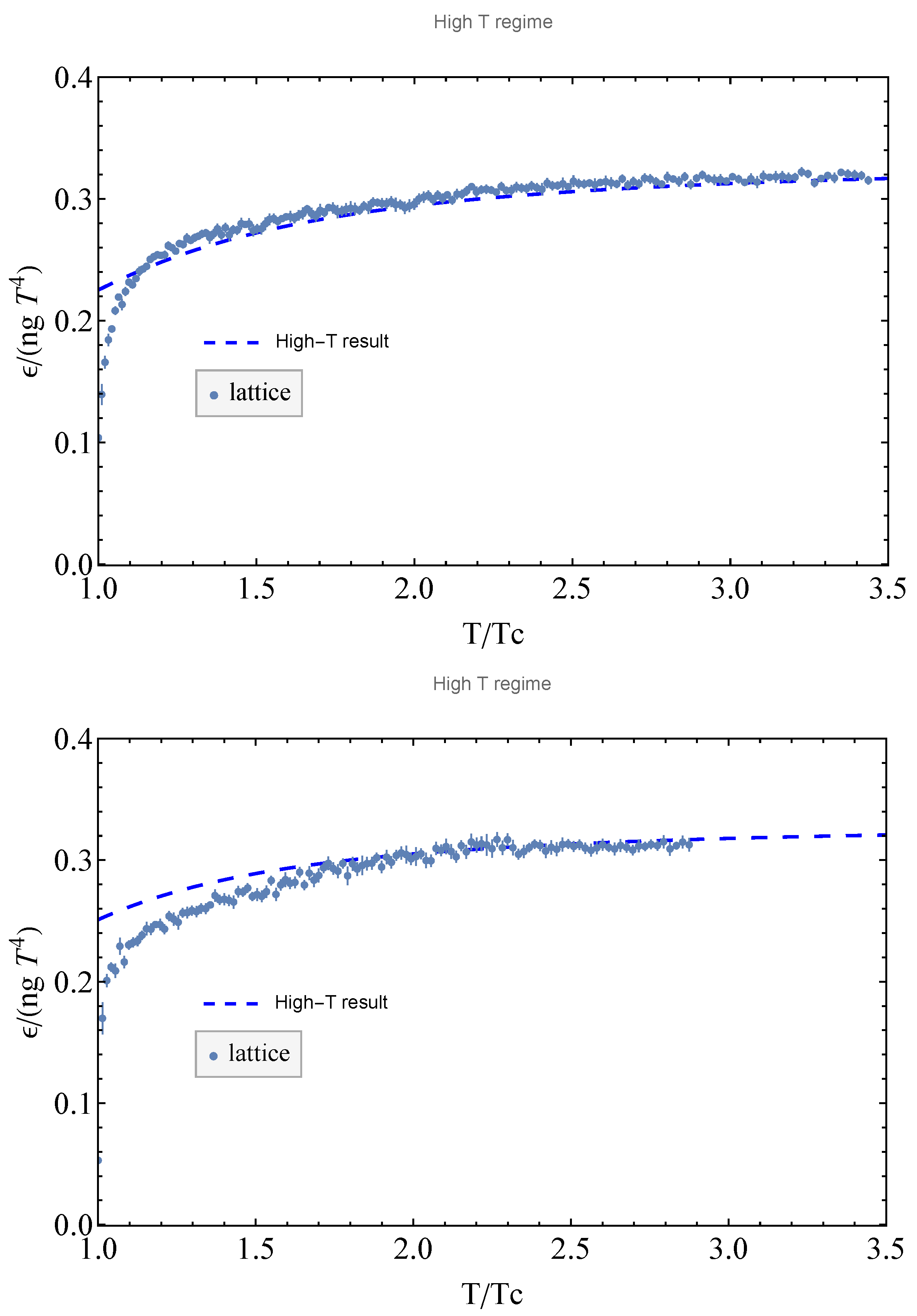
5. Evaluation of the Partition Function
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Two-Point Correlation Function and Spectrum
Appendix B. One-Point Correlation Function
Appendix C. Evaluation of the Partition Function
References
- Pisarski, R. Quark gluon plasma as a condensate of SU(3) Wilson lines. Phys. Rev. D 2000, 62, 111501. [Google Scholar] [CrossRef]
- Sannino, F. Polyakov loops versus hadronic states. Phys. Rev. D 2002, 66, 034013. [Google Scholar] [CrossRef]
- Panero, M. Thermodynamics of the QCD plasma and the large-N limit. Phys. Rev. Lett. 2009, 103, 232001. [Google Scholar] [CrossRef] [PubMed]
- Carenza, P.; Pasechnik, R.; Salinas, G.; Wang, Z. Glueball Dark Matter Revisited. Phys. Rev. Lett. 2022, 129, 261302. [Google Scholar] [CrossRef] [PubMed]
- Frasca, M. Quantum Yang–Mills field theory. Eur. Phys. J. Plus 2017, 132, 38, Erratum in Eur. Phys. J. Plus 2017, 132, 242. [Google Scholar] [CrossRef]
- Frasca, M. Confinement in a three-dimensional Yang–Mills theory. Eur. Phys. J. C 2017, 77, 255. [Google Scholar] [CrossRef]
- Frasca, M. Spectrum of Yang–Mills theory in 3 and 4 dimensions. Nucl. Part. Phys. Proc. 2018, 294–296, 124–128. [Google Scholar] [CrossRef]
- Chaichian, M.; Frasca, M. Condition for confinement in non-Abelian gauge theories. Phys. Lett. B 2018, 781, 33–39. [Google Scholar] [CrossRef]
- Koberinski, A. Mathematical developments in the rise of Yang–Mills gauge theories. Synthese 2021, 198 (Suppl. S16), 3747–3777. [Google Scholar]
- Brink, L.; Phua, K.K. (Eds.) Proceedings of the Conference on 60 Years of Yang–Mills Gauge Field Theories: C.N. Yang’s Contributions to Physics, Nanyang Technological University, Singapore, 25–28 May 2015; World Scientific Publishing Co. Pte Ltd.: Singapore, 2016. [Google Scholar]
- Silva, J.; Khanna, F.; Matos Neto, A.; Santana, A. Generalized Bogolyubov transformation for confined fields: Applications in Casimir effect. Phys. Rev. A 2002, 66, 052101. [Google Scholar] [CrossRef]
- Santos, A.; Khanna, F. Casimir effect and Stefan–Boltzmann law in Yang–Mills theory at finite temperature. Int. J. Mod. Phys. A 2019, 34, 1950128. [Google Scholar] [CrossRef]
- Trotti, E.; Jafarzade, S.; Giacosa, F. Thermodynamics of the glueball resonance gas. Eur. Phys. J. C 2023, 83, 390. [Google Scholar] [CrossRef]
- Frasca, M.; Groote, S. Exact solutions to non-linear classical field theories. Symmetry 2024, 16, 1504. [Google Scholar] [CrossRef]
- Böhm, M.; Denner, A.; Joos, H. Gauge Theories of the Strong and Electroweak Interaction; B.G. Teubner: Stuttgart, Germany, 2001. [Google Scholar]
- Frasca, M. Infrared Gluon and Ghost Propagators. Phys. Lett. B 2008, 670, 73–77. [Google Scholar] [CrossRef]
- Frasca, M. Mapping a massless scalar field theory on a Yang–Mills theory: Classical case. Mod. Phys. Lett. A 2009, 24, 2425–2432. [Google Scholar] [CrossRef]
- Frasca, M.; Ghoshal, A.; Groote, S. Nambu–Jona-Lasinio model correlation functions from QCD. Nucl. Part. Phys. Proc. 2022, 318–323, 138–141. [Google Scholar] [CrossRef]
- Le Bellac, M. Thermal Field Theory; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Lucini, B.; Panero, M. SU(N) gauge theories at large N. Phys. Rept. 2013, 526, 93–163. [Google Scholar] [CrossRef]
- Borsanyi, S.; Endrodi, G.; Fodor, Z.; Katz, S.; Szabo, K. Precision SU(3) lattice thermodynamics for a large temperature range. J. High Energy Phys. 2012, 7, 56. [Google Scholar] [CrossRef]
- Silva, P.J.; Oliveira, O.; Bicudo, P.; Cardoso, N. Gluon screening mass at finite temperature from the Landau gauge gluon propagator in lattice QCD. Phys. Rev. D 2014, 89, 074503. [Google Scholar] [CrossRef]
- Peshier, A.; Kampfer, B.; Pavlenko, O.; Soff, G. A Massive quasiparticle model of the SU(3) gluon plasma. Phys. Rev. D 1996, 54, 2399–2402. [Google Scholar] [CrossRef]
- Castorina, P.; Greco, V.; Jaccarino, D.; Zappalà, D. A Reanalysis of Finite Temperature SU(N) Gauge Theory. Eur. Phys. J. C 2011, 71, 1826. [Google Scholar] [CrossRef]
- Auclair, P.; Bacon, D.; Baker, T.; Barreiro, T.; Bartolo, N.; Belgacem, E.; Bellomo, N.; Ben-Dayan, I.; Bertacca, D.; Besancon, M.; et al. Cosmology with the Laser Interferometer Space Antenna. Living Rev. Rel. 2023, 26, 5. [Google Scholar]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Janssen, G.; Hobbs, G.; McLaughlin, M.; Bassa, C.G.; Deller, A.T.; Kramer, M.; Hobbs, G.; McLaughlin, M.; Bassa, C.G.; Deller, A.T.; et al. Gravitational wave astronomy with the SKA. Proc. Sci. 2015, AASKA14, 37. [Google Scholar]
- Yagi, K.; Seto, N. Detector configuration of DECIGO/BBO and identification of cosmological neutron-star binaries. Phys. Rev. D 2011, 83, 044011, Erratum in Phys. Rev. D 2017, 95, 109901. [Google Scholar]
- Schwaller, P. Gravitational Waves from a Dark Phase Transition. Phys. Rev. Lett. 2015, 115, 181101. [Google Scholar] [CrossRef]
- Breitbach, M.; Kopp, J.; Madge, E.; Opferkuch, T.; Schwaller, P. Dark, Cold, and Noisy: Constraining Secluded Hidden Sectors with Gravitational Waves. J. Cosmol. Astropart. Phys. 2019, 7, 7. [Google Scholar] [CrossRef]
- Fairbairn, M.; Hardy, E.; Wickens, A. Hearing without seeing: Gravitational waves from hot and cold hidden sectors. J. High Energy Phys. 2019, 7, 44. [Google Scholar]
- Svetitsky, B.; Yaffe, L.G. Critical Behavior at Finite Temperature Confinement Transitions. Nucl. Phys. B 1982, 210, 423–447. [Google Scholar]
- Gross, D.J.; Harvey, J.A.; Martinec, E.J.; Rohm, R. The Heterotic String. Phys. Rev. Lett. 1985, 54, 502–505. [Google Scholar]
- Dixon, L.J.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on Orbifolds. Nucl. Phys. B 1985, 261, 678–686. [Google Scholar]
- Dixon, L.J.; Harvey, J.A.; Vafa, C.; Witten, E. Strings on Orbifolds. 2. Nucl. Phys. B 1986, 274, 285–314. [Google Scholar] [CrossRef]
- Acharya, B.S. M theory, Joyce orbifolds and super Yang–Mills. Adv. Theor. Math. Phys. 1999, 3, 227–248. [Google Scholar] [CrossRef]
- Halverson, J.; Morrison, D.R. On gauge enhancement and singular limits in G2 compactifications of M-theory. J. High Energy Phys. 2016, 4, 100. [Google Scholar]
- Asadi, P.; Kramer, E.D.; Kuflik, E.; Ridgway, G.W.; Slatyer, T.R.; Smirnov, J. Thermal squeezeout of dark matter. Phys. Rev. D 2021, 104, 095013. [Google Scholar] [CrossRef]
- Asadi, P.; Kramer, E.D.; Kuflik, E.; Ridgway, G.W.; Slatyer, T.R.; Smirnov, J. Accidentally Asymmetric Dark Matter. Phys. Rev. Lett. 2021, 127, 211101. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Schwaller, P. Scale of dark QCD. Phys. Rev. D 2014, 89, 063522. [Google Scholar] [CrossRef]
- Schwaller, P.; Stolarski, D.; Weiler, A. Emerging Jets. J. High Energy Phys. 2015, 5, 59. [Google Scholar] [CrossRef]
- Halverson, J.; Long, C.; Maiti, A.; Nelson, B.; Salinas, G. Gravitational waves from dark Yang–Mills sectors. J. High Energy Phys. 2021, 5, 154. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Cotrone, A.L.; Paredes, A. Fate of false vacua in holographic first-order phase transitions. J. High Energy Phys. 2020, 12, 200. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Cotrone, A.L.; Paredes, A. Dark Holograms and Gravitational Waves. J. High Energy Phys. 2021, 4, 94. [Google Scholar] [CrossRef]
- Huang, W.C.; Reichert, M.; Sannino, F.; Wang, Z.W. Testing the dark SU(N) Yang–Mills theory confined landscape: From the lattice to gravitational waves. Phys. Rev. D 2021, 104, 035005. [Google Scholar] [CrossRef]
- Wang, X.; Huang, F.P.; Zhang, X. Bubble wall velocity beyond leading-log approximation in electroweak phase transition. arXiv 2011, arXiv:2011.12903. [Google Scholar]
- Kang, Z.; Zhu, J.; Matsuzaki, S. Dark confinement-deconfinement phase transition: A roadmap from Polyakov loop models to gravitational waves. J. High Energy Phys. 2021, 9, 60. [Google Scholar]
- Yamada, M.; Yonekura, K. Cosmic F- and D-strings from pure Yang–Mills theory. Phys. Lett. B 2023, 838, 137724. [Google Scholar]
- Yamada, M.; Yonekura, K. Cosmic strings from pure Yang–Mills theory. Phys. Rev. D 2022, 106, 123515. [Google Scholar] [CrossRef]
- Morgante, E.; Ramberg, N.; Schwaller, P. Gravitational waves from dark SU(3) Yang–Mills theory. Phys. Rev. D 2023, 107, 036010. [Google Scholar] [CrossRef]
- Hindmarsh, M.; Philipsen, O. WIMP dark matter and the QCD equation of state. Phys. Rev. D 2005, 71, 087302. [Google Scholar] [CrossRef]
- Drees, M.; Hajkarim, F.; Schmitz, E. The Effects of QCD Equation of State on the Relic Density of WIMP Dark Matter. J. Cosmol. Astropart. Phys. 2015, 6, 25. [Google Scholar]
- Hajkarim, F.; Schaffner-Bielich, J.; Wystub, S.; Wygas, M. Effects of the QCD equation of state and lepton asymmetry on primordial gravitational waves. Phys. Rev. D 2019, 99, 103527. [Google Scholar]
- Bateman, H. Higher Transcendental Functions [Volumes I–III]; Bateman Manuscript Project; McGraw-Hill Book Company: New York, NY, USA, 1953. [Google Scholar]
- Whittaker, E.T.; Watson, G.N. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- [DLMF]. NIST Digital Library of Mathematical Functions; Olver, F.W.J., Olde Daalhuis, A.B., Lozier, D.W., Schneider, B.I., Boisvert, R.F., Clark, C.W., Miller, B.R., Saunders, B.V., Cohl, H.S., McClain, M.A., Eds.; Release 1.1.6 of 2022-06-30. Available online: https://dlmf.nist.gov/ (accessed on 23 March 2025).
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Translated from the Russian; Jeffrey, A.; Zwillinger, D., Translators; Elsevier; Academic Press: Amsterdam, The Netherlands, 2007; p. xlviii+1171, ISBNs: 978-0-12-373637-6; 0-12-373637-4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frasca, M.; Ghoshal, A.; Groote, S. Non-Perturbative Quantum Yang–Mills at Finite Temperature Beyond Lattice: A Dyson–Schwinger Approach. Symmetry 2025, 17, 543. https://doi.org/10.3390/sym17040543
Frasca M, Ghoshal A, Groote S. Non-Perturbative Quantum Yang–Mills at Finite Temperature Beyond Lattice: A Dyson–Schwinger Approach. Symmetry. 2025; 17(4):543. https://doi.org/10.3390/sym17040543
Chicago/Turabian StyleFrasca, Marco, Anish Ghoshal, and Stefan Groote. 2025. "Non-Perturbative Quantum Yang–Mills at Finite Temperature Beyond Lattice: A Dyson–Schwinger Approach" Symmetry 17, no. 4: 543. https://doi.org/10.3390/sym17040543
APA StyleFrasca, M., Ghoshal, A., & Groote, S. (2025). Non-Perturbative Quantum Yang–Mills at Finite Temperature Beyond Lattice: A Dyson–Schwinger Approach. Symmetry, 17(4), 543. https://doi.org/10.3390/sym17040543






