Fractional Landweber Regularization Method for Identifying the Source Term of the Time Fractional Diffusion-Wave Equation
Abstract
1. Introduction
- (1)
- Riemann–Liouville derivative [1]:
- (2)
- (3)
- Caputo–Fabrizio fractional derivative [4]:
- 1.
- Memory and non-local effects: fractional derivatives inherently account for memory and history dependence, which is crucial in materials science (e.g., viscoelasticity) and processes with long-range temporal correlations. Integer-order models require additional terms or integrals to approximate such effects, increasing complexity.
- 2.
- Anomalous diffusion: in systems like biological tissues or porous media, diffusion often follows a power-law rather than linear growth (as in Fick’s law). Fractional diffusion equations directly model such sub-diffusion or super-diffusion, whereas integer-order models fail to capture these dynamics without unrealistic assumptions.
- 3.
- Power-law dynamics: natural systems frequently exhibit power-law relaxation or frequency responses (e.g., electrochemical impedance, viscoelastic damping). Fractional models naturally describe these behaviors, avoiding the need for infinite exponential terms in integer-order frameworks.
- 4.
- Parsimonious representation: fractional models often require fewer parameters to describe complex behavior. For example, a single fractional-order term can replace multiple integer-order terms, simplifying control systems and reducing computational overhead.
- 5.
- Non-locality in space and time: fractional operators are non-local, making them suitable for phenomena with spatial or temporal long-range interactions. Integer-order models would need ad hoc modifications to incorporate such effects.
- 6.
- Improved data fitting and prediction: experimental data with power-law decay or non-exponential relaxation (e.g., drug transport in tissues, financial time series) often align better with fractional models, yielding lower fitting errors and more accurate predictions.
- 7.
- Robust control systems: fractional-order controllers provide enhanced robustness and tuning flexibility compared traditional PID controllers, particularly for systems with uncertain or complex dynamics.
- Limitations of integer-order models:
- 1.
- Inability to inherently model memory or history-dependent processes.
- 2.
- Require higher-order terms or complex systems to approximate fractional behavior.
- 3.
- Fail to capture power-law dynamics and anomalous diffusion without oversimplification.
- 1.
- Understand the system’s physical/behavioral basis: for systems exhibiting properties between two states (e.g., viscoelastic materials between solid and fluid), choose orders closer to 0 (viscous) or 1 (elastic) based on dominance.
- 2.
- Anomalous diffusion: in sub-diffusion (slower spread) or super-diffusion (faster spread), match the order to the diffusion exponent observed experimentally. Memory effects: lower orders (e.g., ) is called sub-diffusion. is called super-diffusion.
2. Some Auxiliary Results and the Conditional Stability Result of the Problem (1)
2.1. Some Auxiliary Results
2.2. Solution of the Problem (1)
2.3. The Conditional Stability Result of the Problem (1)
3. Preliminary Results of the Problem (1) and Optimal Error Bound
3.1. Preliminary Results of the Problem (1)
- (i).
- Optimal if ;
- (ii).
- The order is optimal if , where .
- According to [29], we obtain
- (i).
- ;
- (ii).
- φ is a strictly monotonically increasing function on ;
- (iii).
- is convex.
- (i).
- , where ;
- (ii).
- , where .
3.2. Optimal Error Bound of the Problem (1)
- (i).
- ;
- (ii).
- is a strictly monotonically increasing function;
- (iii).
- is strictly monotonic and has the following parameter form
- (iv).
- is strictly monotonically increasing and is represented by the following parameter forms
- (v).
- For the function , the following equation holdswhere is a constant related to α and T.
- (i).
- If and , we obtain
- (ii).
- If and , we obtain
4. Fractional Landweber Iterative Regularization Method and Its Convergence Error Estimation
4.1. The Error Estimation Based on a Prior Regularization Parameter Selection Rule
4.2. The Error Estimation Based on a Posterior Regularization Parameter Selection Rule
- (a)
- is a continuous function;
- (b)
- (c)
- (d)
- is a strictly monotonically decreasing function for any .
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Li, C.; Wang, Z. Mathematical analysis and the local discontinuous galerkin method for caputo–hadamard fractional partial differential equation. J. Sci. Comput. 2020, 85, 1–27. [Google Scholar] [CrossRef]
- Gohar, M.; Li, C.; Li, Z. Finite difference methods for caputo–hadamard fractional differential equations. Mediterr. J. Math. 2020, 17, 1–26. [Google Scholar] [CrossRef]
- Al-Salti, N.; Kerbal, E. Boundary-value problems for fractional heat equation involving Caputo-Fabrizio derivative. New Trends Math. Sci. 2016, 4, 79–89. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, Y.B.; Wei, T. Two regularization methods to identify a space-dependent source for the time-fractional diffusion equation-ScienceDirect. Appl. Numer. Math. 2013, 68, 39–57. [Google Scholar] [CrossRef]
- Ruan, Z.S.; Yang, J.Z.; Lu, X.L. Tikhonov regularization method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation. E. Asian J. Appl. Math. 2015, 5, 273–300. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Z.X.; Yue, C.W.; Wang, S.J. Landweber iteration method for simultaneous inversion of the source term and initial data in a time-fractional diffusion equation. J. Appl. Math. Comput. 2022, 68, 3219–3250. [Google Scholar] [CrossRef]
- Zeng, F.H.; Li, C.P.; Liu, F.; Turner, I. The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 2013, 35, A2976–A3000. [Google Scholar] [CrossRef]
- Brunner, H.; Han, H.; Yin, D. Artificial boundary conditions and finite difference approximations for a time-fractional diffusion-wave equation on a two-dimensional unbounded spatial domain. J. Comput. Phys. 2014, 276, 541–562. [Google Scholar] [CrossRef]
- Wei, T.; Xian, J. Determining a time-dependent coefficient in a time-fractional diffusion-wave equation with the Caputo derivative by an additional integral condition. J. Comput. Appl. Math. 2022, 404, 113910–113982. [Google Scholar] [CrossRef]
- Yang, F.; Yan, L.L.; Liu, H.; Li, X.X. Regularization Methods for identifying the unknown source of sobolev equation with fractional Laplacian. J. Appl. Anal. Comput. 2025, 15, 198–225. [Google Scholar]
- Garmatter, D.; Haasdonk, B.; Harrach, B. A reduced basis Landweber method for nonlinear inverse problems. Inverse Probl. 2016, 32, 035001. [Google Scholar] [CrossRef]
- Liang, Y.Q.; Yang, F.; Li, X.X. Two Regularization Methods for Identifying the Initial Value of Time-Fractional Telegraph Equation. J. Appl. Anal. Comput. 2025. [Google Scholar] [CrossRef]
- Cheng, W.; Fu, C.L.; Qian, Z. A modified Tikhonov regularization method for a spherically symmetric three-dimensional inverse heat conduction problem. Math. Comput. Simul. 2007, 75, 97–112. [Google Scholar] [CrossRef]
- Liang, Y.Q.; Yang, F.; Li, X.X. A hybrid regularization method for identifying the source term and the initial value simultaneously for fractional pseudo-parabolic equation with involution. Numer. Algorithms 2024. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, Y.B.; Wei, T. A posteriori regularization parameter choice rule for the quasi-boundary value method for the backward time-fractional diffusion problem. Appl. Math. Lett. 2013, 26, 741–747. [Google Scholar] [CrossRef]
- Wei, T.; Wang, J.G. A modified quasi-boundary value method for the backward time-fractional diffusion problem. Esaim-Math. Model. Num. 2014, 48, 603–621. [Google Scholar] [CrossRef]
- Wang, Y.C.; Wu, B. On the convergence rate of an improved quasi-reversibility method for an inverse source problem of a nonlinear parabolic equation with nonlocal diffusion coefficient. Appl. Math. Lett. 2021, 5, 107491. [Google Scholar] [CrossRef]
- Zhang, H.W.; Wei, T. A Fourier truncated regularization method for a Cauchy problem of a semi-linear elliptic equation. J. Inverse-Ill Probl. 2014, 22, 143–168. [Google Scholar] [CrossRef]
- Yan, X.K.; He, Q.L.; Wang, Y.F. Truncated trust region method for nonlinear inverse problems and application in full-waveform inversion. J. Comput. Appl. Math. 2022, 404, 113896. [Google Scholar] [CrossRef]
- Chen, Z.; Chan, T.H.T. A truncated generalized singular value decomposition algorithm for moving force identification with ill-posed problems. J. Sound Vib. 2017, 401, 297–310. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Fu, C.L.; Ma, Y.J. An a posteriori parameter choice rule for the truncation regularization method for solving backward parabolic problems. J. Comput. Appl. Math. 2014, 255, 150–160. [Google Scholar]
- Murio, D.A. The mollification method and the numerical solution of the inverse heat conduction problem by finite differences. Comput. Math. Appl. 1989, 17, 1385–1396. [Google Scholar]
- Nevolin, V.I. Using numerical solutions in the fourier method for the Fokker-Planck-Kolmogorov equation in the analysis of first-order stochastic nonlinear systems for nonlinear detectors. Radiophys. Quantum Electron. 2003, 46, 288–295. [Google Scholar]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-Leffler Functions and Their Applications. J. Appl. Math. 2009, 2011, 298628. [Google Scholar] [CrossRef]
- Pollard, H. The completely monotonic character of the Mittag-Leffler function. Bull. Amer. Math. Soc. 1948, 54, 1115–1116. [Google Scholar] [CrossRef]
- Tautenhahn, U. Optimality for ill-posed problems under general source conditions. Numer. Funct. Anal. Optim. 2007, 19, 377–398. [Google Scholar]
- Tautenhahn, U. Optimal stable approximations for the sideways heat equation. J. Inverse Ill-Pose Probl. 1997, 5, 287–307. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problems; Springer: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Tautenhahn, U.; Gorenflo, R. On optimal regularization methods for fractional differentiation. J. Math. Anal. Appl. 1999, 18, 449–467. [Google Scholar]
- Tautenhahn, U.; HäMarik, U.; Hofmann, B.; Shao, Y. Conditional stability estimates for ill-posed PDE problems by using interpolation. Numer. Funct. Anal. Optim. 2013, 34, 1370–1417. [Google Scholar] [CrossRef]
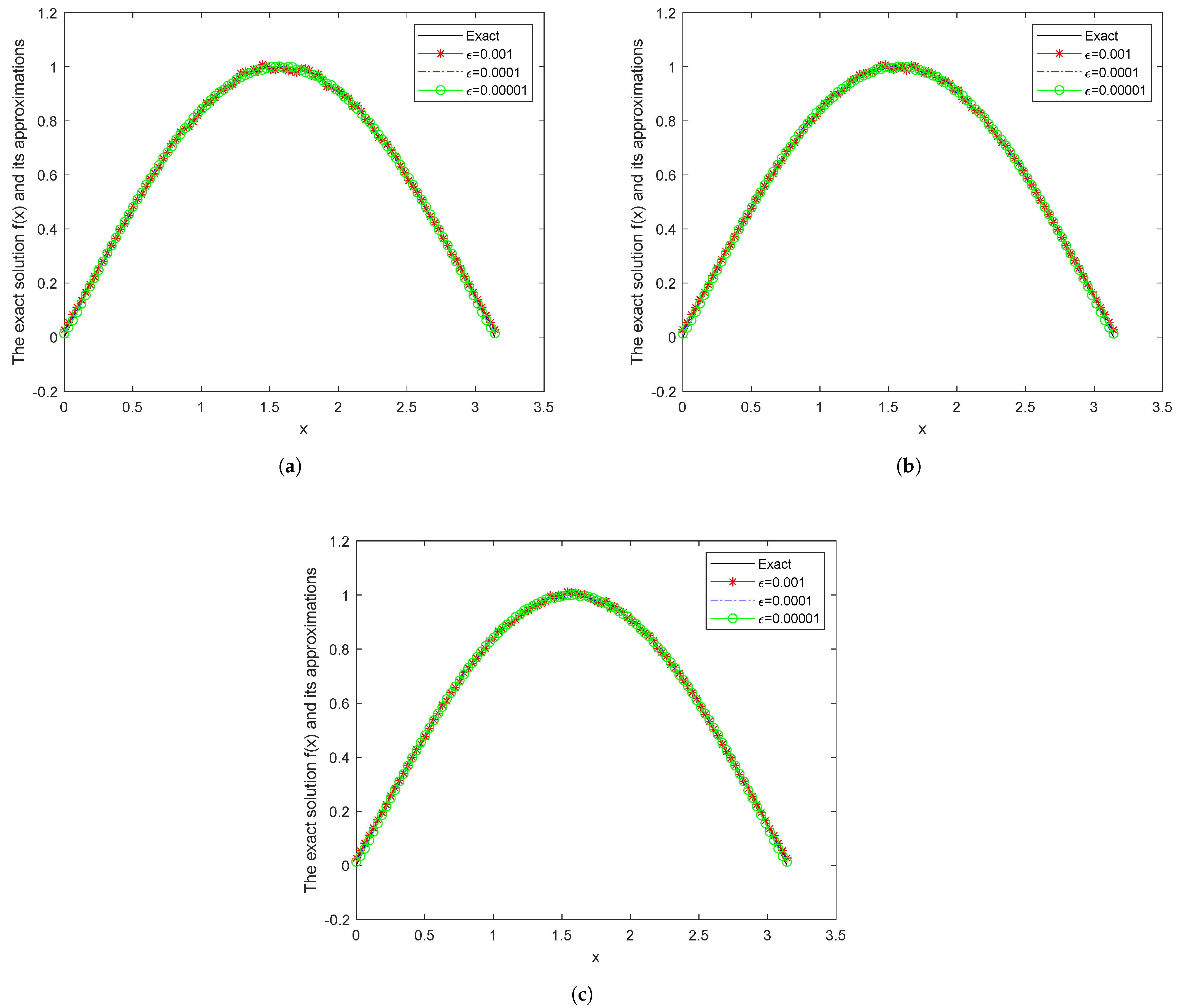
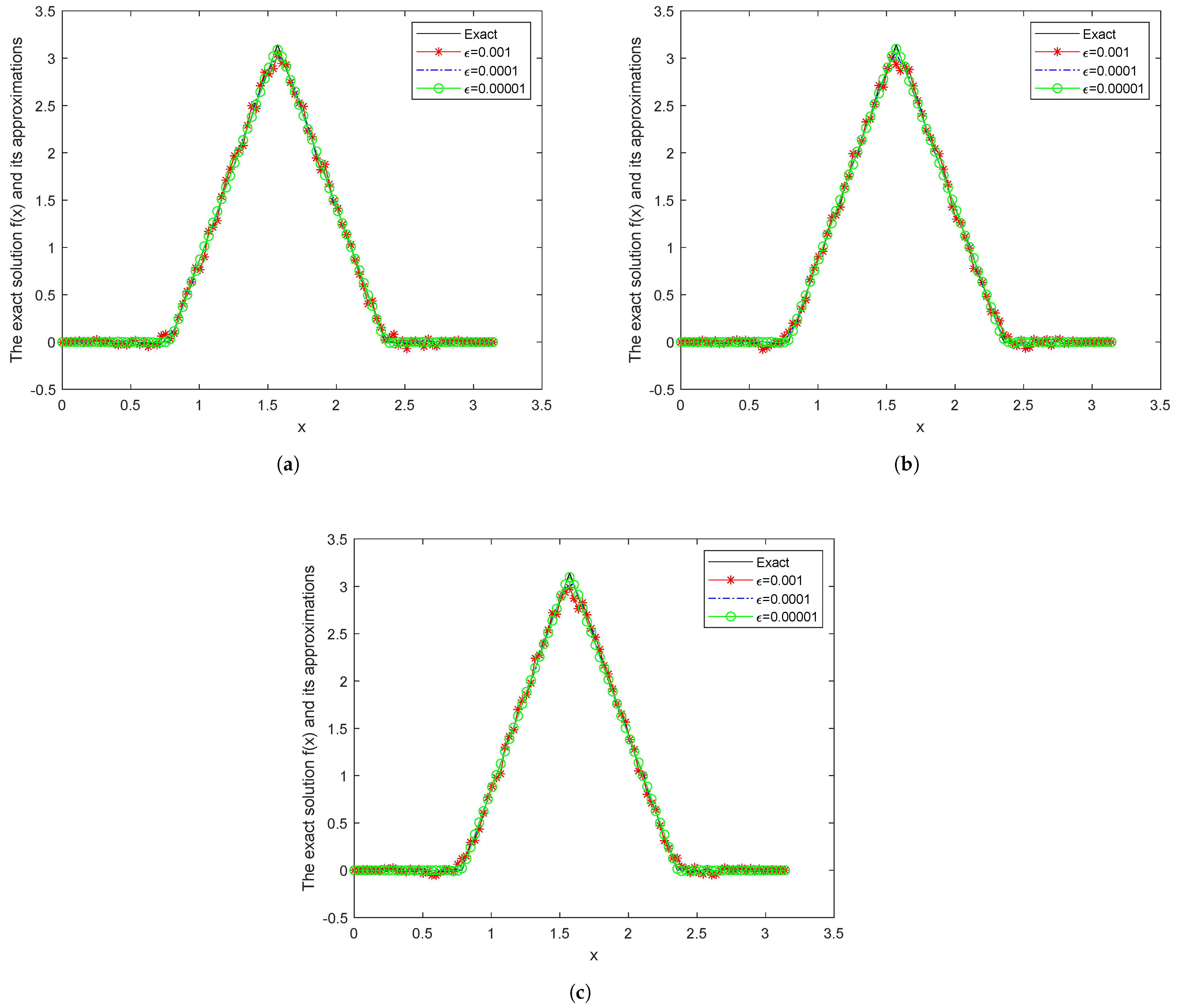

| 0.001 | 0.0001 | 0.00001 | ||
|---|---|---|---|---|
| Fractional Landweber | 19 | 92 | 558 | |
| Fractional Landweber | 20 | 127 | 616 | |
| Fractional Landweber | 22 | 130 | 639 |
| 0.001 | 0.0001 | 0.00001 | ||
|---|---|---|---|---|
| Fractional Landweber | 110 | 350 | 1314 | |
| Fractional Landweber | 113 | 391 | 1421 | |
| Fractional Landweber | 118 | 434 | 1613 |
| 0.001 | 0.0001 | 0.00001 | ||
|---|---|---|---|---|
| Fractional Landweber | 749 | 5162 | 15,481 | |
| Fractional Landweber | 782 | 5637 | 15,724 | |
| Fractional Landweber | 840 | 5648 | 15,766 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Z.; Jiang, Q.; Liu, Q.; Xu, L.; Yang, F. Fractional Landweber Regularization Method for Identifying the Source Term of the Time Fractional Diffusion-Wave Equation. Symmetry 2025, 17, 554. https://doi.org/10.3390/sym17040554
Liang Z, Jiang Q, Liu Q, Xu L, Yang F. Fractional Landweber Regularization Method for Identifying the Source Term of the Time Fractional Diffusion-Wave Equation. Symmetry. 2025; 17(4):554. https://doi.org/10.3390/sym17040554
Chicago/Turabian StyleLiang, Zhenyu, Qin Jiang, Qingsong Liu, Luopeng Xu, and Fan Yang. 2025. "Fractional Landweber Regularization Method for Identifying the Source Term of the Time Fractional Diffusion-Wave Equation" Symmetry 17, no. 4: 554. https://doi.org/10.3390/sym17040554
APA StyleLiang, Z., Jiang, Q., Liu, Q., Xu, L., & Yang, F. (2025). Fractional Landweber Regularization Method for Identifying the Source Term of the Time Fractional Diffusion-Wave Equation. Symmetry, 17(4), 554. https://doi.org/10.3390/sym17040554





