Parameter Estimation in Multifactor Uncertain Differential Equation with Symmetry Analysis for Stock Prediction
Abstract
1. Introduction
1.1. Background on SDEs and UDEs
1.2. Literature Review
1.3. Research Gap and Contribution
2. Parameter Estimation
3. Numerical Examples
4. Parameter Estimation for Time-Varying Functions
5. Algorithm for General Multifactor Mean-Reverting Model
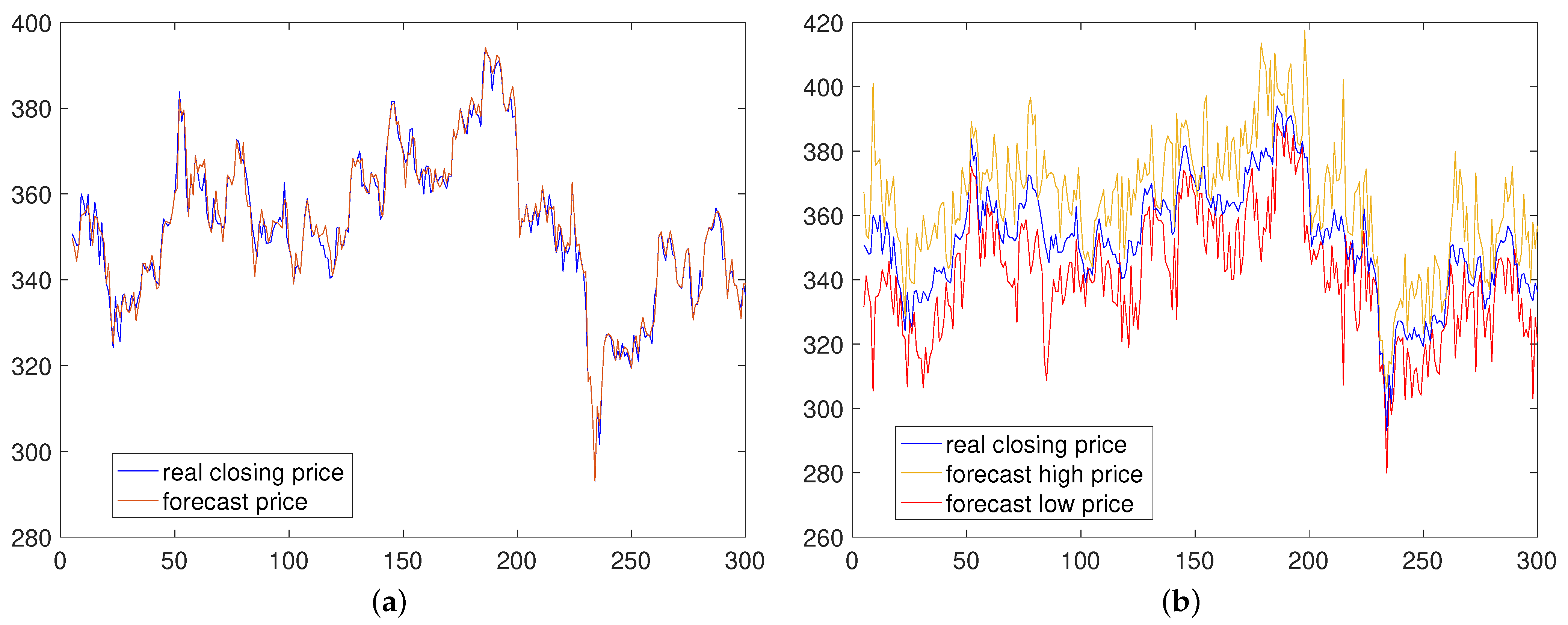
6. Application to China Merchants Bank Stock
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taraskin, A. On the asymptotic normality of vector-valued stochastic integrals and estimates of drift parameters of a multidimensional diffusion process. Theory Probab. Math. Stat. 1974, 2, 209–224. [Google Scholar]
- Kutoyants, Y.A. Estimation of the trend parameter of a diffusion process in the smooth case. Theory Probab. Its Appl. 1977, 22, 399–406. [Google Scholar] [CrossRef]
- Prakasa, R. The Bernstein-von Mises theorem for a class of diffusion processes. Theory Random Process. 1980, 9, 95–101. [Google Scholar]
- Lanksa, V. Minimum contrast estimation in diffusion processes. J. Appl. Probab. 1979, 16, 65–75. [Google Scholar] [CrossRef]
- Yoshida, N. Robust M-estimators in diffusion processes. Ann. Inst. Stat. Math. 1988, 40, 799–820. [Google Scholar] [CrossRef]
- Dietz, H.M.; Kutoyants, Y.A. A class of minimum-distance estimators for diffusion processes with ergodic properties. Stat. Risk Model. 1997, 15, 211–227. [Google Scholar] [CrossRef]
- Kutoyants, Y.A. Parameter estimation for stochastic processes. Acta Math. 1984, 112, 1–40. [Google Scholar]
- Liu, B. Toward uncertain finance theory. J. Uncertain. Anal. Appl. 2013, 1, 1. [Google Scholar] [CrossRef]
- Yang, X.; Yao, K. Uncertain partial differential equation with application to heat conduction. Fuzzy Optim. Decis. Mak. 2017, 16, 379–403. [Google Scholar] [CrossRef]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Ye, T.Q. Partial derivatives of uncertain fields and uncertain partial differential equations. Fuzzy Optim. Decis. Mak. 2024, 23, 199–217. [Google Scholar] [CrossRef]
- Zhu, Y. On uncertain partial differential equations. Fuzzy Optim. Decis. Mak. 2024, 23, 219–237. [Google Scholar] [CrossRef]
- Jia, L.; Li, D.; Guo, F.; Zhang, B. Knock-in options of mean-reverting stock model with floating interest rate in uncertain environment. Int. J. Gen. Syst. 2024, 53, 331–351. [Google Scholar] [CrossRef]
- Zhu, Y. Uncertain optimal control with application to a portfolio selection model. Cybern. Syst. 2010, 41, 535–547. [Google Scholar] [CrossRef]
- Yang, X.; Gao, J. Uncertain differential games with application to capitalism. J. Uncertain. Anal. Appl. 2013, 1, 17. [Google Scholar] [CrossRef]
- Yao, K.; Liu, B. Parameter estimation in uncertain differential equations. Fuzzy Optim. Decis. Mak. 2020, 19, 1–12. [Google Scholar] [CrossRef]
- Liu, Z. Generalized moment estimation for uncertain differential equations. Appl. Math. Comput. 2021, 392, 125724. [Google Scholar] [CrossRef]
- Yang, X.F.; Liu, Y.; Park, G. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fract. 2021, 139, 110026. [Google Scholar] [CrossRef]
- Sheng, Y.H.; Yao, K.; Chen, X. Least squares estimation in uncertain differential equations. IEEE Trans. Fuzzy Syst. 2020, 28, 2651–2655. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y. Moment estimations for parameters in high-order uncertain differential equations. J. Intell. Fuzzy Syst. 2020, 39, 1–9. [Google Scholar] [CrossRef]
- Ye, T.Q.; Liu, B. Uncertain hypothesis test for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2023, 22, 195–211. [Google Scholar] [CrossRef]
- Ye, T.Q.; Liu, B. Uncertain hypothesis test with application to uncertain regression analysis. Fuzzy Optim. Decis. Mak. 2022, 21, 157–174. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Xiao, C.; Yang, P. Numerical solution and parameter estimation for uncertain SIR model with application to COVID-19. Fuzzy Optim. Decis. Mak. 2021, 20, 189–208. [Google Scholar] [CrossRef]
- Jia, L.; Chen, W. Uncertain SEIAR model for COVID-19 cases in China. Fuzzy Optim. Decis. Mak. 2021, 20, 243–259. [Google Scholar] [CrossRef]
- Lio, W.; Liu, B. Initial value estimation of uncertain differential equations and zero-day of COVID-19 spread in China. Fuzzy Optim. Decis. Mak. 2021, 20, 177–188. [Google Scholar] [CrossRef]
- Jia, L.F.; Dai, W. Uncertain spring vibration equation. J. Ind. Manag. Optim. 2022, 18, 2401. [Google Scholar] [CrossRef]
- Xie, J.; Lio, W.; Kang, R. Analysis of simple pendulum with uncertain differential equation. Chaos Solitons Fract. 2024, 185, 115145. [Google Scholar] [CrossRef]
- Tang, H.; Yang, X.F. Uncertain chemical reaction equation. Appl. Math. Comput. 2021, 411, 126479. [Google Scholar] [CrossRef]
- Wu, C.Y.; Yang, L.; Zhang, C.K. Uncertain stochastic optimal control with jump and its application in a portfolio game. Symmetry 2022, 14, 1885. [Google Scholar] [CrossRef]
- Li, Z.X.; Ye, T.Q.; Jin, T.; Song, Y.F.; Xiao, S.J. Uncertain optimal control problem of production and inventory under time-varying customer demand. J. Ind. Manag. Optim. 2025, 21, 2175–2193. [Google Scholar] [CrossRef]
- Li, S.; Peng, J.; Zhang, B. Multifactor uncertain differential equation. J. Uncertain. Anal. Appl. 2015, 3, 7. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y. Pharmacokinetic model based on multifactor uncertain differential equation. Appl. Math. Comput. 2020, 392, 125722. [Google Scholar] [CrossRef]
- Zhang, N.; Sheng, Y.H.; Zhang, J.; Wang, X.L. Parameter estimation in multifactor uncertain differential equation. J. Intell. Fuzzy Syst. 2021, 41, 2865–2878. [Google Scholar] [CrossRef]
- Wu, N.X.; Liu, Y. Least squares estimation of multifactor uncertain differential equations with applications to the stock market. Symmetry 2024, 16, 904. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, L.J. Modeling RL electrical circuit by multifactor uncertain differential equation. Symmetry 2021, 13, 2103. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ma, G.Z.; Yang, X.F.; Yao, X. A relation between moments of Liu process and Bernoulli numbers. Fuzzy Optim. Decis. Mak. 2021, 20, 261–272. [Google Scholar] [CrossRef]
- Poterba, J.; Summers, L. Mean reversion in stock prices: Evidence and implications. J. Financ. Econ. 1988, 22, 27–59. [Google Scholar] [CrossRef]

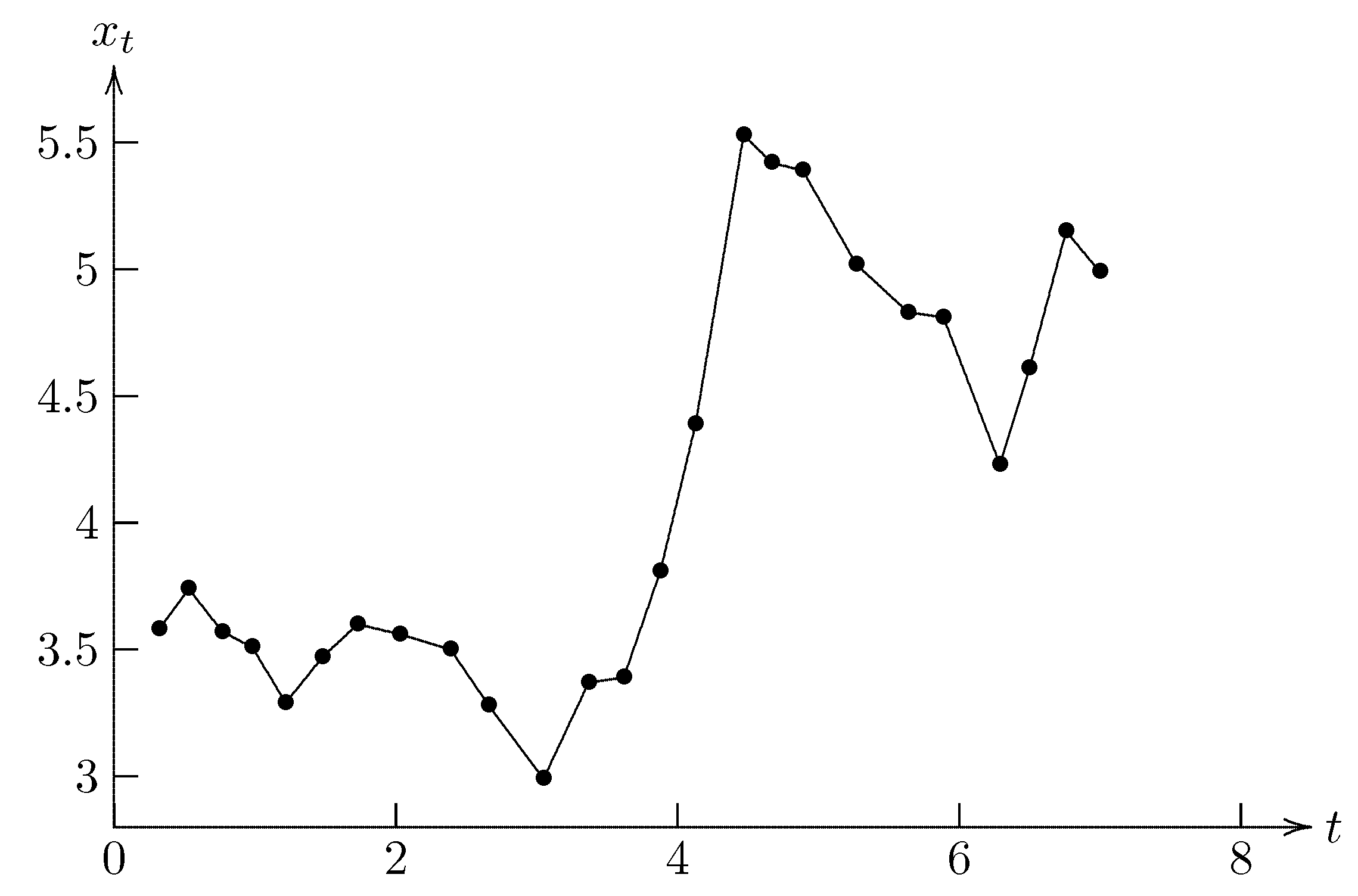



| t | 0.24 | 0.49 | 0.84 | 1.1 | 1.33 | 1.58 | 1.8 | 2.05 | 2.44 |
| 3.74 | 4.85 | 3.95 | 4.31 | 1.67 | 1.17 | 1.98 | 2.36 | 2.03 | |
| t | 2.7 | 3.08 | 3.34 | 3.62 | 3.98 | 4.35 | 4.57 | 4.81 | 5.15 |
| 3.13 | 5.16 | 2.73 | 3.14 | 5.72 | 6.48 | 10.23 | 10 | 11.88 | |
| t | 5.43 | 5.68 | 5.95 | 6.28 | 6.61 | 6.94 | 7.23 | ||
| 14.51 | 13.39 | 10.09 | 5.94 | 7.96 | 8.53 | 10.92 |
| t | 0.32 | 0.53 | 0.77 | 0.98 | 1.22 | 1.48 | 1.73 | 2.03 | 2.39 |
| 3.58 | 3.74 | 3.57 | 3.51 | 3.29 | 3.47 | 3.6 | 3.56 | 3.5 | |
| t | 2.66 | 3.05 | 3.37 | 3.62 | 3.88 | 4.13 | 4.47 | 4.67 | 4.89 |
| 3.28 | 2.99 | 3.37 | 3.39 | 3.81 | 4.39 | 5.53 | 5.42 | 5.39 | |
| t | 5.27 | 5.64 | 5.89 | 6.29 | 6.5 | 6.76 | 7 | ||
| 5.02 | 4.83 | 4.81 | 4.23 | 4.61 | 5.15 | 4.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Ye, T.; Xu, X.; Liu, Y.; Zheng, H. Parameter Estimation in Multifactor Uncertain Differential Equation with Symmetry Analysis for Stock Prediction. Symmetry 2025, 17, 620. https://doi.org/10.3390/sym17040620
Zhang J, Ye T, Xu X, Liu Y, Zheng H. Parameter Estimation in Multifactor Uncertain Differential Equation with Symmetry Analysis for Stock Prediction. Symmetry. 2025; 17(4):620. https://doi.org/10.3390/sym17040620
Chicago/Turabian StyleZhang, Jiashuo, Tingqing Ye, Xiaoya Xu, Yang Liu, and Haoran Zheng. 2025. "Parameter Estimation in Multifactor Uncertain Differential Equation with Symmetry Analysis for Stock Prediction" Symmetry 17, no. 4: 620. https://doi.org/10.3390/sym17040620
APA StyleZhang, J., Ye, T., Xu, X., Liu, Y., & Zheng, H. (2025). Parameter Estimation in Multifactor Uncertain Differential Equation with Symmetry Analysis for Stock Prediction. Symmetry, 17(4), 620. https://doi.org/10.3390/sym17040620








