Asymmetry, Symmetry and Beauty
Abstract
:1. Introduction
2. Methods
3. Results
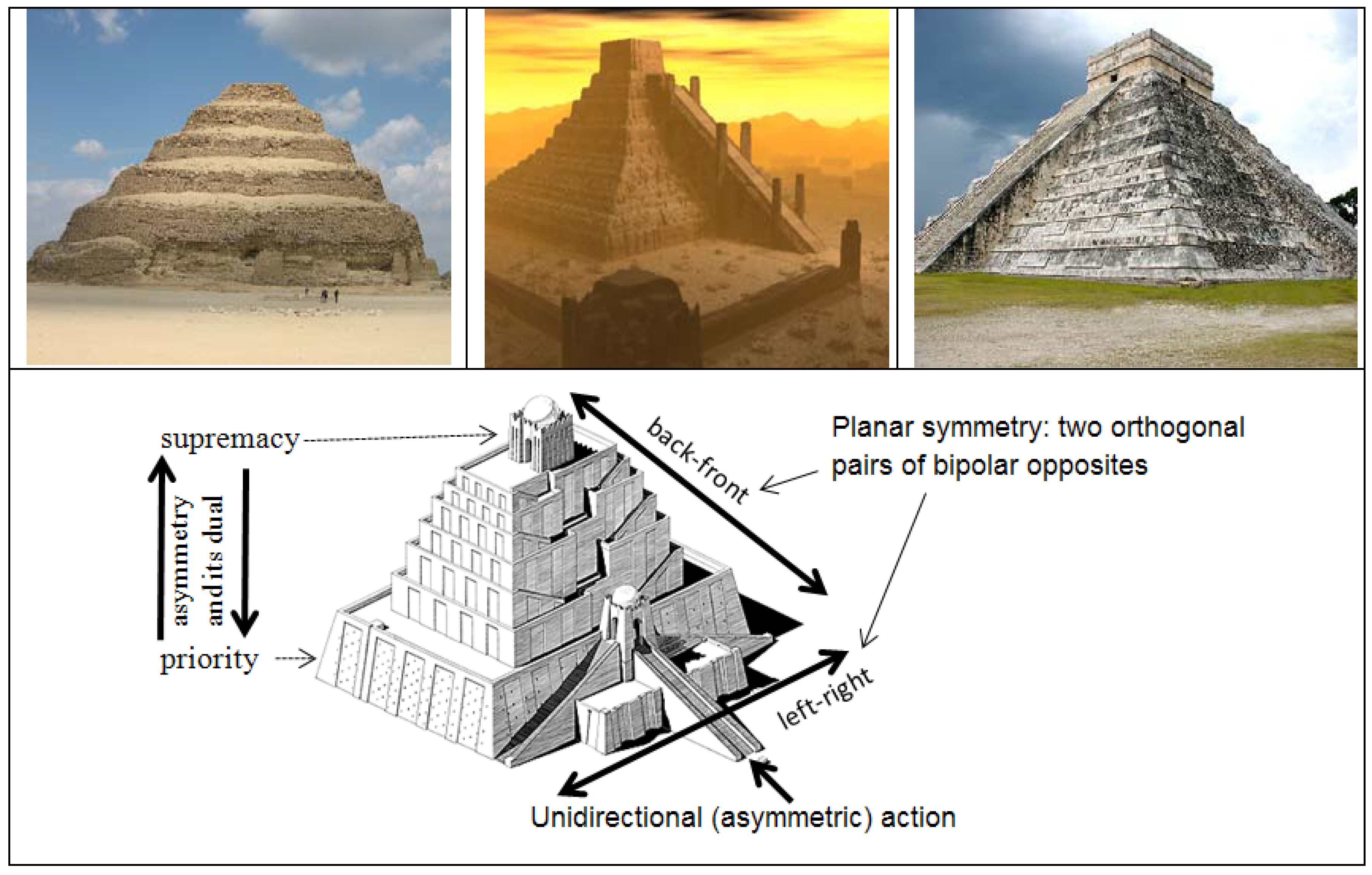
3.1. Asymmetry and Symmetry
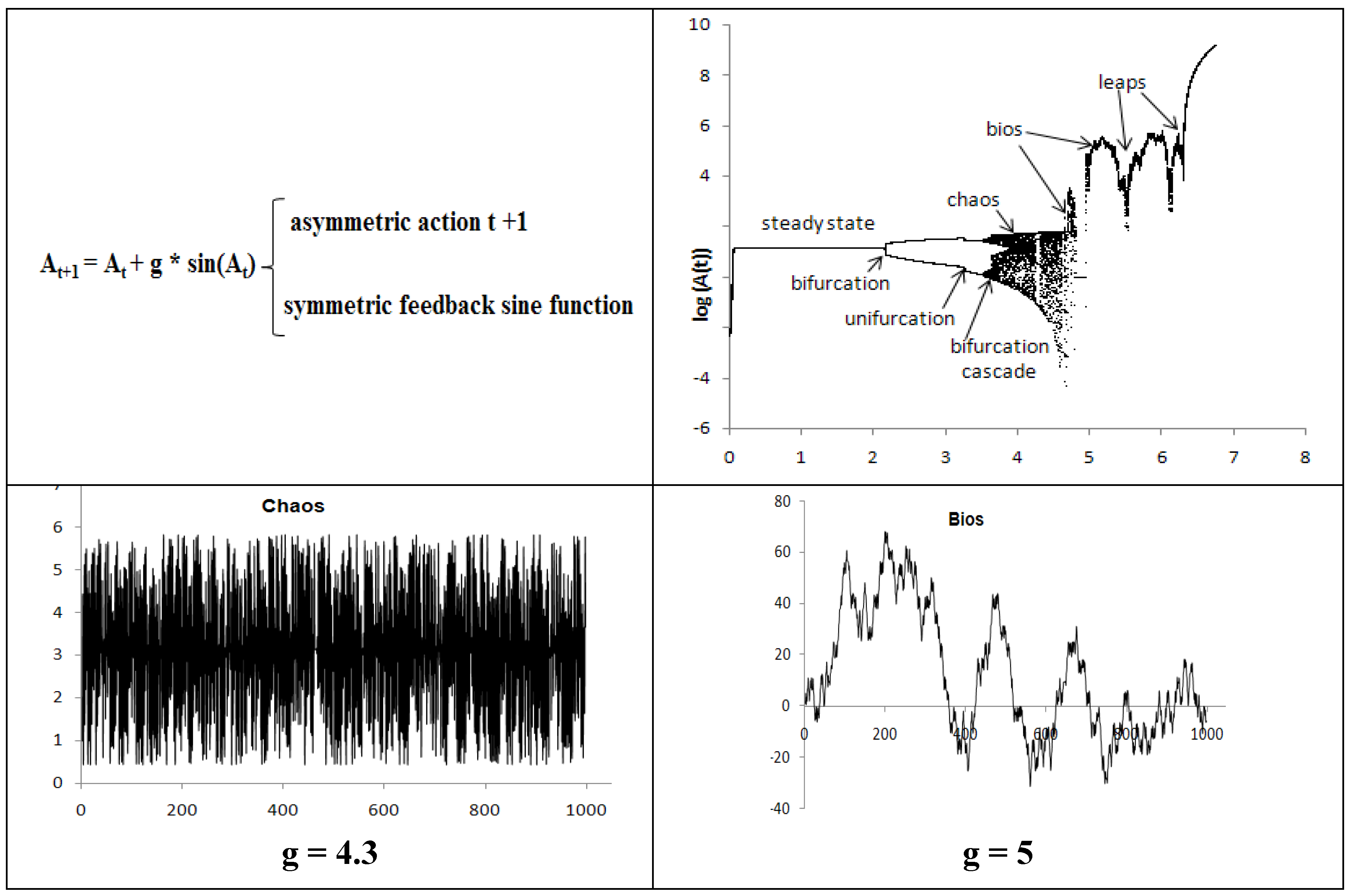
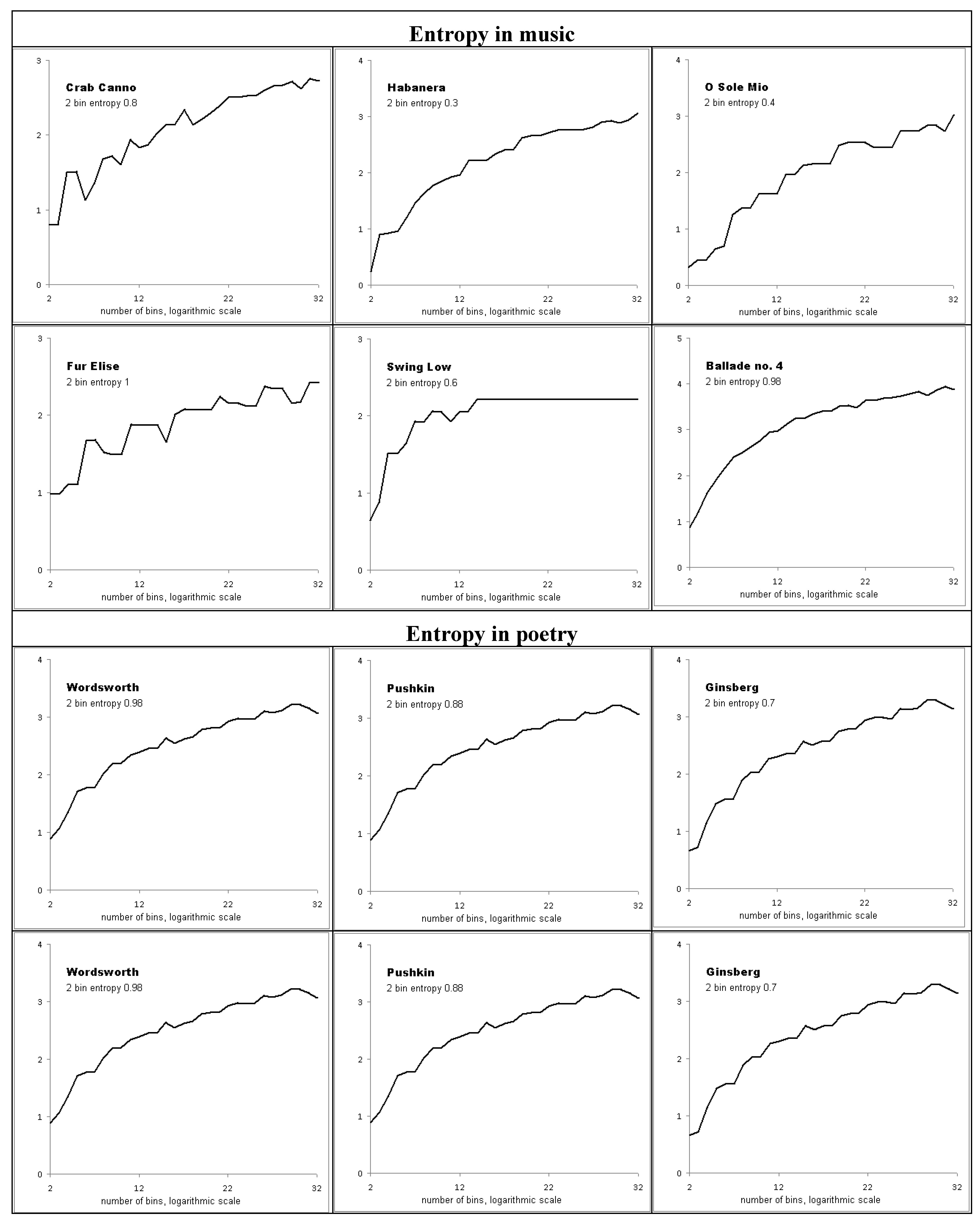
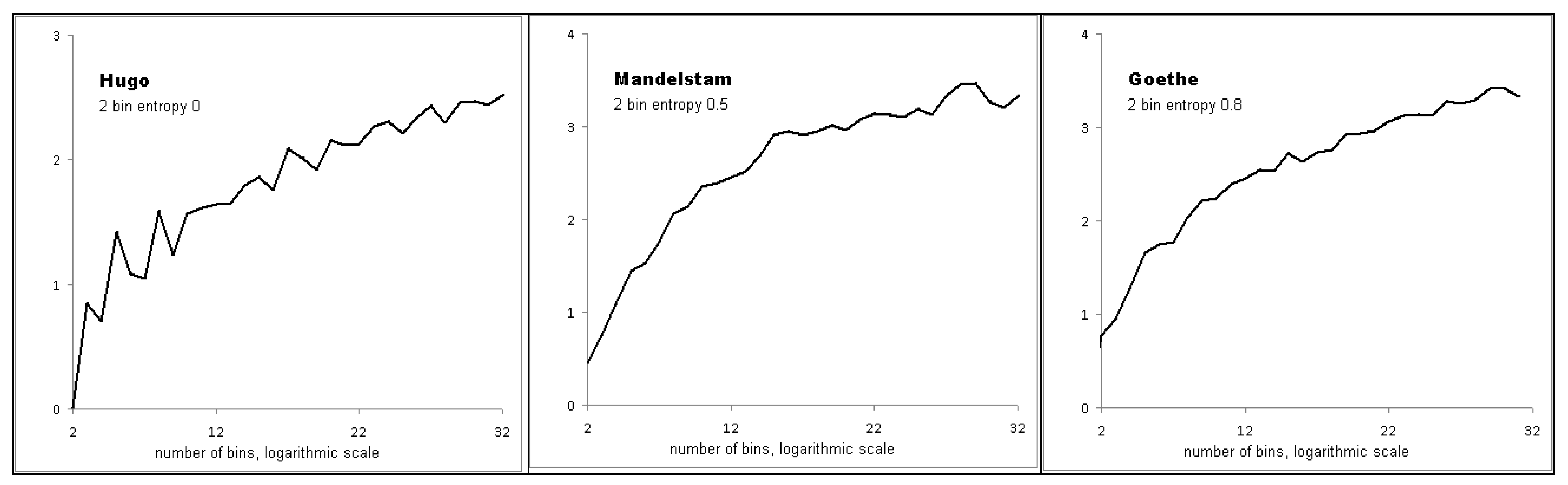
3.2. Entropy
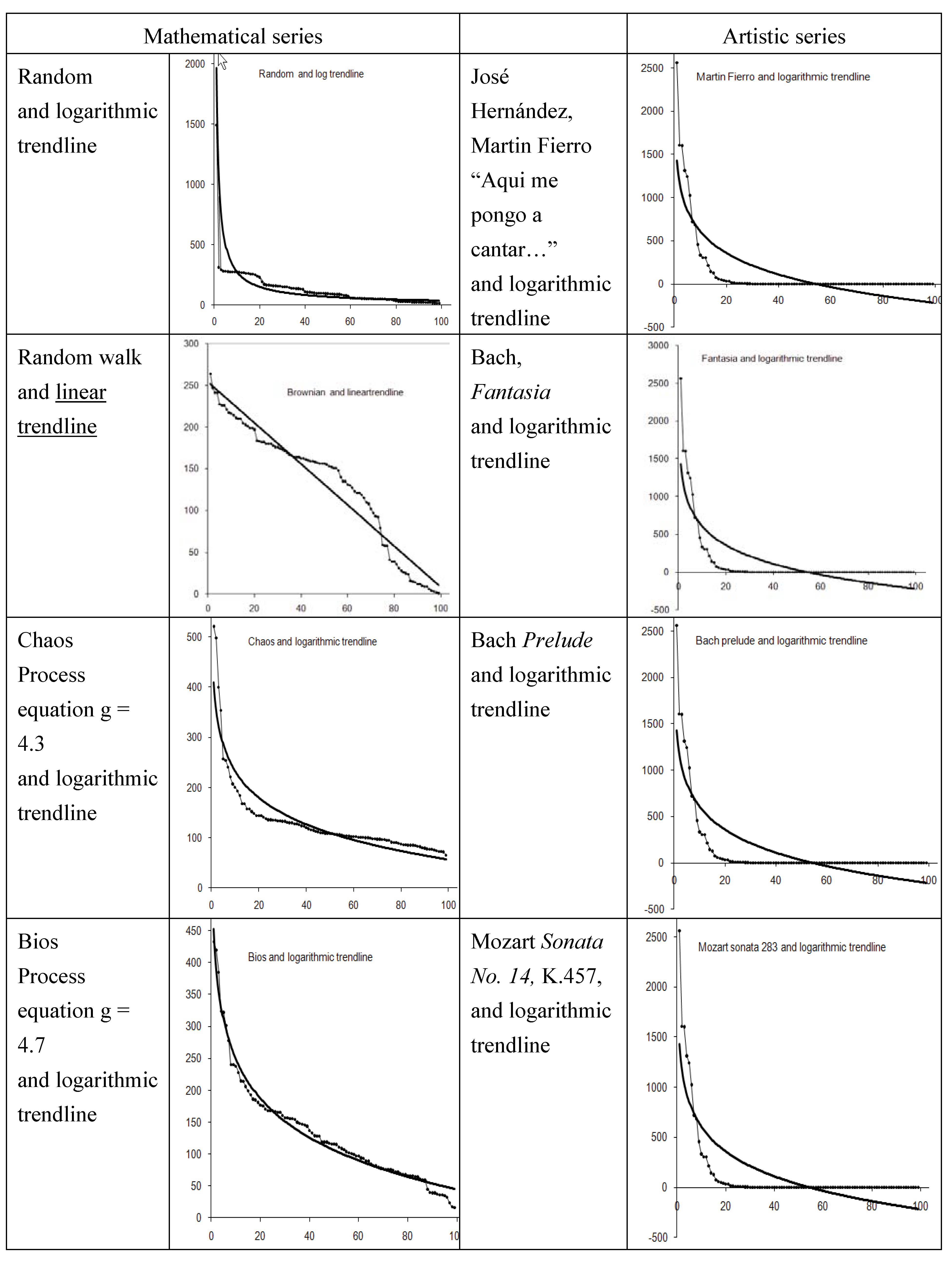
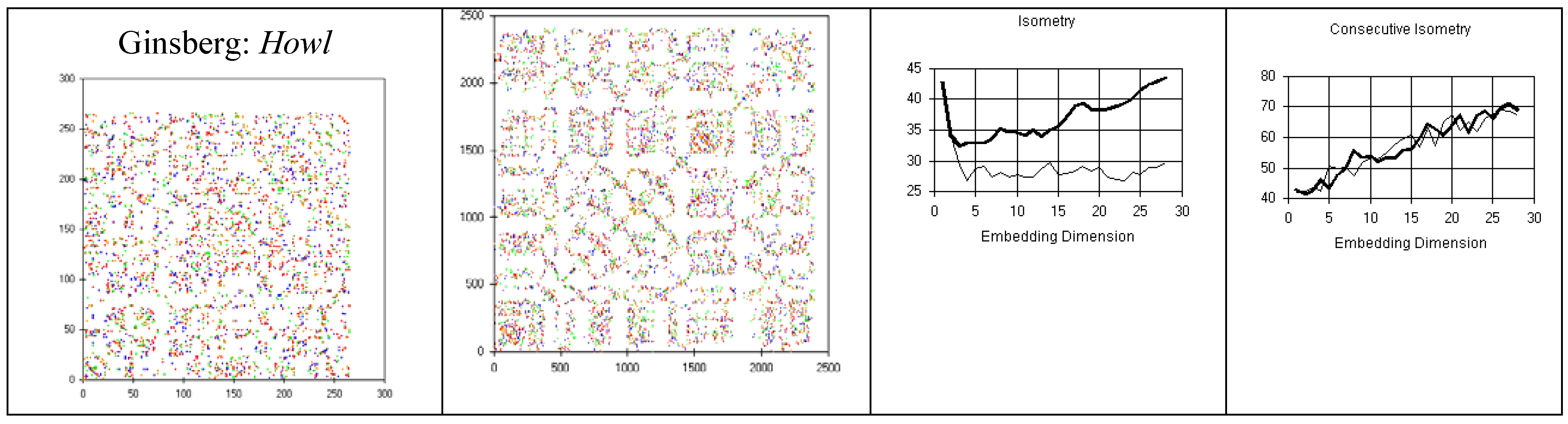
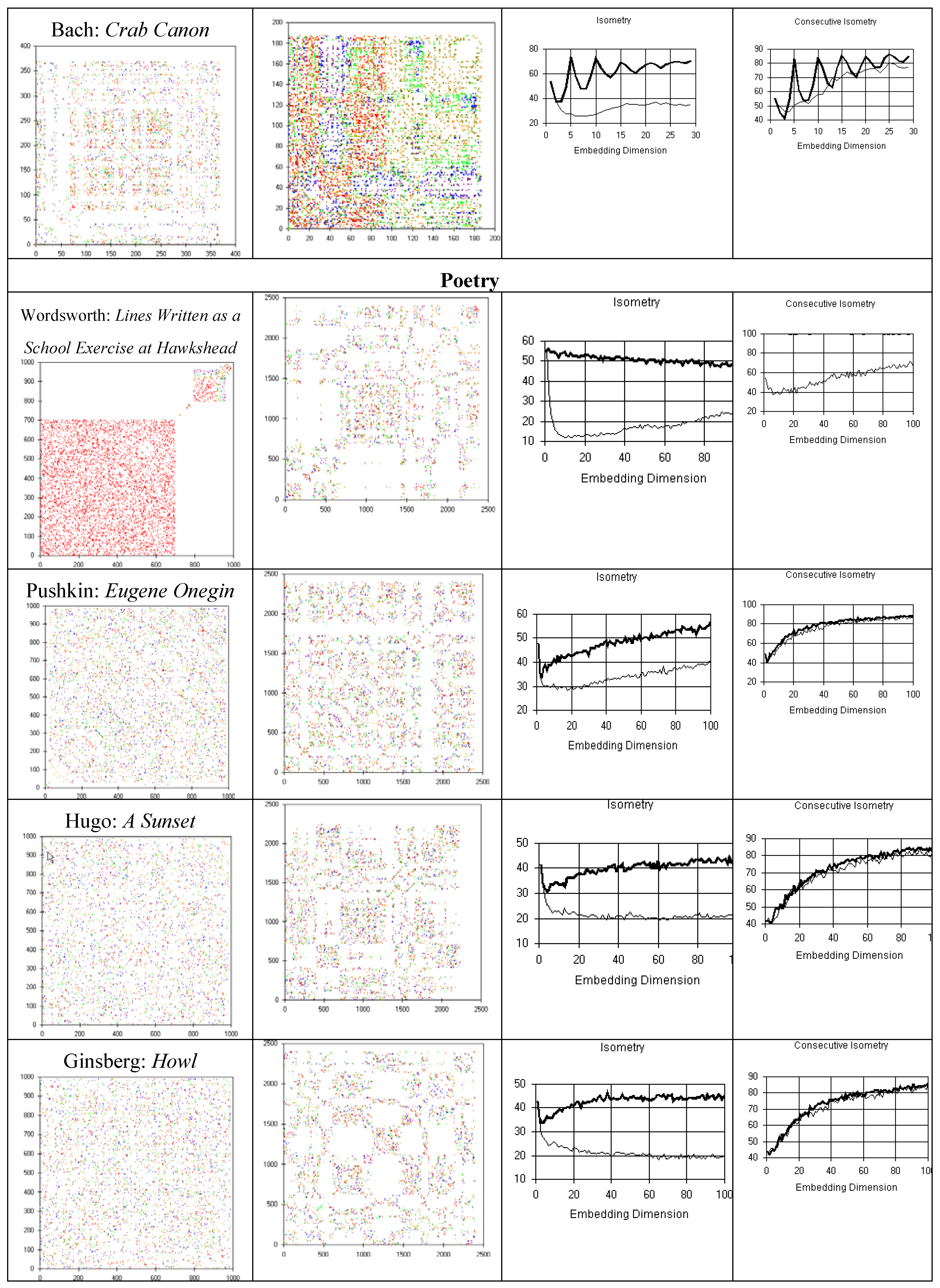
3.3. Power Spectrum Analysis
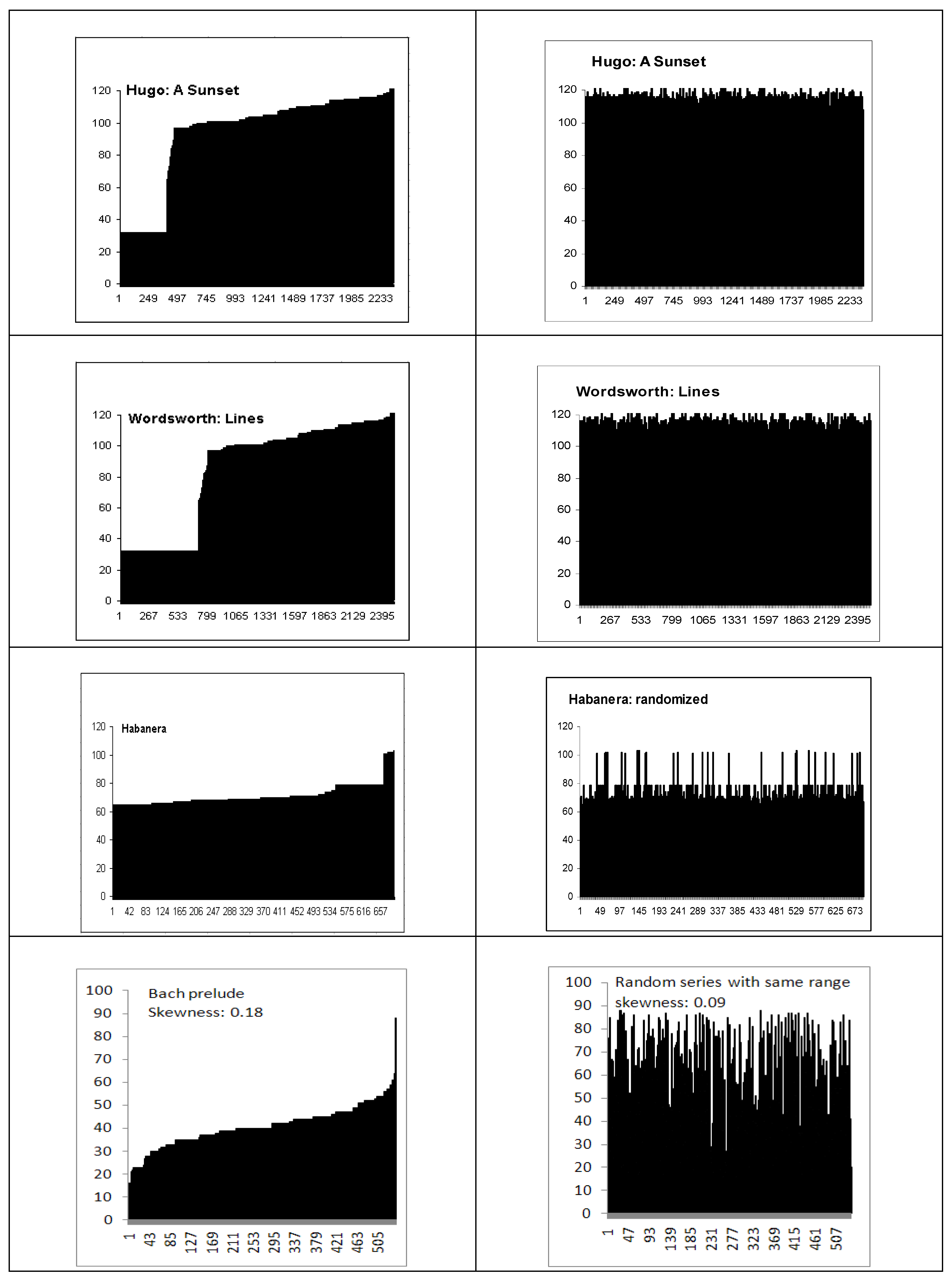
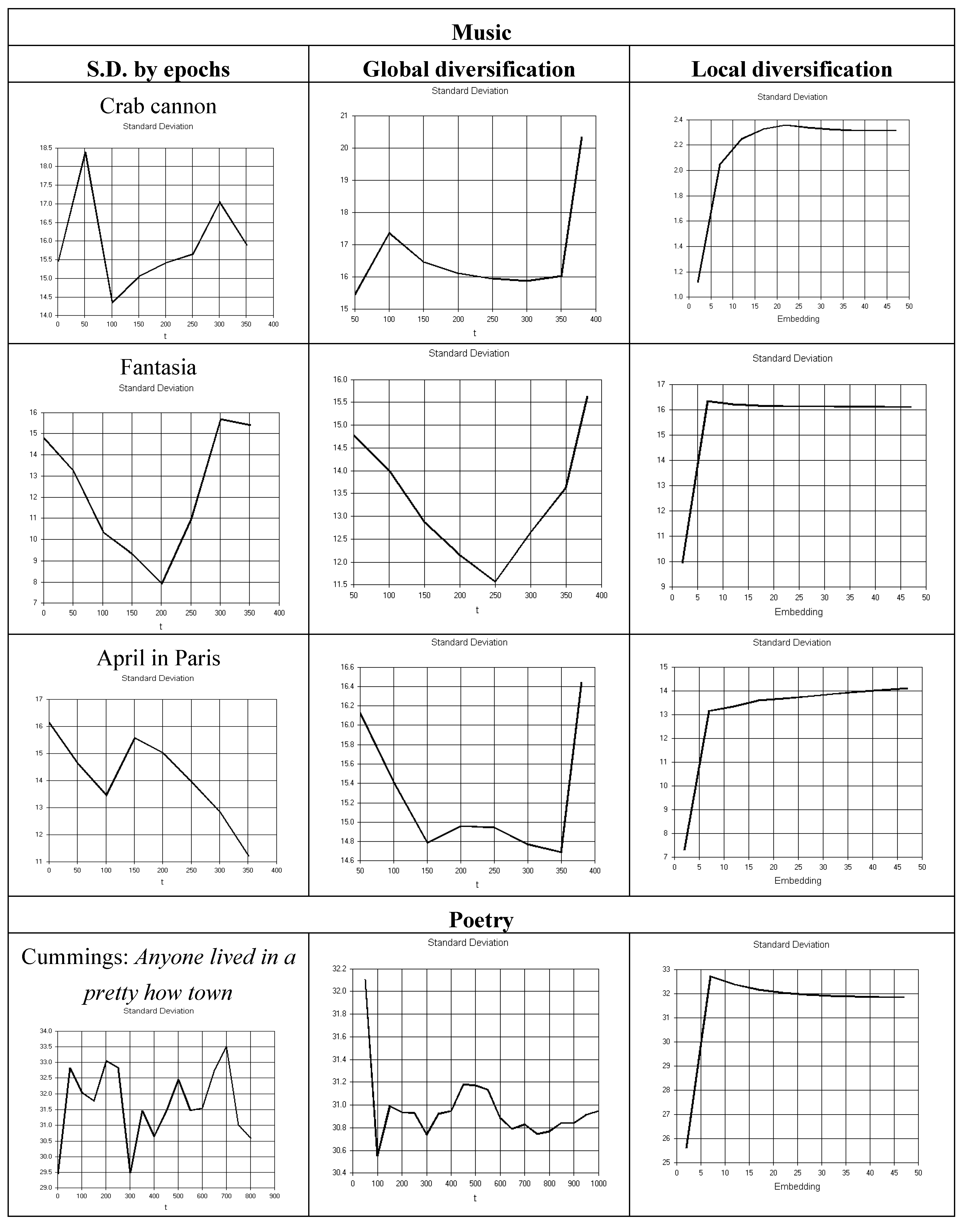
3.4. Biotic Patterns in Music and Poetry
4. Discussion
Acknowledgements
References
- Anderson, P.W. More Is Different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Bourbaki, N. Éléments de mathématique; Actualités Scientifiques et Industrielles: Paris, France, 1952. [Google Scholar]
- Beth, E.W.; Piaget, J. Epistémologie mathématique et psychologie; Essai sur les relations entre la logique formelle et la pensée réelle: Paris, France, 1961. [Google Scholar]
- Sabelli, H. Union of Opposites: A Comprehensive Theory of Natural and Human Processes; Brunswick Publishing: Lawrenceville, VA, USA, 1989. [Google Scholar]
- Sabelli, H. Bios: A Study of Creation; World Scientific: Singapore, 2005. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L. As simple as one, two, three. Arithmetic: a simple, powerful, natural and dynamic logic. In Sustainable Peace in the World System and the Next Evolution of Human Consciousness, Proceeding of International Systems Society 40th meeting; Hall, M.L.W., Ed.; Louisville, KY, USA, 1996; pp. 543–554. [Google Scholar]
- Sabelli, H.; Kovacevic, L. Quantum Bios and Biotic Complexity in the Distribution of Galaxies. Complexity 2006, 11, 14–25. [Google Scholar] [CrossRef]
- Sabelli, H.; Kovacevic, L. Biotic Expansion of the Universe. In International Conference on Advances in Internet, Processing, Systems, and Interdisciplinary Research; Sveti Stefan, Montenegro, 2003; Electronic Publication IPSI-2003. [Google Scholar]
- Thomas, G.; Sabelli, H.; Kauffman, L.; Kovacevic, L. Biotic patterns in Schrödinger’s equation and the evolution of the universe. InterJournal 2006, 1787. [Google Scholar]
- Sabelli, H.; Thomas, J.; Kovacevic, L.; Horan, D. Biotic Dynamics of Galactic Distribution, Gravitational Waves, and Quantum Processes. A Causal Theory of Cosmological Evolution. In Black Holes and Galaxy Formation; Wachter, A.D., Propst, R.J., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2009. [Google Scholar]
- Sabelli, H. Complex Biotic Patterns in LIGO Recordings point to the creativity of gravitational interactions. Complexity 2010, 15, 12–24. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Zbilut, J.; Patel, M.; Messer, J.; Walthall, K.; Tom, C.; Fink, P.; Sugerman, A.; Zdanovics, O. How the heart informs about the brain. A process analysis of the electrocardiogram. In Cybernetics and Systems 94; Trappl, R., Ed.; World Scientific: Singapore, 1994. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Patel, M.; Messer, J.; Zbilut, J.; Sugerman, A.; Walthall, K.; Tom, C.; Zdanovics, O. Electropsychocardiography. Illustrating the Application of Process Methods and Chaos Theory to the Comprehensive Evaluation of Coronary Patients. Complex. Chaos Nurs. 1995, 2, 16–24. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H.; Messer, J.; Patel, M.; Sugerman, A.; Kauffman, L.; Walthall, K. Process method: Part I. An empirical measure of novelty differentiates creative organization from static order and chaos. In Systems thinking, globalization of knowledge, and communitarian ethics, Proceeding of International Systems Society; Rhee, Y.P., Bailey, K.D., Eds.; Kwanak Press: Seoul, Korea, 1997; pp. 1072–1090. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L.; Patel, M.; Zbilut, J.; Messer, J.; Walthall, K. Psychocardiological portraits: A clinical application of process theory. In Chaos theory in Psychology; Abraham, F.D., Gilgen, A.R., Eds.; Greenwood Publishing Group: Westport, CT, USA, 1995; pp. 107–125. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L.; Patel, M.; Sugerman, A. Dynamics and psychodynamics: Process Foundations of Psychology. J. Mind Behav. 1997, 18, 305–334. [Google Scholar]
- Sabelli, H.; Messer, J.; Kovacevic, L.; Walthall, K. The biotic pattern of heartbeat intervals. Int. J. Cardiol. 2010, (in press). [Google Scholar] [CrossRef]
- Sabelli, H.; Kovacevic, L. Biotic Complexity of Population Dynamics. Complexity 2008, 13, 47–55. [Google Scholar] [CrossRef]
- Patel, M.; Sabelli, H. Autocorrelation and Frequency Analysis Differentiate Cardiac And Economic Bios From 1/F Noise. Kybernetes 2003, 32, 692–702. [Google Scholar] [CrossRef]
- Sabelli, H. Bios, creative organization in economic, biological, and meteorological data. In International Conference on Advances in Internet, Processing, Systems, and Interdisciplinary Research; Sveti Stefan, Montenegro, 2003; Electronic Publication IPSI-2003. [Google Scholar]
- Sabelli, H.; Sugerman, A.; Kauffman, L.; Kovacevic, L.; Carlson-Sabelli, L.; Patel, M.; Messer, J.; Konecki, J.; Walthall, K.; Kane, K. Biotic Patterns in Biological, Economic and Physical Processes. J. Appl. Syst. Stud. 2004, 5, 14–26. [Google Scholar]
- Sabelli, H. The Biotic Pattern of Prime Numbers. Cybern. Syst. J. 2008, (in press). [Google Scholar]
- Levy, A.; Alden, D.; Levy, C. Biotic patterns in music. In Society for Chaos Theory in Psychology and Life Sciences Meeting, SCTPLS2006; Johns Hopkins University: Baltimore, MD, USA, 4-6 August 2006. [Google Scholar]
- Sabelli, H. Music, Poetry, Painting, and Bipolar Illness. Nonlinear. Dynam. Psychol. Life Sci. 2010, (in press). [Google Scholar]
- Kauffman, L.; Sabelli, H. The Process equation. Cybern. Syst. 1998, 29, 345–362. [Google Scholar]
- Sabelli, H. Complement plots: Analyzing opposites reveals Mandala-like patterns in human heartbeats. Int. J. Gen. Syst. 2000, 29, 799–830. [Google Scholar] [CrossRef]
- Dekking, M.; Mendès-France, M. Uniform Distribution Modulo One. Journal für die reine und angewandte Mathematik 1981, 239, 149–153. [Google Scholar]
- Sabelli, H.; Sugerman, A.; Kovacevic, L.; Kauffman, L.; Carlson-Sabelli, L.; Patel, M.; Konecki, J. Bios Data Analyzer. Nonlinear. Dynam. Psychol. Life Sci. 2005, 9, 505–538. [Google Scholar]
- Sabelli, H. Novelty, a Measure of Creative Organization in Natural and Mathematical Time Series. Nonlinear. Dynam. Psychol. Life Sci. 2001, 5, 89–113. [Google Scholar] [CrossRef]
- Sabelli, H.; Abouzeid, A. Definition and Empirical Characterization of Creative Processes. Nonlinear. Dynam. Psychol. Life Sci. 2003, 7, 35–47. [Google Scholar] [CrossRef]
- Sabelli, H.; Patel, M.; Sugerman, A.; Kovacevic, L.; Kauffman, L. Process Entropy, a Multidimensional Measure of Diversity and Symmetry. http://creativebios.net/webjass/10Entropy.pdf.
- Sabelli, H.; Sugerman, A.; Carlson-Sabelli, L.; Patel, M.; Kauffman, L. Embedding Plots: A Tool to Measure Simplicity, Complexity and Creativity. J. Appl. Syst. Stud. 2004, 5, 159–201. [Google Scholar]
- Sabelli, H.; Carlson-Sabelli, L. Biological Priority and Psychological Supremacy, a New Integrative Paradigm Derived from Process Theory. Am. J. Psychiatry 1989, 146, 1541–1551. [Google Scholar]
- Torre, C. Chaos, Triadic Theory of Psychological Competence in the Academic Setting. In Chaos Theory in Psychology; Gilgen, A., Abraham, F., Eds.; Praeger/Greenwood Publishing: Westport, CT, USA, 1995; pp. 279–294. [Google Scholar]
- Carlson-Sabelli, L.; Sabelli, H. Phase plane of opposites: A Method to study change in complex processes, and its application to sociodynamics and psychotherapy. Social Dynam. 1992, 3, 1–6. [Google Scholar]
- Sabelli, H. Biothermodynamics. Open Cybern. Syst. J. 2009, (in press). [Google Scholar]
- Schrödinger, E. What is Life? The Physical Aspect of the Living Cell; The Macmillan Company: New York, NY, USA, 1945. [Google Scholar]
- Prigogine, I. From Being to Becoming: The New Science of Connectedness; Doubleday: New York, NY, USA, 1987. [Google Scholar]
- Prigogine, I. The End of Certainty; The Free Press: New York, NY, USA, 1997. [Google Scholar]
- Cohen, J.; Steward, I. The Collapse of Chaos; Penguin: New York, NY, USA, 1994. [Google Scholar]
- Leyton, M. Symmetry, Causality, Mind; MIT Press: Cambridge, UK, 1992. [Google Scholar]
- Petitjean, M. Order, entropy and symmetry: An awkward relation? Symmetry Cult. Sci. 2005, 16, 5–6. [Google Scholar]
- Jakulin, A. Symmetry and information theory. Symmetry Cult. Sci. 2005, 16, 7–26. [Google Scholar]
- Matsuno, K. Symmetry and Information: Symmetry as an Emergent Property of Information. Symmetry Cult. Sci. 2005, 16, 27–36. [Google Scholar]
- Smith, A. A hierarchical perspective. Symmetry Cult. Sci. 2005, 16, 37–46. [Google Scholar]
- Salthe, N. Asymmetry and self-organization. Symmetry Cult. Sci. 2005, 16, 71–90. [Google Scholar]
- Darvas, G. Order, entropy and symmetry. Symmetry Cult. Sci. 2005, 16, 91–108. [Google Scholar]
- Lin, S.K. The Nature of the Chemical Process. 1. Symmetry Evolution—Revised Information Theory, Similarity Principle and Ugly Symmetry. Int. J. Mol. Sci. 2001, 2, 10–39. [Google Scholar] [CrossRef]

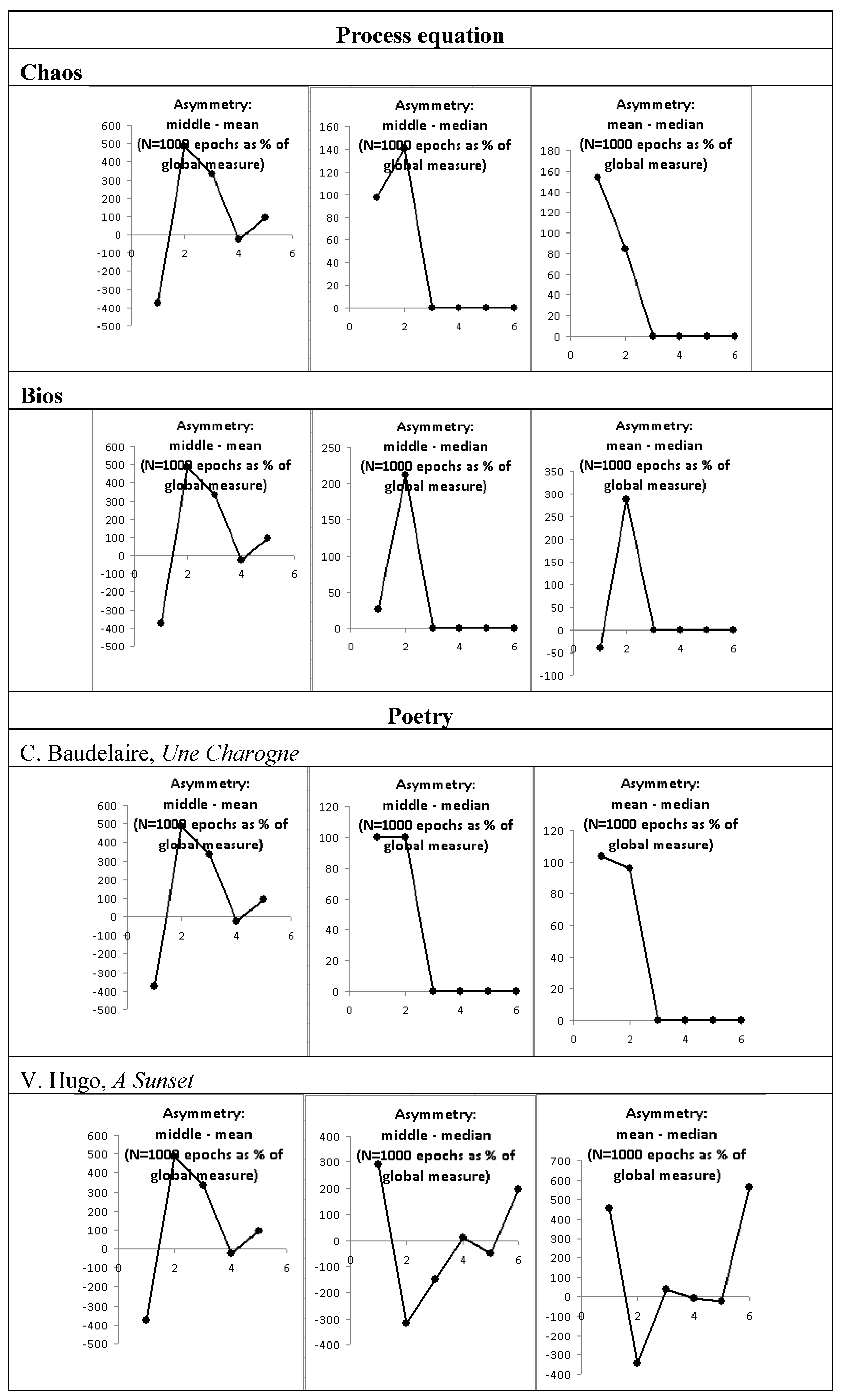
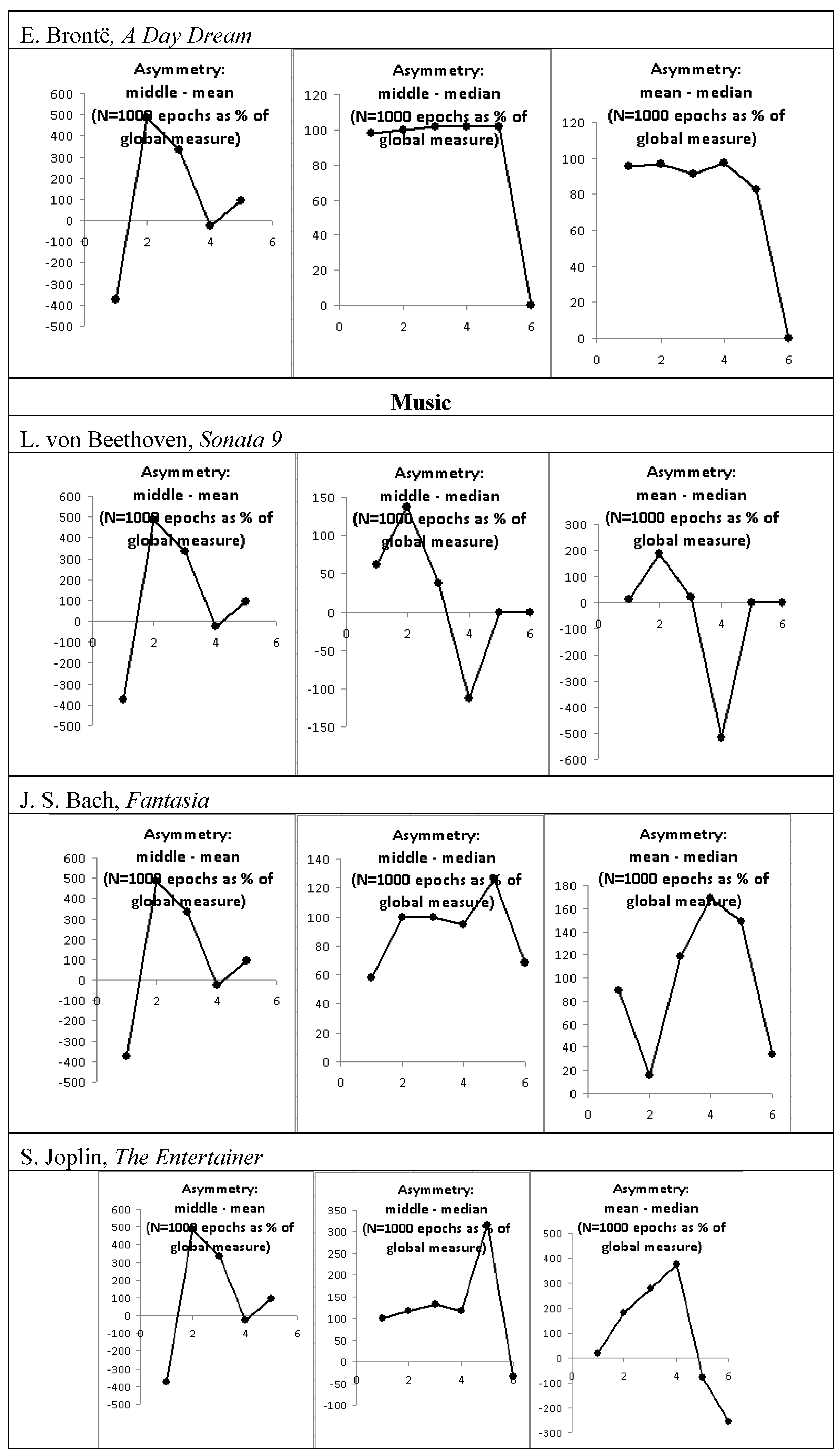


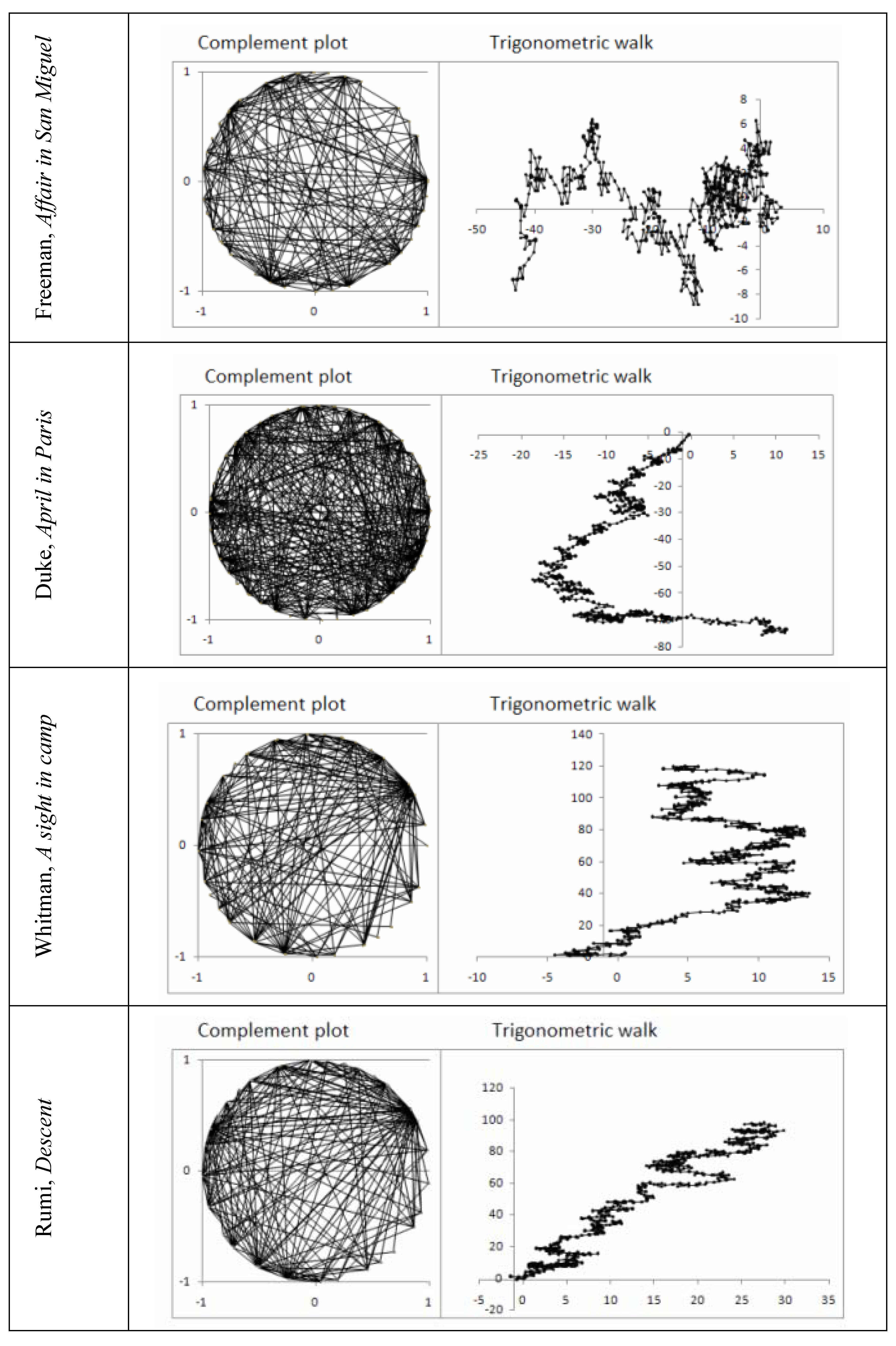










| Series | Max | Min | Middle | Mean | Median | Mean - median | Middle - median | Middle– mean | Cosine/sine average |
|---|---|---|---|---|---|---|---|---|---|
| Random | 9.97 | 0.02 | 5.00 | 4.91 | 4.94 | -0.03 | 0.039 | 0.065 | 4.91 |
| Random Walk | 5.97 | -5.00 | 5.49 | 0.33 | 0.16 | 0.16 | 5.32 | 5.159 | 0.33 |
| Chaos | 5.79 | 0.49 | 2.65 | 3.16 | 3.10 | 0.06 | -0.45 | -0.50 | 3.16 |
| Bios | 17 | -43.87 | 30.43 | -14.02 | -13.02 | -1.00 | 43.45 | 44.45 | -14.02 |
| Prime Numbers | 7919 | 2 | 3959 | 3683 | 3576 | 106.91 | 382.5 | 275.59 | -0.004 |
| Music | |||||||||
| Bach: Prelude | 63 | 16 | 23.5 | 40.52 | 40 | 0.522 | -16.5 | -17.02 | 40.52 |
| Bach: Fantasia | 59 | 11 | 24 | 39.2 | 41 | -1.80 | -17 | -15.20 | 39.20 |
| Freeman: Affair in San Miguel | 59 | 8 | 25.5 | 36.33 | 42 | -5.67 | -16.5 | -10.83 | 36.33 |
| Duke: April in Paris | 59 | 3 | 28 | 37.47 | 36.5 | 0.97 | -8.5 | -9.47 | 37.47 |
| Poetry | |||||||||
| Whitman: A Sight in Camp | 121 | 32 | 44.5 | 92.3 | 104 | -11.70 | -59.5 | -47.80 | 92.30 |
| Rumi: Descent | 122 | 32 | 45 | 90.59 | 104 | -13.41 | -59 | -45.59 | 90.59 |
| Neruda: Puedo escribir | 122 | 32 | 45 | 92.16 | 105 | -12.84 | -60 | -47.16 | 92.16 |
| Fierro: Aquí me pongo a cantar | 243 | 32 | 105.5 | 96.12 | 105 | -8.88 | 0.5 | 9.38 | 96.12 |
| Zorrilla: Don Juan Tenorio | 233 | 32 | 100.5 | 87.1 | 101 | -13.90 | -0.5 | 13.4 | 87.10 |
| Series | Entropy at 16 bins |
|---|---|
| Music | |
| Debussy, Études | 3.20296 |
| Di Capua, O Sole Mio | 2.15 |
| Beethoven, Für Elise | 2.07 |
| Chopin, Ballade No. 4 in F | 3.54696 |
| Denver, Country Roads | 3.638 |
| Bach, Fantasia | 3.65822 |
| Poetry | |
| Hugo, A sunset | 1.75256 |
| Pushkin, Eugene Onegin book I & II | 1.8449 |
| Goethe, To Luna | 2.99606 |
| Mandelstam, Tristia | 2.94824 |
| Blake, On Another’s Sorrow | 2.62664 |
| Whitman, A Sight in Camp | 2.67581 |
| Mathematical series | |
| Random | 3.57727 |
| Random walk | 3.54639 |
| Linearly increasing numbers | 4 |
| Leap (process equation, g = 2*п) | 4 |
| Sine wave | 3.78594 |
| Devil staircase | 3.17955 |
| Lorenz chaos | 3.83145 |
| Rossler chaos | 3.94242 |
| Process equation chaos At+1 = At + 4.3 * sin(At) | 3.76694 |
| Bios: Process equation At+1 = At + 4.65 * sin(At) | 3.62817 |
| Bios: Sum of 4 sine waves | 3.75031 |
| Bios: Sum of 3 sine waves | 3.93651 |
| Natural and social processes | |
| Distance between galaxies | 3.96239 |
| Schrödinger’s equation | 3.64343 |
| El Niño | 3.66817 |
| Air Temperatures | 3.23883 |
| Clear Water River | 2.48224 |
| Earthquakes | 2.37551 |
| MSN Temperature | 3.67427 |
| Heartbeat intervals | 3.50399 |
| Electroencephalogram | 3.19064 |
| Human DNA | 3.67782 |
| Human RND | 3.96081 |
| France population | 3.51594 |
| Daily bond yield DAAA | 3.62622 |
| Model time series | Slope + standard error | Model time series | Slope |
|---|---|---|---|
| Random | 0 | Random walk | 0 |
| Process Chaos | 0.06 | Logistic chaos | -0.28 |
| Bios | -1.76 | Sum of sine waves | -3.64+ 0.02 |
| Pink noise | -1.00 | Brownian noise | -2.11 |
| Physical processes | Slope + standard error | Human processes | Slope + standard error |
| Quantum | -4.08 + 0.11 | Heartbeat intervals | -1.4943 + 0.03 |
| Gravitational waves | -0.27 + 0.04 | Economic | -0.1396 + .03 |
| Music | Slope + standard error | Poetry | Slope + standard error |
| Piano Sonata | -0.33 + 0.06 | Ginsberg: Howl | 0.4087 + 0.04 |
| April in Paris | -0.49 + 0.06 | Wordsworth | -0.1182 + 0.04 |
| Fantasia | -0.29 + 0.06 | Hugo | 0.3746 + 0.04 |
| Chopin Ballad | -0.151 + 0.06 | Mandelstam: Tristia | 0.065 + 0.12 |
| Asymmetry | Dyadic asymmetry and symmetry | Triadic asymmetry and symmetry | |
|---|---|---|---|
| Integers | 1 | 2 | 3 |
| Examples of numerical form | Uni-directional time | Bi-polar and bi-dimensional electro-magnetic charge | Tri-polar nuclear forces |
| Numerical archetypes | Divine proportion φ = 1.618… | Perfect circular symmetry: Π = 3.1415… | e = 2.71828 |
| Form | Asymmetry < | Opposition, asymmetric and symmetric | Triadicity |
| Bourbaki’s structures | Order: lattices | Group opposition and other algebras | Structure: 3D geometry |
| Physics | Action: energy flow in time | Communication (two-valued information: opposites) | Tri-dimensional matter |
| Physical forces | Gravitation (attraction) | Electromagnetic (attraction and repulsion) | Strong nuclear force creates structure. Weak nuclear force creates asymmetry. |
| Light | Linear propagation | Sine wave | Color Spatial radiation |
| Schrodinger equation | Energy, total E and potential U | Sine and cos. if E> U; sinh and cosh if E < U | Momentum = mass * velocity |
| Einstein equation | E | c2 | m |
| Chemistry | Asymmetric molecules and biomolecules (Pasteur) | Covalent and | Asymmetric carbons |
| Biology | Metabolism | Anabolism and catabolism. Sexuality (Linnaeus). | Organisms. Mother, father and child. |
| Evolutionary theory | Life, survival, evolution | Competition and (Darwin) and mutual aid (Kropotkin) | Multicellularity, symbiosis, mutual aid, sociality |
| Central Nervous System | Asymmetric dorsal- sensory to ventral motor axis | Quasi-symmetric right-left axis | Vertical axis from simple to complex |
| Physiology, Medicine | Homeostasis: equilibrium. | Sympathetic and parasympathetic. Periodicity. | Anatomy. |
| Social groups | Age, generations | Sexes. Parent / child. Master / slave. | Upper, middle and lower classes |
| Social aims/organization | Health of persons and environment | Sexes. Class cooperation (socialism) and competition (Smith) and struggle (Marx) | Executive, Legislative and Judicial powers |
| Economics | Consumption | Distribution, trade | Production |
| Psychology | Flux (James). Action (Moreno) | Conflict (Freud). Fight or flight (Cannon). Role reversal (Moreno). | Id, ego, superego (Freud). Creativity: (Moreno). Conflict behaviors and emotions [4]. |
| Cognition [3] | Mental operations regarding order | Mental operations regarding classes | Mental operations regarding space |
| Education [34] | Pragmatic | Emotional | Cognitive and artistic |
| Methodology | Priority of the simple and objective [6, 33]. | Analyze synergy and conflict of opposites | Supremacy of the complex or the subjective [6, 33]. |
| Research techniques | Time series | Phase plane of opposites [35], trigonometric analysis | N-dimensional recurrence |
| Dynamics | Asymmetric factor of catastrophes | Bifurcation. Bifurcating factor of catastrophes | Form and transformation. Complex patterns: fractal, chaos, bios. |
| Process philosophy | Process (not isolated events or stability) | Dialectic: coexisting, interacting, opposites. | Material embodiment. Creative synthesis of opposites and triads. Supremacy of complex |
| Logic / Biotic logic | Implication. Evolving concepts. | Mutual exclusion (Aristotle, Boole) and implication (Sabelli) of opposites. | Triadic categories (Hegel, Pierce) and operations. |
| Process equation | Recursion: A(t + 1) | Sin(A(t)) | Sequence of patterns: convergence, periodicity, chaos, bios |
| Music | Rhythm, tempo | Melody | Harmony |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sabelli, H.; Lawandow, A.; Kopra, A.R. Asymmetry, Symmetry and Beauty. Symmetry 2010, 2, 1591-1624. https://doi.org/10.3390/sym2031591
Sabelli H, Lawandow A, Kopra AR. Asymmetry, Symmetry and Beauty. Symmetry. 2010; 2(3):1591-1624. https://doi.org/10.3390/sym2031591
Chicago/Turabian StyleSabelli, Hector, Atoor Lawandow, and Abbe R. Kopra. 2010. "Asymmetry, Symmetry and Beauty" Symmetry 2, no. 3: 1591-1624. https://doi.org/10.3390/sym2031591
APA StyleSabelli, H., Lawandow, A., & Kopra, A. R. (2010). Asymmetry, Symmetry and Beauty. Symmetry, 2(3), 1591-1624. https://doi.org/10.3390/sym2031591




