Gypsum Precipitation under Saline Conditions: Thermodynamics, Kinetics, Morphology, and Size Distribution
Abstract
:1. Introduction
2. Thermodynamics
2.1. Determination of Saturation, Solubility, and Activity Coefficients
2.2. The Pitzer Formalism
2.3. Effects of Temperature and Composition on Gypsum Solubility
2.3.1. Range of Gypsum Stability
2.3.2. Effect of Temperature
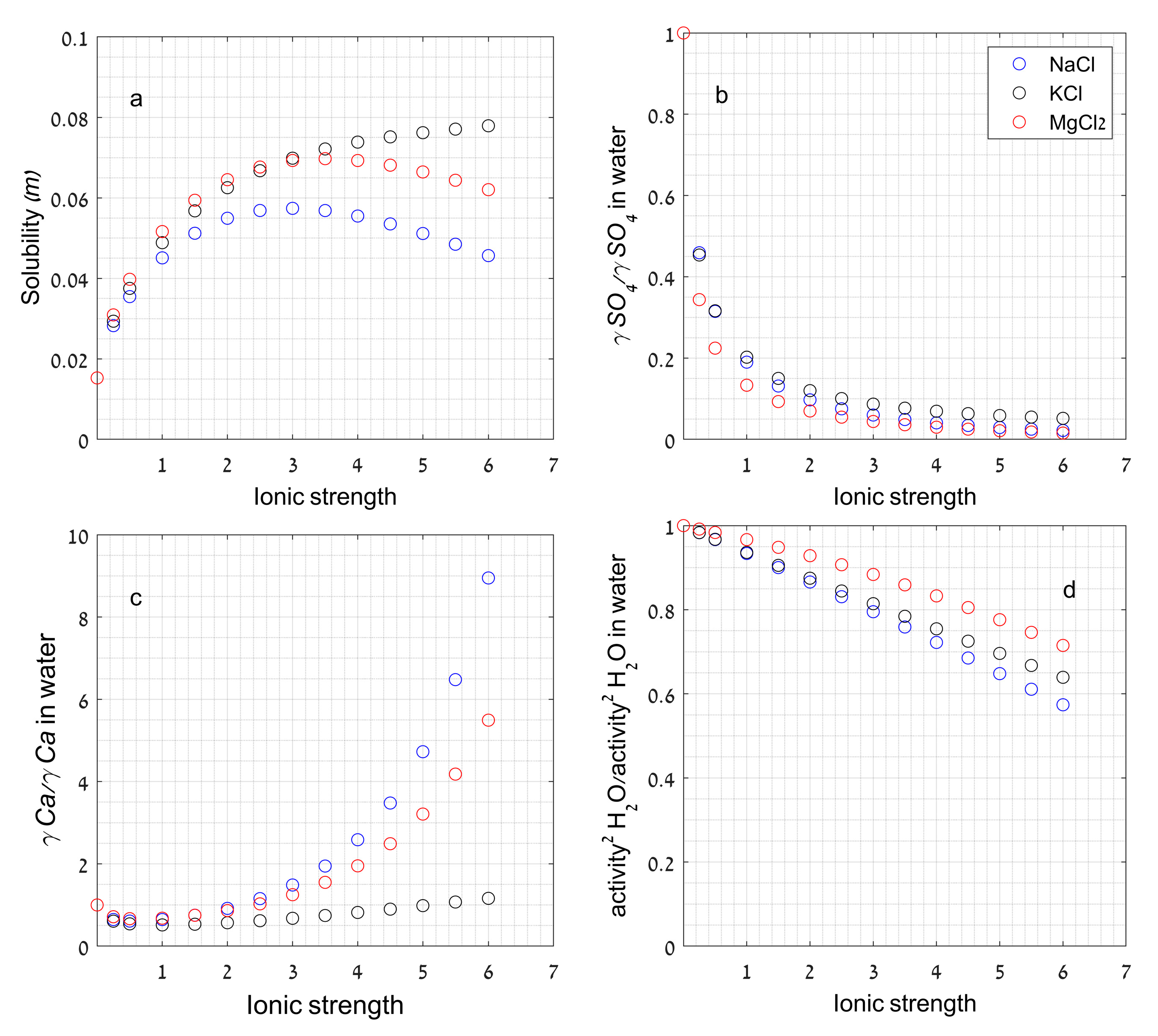
2.3.3. Effect of Ionic Strength
2.3.4. Effect of Ca2+/SO42− Ratio
3. Gypsum Precipitation in Saline Environments: Mechanisms and Rates
3.1. Gypsum Nucleation
3.1.1. Pathways of Nucleation
3.1.2. Gypsum Nucleation—Microscopic Observations
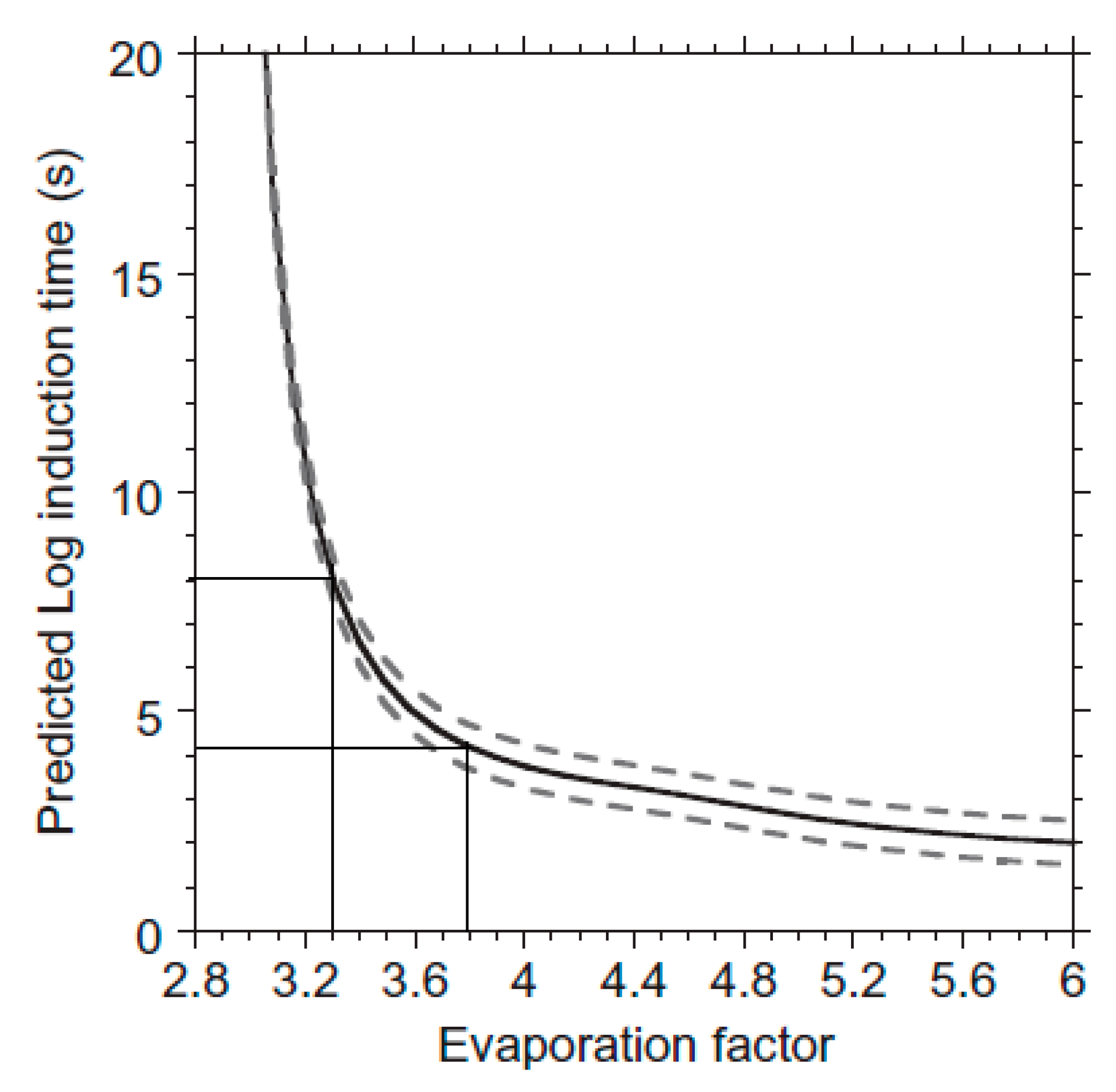
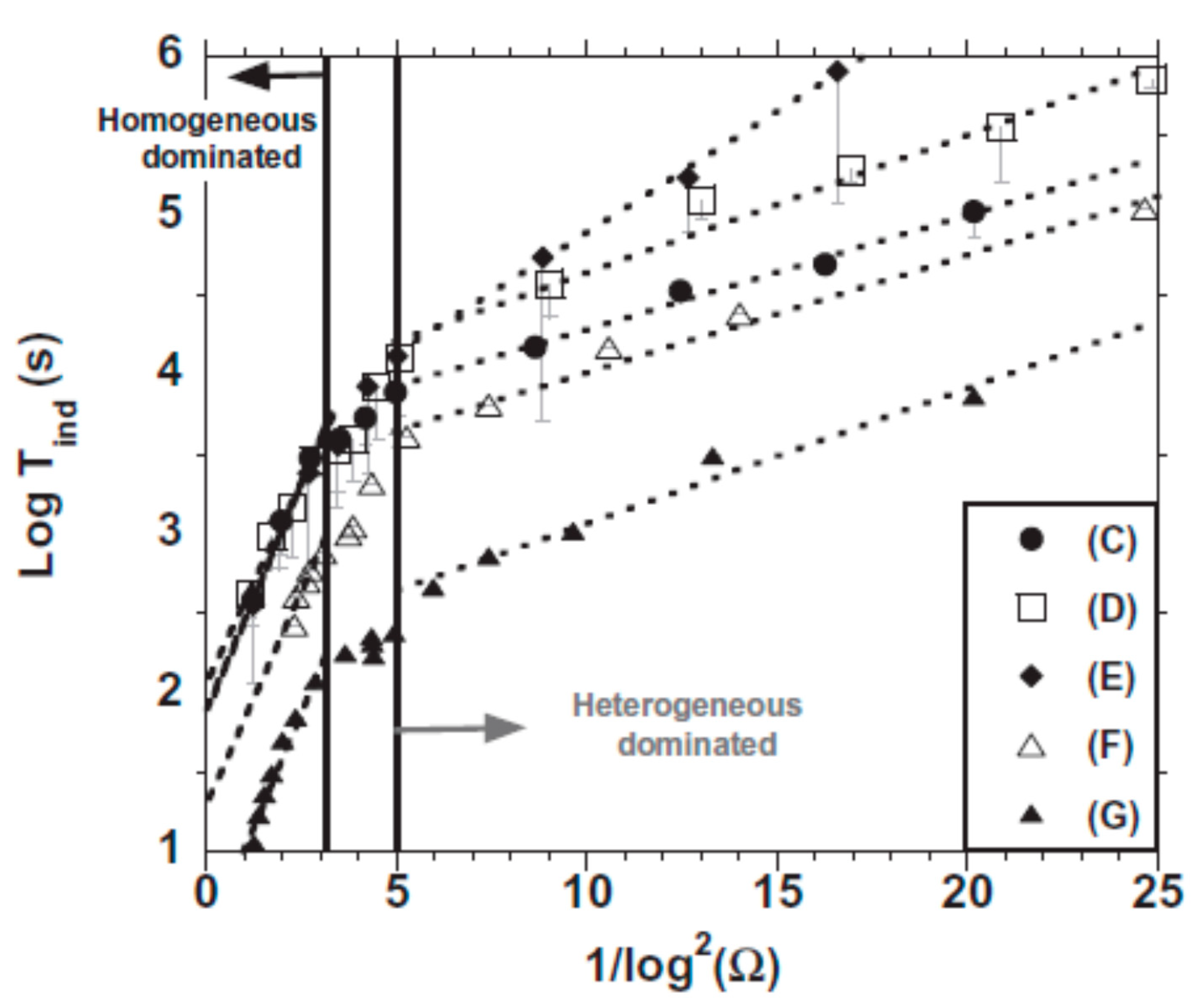
3.1.3. Macroscopic Observations and Nucleation Kinetics
3.2. Gypsum Crystal Growth: Mechanisms and Kinetics
3.2.1. Crystal Growth
3.2.2. Gypsum Crystal Growth—Microscopic Observations
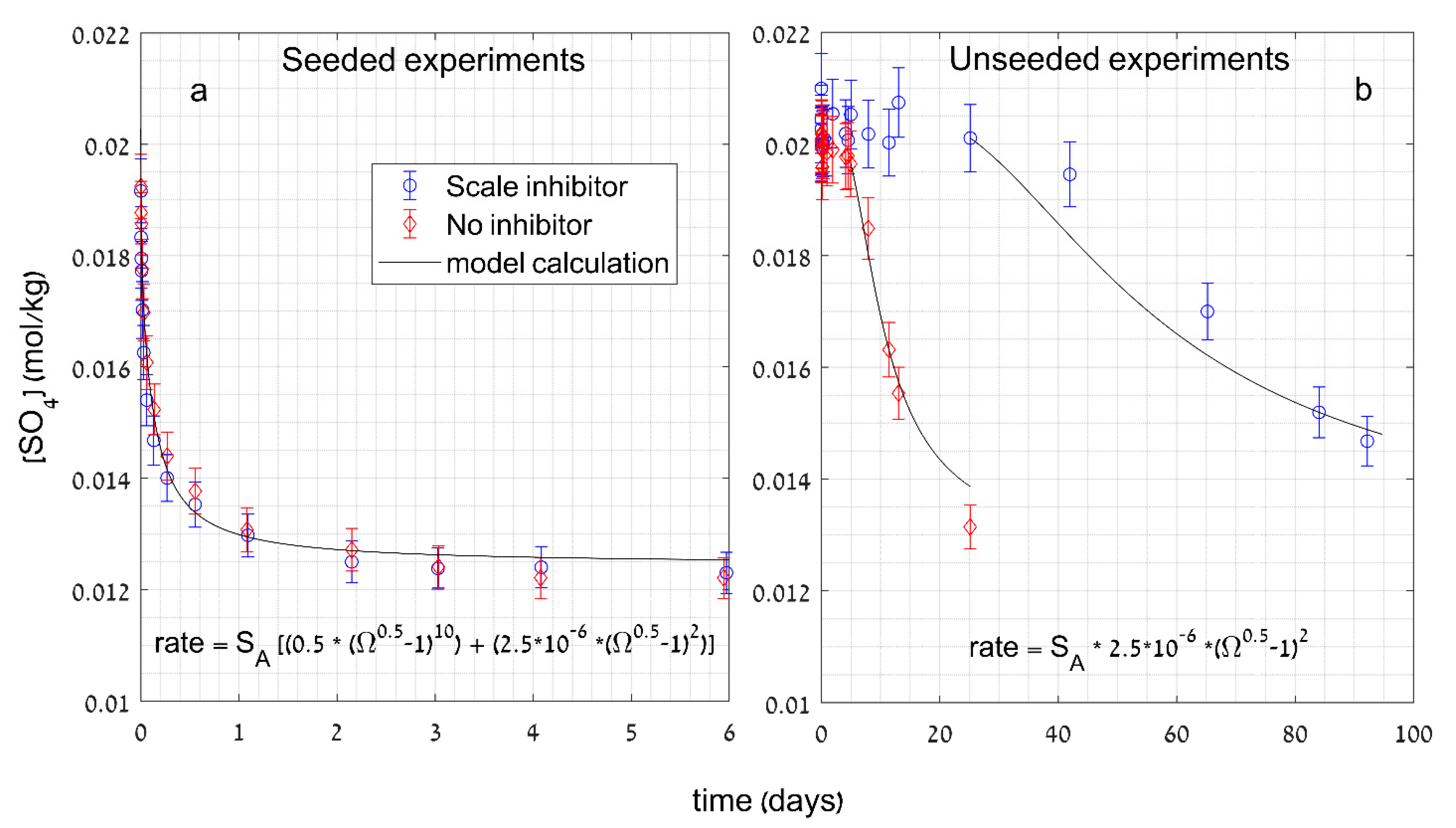
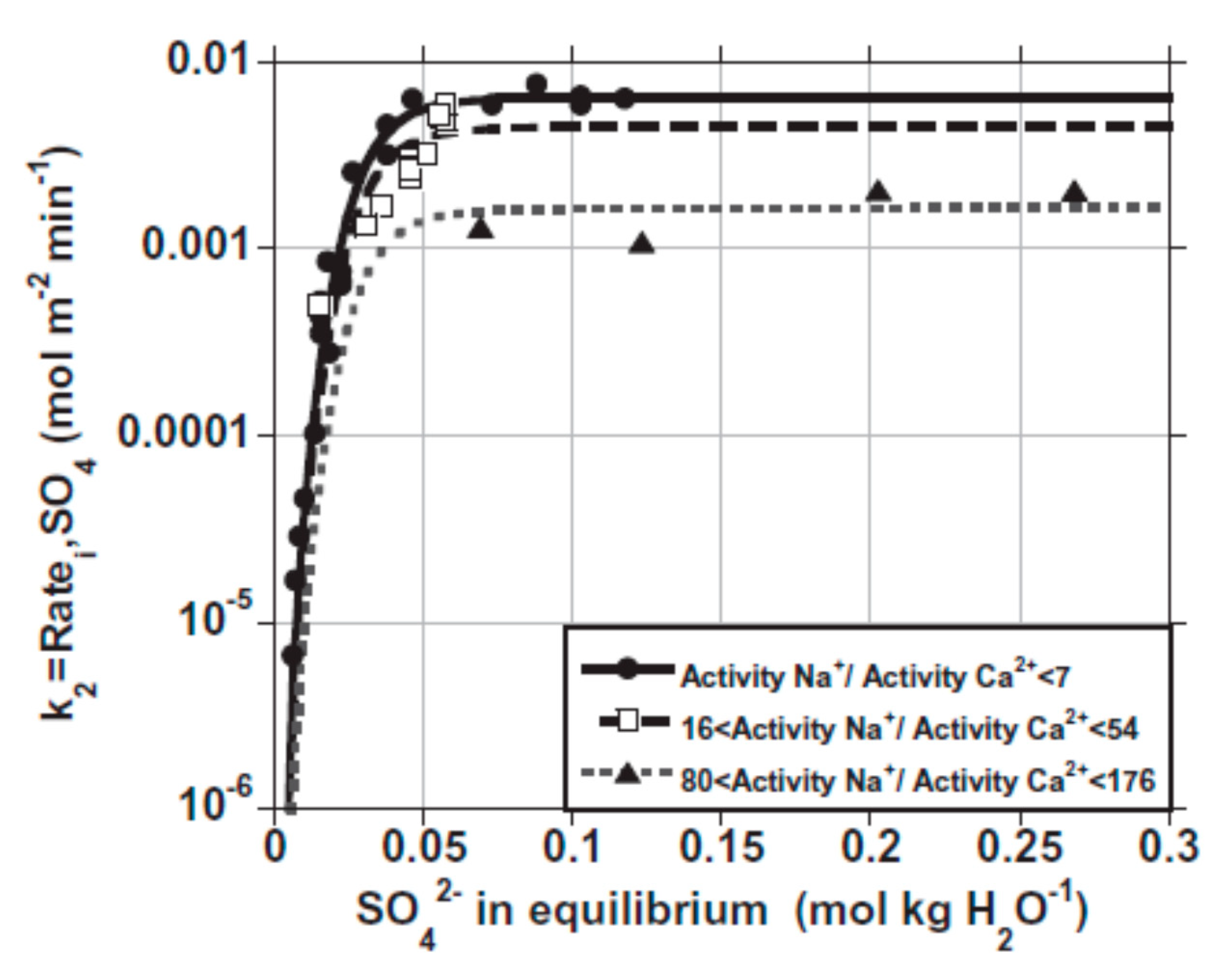
3.2.3. Rate Equations of Gypsum Crystal Growth
Reaction Order for Gypsum Growth
Crystal Growth’s Rate Coefficient (k)
3.3. Gypsum Precipitation in Large-Scale Systems
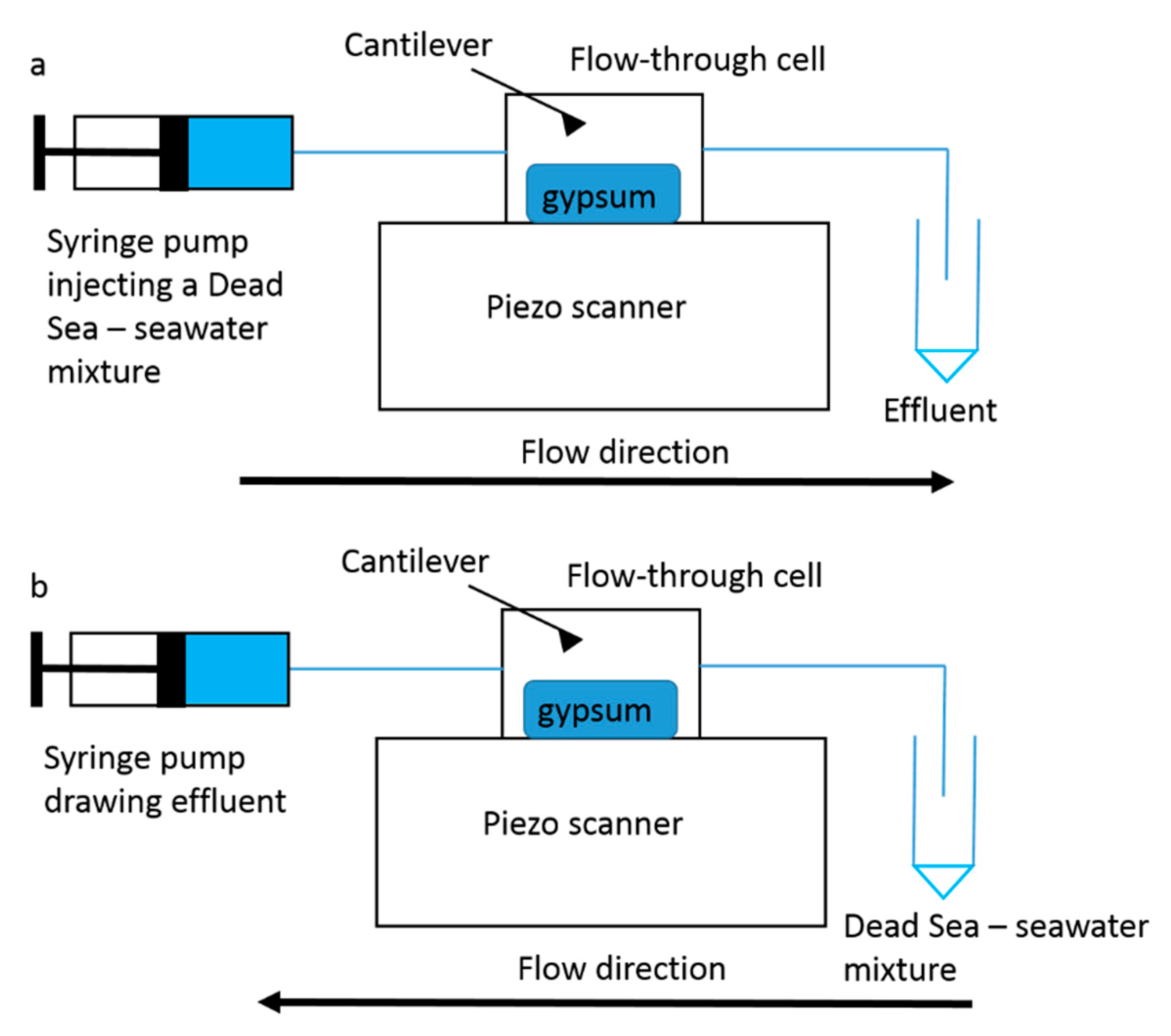
3.4. Challenges of Imaging Precipitation in Brines
4. Crystal Habit and Size Distribution
4.1. Gypsum Morphology
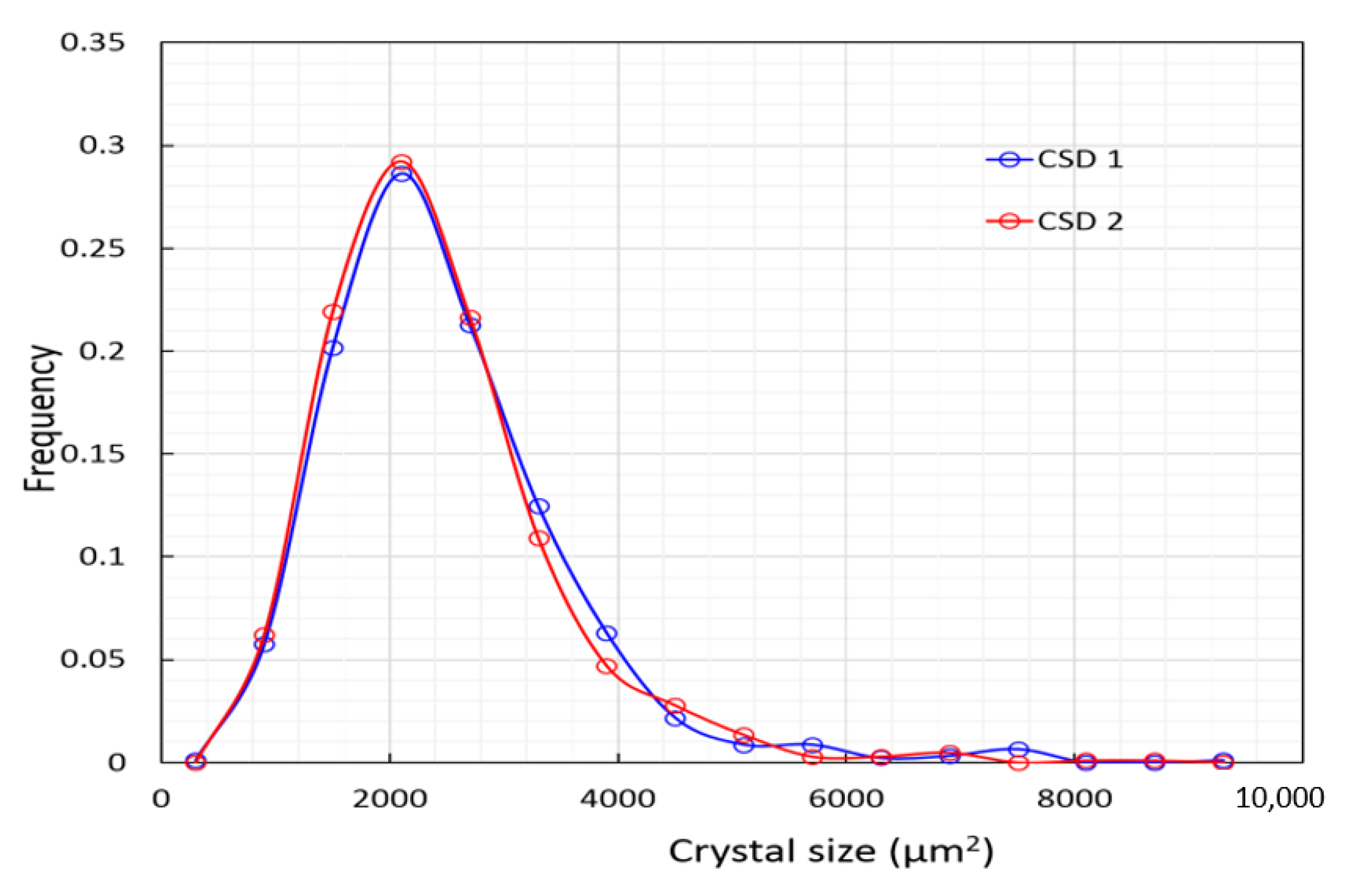
4.2. Gypsum—Crystal Size Distribution and Its Implications
5. Summary and Outline for Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nabhan, S.; Luber, T.; Scheffler, F.; Heubeck, C. Climatic and geochemical implications of Archean pedogenic gypsum in the Moodies Group (~3.2Ga), Barberton Greenstone Belt, South Africa. Precambrian Res. 2016, 275, 119–134. [Google Scholar] [CrossRef]
- Lugli, S.; Manzi, V.; Roveri, M.; Schreiber, B.C. The Primary Lower Gypsum in the Mediterranean: A new facies interpretation for the first stage of the Messinian salinity crisis. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2010, 297, 83–99. [Google Scholar] [CrossRef]
- Thompson, J.B.; Ferris, F.G. Cyanobacterial precipitation of gypsum, calcite, and magnesite from natural alkaline lake water. Geology 1990, 18, 995–998. [Google Scholar] [CrossRef]
- Levy, E.J.; Sivan, O.; Antler, G.; Lazar, B.; Stein, M.; Yechieli, Y.; Gavrieli, I. Mount Sedom salt diapir - Source for sulfate replenishment and gypsum supersaturation in the last glacial Dead Sea (Lake Lisan). Quat. Sci. Rev. 2019, 221, 105871. [Google Scholar] [CrossRef]
- White, S.N.; Dunk, R.M.; Peltzer, E.T.; Freeman, J.J.; Brewer, P.G. In situ Raman analyses of deep-sea hydrothermal and cold seep systems (Gorda Ridge and Hydrate Ridge). Geochemistry, Geophys. Geosystems 2006, 7. [Google Scholar] [CrossRef]
- Tang, M.; Ehreiser, A.; Li, Y.-L. Gypsum in modern Kamchatka volcanic hot springs and the Lower Cambrian black shale: Applied to the microbial-mediated precipitation of sulfates on Mars. Am. Mineral. 2014, 99, 2126–2137. [Google Scholar] [CrossRef] [Green Version]
- Alt, J.C.; Davidson, G.J.; Teagle, D.A.H.; Karson, J.A. Isotopic composition of gypsum in the Macquarie Island ophiolite: Implications for the sulfur cycle and the subsurface biosphere in oceanic crust. Geology 2003, 31, 549–552. [Google Scholar] [CrossRef]
- Ochsenius, C. On the Formation of Rock-Salt Beds and Mother-Liquor Salts. Proc. Acad. Nat. Sci. Philadelphia 1888, 40, 181–187. [Google Scholar]
- Raup, O.B. Gypsum Precipitation By Mixing Seawater Brines. Am. Assoc. Pet. Geol. Bull. 1982, 66, 363–367. [Google Scholar] [CrossRef]
- McCaffrey, M.A.; Lazar, B.; Holland, H.D. The evaporation path of seawater and the coprecipitation of Br− and K+ with halite. J. Sediment. Petrol. 1987, 57, 928–937. [Google Scholar] [CrossRef]
- Lazar, B.; Starinsky, A.; Katz, A.; Sass, E.; Ben-Yaakov, S. The carbonate system in hypersaline solutions: Alkalinity and CaCO3 solubility of evaporated seawater. Limnol. Oceanogr. 1983, 28, 978–986. [Google Scholar] [CrossRef]
- Rosenberg, Y.O.; Sade, Z.; Ganor, J. The precipitation of gypsum, celestine, and barite and coprecipitation of radium during seawater evaporation. Geochim. Cosmochim. Acta 2018, 233, 50–65. [Google Scholar] [CrossRef]
- Braitsch, O. Salt Deposits Their Origin and Composition; Springer Science & Business Media: Salt Lake City, UT, USA, 1971. [Google Scholar]
- Stein, M. The sedimentary and geochemical record of neogene-quaternary water bodies in the Dead Sea basin - Inferences for the regional paleoclimatic history. J. Paleolimnol. 2001, 26, 271–282. [Google Scholar] [CrossRef]
- Stein, M.; Starinsky, A.; Katz, A.; Goldstein, S.L.; Machlus, M.; Schramm, A. Strontium isotopic, chemical, and sedimentological evidence for the evolution of Lake Lisan and the Dead Sea. Geochim. Cosmochim. Acta 1997, 61, 3975–3992. [Google Scholar] [CrossRef]
- Szynkiewicz, A.; Ewing, R.C.; Moore, C.H.; Glamoclija, M.; Bustos, D.; Pratt, L.M. Origin of terrestrial gypsum dunes-Implications for Martian gypsum-rich dunes of Olympia Undae. Geomorphology 2010, 121, 69–83. [Google Scholar] [CrossRef]
- Ryan, W.B.F. Decoding the mediterranean salinity crisis. Sedimentology 2009, 56, 95–136. [Google Scholar] [CrossRef]
- Eardley, A. Gypsum dunes and evaporite history of the Great Salt Lake Desert. Utah Geological and Mineralogical Survey 1962.
- Langevin, Y.; Poulet, F.; Bibring, J.P.; Gondet, B. Sulfates in the north polar region of Mars detected by OMEGA/Mars express. Science 2005, 307, 1584–1586. [Google Scholar] [CrossRef]
- Gendrin, A.; Mangold, N.; Bibring, J.P.; Langevin, Y.; Gondet, B.; Poulet, F.; Bonello, G.; Quantin, C.; Mustard, J.; Arvidson, R.; et al. Sulfates in Martian layered terrains: The OMEGA/Mars express view. Science 2005, 307, 1587–1591. [Google Scholar] [CrossRef] [Green Version]
- Squyres, S.W.; Grotzinger, J.P.; Arvidson, R.E.; Bell, J.F.; Calvin, W.; Christensen, P.R.; Clark, B.C.; Crisp, J.A.; Farrand, W.H.; Herkenhoff, K.E.; et al. In situ evidence for an ancient aqueous environment at Meridiani Planum, Mars. Science 2004, 306, 1709–1714. [Google Scholar] [CrossRef] [Green Version]
- Kah, L.C.; Stack, K.M.; Eigenbrode, J.L.; Yingst, R.A.; Edgett, K.S. Syndepositional precipitation of calcium sulfate in Gale Crater, Mars. Terra Nova 2018, 30, 431–439. [Google Scholar] [CrossRef]
- Farías, M.E.; Contreras, M.; Rasuk, M.C.; Kurth, D.; Flores, M.R.; Poiré, D.G.; Novoa, F.; Visscher, P.T. Characterization of bacterial diversity associated with microbial mats, gypsum evaporites and carbonate microbialites in thalassic wetlands: Tebenquiche and La Brava, Salar de Atacama, Chile. Extremophiles 2014, 18, 311–329. [Google Scholar] [CrossRef] [PubMed]
- Warren, J.K. The hydrological setting, occurrence and significance of gypsum in late Quaternary salt lakes in South Australia. Sedimentology 1982, 29, 609–637. [Google Scholar] [CrossRef]
- Sinha, R.; Raymahashay, B.C. Evaporite mineralogy and geochemical evolution of the Sambhar Salt Lake, Rajasthan, India. Sediment. Geol. 2004, 166, 59–71. [Google Scholar] [CrossRef]
- Hacini, M.; Kherici, N.; Oelkers, E.H. Mineral precipitation rates during the complete evaporation of the Merouane Chott ephemeral lake. Geochim. Cosmochim. Acta 2008, 72, 1583–1597. [Google Scholar] [CrossRef]
- Gibson, G.W. Geological Investigations in Southern Victoria Land, Antarctica. New Zeal. J. Geol. Geophys. 1962, 5, 361–374. [Google Scholar] [CrossRef]
- Rosenberg, Y.O.; Reznik, I.J.; Zmora-Nahum, S.; Ganor, J. The effect of pH on the formation of a gypsum scale in the presence of a phosphonate antiscalant. Desalination 2012, 284, 207–220. [Google Scholar] [CrossRef]
- Karabelas, A.J.; Karanasiou, A.; Mitrouli, S.T. Incipient membrane scaling by calcium sulfate during desalination in narrow spacer-filled channels. Desalination 2014, 345, 146–157. [Google Scholar] [CrossRef]
- Uchymiak, M.; Lyster, E.; Glater, J.; Cohen, Y. Kinetics of gypsum crystal growth on a reverse osmosis membrane. J. Memb. Sci. 2008, 314, 163–172. [Google Scholar] [CrossRef]
- Rosenbauer, R.J.; Bischoff, J.L.; Kharaka, Y.K. Geochemical effects of deep-well injection of the Paradox Valley brine into Paleozoic carbonate rocks, Colorado, U.S.A. Appl. Geochemistry 1992, 7, 273–286. [Google Scholar] [CrossRef]
- Regenspurg, S.; Feldbusch, E.; Byrne, J.; Deon, F.; Driba, D.L.; Henninges, J.; Kappler, A.; Naumann, R.; Reinsch, T.; Schubert, C. Mineral precipitation during production of geothermal fluid from a Permian Rotliegend reservoir. Geothermics 2015, 54, 122–135. [Google Scholar] [CrossRef]
- Rendel, P.M.; Gavrieli, I.; Wolff-Boenisch, D.; Ganor, J. Gypsum solubility under pressure conditions relevant to CO2 geological storage. Int. J. Greenh. Gas Control 2016, 55, 15–22. [Google Scholar] [CrossRef]
- Rendel, P.M.; Gavrieli, I.; Ben-Eliahu, N.; Wolff-Boenisch, D.; Ganor, J. Gypsum crystal growth kinetics under conditions relevant to CO2 geological storage. Int. J. Greenh. Gas Control 2019, 91, 102829. [Google Scholar] [CrossRef]
- Dávila, G.; Luquot, L.; Soler, J.M.; Cama, J. Interaction between a fractured marl caprock and CO2-rich sulfate solution under supercritical CO2 conditions. Int. J. Greenh. Gas Control 2016, 48, 105–119. [Google Scholar] [CrossRef] [Green Version]
- Lattemann, S.; Höpner, T. Environmental impact and impact assessment of seawater desalination. Desalination 2008, 220, 1–15. [Google Scholar] [CrossRef]
- Mady, M.F.; Charoensumran, P.; Ajiro, H.; Kelland, M.A. Synthesis and Characterization of Modified Aliphatic Polycarbonates as Environmentally Friendly Oilfield Scale Inhibitors. Energy and Fuels 2018, 32, 6746–6755. [Google Scholar] [CrossRef]
- Hasson, D.; Shemer, H.; Sher, A. State of the art of friendly “green” scale control inhibitors: A review article. Ind. Eng. Chem. Res. 2011, 50, 7601–7607. [Google Scholar] [CrossRef]
- Reiss, A.G.; Gavrieli, I.; Ganor, J. The effect of phosphonate-based antiscalant on gypsum precipitation kinetics and habit in hyper-saline solutions: An experimental and modeling approach to the planned Red Sea – Dead Sea Project. Desalination 2020, 496, 114638. [Google Scholar] [CrossRef]
- Van Santen, R.A. The Ostwald step rule. J. Phys. Chem. 1984, 88, 5768–5769. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef] [Green Version]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J. Phys. Chem. 1973, 77, 2300–2308. [Google Scholar] [CrossRef] [Green Version]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. III. Activity and osmotic coefficients for 2-2 electrolytes. J. Solution Chem. 1974, 3, 539–546. [Google Scholar] [CrossRef] [Green Version]
- Pitzer, K.S. Thermodynamics of electrolytes. V. effects of higher-order electrostatic terms. J. Solution Chem. 1975, 4, 249–265. [Google Scholar] [CrossRef] [Green Version]
- Pitzer, K.S.; Kim, J.J. Thermodynamics of Electrolytes. IV. Activity and Osmotic Coefficients for Mixed Electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef] [Green Version]
- Harvie, C.E.; Weare, J.H. The prediction of mineral solubilities in natural waters: The NaKMgCaClSO4H2O system from zero to high concentration at 25° C. Geochim. Cosmochim. Acta 1980, 44, 981–997. [Google Scholar] [CrossRef]
- Moeller, N. The prediction of mineral solubilities in natural waters: A chemical equilibrium model for the Na-Ca-Cl-SO_4-H_2O system, to high temperature and concentration. Geochim. Cosmochim. Acta 1988, 52, 821–837. [Google Scholar] [CrossRef]
- Krumgalz, B.S.; Millero, F.J. Physico-chemical study of dead sea waters. III. On gypsum saturation in Dead Sea waters and their mixtures with Mediterranean Sea water. Mar. Chem. 1983, 13, 127–139. [Google Scholar] [CrossRef]
- Krumgalz, B.S.; Millero, F.J. Physico-chemical study of the dead sea waters. I. Activity coefficients of major ions in dead sea water. Mar. Chem. 1982, 11, 209–222. [Google Scholar] [CrossRef]
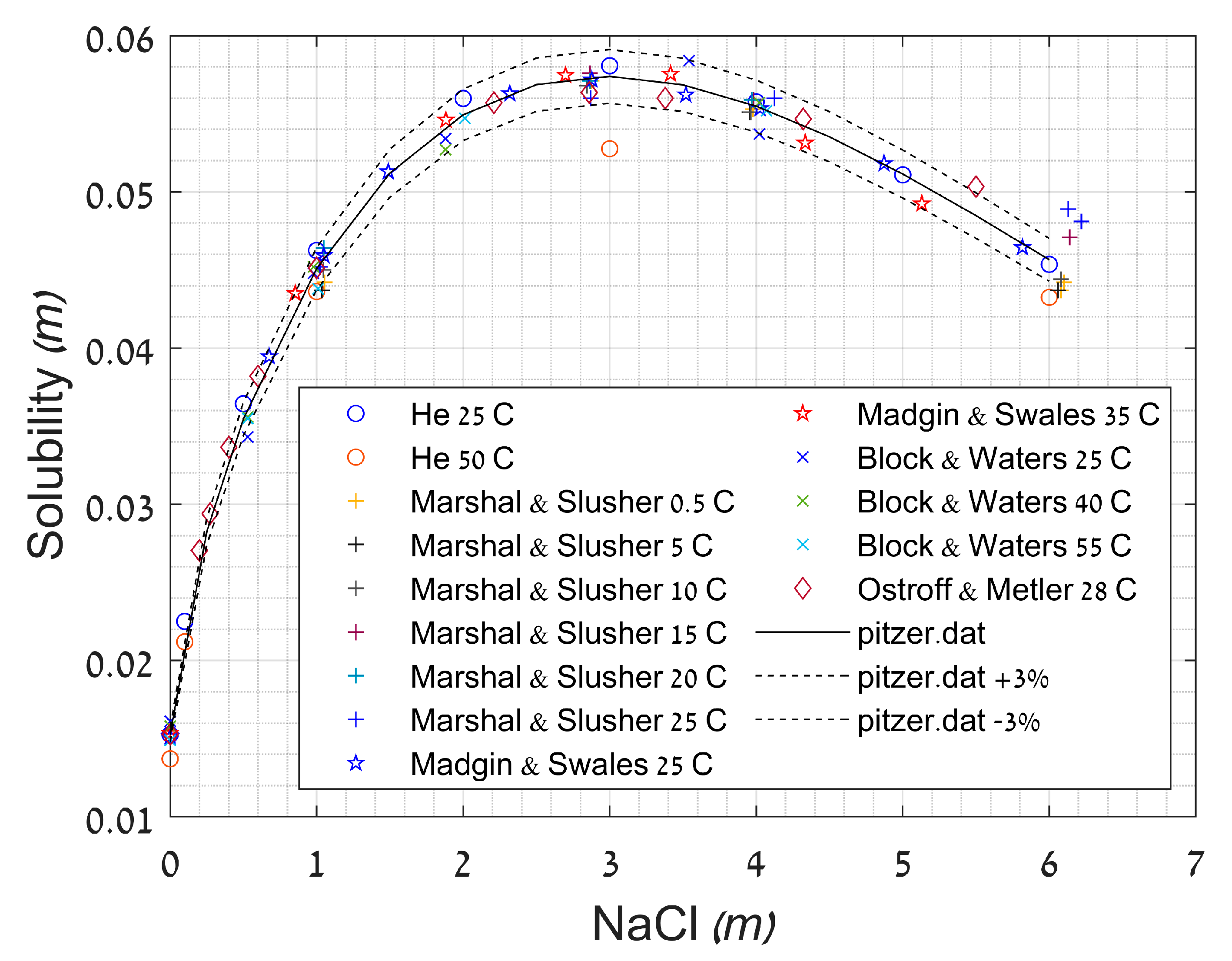
- Krumgalz, B.S. Application of the pitzer ion interaction model to natural hypersaline brines. J. Mol. Liq. 2001, 91, 3–19. [Google Scholar] [CrossRef]
- Harvie, C.E.; Møller, N.; Weare, J.H. The prediction of mineral solubilities in natural waters: The Na-K-Mg-Ca-H-Cl-SO4-OH-HCO3-CO3-CO2-H2O system to high ionic strengths at 25°C. Geochim. Cosmochim. Acta 1984, 48, 723–751. [Google Scholar] [CrossRef]
- Toner, J.D.; Catling, D.C.; Light, B. A revised Pitzer model for low-temperature soluble salt assemblages at the Phoenix site, Mars. Geochim. Cosmochim. Acta 2015, 166, 327–343. [Google Scholar] [CrossRef]
- Appelo, C.A.J. Principles, caveats and improvements in databases for calculating hydrogeochemical reactions in saline waters from 0 to 200°C and 1 to 1000atm. Appl. Geochem. 2015, 55, 62–71. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Bénézeth, P.; Pokrovski, G.S. Thermodynamic databases for water-rock interaction. Rev. Mineral. Geochem. 2009, 70, 1–46. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. User’s Guide to PHREEQC (Version 2): A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. In Water-resources investigations report 99.4259; USGS: Reston, VA, USA, 1999. [Google Scholar]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. In U.S. Geological Survey Techniques and Methods; book 6, chapter A43; USGS: Reston, VA, USA, 2013; ISBN 0092-332X. [Google Scholar]
- Plummer, L.N.; Parkhurst, D.L.; Fleming, G.W.; Dunkle, S. A Computer Program Incorporating Pitzer’s Equations for Calculation of Geochemical Reactions in Brines; U.S. Geological Survey: Washington, DC, USA, 1988. [Google Scholar]
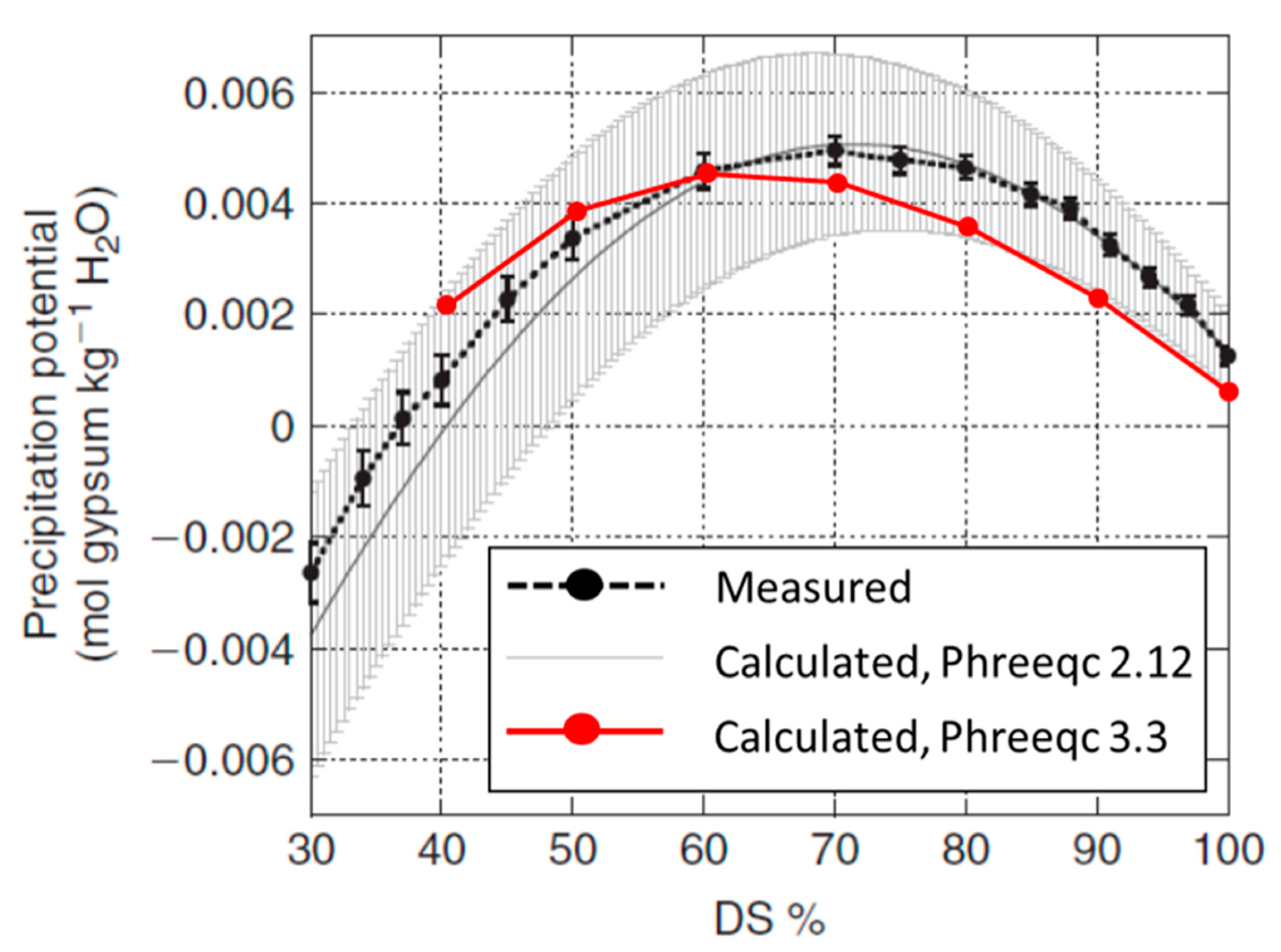
- Reznik, I.J.; Ganor, J.; Gal, A.; Gavrieli, I. Gypsum saturation degrees and precipitation potentials from Dead Seaseawater mixtures. Environ. Chem. 2009, 6, 416–423. [Google Scholar] [CrossRef]
- Appelo, C.A.J.; Parkhurst, D.L.; Post, V.E.A. Equations for calculating hydrogeochemical reactions of minerals and gases such as CO 2 at high pressures and temperatures. Geochim. Cosmochim. Acta 2014, 125, 49–67. [Google Scholar] [CrossRef]
- Rendel, P.M.; Wolff-Boenisch, D.; Gavrieli, I.; Ganor, J. A novel experimental system for the exploration of CO2-water-rock interactions under conditions relevant to CO2 geological storage. Chem. Eng. J. 2018, 334, 1206–1213. [Google Scholar] [CrossRef] [Green Version]
- Hardie, L.A. The gypsum-anhydrite equilibrium at one atmosphere pressure. Am. Mineral. 1967, 52, 171–200. [Google Scholar]
- Blount, C.W.; Dickson, F.W. Gypsum - Anhydrite equilibriua in systems CaSO4-H2O and CaCO4-NaCl-H2O. Am. Mineral. 1973, 58, 323–331. [Google Scholar]
- Raju, K.U.G.; Atkinson, G. The Thermodynamics of “Scale” Mineral Solubilities. 3. Calcium Sulfate in Aqueous NaCl. J. Chem. Eng. Data 1990, 35, 361–367. [Google Scholar] [CrossRef]
- Freyer, D.; Voigt, W. The measurement of sulfate mineral solubilities in the Na-K-Ca-Cl-SO4-H2O system at temperatures of 100, 150 and 200°C. Geochim. Cosmochim. Acta 2004, 68, 307–318. [Google Scholar] [CrossRef]
- Dai, Z.; Kan, A.T.; Shi, W.; Zhang, N.; Zhang, F.; Yan, F.; Bhandari, N.; Zhang, Z.; Liu, Y.; Ruan, G.; et al. Solubility Measurements and Predictions of Gypsum, Anhydrite, and Calcite Over Wide Ranges of Temperature, Pressure, and Ionic Strength with Mixed Electrolytes. Rock Mech. Rock Eng. 2017, 50, 327–339. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; Stawski, T.M.; Kellermeier, M. Calcium sulfate precipitation pathways in natural and engineered environments. Chem. Geol. 2019, 530. [Google Scholar] [CrossRef]
- Madgin, W.M.; Swales, D.A. SOLUBILITIES IN THE SYSTEM CaS04-NaCl-H2O at 25° AT 35°C. J. Appl. Chem. 1956, 6, 482–487. [Google Scholar] [CrossRef]
- Marshall, W.L.; Slusher, R. Thermodynamics of calcium sulfate dihydrate in aqueous sodium chloride solutions, 0–110°. J. Phys. Chem. 1966, 70, 4015–4027. [Google Scholar] [CrossRef]
- Ostroff, A.G.; Metler, A.V. Solubility of Calcium Sulfate Dihydrate in the System NaCI-MgCI2-H20 from 28° to 70 °C. J. Chem. Eng. Data 1966, 11, 346–350. [Google Scholar] [CrossRef]
- Block, J.; Waters, O.B. The CaSO4-Na2SO4-NaCl-H2O System at 25° to 100°C. J. Chem. Eng. Data 1968, 13, 336–344. [Google Scholar] [CrossRef]
- He, S.; Oddo, J.E.; Tomson, M.B. The seeded growth of calcium sulfate dihydrate crystals in NaCl solutions up to 6 m and 90 C. J. Colloid Interface Sci. 1994, 163, 372–378. [Google Scholar] [CrossRef]
- Karthika, S.; Radhakrishnan, T.K.; Kalaichelvi, P. A Review of Classical and Nonclassical Nucleation Theories. Cryst. Growth Des. 2016, 16, 6663–6681. [Google Scholar] [CrossRef]
- De Yoreo, J.J.; Sommerdijk, N.A.J.M.; Dove, P.M. Nucleation Pathways in Electrolyte Solutions. In New Perspectives on Mineral Nucleation and Growth; Springer Science & Business Media: Berlin, Germany, 2017. [Google Scholar]
- Oshchepkov, M.; Popov, K.; Kovalenko, A.; Redchuk, A.; Dikareva, J.; Pochitalkina, I. Initial stages of gypsum nucleation: The role of “nano/microdust”. Minerals 2020, 10, 1083. [Google Scholar] [CrossRef]
- Gebauer, D.; Cölfen, H. Prenucleation clusters and non-classical nucleation. Nano Today 2011, 6, 564–584. [Google Scholar] [CrossRef] [Green Version]
- Furedi-Milhofer, H. Spontaneous precipitation from electrolytic solutions. Pure Appl. Chem. 1981, 53, 2041–2055. [Google Scholar] [CrossRef] [Green Version]
- He, S.; Oddo, J.E.; Tomson, M.B. The Nucleation Kinetics of Calcium Sulfate Dihydrate in NaCl Solutions up to 6 m and 90 °C. J. Colloid Interface Sci. 1994, 162, 297–303. [Google Scholar] [CrossRef]
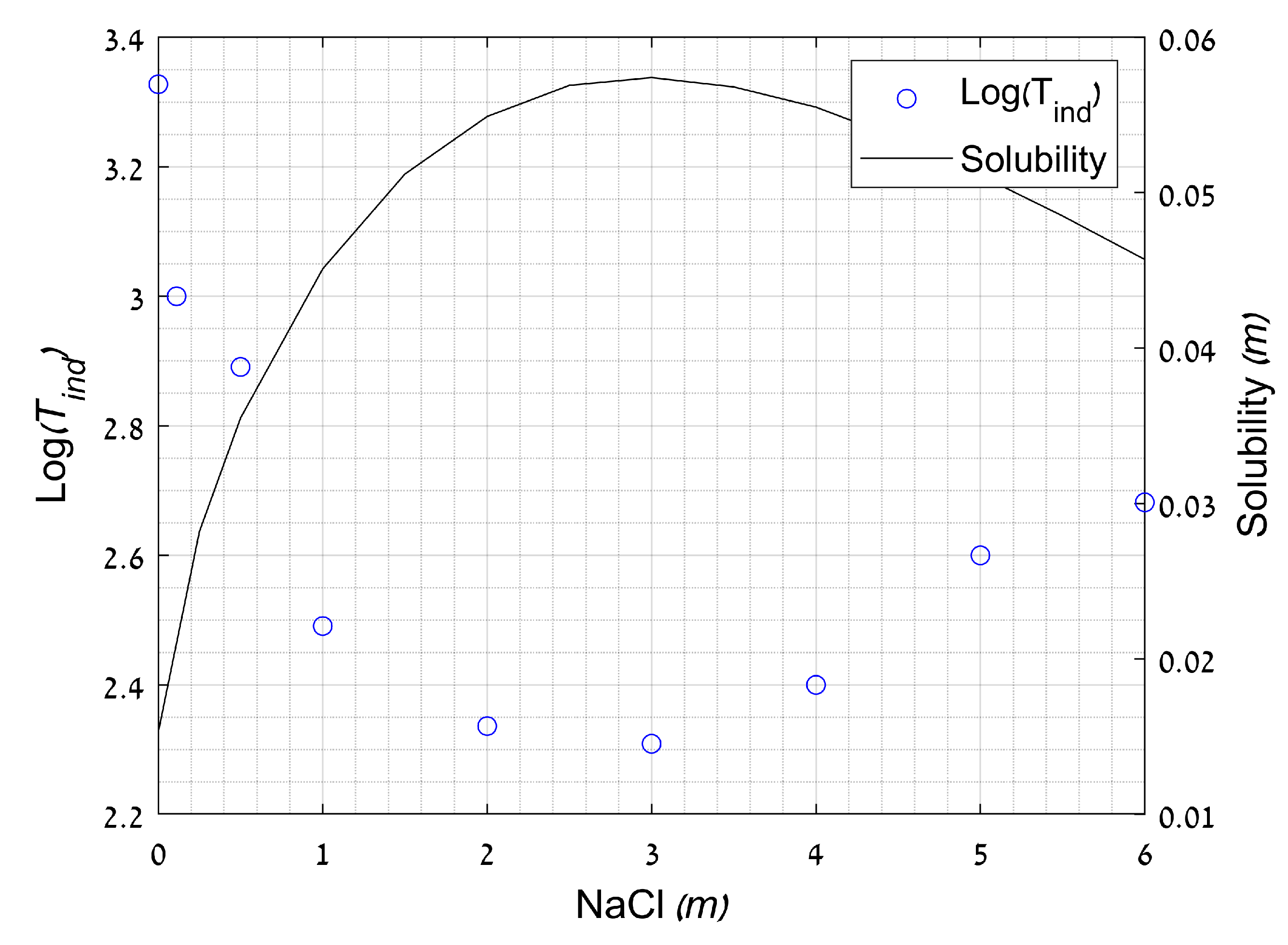
- Söhnel, O.; Mullin, J.W. Interpretation of crystallization induction periods. J. Colloid Interface Sci. 1988, 123, 43–50. [Google Scholar] [CrossRef]
- Reznik, I.J.; Ganor, J.; Gruber, C.; Gavrieli, I. Towards the establishment of a general rate law for gypsum nucleation. Geochim. Cosmochim. Acta 2012, 85, 75–87. [Google Scholar] [CrossRef]
- Rendel, P.M.; Gavrieli, I.; Wolff-Boenisch, D.; Ganor, J. Towards establishing a combined rate law of nucleation and crystal growth – The case study of gypsum precipitation. J. Cryst. Growth 2018, 485, 28–40. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; Benning, L.G.; Rodriguez-Blanco, J.D.; Ossorio, M.; Bots, P.; García-Ruiz, J.M. The Role and Implications of Bassanite as a Stable Precursor Phase to Gypsum Precipitation. Science 2012, 336, 69–72. [Google Scholar] [CrossRef]
- Wang, Y.W.; Kim, Y.Y.; Christenson, H.K.; Meldrum, F.C. A new precipitation pathway for calcium sulfate dihydrate (gypsum) via amorphous and hemihydrate intermediates. Chem. Commun. 2012, 48, 504–506. [Google Scholar] [CrossRef]
- Saha, A.; Lee, J.; Pancera, S.M.; Bräeu, M.F.; Kempter, A.; Tripathi, A.; Bose, A. New insights into the transformation of calcium sulfate hemihydrate to gypsum using time-resolved cryogenic transmission electron microscopy. Langmuir 2012, 28, 11182–11187. [Google Scholar] [CrossRef]
- Stawski, T.M.; Van Driessche, A.E.S.; Ossorio, M.; Diego Rodriguez-Blanco, J.; Besselink, R.; Benning, L.G. Formation of calcium sulfate through the aggregation of sub-3 nanometre primary species. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Jones, F. Infrared investigation of barite and gypsum crystallization: Evidence for an amorphous to crystalline transition. CrystEngComm 2012, 14, 8374–8381. [Google Scholar] [CrossRef] [Green Version]
- Ossorio, M.; Stawski, T.M.; Rodríguez-Blanco, J.D.; Sleutel, M.; García-Ruiz, J.M.; Benning, L.G.; Van Driessche, A.E.S. Physicochemical and additive controls on the multistep precipitation pathway of gypsum. Minerals 2017, 7, 140. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Nie, A.; Yuan, Y.; Ghodsi, S.M.; Song, B.; Firlar, E.; Lu, J.; Lu, Y.P.; Shokuhfar, T.; Megaridis, C.M.; et al. In Situ Transmission Electron Microscopy Explores a New Nanoscale Pathway for Direct Gypsum Formation in Aqueous Solution. ACS Appl. Nano Mater. 2018, 1, 5430–5440. [Google Scholar] [CrossRef]
- Rabizadeh, T.; Stawski, T.M.; Morgan, D.J.; Peacock, C.L.; Benning, L.G. The effects of inorganic additives on the nucleation and growth kinetics of calcium sulfate dihydrate crystals. Cryst. Growth Des. 2017, 17, 582–589. [Google Scholar] [CrossRef]
- Ben Ahmed, S.; Tlili, M.M.; Amami, M.; Ben Amor, M. Gypsum precipitation kinetics and solubility in the NaCl-MgCl 2-CaSO4-H2O system. Ind. Eng. Chem. Res. 2014, 53, 9554–9560. [Google Scholar] [CrossRef]
- Keller, D.M.; Massey, R.E.; Hileman, O.E., Jr. Studies on nucleation phenomena occurring in aqueous solutions supersaturated with calcium sulfate. Can. J. Chem. 1978, 56, 831–838. [Google Scholar] [CrossRef]
- Keller, D.M.; Massey, R.E.; Hileman, O.E., Jr. Studies on nucleation phenomena occurring in aqueous solutions supersaturated with calcium sulfate. III. The cation:anion ratio. Can. J. Chem. 1980, 58, 2127–2131. [Google Scholar] [CrossRef] [Green Version]
- Smith, B.R.; Sweett, F. The crystallization of calcium sulfate dihydrate. J. Colloid Interface Sci. 1971, 37, 612–618. [Google Scholar] [CrossRef]
- Liu, S.T.; Nancollas, G.H. Linear crystallization and induction-period studies of the growth of calcium sulphate dihydrate crystals. Talanta 1973, 20, 211–216. [Google Scholar] [CrossRef]
- Packter, A. The precipitation of calcium sulphate dihydrate from aqueous solution. Induction periods, crystal numbers and final size. J. Cryst. Growth 1974, 21, 191–194. [Google Scholar] [CrossRef]
- Klepetsanis, P.G.; Koutsoukos, P.G. Spontaneous precipitation of calcium sulfate at conditions of sustained supersaturation. J. Colloid Interface Sci. 1991, 143, 299–308. [Google Scholar] [CrossRef]
- Klepetsanis, P.G.; Dalas, E.; Koutsoukos, P.G. Role of Temperature in the Spontaneous Precipitation of Calcium Sulfate Dihydrate. Langmuir 1999, 15, 1534–1540. [Google Scholar] [CrossRef]
- Ziegenheim, S.; Peintler, G.; Pálinkó, I.; Sipos, P. The kinetics of the precipitation of gypsum, CaSO4·2H2O, over a wide range of reactant concentrations. React. Kinet. Mech. Catal. 2020, 131, 75–88. [Google Scholar] [CrossRef]
- Prisciandaro, M.; Lancia, A.; Musmarra, D. Gypsum nucleation into sodium chloride solutions. AIChE J. 2001, 47, 929–934. [Google Scholar] [CrossRef]
- Lancia, A.; Musmarra, D.; Prisciandaro, M. Measuring induction period for calcium sulfate dihydrate precipitation. AIChE J. 2004, 45, 390–397. [Google Scholar] [CrossRef]
- Prisciandaro, M.; Lancia, A.; Musmarra, D. Calcium Sulfate Dihydrate Nucleation in the Presence of Calcium and Sodium Chloride Salts. Ind. Eng. Chem. Res. 2001, 40, 2335–2339. [Google Scholar] [CrossRef]
- Linnikov, O.D. Investigation of the initial period of sulphate scale formation. Part 1. Kinetics and mechanism of calcium sulphate surface nucleation at its crystallization on a heat-exchange surface. Desalination 1999, 122, 1–14. [Google Scholar] [CrossRef]
- Abdel-Aal, E.A.; Rashad, M.M.; El-Shall, H. Crystallization of calcium sulfate dihydrate at different supersaturation ratios and different free sulfate concentrations. Cryst. Res. Technol. 2004, 39, 313–321. [Google Scholar] [CrossRef]
- Keller, D.M.; Massey, R.E.; Hileman, O.E., Jr. Studies on nucleation phenomena occurring in aqueous solutions supersaturated with calcium sulfate. II. The induction time. Can. J. Chem. 1978, 56, 3096–3103. [Google Scholar] [CrossRef]
- Nielsen, A.E.; Söhnel, O. Interfacial tensions electrolyte crystal-aqueous solution, from nucleation data. J. Cryst. Growth 1971, 11, 233–242. [Google Scholar] [CrossRef]
- Söhnel, O. Electrolyte crystal-aqueous solution interfacial tensions from crystallization data. J. Cryst. Growth 1982, 57, 101–108. [Google Scholar] [CrossRef]
- Hina, A.; Nancollas, G.H. Precipitation and dissolution of alkaline earth sulfates: Kinetics and surface energy. Rev. Mineral. Geochemistry 2000, 40, 277–301. [Google Scholar] [CrossRef]
- Hasson, D.; Drak, A.; Semiat, R. Induction times induced in an RO system by antiscalants delaying CaSO4 precipitation. Desalination 2003, 157, 193–207. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton Series in Geochemistry; x+811 pp; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Teng, H.H.; Dove, P.M.; De Yoreo, J.J. Kinetics of calcite growth: Surface processes and relationships to macroscopic rate laws. Geochim. Cosmochim. Acta 2000, 64, 2255–2266. [Google Scholar] [CrossRef]
- Reznik, I.J.; Gavrieli, I.; Antler, G.; Ganor, J. Kinetics of gypsum crystal growth from high ionic strength solutions: A case study of Dead Sea - seawater mixtures. Geochim. Cosmochim. Acta 2011, 75, 2187–2199. [Google Scholar] [CrossRef]
- Witkamp, G.J.; Van Der Eerden, J.P.; Rosmalen, G.M. Van Growth of gypsum I. Kinetics. J. Cryst. Growth 1990, 102, 281–289. [Google Scholar] [CrossRef]
- Christoffersen, J.; Christoffersen, M.R. The kinetics of dissolution of calcium sulphate dihydrate in water. J. Cryst. Growth 1976, 35, 79–88. [Google Scholar] [CrossRef]
- Fischer, C.; Kurganskaya, I.; Schäfer, T.; Lüttge, A. Variability of crystal surface reactivity: What do we know? Appl. Geochemistry 2014, 43, 132–157. [Google Scholar] [CrossRef]
- Fischer, C.; Luttge, A. Beyond the conventional understanding of water–rock reactivity. Earth Planet. Sci. Lett. 2017, 457, 100–105. [Google Scholar] [CrossRef]
- Stack, A.G.; Grantham, M.C. Growth rate of calcite steps as a function of aqueous calcium-to-carbonate ratio: Independent attachment and detachment of calcium and carbonate ions. Cryst. Growth Des. 2010, 4, 1409–1413. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; García-Ruiz, J.M.; Delgado-López, J.M.; Sazaki, G. In situ observation of step dynamics on gypsum crystals. Cryst. Growth Des. 2010, 10, 3909–3916. [Google Scholar] [CrossRef]
- Van Driessche, A.E.S.; García-Ruíz, J.M.; Tsukamoto, K.; Patiño-Lopez, L.D.; Satoh, H. Ultraslow growth rates of giant gypsum crystals. Proc. Natl. Acad. Sci. USA 2011, 108, 15721–15726. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bracco, J.N.; Gooijer, Y.; Higgins, S.R. Hydrothermal atomic force microscopy observations of barite step growth rates as a function of the aqueous barium-to-sulfate ratio. Geochim. Cosmochim. Acta 2016, 183, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bracco, J.N.; Gooijer, Y.; Higgins, S.R. Growth kinetics of step edges on celestite (001) surfaces as a function of temperature, saturation state, ionic strength, and aqueous strontium: Sulfate ratio: An in-situ atomic force microscopy study. Geochim. Cosmochim. Acta 2016, 175, 222–238. [Google Scholar] [CrossRef] [Green Version]
- Shindo, H.; Kaise, M.; Kondoh, H.; Nishihara, C.; Hayakawa, H.; Ono, S.; Nozoye, H. Structure of cleaved surfaces of gypsum studied with atomic force microscopy. J. Chem. Soc. Chem. Commun. 1991, 1097–1099. [Google Scholar] [CrossRef]
- Bosbach, D.; Junta-Rosso, J.L.; Becker, U.; Hochella, M.F. Gypsum growth in the presence of background electrolytes studied by scanning force microscopy. Geochim. Cosmochim. Acta 1996, 60, 3295–3304. [Google Scholar] [CrossRef]
- Bosbach, D.; Rammensee, W. In situ investigation of growth and dissolution on the (010) surface of gypsum by Scanning Force Microscopy. Geochim. Cosmochim. Acta 1994, 58, 843–849. [Google Scholar] [CrossRef]
- Bosbach, D.; Jordan, G.; Rammensee, W. Investigation of surface processes by scanning force microscopy: Crystal growth and dissolution. Microsc. Anal. 1994, 58, 27–29. [Google Scholar]
- Hall, C.; Cullen, D.C. Scanning Force Microscopy of Gypsum Dissolution and Crystal Growth. AIChE J. 1996, 42, 232–238. [Google Scholar] [CrossRef]
- Jordan, G.; Astilleros, J.M. In situ HAFM study of the thermal dehydration on gypsum (010) surfaces. Am. Mineral. 2006, 91, 619–627. [Google Scholar] [CrossRef]
- Morales, J.; Astilleros, J.M.; Matesanz, E.; Fernández-Díaz, L. The growth of gypsum in the presence of hexavalent chromium: A multiscale study. Minerals 2016, 6, 22. [Google Scholar] [CrossRef] [Green Version]
- Mbogoro, M.M.; Peruffo, M.; Adobes-Vidal, M.; Field, E.L.; O’Connell, M.A.; Unwin, P.R. Quantitative 3D Visualization of the Growth of Individual Gypsum Microcrystals: Effect of Ca2+:SO42- Ratio on Kinetics and Crystal Morphology. J. Phys. Chem. C 2017, 121, 12726–12734. [Google Scholar] [CrossRef]
- Criado-Reyes, J.; Pastero, L.; Bruno, M.; García-Ruiz, J.M.; Aquilano, D.; Otálora, F. Equilibrium Shape of 2D Nuclei Obtained from Spiral Hillocks on {010} Form of Gypsum. Cryst. Growth Des. 2020, 20, 1526–1530. [Google Scholar] [CrossRef]
- Aquilano, D.; Otálora, F.; Pastero, L.; García-Ruiz, J.M. Three study cases of growth morphology in minerals: Halite, calcite and gypsum. Prog. Cryst. Growth Charact. Mater. 2016, 62, 227–251. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.T.; Nancollas, G.H. The kinetics of crystal growth of calcium sulfate dihydrate. J. Cryst. Growth 1970, 6, 281–289. [Google Scholar] [CrossRef]
- Liu, S.T.; Nancollas, G.H. The crystal growth of calcium sulfate dihydrate in the presence of additives. J. Colloid Interface Sci. 1973, 44, 422–429. [Google Scholar] [CrossRef]
- Brandse, W.P.; Van Rosmalen, G.M. The influence of sodium chlorine on the crystallization rate of gypsum. J. Inorg. Nucl. Chem. 1977, 39, 2007–2010. [Google Scholar] [CrossRef]
- Amjad, Z. Applications of antiscalants to control calcium sulfate scaling in reverse osmosis systems. Desalination 1985, 54, 263–276. [Google Scholar] [CrossRef]
- Barcelona, M.J.; Atwood, D.K. Gypsum-organic interactions in natural seawater: Effect of organics on precipitation kinetics and crystal morphology. Mar. Chem. 1978, 6, 99–115. [Google Scholar] [CrossRef]
- De Meer, S.; Spiers, C.J.; Peach, C.J. Kinetics of precipitation of gypsum and implications for pressure-solution creep. J. Geol. Soc. London. 2000, 157, 269–281. [Google Scholar] [CrossRef]
- Gill, J.S.; Nancollas, G.H. Kinetics of growth of calcium sulfate crystals at heated metal surfaces. J. Cryst. Growth 1980, 48, 34–40. [Google Scholar] [CrossRef]
- Reznik, I.J.; Gavrieli, I.; Ganor, J. Kinetics of gypsum nucleation and crystal growth from Dead Sea brine. Geochim. Cosmochim. Acta 2009, 73, 6218–6230. [Google Scholar] [CrossRef]
- Christoffersen, M.R.; Christoffersen, J.; Weijnen, M.P.C.; Van Rosmalen, G.M. Crystal growth of calcium sulphate dihydrate at low supersaturation. J. Cryst. Growth 1982, 58, 585–595. [Google Scholar] [CrossRef]
- Zhang, J.; Nancollas, G.H. Influence of calcium/sulfate molar ratio on the growth rate of calcium sulfate dihydrate at constant supersaturation. J. Cryst. Growth 1992, 118, 287–294. [Google Scholar] [CrossRef]
- Steinhorn, I.; Assaf, G.; Gat, J.R.; Nishry, A.; Nissenbaum, A.; Stiller, M.; Beyth, M.; Neev, D.; Garber, R.; Friedman, G.M.; et al. The Dead Sea: Deepening of the mixolimnion signifies the overture to overturn of the water column. Science 1979, 206, 55–57. [Google Scholar] [CrossRef] [PubMed]
- Neev, D.; Emery, K. The Dead Sea—Depositional Processes and Environments of Evaporites; State of Israel, Ministry of Development, Geological Survey: Jerusalem, Israel, 1967; Bulletin report 41.
- Katz, A.; Starinsky, A.; Taitel-Goldman, N.; Beyth, M. Solubilities of gypsum and halite in the Dead Sea and in its mixtures with seawater. Limnol. Oceanogr. 1981, 26, 709–716. [Google Scholar] [CrossRef]
- Reznik, I.J.; Ganor, J.; Lati, J.; Aharoni, M.; Cohen, O.; Maymon, M.; Gavrieli, I. Gypsum precipitation dynamics in a large experiment. proceeding of the 13th International Conference on Water-rock Interaction WRI-13, Guanajuato, Mexico, 16–10 August 2010; pp. 489–492. [Google Scholar]
- Soltis, J. Passivity breakdown, pit initiation and propagation of pits in metallic materials - Review. Corros. Sci. 2015, 90, 5–22. [Google Scholar] [CrossRef]
- Bosbach, D.; Hochella, M.F. Gypsum growth in the presence of growth inhibitors: A scanning force microscopy study. Chem. Geol. 1996, 132, 227–236. [Google Scholar] [CrossRef]
- Arvidson, R.S.; Luttge, A. System and method of fluid exposure and data acquisition. U.S. Patent US8164756B2, 29 September 2009. [Google Scholar]
- Luttge, A.; Arvidson, R.S. Reactions at surfaces: A new approach integrating interferometry and kinetic simulations. J. Am. Ceram. Soc. 2010, 93, 3519–3530. [Google Scholar] [CrossRef]
- Rubbo, M.; Bruno, M.; Massaro, F.R.; Aquilano, D. The five twin laws of gypsum (CaSO 4•2H 2O): A theoretical comparison of the interfaces of the penetration twins. Cryst. Growth Des. 2012, 12, 3018–3024. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Villasuso, R.; Ayora, C.; Canals, A.; Otálora, F. Formation of natural gypsum megacrystals in Naica, Mexico. Geology 2007, 35, 327–330. [Google Scholar] [CrossRef] [Green Version]
- Pinto, A.J.; Ruiz-Agudo, E.; Putnis, C.V.; Putnis, A.; Jiménez, A.; Prieto, M. AFM study of the epitaxial growth of brushite (CaHPO4· 2H2O) on gypsum cleavage surfaces. Am. Mineral. 2010, 95, 1747–1757. [Google Scholar] [CrossRef]
- Massaro, F.R.; Rubbo, M.; Aquilano, D. Theoretical equilibrium morphology of gypsum (CaSO4· 2H2O).1.A syncretic strategy to calculate the morphology of crystals. Cryst. Growth Des. 2010, 10, 2870–2878. [Google Scholar] [CrossRef]
- Massaro, F.R.; Rubbo, M.; Aquilano, D. Theoretical equilibrium morphology of gypsum (CaSO4· 2H2O).2. The stepped faces of the main [001] zone. Cryst. Growth Des. 2011, 11, 1607–1614. [Google Scholar] [CrossRef]
- Rubbo, M.; Massaro, F.R.; Aquilano, D.; Vanzetti, W. Morphology of gypsum: A case study. Cryst. Res. Technol. 2011, 46, 779–783. [Google Scholar] [CrossRef]
- Rabizadeh, T.; Peacock, C.L.; Benning, L.G. Carboxylic acids: Effective inhibitors for calcium sulfate precipitation? Mineral. Mag. 2014, 78, 1465–1472. [Google Scholar] [CrossRef] [Green Version]
- Shukla, J.; Mehta, M.J.; Kumar, A. Solubility Behavior of Calcium Sulfate Dihydrate (Gypsum) in an Aqueous Sodium Chloride System in the Presence of Hydroxyalkyl Ammonium Acetate Ionic Liquids Additives: Morphology Changes and Physicochemical Solution Properties at 35 °C. J. Chem. Eng. Data 2019, 64, 5132–5141. [Google Scholar] [CrossRef]
- Cody, R.D.; Cody, A.M. Gypsum nucleation and crystal morphology in analog saline terrestrial environments. J. Sediment. Petrol. 1988, 58, 247–255. [Google Scholar] [CrossRef]
- Polat, S.; Sayan, P. Effect of various metal ions on gypsum precipitation. Indian Chem. Eng. 2020, 1–11. [Google Scholar] [CrossRef]
- Reiss, A.G.; Ganor, J.; Gavrieli, I. Size Distribution and Morphology of Gypsum Crystals Precipitating from Hypersaline Solutions. Cryst. Growth Des. 2019, 19, 6954–6962. [Google Scholar] [CrossRef]
- Montagnino, D.; Costa, E.; Massaro, F.R.; Artioli, G.; Aquilano, D. Growth morphology of gypsum in the presence of copolymers. Cryst. Res. Technol. 2011, 46, 1010–1018. [Google Scholar] [CrossRef]
- Hoang, T.A.; Ang, H.M.; Rohl, A.L. Effects of Organic Additives on Calcium Sulfate Scaling in Pipes. Aust. J. Chem. 2009, 62, 927. [Google Scholar] [CrossRef]
- Gránásy, L.; Pusztai, T.; Tegze, G.; Warren, J.A.; Douglas, J.F. Growth and form of spherulites. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 72, 011605. [Google Scholar] [CrossRef] [Green Version]
- Alimi, F.; Gadri, A. Kinetics and morphology of formed gypsum. Desalination 2004, 166, 427–434. [Google Scholar] [CrossRef]
- Andreassen, J.-P.; Lewis, A.E. Classical and Nonclassical Theories of Crystal Growth. In New Perspectives on Mineral Nucleation and Growth; Springer: Berlin, Germany, 2017. [Google Scholar]
- Stawski, T.M.; Freeman, H.M.; Van Driessche, A.E.S.; Hövelmann, J.; Besselink, R.; Wirth, R.; Benning, L.G. Particle-Mediated Nucleation Pathways Are Imprinted in the Internal Structure of Calcium Sulfate Single Crystals. Cryst. Growth Des. 2019, 19, 3714–3721. [Google Scholar] [CrossRef] [Green Version]
- Reiss, A.G.; Gavrieli, I.; Ganor, J. The Morphology of Gypsum Precipitated Under Hyper-saline Conditions – Preliminary Results from Dead Sea - Red Sea Mixtures. Procedia Earth Planet. Sci. 2017, 17, 376–379. [Google Scholar] [CrossRef]
- El-Shall, H.; Abdel-Aal, E.A.; Moudgil, B.M. Effect of surfactants on phosphogypsum crystallization and filtration during wet-process phosphoric acid production. Sep. Sci. Technol. 2000, 35, 395–410. [Google Scholar] [CrossRef]
- Reiss, A.G.; Ganor, J.; Hamawi, M.; Gavrieli, I. Dynamics of turbidity in gypsum-precipitating brines: the case of the Red Sea - Dead Sea project. 2021. Under review. [Google Scholar]
- Eberl, D.D.; Kile, D.E.; Drits, V.A. On geological interpretations of crystal size distributions: Constant vs. proportionate growth. Am. Mineral. 2002, 87, 1235–1241. [Google Scholar] [CrossRef]
- Middleton, G.V. Generation of the Log-Normal Frequency Distribution in Sediments. In Topics in Mathematical Geology; Springer: Berlin, Germany, 1970. [Google Scholar]
- Eberl, D.D.; Drits, V.A.; Środoń, J. Deducing growth mechanisms for minerals from the shapes of crystal size distributions. Am. J. Sci. 1998, 298, 499–533. [Google Scholar] [CrossRef]
- Koch, A.L. The logarithm in biology. J. Theor. Biol. 1969, 12, 276–290. [Google Scholar] [CrossRef]
- Crow, E.L.; Shimizu, K. Lognormal Distributions: Theory and Applications, 1 st ed.; Marcel Dekker: New York, NY, USA, 1987. [Google Scholar]
- Kile, D.E.; Eberl, D.D.; Hoch, A.R.; Reddy, M.M. An assessment of calcite crystal growth mechanisms based on crystal size distributions. Geochim. Cosmochim. Acta 2000, 64, 2937–2950. [Google Scholar] [CrossRef]
- Kile, D.E.; Eberl, D.D. On the origin of size-dependent and size-independent crystal growth: Influence of advection and diffusion. Am. Mineral. 2003, 88, 1514–1521. [Google Scholar] [CrossRef]
- Srodor, J.; Eberl, D.D.; Drits, V.A. Evolution of fundamental-particle size during illitization of smectite and implications for reaction mechanism. Clays Clay Miner. 2000, 48, 446–458. [Google Scholar] [CrossRef]
- Emmanuel, S.; Ague, J.J. Impact of nano-size weathering products on the dissolution rates of primary minerals. Chem. Geol. 2011, 282, 11–18. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reiss, A.G.; Gavrieli, I.; Rosenberg, Y.O.; Reznik, I.J.; Luttge, A.; Emmanuel, S.; Ganor, J. Gypsum Precipitation under Saline Conditions: Thermodynamics, Kinetics, Morphology, and Size Distribution. Minerals 2021, 11, 141. https://doi.org/10.3390/min11020141
Reiss AG, Gavrieli I, Rosenberg YO, Reznik IJ, Luttge A, Emmanuel S, Ganor J. Gypsum Precipitation under Saline Conditions: Thermodynamics, Kinetics, Morphology, and Size Distribution. Minerals. 2021; 11(2):141. https://doi.org/10.3390/min11020141
Chicago/Turabian StyleReiss, Amit G., Ittai Gavrieli, Yoav O. Rosenberg, Itay J. Reznik, Andreas Luttge, Simon Emmanuel, and Jiwchar Ganor. 2021. "Gypsum Precipitation under Saline Conditions: Thermodynamics, Kinetics, Morphology, and Size Distribution" Minerals 11, no. 2: 141. https://doi.org/10.3390/min11020141
APA StyleReiss, A. G., Gavrieli, I., Rosenberg, Y. O., Reznik, I. J., Luttge, A., Emmanuel, S., & Ganor, J. (2021). Gypsum Precipitation under Saline Conditions: Thermodynamics, Kinetics, Morphology, and Size Distribution. Minerals, 11(2), 141. https://doi.org/10.3390/min11020141







