Microstructural Analysis of a Mylonitic Mantle Xenolith Sheared at Laboratory-like Strain Rates from the Edge of the Wyoming Craton
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Description
2.2. Analytical Methods
3. Results
3.1. Microstructures, CPO, and Inter- and Intra-Grain Misorientations
3.2. Olivine Monophase and Multiphase Bands
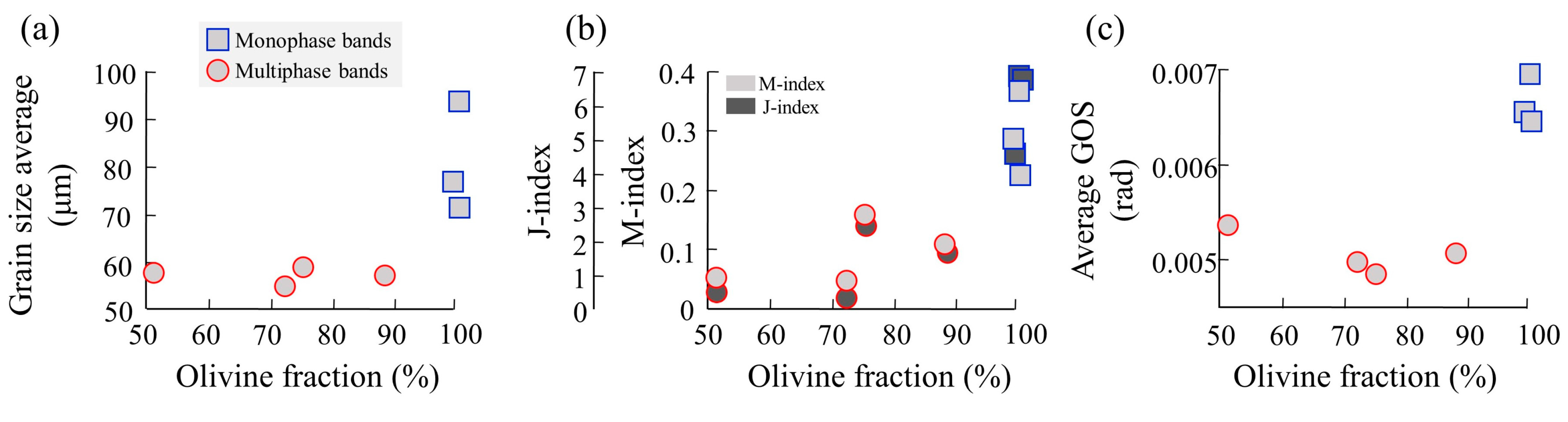
3.2.1. Intragrain Misorientations, Recrystallization, and CPO Strength
3.2.2. Subgrain Boundary Analysis
4. Discussion
4.1. Crystallographic Fabric
4.2. Deformation Mechanisms and Deformation Rates
5. Conclusions and Summary
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ave Lallemant, H.; Mercier, J.C.; Carter, N.; Ross, J. Rheology of the upper mantle: Inferences from peridotite xenoliths. Tectonophysics 1980, 70, 85–113. [Google Scholar] [CrossRef]
- Baptiste, V.; Tommasi, A.; Demouchy, S. Deformation and hydration of the lithospheric mantle beneath the Kaapvaal craton, South Africa. Lithos 2012, 149, 31–50. [Google Scholar] [CrossRef]
- Mercier, J.C.C. Peridotite xenoliths and the dynamics of kimberlite intrusion. In The Mantle Sample: Inclusion in Kimberlites and Other Volcanics; Boyd, F., Meyer, H.O., Eds.; American Geophysical Union: Washington, DC, USA, 1979; Volume 16, pp. 197–212. [Google Scholar]
- Michibayashi, K.; Mainprice, D. The role of pre-existing mechanical anisotropy on shear zone development within oceanic mantle lithosphere: An example from the Oman ophiolite. J. Petrol. 2004, 45, 405–414. [Google Scholar] [CrossRef] [Green Version]
- Michibayashi, K.; Oohara, T. Olivine fabric evolution in a hydrated ductile shear zone at the Moho Transition Zone, Oman Ophiolite. Earth Planet. Sci. Lett. 2013, 377, 299–310. [Google Scholar] [CrossRef]
- Skemer, P.; Karato, S.I. Sheared lherzolite xenoliths revisited. J. Geophys. Res. 2008, 113, B07205. [Google Scholar] [CrossRef] [Green Version]
- Tommasi, A.; Vauchez, A.; Ionov, D.A. Deformation, static recrystallization, and reactive melt transport in shallow subcontinental mantle xenoliths (Tok Cenozoic volcanic field, SE Siberia). Earth Planet. Sci. Lett. 2008, 272, 65–77. [Google Scholar] [CrossRef]
- Tommasi, A.; Baptiste, V.; Vauchez, A.; Holtzman, B. Deformation, annealing, reactive melt percolation, and seismic anisotropy in the lithospheric mantle beneath the southeastern Ethiopian rift: Constraints from mantle xenoliths from Mega. Tectonophysics 2016, 682, 186–205. [Google Scholar] [CrossRef]
- Toy, V.G.; Newman, J.; Lamb, W.; Tikoff, B. The role of pyroxenites in formation of shear instabilities in the mantle: Evidence from an ultramafic ultramylonite, Twin Sisters massif, Washington. J. Petrol. 2010, 51, 55–80. [Google Scholar] [CrossRef] [Green Version]
- Warren, J.M.; Hirth, G.; Kelemen, P.B. Evolution of olivine lattice preferred orientation during simple shear in the mantle. Earth Planet. Sci. Lett. 2008, 272, 501–512. [Google Scholar] [CrossRef] [Green Version]
- Webber, C.; Newman, J.; Holyoke, C.W., III; Little, T.; Tikoff, B. Fabric development in cm-scale shear zones in ultramafic rocks, Red Hills, New Zealand. Tectonophysics 2010, 489, 55–75. [Google Scholar] [CrossRef]
- Boneh, Y.; Skemer, P. The effect of deformation history on the evolution of olivine CPO. Earth Planet. Sci. Lett. 2014, 406, 213–222. [Google Scholar] [CrossRef]
- Couvy, H.; Frost, D.J.; Heidelbach, F.; Nyilas, K.; Ungár, T.; Mackwell, S.J.; Cordier, P. Shear deformation experiments of forsterite at 11 GPa-1400 °C in the multianvil apparatus. Eur. J. Mineral. 2004, 16, 877–889. [Google Scholar] [CrossRef]
- Hansen, L.; Zimmerman, M.; Dillman, A.; Kohlstedt, D. Strain localization in olivine aggregates at high temperature: A laboratory comparison of constant-strain-rate and constant-stress boundary conditions. Earth Planet. Sci. Lett. 2012, 333, 134–145. [Google Scholar] [CrossRef]
- Jung, H.; Karato, S.-I. Water-induced fabric transitions in olivine. Science 2001, 293, 1460–1463. [Google Scholar] [CrossRef] [Green Version]
- Karato, S.-I.; Jung, H. Effects of pressure on high-temperature dislocation creep in olivine. Philos. Mag. 2003, 83, 401–414. [Google Scholar] [CrossRef]
- Ohuchi, T.; Kawazoe, T.; Nishihara, Y.; Nishiyama, N.; Irifune, T. High pressure and temperature fabric transitions in olivine and variations in upper mantle seismic anisotropy. Earth Planet. Sci. Lett. 2011, 304, 55–63. [Google Scholar] [CrossRef]
- Ohuchi, T.; Kawazoe, T.; Nishihara, Y.; Irifune, T. Change of olivine a-axis alignment induced by water: Origin of seismic anisotropy in subduction zones. Earth Planet. Sci. Lett. 2012, 317, 111–119. [Google Scholar] [CrossRef]
- Wallis, D.; Hansen, L.N.; Tasaka, M.; Kumamoto, K.M.; Parsons, A.J.; Lloyd, G.; Kohlstedt, D.; Wilkinson, A.J. The impact of water on slip system activity in olivine and the formation of bimodal crystallographic preferred orientations. Earth Planet. Sci. Lett. 2019, 508, 51–61. [Google Scholar] [CrossRef]
- Ave’lallemant, H.G.; Carter, N.L. Syntectonic recrystallization of olivine and modes of flow in the upper mantle. Geol. Soc. Am. Bull. 1970, 81, 2203–2220. [Google Scholar] [CrossRef]
- Hirth, G.; Kohlstedt, D. Rheology of the upper mantle and the mantle wedge: A view from the experimentalists. Inside Subduction Fact. 2003, 138, 83–105. [Google Scholar]
- Karato, S.-I.; Wu, P. Rheology of the upper mantle: A synthesis. Science 1993, 260, 771–778. [Google Scholar] [CrossRef]
- Long, M.D.; Becker, T.W. Mantle dynamics and seismic anisotropy. Earth Planet. Sci. Lett. 2010, 297, 341–354. [Google Scholar] [CrossRef]
- Hansen, L.N.; Zhao, Y.-H.; Zimmerman, M.E.; Kohlstedt, D.L. Protracted fabric evolution in olivine: Implications for the relationship among strain, crystallographic fabric, and seismic anisotropy. Earth Planet. Sci. Lett. 2014, 387, 157–168. [Google Scholar] [CrossRef]
- Mainprice, D. 2.20—Seismic Anisotropy of the Deep Earth from a Mineral and Rock Physics Perspective. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 487–538. [Google Scholar] [CrossRef]
- Zhang, S.; Karato, S.-I. Lattice preferred orientation of olivine aggregates deformed in simple shear. Nature 1995, 375, 774–777. [Google Scholar] [CrossRef]
- Karato, S.-I.; Jung, H.; Katayama, I.; Skemer, P. Geodynamic significance of seismic anisotropy of the upper mantle: New insights from laboratory studies. Annu. Rev. Earth Planet. Sci. 2008, 36, 59–95. [Google Scholar] [CrossRef] [Green Version]
- Bernard, R.E.; Behr, W.M.; Becker, T.W.; Young, D.J. Relationships between olivine CPO and deformation parameters in naturally deformed rocks and implications for mantle seismic anisotropy. Geochem. Geophys. Geosyst. 2019, 20, 3469–3494. [Google Scholar] [CrossRef] [Green Version]
- Kumamoto, K.M.; Warren, J.M.; Hansen, L.N. Evolution of the Josephine Peridotite Shear Zones: 2. Influences on Olivine Cpo Evolution. J. Geophys. Res. Solid Earth 2019, 124, 12763–12781. [Google Scholar] [CrossRef]
- Herwegh, M.; Linckens, J.; Ebert, A.; Berger, A.; Brodhag, S. The role of second phases for controlling microstructural evolution in polymineralic rocks: A review. J. Struct. Geol. 2011, 33, 1728–1750. [Google Scholar] [CrossRef]
- Sundberg, M.; Cooper, R.F. A composite viscoelastic model for incorporating grain boundary sliding and transient diffusion creep; correlating creep and attenuation responses for materials with a fine grain size. Philos. Mag. 2010, 90, 2817–2840. [Google Scholar] [CrossRef]
- Tasaka, M.; Zimmerman, M.E.; Kohlstedt, D.L. Rheological weakening of olivine+ orthopyroxene aggregates due to phase mixing: 1. Mechanical behavior. J. Geophys. Res. Solid Earth 2017, 122, 7584–7596. [Google Scholar] [CrossRef]
- Tasaka, M.; Zimmerman, M.E.; Kohlstedt, D.L.; Stünitz, H.; Heilbronner, R. Rheological weakening of olivine+ orthopyroxene aggregates due to phase mixing: Part 2. Microstructural development. J. Geophys. Res. Solid Earth 2017, 122, 7597–7612. [Google Scholar] [CrossRef] [Green Version]
- Zhao, N.; Hirth, G.; Cooper, R.F.; Kruckenberg, S.C.; Cukjati, J. Low viscosity of mantle rocks linked to phase boundary sliding. Earth Planet. Sci. Lett. 2019, 517, 83–94. [Google Scholar] [CrossRef]
- Storey, C.; Prior, D. Plastic deformation and recrystallization of garnet: A mechanism to facilitate diffusion creep. J. Petrol. 2005, 46, 2593–2613. [Google Scholar] [CrossRef] [Green Version]
- Burnley, P. The importance of stress percolation patterns in rocks and other polycrystalline materials. Nat. Commun. 2013, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Cross, A.; Skemer, P. Ultramylonite generation via phase mixing in high-strain experiments. J. Geophys. Res. Solid Earth 2017, 122, 1744–1759. [Google Scholar] [CrossRef]
- Hansen, L.N.; Warren, J.M. Quantifying the effect of pyroxene on deformation of peridotite in a natural shear zone. J. Geophys. Res. Solid Earth 2015, 120, 2717–2738. [Google Scholar] [CrossRef] [Green Version]
- Paterson, M. Relating experimental and geological rheology. Int. J. Earth Sci. 2001, 90, 157–167. [Google Scholar] [CrossRef]
- Katayama, I.; Michibayashi, K.; Terao, R.; Ando, J.I.; Komiya, T. Water content of the mantle xenoliths from Kimberley and implications for explaining textural variations in cratonic roots. Geol. J. 2011, 46, 173–182. [Google Scholar] [CrossRef]
- Goetze, C. Sheared Iherzolites: From the point of view of rock mechanics. Geology 1975, 3, 172–173. [Google Scholar] [CrossRef]
- Chin, E.J.; Chilson-Parks, B.; Boneh, Y.; Hirth, G.; Saal, A.; Hearn, B.C.; Hauri, E. The peridotite deformation cycle in cratons and the deep impact of subduction. Tectonophysics 2021, 229029. [Google Scholar] [CrossRef]
- Carlson, R.; Irving, A.; Hearn, B., Jr. Chemical and isotopic systematics of peridotite xenoliths from the Williams kimberlite, Montana: Clues to processes of lithosphere formation, modification and destruction. In Proceedings of the VIIth International Kimberlite Conference; University of Cape Town: Rondebosch, South Africa, 1999; pp. 90–98. [Google Scholar]
- Carlson, R.W.; Irving, A.J.; Schulze, D.J.; Hearn Jr, B.C. Timing of Precambrian melt depletion and Phanerozoic refertilization events in the lithospheric mantle of the Wyoming Craton and adjacent Central Plains Orogen. Lithos 2004, 77, 453–472. [Google Scholar] [CrossRef]
- Hearn, J.B.C. The Homestead kimberlite, central Montana, USA: Mineralogy, xenocrysts, and upper-mantle xenoliths. Lithos 2004, 77, 473–491. [Google Scholar]
- Boneh, Y.; Chin, E.J.; Chilson-Parks, B.H.; Saal, A.E.; Hauri, E.H.; Carter Hearn, B., Jr.; Hirth, G. Microstructural shift due to post-deformation annealing in the upper mantle. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009377. [Google Scholar] [CrossRef]
- Warren, J.M.; Hauri, E.H. Pyroxenes as tracers of mantle water variations. J. Geophys. Res. Solid Earth 2014, 119, 1851–1881. [Google Scholar] [CrossRef]
- Demouchy, S.; Jacobsen, S.D.; Gaillard, F.; Stern, C.R. Rapid magma ascent recorded by water diffusion profiles in mantle olivine. Geology 2006, 34, 429–432. [Google Scholar] [CrossRef]
- Mainprice, D.; Bachmann, F.; Hielscher, R.; Schaeben, H. Descriptive tools for the analysis of texture projects with large datasets using MTEX: Strength, symmetry and components. Geol. Soc. Lond. Spec. Publ. 2014, 409, 251–271. [Google Scholar] [CrossRef]
- Hielscher, R.; Schaeben, H. A novel pole figure inversion method: Specification of the MTEX algorithm. J. Appl. Crystallogr. 2008, 41, 1024–1037. [Google Scholar] [CrossRef]
- Bunge, H.-J. Texture Analysis in Materials Science: Mathematical Methods; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Skemer, P.; Katayama, I.; Jiang, Z.; Karato, S.-I. The misorientation index: Development of a new method for calculating the strength of lattice-preferred orientation. Tectonophysics 2005, 411, 157–167. [Google Scholar] [CrossRef]
- Chin, E.J.; Soustelle, V.; Liu, Y. An SPO-induced CPO in composite mantle xenoliths correlated with increasing melt-rock interaction. Geochim. Cosmochim. Acta 2020, 278, 199–218. [Google Scholar] [CrossRef]
- Urai, J.; Means, W.; Lister, G. Dynamic recrystallization of minerals. In Mineral and Rock Deformation: Laboratory Studies; American Geophysical Union: Washington, DC, USA, 1986; Volume 36, pp. 161–199. [Google Scholar]
- Platt, J.P. Rheology of two-phase systems: A microphysical and observational approach. J. Struct. Geol. 2015, 77, 213–227. [Google Scholar] [CrossRef] [Green Version]
- Mehl, L.; Hacker, B.R.; Hirth, G.; Kelemen, P.B. Arc-parallel flow within the mantle wedge: Evidence from the accreted Talkeetna arc, south central Alaska. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Skemer, P.; Warren, J.M.; Kelemen, P.B.; Hirth, G. Microstructural and Rheological Evolution of a Mantle Shear Zone. J. Petrol. 2010, 51, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Prior, D.J.; Wheeler, J.; Peruzzo, L.; Spiess, R.; Storey, C. Some garnet microstructures: An illustration of the potential of orientation maps and misorientation analysis in microstructural studies. J. Struct. Geol. 2002, 24, 999–1011. [Google Scholar] [CrossRef]
- Kaczmarek, M.-A.; Reddy, S.M. Mantle deformation during rifting: Constraints from quantitative microstructural analysis of olivine from the East African Rift (Marsabit, Kenya). Tectonophysics 2013, 608, 1122–1137. [Google Scholar] [CrossRef]
- Katayama, I.; Jung, H.; Karato, S.-I. New type of olivine fabric from deformation experiments at modest water content and low stress. Geology 2004, 32, 1045–1048. [Google Scholar] [CrossRef] [Green Version]
- Christensen, N.I.; Lundquist, S.M. Pyroxene orientation within the upper mantle. Geol. Soc. Am. Bull. 1982, 93, 279–288. [Google Scholar] [CrossRef]
- Drury, M.; Roermund, H.V. Fluid assisted recrystallization in upper mantle peridotite xenoliths from kimberlites. J. Petrol. 1989, 30, 133–152. [Google Scholar] [CrossRef]
- Chin, E.J.; Soustelle, V.; Hirth, G.; Saal, A.E.; Kruckenberg, S.C.; Eiler, J.M. Microstructural and geochemical constraints on the evolution of deep arc lithosphere. Geochem. Geophys. Geosyst. 2016, 17, 2497–2521. [Google Scholar] [CrossRef] [Green Version]
- Précigout, J.; Hirth, G. B-type olivine fabric induced by grain boundary sliding. Earth Planet. Sci. Lett. 2014, 395, 231–240. [Google Scholar] [CrossRef] [Green Version]
- Tommasi, A.; Tikoff, B.; Vauchez, A. Upper mantle tectonics: Three-dimensional deformation, olivine crystallographic fabric and seismic properties. Earth Planet. Sci. Lett. 1999, 168, 173–186. [Google Scholar] [CrossRef]
- Hidas, K.; Garrido, C.J.; Booth-Rea, G.; Marchesi, C.; Bodinier, J.-L.; Dautria, J.-M.; Louni-Hacini, A.; Azzouni-Sekkal, A. Lithosphere tearing along STEP faults and synkinematic formation of lherzolite and wehrlite in the shallow subcontinental mantle. Solid Earth 2019, 10, 1099–1121. [Google Scholar] [CrossRef] [Green Version]
- Boneh, Y.; Morales, L.F.; Kaminski, E.; Skemer, P. Modeling olivine CPO evolution with complex deformation histories: Implications for the interpretation of seismic anisotropy in the mantle. Geochem. Geophys. Geosyst. 2015, 16, 3436–3455. [Google Scholar] [CrossRef] [Green Version]
- Hansen, L.N.; Conrad, C.P.; Boneh, Y.; Skemer, P.; Warren, J.M.; Kohlstedt, D.L. Viscous anisotropy of textured olivine aggregates: 2. Micromechanical model. J. Geophys. Res. Solid Earth 2016, 121, 7137–7160. [Google Scholar] [CrossRef]
- Skemer, P.; Warren, J.M.; Hirth, G. The influence of deformation history on the interpretation of seismic anisotropy. Geochem. Geophys. Geosyst. 2012, 13, Q03006. [Google Scholar] [CrossRef] [Green Version]
- Bell, D.R.; Rossman, G.R.; Maldener, J.; Endisch, D.; Rauch, F. Hydroxide in olivine: A quantitative determination of the absolute amount and calibration of the IR spectrum. J. Geophys. Res. Solid Earth 2003, 108, 2105. [Google Scholar] [CrossRef] [Green Version]
- Paterson, M. The determination of hydroxyl by infrared-absorption in quartz, silicate-glasses and similar materials. Bull. Minéral. 1982, 105, 20–29. [Google Scholar] [CrossRef]
- Jung, H. Crystal preferred orientations of olivine, orthopyroxene, serpentine, chlorite, and amphibole, and implications for seismic anisotropy in subduction zones: A review. Geosci. J. 2017, 21, 985–1011. [Google Scholar] [CrossRef]
- Soustelle, V.; Manthilake, G. Deformation of olivine-orthopyroxene aggregates at high pressure and temperature: Implications for the seismic properties of the asthenosphere. Tectonophysics 2017, 694, 385–399. [Google Scholar] [CrossRef]
- Van der Wal, D.; Chopra, P.; Drury, M.; Gerald, J.F. Relationships between dynamically recrystallized grain size and deformation conditions in experimentally deformed olivine rocks. Geophys. Res. Lett. 1993, 20, 1479–1482. [Google Scholar] [CrossRef]
- Linckens, J.; Herwegh, M.; Müntener, O.; Mercolli, I. Evolution of a polymineralic mantle shear zone and the role of second phases in the localization of deformation. J. Geophys. Res. 2011, 116, B06210. [Google Scholar] [CrossRef]
- Linckens, J.; Bruijn, R.H.; Skemer, P. Dynamic recrystallization and phase mixing in experimentally deformed peridotite. Earth Planet. Sci. Lett. 2014, 388, 134–142. [Google Scholar] [CrossRef]
- De Bresser, J.; Peach, C.; Reijs, J.; Spiers, C. On dynamic recrystallization during solid state flow: Effects of stress and temperature. Geophys. Res. Lett. 1998, 25, 3457–3460. [Google Scholar] [CrossRef]
- Zhang, G.; Mei, S.; Song, M. Effect of water on the dislocation creep of enstatite aggregates at 300 MPa. Geophys. Res. Lett. 2020, 47, e2019GL085895. [Google Scholar] [CrossRef]
- Zhang, G.; Mei, S.; Song, M.; Kohlstedt, D.L. Diffusion creep of enstatite at high pressures under hydrous conditions. J. Geophys. Res. Solid Earth 2017, 122, 7718–7728. [Google Scholar] [CrossRef]
- Hirth, G. Laboratory constraints on the rheology of the upper mantle. Rev. Mineral. Geochem. 2002, 51, 97–120. [Google Scholar] [CrossRef]
- Cross, A.; Skemer, P. Rates of dynamic recrystallization in geologic materials. J. Geophys. Res. Solid Earth 2019, 124, 1324–1342. [Google Scholar] [CrossRef] [Green Version]



| Microstructural Observations (This Study) | Experimental Work | References | ||
|---|---|---|---|---|
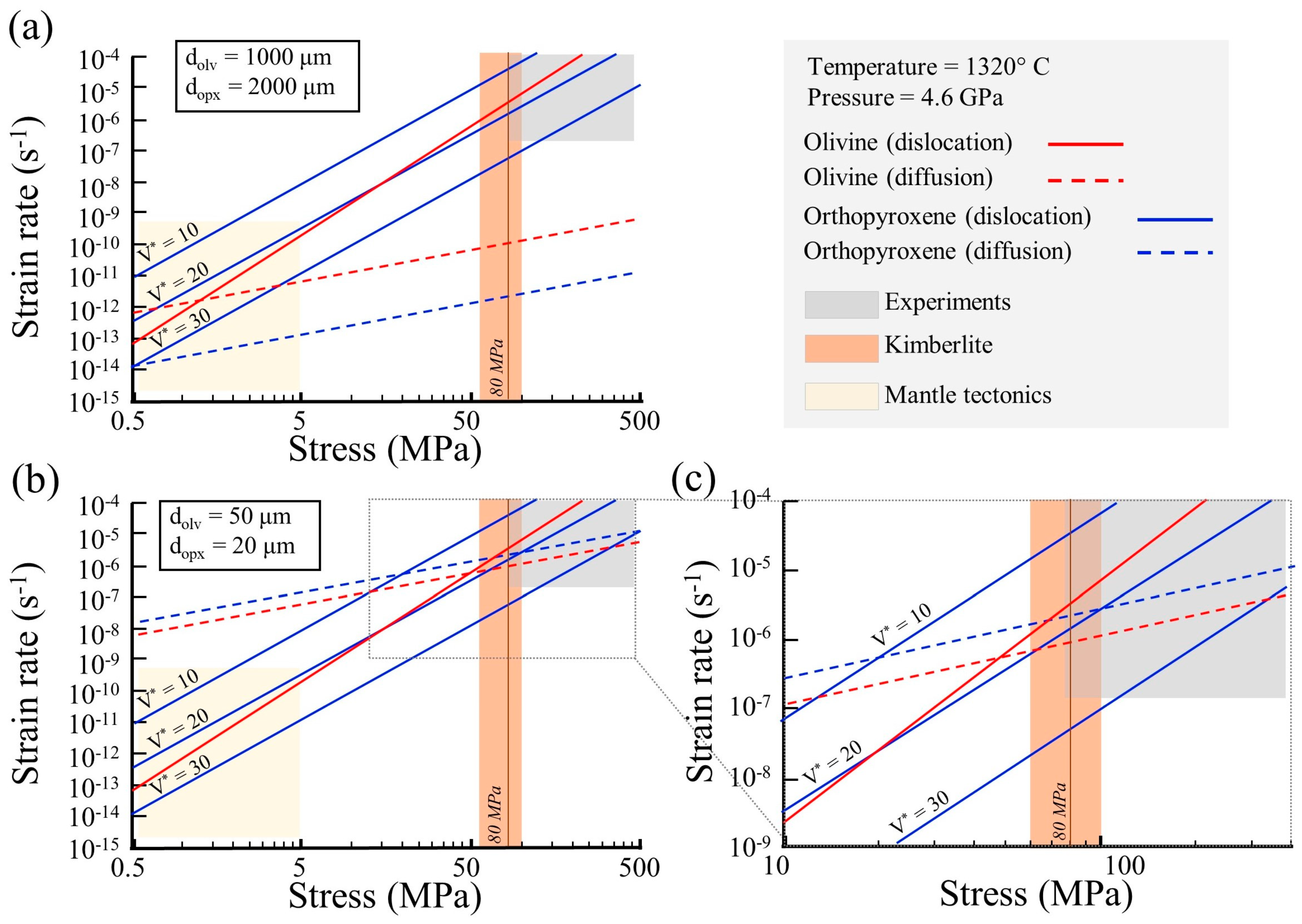
| Olivine–orthopyroxene piezometers | ☑ | Grain size of olivine (50 μm) is larger than orthopyroxene (opx) (20 μm). | Existing olivine and opx piezometers give similar stresses and agree with observations that dopx < dolv for a given stress conditions (Figure 10a) | van der Wal et al., 1993; Linckens et al., 2014 |
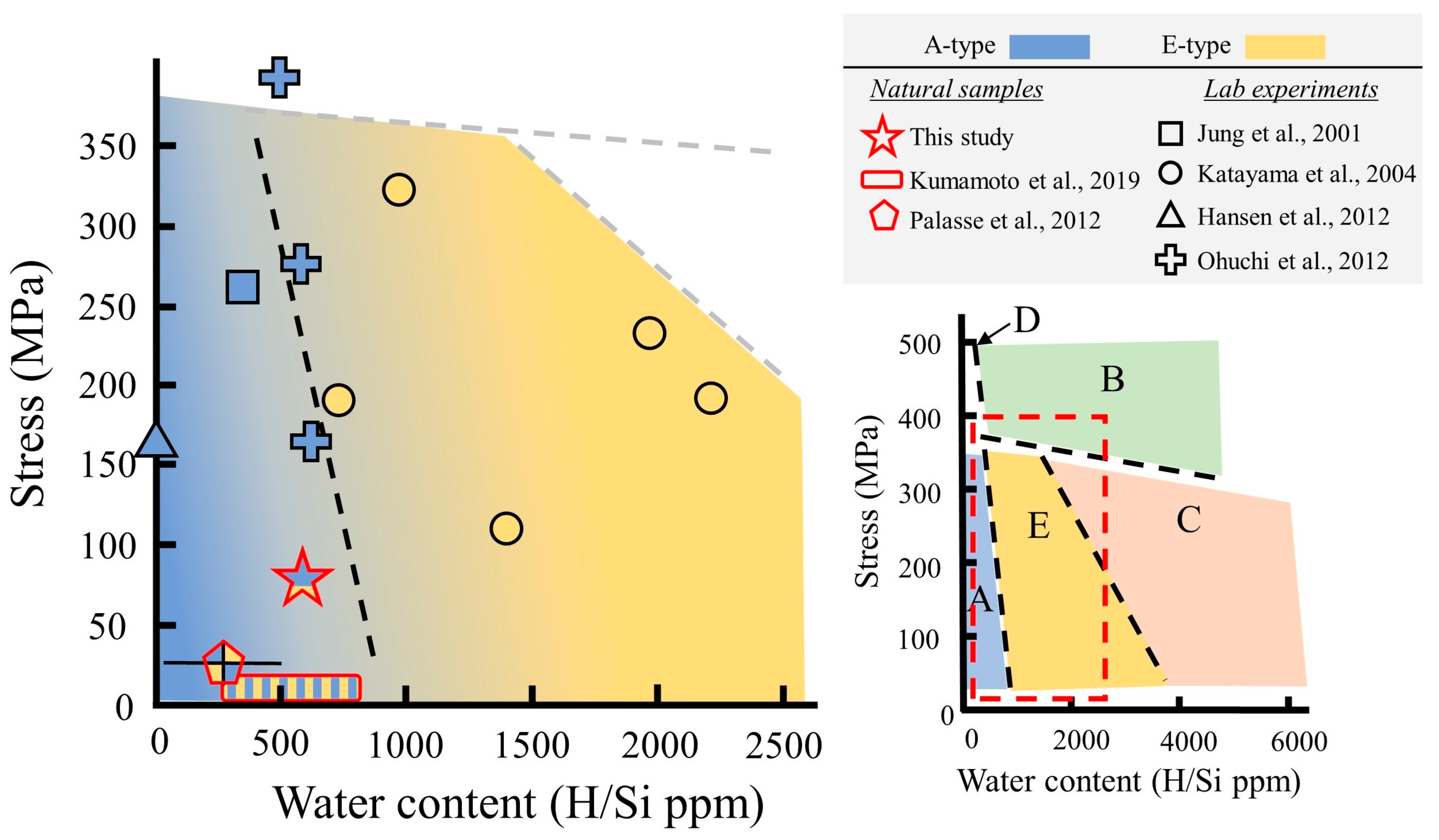
| Olivine CPO fabric | ☑ | A-type with secondary E-type | The experimentally-based stress-H2O space predicts A-type fabric near the A-E transition (Figure 9). | Karato et al., 2008; Katayama et al., 2004 |
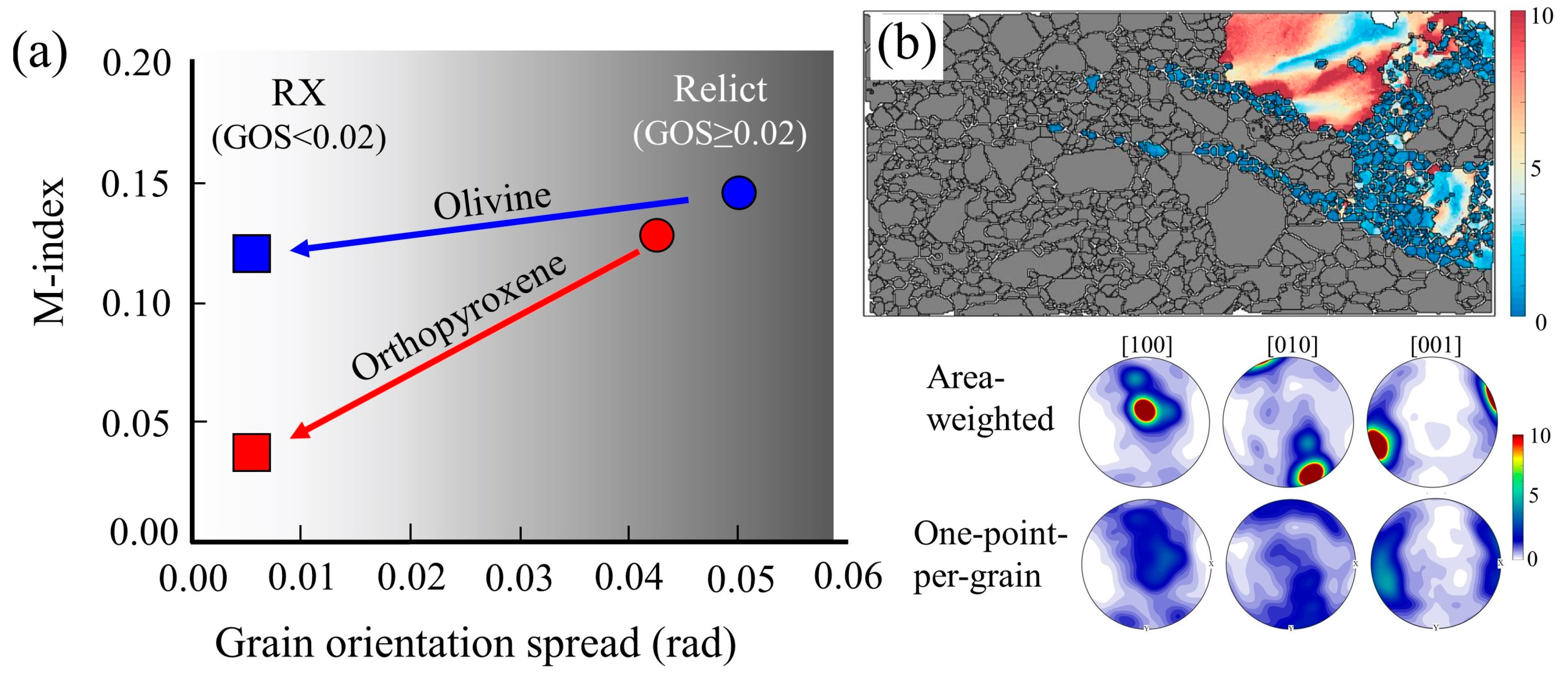
| Olivine mechanism of deformation | ☑ | CPO and grains with high intragrain misorientation suggest dislocation creep. In recrystallized grains, low intragrain misorientation suggests transition to grain size sensitive mechanism. | Flow laws predict dislocation creep in the porphyroclasts and transition to a contribution of both dislocation and diffusion after recrystallization (Figure 10b). | Hirth and Kohlstedt, 2003; De Bresser et al., 1998 |
| Orthopyroxene mechanism of deformation | ☑ ⊠ | Large porphyroclastic grains with high intragrain misorientations suggest dislocation creep. Recrystallized grains with low intragrain misorientation and dispersed CPO suggest diffusion creep. | Existing wet opx flow laws for dislocation creep lack the pressure effect on deformation. Our observations (left column) can be predicted using activation energy of V* > 20 (m3 106/mol) (Figure 11). | Zhang et al., 2020; Zhang et al., 2017 |
| Viscosity ratio Olv/OPx | ☑ ⊠ | High/low recrystallization fraction for olivine and opx, respectively, and olivine-rich bands with stronger CPO suggest that more strain was accommodated by the monophase bands. Tail-shaped structure of recrystallized opx suggest that high strain was accommodated also along opx recrystallized grains. | See cell above. Using high activation volume can result in consistency of flow laws with the observed microstructure-weaker olivine porphyroclasts grains while weaker olivine + opx recrystallized grains (Figure 11c) | Hirth and Kohlstedt, 2003; Zhang et al., 2020; Zhang et al., 2017 |
| Garnet deformation and relative viscosity | ☑ | Garnets have rounded grain morphology with no evidence for recrystallization or intragrain misorientations suggesting that it was not internally deformed. | No existing flow laws for wet garnet (pyrope composition) under high pressures. However, Mg-rich pyrope was showed to be stronger than olivine. | Karato et al., 1995; Katayama and Karato, 2008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boneh, Y.; Chin, E.J.; Hirth, G. Microstructural Analysis of a Mylonitic Mantle Xenolith Sheared at Laboratory-like Strain Rates from the Edge of the Wyoming Craton. Minerals 2021, 11, 995. https://doi.org/10.3390/min11090995
Boneh Y, Chin EJ, Hirth G. Microstructural Analysis of a Mylonitic Mantle Xenolith Sheared at Laboratory-like Strain Rates from the Edge of the Wyoming Craton. Minerals. 2021; 11(9):995. https://doi.org/10.3390/min11090995
Chicago/Turabian StyleBoneh, Yuval, Emily J. Chin, and Greg Hirth. 2021. "Microstructural Analysis of a Mylonitic Mantle Xenolith Sheared at Laboratory-like Strain Rates from the Edge of the Wyoming Craton" Minerals 11, no. 9: 995. https://doi.org/10.3390/min11090995
APA StyleBoneh, Y., Chin, E. J., & Hirth, G. (2021). Microstructural Analysis of a Mylonitic Mantle Xenolith Sheared at Laboratory-like Strain Rates from the Edge of the Wyoming Craton. Minerals, 11(9), 995. https://doi.org/10.3390/min11090995






